Штирлиц — Сеть печатных салонов в Перми

Весь комплекс печатных услуг в Перми. Общирная сеть печатных салонов в Перми. Цифровая печать, цветное и черно-белое копирование документов, сканирование документов, ризография в Перми

Проранжируйте что это значит: проранжировать | Перевод проранжировать?

Содержание

4.1. Правила ранжирования

А. Ранжирование качественных признаков

Пример 1.

Испытуемому предлагается задание, в котором семь личностных качеств необходимо упорядочить (проранжировать) в двух столбцах: в левом столбце в соответствии с особенностями его «Я реального», а в правом столбце в соответствии с особенностями его «Я идеального». Результаты ранжирования даны в таблице 2.

Таблица 2.

Я реальное

Качества личности

Я идеальное

7

ответственность

1

1

общительность

5

3

настойчивость

7

2

энергичность

6

5

жизнерадостность

4

4

терпеливость

3

6

решительность

2

Б. Ранжирование количественных признаков

Пример 2.

В результате диагностики невроза у пяти испытуемых по методике К.Хека и Х. Хесса были получены следующие баллы: 24, 25, 37, 13, 12. Этому ряду чисел можно проставить ранги двумя способами:

  1. большему числу в ряду ставится больший ранг, в этом случае получится: 3, 4, 5, 2, 1;

  2. большему числу в ряду ставится меньший ранг: в этом случае получится: 3, 2, 1, 4, 5.

А. Формула для подсчета суммы рангов по столбцу (строчке)

Если ранжируется N чисел, то сумма рангов расчитывается по формуле (1.1):

1+2+3+…+N=N(N+1)/2 (1.1)

В случае примера 1 число ранжируемых признаков было равно N =7, поэтому сумма рангов, подсчитанная по формуле (1.1), должна равняться 7(7+1)/2=28.

Сложим величины рангов отдельно для левого и правого столбца таблицы:

7 + 1 + 3+ 2 + 5 + 4 + 6 = 28 — для левого столбца и

1 + 5+ 7+ 6 + 4 + 3 + 2 = 28 — для правого столбца.

Суммы рангов совпали.

Б. Формула для расчета суммы рангов в таблице

Ранжирование по столбцам.

Пример 3. Результаты тестирования двух групп испытуемых по 5 человек в каждой по методике дифференциальной диагностики депрессивных состояний В. А. Жмурова представлены в таблице 3.

Таблица 3.

Номер испытуемого

Группа 1

Группа 2

1

15

26

2

45

67

3

44

23

4

14

78

5

21

3

Задача: проранжировать обе группы испытуемых как одну, т.  е. объединить выборки и проставить ранги объединенной выборке, сохраняя, однако различие между группами. Сделаем это в таблице 4, причем так, что максимальной величине будем ставить минимальный ранг.

Таблица 4.

Номер испытеумого

Группа 1

Ранги

Группа 2

Ранги

1

15

8

26

5

2

45

3

67

2

3

44

4

23

6

4

14

9

78

1

5

21

7

3

10

Сумма

31

24

Поскольку у нас получены суммы ранга по столбцам, то общую сумму рангов можно получить, сложив эти суммы: 31+24= 55.

Чтобы применить формулу (1.1), нужно подсчитать общее количество испытуемых — это 5+5=10.

Тогда по формуле (1.1) получаем: 10(10+1)/2=55.

Ранжирование прведено правильно.

Если в таблице имеется большое число строк и столбцов, то можно использовать модификацию формулы (1.1)

Сумма рангов в таблице

= (kc+1)kc/2 , (1.2)

где k — число строк, с — число столбцов.

Вычислим сумму рангов по формуле (1.2.) для нашего примера. В таблице 2 имеется 5 строк и 2 столбца, сумма рангов = ((5·2+1)·5·2)/2=55

Ранжирование по строкам

Пример 4.

В предыдущем примере добавили еще одну группу испытуемых 5 человек

.

Таблица 5. Проведем ранжирование по строчкам.

Номер испытуемого

Группа 1

Ранги

Группа 2

Ранги

Группа 3

Рагни

1

15

1

26

2

37

3

2

45

2

67

3

24

1

3

44

3

23

1

55

3

4

14

1

78

3

36

2

5

21

2

3

1

33

1

Суммы по столбцам

8

10

12

В этой таблице минимальному по величине числу ставится минимальный ранг. Сумма рангов по каждой строчке должна быть равна 6, поскольку у нас ранжируется три величины: 1+2+3= 6. В нашем случае так оно и есть. Теперь просуммируем ранги по каждому столбцу отдельно и сложим их.

Расчетная формула общей суммы рангов для ранжирования по строчкам для таблицы определяется по формуле:

Сумма рангов = nc(c+1)/2, (1.3.)

где n – количество испытуемых в столбце, с — количество столбцов (групп).

Проверим правильность ранжирования для нашего примера.

Реальная сумма рангов в таблице 8+10+12= 30

По формуле (1.3): 5·3·(3+1)/2=30.

Следовательно, ранжирование проведено правильно.

Случай одинаковых рангов

Ранжирование качественных признаков

А. Ранжирование качественных признаков

Модифицируем пример 1. и перепишем его в табл. 6. Предположим, что при оценке особенностей «Я реального» испытуемый считает, что такие качества, как «настойчи­вость» и «энергичность», должны иметь один и тот же ранг. При проведении ранжирования (столбец 1 табл. 6) этим качествам необходимо проставить мысленные ранги (М.Р.), как числа, обязательно идущие по порядку друг за другом, и от­метить эти ранги круглыми скобками — ( ). Однако посколь­ку эти качества, по мнению испытуемого, должны иметь одинаковые ранги, то во втором столбце табл. 6, относяще­муся к «Я реальному», следует поместить среднее арифмети­ческое рангов, проставленных в скобках, т.е. (2 + 3)/2 = 2,5. Таким образом, второй столбец табл. 6 и будет окончатель­ным итогом ранжирования особенностей «Я реального», данным испытуемым, а проставленные в этом столбце ран­ги будут носить название — реальные ранги (P.P.).

Аналогично при ранжировании «Я идеального» испыту­емый считает, что такие качества, как «общительность», «энергичность» и «жизнерадостность», должны иметь один и тот же ранг. Тогда при проведении ранжирования (см. столбец 5 табл. 6) этим качествам необходимо проставить мысленные ранги, как числа, обязательно идущие по поряд­ку друг за другом, и отметить эти ранги круглыми скобка­ми — ( ). Однако поскольку эти качества, по мнению испы­туемого, должны иметь одинаковые ранги — то в четвертом столбце табл. 6, относящемся к «Я идеальному», следует поместить среднее арифметическое рангов, проставленных в скобках, т.е. (4 + 5 + 6)/3 = 5. Таким образом, четвертый столбец таблицы 6 и будет окончательным итогом ранжи­рования особенностей «Я идеального», данным испытуе­мым, а проставленные в этом столбце ранги будут носить название — реальные ранги. Подчеркнем еще раз, что мыс­ленные (условные) ранги, как числа, должны располагаться друг за другом по порядку, несмотря на то что ранжируемые качества в таблице данных не находятся рядом друг с дру­гом.

Таблица 6.

Я реальное

Качества личности

Я идеальное

М. Р.

P.P.

P.P.

М.Р.

7

7

Ответственность

1

1

1

1

Общительность

5

(4)

(2)

2,5

Настойчивость

7

7

(3)

2,5

Энергичность

5

(5)

5

5

Жизнерадостность

5

(6)

4

4

Терпеливость

3

3

6

6

Решительность

2

2

Обозначения: М. Р. — мысленные, или условные, ранги; P.P. — ре­альные ранги.

Проверим правильность ранжирования во втором столб­це табл. 6, т.е. реальные ранги, относящиеся к «Я реаль­ному»:

1 + 2,5 + 2,5 + 5 + 4 + 6 = 28.

По формуле (1.1) сумма рангов также равняется 28. Сле­довательно, ранжирование проведено правильно.

Проверим правильность ранжирования в четвертом столбце табл. 6, т.е. реальные ранги, относящиеся к «Я идеальному»:

1 + 2 + 3 + 5 + 5 + 5 + 7 = 28.

По формуле (1.1) сумма рангов также равняется 28. Сле­довательно, ранжирование проведено правильно.

Б. Ранжирование количественных характеристик (чисел)

Ранжирование чисел рассмотрим на примере.

Пример. Психолог получил у 11 испытуемых следующие значения показателя невербального интеллекта: 113,102,123,122, 117, 117, 102, 108, 114, 102, 104. Необходимо проранжировать эти показатели, и лучше всего это сделать в таблице 7.

Таблица 7

Номер испытуемых

Показатели интеллекта

Мысленные ранги (М.Р.)

Реальные ранги (P.P.)

1

113

6

6

2

102

(1)

2

3

123

11

11

4

122

10

10

5

117

[8]

8,5

6

117

[9]

8,5

7

102

(2)

2

8

108

5

5

9

114

7

7

10

102

(3)

2

11

104

4

4

В примере встретились две группы из равных чисел (102, 102 и 102; 117 и 117), поскольку числа в группах раз­личны, то и скобки, проставленные этим группам чисел, также различны.

Проверим правильность ранжирования по формуле (1.1). Под­ставив исходные значения в формулу, получим: 11·12/2 = 66. Суммируя реальные ранги, получим:

6 + 2 + 11 + 10 + 8,5 + 8,5 + 2 + 5 + 7 + 2 + 4 = 66.

Поскольку суммы совпали, следовательно, ранжирование про­ведено правильно.

Правила ранжирования чисел таковы.

1. Наименьшему (наибольшему) числовому значению приписывается ранг 1.

2. Наибольшему (наименьшему) числовому значению приписывается ранг, равный количеству ранжируемых ве­личин.

3. Одинаковым по величине числам должны проставлять­ся одинаковые ранги.

4. Если в ранжируемом ряду несколько чисел оказались равными, то им приписывается реальный ранг, равный средней арифметической величине тех рангов, которые эти числа получили бы, если бы стояли по порядку друг за дру­гом.

5. Если в ранжируемом ряду имеется две и больше групп равных между собой чисел, то для каждой такой группы применяется правило 4, и мысленные ранги каждой группы заключаются в разные скобки.

6. Общая сумма реальных рангов должна совпадать с расчетной, определяемой по формуле (1.1).

7. Не рекомендуется ранжировать более чем 20 величин (признаков, качеств, свойств и т.п.), поскольку в этом слу­чае ранжирование в целом оказывается малоустойчивым.

При необходимости ранжирования достаточно большого числа объектов следует объединять их по какому-либо при­знаку в достаточно однородные классы (группы), а затем уже ранжировать полученные классы (группы).

Наиболее часто к измерениям, полученным в ранговой шкале, применяются коэффициенты корреляции Спирмена и Кэндалла, и, кроме того, используются разнообразные критерии различий.

Вопрос с ранжированием | SurveyMonkey Help

СТАТЬЯ

В вопросе с ранжированием респондентов просят сравнить элементы между собой, разместив их в порядке предпочтения. В разделе «Анализ результатов» для каждого варианта ответа вычисляется среднее ранжирование, позволяя быстро оценить наиболее предпочитаемый вариант.

Видеообзор

Создание вопроса с ранжированием

Как добавить вопрос такого типа

  1. В разделе «Составление» перетащите в свой опрос элемент Ранжирование.
  2. В поле текста вопроса введите инструкции, указывающие респондентам проранжировать варианты ответа в порядке предпочтения (где 1 – самая высокая позиция). Рекомендуется также объяснить, что общего имеют между собой все доступные варианты ответа. Например: «Расположите вкусы мороженого в порядке предпочтения (где 1 – Ваш любимый вкус)».
  3. В полях вариантов ранжирования введите варианты ответов, по которым следует ранжировать респондентов. Вы можете добавить до 250 вариантов ответов.
  4. При необходимости задайте другие дополнительные параметры.
  5. Нажмите кнопку Сохранить.

Добавление варианта «Неприменимо»

На вкладке Изменить вы можете добавить столбец «Неприменимо» и настроить метку.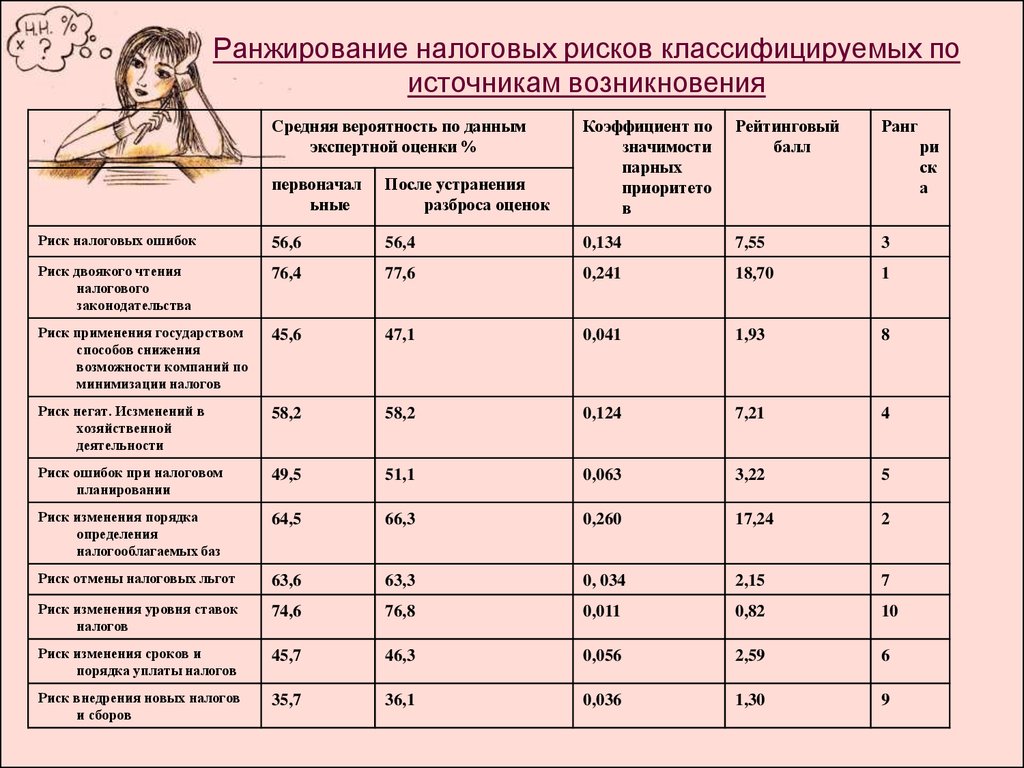 При добавлении параметра «Не указано» в вопрос с ранжированием, в конец каждой строки добавляется флажок «Не указано». Если респондент выбирает флажок «Не указано», эта строка становится серой и не будет включаться в порядок ранжирования для данного респондента.

Важно убедиться, что к респонденту применяются даже варианты с самым низким рангом. Если у респондента нет возможности заявить, что элемент ранжирования к нему не относится, ему придется все равно выполнить ранжирование, что может привести к искажению данных.

Характеристика прохождения опроса

Перед отправкой опроса необходимо выполнить предварительный просмотр его схемы, чтобы проверить, как будет выглядеть опрос для респондентов.

Респонденты могут отвечать на вопросы с ранжированием двумя способами:

  • Перетаскивать варианты ответа в соответствии со степенью предпочтения.
  • В раскрывающихся меню выбирать числовое значение ранга для каждого варианта ответа.

Анализ результатов

Ознакомьтесь с примерами результатов (только на английском языке) »

Среднее ранжирование

В вопросах с ранжированием для каждого варианта ответа рассчитывается среднее ранжирование, позволяя определить, какой из вариантов ответа был наиболее предпочитаемым для респондентов.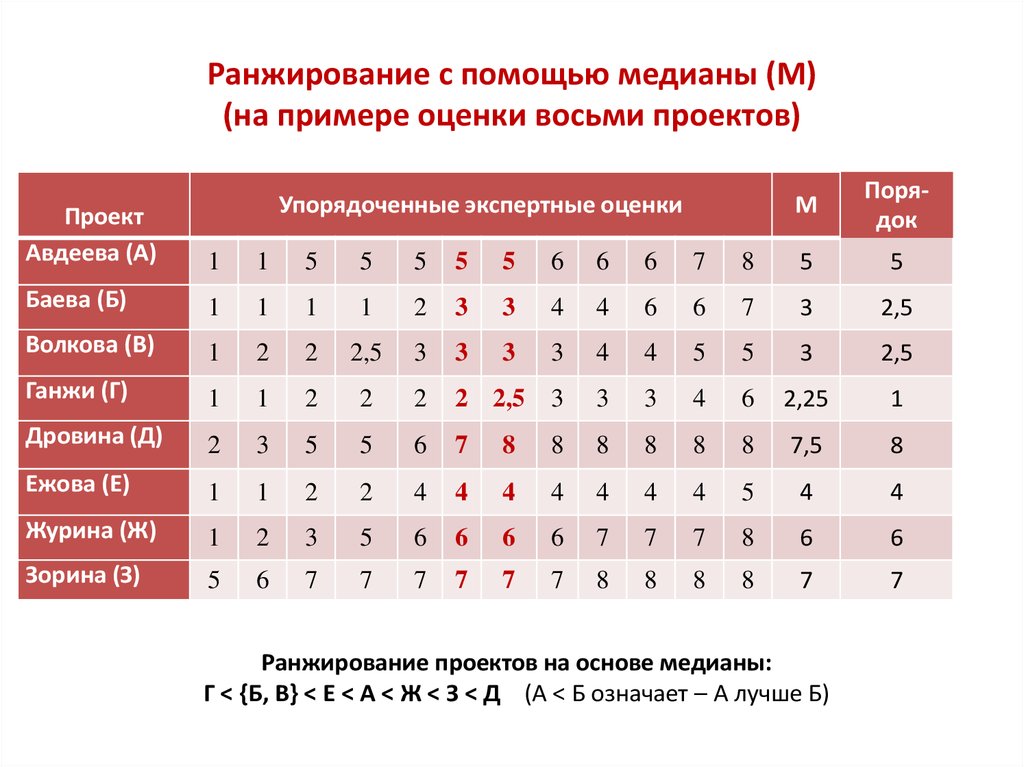 Вариант ответа с самым высоким средним ранжированием является самым предпочитаемым ответом среди респондентов.

Среднее ранжирование рассчитывается по следующей формуле, где:

w = весовой коэффициент ранга
x = кол-во ответов для варианта ответа

1w1 + x2w2 + x3w3 … xnwn
————————
Общее количество ответов

Весовой коэффициент прямо пропорционален среднему значению ранжирования. Другими словами, самый предпочитаемый среди респондентов вариант ответа (ранг которого равен единице) имеет наибольший весовой коэффициент, а наименее предпочитаемый вариант ответа (с рангом, равным номеру последней позиции) имеет весовой коэффициент, равный единице. Весовой коэффициент по умолчанию изменить нельзя.

Например, если вопрос с ранжированием имеет 5 вариантов ответов, значения весового коэффициента для этих ответов распределяются следующим образом:

  • Вариант ответа с рангом, равным 1, имеет весовой коэффициент, равный 5
  • Вариант ответа с рангом, равным 2, имеет весовой коэффициент, равный 4
  • Вариант ответа с рангом, равным 3, имеет весовой коэффициент, равный 3
  • Вариант ответа с рангом, равным 4, имеет весовой коэффициент, равный 2
  • Вариант ответа с рангом, равным 5, имеет весовой коэффициент, равный 1

Мы присваиваем вариантам ответов значения весового коэффициента именно таким образом, чтобы во время представления собранных данных в виде таблицы было ясно, какой из вариантов ответов является наиболее предпочитаемым.

Если в вопрос с ранжированием включен вариант ответа «Неприменимо», такие ответы не будут учитываться при определении среднего ранжирования.

Диаграммы

Для параметра отображения «Глубина» можно выбрать один из перечисленных ниже вариантов.

  • Взвешенное среднее значение: на диаграмме отображается среднее значение ранжирования для каждого варианта ответа.
  • Распространение: на диаграмме отображается абсолютное или процентное количество респондентов, которые выбрали каждый вариант ответа

Доступные типы диаграммы зависят от типа вопроса и настроенных вами параметров отображения. Подробнее: Пользовательские диаграммы и таблицы данных

ПОНИМАТЬ ЧТО-ТО/ЧТО-ТО ИЗ определение | Кембриджский словарь английского языка

Примеры вычислить что-то/кого-то

вычислить что-то/кого-то

Трудно вычислить из того, что принесет будущее.

От Рейтер