Образцы и бланки журналов регистраций 2022 года
Журнал регистрации нужен для отражения факта формирования/поступления в компанию какого-либо документа. Он подразделяется на множество видов. Некоторые виды книг нужно вести на протяжении всего года, другие заводятся на короткий срок. Журналы позволяют упорядочить документооборот, систематизировать его по хронологическому принципу.
Функции журнала регистрации
Журнал регистрации наделен следующими функциями:
- Фиксация даты регистрации, от которой будет отсчитываться срок выполнения документа.
- Упорядочивание справочных данных о документации.
- Быстрый и простой поиск нужной бумаги.
- Упорядочивание всей документации.
Регистрация представляет собой присвоение документу определенного регистрационного номера. Последний включает в себя 12 символов. Эти 12 символов могут быть дополнены указанием наименования документа, ФИО подписавшего, корреспондента, исполнителя. Регистрировать требуется все документы, которые были созданы в компании или поступили извне.
Регистрация – это внесение записи о документе в журнале, присвоение номера и проставление его на бумаге. Наличие номера обозначает, что бумага входит в документооборот компании. Регистрационный номер может составляться несколькими фирмами. В этом случае каждая компания ставит свой регистрационный номер. Можно указывать обозначения через черту.
ВНИМАНИЕ! Где проставлять номер? Все зависит от конкретного документа, его формы.
Какие журналы должны быть в компании?
В любой организации должен быть обязательный перечень журналов:
- По учету входящей корреспонденции.
- По учету исходящей корреспонденции.
- По учету приказов, касающихся главной деятельности компании.
- По учету соглашений.
Рассмотренный перечень книг используется в работе практически любой организации. При этом не имеет значение размер компании, размер ее штата, форма собственности. При этом нужно учитывать, что чем больше фирма, тем большее количество видов журналов она использует. Формы этих книг не утверждены, а потому организация может определять их самостоятельно. При этом следует пользоваться образцом.
Формы этих книг не утверждены, а потому организация может определять их самостоятельно. При этом следует пользоваться образцом.
Требуется ли регистрировать каждый документ?
Компания имеет полное право регистрировать каждый документ. Однако делать это в обязательном порядке не требуется. Более того, регистрация каждой бумаги даже не желательна. Связано это с тем, что регистрация занимает много времени. Она заставляет сотрудников компании бросать свои дела ради рутинной работы.
Как определить, какой документ нуждается в регистрации? Регистрировать следует те бумаги, которые потенциально нужно будет отслеживать.
Электронная или бумажная форма?
Журналы регистрации могут вестись и в бумажной, и в электронной форме. Большая часть фирм уже использует электронную форму. Она более проста, более удобна в использовании. Для ведения таких книг нужны специальные программы. Они могут быть как простейшими, так и сложными.
Однако остались еще предприятия, которые ведут бумажный документооборот.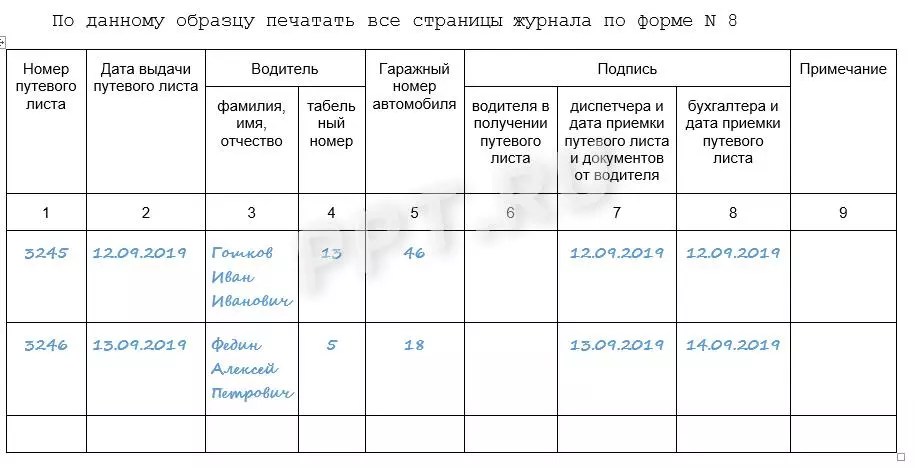 Он актуален для тех книг, в которых нужно ставить росписи сотрудников. К примеру, к таким книгам относится Журнал регистрации печатей и штампов. Для ведения бумажных книг могут использоваться тетради, специальные журналы.
Он актуален для тех книг, в которых нужно ставить росписи сотрудников. К примеру, к таким книгам относится Журнал регистрации печатей и штампов. Для ведения бумажных книг могут использоваться тетради, специальные журналы.
Как хранить журналы?
Все журналы нужно внести в номенклатуру. Электронные книги требуется включить в систему электронного документооборота. Срок хранения документов установлен Перечнем типовых бумаг, утвержденным приказом Минкультуры №558 от 25 августа 2010 года. Для обычных книг этот срок составляет 5 лет. Если это журнал регистрации приказов о приеме/увольнении, срок увеличивается до 75 лет.
Программы
Ведение электронных книг осуществляется посредством специальных программ:
- Microsoft Excel. В этой программе реализован самый минимум функций, который потребуется секретарю.
- Microsoft Access. Программа с расширенным функционалом. Поможет сформировать единую базу данных. Позволяет связывать регистрационные журналы между собой, фильтровать бумаги по определенным параметрам.
- Гугл.Драйв и Яндекс.Диск. Системы работают по принципу, аналогичному Excel. Отличие заключается в том, что с этими программами можно работать удаленно.
Это наиболее экономичные решения, которые подходят небольшим компаниям. Но большие предприятия пользуются более серьезными системами.
ОБРАЗЕЦ ведения журнала на рабочем месте
Версия сайта для слабовидящих
Вход для зарегистрированных
пользователей
Информация
общие сведенияАкадемия
новости и информацияНаука
и исследованияОбучение
учебный отделВоспитание
общественная
и спортивная жизньАккредитационно-
симуляционный центрПодготовка кадров
высшей квалификацииДополнительное
профессиональное образованиеАбитуриенту
поступление в ЧГМАСведения
об образовательной
организации
Читинская государственная медицинская академия
Наша миссия: сохранение здоровья общества через обеспечение отрасли высококвалифицированными кадрами, подготовленными на основе научных достижений, с использованием принципов гуманизма, нравственности и духовности.
Читинская государственная медицинская академия
Наша миссия: сохранение здоровья общества через обеспечение отрасли высококвалифицированными кадрами, подготовленными на основе научных достижений, с использованием принципов гуманизма, нравственности и духовности.
Дополнительное меню
События и новости
ОБРАЗЕЦ ведения журнала на рабочем месте
Зыкова Ольга Витальевна — специалист по охране труда
21.08.2013 06:15:10
Образец заполнения журнала инструктажа на рабочем месте
- Журнал инструктажа на рабочем месте должен быть пронумерован, прошнурован, подписан лицом, ответственным за его ведение и скреплен печатью.
- На первой странице Журнала указывается наименование структурного подразделения, дата начала и окончания ведения Журнала.
- Первичный инструктаж на рабочем месте, повторный, внеплановый и целевой инструктажи проводит непосредственный руководитель (производитель) работ, прошедший в установленном порядке обучение по охране труда и проверку знаний требований охраны труда.

4. Следует обратить внимание на следующее: Фамилия Имя Отчество сотрудников (обучающихся) указываются полностью.
- Для каждого сотрудника заполняется строка с № инструкции, видом инструктажа, фамилией инструктирующего. Заполнение по вертикали запрещено.
- Графа 6 заполняется только при проведении внепланового инструктажа. В остальных случаях графа 6 остаётся пустой.
Графы 10,11,12 заполняются при первичном инструктаже на рабочем месте и только в случае, когда требуется стажировка.
В остальных случаях графы 10,11,12 остаются пустыми.
*Важно! При заполнении журналов страницы и строки не пропускаются!
- Журнал регистрации инструктажа на рабочем месте (заполняется 1 раз в 6 месяцев); Для работ с повышенной опасностью 1 раз в квартал.
- Журнал инструктажа для студентов (заполняется при проведении циклов лабораторных работ, практических, при прохождении практики (учебной, производственной), для целевого инструктажа (при выполнении обучающимися разовых работ, не связанных с прямыми обязанностями (организация массовых мероприятий (субботники, экскурсии, походы, спортивные соревнования и др)).

ОБРАЗЕЦ ведения журнала на рабочем месте.docx
19.15 КБ
21.08.2013 00:00:00
Логарифм | Правила, примеры и формулы
- Ключевые люди:
- Джон Напье Генри Бриггс Йоост Бюрги
- Похожие темы:
- натуральный логарифм десятичный логарифм мантисса сила
Просмотреть весь связанный контент →
Резюме
Прочтите краткий обзор этой темы
логарифм , показатель или степень, в которую необходимо возвести основание, чтобы получить данное число. Выражаясь математически, x — это логарифм N до базы B , если B x = N , в этом случае один из них пишет x = log B . Например, 2 3 = 8; следовательно, 3 — это логарифм 8 по основанию 2, или 3 = log 2 8. Таким же образом, поскольку 10 2 = 100, то 2 = log 10 100. Логарифмы последнего вида (что логарифмы с основанием 10) называются обычными или бриггсовскими логарифмами и записываются просто log п .
Логарифмы последнего вида (что логарифмы с основанием 10) называются обычными или бриггсовскими логарифмами и записываются просто log п .
Логарифмы, изобретенные в 17 веке для ускорения вычислений, значительно сократили время, необходимое для умножения многозначных чисел. Они были основными в численной работе более 300 лет, пока совершенствование механических вычислительных машин в конце 19 века и компьютеров в 20 веке не сделало их устаревшими для крупномасштабных вычислений. Натуральный логарифм (с основанием e ≅ 2,71828 и записанный как ln n ), однако, продолжает оставаться одной из самых полезных функций в математике, с приложениями к математическим моделям во всех физических и биологических науках.
Свойства логарифмов
Логарифмы были быстро приняты учеными из-за различных полезных свойств, которые упрощали долгие и утомительные вычисления. В частности, ученые могли найти произведение двух чисел m и n , просматривая логарифм каждого числа в специальной таблице, складывая логарифмы вместе, а затем снова обращаясь к таблице, чтобы найти число с этим вычисленным логарифмом (известным как его антилогарифм). Выраженная в виде десятичных логарифмов, эта связь определяется как log m n = log m + log n . Например, 100 × 1000 можно вычислить, найдя логарифмы 100 (2) и 1000 (3), сложив логарифмы (5), а затем найдя антилогарифм (100 000) в таблице. Точно так же задачи деления преобразуются в задачи вычитания с логарифмами: log m / n = log m − log n . Это еще не все; вычисление степеней и корней можно упростить с помощью логарифмов. Логарифмы также можно преобразовывать между любыми положительными основаниями (за исключением того, что 1 нельзя использовать в качестве основания, поскольку все его степени равны 1), как показано в Щелкните здесь, чтобы увидеть полноразмерную таблицу логарифмических законов.
Выраженная в виде десятичных логарифмов, эта связь определяется как log m n = log m + log n . Например, 100 × 1000 можно вычислить, найдя логарифмы 100 (2) и 1000 (3), сложив логарифмы (5), а затем найдя антилогарифм (100 000) в таблице. Точно так же задачи деления преобразуются в задачи вычитания с логарифмами: log m / n = log m − log n . Это еще не все; вычисление степеней и корней можно упростить с помощью логарифмов. Логарифмы также можно преобразовывать между любыми положительными основаниями (за исключением того, что 1 нельзя использовать в качестве основания, поскольку все его степени равны 1), как показано в Щелкните здесь, чтобы увидеть полноразмерную таблицу логарифмических законов.
Обычно в таблицы логарифмов включались только логарифмы чисел от 0 до 10. Чтобы получить логарифм некоторого числа за пределами этого диапазона, число сначала было записано в научной записи как произведение его значащих цифр и его экспоненциальной степени — например, 358 будет записано как 3,58 × 10 2 , а 0,0046 будет можно записать как 4,6 × 10 −3 . Затем в таблице можно было найти логарифм значащих цифр — десятичную дробь от 0 до 1, известную как мантисса. Например, чтобы найти логарифм числа 358, нужно найти log 3,58 ≅ 0,55388. Следовательно, log 358 = log 3,58 + log 100 = 0,55388 + 2 = 2,55388. В примере числа с отрицательным показателем степени, например 0,0046, можно найти log 4,6 ≅ 0,66276. Следовательно, log 0,0046 = log 4,6 + log 0,001 = 0,66276 — 3 = -2,33724.
Затем в таблице можно было найти логарифм значащих цифр — десятичную дробь от 0 до 1, известную как мантисса. Например, чтобы найти логарифм числа 358, нужно найти log 3,58 ≅ 0,55388. Следовательно, log 358 = log 3,58 + log 100 = 0,55388 + 2 = 2,55388. В примере числа с отрицательным показателем степени, например 0,0046, можно найти log 4,6 ≅ 0,66276. Следовательно, log 0,0046 = log 4,6 + log 0,001 = 0,66276 — 3 = -2,33724.
История логарифмов
Изобретение логарифмов было предвосхищено сравнением арифметических и геометрических последовательностей. В геометрической последовательности каждый член образует постоянное отношение со своим последующим; Например,
…1/1000, 1/100, 1/10, 1, 10, 100, 1000…
имеет обыкновенное отношение 10. В арифметической последовательности каждый последующий член отличается на константу, известную как общая разность; Например,
…−3, −2, −1, 0, 1, 2, 3…
имеет общую разность, равную 1. Обратите внимание, что геометрическую последовательность можно записать в терминах ее общего отношения; для приведенного выше примера геометрической последовательности:
…10 −3 , 10 −2 , 10 −1 , 10 0 , 10 1 , 10 2 , 10 3 … . Умножение двух чисел в геометрической последовательности, скажем, 1/10 и 100, равносильно сложению соответствующих показателей степени обыкновенного отношения, -1 и 2, чтобы получить 10 1 = 10. Таким образом, умножение превращается в сложение. Однако первоначальное сравнение двух серий не было основано на каком-либо явном использовании экспоненциальной записи; это была более поздняя разработка. В 1620 г. швейцарский математик Йост Бюрги опубликовал в Праге первую таблицу, основанную на концепции соотношения геометрических и арифметических последовательностей.
Умножение двух чисел в геометрической последовательности, скажем, 1/10 и 100, равносильно сложению соответствующих показателей степени обыкновенного отношения, -1 и 2, чтобы получить 10 1 = 10. Таким образом, умножение превращается в сложение. Однако первоначальное сравнение двух серий не было основано на каком-либо явном использовании экспоненциальной записи; это была более поздняя разработка. В 1620 г. швейцарский математик Йост Бюрги опубликовал в Праге первую таблицу, основанную на концепции соотношения геометрических и арифметических последовательностей.
Шотландский математик Джон Нейпир опубликовал свое открытие логарифмов в 1614 году. Его цель состояла в том, чтобы помочь в умножении величин, которые тогда назывались синусами. Весь синус был величиной стороны прямоугольного треугольника с большой гипотенузой. (Первоначальная гипотенуза Непера была 10
Оформите подписку Britannica Premium и получите доступ к эксклюзивному контенту. Подпишитесь сейчас
Подпишитесь сейчас
Таким образом, логарифм любого синуса представляет собой число, очень точно выражающее линию, которая одинаково увеличивалась в течение определенного времени, в то время как линия всего синуса пропорционально уменьшалась в этом синусе, причем оба движения были равновременны и начало смещалось одинаково.
В сотрудничестве с английским математиком Генри Бриггсом Нейпир привел свой логарифм в его современную форму. Для логарифма Напера сравнение будет между точками, движущимися по градуированной прямой линии, L точка (для логарифма) движется равномерно от минус бесконечности до плюс бесконечности, X точка (для синуса) движется от нуля до бесконечности со скоростью, пропорциональной ее расстоянию от нуля. Кроме того, L равно нулю, когда X равно единице, и их скорости в этой точке равны. Суть открытия Непера состоит в том, что оно представляет собой обобщение отношения между арифметическим и геометрическим рядами; т. е. умножение и возведение в степень значений 9Точка 0023 X соответствует сложению и умножению значений точки L соответственно. На практике удобно ограничить движение L и X требованием, чтобы L = 1 при X = 10 в дополнение к условию, что X = 1 при L = 0. Это изменение привело к бриггсовскому или десятичному логарифму.
е. умножение и возведение в степень значений 9Точка 0023 X соответствует сложению и умножению значений точки L соответственно. На практике удобно ограничить движение L и X требованием, чтобы L = 1 при X = 10 в дополнение к условию, что X = 1 при L = 0. Это изменение привело к бриггсовскому или десятичному логарифму.
Нейпир умер в 1617 году, и Бриггс продолжил работу в одиночку, опубликовав в 1624 году таблицу логарифмов, рассчитанных до 14 знаков после запятой для чисел от 1 до 20 000 и от 9.от 0 000 до 100 000. В 1628 году голландский издатель Адриан Влак опубликовал 10-местную таблицу для значений от 1 до 100 000, добавив недостающие 70 000 значений. И Бриггс, и Влак занимались созданием логарифмических тригонометрических таблиц. Такие ранние таблицы были либо с точностью до одной сотой градуса, либо с точностью до одной угловой минуты. В 18 веке таблицы были опубликованы для 10-секундных интервалов, которые были удобны для таблиц с семью десятичными знаками. В общем случае требуются более тонкие интервалы для вычисления логарифмических функций меньших чисел, например, при вычислении функций log sin x и логарифмический тангенс x .
В общем случае требуются более тонкие интервалы для вычисления логарифмических функций меньших чисел, например, при вычислении функций log sin x и логарифмический тангенс x .
Наличие логарифмов сильно повлияло на форму плоской и сферической тригонометрии. Процедуры тригонометрии были переработаны для получения формул, в которых операции, зависящие от логарифмов, выполняются одновременно. Тогда обращение к таблицам состояло всего из двух шагов: получения логарифмов и, после выполнения вычислений с логарифмами, получения антилогарифмов.
Фрэнсис Дж. МюррейЛогарифм (Журналы) — Примеры | Натуральное бревно и обыкновенное бревно
Логарифмы — это еще один способ записи показателей степени. Мы знаем, что 2 5 = 32. Но если нас попросят найти, какое число заменяет знак вопроса в 2 ? = 32, то методом проб и ошибок мы можем просто найти, что ответ равен 5. Но что, если нас попросят найти вопросительный знак в 2 ? = 30? Существует ли такое число, что при возведении к нему 2 будет 30? Нет, тогда как решить? Решение — логарифмы (или журналы).
Давайте узнаем больше о логарифмах и их свойствах на примерах.
| 1. | Что такое логарифм? |
| 2. | Определение журналов |
| 3. | Натуральное бревно и обыкновенное бревно |
| 4. | Правила журналов |
| 5. | Как сжимать/расширять логарифмы? |
| 6. | Часто задаваемые вопросы о логарифмах |
Что такое логарифм?
Логарифм — это не что иное, как другой способ выражения показателей степени, и его можно использовать для решения задач, которые нельзя решить, используя только понятие показателей степени. Разобраться в логах не так уж и сложно. Чтобы понимать логарифмы, достаточно знать, что логарифмическое уравнение — это просто еще один способ записи показательного уравнения.
Логарифм и показатель степени являются обратными формами друг друга. Это можно понять из раздела ниже. Первоначально математик по имени Джон Нейпир ввел логарифмы для упрощения расчетов, и эта концепция быстро была принята другими учеными, инженерами и т. д.
Это можно понять из раздела ниже. Первоначально математик по имени Джон Нейпир ввел логарифмы для упрощения расчетов, и эта концепция быстро была принята другими учеными, инженерами и т. д.
Вот математическое определение бревен.
Определение журналов
Логарифм определяется с помощью показателя степени.
- б х = а ⇔ log б а = х
Здесь «log» означает логарифм. Правая часть стрелки читается как «Логарифм а по основанию b равен х».
Очень простой способ запомнить это: «база остается базой в обеих формах» и «база не остается с показателем степени в логарифмической форме». Обратите внимание, что «b» является основанием как в левой, так и в правой частях подразумеваемого символа, а в логарифмической форме видно, что основание b и показатель степени x не остаются на одной стороне уравнения.
Здесь
- a и b — два положительных действительных числа.

- х — действительное число.
- а, который внутри лога называется «аргумент».
- б, который внизу журнала называется «база».
В приведенном выше уравнении нужно понять две вещи (из символа ⇔):
- b x = a ⇒ log b a = x. Это называется «экспоненциальной формой в логарифмическую форму»
- log б а = х ⇒ б х = а . Это называется «переведение в экспоненциальную форму»
Вот таблица для понимания преобразований из одной формы в другую.
| Экспоненциальная форма | Логарифмическая форма |
|---|---|
| 2 5 = 32 | журнал 2 32 = 5 |
| 6 2 = 36 | журнал 6 36 = 2 |
| 3 -2 = 1/9 | журнал 3 (1/9) = -2 |
| e 2 = 7,389 | журнал e 7,389 = 2 |
| 10 3 = 1000 | журнал 10 1000 = 3 |
Натуральное бревно и обыкновенное бревно
Обратите внимание на две последние строки приведенной выше таблицы. У них лог e и журнал 10 . Эти два журнала имеют особое значение и определенные имена в логарифмах.
У них лог e и журнал 10 . Эти два журнала имеют особое значение и определенные имена в логарифмах.
- бревно e называется натуральным бревном
- журнал 10 называется общим журналом
Давайте узнаем больше о каждом из них.
Натуральный логарифм
Натуральный логарифм есть не что иное, как логарифм с основанием e. То есть натуральный журнал означает log e . Но обычно он не представляется как log e 9.0042 . Вместо этого он представлен как пер. т. е.
- log e = ln
Примеры:
- e x = 2 ⇒ log e 2 = x (или) ln 2 = x.
- e x = 7 ⇒ log e 7 = x (или) ln 7 = x.
Десятичный логарифм
Десятичный логарифм — это не что иное, как логарифм с основанием 10. То есть десятичный логарифм означает log 10 . Но обычно вместо записи log 9 достаточно написать «log».0039 10 . т. е.
Но обычно вместо записи log 9 достаточно написать «log».0039 10 . т. е.
- логарифм 10 = логарифм
т.е. если нет базы для лога значит его лог 10 . Другими словами, это десятичный логарифм.
Примеры:
- 10 2 = 100 ⇒ log 10 100 = 2 (или) log 100 = 2
- 10 -2 = 0,01 ⇒ log 10 0,01 = -2 (или) log 0,01 = -2
Обратите внимание, что в этих примерах мы не написали 10 в качестве основы, потому что это очевидно.
Правила журналов
Правила журналов используются для упрощения логарифма, расширения логарифма или сжатия группы логарифмов в один логарифм. Вот правила (или) свойства журналов. Если вы хотите увидеть, как выводятся все эти правила, нажмите здесь.
Давайте рассмотрим каждое из этих правил одно за другим.
Log 1
Значение log 1 независимо от основания равно 0. Поскольку из свойств показателей мы знаем, что 0 = 1 для любого «а». Преобразовав это в логарифмическую форму, запишите a 1 = 0 для любого «а». Очевидно, что при a = 10 log 10 1 = 0 (или) просто log 1 = 0.
Поскольку из свойств показателей мы знаем, что 0 = 1 для любого «а». Преобразовав это в логарифмическую форму, запишите a 1 = 0 для любого «а». Очевидно, что при a = 10 log 10 1 = 0 (или) просто log 1 = 0.
Если мы расширим это до натурального логарифма, то получим, поскольку e 0 = 1 ⇒ ln 1 = 0
Log
a aПоскольку a 1 = a, для любого «a», преобразуя это уравнение в логарифмическую форму, log a a = 1. Таким образом, логарифм любого числа к одному и тому же основание всегда равно 1. Например:
- журнал 2 2 = 1
- журнал 3 3 = 1
- журнал 10 = 1
- лн е = 1
Логарифм произведения
Логарифм произведения двух чисел равен сумме логарифмов отдельных чисел, т. е.
Обратите внимание, что основания всех журналов здесь должны быть одинаковыми. Это напоминает / получено из правила произведения показателей степени: x м ⋅ х n = х м+n .
Примеры:
- log 6 = log (3 x 2) = log 3 + log 2
- журнал (5x) = журнал 5 + журнал x
Правило частного логарифма
Логарифм частного двух чисел представляет собой разность между логарифмами отдельных чисел, т. е. а п
Обратите внимание, что основания всех журналов здесь также должны быть одинаковыми. Это напоминает / получено из частного правила показателей степени: x м / х н = х м-н .
Примеры:
- лог. 4 = лог. (8/2) = лог. 8 — лог. 2
- лог (х/2) = лог х — лог 2
Степенное правило логарифма
Показатель степени аргумента логарифма может быть поставлен перед логарифмом, т. е.
- log a m n = n log 22 m a
Здесь основания должны быть одинаковыми с обеих сторон. Это напоминает / происходит из правила степени степени показателей: (x м ) н = х мн .
Правило изменения основания
С помощью этого свойства можно изменить основание логарифма. Он говорит:
- log b a = (log꜀ a) / (log꜀ b)
Другой способ записи этого правила: log b a · log꜀ b = log꜀ a.
Используя это свойство, мы можем изменить основание на любое другое число. Следовательно, мы также можем изменить основание на 10. Тогда получаем: лог b a = (log a) / (log b). Таким образом:
- log 2 3 = (log 3) / (log 2)
- журнал 3 2 = (лог 2) / (лог 3)
Правило равенства логарифмов
Это правило используется при решении уравнений с логарифмами. т. е.
- log b a = log b c ⇒ a = c
Это своего рода журнал отмены с обеих сторон.
Число поднято до свойства журнала
Когда число возводится в логарифм, основание которого совпадает с числом, тогда результатом является просто аргумент логарифма. т. е.
т. е.
- a log a x = x
Вот несколько примеров этого свойства.
- 2 журнал 2 5 = 5
- 10 журнал 6 = 6
- е пер. 3 = 3
Свойство отрицательного журнала
Негативные журналы имеют форму -log б а. Мы можем вычислить это, используя правило степени логарифмов.
−log b a = log b a -1 = log b (1/a)
Thus,
- −log b a = log b (1/ а)
т. е., чтобы преобразовать отрицательный журнал в положительный, мы можем просто взять обратное значение аргумента. Кроме того, чтобы преобразовать отрицательный логарифм в положительный логарифм, мы можем взять обратное основание, то есть
- −log b a = log 1/b a
Как сжимать/расширять логарифмы?
Мы можем либо сжать группу журналов в один журнал, либо развернуть один журнал в группу журналов, используя приведенные выше правила журналов. Но важные правила, которые мы используем в этом процессе, следующие:
Но важные правила, которые мы используем в этом процессе, следующие:
- log a mn = log a m + log a n (правило произведения логарифмов)
- log a m/n = log a m — log a n (частное правило логарифмов)
- log a m n = n log a m (Степенное правило логарифмов)
Расширение логарифмов
Расширим логарифм (3x 2 y 3 ).
журнал (3x 2 и 3 )
= log (3) + log (x 2 ) + log (y 3 ) (по правилу произведения)
= log 3 + 2 log x + 3 log y (по степенному правилу)
Сокращение логарифмов
Давайте просто возьмем приведенную выше сумму логарифмов и сократим ее. Мы должны вернуть лог (3x 2 y 3 ).
лог. 3 + 2 лог. x + 3 лог. у
= log (3) + log (x 2 ) + log (y 3 ) (по степенному правилу)
= log (3x 2 y 3 ) (По правилу произведения)
Важные примечания по логарифмам:
- Логарифм 0 НЕ определяется, так как одно число, возведенное в другое число, никогда не дает 0 в результате.

- Показательное уравнение преобразуется в логарифмическое уравнение и наоборот, используя b x = a ⇔ log b a = x.
- Обыкновенный логарифм — это логарифм по основанию 10, т. е. логарифм 10 = логарифм.
- Натуральный логарифм — это логарифм по основанию e, т. е. log e = ln.
- Логарифмы используются для самых сложных вычислений умножения и деления.
☛ Похожие темы:
- Общий калькулятор журнала
- Калькулятор естественного бревна
Часто задаваемые вопросы о логарифмах
Что такое журналы в математике?
Журналы — это другой способ записи показателя степени. Формула преобразования экспоненциальной формы в логарифмическую: b x = a ⇔ log b a = x. Логарифмы очень полезны при решении уравнений с показателями степени.
Каковы значения логарифмов log 0, log 1, log 2, log 3, log 4, log 5, log 10, log 100 и log inf?
Вот значения данных журналов:
- log 0 не определен ни для какой базы, потому что число, возведенное в любое число, не дает 0.
- журнал 1 = 0 как 10 0 = 1
- log 2 ≈ 0,3010 (с помощью калькулятора)
- log 3 ≈ 0,4771 (с помощью калькулятора)
- log 4 ≈ 0,6021 (с помощью калькулятора)
- log 5 ≈ 0,6990 (с помощью калькулятора)
- log 10 = 1 как 10 1 = 10
- log 100 = 2 как 10 2 = 100
- журнал ∞ = ∞
Что такое ln в математике?
Ln в математике используется для представления натуральных логарифмов. т. е. ln = «логарифм с основанием e». Например, e 2 = x ⇔ ln x = 2.
Какие 3 типа логарифмов существуют?
Существуют три основных типа логарифмов:
- Десятичный логарифм, который записывается как логарифм без основания. Например: журнал 2
- Натуральный логарифм, который записывается как «ln» (означает log и ). Например: пер. 2
- Логарифм по любому другому основанию (без конкретного названия). Например: журнал 3 2.

Каковы значения логарифмов ln e, ln 1 и ln от 0?
Здесь значения заданных натуральных бревен.
- In e = 1 как e 1 = e
- In 1 = 0 как e 0 = 1
- In 0 НЕ определено
Что такое важные логарифмические свойства?
Важными логарифмическими свойствами являются:
- Правило произведения: log a mn = log a m + log a n
- Частное правило: log a m/n = log a m — log a n
- Степенное правило: log a m n = n log a m
Как рассчитать журналы?
Мы можем вычислять логи, используя свойства логарифмов. т. е., используя правила журналов, мы можем либо сжать набор логарифмов в один, либо разложить один логарифм на множество. Мы также используем логарифмическую таблицу и антилогарифмическую таблицу в расчетах.
Какая производная от ln x и log x?
Вот производные:
- Производная от ln x равна d/dx (ln x) = 1/x.

