Операции сравнения чисел
Операции сравнения чиселВ условных инструкциях, в инструкциях цикла, как правило используются сравнения вида x > 0 или a != b (числа a и b не равны), то есть некоторое логическое выражение. В таких выражениях как правило используются операции сравнения (равно, неравно, меньше, больше и т.д.).
В языке C подобные операции возвращают значение типа int, либо 0, что считается ложью, либо 1, которое означает истину. В языке C++ для этого есть специальный логический тип bool.
Переменные логического типа bool принимают два значения: true (истина) и false (ложь). Также любое целочисленное выражение можно трактовать, как логическое выражение, при этом нулевое целое число означает ложь, а ненулевое — истину. Таким образом, если вместо условия написать false или 0, то оно будет всегда ложно, если же указать true, 1 или любое ненулевое число, то условие будет истинно.
Как правило, в качестве проверяемого условия используется результат вычисления одного из следующих операторов сравнения:
| < | Меньше — возвращает true, если первый операнд меньше второго. |
| > | Больше — возвращает true, если первый операнд больше второго. |
| <= | Меньше или равно. |
| >= | Больше или равно. |
| == | Равенство. Возвращает true, если два операнда равны. |
| != | Неравенство. Возвращает true, если два операнда неравны. |
Например, условие (x * x < 1000) означает “значение x * x меньше 1000”, а условие (2 * x != y) означает “удвоенное значение переменной x не равно значению переменной y”.
Будьте аккуратны: оператор == (два знака равенства) — это проверка на равенство двух выражений, а оператор = (один знак равенства) — это присваивание одной переменной значения выражения и использование его в условии оператора ветвления в большинстве случаев является ошибкой.
Рассмотрим эту типичную ошибку на следующем примере:
int a, b;
cin >> a >> b;
if (a = b)
{
cout << "Числа равны" << endl;
}
else
{
cout << "Числа не равны" << endl;
}Здесь по ошибке вместо операции сравнения == использована операция присваивания =. Поэтому при любых значениях a и b переменной a будет присвоено значение переменной b, при проверке истинности выражения
Поэтому при любых значениях a и b переменной a будет присвоено значение переменной b, при проверке истинности выражения a = b. Но оператор присваивания еще и возвращает значение, поэтому если значение b было ненулевым (а это интерпретируется, как истина), то программа выведет строку «Числа равны», а если нулевым — то строку «Числа не равны». При этом значение переменной
c++ — C — почему &arr не равно arr и как мы получаем размер?
int arr[] = {1, 2, 3, 4, 5, 6};
int size = *(&arr + 1) - arr;
- Массив
arrимеет типint [6], т.е. массив из шести элементов типаint. - Выражение
&arrимеет типint (*)[6], т.е. указатель на (массив из шести элементов типаint). - В выражении
&arr + 1к указателю применяется арифметика указателей. Значение указателя наращивается наsizeof(int[6])байт, что равноsizeof(int) * 6байт. Получившийся указатель указывает на гипотетический массив из шести элементов типа
Получившийся указатель указывает на гипотетический массив из шести элементов типа int, следующий непосредственно за массивомarr. - В выражении
*(&arr + 1)происходит разыменование указателя. Т.е. мы получаем lvalue «ссылающееся» на гипотетический массив после массиваarrUB-1). Тип этого выражения —int[6]3). - В выражении
*(&arr + 1) - arrоба операнда бинарного оператора-имеют тип массива —int [6]. И к обоим операндам применяется неявное преобразование из типа массива к типу указателя на первый элемент массива.
Т.е гипотетический массив*(&arr + 1)после массиваarrтипаint [6]преобразуется к указателю типаint*на свой первый элемент.
Аналогично массивarrпреобразуется к указателю на свой первый элемент. - Разность двух указателей типа
int*даёт знаковое целочисленное значение типа std::ptrdiff_t, равное количеству объектов типаintмежду двумя указателями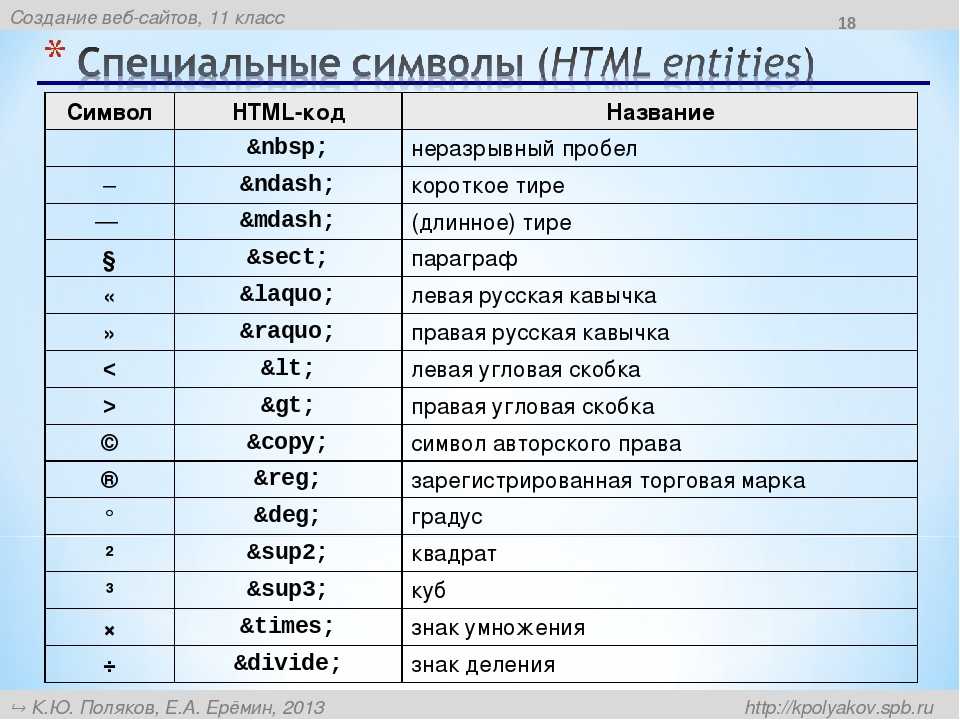
- Разыменование указателя на гипотетический элемент после массива вызывает неопределённое поведение, так как такой указатель не является указателем на объект.
basic.compound / 3:
… Every value of pointer type is one of the following:
- a pointer to an object or function (the pointer is said to point to the object or function), or
- a pointer past the end of an object ([expr.add]), or
- the null pointer value for that type, or
- an invalid pointer value.
expr.unary.op / 1:
The unary
*operator performs indirection: the expression to which it is applied shall be a pointer to an object type, or a pointer to a function type and the result is anlvaluereferring to the object or function to which the expression points.
Код
constexpr static int arr[] = {1, 2, 3, 4, 5, 6};
constexpr std::ptrdiff_t diff = *(&arr + 1) - arr;
может вызвать следующую ошибку компиляции:
//cannot access array element of pointer past the end of object
constexpr std::ptrdiff_t diff = *(&arr + 1) - arr;
^
Даже если бы было известно, что по адресу на который указывает указатель на гипотетический элемент после последнего расположен объект, то такой указатель по прежнему нельзя разыменовывать.
- Разность двух указателей, указывающих на элементы разных массивов, вызывает неопределённое поведение.
expr.add / 5:
When two pointer expressions
PandQare subtracted, the type of the result is an implementation-defined signed integral type; this type shall be the same type that is defined asstd::ptrdiff_tin the<cstddef>header.
- If
PandQboth evaluate to null pointer values, the result is0.- Otherwise, if
PandQpoint to, respectively, array elementsiandjof the same array objectx, the expressionP - Qhas the valuei − j.- Otherwise, the behavior is undefined.
[Note 1: If the valuei − jis not in the range of representable values of typestd::ptrdiff_t, the behavior is undefined.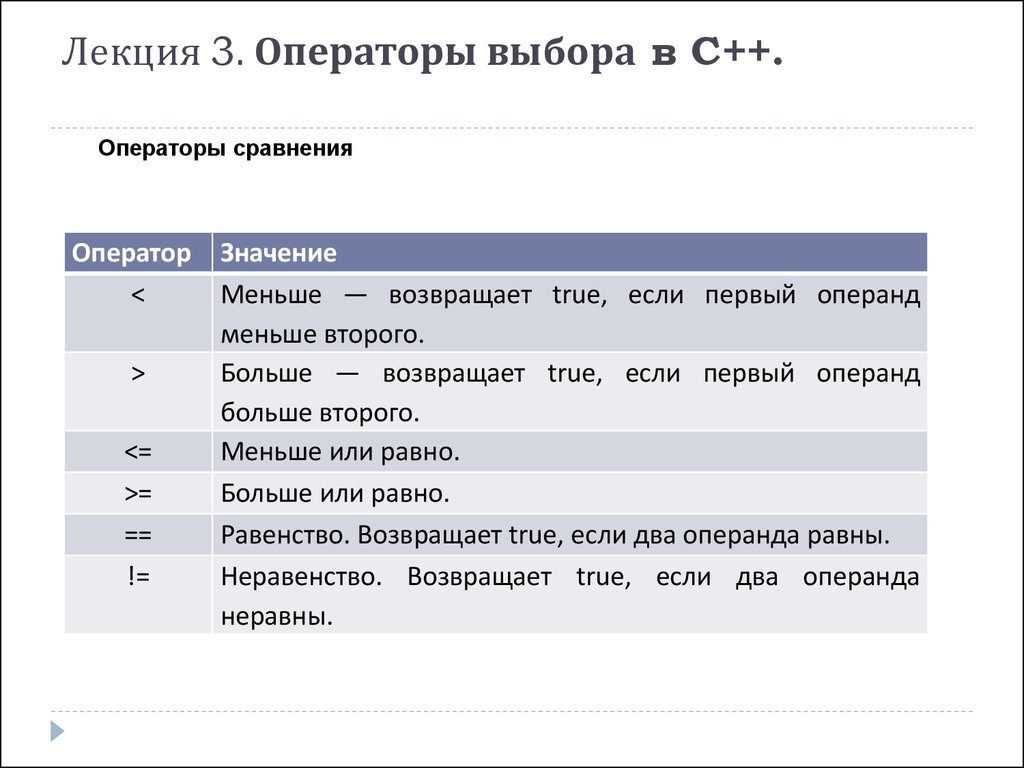
- Результат разыменования указателя на тип
T— это lvalue типаT(не ссылка).expr.unary.op / 1:
The unary
*operator performs indirection: the expression to which it is applied shall be a pointer to an object type, or a pointer to a function type and the result is an lvalue referring to the object or function to which the expression points. If the type of the expression is “pointer toT”, the type of the result is “T”.Выражение наподобие
std::is_same_v< int ( & ) [6], decltype(*(&arr + 1)) >возвращаетtrueв силу особенностей работы спецификатораdecltype, который дляlvalueтипаTв качестве типа выводитT&.dcl.type.decltype / 1:
For an expression
E, the type denoted bydecltype(E)is defined as follows:
...
otherwise, ifEis an lvalue,decltype(E)isT&, whereTis the type ofE;
…Итого: приведённый в вопросе код содержит неопределённое поведение. Результат его выполнения (если вообще скомпилируется) не предсказуем.
Нарушение неравенства Белла в Si
- Опубликовано:
Квантовая информация
- Сьюзен Копперсмит 1
Природа Нанотехнологии том 11 , страницы 216–217 (2016)Процитировать эту статью
1328 Доступ
1 Цитаты
4 Альтметрический
Сведения о показателях
предметов
- Квантовая информация
Было подготовлено и измерено запутанное состояние двух спиновых кубитов в кремнии, что привело к нарушению неравенства Белла, которое до сих пор было самым большим из достигнутых в твердом состоянии.
Помимо того, что кремний является основным материалом для большинства современных электронных устройств, за последние несколько лет было продемонстрировано, что кремний обладает превосходными свойствами для устройств квантовой обработки информации. Электронные спины в кремнии, который был обогащен изотопами, чтобы уменьшить долю ядер с ненулевыми спинами до менее чем 50 частей на миллион, имеют время когерентности больше секунды.0012 1 . За последние несколько лет были продемонстрированы одиночные кубиты, построенные из примесей в кремнии с точностью процесса, превышающей 99,9%, как для электронов, связанных с примесями фосфора, так и из ядер фосфора2,3, что означает, что желаемые квантовые преобразования реализуются операциями вентиля для в пределах 0,1%.
Это предварительный просмотр содержимого подписки, доступ через ваше учреждение
Варианты доступа
Подписка на журнал
Получите полный доступ к журналу на 1 год
118,99 €
всего 9,92 € за выпуск
Подписаться
Расчет налогов будет завершен во время оформления заказа.
Купить статью
Получите ограниченный по времени или полный доступ к статье на ReadCube.
32,00 $
Купить
Все цены указаны без учета стоимости.
Список литературы
Тырышкин А.М. и др. Материя Природы. 11 , 143–147 (2012).
Артикул КАС Google ученый
Muhonen, J. T. et al. Природа Нанотех. 9 , 986–991 (2014).
Артикул КАС Google ученый
Muhonen, J.T. et al. J. Phys. Конденс. Материя 27 , 154205 (2015).
Артикул КАС Google ученый
Dehollain, J. P. et al. Природа Нанотех. 11 , 242–246 (2016).
Артикул КАС Google ученый
Бруннер, Н.
и др. Ред. Мод. физ. 86 , 419–478 (2014).
Артикул Google ученый
Белл, Дж. Физика 1 , 195–200 (1964).
Артикул Google ученый
Клив, Р. и др. в Проц. 19-я годовщина IEEE. конф. Вычислительная сложность 236–249 (IEEE, 2004).
Google ученый
Freedman, S.J. & Clauser, J.F. Phys. Преподобный Летт. 28 , 938–941 (1972).
Артикул КАС Google ученый
Роу М.А. и др. Природа 409 , 791–794 (2001).
Артикул КАС Google ученый
Мацукевич Д. Н., Маунц П., Мёринг Д. Л., Олмшенк С. и Монро С. Phys.
Преподобный Летт. 100 , 150404 (2008 г.).
Артикул КАС Google ученый
Ансманн, М. и др. Природа 461 , 504–506 (2009).
Артикул КАС Google ученый
Хофман, Дж. и др. Наука 337 , 72–75 (2012).
Артикул Google ученый
Пфафф, В. и др. Природа физ. 9 , 29–33 (2013).
Артикул КАС Google ученый
Хенсен, Б. и др. Природа 526 , 682–686 (2015).
Артикул КАС Google ученый
Шалм Л.К. и др. Физ. Преподобный Летт. 115 , 250402 (2015).
Артикул Google ученый
Джустина, М.
и др. Физ. Преподобный Летт. 115 , 250401 (2015).
Артикул Google ученый
Ссылки на скачивание
Информация об авторе
Авторы и организации
Сьюзен Копперсмит работает на физическом факультете Университета Висконсина, Мэдисон, 1150 Юниверсити-авеню, Мэдисон, Висконсин 53706, США,
Susan Coppersmith
Авторы
- Susan Coppersmith
Посмотреть публикации автора
Вы также можете искать этого автора в PubMed Google Scholar
Автор, ответственный за переписку
Сьюзен Копперсмит.
Права и разрешения
Перепечатка и разрешения
Об этой статье
Эта статья цитируется
Защита нелокальности многочастных состояний за счет упреждающего управления
- Сяо-Ган Ли
- Цзянь Цзоу
- Бинь Шао
Квантовая обработка информации (2018)
Глоссарий | DataBank
Код SI. POV.GINI
Название индикатора Индекс GINI Короткий определение 3001 . домохозяйства в экономике отклоняются от совершенно равного распределения. Индекс Джини, равный 0, представляет собой абсолютное равенство, а индекс 100 подразумевает абсолютное неравенство. Полное определение Индекс Джини измеряет степень отклонения распределения доходов (или, в некоторых случаях, расходов на потребление) между отдельными лицами или домохозяйствами в рамках экономики от абсолютно равного распределения. Кривая Лоренца отображает кумулятивные проценты общего полученного дохода от совокупного числа получателей, начиная с самого бедного человека или домохозяйства. Индекс Джини измеряет площадь между кривой Лоренца и гипотетической линией абсолютного равенства, выраженную в процентах от максимальной площади под линией. Таким образом, индекс Джини, равный 0, представляет собой абсолютное равенство, а индекс 100 подразумевает абсолютное неравенство. Источник Всемирный банк, Платформа борьбы с бедностью и неравенством. Данные основаны на данных первичного обследования домохозяйств, полученных от государственных статистических органов и страновых отделений Всемирного банка. Данные по странам с высоким уровнем доходов в основном взяты из базы данных Люксембургского исследования доходов. Дополнительную информацию и методологию см. на http://pip.worldbank.org. Тема Экономический и социальный контекст Единица измерения % Периодичность Годовой Статистическая концепция и методология Индекс Джини измеряет площадь между кривой Лоренца и гипотетической линией абсолютного равенства, выраженную в процентах от максимальной площади под линией. Кривая Лоренца отображает кумулятивные проценты от общего полученного дохода по сравнению с кумулятивным числом получателей, начиная с самого бедного человека. Таким образом, индекс Джини, равный 0, представляет собой абсолютное равенство, а индекс 100 подразумевает абсолютное неравенство. Индекс Джини представляет собой удобную сводную меру степени неравенства. Данные о распределении доходов или потребления поступают из общенациональных репрезентативных обследований домохозяйств. Там, где были доступны первоначальные данные обследования домохозяйств, они использовались для расчета доли дохода или потребления по квинтилям. В противном случае доли оценивались на основе наилучших доступных сгруппированных данных. Данные о распределении были скорректированы с учетом размера домохозяйства, что обеспечивает более последовательную оценку дохода или потребления на душу населения. Год отражает год, в котором были собраны данные основного обследования домохозяйств, или, если период сбора данных перекрывает два календарных года, год начала сбора данных.
Актуальность для развития Цель Группы Всемирного банка по содействию всеобщему процветанию была определена как содействие росту доходов беднейших 40 процентов распределения благосостояния в каждой стране. Коэффициенты Джини — важная справочная информация для всеобщего процветания.
Ограничения и исключения Коэффициенты Джини не уникальны. Две разные кривые Лоренца могут давать один и тот же коэффициент Джини. Более того, коэффициент Джини в развивающейся стране может возрасти (из-за увеличения неравенства доходов), в то время как число людей, живущих в абсолютной бедности, уменьшится. Это связано с тем, что коэффициент Джини измеряет относительное, а не абсолютное богатство. Еще одно ограничение коэффициента Джини заключается в том, что он не является аддитивным по группам, т. Е. Общий коэффициент Джини общества не равен сумме коэффициентов Джини для его подгрупп. Таким образом, коэффициенты Джини на уровне страны не могут быть объединены в региональные или глобальные коэффициенты Джини, хотя коэффициент Джини может быть рассчитан для совокупности. Поскольку лежащие в основе обследования домохозяйств различаются по методам и типам собираемых показателей благосостояния, данные не являются строго сопоставимыми по странам или даже по годам внутри страны. В частности, для распределения доходов следует отметить два источника несопоставимости. Во-первых, обследования могут различаться по многим параметрам, в том числе по тому, используют ли они доходы или расходы на потребление в качестве показателя уровня жизни. Распределение доходов обычно более неравномерно, чем распределение потребления. Кроме того, в разных обследованиях чаще используются разные определения дохода. Потребление обычно является гораздо лучшим показателем благосостояния, особенно в развивающихся странах. Во-вторых, домохозяйства различаются по размеру (количеству членов) и степени распределения доходов между членами. И люди различаются по возрасту и потребительским потребностям. Различия между странами в этих отношениях могут исказить сравнение распределения. Сотрудники Всемирного банка приложили усилия для обеспечения максимально возможной сопоставимости данных. Везде, где это возможно, использовалось потребление, а не доход. Распределение доходов и индексы Джини для стран с высоким уровнем доходов рассчитываются непосредственно из базы данных Люксембургского исследования доходов с использованием метода оценки, совместимого с тем, который применяется для развивающихся стран.
Оставить комментарий




