Переменная x: ПЕРЕМЕННАЯ | это... Что такое ПЕРЕМЕННАЯ?

Содержание

Использование переменных в под процедурах Excel в Visual Basic для приложений

Введение

В этой статье описано, как использовать переменные Microsoft Excel под процедурах в Microsoft Visual Basic для приложений.

Дополнительные сведения

Переменные в под процедуре

Мощной функцией языков программирования является возможность хранить данные в переменной, чтобы содержимое переменной можно было использовать или менять позже. В этом документе обсуждается следующее использование переменных в Visual Basic:

Как объявляются переменные.
Процедуры и проекты, которые могут использовать переменную.
Время жизни переменной.

Объявление переменной в макросе

Самый простой способ объявить переменную в макросах — использовать отчет Dim. В следующей строке две переменные объявлялись как integers(integers).

Dim x As Integer, y As Integer

Если для переменных x и y заданы целые числа, вы указываете Visual Basic выделить достаточно памяти для переменной целого числа (по 2 на x и y) и что данные, хранимые в x или y, являются целым числом в период между -32768 и 32767.

ПРИМЕЧАНИЕ: Если вы объявляете несколько переменных с помощью одной выписки Dim, необходимо указать тип данных для каждой переменной.

Если не указать тип данных для каждой переменной, как в следующем коде Visual Basic, то переменная y будет настроена как переменная с типом данных типа integer.

Переменная x будет иметь тип типа variant:

Dim x, y As Integer

Дополнительные сведения см. в приведенной ниже таблице Variant.

Чтобы выполнить проверку переменной, выполните следующие действия:

Сохраните и закроите все открытые книги, а затем откройте новую книгу.
Запустите редактор Visual Basic (нажмите ALT+F11).
В меню Вставка выберите пункт Модуль.
Введите следующий код:
Sub Variable_Test()
Dim x As Integer, y As Integer
x = 10
y = 100
MsgBox «значение x — » & x & _
Chr(13) & «значение y — » & y
End Sub
Запустите Variable_Test макрос. Вы получаете следующее сообщение:the value of x is 10
the value of y is 100
Нажмите кнопку ОК.
В макро Variable_Test изменить следующую строку:
x = 10
org/ListItem»>
to:
x = «error»
Запустите Variable_Test макрос.

Вы получите ошибку во время запуска, так как «ошибка» не является integer, и вы пытаетесь назначить это строковую величину для переменной x.

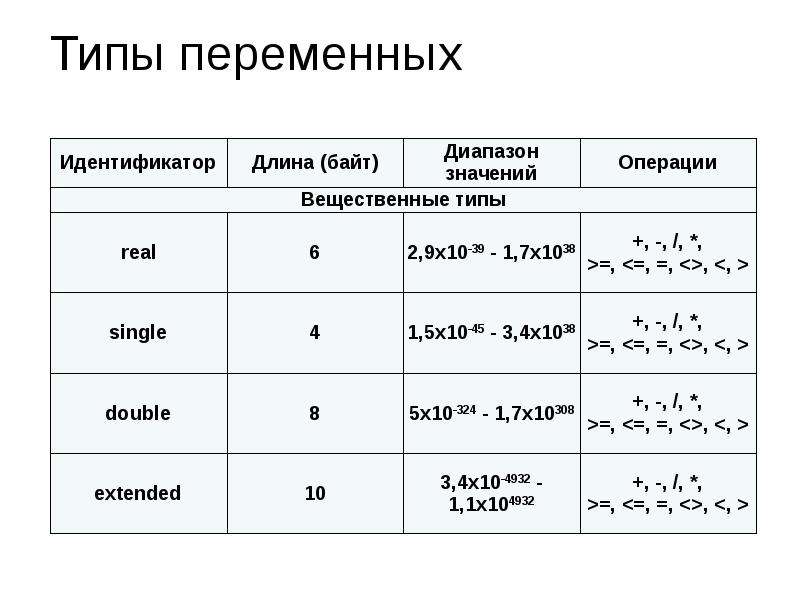
Сводка по типам данных

Это распространенные типы данных переменных:

тип данных Variant

Если не указать тип данных при объявлении переменной или вообще не объявлять переменную, Visual Basic автоматически определяет тип данных переменной типа переменной. Ниже следующую информацию о преимуществах переменных, объявленных в качестве этого типа данных:

org/ListItem»>
Переменные могут содержать строку, дату, время, boolean или числовую величину.
Переменные могут автоматически преобразовывать содержащиеся в них значения.

Недостатком является то, что для переменных требуется не менее 16байт памяти. 16 bytes of memory can be significant in large procedures or in complex modules.

Чтобы узнать, как это работает в макросе Variable_Test, выполните следующие действия:

Измените код макроса Variable_Test на:


Sub Variable_Test()
    Dim x, y
    x = "string"
    y = 1.23
    MsgBox "the value of x is " & x & _
    Chr(13) & "the value of y is " & y
End Sub

Запустите Variable_Test макрос.

Вы не получите сообщение об ошибке, так как вы можете назначить что-либо переменным x и y.

ПРИМЕЧАНИЕ: Вы также можете не использовать следующую строку, и макрос будет по-прежнему работать, так как переменные x и y будут рассматриваться как типы данных Variant:

Dim x, y

Область действия переменной

Когда вы объявляете переменную, она может быть видна другими макросами в том же модуле, в других модулях или в других проектах. Такое доступность переменной в модулях называется областью действия. Область действия может быть трех типов: на уровне процедуры, на уровне частного модуля и на уровне общего модуля. Область действия зависит от того, как и где объявлять переменные или переменные.

Область на уровне процедуры

Переменная с областью на уровне процедуры не видна за пределами процедуры, в которой она объявлена.

Если установить значение переменной, которая имеет область действия на уровне процедуры, ее содержимое не будет видно другими макросами.

Чтобы убедиться, что переменная с областью на уровне процедуры не видна за пределами процедуры, в которой она объявлена, выполните указанные ниже действия.

Вставка нового модуля в проект.
Введите в этот модуль оба макроса:
Sub Macro1() Dim x As Integer x = 10 MsgBox «x, as seen by Macro1 is » & x ‘next line runs Macro2 Macro2 End Sub Macro2() MsgBox «x, as seen by Macro2 is » & x End Sub
org/ListItem»>
Запустите Макрос1, и вы получите следующее сообщение:
x, as seen by Macro1 is 10
Нажмите кнопкуОК, и вы получите следующее сообщение:
x, as seen by Macro2 is
Нажмите кнопку
ОК.

Макрос2 не отображает значение переменной x, так как переменная x является локальной для параметра Macro1.

Объем личных и общедоступных модулей

Вы можете определить переменные в разделе объявлений модуля (в верхней части модуля, над всеми под процедурами) и настроить область действия переменной с помощью открытой выписки, затемной или закрытой выписки. Если перед переменной поместить открытое заявление, переменная будет доступна всем макросам во всех модулях проекта. Если перед переменной поместить перед переменной утверждение Dim или Private, переменная будет доступна только макросам в модуле, в котором она объявлена.

Чтобы увидеть разницу между общедоступным заявлением и заявлением Dim, выполните следующие действия:

Сохраните и закроите все открытые книги, а затем откройте новую книгу.
Запустите редактор Visual Basic редактора.
Вставка модуля в проект.


Type the following code into this module:

Public x As Integer
Sub Macro_1a()
    x = 10
    MsgBox x
    Macro_1b
End Sub
Sub Macro_1b()
    x = x * 2
    MsgBox x
    Macro2
End Sub

Вставка другого модуля в проект.
Введите следующий код в этот модуль:

Sub Macro2() x = x * 3
MsgBox x
End Sub
org/ListItem»>
Запустите Macro_1a макрос в первом модуле.
С переменной x, объявленной как «Public x As Integer», все три макроса в проекте имеют доступ к значению x. В первом окне сообщения отображается значение 10. Во втором поле сообщения отображается значение 20 (поскольку x умножается на 2 в Macro_1b). В третьем окне сообщения отображается значение 60 (поскольку значение x было изменено на 20 в Macro_1b а затем умножено на 3 в Макросе2).
Измените строку объявления в первом модуле из:
Public x As Integer
to:
Dim x As Integer
org/ListItem»>
Запустите Macro_1a макрос.
Если переменная x объявлена как «Dim x As Integer», только макрос в первом модуле имеет доступ к значению x. В первом поле сообщения отображается значение 10, во втором — 20 (поскольку x умножается на 2 в Macro_1b), а в третьем — значение 0 (так как в Макросе2 не отображается значение x, а в макросе 2 используется неинициализированное значение нуля).
Измените строку объявления в первом модуле из:
Dim x As Integer
Кому:
Private x As Integer
Запустите Macro_1a макрос.
Те же поля сообщений отображаются с использованием области Private statement, как при использовании statement Dim. Переменная x имеет ту же область действия, что и модуль, где она объявлена.

ПРИМЕЧАНИЕ: Если вы хотите ограничить область действия переменной модулем, в котором она объявлена, используйте privatestatement вместо dim. Оба этих эффекта будут одинаковыми, но при использовании закрытой выписки область действия будет более четкой.

Срок жизни переменной

Время, в течение которого переменная сохраняет значение, называется сроком жизни. Значение переменной может изменяться в течение ее жизненного времени, но при этом сохраняется значение. Кроме того, если переменная теряет область действия, она теряет значение.

Инициализация значения переменной

При запуске макроса все переменные инициализируются со значением. Числовая переменная инициализирована до нуля, строка переменной длины — в нулевую строку («»), а строка фиксированной длины заполняется кодом ASCII 0. Переменные Variant инициализируются как пустые. Пустая переменная представлена нулем в числовом контексте и пустой строкой («») в строковом контексте.

Переменные уровня процедуры

Если переменная объявляется в макрос с помощью макроса Dim, значение переменной сохраняется до тех пор, пока работает макрос. Если этот макрос вызывает другие макрос, значение переменной сохраняется (но не доступно другим макросам), пока работают и другие макросы.

Чтобы продемонстрировать работу переменных на уровне процедуры, выполните указанные ниже действия.

Вставка нового модуля в проект.
В этом модуле введите оба макроса:
Sub Macro1()
    ‘set x as a procedure level variable
   Dim x As Integer
   MsgBox «инициализированное значение x — » & x
   x = 10
    MsgBox «x is » & x
    ‘следующая строка запускает Макрос2
    Макрос2
    MsgBox «x is still » & x
End Sub
Sub Macro2()
    MsgBox «x, as seen by Macro2 is » & x
End Sub
org/ListItem»>
Запустите Макрос1.
Вы получаете следующее сообщение:
the initialized value of x is 0
Нажмите кнопкуОК, и вы получите сообщение:
x is 10
Нажмите кнопкуОК, и вы получите следующее сообщение:
x, as seen by Macro2 is
Нажмите кнопку ОК.
org/ListItem»>
Макрос2 не отображает значение переменной x, так как переменная x является локальной для параметра Macro1. Вы получите следующее сообщение:
x is still 10
Нажмите кнопку ОК.
Запуск макроса1.

Вы получаете те же сообщения, что и в шагах 3–6, так как как макрос1 перестал работать на шаге 6, значение переменной x было потеряно. Таким образом, при повторном повторе макроса 1 в шаге 7 в первом сообщении будет показано значение x в качестве нуля (инициализированное значение).

Статическое ключевое слово

Если переменная на уровне процедуры объявлена с помощью статического ключевого слова, переменная сохраняет значение до сброса проекта. Таким образом, если у вас есть статическая переменная, то при следующем вызове процедуры статическая переменная инициализирована до последнего значения.

Чтобы узнать, как работает статическое ключевое слово, выполните следующие действия:


Change the code in Macro1 to:

Sub Macro1()
    'set x as a procedure level variable
    Static x As Integer
       MsgBox "the initialized value of x is " & x
    x = x + 10
    MsgBox "x is " & x
End Sub

Запустите Макрос1.
org/ListItem»>
Вы получите сообщение:the initialized value of x is 0
Нажмите кнопкуОК, и вы получите сообщение:
x is 10
Нажмите кнопку ОК.
Запустите Макрос1, и вы получите следующее
сообщение:the initialized value of x is 10
Нажмите кнопкуОК, и вы получите следующее сообщение:
x is 20
org/ListItem»>
Нажмите кнопку ОК.

Значения, которые отображаются в сообщениях, во второй раз отличаются, так как переменная x объявляется как статическая переменная, а значение переменной сохраняется после первого запуска макроса Macro1.

ПРИМЕЧАНИЕ: Если у вас есть переменная уровня модуля, ее время существования будет таким же, как если бы она была статической переменной на уровне процедуры.

Чтобы проверить срок жизни переменной уровня модуля, выполните указанные ниже действия.


Change the code in the module that contains Macro1 to the following:

Dim x As Integer  'create a module-level variable
Sub Macro1()
   MsgBox "the initialized value of x is " & x
   x = x + 10
   MsgBox "x is " & x
End Sub

org/ListItem»>
Запустите Макрос1, и вы получите следующее сообщение:
the initialized value of x is 0
Нажмите кнопку ОК, и вы получите следующее сообщение:
x is 10
Нажмите кнопку ОК,
Запустите Макрос1, и вы получите сообщение:
the initialized value of x is 10
Нажмите кнопку ОК.
org/ListItem»>
Вы получаете следующее сообщение:
x is 20
Нажмите кнопку ОК.

Значения, которые отображаются в сообщениях, во второй раз отличаются, так как переменная x объявлена как статическая переменная и сохраняет значение после первого запуска макроса Macro1.

Сброс проектов для сброса переменных

Если вы хотите сбросить значение статической переменной или переменной на уровне модуля, нажмите кнопку Сброс на
Стандартная панель инструментов или нажмите кнопку Сброс в меню Выполнить.

Если вы сделаете это для проекта Macro1, а затем повторно запроизводили макрос1,значение переменной x инициализировано до нуля, и вы получите первое сообщение:

the initialized value of x is 0

Переменные для «инклюзивных» измерений

5.

1 Переменная Фейнмана х_F

Пусть при рассеянии частиц a, b после их взаимодействия регистрируется частица c, а остальные продукты реакции не регистрируются (система X), то есть проводятся инклюзивные измерения реакции

a + b → c + X.

(5.1)

Чтобы не загромождать формулы, под 4-импульсом (или компонентами его, то есть энергией и 3-импульсом) регистрируемой частицы будем понимать (E_c,p_c), опуская индекс c . В случае обращения к системе центра масс реакции, как всегда, соответствующие неинвариантные величины будем помечать символом *.
Кинематическую область возможных значений импульса регистрируемой частицы можно легко определить, пользуясь формулами для «круга импульсов» (если речь идет о системе центра масс) или «эллипса импульсов» (если речь идет о любой другой системе отсчета, например, лабораторной), рассмотренными ранее. В частности, продольный импульс регистрируемой частицы может лежать в пределах

(5.2)

где

(5.3)

здесь m_X,min − минимальное допустимое значение эффективной массы системы X, равное сумме масс входящих в нее частиц (имеется в виду, допустимое законами сохранения квантовых чисел для рассматриваемой реакции). Если графически представить круг импульсов, то принадлежит хорде круга, проведенной перпендикулярно его вертикальному диаметру на расстоянии от горизонтального диаметра, а границы изменения определяются крайними точками этой хорды. В лабораторной системе, где круг импульсов превращается в эллипс импульсов, величина принадлежит хорде эллипса, проведенной перпендикулярно его малой полуоси на расстоянии от большой оси, а границы изменения определяются крайними точками этой хорды (см. рис. 5.1, эллипс импульсов для реакции p(p,π)X). Т. о. экстремальные (максимальное и минимальное) возможные значения для реакции (5.1) определяются крайними точками большой оси этого эллипса (см. пример на рис. 5.1, точки A, B и C для соответствующих процессов).
Вспомнив о партонной картине взаимодействия адронов, можно заподозрить, что инвариантная безразмерная переменная

x_F = /_max,

(5.4)

может быть хорошей переменной для анализа данных инклюзивных измерений реакций типа (5.1). Опыт показал, что так оно и есть. Переменная (5.4) называется фейнмановской скейлинговой переменной.

Рис. 5.1. Эллипс импульсов пиона в лабораторной системе для реакций p(p,π)X и p(d, π)X, обсужденный в Части II. Область внутри меньшего эллипса разрешена для пиона, рожденного в реакции p(p, π)X (оба нуклона — свободные). Граница большего эллипса соответствует реакции p(d,π)X, когда дейтрон рассматривается как «материальная точка», а эффективная масса системы X минимально возможная (после учета всех законов сохранения и правил отбора по квантовым числам). Область импульсов вне большего эллипса − абсолютно запрещена для пиона вследствие законов сохранения энергии и импульса. Между внешним и внутренним эллипсами − «кумулятивная» область, недоступная для реакции p(p,π)X вследствие тех же законов сохранения энергии и импульса.

Ясно, что при анализе дифференциальных распределений, проинтегрированных по поперечному импульсу, под _max следует понимать экстремальное значение продольного импульса (например, соответствующее точке В на рис. 5.1). Кроме того, в партонной картине Фейнмана считается, что поперечный импульс партонов невелик, то есть их импульсное распределение в адроне «прижато» к оси абсцисс рис. 5.1, что дает некоторое дополнительное оправдание такому рецепту определения _max.
В литературе часто употребляют и другое определение х_F, а именно:

= 2/√s,

(5.5)

практически совпадающее с (5.4), когда s намного больше значений всех масс, входящих в определение (5.2), равно как и значений поперечного импульса . Определение (5.4) представляется более точным при конечных энергиях или при работе вблизи кинематических границ рассматриваемого процесса (но все же при невысоких , если для максимального значения продольного импульса принимается его экстремальная величина).

5.2 Быстрота и псевдобыстрота

Можно убедиться, что определенная в Части I безразмерная переменная, называемая быстротой, может быть выражена через энергии и импульсы регистрируемой частицы так:

(5.6)

а продольная быстрота как

(5.

Переменные, соответствующие динамике на световом фронте, в импульсном пространстве можно выразить через через импульсы и энергии в с.ц.м.:

(5.8)

откуда видно, что

(5.9)

Таким образом, существенными кинематическими переменными для анализа реакций типа (5.1), являются пары (,x_F) или (,η_long). Однако значения пределов изменения одной из переменных в указанных парах зависят от значений другой переменной. Это интуитивно ясно из рассмотрения рис. 5.1; подробнее это обсуждено в книге [4]. Там же детально рассмотрена еще одна, часто употребляемая при высоких энергиях переменная, а именно − псевдобыстрота. Ее практическая ценность в том, что измерять псевдобыстроту проще, чем быстроту: не нужно измерять величины импульсов, равно как и нет особой необходимости идентифицировать частицы, чтобы правильно вычислять их энергии. Дело в том, что для измерения псевдобыстроты достаточно измерить угол θ вылета частицы. При этом псевдобыстрота почти везде достаточно близка к продольной быстроте.

Вначале заметим, что

(5.10)

(величина называется «поперечной массой»), если выполнены условия:

угол вылета много меньше 1 но не слишком мал:

m/p < θ <<1;

(5.11)

поперечный импульс много меньше продольного:

<< ||;

(5.12)

импульсы велики по сравнению с массами:

p ≥ .

(5.

13)

Если несколько ослабить первое условие, то есть допустить, что

m/p < θ <1,

(5.14)

то можно увидеть, что

(5.15)

Последнее приближенное равенств в этой формуле используется как определение псевдобыстроты, позволяющее ограничиться измерениями углов вылета частиц в лабораторной системе:

(5.16)

    Следует заметить, что в разных работах по изучению процессов множественного рождения частиц в инклюзивной постановке экспериментов при высоких энергиях нередко используются слегка разные определения псевдобыстроты (см. например [4]). Поэтому небесполезно внимательно следить за тем, какое именно определение псевдобыстроты используется в той или иной работе, хотя все такие определения отталкиваются от углов вылета регистрируемой частицы.
    Безусловно, необходимо помнить о различии между псевдобыстротой и настоящей быстротой.
    Наконец, нельзя не сказать и о том, что (уступая давлению жаргона) продольную быстроту иногда также называют просто быстротой (см. примеры в [4]).
    Рисунок 5.1 помогает понять, почему переменная псевдобыстроты в свое время стала популярной. Действительно, партонная картина неупругого взаимодействия подразумевает, что при высоких энергиях средние поперечные импульсы вторичных частиц почти не растут с ростом начальной энергии (или растут достаточно медленно). Иными словами, область внутри разрешенного кинематикой эллипса «заселяется» частицами неравномерно: они концентрируются вблизи оси абсцисс в довольно узкой полосе. С ростом энергии эллипс расширяется, но частицы остаются почти в той же полосе: распределение по поперечному импульсу при фиксированной быстроте почти не меняется, и когда поперечный импульс частицы много меньше ее полного импульса, распределение по продольному импульсу становится (приближенно) распределением по углу вылета частицы. Это означает, что характер распределения событий внутри эллипса не зависит (или слабо зависит) от его абсолютных размеров: важно лишь относительное расстояние точки, изображающей событие, от центра эллипса (круга в с.ц.м.).

5.3 Связь быстроты и переменной х

_F.

В определениях (5.4) фейнмановской переменной и продольной быстроты (5.7) фигурирует один и тот же продольный импульс регистрируемой частицы с. Отсюда следует, что эти переменные связаны между собой. Эту связь нетрудно установить:

(5.17)

Можно убедиться, что вблизи |_{x_F| ~ 0 продольная быстрота тоже мала: || ~ 0, но в этой, т. н.
«центральной» области, данный конечный фиксированный
интервал ∆x_F с ростом энергии столкновения (√s) отображается на растущий с √s интервал быстроты (см. например, [4]). Иными словами, быстрота
«растягивает» центральную область по сравнению с |_{x_F|.
Вблизи кинематических границ можно переписать связь x_F с быстротой в другой
форме. В самом деле, рассмотрим выражения для них в системе центра масс вблизи
границы x_F ≈ 1 и
≈
.}}

(5.18)

Поскольку сами эти переменные обычно применяются в области высоких энергий и, как правило, при анализе неупругих процессов с довольно высокой множественностью, можно считать >> m_c. Это вполне оправдано вблизи кинематических пределов. Приняв это приближение, из (5.18) имеем

(5.19)

поскольку вблизи границы |_{x_F| ≈ 1 перпендикулярный импульс
много меньше
продольного
.
В результате, приходим к формуле}

(5.

20)

которую удобнее выписать в окончательной форме [4]

x_F ≈ exp_{(−
), x_F > 0,
x_F ≈ exp_{(|| −
), x_F < 0.}}

(5.21)

Что такое переменная в математике? Определение, типы, примеры, факты

В реальной жизни есть вещи, которые остаются неизменными, например дата вашего рождения. Однако есть вещи, которые меняются со временем и местом, такие как температура, возраст, рост и т. д. Поскольку эти величины меняются, их можно назвать переменными.

В алгебре — символ (обычно буква), заменяющий неизвестное числовое значение в уравнении или алгебраическом выражении. Простыми словами, переменная – это величина, которая может быть изменена и не является фиксированной. Переменные необходимы, поскольку они составляют основной компонент алгебры.

Обычно мы используем « x » и « y » для выражения неизвестного целого числа. Однако это не обязательно, и мы можем использовать любую букву.

Пример-
Возьмем в качестве примера алгебраическое выражение 2x + 6. Здесь x является переменной и может принимать любое значение. Если x = 1, значение этого алгебраического выражения будет 2(1) + 6, т. е. 8, и

, если x = 2, значение алгебраического выражения изменится на 10. Следовательно, мы можем сказать, что значение алгебраического выражения изменяется при изменении x.

Переменная x также может принимать любое значение в уравнении. Он может удовлетворять или не удовлетворять уравнению. Если да, то это называется решением уравнения.

Зависимая переменная — это переменная, значение которой определяется величиной, которую принимает другая переменная.

Например, в уравнении y = 2x + 3 x может принимать любое значение, например 1, 2, 3. Однако значение y будет зависеть от значения x. Таким образом, если x = 1, y станет равным 5, а если x = 2, y станет равным 7 и так далее. Поэтому у называется зависимой переменной, а х называется независимой переменной.

Независимая переменная в алгебраическом уравнении — это переменная, на значения которой не влияют изменения. Если алгебраическое уравнение имеет две переменные, x и y, и каждое значение x связано с любым другим значением y, то x является независимой переменной, а y является зависимой переменной.

Например, в уравнении y = 2x x может принимать любое значение. Следовательно, это независимая переменная в уравнении.

Переменные — очень важная концепция, если вы хотите понять алгебру. В SplashLearn , вы найдете различные ресурсы, такие как игры и рабочие листы, которые помогут вам понять концепцию переменных. Решенные примеры и практические задачи дают пошаговое понимание, облегчая самостоятельное решение задач.

x = 3 удовлетворяют уравнению, поскольку LHS равно RHS. Итак, x = 3 является решением данного уравнения.

Значение a в уравнении a + 6

² = 39 равно

Правильный ответ: 3
3 + 6 ² = 3 + 36 = 39

Рассмотрим уравнение x + y = 20. Если значение x равно 14, значение y будет

Правильный ответ: 6
14 + 6 = 20

Решением какого из следующих уравнений является y = 3?

у — 4 = 1

у + 3 = 0

2у — 5 = 2

y — 3 = 0

Правильный ответ: y — 3 = 0
3 — 3 = 0

Переменные A

могут принимать только 1 значение

могут принимать только 2 значения

имеет фиксированное значение

может принимать разные значения

Правильный ответ: может принимать разные значения
Переменная может принимать любое значение и, следовательно, не имеет фиксированного значения.

Почему мы используем переменные в математике?

Переменные используются для представления неизвестной величины.

Можем ли мы использовать буквы или символы греческих языков в качестве переменных?

Да, мы можем использовать α (альфа), 𝛽 (бета), 𝛾 (гамма), 𝛳 (тета) и другие буквы также в качестве переменной.

Могут ли переменные принимать любое значение?

Да, переменные могут принимать любые значения.

Что такое переменное выражение?

Комбинация символов, переменных и констант называется переменным выражением. Например: 5x – 42

Переменные, функции и уравнения

Экономисты заинтересованы в изучении типов отношений. Например экономист может посмотреть на сумму денег, которую зарабатывает человек, и на сумму, которую человек выбирает тратить. Это отношение или функция потребления. Как другой пример, экономист может посмотреть на сумму денег, которую коммерческая фирма имеет и сумму, которую он хочет потратить на новое оборудование. это инвестиции отношения или инвестиционная функция.

Функция пытается определить эти отношения. Он пытается придать отношениям математическую форму. Уравнение – это математическое способ рассмотрения отношений между понятиями или элементами. Эти концепции или элементы представлены тем, что называется переменными.

Переменная представляет понятие или элемент, величина которого может быть представлен числом, т.е. измерен количественно. Переменные называются переменными, потому что они изменяются, т. е. могут иметь различные значения. Таким образом, переменную можно рассматривать как величину, которая принимает различные значения. в конкретной проблеме. Многие элементы в экономике могут принимать различные значения. Математика обычно использует буквы с конца алфавита для обозначения переменных. Однако в экономике часто используется первая буква элемента, которая варьируется для обозначения переменные. Таким образом, p используется для переменной цены, а q используется для переменной количество.

Выражение, такое как 4x ³, является переменной. Он может предполагать разные значения, потому что x может принимать разные значения. В этом выражении x является переменной 4 – коэффициент при x. Коэффициент означает, что 4 работает вместе с x. Выражения например, 4x ³, которое состоит из коэффициента, умноженного на переменную, поднятую степени называются мономами.

Одночлен — это алгебраическое выражение, которое является либо числом, переменная или произведение чисел и переменных. (мономиал происходит от Греческое слово, монос, что означает один.) Действительные числа, такие как 5, которые не умножаются по переменной также называются мономами. Одночлены также могут иметь более одного переменная. 4x ³ y ² является таким примером. В этом выражении и x, и y — переменные, а 4 — их коэффициент.

Ниже приведены примеры одночленов:

х, 4х ², -6xy ² z, 7

Один или несколько мономов можно комбинировать путем сложения или вычитания, чтобы получить то, что называются полиномами . (Полиномиальный происходит от греческого слова поли, что означает много.) Многочлен имеет два или несколько терминов, то есть два или более монома. Если в многочлене всего два члена, многочлен называется двучленом.

Выражение 4x ³ y ² — 2xy ² +3 является многочленом с тремя терминами.

Эти условия равны 4x ³ y ² , — 2xy ² и 3. коэффициенты членов равны 4, -2 и 3.

Степень термина или монома представляет собой сумму показателей степени переменных. Степень многочлена – это степень члена старшей степени. в В приведенном выше примере степени членов равны 5, 3 и 0. Степень многочлена 5,

Помните, что переменные — это элементы, которые могут принимать разные значения. Функция пытается объяснить одну переменную через другую.

Рассмотрим приведенный выше пример, в котором сумма, которую вы решите потратить, зависит от Ваш заработная плата. Здесь есть две переменные: ваша зарплата и сумма, которую вы тратите.

Независимые переменные — это те, которые не зависят от других переменных. Зависимый переменные — это те, которые изменяются независимыми переменными. Изменение вызывается независимой переменной. В нашем примере заработная плата является независимой переменная, а сумма, которую вы тратите, является зависимой переменной.

Чтобы продолжить тот же пример, что, если сумма, которую вы решите потратить, зависит не только от вашей зарплаты, но и от дохода, который вы получаете от инвестиций на фондовом рынке. Теперь есть три переменных: ваша зарплата и ваши инвестиции. доходы являются независимыми переменными, а сумма, которую вы тратите, является зависимой переменной.

Определение: Функция — это математическое соотношение, в котором значения одной зависимой переменной определяются значениями одного или более независимых переменных. Функция означает, что зависимая переменная определяется по независимой переменной (переменным).

Цель экономического анализа состоит в том, чтобы определить независимую(ые) переменную(ые), которые объяснить некоторые зависимые переменные. Например, что объясняет изменения в занятости, в потребительских расходах, в бизнес-инвестициях и т. д.?

Функции с одной независимой переменной называются одномерными функциями. Идет переписка один в один. Функции с более чем одним независимым переменных называются многомерными функциями.

Независимая переменная часто обозначается x. Зависимая переменная часто обозначается y.

Мы говорим, что y является функцией x. Это означает, что у зависит от х или определяется им.

Математически мы пишем y = f(x)

Это означает, что математически y зависит от x. Если мы знаем значение х, то мы можем найти значение y.

В произношении мы говорим «y есть f of x». Это не означает, что y является продуктом двух отдельных величин, f и x, а скорее то, что f используется для обозначения идея функции. Другими словами, скобки не означают, что f умножается по х.

Не обязательно использовать букву f. Например, мы могли бы сказать
y = g(x), что также означает, что y является функцией x, или мы могли бы сказать y = h(x) что также означает, что y является функцией x.

Мы можем рассматривать функции алгебраически или графически. Если мы используем алгебру, мы посмотри уравнения. Если мы используем геометрию, мы используем графики.

Простой пример функциональной записи

Q _d = количество требуемых пицц

P _p = цена пиццы

P _t = цена томатного соуса

P _c = цена сыра

P _d = цена теста для пиццы

N = число потенциальных едоков пиццы

P _p = f(P _t , P _c , P _d )

Это пример функции, которая говорит, что цена пиццы зависит от цены на томатный соус, сыр и тесто для пиццы. Есть одна зависимая переменная, цена пиццы и есть три независимые переменные, цены на томатный соус, сыр и тесто для пиццы.

Q _d = f(P _p , N)

Это еще один пример функции. В нем говорится, что требуемое количество пиццы зависит от цены пиццы и количества потенциальных едоков пиццы. Там есть одна зависимая переменная, количество требуемой пиццы, и есть две независимые переменные, цена пиццы и количество потенциальных пицц Пожиратели.

Общий экономический пример функциональной записи

C = потребление, сумма, потраченная на товары и услуги

Y = доход, сумма, которую можно потратить

С = С(У)

Это пример функции, которая говорит о сумме, потраченной на потребление зависит от дохода. Это очень общая форма функции потребления. Чтобы использовать его, экономисты должны облечь его в более точную математическую форму. Например

С = 25 + 0,75 Y

Это функция, которая говорит, что потребление равно 25 независимо от уровня дохода и что на каждый дополнительный доллар дохода тратится 75 центов на потребление.

Использование функциональной записи: некоторые примеры

Пример 1

у = f(х) = 3х + 4

Это функция, которая говорит, что y, зависимая переменная, зависит от x, независимая переменная. Независимая переменная x может принимать разные значения. При изменении х меняется и у.

Найти f(0). Это означает, что нужно найти значение y, когда x равно 0.
f(0) = 3 умножить на 0 плюс 4
f(0) = 3(0) + 4 = 4
Найти f(1). Это означает, что нужно найти значение y, когда x равно 1.
f(1) = 3 умножить на 1 плюс 4
f(1) = 3(1) + 4 = 7
Найти f(-1). Это означает, что нужно найти значение y, когда x равно -1.
f(-1) = 3 раза (-1) плюс 4
f(1) = 3(-1) + 4 = 1

Пример 2

d(p) = p ² -20p + 125
Это функция, описывающая спрос на товар, где p — доллар.

Штирлиц — Сеть печатных салонов в Перми

Переменная x: ПЕРЕМЕННАЯ | это… Что такое ПЕРЕМЕННАЯ?