Основы алгоритмов: Основы алгоритмизации. Алгоритмы

Лекции Технопарка. 1 семестр. Алгоритмы и структуры данных

Очередной пост в рамках нашего цикла лекций Технопарка. В этот раз мы предлагаем вашему вниманию курс, посвящённый алгоритмам и структурам данных. Автор курса — Степан Мацкевич, сотрудник компании ABBYY.

Лекция 1. Основы

Начало первой лекции посвящено обсуждению основных понятий, на которых строится вся дальнейшая программа курса: что такое алгоритм и структура данных. Описаны базовые виды алгоритмов, их характеристики и методы анализа. Далее рассматриваются примеры создания алгоритмов для вычисления чисел Фибоначчи, проверки числа на простоту, быстрого возведения числа в целую степень. В конце лекции рассказывается об особенностях использования алгоритмов для работы с массивами: создание однопроходных алгоритмов, поиск минимального элемента, бинарный поиск.

Лекция 2.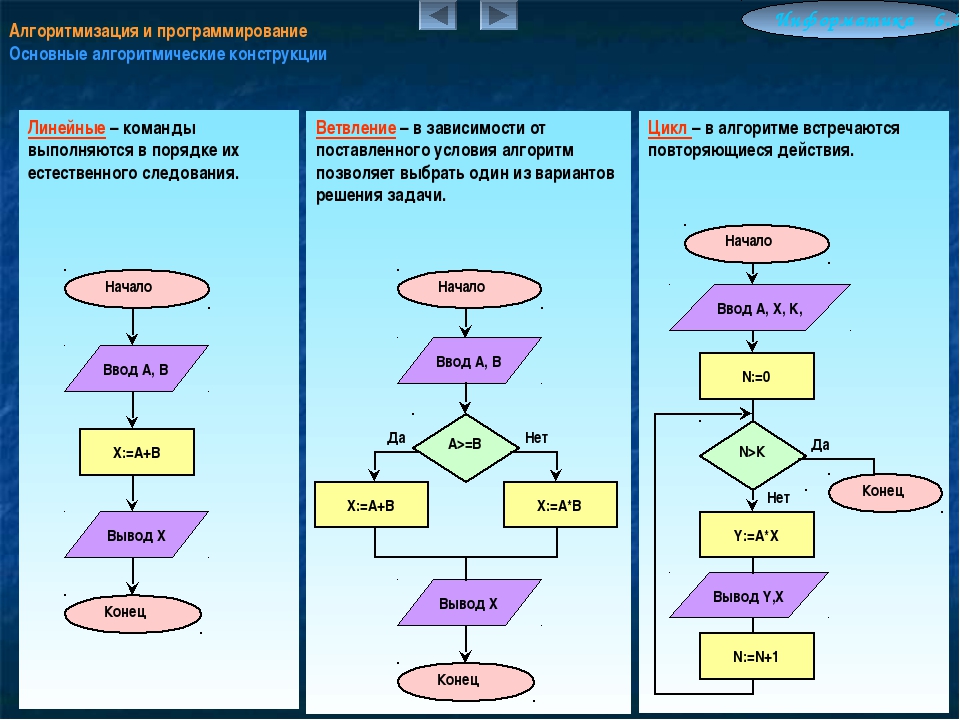 Элементарные структуры данных

Вторая лекция посвящена изучению элементарных структур данных. В начале даётся определение понятия «абстрактного типа данных». Далее лектор рассказывает о том, что такое амортизационный анализ и каковы его особенности.

Рассматриваются такие виды структур и абстрактные типы данных, как:

• массив и динамический массив;
• стек, очередь и дэк;
• очередь с приоритетом;
• связные списки: однонаправленные и двунаправленные;
• двоичная куча.

Разбираются недостатки и преимущества каждого вида структур, а также их реализация в виде программного кода.

Лекция 3. Сортировки (часть 1)

Тема сортировок оказалась настолько объёмной, что её пришлось разделить на две лекции. В первой части подробно рассматриваются такие виды алгоритмов, как:

• сортировка одного, двух и трёх элементов;
• сортировка выбором;
• сортировка вставками;
• сортировка пузырьком;
• быстрая сортировка Хоара.

Описывается, как можно оценить скорость работы того или иного алгоритма сортировки, как проанализировать алгоритмы по количеству сравнений и т.д.

Лекция 4. Сортировки (часть 2)

На этой лекции рассматриваются другие виды алгоритмов и их применение:

• сортировка слиянием, в том числе двух упорядоченных массивов;
• сортировка подсчётом;
• поразрядная сортировка;
• пирамидальная сортировка и ряд других.

Напоследок проводится сравнительный анализ разных алгоритмов.

Лекция 5. Хеш-таблицы

Из этой лекции вы сначала узнаете, что такое метод поиска хешированием, какие бывают хеш-функции (в том числе хеш-функции строк). Затем идёт подробное рассмотрение хеш-таблиц и способов их применения: что они собой представляют, каковы основные методы разрешения коллизий (метод цепочек и метод открытой адресации), а также методы вставки, удаления и поиска элементов. Напоследок проводится сравнение хеш-таблиц по затратам времени и памяти.

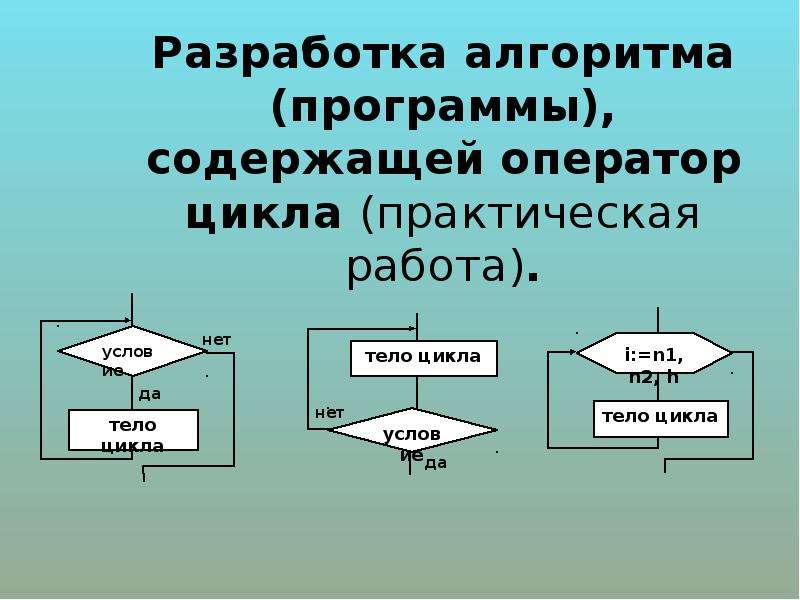
Лекция 6. Деревья

Последняя лекция в рамках курса АиСД посвящена таким структурам данных, как деревья. Разумеется, в начале лекции дается определение понятия «деревья», рассматриваются их характеристики и приводятся примеры. Затем вы узнаете, как деревья представлены в памяти, какие есть способы обхода дерева. Далее рассматриваются так называемые двоичные деревья поиска и группа самобалансирующихся деревьев: декартовы и АВЛ-деревья. И в завершение лекции рассказывается об абстрактном типе данных «ассоциативный массив».

Введение в анализ сложности алгоритмов (часть 1) / Хабр

От переводчика: данный текст даётся с незначительными сокращениями по причине местами излишней «разжёванности» материала. Автор абсолютно справедливо предупреждает, что отдельные темы покажутся чересчур простыми или общеизвестными. Тем не менее, лично мне этот текст помог упорядочить имеющиеся знания по анализу сложности алгоритмов. Надеюсь, что он будет полезен и кому-то ещё.
Из-за большого объёма оригинальной статьи я разбила её на части, которых в общей сложности будет четыре.
Я (как всегда) буду крайне признательна за любые замечания в личку по улучшению качества перевода.

Введение

Многие современные программисты, пишущие классные и широко распространённые программы, имеют крайне смутное представление о теоретической информатике. Это не мешает им оставаться прекрасными творческими специалистами, и мы благодарны за то, что они создают.

Тем не менее, знание теории тоже имеет свои преимущества и может оказаться весьма полезным. В этой статье, предназначенной для программистов, которые являются хорошими практиками, но имеют слабое представление о теории, я представлю один из наиболее прагматичных программистских инструментов: нотацию «большое О» и анализ сложности алгоритмов. Как человек, который работал как в области академической науки, так и над созданием коммерческого ПО, я считаю эти инструменты по-настоящему полезными на практике. Надеюсь, что после прочтения этой статьи вы сможете применить их к собственному коду, чтобы сделать его ещё лучше. Также этот пост принесёт с собой понимание таких общих терминов, используемых теоретиками информатики, как «большое О», «асимптотическое поведение», «анализ наиболее неблагоприятного случая» и т.п.

Этот текст также ориентирован на учеников средней школы из Греции или любой другой страны, участвующих в Международной олимпиаде по информатике, соревнованиях по алгоритмам для учащихся и тому подобном. Как таковой, он не требует предварительного знания каких-либо сложных математических моментов и просто даст вам основу для дальнейшего исследования алгоритмов с твёрдым пониманием стоящей за ними теории. Как тот, кто в своё время много участвовал в различных состязаниях, я настоятельно рекомендую вам прочитать и понять весь вводный материал. Эти знания будут просто необходимы, когда вы продолжите изучать алгоритмы и различные передовые технологии.

Я надеюсь, что это текст будет полезен для тех программистов-практиков, у которых нет большого опыта в теоретической информатике (то, что самые вдохновлённые инженеры-программисты никогда не ходили в колледж, уже давно свершившийся факт). Но поскольку статья предназначена и для студентов тоже, то временами она будет звучать, как учебник. Более того, некоторые темы могут показаться вам чересчур простыми (например, вы могли сталкиваться с ними во время своего обучения). Так что, если вы чувствуете, что понимаете их — просто пропускайте эти моменты. Другие секции идут несколько глубже и являются более теоретическими, потому что студенты, участвующие в соревнованиях, должны разбираться в теории алгоритмов лучше, чем средний практик. Но знать эти вещи не менее полезно, а следить за ходом повествования не так уж сложно, так что они, скорее всего, заслуживают вашего внимания. Оригинальный текст был направлен учащимся старшей школы, никаких особых математических знаний он не требует, поэтому каждый, имеющий опыт программирования (например, знающий, что такое рекурсия) способен понять его без особых проблем.

В этой статье вы найдёте много интересных ссылок на материалы, выходящие за рамки нашего обсуждения. Если вы — работающий программист, то вполне возможно, что знакомы с большинством из этих концепций. Если же вы просто студент-новичок, участвующий в соревнованиях, переход по этим ссылкам даст вам информацию о других областях информатики и разработки программного обеспечения, которые вы ещё не успели изучить. Просмотрите их ради увеличения собственного багажа знаний.

Нотация «большого О» и анализ сложности алгоритмов — это те вещи, которые и программисты-практики, и студенты-новички часто считают трудными для понимания, боятся или вообще избегают, как бесполезные. Но они не так уж сложны и заумны, как может показаться на первый взгляд. Сложность алгоритма — это всего лишь способ формально измерить, насколько быстро программа или алгоритм работают, что является весьма прагматичной целью. Давайте начнём с небольшой мотивации по этой теме.

Мотивация

Мы уже знаем, что существуют инструменты, измеряющие, насколько быстро работает код. Это программы, называемые профайлерами (profilers), которые определяют время выполнения в миллисекундах, помогая нам выявлять узкие места и оптимизировать их. Но, хотя это и полезный инструмент, он не имеет отношения к сложности алгоритмов. Сложность алгоритма — это то, что основывается на сравнении двух алгоритмов на идеальном уровне, игнорируя низкоуровневые детали вроде реализации языка программирования, «железа», на котором запущена программа, или набора команд в данном CPU. Мы хотим сравнивать алгоритмы с точки зрения того, чем они, собственно, являются: идеи, как происходит вычисление. Подсчёт миллисекунд тут мало поможет. Вполне может оказаться, что плохой алгоритм, написанный на низкоуровневом языке (например, ассемблере) будет намного быстрее, чем хороший алгоритм, написанный языке программирования высокого уровня (например, Python или Ruby). Так что пришло время определиться, что же такое «лучший алгоритм» на самом деле.

Алгоритм — это программа, которая представляет из себя исключительно вычисление, без других часто выполняемых компьютером вещей — сетевых задач или пользовательского ввода-вывода. Анализ сложности позволяет нам узнать, насколько быстра эта программа, когда она совершает вычисления. Примерами чисто вычислительных операций могут послужить операции над числами с плавающей запятой (сложение и умножение), поиск заданного значения из находящейся в ОЗУ базы данных, определение игровым искусственным интеллектом (ИИ) движения своего персонажа таким образом, чтобы он передвигался только на короткое расстояние внутри игрового мира, или запуск шаблона регулярного выражения на соответствие строке. Очевидно, что вычисления встречаются в компьютерных программах повсеместно.

Анализ сложности также позволяет нам объяснить, как будет вести себя алгоритм при возрастании входного потока данных. Если наш алгоритм выполняется одну секунду при 1000 элементах на входе, то как он себя поведёт, если мы удвоим это значение? Будет работать также быстро, в полтора раза быстрее или в четыре раза медленнее? В практике программирования такие предсказания крайне важны. Например, если мы создали алгоритм для web-приложения, работающего с тысячей пользователей, и измерили его время выполнения, то используя анализ сложности, мы получим весьма неплохое представление о том, что случится, когда число пользователей возрастёт до двух тысяч. Для соревнований по построению алгоритмов анализ сложности также даст нам понимание того, как долго будет выполняться наш код на наибольшем из тестов для проверки его правильности. Так что, если мы определим общее поведение нашей программы на небольшом объёме входных данных, то сможем получить хорошее представление и о том, что будет с ней при больших потоках данных. Давайте начнём с простого примера: поиска максимального элемента в массиве.

Подсчёт инструкций

В этой статье для реализации примеров я буду использовать различные языки программирования. Не переживайте, если вы не знакомы с каким-то из них — любой, кто умеет программировать, способен прочитать этот код без особых проблем, поскольку он прост, и я не собираюсь использовать какие-либо экзотические фенечки языка реализации. Если вы — студент-олимпиадник, то, скорее всего, пишите на С++, поэтому у вас тоже не должно возникать проблем. В этом случае я также рекомендую прорабатывать упражнения, используя С++ для большей практики.

Максимальный элемент массива можно найти с помощью простейшего отрывка кода. Например, такого, написанного на Javascript. Дан входной массив А размера n:

var M = A[ 0 ];
 
for ( var i = 0; i < n; ++i ) {
    if ( A[ i ] >= M ) {
        M = A[ i ];
    }
}

Сначала подсчитаем, сколько здесь вычисляется фундаментальных инструкций. Мы сделаем это только один раз — по мере углубления в теорию такая необходимость отпадёт. Но пока наберитесь терпения на то время, которое мы потратим на это. В процессе анализа данного кода, имеет смысл разбить его на простые инструкции — задания, которые могут быть выполнены процессором тотчас же или близко к этому. Предположим, что наш процессор способен выполнять как единые инструкции следующие операции:

• Присваивать значение переменной
• Находить значение конкретного элемента в массиве
• Сравнивать два значения
• Инкрементировать значение
• Основные арифметические операции (например, сложение и умножение)

Мы будем полагать, что ветвление (выбор между if и else частями кода после вычисления if-условия) происходит мгновенно, и не будем учитывать эту инструкцию при подсчёте. Для первой строки в коде выше:

var M = A[ 0 ]; 

требуются две инструкции: для поиска A[0] и для присвоения значения M (мы предполагаем, что n всегда как минимум 1). Эти две инструкции будут требоваться алгоритму, вне зависимости от величины n. Инициализация цикла for тоже будет происходить постоянно, что даёт нам ещё две команды: присвоение и сравнение.

i = 0;
i < n;

Всё это происходит до первого запуска for. После каждой новой итерации мы будем иметь на две инструкции больше: инкремент i и сравнение для проверки, не пора ли нам останавливать цикл.

++i;
i < n;

Таким образом, если мы проигнорируем содержимое тела цикла, то количество инструкций у этого алгоритма 4 + 2n — четыре на начало цикла for и по две на каждую итерацию, которых мы имеем n штук. Теперь мы можем определить математическую функцию f(n) такую, что зная n, мы будем знать и необходимое алгоритму количество инструкций. Для цикла for с пустым телом f( n ) = 4 + 2n.

Анализ наиболее неблагоприятного случая

В теле цикла мы имеем операции поиска в массиве и сравнения, которые происходят всегда:

if ( A[ i ] >= M ) { ...

Но тело if может запускаться, а может и нет, в зависимости от актуального значения из массива. Если произойдёт так, что A[ i ] >= M, то у нас запустятся две дополнительные команды: поиск в массиве и присваивание:

M = A[ i ]

Мы уже не можем определить f(n) так легко, потому что теперь количество инструкций зависит не только от n, но и от конкретных входных значений. Например, для A = [ 1, 2, 3, 4 ] программе потребуется больше команд, чем для A = [ 4, 3, 2, 1 ]. Когда мы анализируем алгоритмы, мы чаще всего рассматриваем наихудший сценарий. Каким он будет в нашем случае? Когда алгоритму потребуется больше всего инструкций до завершения? Ответ: когда массив упорядочен по возрастанию, как, например, A = [ 1, 2, 3, 4 ]. Тогда M будет переприсваиваться каждый раз, что даст наибольшее количество команд. Теоретики имеют для этого причудливое название — анализ наиболее неблагоприятного случая, который является ни чем иным, как просто рассмотрением максимально неудачного варианта. Таким образом, в наихудшем случае в теле цикла из нашего кода запускается четыре инструкции, и мы имеем f( n ) = 4 + 2n + 4n = 6n + 4.

Асимптотическое поведение

С полученной выше функцией мы имеем весьма хорошее представление о том, насколько быстр наш алгоритм. Однако, как я и обещал, нам нет нужды постоянно заниматься таким утомительным занятием, как подсчёт команд в программе. Более того, количество инструкций у конкретного процессора, необходимое для реализации каждого положения из используемого языка программирования, зависит от компилятора этого языка и доступного процессору (AMD или Intel Pentium на персональном компьютере, MIPS на Playstation 2 и т.п. ) набора команд. Ранее же мы говорили, что собираемся игнорировать условия такого рода. Поэтому сейчас мы пропустим нашу функцию f через «фильтр» для очищения её от незначительных деталей, на которые теоретики предпочитают не обращать внимания.

Наша функция 6n + 4 состоит из двух элементов: 6n и 4. При анализе сложности важность имеет только то, что происходит с функцией подсчёта инструкций при значительном возрастании n. Это совпадает с предыдущей идеей «наихудшего сценария»: нам интересно поведение алгоритма, находящегося в «плохих условиях», когда он вынужден выполнять что-то трудное. Заметьте, что именно это по-настоящему полезно при сравнении алгоритмов. Если один из них побивает другой при большом входном потоке данных, то велика вероятность, что он останется быстрее и на лёгких, маленьких потоках. Вот почему мы отбрасываем те элементы функции, которые при росте n возрастают медленно, и оставляем только те, что растут сильно. Очевидно, что 4 останется 4 вне зависимости от значения n, а 6n наоборот будет расти. Поэтому первое, что мы сделаем, — это отбросим 4 и оставим только f( n ) = 6n.

Имеет смысл думать о 4 просто как о «константе инициализации». Разным языкам программирования для настройки может потребоваться разное время. Например, Java сначала необходимо инициализировать свою виртуальную машину. А поскольку мы договорились игнорировать различия языков программирования, то попросту отбросим это значение.

Второй вещью, на которую можно не обращать внимания, является множитель перед n. Так что наша функция превращается в f( n ) = n. Как вы можете заметить, это многое упрощает. Ещё раз, константный множитель имеет смысл отбрасывать, если мы думаем о различиях во времени компиляции разных языков программирования (ЯП). «Поиск в массиве» для одного ЯП может компилироваться совершенно иначе, чем для другого. Например, в Си выполнение A[ i ] не включает проверку того, что i не выходит за пределы объявленного размера массива, в то время как для Паскаля она существует. Таким образом, данный паскалевский код:

M := A[ i ]

эквивалентен следующему на Си:

if ( i >= 0 && i < n ) {
    M = A[ i ];
}

Так что имеет смысл ожидать, что различные языки программирования будут подвержены влиянию различных факторов, которые отразятся на подсчёте инструкций. В нашем примере, где мы используем «немой» паскалевский компилятор, игнорирующий возможности оптимизации, требуется по три инструкции на Паскале для каждого доступа к элементу массива вместо одной на Си. Пренебрежение этим фактором идёт в русле игнорирования различий между конкретными языками программирования с сосредоточением на анализе самой идеи алгоритма как таковой.

Описанные выше фильтры — «отбрось все факторы» и «оставляй только наибольший элемент» — в совокупности дают то, что мы называем асимптотическим поведением. Для f( n ) = 2n + 8 оно будет описываться функцией f( n ) = n. Говоря языком математики, нас интересует предел функции f при n, стремящемся к бесконечности. Если вам не совсем понятно значение этой формальной фразы, то не переживайте — всё, что нужно, вы уже знаете. (В сторону: строго говоря, в математической постановке мы не могли бы отбрасывать константы в пределе, но для целей теоретической информатики мы поступаем таким образом по причинам, описанным выше). Давайте проработаем пару задач, чтобы до конца вникнуть в эту концепцию.

Найдём асимптотики для следующих примеров, используя принципы отбрасывания константных факторов и оставления только максимально быстро растущего элемента:

1. f( n ) = 5n + 12 даст f( n ) = n.
   Основания — те же, что были описаны выше
2. f( n ) = 109 даст f( n ) = 1.
   Мы отбрасываем множитель в 109 * 1 , но 1 по-прежнему нужен, чтобы показать, что функция не равна нулю
3. f( n ) = n² + 3n + 112 даст f( n ) = n²
   Здесь n² возрастает быстрее, чем 3n, который, в свою очередь, растёт быстрее 112
4. f( n ) = n³ + 1999n + 1337 даст f( n ) = n³
   Несмотря на большую величину множителя перед n, мы по прежнему полагаем, что можем найти ещё больший n, поэтому f( n ) = n³ всё ещё больше 1999n (см. рисунок выше)
5. f( n ) = n + sqrt( n ) даст f( n ) = n
   Потому что n при увеличении аргумента растёт быстрее, чем sqrt( n )

Упражнение 1

1. f( n ) = n⁶ + 3n
2. f( n ) = 2ⁿ + 12
3. f( n ) = 3ⁿ + 2ⁿ
4. f( n ) = nⁿ + n

Если у вас возникли проблемы с выполнением этого задания, то просто подставьте в выражение достаточно большое n и посмотрите, какой из его членов имеет большую величину. Всё очень просто, не так ли?

Про алгоритмы для новичков

Если вы когда-либо слышали, что алгоритмы нужно знать всем разработчикам, но что это такое представляете с трудом – вам сюда.

Для опытных программистов некоторые понятия, в том числе и алгоритмы, настолько фундаментальны, что не возникает даже мыслей о том, что, то или иное определение может оказаться непонятным, сложным или вообще, пугающим, для новичка.

Алгоритм – вызывает ассоциации ни то с логарифмами, ни то с арифметикой.

И это слово действительно пришло из математики и использовалось для описания алгоритма Евклида, который применяется для нахождения наибольшего общего делителя двух целых чисел.

Если говорить нормальным языком, алгоритм – это пошаговая инструкция, где результат прошлого шага строго определен и используется в качестве входных данных для следующего шага.

Однако, поскольку в реальной жизни при написании программы совсем нечасто нужно искать общий делитель у целых чисел, раскладывать на множители и вообще думать о математиках, творивших в 300-е года до н.э., рассмотрим немного более жизненный пример применения алгоритмов.

Давайте представим, что телефонный справочник все еще актуален (да, тот бумажный, если вы их застали). Допустим, мы хотим набрать Николая Должанского. Принимая во внимание, что Николай есть в телефонном справочнике, мы можем найти его номер несколькими различными способами.

Самый простой способ найти что-то в списке – пройти по нему по порядку, сравнивая с искомым значением. То есть:

1. Надежда Александрова –> не подходит

2. Николай Алексеев –> не подходит

…

И так далее, пока вы не найдете наконец Николая Должанского. Вероятно, понадобятся десятки и даже сотни операций сравнения. То есть, если вы захотите поболтать с Ярославом Яковлевым, то это займет порядком больше времени.

Как вы уже поняли, смысл алгоритма линейного поиска заключается в простом переборе значений от начала списка и до конца (или искомого результата). Это брутфорс. Этот алгоритм крайне прост и может возникнуть множество ситуаций, где его использование будет иметь смысл.

Например, если нужно найти телефон приятеля не в целой книге, а, предположим, на клочке бумаги, где помимо его номера всего десяток других записей – пройти список сверху вниз, в этом случае, будет умным решением.

У большинства людей просто не хватит терпения перебирать весь справочник. Поэтому они пойдут более прагматичным путем – будут разделять книгу на части.

Процесс деления на части предполагает сначала нахождение основной области, где, предположительно, находится искомое значение. Мы тут все еще ищем Николая Должанского.

Поиск начнем, перелистнув книгу на 30 страниц вперед. Мы увидим, что все фамилии начинаются на «Б». Перейдем еще на 60 вперед и увидим «Г». Достоверно известно, что «Г» находится прямо перед «Д», а значит, Коля где-то рядом и с этого момента мы будем двигаться осторожнее.

Этот алгоритм описывает, как большинство людей ищут что-то в справочниках. Но поскольку мы, люди, часто выбираем неоптимальные пути решения задач, рассмотрим правильный подход к делению на части – бинарный алгоритм поиска.

Вот это уже звучит серьезно, да? На самом деле, ничего сложного. Бинарный поиск предполагает, что мы будем делить исходный массив данных пополам, отбрасывать ту часть, где искомого значения быть не может и делить остаток пополам снова, пока область поиска не сократится до минимально возможной.

В терминах телефонной книги, работа будет строиться следующим образом. Наш справочник содержит 400 страниц. Даже если мы все еще ищем Николая Должанского, который находится на 136 странице, мы можем воспользоваться бинарным поиском. Делим книгу пополам и по счастливой случайности попадаем прямо между буквами «М» и «Н» на 199 и 200 страницах соответственно. Мы знаем, что буква «Д» в алфавите находится перед «М», так что справедливо будет утверждение:

Николай Должанский находится на странице между 0 и 199

Ту часть, что начинается с «Н» мы выбрасываем.

Далее, мы делим на две части первые 200 страниц телефонного справочника и видим, что попали мы прямо на страницу с буквой «Г», а «Г», как известно, идет перед «Д». То есть нам снова стал известен неоспоримый факт:

Телефон Николая Должанского находится между 99 и 199 страницами

И вот, стартовав с 400 страниц, мы, всего через две операции сравнения, сократили область поиска на 3/4. Учитывая, что телефон Коли находится на 136 странице, нам предстоит сделать следующие операции:

[99-199] -> [99-149] -> [124-149] -> [124-137] -> [130-137] -> [133-137] -> [135-137] -> [136]

Еще 6 сравнений. Чтобы рассчитать количество операций необходимых для нахождения нужной страницы бинарным поиском, мы можем взять логарифм от количества страниц с основанием 2 и получим:

log2(400) = 8.644

то есть, округлив, в худшем случае – 9 операций сравнения. Рядом с исходным числом страниц, конечно, ерунда. Но давайте поговорим о по-настоящему серьезных книгах. Пусть в нашем справочнике будет не 400, а 4 000 000 страниц. Попробуйте представить, сколько операций сравнения нам потребуется? На самом деле, немного:

log2(4000000) = 21.932

то есть, 22 раза нужно будет провести сравнение частей справочника, прежде, чем 4 000 000 превратятся в 1.

Сравните скорость работы линейного и бинарного алгоритмов поиска для такого количества страниц.

В общем, так и со всеми алгоритмами. Изучение алгоритмов – это изучение способов решать проблемы и задачи наиболее оптимальным путем. Алгоритм – это решение, рассмотренное со всех сторон и преобразованное в эдакий todo-list действий, которые нужно совершить, чтобы воспроизвести его.

И отдельная тема, это преобразование алгоритма в код на конкретном языке, ведь в разных языках алгоритмы (особенно поисковые) могут реализовываться по-разному. Иногда, это может быть уже встроенная в язык функция, которая выдаст нужный результат из массива одной строкой, а где-то понадобиться пара-тройка десятков строк.

И, для примера, вот так будет реализован бинарный поиск на Ruby:

def binary_search(target, list)
  position = (list.count / 2).floor
  mid = list[position]

  return mid if mid == target

  if(mid < target)
    return binary_search(target, list.slice(position + 1, list.count/2))
  else
    return binary_search(target, list.slice(0, list.count/2))
  end
end


puts binary_search(9, [1,2,3,4,5,6,7,8,9,10])

Изучаем алгоритмы: полезные книги, веб-сайты, онлайн-курсы и видеоматериалы

полезные книги, веб-сайты, онлайн-курсы и видеоматериалы

В этой подборке представлен список книг, веб-сайтов и онлайн-курсов, дающих понимание как простых, так и продвинутых алгоритмов.

Воодушевленный awesome-awesomeness и некоторыми другими шикарными библиотеками, я написал список лучших, на мой взгляд, источников для изучения и практики знаний алгоритмов. Если вы хотите поспособствовать развитию списка, пожалуйста, прочтите Гайд по развитию списка.

Веб-сайты, которые вам стоит использовать, чтоб выучить классические алгоритмы:

• A Visual Guide to Graph Traversal Algorithms — Интерактивная визуализация показывает, как работает алгоритм поиска в глубину графа.
• Algomation — Поучительное и анимированное описание алгоритмов.
• Algorithm Visualizer — Тонны анимированых алгоритмов (с кодом, конечно же), можно также создавать свои алгоритмы.
• Algorithms Visualization — Коротенькая статья, посвящённая визуализации алгоритмов.
• Big-O Cheat Sheet — Сложности повседневных алгоритмов, используемых в анализе данных.
• Data Structure Visualizations — Визуализируйте поведение структур данных и делайте операции с ними.
• Geeks for Geeks — Много-много хорошо объяснённых и реализованных алгоритмов.
• Rosetta Code — Хрестоматия по программированию, цель которой — показать использование множества алгоритмов и структур данных в разных языках программирования.
• Sorting Algorithms — Красивые и простые анимации алгоритмов сортировки, не без коротеньких примеров с кодом и их обсуждений.
• Stoimen’s web log — Некоторые алгоритмы, которые очень понятно объяснены.
• VisuAlgo — Визуализация структур данных и алгоритмов посредством анимации.
• Wikipedia — Algorithms — Ко-неч-но-же!
• Wikipedia — Data Structures — А почему бы и нет?

Бесплатные и качественные курсы онлайн:

• Algorithms: Divide and Conquer, Sorting and Searching, and Randomized Algorithms — Основные темы: асимптотика («Большое О(х)»), сортировка и поиск, разделяй и властвуй, а также другие разные алгоритмы.
• Algorithms: Graph Search, Shortest Paths, and Data Structures — Основные темы: структуры данных, графы и их применения.
• Algorithms: Greedy Algorithms, Minimum Spanning Trees, and Dynamic Programming — Основные темы: жадные алгоритмы и динамическое программирование.
• Algorithms: Shortest Paths Revisited, NP-Complete Problems and What To Do About Them — Основные темы: кратчайший путь, NP-полные задачи и что это все значит для разработчика.
• Algorithms, Part 1 — Этот курс затрагивает необходимую информацию об алгоритмах и структурах данных, в которой нуждается каждый программист, который серьезно относится к своему делу. Курс рассказывает о структурах данных, сортировке и алгоритмах поиска.
• Algorithms, Part 2 — Вторая часть курса, которая сфокусирована на жадном алгоритме и динамических парадигмах, а также на NP-полных задачах.
• Khan Academy Algorithms — курс по алгоритмам, созданный Томасом Корменом и Девином Балккомом.
• MIT-6-006 — Хорошо описанные алгоритмы.
• MIT-6-046j — Такой же курс, как и предыдущий, только с другими алгоритмами.
• MIT-6-00sc — Простое и понятное введение в алгоритмы.
• Udacity Intro to Algorithms — Курс по алгоритмам на Python.

Самые популярные книги для изучения алгоритмов:

Англоязычные:

• Algorithm Design — Раскрывает суть решения задач, встречающихся в жизни.
• Algorithms — Решения задач на Java, описание хороших практик ООП и бесплатные онлайн-курсы.
• Data Structures Using C — Примеры использования структур данных.
• Elementary Algorithms — Потрясающая книга об алгоритмах и структурах данных.
• Grokking Algorithms — Книга об алгоритмах и их практических применениях с множеством иллюстраций.
• Introduction to Algorithms — Необходима к прочтению!
• Swift Algorithms and Data Structures — Практическое руководство по теории и коду.
• The Algorithm Design Manual — Книгу легко читать, и она полна примеров из жизни.
• The Art of Computer Programming — Просто хорошая книга.

Русскоязычные:

Новичку

• Алгоритмы на Java — Исчерпывающее толкование структур данных и алгоритмов сортировки, поиска, обработки графов и строк, включая пятьдесят алгоритмов, которые должен знать каждый программист.
• Алгоритмы. Вводный курс — Книга предназначена для всех, кого интересуют вопросы, связанные с компьютерными алгоритмами, но отсутствие времени не позволяет взяться за серьезный труд.
• Карты метро и нейронные сети. Теория графов — Отличная книга для тех, кому не терпится познать такой раздел математики, как Теория графов.
• Дискретная математика для программистов — Основополагающее введение в дискретную математику, без знания которой невозможно успешно заниматься информатикой и программированием.
• Дискретный анализ — Пособие написано по материалам вводного лекционного курса математико-механического факультета Санкт-Петербургского государственного университета.
• Дискретная математика — В этом учебнике изложены все основные разделы дискретной математики и описаны важнейшие алгоритмы на дискретных структурах данных.
• Problem Solving with Algorithms and Data Structures (перевод) — Изложение в книге идёт от простого (что такое алгоритм, как оценить его производительность) к сложному (деревья, графы) с живыми примерами и кодом.
• Алгоритмы — В этой книге подробно разбираются основные методы построения и анализа эффективных алгоритмов.
• Структуры данных и алгоритмы в Java — Помимо простых и ясных примеров, автор приводит небольшую демонстрационную программу, которую можно запустить в веб-браузере.
• Анализ алгоритмов. Вводный курс — Особое внимание уделено алгоритмам параллельной обработки, редко освещаемым в литературе на русском языке.
• Программирование: теоремы и задачи — Книга содержит задачи (с решениями) по программированию различной трудности.
• Алгоритмы. Теория и практическое применение — Из этой книги вы узнаете, где алгоритмы применяются и как их анализировать, чтобы понять их поведение.

Знающему основы для углубленного изучения

Профессионалу

• Теория и практика С++ — Книга посвящена обсуждению сложных вопросов программирования., каких как реализация разреженных массивов, алгоритмы шифрования и сжатия данных, а также проблемы разработки собственных языков программирования и написания интерпретаторов для них.
• Искусство программирования — Эта книга была признана одной из двенадцати лучших физико-математических монографий столетия.
• Алгоритмы. Построение и анализ — Книга удачно объединяет в себе полноту охвата и строгость изложения материала.
• Algolist. Алгоритмы, методы, исходники — Огромный список разнообразных алгоритмов по математике, графике, кодированию, сортировкам, структурам данных, нервным сетям и многому другому.

Реализация большинства классических алгоритмов во многих языках программирования

C

CoffeeScript

C#

C++

Erlang

Go

Java

JavaScript

Objective-C

Python

Ruby

Scala

Swift

Языково-независимые

Онлайн-практика для того, чтоб оттачивать свои навыки:

• ACM-ICPC Live Archive — Сотни задач с предыдущих региональных состязаний ACM-ICPC и мировых состязаний World Finals.
• AIZU ONLINE JUDGE — Японская онлайн практика.
• CodeChef — Больше задач и ежемесячные состязания.
• Codeforces — Единственный сайт, где можно посостязаться в знаниях платформы Web 2.0.
• CodeWars — Веб-сайт, который предлагает задачи по алгоритмам на многих языках и для многих уровней сложности.
• CoderByte — Скромный веб-сайт с задачами на оттачивание алгоритмов для начального и продвинутого уровней. Поддерживает множество популярных языков программирования, таких как С++, Python, JavaScript, Ruby и так далее.
• HackerEarth — Решайте задачи, используя алгоритмы и принимайте участие в решении задач, которые задают при приёме на работу.
• HackerRank — Онлайн практика по известным алгоритмам и функциональном программировании.
• Infoarena — Румынская онлайн-практика. 1500+ задач по алгоритмам.
• LavidaOnlineJudge — Корейская онлайн-практика(около половины на английском) 1300+ задач.
• Learneroo Algorithms Tutorials — Учитесь и практикуйтесь в написании алгоритмов, решая задачи онлайн.
• LeetCode — Выучите алгоритмы и подготовьтесь к интервью.
• PKU JudgeOnline — Китайская онлайн-практика.
• ProjectEuler — Математические задачи, которые могут быть решены с использованием алгоритмов (или даже с помощью карандаша, зависит от того, сколько вы уже знаете).
• Rosalind — Платформа для изучения биоинформатики и программирования, решая задачи.
• ShareCode — Онлайн практика и состязания с множеством задач по алгоритмам.
• Snakify — Вводный курс по Python с 100+ задачами по алгоритмам и отладке (российский).
• SPOJ — Еще больше задач.
• TopCoder — Множество задач по графическому дизайну, анализу данных и разработки в целом.
• URI — Бразильская онлайн-практика. Не так много задач по сравнению с конкурентами, но их база растет, а также у них есть онлайн-состязания.
• UVA — Ещё много задач с предыдущих региональных состязаний ACM-ICPC и мировых состязаний World Finals.

Некоторые инструменты, которые помогут вам в освоении алгоритмов

• flow-chart.js — Иструмент, помогающий вам создавать диаграммы и схемы, которые могут моделировать алгоритмы.
• interactive-coding-challenges — Интерактивные задачки по алгоритмам и структурам данных.

Лицензия
И в интересах авторского лева(материал свободный, и все его изменённые или дополненные формы должны оставаться свободными — прим. переводчика) вот наша лицензия:

Эта работа находится под лицензией Creative Commons Attribution 4.0 International License(ссылка).

Алгоритмы и структуры данных: развернутый видеокурс

Объясняем известные алгоритмы сортировки на пальцах

Изучаем алгоритмы и структуры данных правильно

Любой программист сталкивается с такими понятиями, как алгоритмы и структуры данных. Предлагаем вашему вниманию статью, которая поможет вам освоить столь сложные вещи.

Структуры данных и алгоритмы сложны в изучении. К тому же, их много, взгляните лишь на небольшой список из различных структур данных и алгоритмов: Data Structures and Algorithms.

Так что же делать?

Для освоения данных областей программирования требуются две вещи: понимание и практика. Мы составили для вас список шагов, выполнение которых, мы надеемся, поможет вам на вашем пути.

Как и теория — ничто без практики, так и практика — ничто без теории. Постоянно учиться, читать, поглощать новые знания — всё это без преувеличения является обязанностью любого уважающего себя программиста. Хоть сегодня заучивание алгоритмов не является таким обязательным правилом, каким оно было раньше, знание алгоритмов является хорошим тоном для программиста. Помимо списка, который мы привели в начале данной статьи, советуем обратить ваше внимание на список алгоритмов, полезных для решения олимпиадных задач по программированию.

Чтение книг по теории алгоритмов является также хорошей практикой. Советуем вам обратить внимание на книгу Introduction to Algorithms, которая была издана MIT.

Изучая всё новые алгоритмы и структуры данных, вы начнёте замечать такую тенденцию: чем больше вы учите, тем меньше вы знаете. Чем больше вы знаете, тем больше вам нужно знать дополнительно.

Не стоит сразу браться за реализацию. Сначала убедитесь в том, что вы поняли все аспекты изученного. Попробуйте «стать компьютером», проделывая каждый шаг алгоритма вручную, на бумаге.

Также у нас есть замечательная подборка материалов по алгоритмам, который мы не можем с вами не поделиться.

Данный шаг должен выполняться одновременно с предыдущим. Практика поможет закрепить знания и даст вам умение по-разному оперировать алгоритмом или структурой данных для решения своих задач.

Практиковаться можно, конечно, и по книжке, однако существует целый ряд платформ, которые могут стать вашей площадкой для изучения. Предлагаем вашему вниманию список подобных онлайн-платформ:

• CodeForces (структуры данных). Еженедельные испытания, возможность учиться на решениях других людей, а также постоянное наличие новых задач делает данный ресурс очень интересным для изучения.
• HackerRank (алгоритмы). Ресурс похож на CodeForces: постоянные состязания программистов на скорость или на эффективность решения добавят долю азарта в процесс обучения. Кроме того, мотивацией может являться то, что вы можете даже быть приглашены на работу, используя данную платформу, так как она постоянно мониторится различными IT-компаниями.
• Можно сказать ещё много слов про следующие платформы, но мы ограничимся списком, иначе статья будет слишком длинной: USACO, HackerEarth, TopCoder, SPOJ, CodeChef

Напишите рабочий код, готовый и отлаженный, если необходимо. Вы должны уметь с нуля написать структуру данных или алгоритм, просто глядя на листок бумаги. Если же вы застряли, то, возможно, вы что-то упустили и вам следует вернуться к первому шагу.

Предлагаем вам взглянуть на ряд обучающих ресурсов, которые могут помочь вам в изучении структур данных:

Изучение структур данных — это в первую очередь их понимание, а не просто реализация. Связано это с тем, что манипулирование структурой данных, чтобы она подходила к определённой проблеме, требует от вас понимания принципов работы этой структуры данных. Таким образом, не имеет значения, на каком языке написана структура данных. Вместо этого лучше попытайтесь представить принципы её работы, используя листок бумаги и карандаш.

Признание поражения, решение сдаться — это то, что вставало на пути почти каждого программиста, но только те, у кого хватало силы воли не сдаться, а продолжать, чего-то добились, будучи программистом.

• Читайте код других программистов. Не следует бездумно копировать и вставлять код, лучше попробуйте понять главную идею решения. После этого закройте код и попытайтесь написать своё собственное решение, основываясь на том, что вы только что прочитали, но не смотря на код. Это очень важно, потому что только если у вас получилось решить проблему таким путём, можно точно утверждать, что вы действительно поняли, как всё работает.
• Все задачи, с которыми вы будете сталкиваться как программист, имеют схожие проблемы. Таким образом, во время кропотливой работы с алгоритмами и структурами данных вы научитесь решать проблемы, которые некогда казались вам нерешаемыми.

Есть мнение, что соревнования — лучшая практика. Подобные мероприятия помогут вам научиться лучше контролировать себя в стрессовых ситуациях, а также проверят, насколько хорошо вы знакомы с определённой темой. После каждого соревнования убедитесь, что вы поняли и решели все задачи, которые вы не решили во время соревнования. Это самое главное!

Вы не сможете достичь определённых высот в чём бы то ни было, если это что-то не доставляет вам удовольствия.

Основы программирования. Лекции Proginfo — Сайт преподавателя Гусева Ивана Евгеньевича

Оглавление

Раздел 1. Введение в программирование 5

Тема 1.1. Основы алгоритмизации 5

Лекция№1 Алгоритмы. Свойства и способы описания линейных алгоритмов. 5

Лекция№2 Составные команды (следования, ветвления, цикла) 11

Лекция№3 Команда присваивания. Заголовок алгоритма 16

Лекция№4 Табличные величины, виды таблиц 21

Лекция№5 Вспомогательные алгоритмы Тестирование ПО 27

Тема 1.2. Языки программирования 33

Лекция№6 Языки программирования, их классификация. 33

Лекция»7 Принципы построения ПО. Трансляторы 40

Лекция№ 8 Стадии разработки программного продукта. Этапы решения задач на ПК. 47

Лекция №9 Величины. Типы данных. 52

Раздел 2. Основные конструкции языков программирования 57

Тема 2.1. Операторы языка программирования 57

Лекция№10 Синтаксис языка. Арифметические выражения 57

Лекция№ 11 Ввод и вывод данных. 63

Лекция№ 12 Условный оператор. Оператор выбора. 67

Лекция№13 Циклы с пост и предусловием Цикл с параметром Вложенные циклы 72

Раздел 3. Структурное и модульное программирование 78

Тема 3.1. Процедуры и функции 78

Лекция№14 Общие сведения о подпрограммах Определение и вызов подпрограмм 78

Тема 3.2. Структуризация в программировании 84

Лекция№15 Основы и методы структурного программирования 84

Тема 3.3. Модульное программирование 88

Лекция№16 Понятие и структура модуля. Компиляция и компоновка программы 88

Раздел 4. Структуры данных 92

Тема 4.1. Массивы 92

Лекция №17 Понятие массива. Особенности программирования массивов 92

Тема 4.2. Строки 97

Лекция№18 Символьный и строковый типы. Объявление типов. 97

Лекция№19 Поиск, удаление, замена и добавление символов в строке. 103

Лекция№20 Операции со строками. Функции и процедуры. Решение задач. 108

Тема 4.3. Множества 114

Лекция№21 Понятие и объявление множества. Операции над множествами. 114

Тема 4.4. Записи 121

Лекция№22 Определение типа записи. Правила работы с записями. 121

Тема 4.5. Файлы 125

Лекция№23 Типы файлов. Файлы последовательного доступа. 125

Тема 4.6. Указатели 131

Лекция№ 25. Указатели и применение динамически распределяемой памяти. 131

Тема 4.6 137

Лекция№26. Структуры данных на основе указателей. 137

Раздел 5. Объектно-ориентированное программирование 143

Тема 5.1 Основные принципы объектно-ориентированного программирования (ООП) 143

Лекция№27. Базовые понятия ООП. Основные принципы ООП. 143

Тема 5.1 147

Лекция№28. Классы объектов. Компоненты и их свойства. 147

Тема 5.2 Интегрированная среда разработчика 152

Лекция№29. Интерфейс среды разработчика: основные окна, интегрированной среде 152

Тема 5.3 Этапы разработки приложения 158

Лекция№30. Проектирование, тестирование и отладка приложения. 158

Тема 5.4 Иерархия классов 164

Лекция№31. Классы объектно-ориентированного языка программирования. 164

Лекция№32. Наследование. Перегрузка методов 170

Тема 5.5. Визуальное событийно-управляемое программирование 174

Лекция№33. Основные компоненты интегрированной среды разработки 174

Тема 5.5. 179

Лекция№34. События компонентов Процедуры, определенные пользователем. 179

Тема 5.6. Разработка оконного приложения 183

Лекция№35. Создание интерфейса оконного приложения. Компиляция и запуск приложения. 183

Раздел 1. Введение в программирование 188

Тема 1.1. Основы алгоритмизации 188

Лекция№1 Алгоритмы. Свойства и способы описания линейных алгоритмов. 188

Лекция№2 Составные команды (следования, ветвления, цикла) 193

Лекция№3 Команда присваивания. Заголовок алгоритма 198

Лекция№4 Табличные величины, виды таблиц 203

Лекция№5 Вспомогательные алгоритмы Тестирование ПО 209

Тема 1.2. Языки программирования 215

Лекция№6 Языки программирования, их классификация. 215

Лекция»7 Принципы построения ПО. Трансляторы 221

Лекция№ 8 Стадии разработкт программного продукта. Этапы решения задач на ПК. 227

Лекция №9 Величины. Типы данных. 232

Раздел 2. Основные конструкции языков программирования 238

Тема 2.1. Операторы языка программирования 238

Лекция№10 Синтаксис языка. Арифметические выражения 238

Лекция№ 11 Ввод и вывод данных. 244

Лекция№ 12 Условный оператор. Оператор выбора. 247

Лекция№13 Циклы с пост и предусловием Цикл с параметром Вложенные циклы 253

Раздел 3. Структурное и модульное программирование 259

Тема 3.1. Процедуры и функции 259

Лекция№14 Общие сведения о подпрограммах Определение и вызов подпрограмм 259

Тема 3.2. Структуризация в программировании 265

Лекция№15 Основы и методы структурного программирования 265

Тема 3.3. Модульное программирование 269

Введение в алгоритмы — GeeksforGeeks

Введение в алгоритмы

Что такое алгоритм? Основы алгоритмов

Слово Алгоритм означает «процесс или набор правил, которым необходимо следовать при вычислениях или других операциях по решению проблем». Следовательно, алгоритм относится к набору правил / инструкций, которые шаг за шагом определяют, как должна выполняться работа, чтобы получить ожидаемые результаты.

Это можно понять на примере приготовления нового рецепта. Чтобы приготовить новый рецепт, нужно прочитать инструкции и шаги и выполнить их один за другим в заданной последовательности. В результате получается идеально приготовленное новое блюдо. Точно так же алгоритмы помогают выполнить задачу программирования, чтобы получить ожидаемый результат.
Разработанный алгоритм не зависит от языка, то есть это просто простые инструкции, которые могут быть реализованы на любом языке, и все же результат будет таким же, как и ожидалось.

Каковы характеристики алгоритма?

Поскольку при приготовлении рецепта нельзя следовать никаким письменным инструкциям, а только стандартным. Точно так же не все письменные инструкции по программированию представляют собой алгоритм. Чтобы некоторые инструкции были алгоритмом, он должен иметь следующие характеристики:

• Ясный и однозначный : Алгоритм должен быть четким и однозначным. Каждый его шаг должен быть ясным во всех аспектах и ​​иметь только одно значение.
• Хорошо определенные входы : Если алгоритм требует принимать входные данные, это должны быть четко определенные входы.
• Четко определенные выходы: Алгоритм должен четко определять, какой результат будет получен, и он также должен быть четко определен.
• Конечность: Алгоритм должен быть конечным, то есть он не должен заканчиваться бесконечными циклами и т.п.
• Выполнимо: Алгоритм должен быть простым, универсальным и практичным, чтобы его можно было выполнять при наличии доступных ресурсов.Он не должен содержать какие-то технологии будущего или что-то еще.
• Независимость от языка: Разработанный алгоритм должен быть независимым от языка, то есть это должны быть простые инструкции, которые могут быть реализованы на любом языке, и все же результат будет таким же, как и ожидалось.

Преимущества алгоритмов:

• Это легко понять.
• Алгоритм — это пошаговое представление решения данной проблемы.
• В алгоритме проблема разбита на более мелкие части или шаги, поэтому программисту легче преобразовать ее в реальную программу.

Недостатки алгоритмов:

• Написание алгоритма занимает много времени, поэтому требует много времени.
• Операторы ветвления и цикла трудно отобразить в алгоритмах.

Как разработать алгоритм?

Для написания алгоритма необходимы следующие вещи:

1. Задача , которую должен решить этот алгоритм.
2. ограничивает задачи, которые необходимо учитывать при решении задачи.
3. Вход , который нужно использовать для решения проблемы.
4. Выход следует ожидать, когда проблема будет решена.
5. Решение этой проблемы в заданных ограничениях.

Затем алгоритм записывается с помощью вышеуказанных параметров, так что он решает проблему.
Пример: Рассмотрим пример сложения трех чисел и вывода суммы.

• Шаг 1: Выполнение предварительных условий
  Как обсуждалось выше, для написания алгоритма должны быть выполнены его предварительные условия.
  1. Задача, которую решает этот алгоритм : сложить 3 числа и вывести их сумму.
  2. Ограничения задачи, которые необходимо учитывать при решении задачи : числа должны содержать только цифры и никаких других символов.
  3. Ввод, который необходимо предпринять для решения проблемы: Три числа, которые нужно сложить.
  4. Ожидаемый результат, когда проблема решена: Сумма трех чисел, взятых в качестве входных.
  5. Решение этой проблемы с учетом заданных ограничений: Решение состоит в сложении 3 чисел. Это можно сделать с помощью оператора «+», побитовым или любым другим способом.
• Шаг 2: Разработка алгоритма
  Теперь давайте спроектируем алгоритм с помощью вышеуказанных предварительных условий:
  Алгоритм сложения трех чисел и вывода их суммы:
  1. СТАРТ
  2. Объявите 3 целочисленные переменные num1, num2 и num3.
  3. Возьмите три числа, которые нужно сложить, как входные данные в переменных num1, num2 и num3 соответственно.
  4. Объявите целочисленную переменную sum для хранения итоговой суммы трех чисел.
  5. Сложите 3 числа и сохраните результат в переменной sum.
  6. Вывести значение переменной суммы
  7. КОНЕЦ
• Шаг 3: Тестирование алгоритма путем его реализации.
  Для проверки алгоритма реализуем его на языке Си.

Программа:

C ++

#include с использованием пространства имен std; внутренний основной () { интервал число1, число2, число3; внутр сумма; cout << "Введите 1-е число:" ; cin >> num1; cout << "" << num1 << endl; cout << "Введите 2-е число:" ; cin >> число2; cout << "" << num2 << endl; cout << "Введите 3-е число:" ; cin >> num3; cout << "" << num3; сумма = число1 + число2 + число3; cout << "\ nСумма трех чисел:" << сумма; возврат 0; }

Руководство по алгоритму - основы алгоритма

Предупреждение: TT: undefined function: 32

РУКОВОДСТВО ПО АЛГОРИТМУ И СХЕМА ДАННЫХ

для

СТУДЕНТОВ

(Рави К.Валиа) Ассистент профессора и Incharge Компьютерный и приборный центр Университет садоводства и лесоводства доктора Я. С. Пармара, Науни Солан ИНДИЯ (л.с.)

ПРЕДИСЛОВИЕ

Этот документ подготовлен для студентов Университета садоводства доктора Я. С. Пармара. И лесное хозяйство, Науни, Солан (HP), Индия. Инженер-программист использует различное программирование языки для создания программ. Прежде чем писать программу, сначала нужно найти процедуру для решение проблемы. Программа, написанная без должного предварительного планирования, имеет более высокие шансы ошибки.

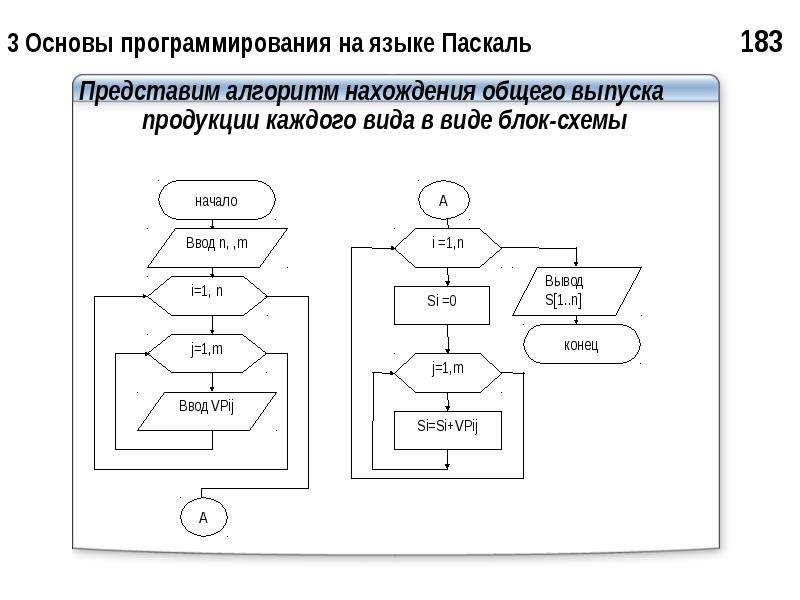
Алгоритм и блок-схема - мощные инструменты для обучения программированию. Алгоритм - это пошаговый анализ процесса, в то время как блок-схема объясняет шаги программы в графический способ. Алгоритм и блок-схемы помогают прояснить все этапы решения проблемы. Новичкам всегда рекомендуется сначала написать алгоритм и нарисовать блок-схему для решение проблемы, а затем только написать программу.

Новичкам сложно написать алгоритм и нарисовать блок-схему.Алгоритм может варьироваться от от человека к человеку, чтобы решить конкретную проблему. Пособие будет полезно студентам для узнать алгоритм и блок-схему. Он включает в себя основы алгоритма и блок-схему, а также количество примеров. Программное обеспечение ClickCharts от NCH (нелицензионная версия) использовалось для нарисуйте все схемы в руководстве.

КАК ЗАПИСАТЬ АЛГОРИТМЫ

Шаг 1 Определите входные данные вашего алгоритма: многие алгоритмы принимают данные для обработки, например для вычисления площади прямоугольника ввода могут быть высота прямоугольника и ширина прямоугольника.

Шаг 2 Определите переменные: переменные алгоритма позволяют использовать его для более чем одного место. Мы можем определить две переменные для высоты прямоугольника и ширины прямоугольника как HEIGHT и ШИРИНА (или H&W). Мы должны использовать осмысленное имя переменной, например вместо использования H&W используйте HEIGHT и WIDTH в качестве имени переменной.

Шаг 3 Опишите операции алгоритма: используйте входную переменную для целей вычисления, например чтобы найти площадь прямоугольника, умножьте переменные HEIGHT и WIDTH и сохраните значение в новая переменная (скажем) AREA.Операции алгоритма могут принимать форму нескольких шагов и четная ветвь, в зависимости от значения входных переменных.

Шаг 4 Выведите результаты работы вашего алгоритма: В случае площади прямоугольника output будет значением, хранящимся в переменной AREA. если входные переменные описывают прямоугольник при ВЫСОТЕ 2 и ШИРИНАХ 3 алгоритм выдаст значение 6.

СХЕМА:

Первый дизайн блок-схемы восходит к 1945 году, он был разработан Джоном фон Нейманом.В отличие от алгоритма, блок-схема использует разные символы для разработки решения проблемы. это еще один широко используемый инструмент программирования. Глядя на блок-схему, можно понять операции и последовательность операций, выполняемых в системе. Блок-схема часто рассматривается в качестве эскиза дизайна, используемого для решения конкретной проблемы.

Преимущества блок-схемы: - Блок-схема - отличный способ передать логику программы. - Легко и эффективно анализировать проблему с помощью блок-схемы.- Во время цикла разработки программы блок-схема играет роль плана, который упрощает процесс разработки программы. - После успешного развития программы она требует постоянного своевременного обслуживания. в процессе его эксплуатации. Блок-схема делает программу или систему обслуживание проще. - Блок-схему легко преобразовать в код любого языка программирования.

Блок-схема представляет собой схематическое / графическое представление последовательности шагов для решения проблема.Для построения блок-схемы используются следующие стандартные символы

.

Символ Название Символ Функция

Овальный

Используется для обозначения начала и конец блок-схемы

параллелограмм Используется для ввода и вывода операция

Прямоугольник

null

Обработка: Используется для арифметические операции и манипуляции с данными

Алмаз

Принятие решения. Привык к представляют собой операцию, в которой есть два / три альтернативы, правда и ложь и т. д.

Стрелки

Проточная линия Используется для индикации поток логики путем соединения символов

Круг Соединитель страниц

Разъем Off Page

null

Предопределенный процесс / функция Используется для представления группа заявлений выполнение одной задачи обработки.

null

Препроцессор | -------------- --------- | | --------------

Комментарии

Логические операторы

Оператор Пример Значение AND A B) Результат истинен, если A> B ложно иначе верно

Заявления о контроле отбора Пример управления выделением Значение ЕСЛИ (условие) Тогда... ENDIF

IF (X> 10) T Y = Y + 5 HEN

ENDIF

Если условие X> 10 истинно, выполнить инструкцию между THEN и ENDIF ЕСЛИ (Условие) Тогда ... ELSE ..... ENDIF

IF (X> 10) THEN Y = Y +

ELSE

Y = Y + 8 Z = Z +

ENDIF

Если условие X> 10 истинно, выполните инструкцию между THEN и ELSE в противном случае выполните инструкции между ELSE и ENDIF

Контроллер контура Пример управления выделением Значение WHILE (Состояние) ДЕЛАТЬ .. .. ENDDO

WHILE (X <10)

DO

печать x x = x + ENDDO

Выполнять цикл, пока условие ИСТИНА

DO

.......

UNTILL (Состояние)

DO

печать x x = x + UNTILL (X> 10)

Выполнять цикл, пока условие ложно

Оператор GO TO, также называемый оператором безусловной передачи управления, используется для передачи контроль исполнения до следующего шага / оператора.. например заявление GOTO n передаст контроль к шагу / оператору n. Примечание. Мы можем использовать ключевое слово INPUT или READ или GET для приема ввода (значений) / значения (значений) и ключевые слова PRINT, WRITE или DISPLAY для вывода результата (ов).

..

Алгоритм и блок-схема для нахождения суммы двух чисел

Алгоритм

Шаг-1 Старт Шаг 2 Введите первые цифры, например A Шаг 3 Введите второе число, скажем B Шаг 4 СУММ = A + B Шаг 5: отображение суммы Шаг-6 Остановка

OR

Алгоритм Шаг-1 Начало Шаг 2 Введите два числа, например A и B Шаг 3 СУММ = A + B Шаг 4: отображение суммы Шаг 5 Остановка

..

Алгоритм и блок-схема для определения площади и периметра квадрата

L: длина стороны квадрата ПЛОЩАДЬ: Площадь ПЕРИМЕТРА: Периметр площади

Алгоритм Шаг-1 Начало Шаг 2 Введите длину стороны квадрата, например L Шаг-3 Площадь = L x L Шаг-4 ПЕРИМЕТР = 4 x L Шаг 5 Отображение ОБЛАСТИ, ПЕРИМЕТРА Шаг-6 Остановка

Алгоритм и блок-схема для определения площади и периметра прямоугольника

L: длина прямоугольника B: Ширина прямоугольника ОБЛАСТЬ: Площадь прямоугольника ПЕРИМЕТР: Периметр прямоугольника

Алгоритм Шаг-1 Начало Шаг 2 Введите длину и ширину стороны, например L, B Шаг-3 Площадь = L x B Шаг-4 ПЕРИМЕТР = 2 x (L + B) Шаг 5 Отображение ОБЛАСТИ, ПЕРИМЕТРА Шаг-6 Остановка

..

Алгоритм и блок-схема для определения площади и периметра окружности

R: Радиус окружности ОБЛАСТЬ: Площадь круга ПЕРИМЕТР: Периметр круга

Алгоритм Шаг-1 Начало Шаг 2 Введите радиус круга, например R Шаг-3 Площадь = 22,0 / 7,0 x R x R Шаг-4 ПЕРИМЕТР = 2 x 22,0 / 7,0 x R Шаг 5 Отображение ОБЛАСТИ, ПЕРИМЕТРА Шаг-6 Остановка

Алгоритм и блок-схема для определения площади и периметра треугольника

(если указаны три стороны)

A: Первая сторона треугольника B: Вторая сторона треугольника C: Третья сторона треугольника ОБЛАСТЬ: Площадь треугольника. ПЕРИМЕТР: Периметр треугольника

.

Алгоритм Шаг-1 Начало Шаг 2: входные стороны треугольника A, B, C Шаг-3 S = (A + B + C) / 2.Шаг 4 ОБЛАСТЬ = КОРЕНЬ (S x (S-A) x (S-B) x (S-C)) Шаг 5 ПЕРИМЕТР = S1 + S2 + S Шаг-6 Отображение ОБЛАСТИ, ПЕРИМЕТРА Шаг-7 Остановка

Начало

Ввод значения R

ПЛОЩАДЬ x R = 22.0 / 7.0 x R

PPR Ein Rt I A M R T E E AR,

Остановка

ПЕРИМТЕР 22,0 / 7,0 x = R 2 X

..

Алгоритм и блок-схема для замены двух чисел с использованием временной переменной

null

Алгоритм Шаг-1 Начало Шаг 2. Введите два числа. Произнесите NUM1, NUM. Шаг 3: Отображение перед заменой значений NUM1, NUM Шаг 4 TEMP = NUM Шаг 5 ЧИСЛО1 = ЧИСЛО Шаг 6 ЧИСЛО2 = ЧИСЛО Шаг-7 Отображение после замены значений NUM1, NUM Шаг-8 Остановка

Алгоритм и блок-схема для замены двух чисел без использования временной

переменной

Алгоритм

Шаг-1 Старт Шаг 2: введите два числа, произнесите A, B Шаг-3 Отображение перед заменой значений A, B Шаг-4 A = A + B Шаг-5 B = A - B Шаг-6 A = A - B Шаг-7 Отображение после обмена значениями A, B Шаг-8 Остановка

..

Алгоритм и блок-схема для поиска наименьшего из двух чисел

Алгоритм

Шаг-1 Старт Шаг 2 Введите два числа, скажем NUM1, NUM Шаг 3, ЕСЛИ ЧИСЛО1 <ЧИСЛО2, ТО печать наименьшего размера - ЧИСЛО ELSE печать наименьшего размера - ЧИСЛО ENDIF Шаг-4 Остановка

Алгоритм и блок-схема для нахождения наибольшего из двух чисел

Алгоритм Шаг-1 Начало Шаг 2 Введите два числа, скажем NUM1, NUM Шаг-3 ЕСЛИ ЧИСЛО1> ЧИСЛО2 ТО максимальный размер печати - NUM ELSE максимальный размер печати - NUM ENDIF Шаг-4 Остановка

Начало

I no p fu NUM1 t V al u e

Ввод значения NUM2

Остановка

NUM1>, если наибольшее число отпечатков NUM2 NUM Самый большой отпечаток НОМ

Да Нет

..

Алгоритм и блок-схема для нахождения наибольшего из трех чисел (другой способ)

Алгоритм Шаг-1 Начало Шаг 2 Прочитайте три цифры, скажем A, B, C Шаг-3 БОЛЬШОЙ = A Шаг 4 ЕСЛИ B> БОЛЬШОЕ ТО БОЛЬШОЙ = B ENDIF Шаг 5, ЕСЛИ C> БОЛЬШОЕ ТО БОЛЬШОЙ = C ENDIF Шаг 6 Напишите БОЛЬШОЙ Шаг-7 Остановка

..

Алгоритм и блок-схема для поиска четного числа от 1 до 50

Алгоритм Шаг-1 Начало Шаг-2 I = 1 Шаг-3 ЕСЛИ (I> 50) ТО ПЕРЕЙТИ К Шагу ENDIF Шаг 4 ЕСЛИ ((I% 2) = 0) ТО Дисплей I ENDIF Шаг-5 I = I + 1 Шаг 6 ПЕРЕЙДИТЕ К Шагу - Шаг-7 Остановка

Алгоритм и блок-схема для поиска нечетных чисел от 1 до n, где n - положительное целое число

Алгоритм Шаг-1 Начало Шаг 2 Введите значение N Шаг-3 I = 1 Шаг 4 ЕСЛИ (I> N) ТО ПЕРЕЙТИ К Шагу ENDIF Шаг 5 ЕСЛИ ((I% 2) = 1) ТО Дисплей I ENDIF Шаг-6 I = I + 1 Шаг 7 ПЕРЕЙДИТЕ К Шагу Шаг-8 Остановка

..

Алгоритм и блок-схема для нахождения суммы ряда 1 - X + X 2 - X 3 .... XN

Алгоритм Шаг-1 Начало Шаг 2 Введите значение N, X Шаг-3 I = 1, SUM = 1, TERM = Шаг 4 ЕСЛИ (I> N) ТО ПЕРЕЙТИ К Шагу ENDIF Шаг 5 TERM = - TERM * X Шаг 6 SUM = SUM + TERM Шаг-7 I = I + 1 Шаг 8 Перейти к шагу Шаг 9 Отображение значения SUM Шаг-10 Остановка

Алгоритм и блок-схема для печати таблицы умножения числа

Алгоритм Шаг-1 Начало Шаг 2 Введите значение NUM Шаг-3 I = 1 Шаг 4 ЕСЛИ (I> 10) ТО ПЕРЕЙДИТЕ К Шагу 9 ENDIF Шаг 5 PROD = NUM ​​* I Шаг 6 ЗАПИШИТЕ I «x» НОМЕР «=» ПРОД Шаг-7 I = I + 1 Шаг 8 Перейти к шагу Шаг-9 Остановка

..

Алгоритм и блок-схема для генерации первых n членов Фибоначчи 0,1,1,2,3,5 ... n (n> 2)

Алгоритм Шаг-1 Начало Шаг 2 Введите значение N Шаг-3 A = 0, B = 1, COUNT = Шаг 4 ЗАПИШИТЕ A, B Шаг 5, ЕСЛИ (COUNT> N), перейдите к шагу 12. Шаг 6 ДАЛЕЕ = A + B Шаг-7 ЗАПИСАТЬ ДАЛЕЕ Шаг-8 A = B Шаг 9 B = ДАЛЕЕ Шаг 10 COUNT = COUNT + 1 Шаг-11 Перейти к шагу- Шаг-12 Остановка

видов алгоритмов RL - документация Spinning Up

Теперь, когда мы ознакомились с основами терминологии и обозначений RL, мы можем охватить немного более богатого материала: ландшафт алгоритмов в современном RL и описание виды компромиссов, которые входят в разработку алгоритмов.

Неполная, но полезная таксономия алгоритмов в современном RL. Цитаты ниже.

Мы начнем этот раздел с заявления об отказе от ответственности: действительно довольно сложно составить точную, всеобъемлющую таксономию алгоритмов в современном пространстве RL, потому что модульность алгоритмов плохо представлена ​​древовидной структурой. Кроме того, чтобы сделать что-то, что уместится на странице и будет приемлемо для восприятия во вводном эссе, мы должны опустить довольно много более сложного материала (исследование, переносное обучение, мета-обучение и т. Д.).Тем не менее, наши цели здесь -

.

• , чтобы выделить наиболее основополагающие варианты дизайна в алгоритмах глубокого RL о том, чему учиться и как этому учиться,
• , чтобы выявить компромиссы в этом выборе,
• и поместить несколько известных современных алгоритмов в контекст с учетом этих вариантов.

без модели против модели на основе RL

Одной из наиболее важных точек ветвления в алгоритме RL является вопрос , имеет ли агент доступ (или изучает) модель среды .Под моделью среды мы подразумеваем функцию, которая прогнозирует переходы между состояниями и вознаграждения.

Основным преимуществом модели является то, что она позволяет агенту планировать , думая наперед, видя, что произойдет с рядом возможных вариантов, и явно выбирая один из вариантов. Затем агенты могут преобразовать результаты заблаговременного планирования в усвоенную политику. Особенно известный пример такого подхода - AlphaZero. Когда это работает, это может привести к существенному повышению эффективности выборки по сравнению с методами, в которых нет модели.

Основным недостатком является то, что базовая модель среды обычно недоступна для агента. Если агент хочет использовать модель в этом случае, он должен изучить модель исключительно на опыте, что создает несколько проблем. Самая большая проблема заключается в том, что предвзятость модели может использоваться агентом, в результате чего агент работает хорошо по сравнению с изученной моделью, но ведет себя неоптимально (или очень ужасно) в реальной среде. Изучение моделей по сути своей сложно, поэтому даже интенсивные усилия - желание потратить много времени и вычислений - могут не окупиться.

Алгоритмы, использующие модель, называются методами на основе модели , а те, которые не используют модель, называются методами без модели . В то время как безмодельные методы исключают потенциальный выигрыш в эффективности выборки от использования модели, их легче реализовать и настроить. На момент написания этого введения (сентябрь 2018 г.) безмодельные методы были более популярными и были более тщательно разработаны и протестированы, чем методы, основанные на моделях.

Чему учиться

Еще одна критическая точка ветвления в алгоритме RL - это вопрос, чему учиться. Список обычных подозреваемых включает

• политики, стохастические или детерминированные,
• функций действия-значения (Q-функции),
• функций значений,
• и / или модели окружающей среды.

Чему учиться в RL без модели

Существует два основных подхода к представлению и обучению агентов с помощью безмодельного RL:

Оптимизация политики. Методы этого семейства явно представляют политику как. Они оптимизируют параметры либо напрямую, увеличивая градиент от целевой производительности, либо косвенно, максимизируя локальные приближения.Эта оптимизация почти всегда выполняется на основе политики , что означает, что каждое обновление использует только данные, собранные при действии в соответствии с самой последней версией политики. Оптимизация политики также обычно включает изучение аппроксиматора для функции значения политики, которая используется при выяснении того, как обновить политику.

Вот несколько примеров методов оптимизации политики:

• A2C / A3C, который выполняет градиентный подъем для непосредственного увеличения производительности,
• и PPO, чьи обновления косвенно максимизируют производительность, вместо этого максимизируя функцию суррогатной цели , которая дает консервативную оценку того, сколько изменений изменится в результате обновления.

Q-Learning. Методы этого семейства изучают аппроксиматор для оптимальной функции значение-действие,. Обычно они используют целевую функцию, основанную на уравнении Беллмана. Эта оптимизация почти всегда выполняется вне политики , что означает, что каждое обновление может использовать данные, собранные в любой момент во время обучения, независимо от того, как агент выбирал для исследования среды при получении данных. Соответствующая политика получается через соединение между и: действия, предпринимаемые агентом Q-Learning, задаются

Примеры методов Q-обучения:

• DQN, классика, которая существенно открыла область глубокого RL,
• и C51, вариант, который изучает распределение по доходности, ожидание которого равно.

Компромисс между оптимизацией политики и Q-Learning. Основная сила методов оптимизации политик заключается в их принципиальности в том смысле, что вы напрямую оптимизируете под то, что хотите. Это делает их стабильными и надежными. Напротив, методы Q-обучения только опосредованно, , оптимизируют производительность агента, обучая удовлетворять уравнению самосогласованности. Для этого типа обучения существует множество режимов отказа, поэтому оно, как правило, менее стабильно.Но методы Q-обучения получают преимущество в том, что они значительно более эффективны в отношении выборки, когда они действительно работают, потому что они могут повторно использовать данные более эффективно, чем методы оптимизации политик.

Интерполяция между оптимизацией политики и Q-Learning. По счастливой случайности, оптимизация политики и Q-обучение не являются несовместимыми (а при некоторых обстоятельствах, оказывается, эквивалентными), и существует ряд алгоритмов, которые находятся между двумя крайностями. Алгоритмы, которые живут в этом спектре, могут тщательно выбирать между сильными и слабыми сторонами любой из сторон.Примеры включают

• DDPG, алгоритм, который одновременно изучает детерминированную политику и Q-функцию, используя одну для улучшения другой,
• и SAC, вариант, который использует стохастические политики, регуляризацию энтропии и несколько других уловок для стабилизации обучения и получения более высоких результатов, чем DDPG в стандартных тестах.

Чему учиться в модельно-ориентированном RL

В отличие от безмодельного RL, для основанного на моделях RL не существует небольшого числа легко определяемых кластеров методов: существует множество ортогональных способов использования моделей.Приведем несколько примеров, но список далеко не исчерпывающий. В каждом случае модель можно либо дать, либо изучить.

Предпосылки: Чистое планирование. Самый простой подход никогда не явно представляет политику, а вместо этого использует чистые методы планирования, такие как управление с прогнозированием модели (MPC), для выбора действий. В MPC каждый раз, когда агент наблюдает за окружающей средой, он вычисляет план, который является оптимальным по отношению к модели, где план описывает все действия по выполнению некоторого фиксированного промежутка времени после настоящего.(Будущие награды за горизонтом могут быть учтены алгоритмом планирования с помощью функции усвоенной ценности.) Затем агент выполняет первое действие плана и немедленно отбрасывает остальную часть. Он вычисляет новый план каждый раз, когда готовится к взаимодействию с окружающей средой, чтобы избежать использования действия из плана с горизонтом планирования короче желаемого.

• Работа MBMF исследует MPC с изученными моделями среды на некоторых стандартных тестовых задачах для глубокого RL.

Эксперт Итерация. Прямое продолжение чистого планирования включает использование и изучение явного представления политики,. Агент использует алгоритм планирования (например, поиск по дереву Монте-Карло) в модели, генерируя возможные действия для плана путем выборки из его текущей политики. Алгоритм планирования производит действие, которое лучше, чем то, что произвела бы сама политика, поэтому он является «экспертом» по отношению к политике. Впоследствии политика обновляется, чтобы произвести действие, больше похожее на результат алгоритма планирования.

• Алгоритм ExIt использует этот подход для обучения глубоких нейронных сетей воспроизведению Hex.
• AlphaZero - еще один пример такого подхода.

Увеличение данных для безмодельных методов. Используйте безмодельный алгоритм RL для обучения политики или Q-функции, но либо 1) дополните реальный опыт фиктивным при обновлении агента, либо 2) используйте только фиктивный опыт для обновления агента.

• См. MBVE для примера дополнения реального опыта вымышленным.
• См. «Модели мира» для примера использования чисто вымышленного опыта для обучения агента, который они называют «обучением во сне».

Встраивание циклов планирования в политики. Другой подход включает процедуру планирования непосредственно в политику в качестве подпрограммы - так что полные планы становятся дополнительной информацией для политики - при обучении выходных данных политики с помощью любого стандартного алгоритма без модели. Ключевой концепцией является то, что в этой структуре политика может научиться выбирать, как и когда использовать планы.Это уменьшает проблему смещения модели, потому что, если модель не подходит для планирования в некоторых состояниях, политика может просто научиться игнорировать ее.

• См. I2A для примера агентов, наделенных этим стилем воображения.

Основы двунаправленного алгоритма Unicode

Что в основном делает алгоритм двунаправленного (двунаправленного) Unicode (Bidi)?

В некоторых старых технологиях, таких как мэйнфреймы и системы iSeries, вы все еще можете встретить текст, хранящийся в визуальном порядке.Для получения дополнительной информации см. Визуальный и логический порядок текста .

С самого начала важно понимать, что во всех основных веб-браузерах порядок символов в памяти (логический) не совпадает с порядком, в котором они отображаются (визуально).

Набор правил, применяемых браузером для создания правильного порядка во время отображения, описывается двунаправленным алгоритмом Unicode Bidirectional Algorithm , или для краткости «алгоритмом двунаправленного текста».

На этой странице представлены основные концепции алгоритма двунаправленного текста.Цель состоит не в том, чтобы рассказать вам, как управлять двунаправленным текстом в вашем приложении, формате и т. Д. (См. Ссылки в нижней части страницы), а в том, чтобы помочь вам понять, как работает двунаправленный аглорифм и где он нужен. Помогите понять эту информацию. Однако мы иногда используем примеры из HTML, чтобы помочь тем, кто знаком с этим языком, связать идеи с практическими приложениями.

Символы и направленный набор

Мы уже знаем, что отображается последовательность латинских символов (т.е.отображается) один за другим слева направо (мы видим что в тексте, который вы сейчас читаете). С другой стороны, алгоритм двунаправленного текста будет отображать последовательность арабских или ивритских символов один за другим справа налево. слева.

Последовательности строго типизированных одинаковых символов направления бегут в ожидаемом направлении. Смотрите живую демонстрацию.

Как ваш браузер узнает, является ли это последовательностью символов слева направо или справа налево? Потому что с каждым символом в Юникоде связано свойство направления.Большинство букв сильно набрал как LTR (слева направо). Буквы в сценариях с письмом справа налево строго типизированы как RTL (справа налево).

Последовательность строго типизированных символов RTL будет отображаться справа налево. Это не зависит от окружающего базового направления.

Направленные трассы

Когда текст с разной направленностью смешивается в строке, алгоритм двунаправленного текста создает отдельный направленный прогон из каждой последовательности смежных символов с одинаковыми направленность.

Итак, в следующем примере есть три направленных участка:

Направленные бега. Смотрите живую демонстрацию.

Обратите внимание, что вам не нужна разметка или стили, чтобы это произошло.

Базовое направление, принципиально важная концепция

Порядок, в котором отображается текст, зависит от основного направления , назначенного фразе, абзацу или блоку, содержащему его. Базовое направление - понятие принципиально важное.Он устанавливает направленный контекст, к которому алгоритм двунаправленного текста обращается в различных точках, чтобы решить, как обрабатывать текст.

В HTML базовое направление либо явно задается ближайшим родительским элементом, который использует атрибут dir , либо, при отсутствии любого такого атрибута, наследуется от направления документа по умолчанию, которое находится слева направо. .

Вот важный бит: порядок, в котором направленные участки отображаются на странице, зависит от преобладающего базового направления .

В приведенном выше примере общий в контексте (т. е. базовое направление) ltr , вы должны прочитать «bahrain», затем «مصر», затем «kuwait».

То же направление работает в контексте LTR. Смотрите живую демонстрацию.

Если вы измените контекст направления в приведенном выше примере, указав, что направление элемента html или родительского элемента, такого как div , p или элемент span , равно rtl , вы изменить порядок направленных пробегов.

То же направление работает в контексте RTL. Смотрите живую демонстрацию.

Символы в обоих случаях сохраняются в памяти в одном и том же порядке, но визуальный порядок направленных пробегов при отображении меняется на обратный.

Нейтральные символы

Пробелы и знаки препинания не строго типизированы как LTR или RTL в Unicode, потому что они могут использоваться в любом типе скрипта. Поэтому они классифицируются как нейтральных или слабых символов.

Символы обычно классифицируются как «слабые», когда они связаны с числами. Небольшое количество знаков пунктуации изначально классифицируются как слабые, но в нечисловом контексте рассматриваются как нейтральные. Вследствие этого в этой статье мы будем называть все знаки препинания нейтральными символами.

Здесь начинается самое интересное. Когда алгоритм двунаправленного текста обнаруживает символы с нейтральными свойствами направления (например, как пробелы и знаки препинания), он решает, как их обрабатывать, глядя на окружающие символы.

Нейтральный символ между двумя строго типизированными символами, имеющими один и тот же тип направленности, также будет предполагать эту направленность . Так что нейтральный символ между двумя символами RTL будет рассматриваться как сам символ RTL и будет иметь эффект , расширяющий направленный пробег . Вот почему три арабских слова в следующем примере читаются справа налево как единый направленный бег - , включая два промежуточных пробела , которые в качестве нейтральных принимают направление окружающих символов.(Стрелки показывают порядок чтения.)

Пробелы, как нейтральные символы, увеличивают направленность бега. Смотрите живую демонстрацию.

Даже если между двумя строго типизированными символами есть несколько нейтральных символов, все они будут обрабатываться одинаково.

Обратите внимание, что для этого вам по-прежнему не нужны разметка или стили. И что здесь все еще есть только три направленных маршрута.

Но что происходит , когда пробел или пунктуация попадают между двумя строго типизированными символами, которые имеют разную направленность , т.е.на границе между направленными пробегами? В таком случае нейтральный персонаж (или символы) будет рассматриваться, как если бы они имели ту же направленность, что и преобладающее базовое направление .

Так, например, если мы добавим запятую после последнего арабского символа в приведенном выше примере, это будет рассматриваться как LTR (направление основного направления) и, следовательно, будет отображаться справа от арабского текста, т.е. как часть правостороннего пробега.

Запятая между пробегами в противоположных направлениях предполагает общий направленный контекст.Смотрите живую демонстрацию.

Пока все хорошо, но это не всегда работает в наших интересах, как мы увидим дальше.

Вложение изменений в базовое направление

Если в предыдущем примере заголовок на арабском языке действительно заканчивался восклицательным знаком, то можно было бы ожидать, что он появится у левого края арабского текста.

Знаки препинания после встроенного текста RTL должны быть слева. Смотрите живую демонстрацию.

К сожалению, по умолчанию так не будет.Восклицательный знак будет обрабатываться так же, как запятая, и окажется в том же месте, т.е. справа от арабского названия.

Чтобы исправить это, нам нужно определить базовое направление арабского текста плюс восклицательный знак справа налево. Тогда восклицательный знак примет направление справа налево и будет рассматриваться как продолжение арабского текста.

Язык разметки или приложение, с которым вы работаете, должны предоставлять механизмы, позволяющие вам это делать (например, использование атрибута dir в элементе q в HTML).Мы обсудим это немного подробнее в разделе «Помимо алгоритма двунаправленного текста» ниже.

Не только изменение основного направления важно в некоторых случаях для обработки знаков препинания на границе направленного прохода, но также важно обеспечить правильный порядок направленных проходов во встроенном двунаправленном тексте. Возьмем, например, следующий пример, где верхняя строка показывает ожидаемый рендеринг, а вторая строка показывает обработку по умолчанию с использованием только алгоритма двунаправленного текста.

Множественные сбои в передаче двунаправленного встроенного текста.Смотрите живую демонстрацию.

Не беспокойтесь о значении здесь слишком много: проблема в том, что в нижней строке, без изменения основного направления для цитаты, направленные пробеги внутри цитаты упорядочиваются слева направо. Опять же, способ решить проблему - переопределить базовое направление цитаты.

Номера

Несколько слов о числах. Числа в сценариях RTL идут слева направо в потоке справа налево, но они обрабатываются алгоритмом двунаправленного текста немного иначе, чем слова.Говорят, что они имеют слабую направленность . Два примера на картинке иллюстрируют эту разницу.

Цифровые цифры идут слева направо, но не прерывают направленных. Смотрите живую демонстрацию.

В первом примере используются европейские цифры «1234», во втором то же число выражается арабско-индийскими цифрами, ١٢٣٤. В обоих случаях цифры в номере читаются слева направо.

Поскольку число набрано слабо, число рассматривается как часть предыдущего арабского текста, поэтому два арабских слова, окружающие число, обрабатываются как часть одного и того же направленного прохода - даже если последовательность цифр запускает LTR на экране.

Обратите внимание, что наряду с числом некоторые нейтральные символы, такие как символы валюты, будут рассматриваться как часть числа, а не как нейтральные. Есть и другие незначительные различия в способах обработки чисел, которые нам не нужно подробно обсуждать здесь.

Зеркальные символы

Вы также обнаружите, что некоторые символы имеют зеркальные формы, в зависимости от направления текста, в котором они находятся.

В приведенном ниже примере во всех случаях используется один и тот же символ угловой скобки, но вы видите, что он указывает вправо в контексте письма слева направо и влево в контексте письма справа налево.

В зависимости от направления текста для одного и того же символа угловой скобки отображаются разные формы. Смотрите живую демонстрацию.

Существует ряд таких символов, многие из которых появляются парами, например, круглые и квадратные скобки, а также некоторые, которые появляются сами по себе. Для такого поведения ничего особенного не требуется.

Необходимо указать базовое направление

Из приведенных выше примеров становится ясно, что необходимо использовать дополнительную разметку, метаданные или специальные подходы, чтобы установить правильное базовое направление для диапазона текста.

Это важно не только для встроенного текста, как показано в примерах выше, но также необходимо установить базовое направление для любого фрагмента текста , чтобы отображать его по мере необходимости. Большинство приложений обрабатывают текст по умолчанию как слева направо, и требуется определенное усилие, чтобы указать, что основное направление должно быть справа налево.

Вот несколько примеров строк обычного текста, которые не отображаются правильно, если нет информации, указывающей, что основное направление - справа налево.

Та же последовательность символов, отображаемая с основным направлением LTR или RTL. Смотрите живую демонстрацию.

Любая строка, которая смешивает текст в более чем одном направлении, требует доступа к информации о том, какое базовое направление должно быть установлено. В этом примере W3C должен отображаться слева от текста. Если по умолчанию используется базовое направление слева направо, оно будет отображаться справа от иврита, что может значительно изменить значение, если не вызовет значительную путаницу.

Другая последовательность символов, отображаемая с основным направлением LTR или RTL. Смотрите живую демонстрацию.

Для любого текста с письмом справа налево с завершающими или начальными знаками препинания также необходимо указать базовое направление. В приведенном выше примере восклицательный знак должен стоять слева от текста с письмом справа налево.

Помимо правильного отображения компонентов строки, обычно необходимо выровнять текст справа налево, а иногда и отразить направление окружающей информации.Подсказки для этого также предоставляются настройкой базового направления.

Часто необходимо изолировать соседние диапазоны

В некоторых случаях необходимо изолировать смежные области текста, чтобы произвести желаемый порядок. Например, рассмотрим второй рейтинг ресторана ниже.

Как это должно выглядеть.

Как это выглядит на самом деле.

Цифры, следующие за текстом RTL в контексте LTR, необходимо изолировать от предыдущего текста.Смотрите живую демонстрацию.

Проблема со вторым названием ресторана возникает из-за того, что браузер считает, что -5 является частью текста на иврите. Это то, что говорит ему алгоритм Unicode Bidi, и обычно это правильно. Но не здесь. Нам нужно найти способ сказать, что имя и номер - это разные вещи, т.е. чтобы отделить вставленное имя от числа.

В следующем примере причина сбоя заключается в том, что при наличии строго типизированного символа письма справа налево (RTL) с обеих сторон двунаправленный алгоритм видит нейтральную запятую как часть арабского текста.Он интерпретирует первые два арабских слова и запятую как однонаправленный переход на арабском языке. Фактически, это часть английского текста, и он должен обозначать границу между двумя отдельными направлениями справа налево на арабском языке.

Элементы того же направления в списке с другим базовым направлением необходимо изолировать. Смотрите живую демонстрацию.

Необходимо некоторое вмешательство, чтобы отделить два арабских слова друг от друга. Алгоритм двунаправленного текста не может решить это самостоятельно.

Статья «Встроенная разметка и двунаправленный текст в HTML» предоставляет информацию о том, как управлять встроенным направлением в HTML, и содержит отработанные примеры. Его сопутствующий документ, Структурная разметка и текст с написанием справа налево в HTML, рассказывает вам, как задать направление для абзацев, блоков, форм и целых страниц.

- Справочник по C ++

библиотека

<алгоритм>

Стандартная библиотека шаблонов: алгоритмы

Заголовок определяет набор функций, специально предназначенных для использования с диапазонами элементов.

Диапазон - это любая последовательность объектов, к которой можно получить доступ через итераторы или указатели, например массив или экземпляр некоторых контейнеров STL. Однако обратите внимание, что алгоритмы работают через итераторы непосредственно со значениями, никоим образом не влияя на структуру любого возможного контейнера (это никогда не влияет на размер или распределение памяти контейнера).

Функции в <алгоритме>

Операции с неизменяемой последовательностью :

all_of

Условия проверки для всех элементов в диапазоне (шаблон функции )

any_of

Проверить, удовлетворяет ли какой-либо элемент в диапазоне условию (шаблон функции )

none_of

Проверить, нет ли элементов, удовлетворяющих условию (шаблон функции )

for_each

Применить функцию к диапазону (шаблон функции )

найти

Найти значение в диапазоне (шаблон функции )

find_if

Найти элемент в диапазоне (шаблон функции )

find_if_not

Найти элемент в диапазоне (отрицательное условие) (шаблон функции )

find_end

Найти последнюю подпоследовательность в диапазоне (шаблон функции )

find_first_of

Найти элемент из набора в диапазоне (шаблон функции )

neighbour_find

Найти равные соседние элементы в диапазоне (шаблон функции )

count

Подсчет появления значений в диапазоне (шаблон функции )

count_if

Возвращает количество элементов в диапазоне, удовлетворяющем условию (шаблон функции )

несоответствие

Возвращает первую позицию, где два диапазона различаются (шаблон функции )

равно

Проверить, равны ли элементы в двух диапазонах (шаблон функции )

is_permutation

Проверить, является ли диапазон перестановкой другого (шаблон функции )

поиск

Диапазон поиска для подпоследовательности (шаблон функции )

search_n

Диапазон поиска элементов (шаблон функции )

Операции изменения последовательности :

копировать

Копировать диапазон элементов (шаблон функции )

copy_n

Копировать элементы (шаблон функции )

copy_if

Копирование определенных элементов диапазона (шаблон функции )

copy_backward

Копировать диапазон элементов назад (шаблон функции )

перемещение

Перемещение диапазона элементов (шаблон функции )

move_backward

Перемещение диапазона элементов назад (шаблон функции )

swap

Обмен значениями двух объектов (шаблон функции )

swap_ranges

Обмен значениями двух диапазонов (шаблон функции )

iter_swap

Обмен значениями объектов, на которые указывают два итератора (шаблон функции )

преобразование

Диапазон преобразования (шаблон функции )

replace

Заменить значение в диапазоне (шаблон функции )

replace_if

Заменить значения в диапазоне (шаблон функции )

replace_copy

Копировать заменяющее значение диапазона (шаблон функции )

replace_copy_if

Копировать заменяющее значение диапазона (шаблон функции )

заполнить

заполнить диапазон значением (шаблон функции )

fill_n

Последовательность заполнения значением (шаблон функции )

генерировать

Генерировать значения для диапазона с функцией (шаблон функции )

generate_n

Сгенерировать значения для последовательности с функцией (шаблон функции )

удалить

Удалить значение из диапазона (шаблон функции )

remove_if

Удалить элементы из диапазона (шаблон функции )

remove_copy

Копировать значение удаления диапазона (шаблон функции )

remove_copy_if

Копировать диапазон удаления значений (шаблон функции )

уникальный

Удалить последовательные дубликаты в диапазоне (шаблон функции )

unique_copy

Копирование диапазона удаления дубликатов (шаблон функции )

реверс

реверс диапазона (шаблон функции )

reverse_copy

Обратный диапазон копирования (шаблон функции )

повернуть

Повернуть влево элементы в диапазоне (шаблон функции )

rotate_copy

Область копирования повернута влево (шаблон функции )

random_shuffle

Произвольно переставить элементы в диапазоне (шаблон функции )

перемешать

Произвольно переставить элементы в диапазоне с помощью генератора (шаблон функции )

Разделы :

is_partitioned

Проверить, разделен ли диапазон (шаблон функции )

раздел

Диапазон разделения пополам (шаблон функции )

stable_partition

Диапазон разделов в два стабильных порядка (шаблон функции )

partition_copy

Разделение диапазона на два (шаблон функции )

partition_point

Получить точку разделения (шаблон функции )

Сортировка :

sort

Сортировка элементов в диапазоне (шаблон функции )

stable_sort

Сортировка элементов с сохранением порядка эквивалентов (шаблон функции )

partial_sort

Частично отсортировать элементы в диапазоне (шаблон функции )

partial_sort_copy

Копирование и частичная сортировка диапазона (шаблон функции )

is_sorted

Проверить, отсортирован ли диапазон (шаблон функции )

is_sorted_until

Найти первый несортированный элемент в диапазоне (шаблон функции )

nth_element

Сортировка элемента в диапазоне (шаблон функции )

Двоичный поиск (работа с секционированными / отсортированными диапазонами):

lower_bound

Вернуть итератор к нижней границе (шаблон функции )

upper_bound

Вернуть итератор к верхней границе (шаблон функции )

equal_range

Получить поддиапазон равных элементов (шаблон функции )

binary_search

Проверить, существует ли значение в отсортированной последовательности (шаблон функции )

Объединить (работает с отсортированными диапазонами):

объединить

Объединить отсортированные диапазоны (шаблон функции )

inplace_merge

Объединение последовательных отсортированных диапазонов (шаблон функции )

включает

Проверить, включает ли отсортированный диапазон другой отсортированный диапазон (шаблон функции )

set_union

Объединение двух отсортированных диапазонов (шаблон функции )

set_intersection

Пересечение двух отсортированных диапазонов (шаблон функции )

set_difference

Разница двух отсортированных диапазонов (шаблон функции )

set_symmetric_difference

Симметричная разность двух отсортированных диапазонов (шаблон функции )

Куча :

push_heap

Вставить элемент в диапазон кучи (шаблон функции )

pop_heap

Извлечь элемент из диапазона кучи (шаблон функции )

make_heap

Сделать кучу из диапазона (шаблон функции )

sort_heap

Сортировка элементов кучи (шаблон функции )

is_heap

Проверить, является ли диапазон кучи (шаблон функции )

is_heap_until

Найти первый элемент не в порядке кучи (шаблон функции )

Мин. / Макс. :

мин.

Вернуть наименьшее (шаблон функции )

max

Вернуть наибольшее значение (шаблон функции )

minmax

Возврат наименьших и наибольших элементов (шаблон функции )

min_element

Возвращает наименьший элемент в диапазоне (шаблон функции )

max_element

Вернуть наибольший элемент в диапазоне (шаблон функции )

minmax_element

Возврат наименьшего и наибольшего элементов в диапазоне (шаблон функции )

Другое :

lexicographic_compare

Лексикографическое сравнение типа «меньше чем» (шаблон функции )

next_permutation

Преобразовать диапазон в следующую перестановку (шаблон функции )

prev_permutation

Преобразовать диапазон в предыдущую перестановку (шаблон функции )

Руководство по разработке алгоритмов

Руководство по разработке алгоритмов

Новый выпуск!

Это недавно расширенное и обновленное третье издание классического бестселлера продолжает раскрывать «загадочность» разработки алгоритмов и анализа их действенности и эффективности.Расширяя первое и второе издания, книга теперь служит основным учебником для курсов по разработке алгоритмов, сохраняя при этом статус главного практического справочника по алгоритмам для программистов, исследователей и студентов.

Удобное для чтения «Руководство по разработке алгоритмов» обеспечивает прямой доступ к технологии комбинаторных алгоритмов, делая упор на дизайн над анализом. Первая часть, «Методы», предоставляет доступную инструкцию по методам проектирования и анализа компьютерных алгоритмов.Вторая часть, Ресурсы, предназначена для просмотра и справки и включает в себя каталог алгоритмических ресурсов, реализаций и обширную библиографию.

---

Полезные ссылки

---

Цитаты

«Мне больше всего нравится такой вид подготовки к собеседованию, как« Руководство по разработке алгоритмов »Стивена Скиены. Больше, чем любая другая книга, оно помогло мне понять, насколько удивительно банальны ... графические проблемы - они должны быть частью набора инструментов каждого работающего программиста.В книге также описаны основные структуры данных и алгоритмы сортировки, что является приятным бонусом. … На каждом пейджере есть простая картинка, чтобы ее было легко запомнить. «
- Стив Йегге - Получите эту работу в Google»:

"Руководство по разработке алгоритмов Стивена Скиены сохраняет свое звание лучшего и наиболее полного практического руководства по алгоритмам, помогающего выявлять и решать проблемы.… Каждый программист должен прочитать эту книгу, и любой, кто работает в этой области, должен держать ее под рукой.… Это это лучшее вложение, которое может сделать программист или начинающий программист."
- Гарольд Тимблби, Times Higher Education

" Замечательно открыть случайное место и открыть для себя интересный алгоритм. Это единственный учебник, который я чувствовал себя обязанным взять с собой после студенческих времен… Цвет действительно добавляет много энергии новому изданию книги! »
- Кори Барт, Университет штата Делавэр

---

Прочая продукция высокого качества

---

От издателя

Это недавно расширенное и обновленное третье издание классического бестселлера продолжает раскрывать «загадочность» разработки алгоритмов и анализа их эффективности.Он служит основным учебным пособием для курсов по разработке алгоритмов и самообучения на собеседовании, сохраняя при этом статус главного практического справочника по алгоритмам для программистов, исследователей и студентов.

Удобное для чтения Руководство по разработке алгоритмов обеспечивает прямой доступ к технологии комбинаторных алгоритмов, делая упор на дизайн над анализом. Первая часть, «Практическое проектирование алгоритмов», предоставляет доступную инструкцию по методам проектирования и анализа компьютерных алгоритмов.Вторая часть, Автостопом по алгоритмам, предназначена для просмотра и справки и включает в себя каталог алгоритмических ресурсов, реализаций и обширную библиографию.

---

Дополнительная информация

Дополнительные материалы можно найти на странице моего курса CSE 373 (Анализ алгоритмов). Видео лекций для моих занятий по Наука о данных, Анализ алгоритмов, Вычислительная биология и многое другое можно найти на Youtube.