Операции с множествами python: Операции над множествами. Программирование на Python

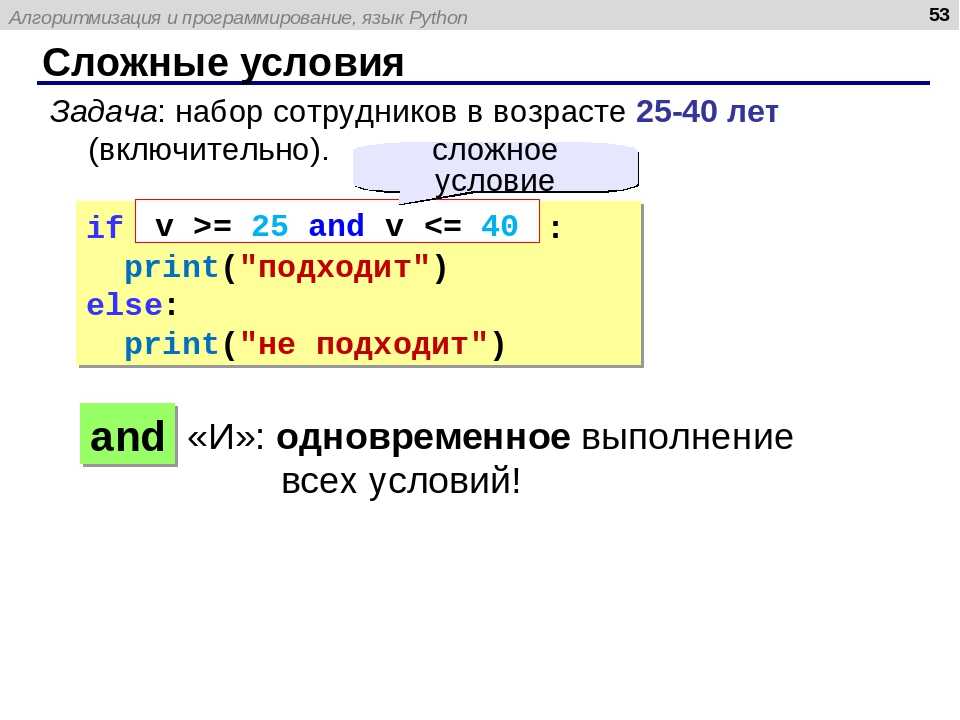
Общие операции с множествами set и frozenset в Python.

Здесь перечислены все доступные операции с неизменяемыми множествами frozenset, с их описанием и примерами использования в коде.

Дополнительно смотрите описание типа frozenset в языке программирования Python.

---

Определение количества элементов в множестве в Python.

Операция len(sets) вернет количество элементов в множестве sets (кардинальное число множества sets). Эта операция поддерживаются как неизменяемыми frozenset, так изменяемыми множествами set.

Проверка вхождения элемента в множество в Python.

Операция x in sets проверяет наличие значения элемента x в множестве sets. Если значение x присутствует в множестве операция вернет True, если нет, то False. Операция x not in sets противоположна.

Метод sets.isdisjoint() в Python, отсутствие элементов в множестве.

Метод sets.isdisjoint() возвращает True, если множество sets не имеет общих элементов с итерируемым объектом other. Итерируемый объект other, это объект поддерживающий итерацию по своим элементам, может быть список, кортеж, другое множество

Метод sets.issubset() в Python, вхождение элементов в множество.

Метод sets.issubset() позволяет проверить находится ли каждый элемент множества sets в последовательности other. Метод возвращает True, если множество sets **является подмножеством** итерируемого объекта other, если нет, т

Проверка множества на правильное подмножество в Python.

Математический оператор < (меньше) позволяет проверить, является ли множество sets подходящим подмножеством другого множества other. Множество меньше другого тогда и только тогда, когда первое множество является правильным подмножеством второго

Метод sets.issuperset() в Python, вхождение элементов в множество.

Метод sets.issuperset() позволяет проверить находится ли каждый элемент последовательности other в множестве sets. Метод возвращает True, если множество sets является надмножеством итерируемого объекта other, если нет, то вернет False.

Проверка множества на правильное надмножество в Python.

Математический оператор > (больше) позволяет проверить, является ли множество sets правильным надмножеством другого множества other, то есть выполняются ли условия sets >= other и set != other.

Метод sets.union() в Python, объединение множеств.

Метод sets.union() позволяет объединить множество с двумя или более последовательностями поддерживающих итерирование. Метод возвращает новое множество с элементами из множества sets и элементами вставленными из всех итерируемых объектов *other.

Метод sets.intersection() в Python, пересечение множеств.

Метод sets.intersection() позволяет найти пересечение множества с одной или более последовательностями поддерживающих итерирование. Метод возвращает новое множество с элементами, общими для множества sets и всех итерируемых объектов *other

Метод sets.difference() в Python, разность множеств.

Метод sets.difference() позволяет получить элементы множества, которых нет в одной или более последовательности поддерживающих итерирование. Метод возвращает новое множество с уникальными элементами множества sets, которых нет

Метод sets.symmetric_difference() в Python, симметричная разница

Метод sets.symmetric_difference() позволяет исключить из результата общие элементы для множества и последовательности, операцию еще называют симметричной разницей.

Метод sets.copy() в Python, копия множества.

Метод sets.copy() вернет мелкую копию множества sets. Эта операция поддерживается как неизменяемым frozenset, так изменяемым множеством set.

Python и теория множеств / Хабр

В Python есть очень полезный тип данных для работы с множествами – это set. Об этом типе данных, примерах использования, и небольшой выдержке из теории множеств пойдёт речь далее.

Следует сразу сделать оговорку, что эта статья ни в коем случае не претендует на какую-либо математическую строгость и полноту, скорее это попытка доступно продемонстрировать примеры использования множеств в языке программирования Python.

• Множество
• Множества в Python
  
  • Хешируемые объекты
• Свойства множеств
  
  • Принадлежность множеству
  • Мощность множества
  • Перебор элементов множества
• Отношения между множествами
  
  • Равные множества
  • Непересекающиеся множества
  • Подмножество и надмножество
• Операции над множествами
  
  • Объединение множеств
  • Добавление элементов в множество
  • Пересечение множеств
  • Разность множеств
  • Удаление элементов из множества
  • Симметрическая разность множеств
• Заключение
• Полезные ссылки

Множество

Множество – это математический объект, являющийся набором, совокупностью, собранием каких-либо объектов, которые называются элементами этого множества. Или другими словами:

Множество – это не более чем неупорядоченная коллекция уникальных элементов.

Что значит неупорядоченная? Это значит, что два множества эквивалентны, если содержат одинаковые элементы.

Элементы множества должны быть уникальными, множество не может содержать одинаковых элементов. Добавление элементов, которые уже есть в множестве, не изменяет это множество.

Множества, состоящие из конечного числа элементов, называются конечными, а остальные множества – бесконечными. Конечное множество, как следует из названия, можно задать перечислением его элементов. Так как темой этой статьи является практическое использование множеств в Python, то я предлагаю сосредоточиться на конечных множествах.

Множества в Python

Множество в Python можно создать несколькими способами. Самый простой – это задать множество перечислением его элементов в фигурных скобках:

fruits = {"banana", "apple", "orange"}

Единственное ограничение, что таким образом нельзя создать пустое множество. Вместо этого будет создан пустой словарь:

wrong_empty_set = {}
print(type(wrong_empty_set))
# Вывод
<class "dict">

Для создания пустого множества нужно непосредственно использовать

set():

correct_empty_set = set()
print(type(correct_empty_set))
# Вывод
<class "set">

Также в set() можно передать какой-либо объект, по которому можно проитерироваться (Iterable):

color_list = ["red", "green", "green", "blue", "purple", "purple"]
color_set = set(color_list)
print(color_set)
# Вывод (порядок может быть другим):
{"red", "purple", "blue", "green"}

Ещё одна возможность создания множества – это использование set comprehension. Это специальная синтаксическая конструкция языка, которую иногда называют абстракцией множества по аналогии с list comprehension (Списковое включение).

numbers = [1, 2, 2, 2, 3, 3, 4, 4, 5, 6]
# Единственное отличие со списковыми включениями - это
# использование фигурных скобок вместо квадратных
even_numbers = {
    number for number in numbers
    if number % 2 == 0
}
print(even_numbers)
# Вывод (порядок может быть другим):
{2, 4, 6}

Хешируемые объекты

Существует ограничение, что элементами множества (как и ключами словарей) в Python могут быть только так называемые хешируемые (Hashable) объекты. Это обусловлено тем фактом, что внутренняя реализация set основана на хеш-таблицах. Например, списки и словари – это изменяемые объекты, которые не могут быть элементами множеств. Большинство неизменяемых типов в Python (int, float, str, bool, и т.д.) – хешируемые. Неизменяемые коллекции, например tuple, являются хешируемыми, если хешируемы все их элементы.

# Множество кортежей (tuple)
records = {
    ("Москва", 17_200_000), 
    ("Санкт-Петербург", 5_400_000), 
    ("Новосибирск", 1_600_000),
    ("Москва", 17_200_000),
}
for city, population in records:
    print(city)
# Вывод (порядок может быть другим):
Москва
Новосибирск
Санкт-Петербург

Объекты пользовательских классов являются хешируемыми по умолчанию. Но практического смысла чаще всего в этом мало из-за того, что сравнение таких объектов выполняется по их адресу в памяти, т.е. невозможно создать два «равных» объекта.

class City:
    def __init__(self, name: str):
        self. name = name
    def __repr__(self) -> str:
        """ Определим метод __repr__ для наглядности следующих примеров
        """
        return f'City("{self.name}")'
print(City("Moscow") == City("Moscow"))
# Вывод:
False
cities = {City("Moscow"), City("Moscow")}
print(cities)
# Вывод
{City("Moscow"), City("Moscow")}

Скорее всего мы предполагаем, что объекты City("Moscow") должны быть равными, и следовательно в множестве cities должен находиться один объект.
Этого можно добиться, если определить семантику равенства для объектов класса

City:

class City:
    def __init__(self, name: str):
        # Атрибут name не должен изменяться, пока объект существует
        # Для простоты пометим этот атрибут как внутренний
        self._name = name
    def __hash__(self) -> int:
        """ Хеш от объекта
        """
        return hash((self._name, self.__class__))
    def __eq__(self, other) -> bool:
        """ Определяем семантику равентсва (оператор ==)
        """
        if not isinstance(other, self. __class__):
            return False
        return self._name == other._name
    def __repr__(self) -> str:
        """ Определим метод __repr__ для наглядности следующих примеров
        """
        return f'City("{self._name}")'

Чтобы протокол хеширования работал без явных и неявных логических ошибок, должны выполняться следующие условия:

• Хеш объекта не должен изменяться, пока этот объект существует
• Равные объекты должны возвращать одинаковый хеш

moscow = City("Moscow")
moscow_again = City("Moscow")
print(moscow == moscow_again and hash(moscow) == hash(moscow_again))
# Вывод:
True
# Теперь множество городов работает более логично и интуитивно
cities = {City("Moscow"), City("Kazan"), City("Moscow")}
print(cities)
# Вывод (порядок может быть другим):
{City("Kazan"), City("Moscow")}

Свойства множеств

Тип set в Python является подтипом Collection (про коллекции), из данного факта есть три важных следствия:

• Определена операция проверки принадлежности элемента множеству
• Можно получить количество элементов в множестве
• Множества являются iterable-объектами

Принадлежность множеству

Проверить принадлежит ли какой-либо объект множеству можно с помощью оператора in.

Это один из самых распространённых вариантов использования множеств. Такая операция выполняется в среднем за O(1) с теми же оговорками, которые существуют для хеш-таблиц.

tremendously_huge_set = {"red", "green", "blue"}
if "green" in tremendously_huge_set:
    print("Green is there!")
else:
    print("Unfortunately, there is no green...")
# Вывод:
Green is there!
if "purple" in tremendously_huge_set:
    print("Purple is there!")
else:
    print("Unfortunately, there is no purple...")
# Вывод:
Unfortunately, there is no purple...

Мощность множества

Мощность множества – это характеристика множества, которая для конечных множеств просто означает количество элементов в данном множестве. Для бесконечных множеств всё несколько сложнее.

even_numbers = {i for i in range(100) if i % 2 == 0}
# Мощность множества
cardinality = len(even_numbers)
print(cardinality)
# Вывод:
50

Перебор элементов множества

Как уже было отмечено выше, множества поддерживают протокол итераторов, таким образом любое множество можно использовать там, где ожидается iterable-объект.

colors = {"red", "green", "blue"}
# Элементы множества можно перебрать с помощью цикла for
for color in colors:
    print(color)
# Вывод (порядок может быть другим):
red
green
blue
# Множества можно использовать там, где ожидается iterable-объект
color_counter = dict.fromkeys(colors, 1)
print(color_counter)
# Вывод (порядок может быть другим):
{"green": 1, "red": 1, "blue": 1}

Отношения между множествами

Между множествами существуют несколько видов отношений, или другими словами взаимосвязей. Давайте рассмотрим возможные отношения между множествами в этом разделе.

Равные множества

Тут всё довольно просто – два множества называются равными, если они состоят из одних и тех же элементов. Как следует из определения множества, порядок этих элементов не важен.

my_fruits = {"banana", "apple", "orange", "orange"}
your_fruits = {"apple", "apple", "banana", "orange", "orange"}
print(my_fruits == your_fruits)
# Вывод:
True

Непересекающиеся множества

Если два множества не имеют общих элементов, то говорят, что эти множества не пересекаются. Или другими словами, пересечение этих множеств является пустым множеством.

even_numbers = {i for i in range(10) if i % 2 == 0}
odd_numbers = {i for i in range(10) if i % 2 == 1}
# Очевидно, что множества чётных и нечётных чисел не пересекаются
if even_numbers.isdisjoint(odd_numbers):
    print("Множества не пересекаются!")
# Вывод:
Множества не пересекаются!

Подмножество и надмножество

Подмножество множества S – это такое множество, каждый элемент которого является также и элементом множества S. Множество S в свою очередь является надмножеством исходного множества.

# Множество чисел Фибоначчи меньших 100
fibonacci_numbers = {0, 1, 2, 3, 34, 5, 8, 13, 21, 55, 89}
# Множество натуральных чисел меньших 100
natural_numbers = set(range(100))
# Множество чисел Фибоначчи является подмножеством множества 
# натуральных чисел
if fibonacci_numbers.issubset(natural_numbers):
    print("Подмножество!")
# Вывод:
Подмножество!
# В свою очередь множество натуральных чисел является
# надмножеством множества чисел Фибоначчи
if natural_numbers.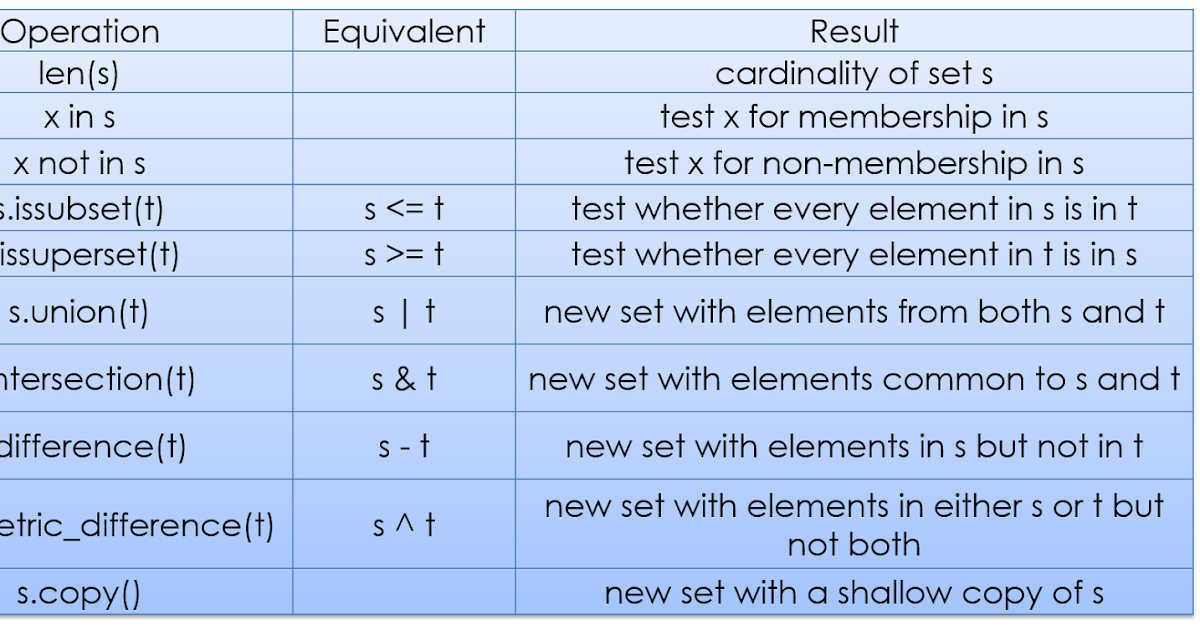 issuperset(fibonacci_numbers):
    print("Надмножество!")
# Вывод:
Надмножество!

Пустое множество является подмножеством абсолютно любого множества.

empty = set()
# Методы issubset и issuperset могут принимать любой iterable-объект
print(
    empty.issubset(range(100))
    and empty.issubset(["red", "green", "blue"])
    and empty.issubset(set())
)
# Вывод:
True

Само множество является подмножеством самого себя.

natural_numbers = set(range(100))
if natural_numbers.issubset(natural_numbers):
    print("Подмножество!")
# Вывод:
Подмножество!

Операции над множествами

Рассмотрим основные операции, опредяляемые над множествами.

Объединение множеств

Объединение множеств – это множество, которое содержит все элементы исходных множеств. В Python есть несколько способов объединить множества, давайте рассмотрим их на примерах.

my_fruits = {"apple", "orange"}
your_fruits = {"orange", "banana", "pear"}
# Для объединения множеств можно использовать оператор `|`,
# оба операнда должны быть объектами типа set
our_fruits = my_fruits | your_fruits
print(our_fruits)
# Вывод (порядок может быть другим):
{"apple", "banana", "orange", "pear"}
# Также можно использовать ментод union. 
# Отличие состоит в том, что метод union принимает не только
# объект типа set, а любой iterable-объект
you_fruit_list: list = list(your_fruits)
our_fruits: set = my_fruits.union(you_fruit_list)
print(our_fruits)
# Вывод (порядок может быть другим):
{"apple", "banana", "orange", "pear"}

Добавление элементов в множество

Добавление элементов в множество можно рассматривать как частный случай объединения множеств за тем исключением, что добавление элементов изменяет исходное множество, а не создает новый объект. Добавление одного элемента в множество работает за O(1).

colors = {"red", "green", "blue"}
# Метод add добаляет новый элемент в множество
colors.add("purple")
# Добавление элемента, который уже есть в множестве, не изменяет
# это множество
colors.add("red")
print(colors)
# Вывод (порядок может быть другим):
{"red", "green", "blue", "purple"}
# Метод update принимает iterable-объект (список, словарь, генератор и т.п.)
# и добавляет все элементы в множество
numbers = {1, 2, 3}
numbers. update(i**2 for i in [1, 2, 3])
print(numbers)
# Вывод (порядок может быть другим):
{1, 2, 3, 4, 9}

Пересечение множеств

Пересечение множеств – это множество, в котором находятся только те элементы, которые принадлежат исходным множествам одновременно.

def is_prime(number: int) -> bool:
    """ Возвращает True, если number - это простое число
    """
    assert number > 1
    return all(number % i for i in range(2, int(number**0.5) + 1))
def is_fibonacci(number: int) -> bool:
    """ Возвращает True, если number - это число Фибоначчи
    """
    assert number > 1
    a, b = 0, 1
    while a + b < number:
        a, b = b, a + b
    return a + b == number
# Множество простых чисел до 100
primes = set(filter(is_prime, range(2, 101)))
# Множество чисел Фибоначчи до 100
fibonacci = set(filter(is_fibonacci, range(2, 101)))
# Множество простых чисел до 100, которые одновременно являются
# числами Фибоначчи
prime_fibonacci = primes.intersection(fibonacci)
# Или используя оператор `&`, который определён для множеств
prime_fibonacci = fibonacci & primes
print(prime_fibonacci)
# Вывод (порядок может быть другим):
{2, 3, 5, 13, 89}

При использовании оператора & необходимо, чтобы оба операнда были объектами типа set. Метод intersection, в свою очередь, принимает любой iterable-объект. Если необходимо изменить исходное множество, а не возращать новое, то можно использовать метод intersection_update, который работает подобно методу intersection, но изменяет исходный объект-множество.

Разность множеств

Разность двух множеств – это множество, в которое входят все элементы первого множества, не входящие во второе множество.

i_know: set = {"Python", "Go", "Java"}
you_know: dict = {
    "Go": 0.4, 
    "C++": 0.6, 
    "Rust": 0.2, 
    "Java": 0.9
}
# Обратите внимание, что оператор `-` работает только
# для объектов типа set
you_know_but_i_dont = set(you_know) - i_know
print(you_know_but_i_dont)
# Вывод (порядок может быть другим):
{"Rust", "C++"}
# Метод difference может работать с любым iterable-объектом,
# каким является dict, например
i_know_but_you_dont = i_know.difference(you_know)
print(i_know_but_you_dont)
# Вывод:
{"Python"}

Удаление элементов из множества

Удаление элемента из множества можно рассматривать как частный случай разности, где удаляемый элемент – это одноэлементное множество. Следует отметить, что удаление элемента, как и в аналогичном случае с добавлением элементов, изменяет исходное множество. Удаление одного элемента из множества имеет вычислительную сложность O(1).

fruits = {"apple", "orange", "banana"}
# Удаление элемента из множества. Если удаляемого элемента
# нет в множестве, то ничего не происходит
fruits.discard("orange")
fruits.discard("pineapple")
print(fruits)
# Вывод (порядок может быть другим):
{"apple", "banana"}
# Метод remove работает аналогично discard, но генерирует исключение,
# если удаляемого элемента нет в множестве
fruits.remove("pineapple")  # KeyError: "pineapple"

Также у множеств есть метод differenсe_update, который принимает iterable-объект и удаляет из исходного множества все элементы iterable-объекта. Этот метод работает аналогично методу difference, но изменяет исходное множество, а не возвращает новое.

numbers = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10}
even_numbers_under_100 = (i for i in range(1, 101) if i % 2 == 0)
numbers. , также существует два специальных метода – symmetric_difference и symmetric_difference_update. Оба этих метода принимают iterable-объект в качестве аргумента, отличие же состоит в том, что symmetric_difference возвращает новый объект-множество, в то время как symmetric_difference_update изменяет исходное множество.
non_positive = {-3, -2, -1, 0}
non_negative = range(4)
non_zero = non_positive.symmetric_difference(non_negative)
print(non_zero)
# Вывод (порядок может быть другим):
{-1, -2, -3, 1, 2, 3}
# Метод symmetric_difference_update изменяет исходное множество
colors = {"red", "green", "blue"}
colors.symmetric_difference_update(["green", "blue", "yellow"])
print(colors)
# Вывод (порядок может быть другим):
{"red", "yellow"}

Заключение
Я надеюсь, мне удалось показать, что Python имеет очень удобные встроенные средства для работы с множествами. На практике это часто позволяет сократить количество кода, сделать его выразительнее и легче для восприятия, а следовательно и более поддерживаемым. Я буду рад, если у вас есть какие-либо конструктивные замечания и дополнения.

Полезные ссылки
Множества (Статья на Википедии)
Документация по типу set
Iterable-объекты (Глоссарий Python)
Hashable-объекты (Глоссарий Python)
Sets in Python
Set Theory: the Method To Database Madness
 Наборы в Python — GeeksforGeeks 
 Набор в программировании на Python — это неупорядоченный тип данных коллекции, который является итерируемым, изменяемым и не имеет повторяющихся элементов.
 Набор представлен { } (значения заключены в фигурные скобки). набор. Это основано на структуре данных, известной как хеш-таблица. Поскольку множества неупорядочены, мы не можем обращаться к элементам с помощью индексов, как в списках.
 Пример наборов Python 
 Python3 
  var   =   {   "Гики"
0,900 для"   ,   "Гики"   } 
  type   (var) 
  Вывод: 
 set 
 Time Сложность: O(1) 
 Тип 9005 Вспомогательное пространство: O(1) Установить метод
 Метод Python set() используется для приведения типов.
 Python3 
  myset   =   набор   ([   "a" 0 9 , 0020  ,   "с"   ]) 
  print   (myset) 
  
  myset.add(   "d"   ) 
  print 30  0 (myset)
  Вывод: 
 Набор Python — это неупорядоченный тип данных, что означает, что мы не можем знать, в каком порядке хранятся элементы набора.
 {'в', 'б', 'а'}
{'d', 'c', 'b', 'a'} 
 Временная сложность: O(n) 
 Вспомогательный пробел: O(n)
 Проверить уникальность и неизменяемость с помощью Python Set 
 Наборы Python не могут иметь повторяющееся значение, и после его создания мы не можем изменить его значение.
 Python3 
55  Вывод: 
 Первый код объясняет, что набор не может иметь дубликатов ценить. Каждый элемент в нем является уникальным значением.
 Второй код генерирует ошибку, поскольку мы не можем присвоить или изменить значение после создания набора. Мы можем только добавлять или удалять элементы в наборе.
 {'Гики', 'для'}
TypeError: объект 'set' не поддерживает назначение элементов 
 Гетерогенный элемент с набором Python 
 Наборы Python могут хранить в себе гетерогенные элементы, т. е. набор может хранить смесь строковых, целых, логических и т. д. типов данных.
 Python3 
  
  myset   =   {   "Гики"   ,   "для"   ,   9 } 0003
  печать   (мой набор) 
  
  myset[   1   ]   =   "Привет" 
  печать   (myset) 
 
  myset   =   {   "Гики"   ,   "для"   ,   10    ,
 0
 ,   Правда   } 
  печать   ( myset) 
  Вывод: 
 {Истина, 10, 'Geeks', 52.7, 'for' 
 Временная сложность: O(n) 900:0103 Вспомогательное пространство) 0 Питон заморожен Наборы
  Наборы Frozen  в Python — это неизменяемые объекты, которые поддерживают только те методы и операторы, которые производят результат, не затрагивая замороженный набор или наборы, к которым они применяются. Это можно сделать с помощью метода Frozenset() в Python.
 Хотя элементы набора можно изменить в любое время, элементы замороженного набора остаются неизменными после создания.
 Если параметры не переданы, возвращается пустой замороженный набор.
 Python 
  
  normal_set   =   набор   ([  "а"   ,   "б"   ,   "с"   0) 2  
  печать   (   "Обычный набор "   ) 
  печать   (обычный_набор) 
  
  замороженный_набор   =   замороженный [0
0набор 9 0  "е"  ,   "ф"  ,  " г"   ]) 
  
  print   (   "\nFrozen Set"   ) 
 9 print 0 0
  
  Выход: 
 Обычный набор
{'а', 'в', 'б'}
Замороженный набор
{'e', 'g', 'f'} 
 Временная сложность: O(n) 
 Вспомогательное пространство: O(n)
 Внутренняя работа Set 
 Это основано на структуре данных, известной как хеш-таблица. . Если несколько значений присутствуют в одной и той же позиции индекса, то значение добавляется к этой позиции индекса для формирования связанного списка.
 В Python Sets реализованы с использованием словаря с фиктивными переменными, где ключевыми являются члены, установленные с большей оптимизацией временной сложности.
  Реализация набора: 
  
 Наборы с многочисленными операциями над одной HashTable:
  
 Методы для наборов 
 функция , где создается соответствующее значение записи для сохранения в хеш-таблице. То же, что и при проверке элемента, т. е. в среднем O(1). Однако в худшем случае может стать 
 О(н)  .
 Python3 
  человек   =   {   "Джей"  9   ,   "Архи"   } 
  
  печать   (   "Люди:"   , конец   =   " "   ) 
  печать 
 0 0 (люди) 2  
  чел. доп(   "Daxit"   ) 
  
  для   i   в   диапазон  
0 (
0 019 ,   6   ): 
         чел.добавить( i) 
  
  print   (   "\nУстановить после добавления элемента:"   , end   =   "2 0 "  )
  печать   (люди) 
  Вывод: 
 Люди: {'Идриш', 'Арчи', 'Джей'}
Установить после добавления элемента: {1, 2, 3, 4, 5, 'Идриш', 'Арчи', 'Джей', 'Даксит'} 
 Временная сложность: O(n) 
 Вспомогательное пространство: O(n)
 Операция объединения на наборах Python 
 Два набора можно объединить с помощью функции union() или | оператор. Доступ к обоим значениям хеш-таблицы и их обход осуществляется с помощью операции слияния, выполняемой над ними для объединения элементов, в то же время дубликаты удаляются. Временная сложность этого  O(len(s1) + len(s2))  где s1 и s2 — два набора, объединение которых необходимо выполнить.
 Python3 
  человек   =   {   "Джей"  9   ,   "Арчил"   } 
  вампиры   =   {   "Каран"   ,   "Арджун"   } 
  Дракула 9Население 0  people.union(vampires) 
  
  print   (   "Объединение с использованием функции union()"   ) 
  print   (население) 
  
  население 
90 =  0 =  0 
  
  print   (   "\nОбъединение с помощью оператора '|'"   ) 
  print  4  (население) 90 4 90 90 90 0046
  Вывод: 
 Объединение с использованием union() функция
{'Каран', 'Идриш', 'Джей', 'Арджун', 'Арчил'}
Союз с использованием '|' оператор
{'Deepanshu', 'Idrish', 'Jay', 'Raju', 'Archil'} 
 Временная сложность: O(n) 
 Вспомогательное пространство: O(n)
 Операция пересечения на наборах Python 
 Это можно сделать с помощью оператора cross() или &. Выбраны общие элементы. Они аналогичны перебору списков хешей и объединению одних и тех же значений в обеих таблицах. Временная сложность этого O(min(len(s1), len(s2)) где s1 и s2 — два набора, объединение которых необходимо выполнить.  набор   () 
  набор2   =   набор   () 
  
  для   i   в диапазоне     (  9  5 ): 0
         set1.add(i) 
  
  для   i   в диапазоне     (   3   ,   9   ): 
 9 00018  набор2.добавить(i) 
  
  набор3   =   set1. intersection(set2) 
  
  print   (   "Пересечение с использованием функции crosse()"   )
30 
30   (набор3) 
  
  set3   =   set1 & set2 
  
  print   (   "\nПересечение с помощью оператора '&' 
 )
 19 печать   (set3) 
  Вывод: 
 Пересечение с использованием функции crosse()
{3, 4}
Пересечение с использованием оператора '&'
{3, 4} 
 Временная сложность: O(n) 
 Вспомогательный пробел: O(n)
 Поиск различий наборов в Python
 Чтобы найти различия между наборами. Аналогично поиску различий в связанном списке. Это делается через разницу() или – оператор. Временная сложность поиска разницы s1 – s2 равна O(len(s1))
 Python3 
  
  набор1   =   набор   ()  
  набор  =   набор   () 
  
  для   i   в диапазоне     (   5   ): 
         set1.add(i) 
0 3
2 
2 8   и   в   диапазон   (   3   ,   9   ): 
         3 900 900
  набор3   =   набор1.разница(набор2) 
  
  печать   (   "Разность двух наборов с использованием функции разность()"   ) 
  печать   (набор3) 0 0030 9 3
  комплект3   =   set1   -   set2 
  
  print   (   "\nРазность двух наборов) с помощью оператора 9002 9000   03
  печать   (набор3) 
  Вывод: 
 Разница двух наборов с использованием функции разность()
{0, 1, 2}
Разница двух наборов с помощью оператора «-»
{0, 1, 2} 
 Временная сложность: O(n) 
 Вспомогательное пространство: O(n)
 Очистка наборов Python
 Метод Set Clear() очищает весь набор на месте.
 Python3
  set1   =   {   1  2
 , 20 ,   3  ,   4  ,   5  ,   6   } 
  
  печать   (   "Исходный набор"   ) 
  печать   (набор1) 
  
  набор1.clear() 
  
0 печать  9 0019 "\nУстановить после использования функции clear()"   ) 
  print   (set1) 
  Вывод: 
 Исходный набор
{1, 2, 3, 4, 5, 6}
Установить после использования функции clear()
set() 
 Временная сложность: O(n) 
 Вспомогательное пространство: O(n)
  Однако в наборах Python есть две основные ловушки: 
 Набор не поддерживает элементы в каком-либо определенном порядке.
 В набор Python можно добавлять только экземпляры неизменяемых типов.
 Временная сложность наборов 
 Операция
 Средний случай
 Наихудший случай
 примечания
 О(1)
 О(н)
  
 Union s|t
 O(len(s)+len(t))
  
  
 Пересечение s&t
 O(min(len 14), 9 04(t), 0len(s)) (len(s) * len(t))
 заменить «min» на «max», если t не является набором ) где l равно max(len(s1),..,len(sn))
  
 Разность s-t
 O(len(s))
  
  
 Операторы для наборов 
 Наборы и фиксированные наборы поддерживают следующие операторы:
 s > 1 4
 Операторы
 919 5 9081  16
 ключ вставлен s
 проверка герметичности
 ключ не вставлен s
 проверка отсутствия содержания
 s1 == s2
 s1 эквивалентно s2
 s1 != s2
 s2 9 не эквивалентно s20044
 s1 <= s2
 s1 является подмножеством s2
 s1 < s2
 s1 является правильным подмножеством s2
6
 s1 является надмножеством s2
 s1 > s2
 s1 является надмножеством s2
 s1 | s2
 объединение s1 и s2
 s1 & s2
 пересечение s1 и s2
 s1 – s2
 но не s1 набор элементов в0044
 s1 ˆ s2
 набор элементов ровно в одном из s1 или s2
  Последние статьи о Python Set. 
 
 Python Set 
 Предыдущий
 Следующий
 Набор — это изменяемый набор различных хэшируемых объектов, таких же, как список и кортеж.
 Это неупорядоченный набор объектов, что означает, что он не записывает позицию элемента или порядок вставки и поэтому не может получить доступ к элементам с помощью индексов.
 Набор представляет собой реализацию Python набора в математике. Объект набора имеет подходящие методы для выполнения математических операций с наборами, таких как объединение, пересечение, разность и т. д.
 Объект набора содержит один или несколько элементов, не обязательно одного типа, разделенных запятой и заключенных в фигурные скобки {}.
 Следующее определяет объект набора с четными номерами.
 even_nums = {2, 4, 6, 8, 10} # набор четных чисел
emp = {1, 'Стив', 10.5, True} # набор различных объектов
 
 Набор не хранит повторяющиеся объекты. Даже если объект добавляется в фигурные скобки более одного раза, в заданном объекте сохраняется только одна копия.
 Следовательно, операции индексации и нарезки не могут выполняться для заданного объекта.
 >>> числа = {1, 2, 2, 3, 4, 4, 5, 5}
>>> числа
{1, 2, 3, 4, 5}
 
 Порядок элементов в наборе не обязательно совпадает с порядком, заданным во время присваивания.
 Python оптимизирует структуру множества для выполнения операций над ним, как это определено в математике.
 Только неизменяемые (и хэшируемые) объекты могут быть частью заданного объекта. Числа (целые, с плавающей запятой, а также комплексные), строки и объекты кортежей принимаются, но объекты наборов, списков и словарей не принимаются.
 >>> myset = {(10,10), 10, 20} # допустимо
>>> мойсет
{10, 20, (10, 10)}
>>> myset = {[10, 10], 10, 20} # не могу добавить список
Traceback (последний последний вызов):
  Файл "", строка 1, в 
    набор = {[10, 10], 10, 20}
TypeError: unhashable type: 'list'
>>> myset = {{10, 10}, 10, 20} # нельзя добавить набор
Traceback (последний последний вызов):
  Файл "", строка 1, в 
    набор = {{10, 10}, 10, 20}
TypeError: unhashable type: 'set'
 
 В приведенном выше примере  (10,10)  — это кортеж, следовательно, он становится частью набора. Однако  [10,10]  — это список, поэтому отображается сообщение об ошибке, в котором говорится, что список нельзя хэшировать.
 (Хеширование — это механизм в информатике, который позволяет быстрее искать объекты в памяти компьютера.)
 Несмотря на то, что изменяемые объекты не хранятся в наборе, сам набор является изменяемым объектом.
 Используйте функцию set() для создания пустого набора. Пустые фигурные скобки создадут пустой словарь вместо пустого множества.
 >>> emp = {} # создает пустой словарь
>>> тип (эмп)
<класс 'дикт'>
>>> s = set() # создает пустой набор
>>> тип(ы)
<класс 'набор'>
 
 Функция set() также используется для преобразования объекта строки, кортежа или словаря в объект набора, как показано ниже.
 >>> s = set('Hello') # преобразует строку в набор
>>> с
{'л', 'ч', 'о', 'е'}
>>> s = set((1,2,3,4,5)) # преобразует кортеж в набор
>>> с
{1, 2, 3, 4, 5}
>>> d = {1: "Один", 2: "Два"}
>>> s = set(d) # преобразует dict в set
>>> с
{1, 2}
 
 Изменить элементы набора 
 Используйте встроенные функции набора методов add(), remove() или update() для изменения набора наборов.
 >>> s = set() # создает пустой набор
>>> s.add(10) # добавить элемент
>>> с.доп(20)
>>> с.доп(30)
>>> с
{10, 20, 30}
>>> PrimeNums = {2, 3, 5, 7}
>>> s.update(primeNums) # обновить набор другим набором
>>> с
{2, 3, 20, 5, 7, 10, 30}
>>> s.remove(2) # удалить элемент
>>> с
{3, 20, 5, 7, 10, 30}
 9выполнять операции объединения, пересечения, разности и симметричной разности соответственно. У каждого из этих операторов есть соответствующий метод, связанный со встроенным классом set. 

         
 
 
 

                            Операция
                         
                         

                            Пример
                         
                     
 
 
 
 

                              Union:  Возвращает новый набор с элементами из обоих наборов. 
  Оператор:  | 
  Метод:  set.union()
                         
 
                         

 
 >>> с1={1,2,3,4,5}
>>> с2={4,5,6,7,8}
>>> с1|с2
{1, 2, 3, 4, 5, 6, 7, 8} 
 >>> с1={1,2,3,4,5}
>>> с2={4,5,6,7,8}
>>> s1. union(s2)
{1, 2, 3, 4, 5, 6, 7, 8}
>>> s2.union(s1)
{1, 2, 3, 4, 5, 6, 7, 8} 
  Пересечение:  Возвращает новый набор, содержащий элементы, общие для обоих наборов.
  Оператор:  и 
  Метод:  set.intersection()
 >>> с1={1,2,3,4,5}
>>> с2={4,5,6,7,8}
>>> с1 и с2
{4, 5}
>>> с2 и с1
{4, 5} 
 >>> с1={1,2,3,4,5}
>>> с2={4,5,6,7,8}
>>> s1.intersection(s2)
{4, 5}
>>> s2.intersection(s1)
{4, 5} 
  Отличие:  Возвращает набор, содержащий элементы только из первого набора, но не из второго набора.
  Оператор  : - 
  Метод:  set.difference()
 >>> с1={1,2,3,4,5}
>>> с2={4,5,6,7,8}
>>> с1-с2
{1, 2, 3}
>>> с2-с1
{8, 6, 7} 
 >>> с1={1,2,3,4,5}
>>> с2={4,5,6,7,8}
>>> s1. difference(s2)
{1, 2, 3}
>>> s2.difference(s1)
{8, 6, 7} 9с1
{1, 2, 3, 6, 7, 8} 
 >>> с1={1,2,3,4,5}
>>> с2={4,5,6,7,8}
>>> s1.symmetric_difference(s2)
{1, 2, 3, 6, 7, 8}
>>> s2.symmetric_difference(s1)
{1, 2, 3, 6, 7, 8} 
 Установить методы 
 В следующей таблице перечислены встроенные методы установки:
 Метод
 Описание
 установить.добавить()
 Добавляет элемент в набор. Если элемент уже существует в наборе, он не добавляет этот элемент.
 установить.очистить()
 Удаляет все элементы из набора.
 set.copy()
 Возвращает поверхностную копию набора.
 set.difference()
 Возвращает новый набор с уникальными элементами, которых нет в другом наборе, переданном в качестве параметра.
 set.difference_update()
 Обновляет набор, для которого вызывается метод, элементами, общими для другого набора, переданного в качестве аргумента.
 set.discard()
 Удаляет определенный элемент из набора.
 set.intersection()
 Возвращает новый набор с элементами, общими для заданных наборов.
 set. intersection_update()
 Обновляет набор, для которого вызывается метод instersection_update(), с общими элементами среди указанных наборов.
 set.isdisjoint()
 Возвращает true, если заданные множества не имеют общих элементов. Множества не пересекаются тогда и только тогда, когда их пересечение является пустым множеством.
 set.issubset()
 Возвращает true, если набор (для которого вызывается issubset()) содержит все элементы другого набора, переданного в качестве аргумента.
 set.pop()
 Удаляет и возвращает случайный элемент из набора.
 установить.удалить()
 Удаляет указанный элемент из набора. Если указанный элемент не найден, возникает ошибка.
 Оставить комментарий
Добавить комментарий Отменить ответ
Ваш адрес email не будет опубликован. Обязательные поля помечены *
Комментарий *
Имя * 
Email * 
Сайт