Коды шифрования – Онлайн калькулятор: Шифр Виженера

Содержание

Онлайн калькулятор: Шифр Виженера

Так как Шифр Цезаря у нас уже есть, было бы логично дополнить его калькулятором, который шифрует/расшифровывает текст используя шифр Виженера.

Суть алгоритма шифрования проста. Шифр Виженера — это последовательность шифров Цезаря с различными значениями сдвига (ROTX — см. Шифр Цезаря). То есть к первой букве текста применяется преобразование, например, ROT5, ко второй, например, ROT17, и так далее. Последовательность применяемых преобразований определяется ключевой фразой, в которой каждая буква слова обозначает требуемый сдвиг, например, фраза ГДЕ ОН задает такую последовательность шифров Цезаря: ROT3-ROT4-ROT5-ROT15-ROT14, которая повторяется, пока не будет зашифрован весь текст сообщения.

Как повествует Википедия, шифр Виженера является шифром подстановки, то есть шифром, в котором каждая буква исходного текста заменяется буквой шифр-текста. Для вскрытия подобных шифров используется частотный криптоанализ.

Еще там можно прочитать про вариант шифра с бегущим ключом (running key), который был когда-то был невзламываемым. Этот вариант заключается в использовании в качестве ключа блока текста, равного по длине исходному тексту. Впрочем, и этот вариант, как оказалось, успешно поддается взлому. Проблема с бегущим ключом шифра Виженера состоит в том, что криптоаналитик имеет статистическую информацию о ключе (учитывая, что блок текста написан на известном языке) и эта информация будет отражаться в шифрованном тексте. Если ключ действительно случайный, его длина равна длине сообщения и он использовался единожды, то шифр Виженера теоретически будет невзламываемым, но такие системы уже относятся к классу систем

одноразового кода, или одноразового шифр-блокнота (one-time pad). Они действительно не поддаются взлому, однако их практическое применение довольно затруднительно.

Шифр Виженера

АлфавитАнглийскийИспанскийРусскийРусский (без ё)Квадрат Виженера начинается сROT0 («a» преобразуется в «а»)ROT1 («а» преобразуется в «б») Карл у Клары украл кораллыПреобразование
Преобразованный текст

save Сохранить share Поделиться extension Виджет
planetcalc.ru
NoZDR — Шифры замены

В шифрах замены (или шифрах подстановки), в отличие от перестановочных шифров, элементы текста не меняют свою последовательность, а изменяются сами, т.е. происходит замена исходных букв на другие буквы или символы (один или несколько) по неким правилам.
На этой страничке описаны шифры, в которых замена происходит на буквы или цифры. Когда же замена происходит на какие-то другие не буквенно-цифровые символы, на комбинации символов или рисунки, это называют прямым кодированием.
Моноалфавитные шифры
В шифрах с моноалфавитной заменой каждая буква заменяется на одну и только одну другую букву/символ или группу букв/символов. Если в алфавите 33 буквы, значит есть 33 правила замены: на что менять А, на что менять Б и т.д.

Такие шифры довольно легко расшифровать даже без знания ключа. Делается это при помощи частотного анализа зашифрованного текста — надо посчитать, сколько раз каждая буква встречается в тексте, и затем поделить на общее число букв. Получившуюся частоту надо сравнить с эталонной. Самая частая буква для русского языка — это буква О, за ней идёт Е и т.д. Правда, работает частотный анализ на больших литературных текстах. Если текст маленький или очень специфический по используемым словам, то частотность букв будет отличаться от эталонной, и времени на разгадывание придётся потратить больше. Ниже приведена таблица частотности букв (то есть относительной частоты встречаемых в тексте букв) русского языка, рассчитанная на базе НКРЯ.

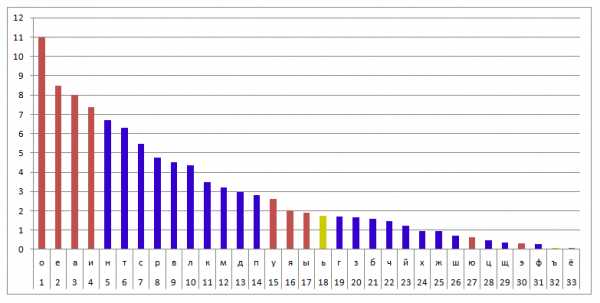
Использование метода частотного анализа для расшифровки шифрованных сообщений красиво описано во многих литературных произведениях, например, у Артура Конана Дойля в романе «Пляшущие человечки» или у Эдгара По в «Золотом жуке».
Составить кодовую таблицу для шифра моноалфавитной замены легко, но запомнить её довольно сложно и при утере восстановить практически невозможно, поэтому обычно придумывают какие-то правила составления таких кодовых страниц. Ниже приведены самые известные из таких правил.
Случайный код
Как я уже писал выше, в общем случае для шифра замены надо придумать, какую букву на какую надо заменять. Самое простое — взять и случайным образом перемешать буквы алфавита, а потом их выписать под строчкой алфавита. Получится кодовая таблица. Например, вот такая:
Число вариантов таких таблиц для 33 букв русского языка = 33! ≈ 8.683317618811886*10³⁶. С точки зрения шифрования коротких сообщений — это самый идеальный вариант: чтобы расшифровать, надо знать кодовую таблицу. Перебрать такое число вариантов невозможно, а если шифровать короткий текст, то и частотный анализ не применишь.

Но для использования в квестах такую кодовую таблицу надо как-то по-красивее преподнести. Разгадывающий должен для начала эту таблицу либо просто найти, либо разгадать некую словесно-буквенную загадку. Например, отгадать ключевое слово или решить лабиринт-алфавит.
Ключевое слово
Один из вариантов составления кодовой таблицы — использование ключевого слова. Записываем алфавит, под ним вначале записываем ключевое слово, состоящее из неповторяющихся букв, а затем выписываем оставшиеся буквы. Например, для слова «манускрипт» получим вот такую таблицу:
Как видим, начало таблицы перемешалось, а вот конец остался неперемешенным. Это потому, что самая «старшая» буква в слове «манускрипт» — буква «У», вот после неё и остался неперемешенный «хвост». Буквы в хвосте останутся незакодированными. Можно оставить и так (так как большая часть букв всё же закодирована), а можно взять слово, которое содержит в себе буквы А и Я, тогда перемешаются все буквы, и «хвоста» не будет.

Само же ключевое слово можно предварительно тоже загадать, например при помощи ребусов или рамок. Например, вот так:
Разгадав арифметический ребус-рамку и сопоставив буквы и цифры зашифрованного слова, затем нужно будет получившееся слово вписать в кодовую таблицу вместо цифр, а оставшиеся буквы вписать по-порядку. Получится вот такая кодовая таблица:
Атбаш
Изначально шифр использовался для еврейского алфавита, отсюда и название. Слово атбаш (אתבש) составлено из букв «алеф», «тав», «бет» и «шин», то есть первой, последней, второй и предпоследней букв еврейского алфавита. Этим задаётся правило замены: алфавит выписывается по порядку, под ним он же выписывается задом наперёд. Тем самым первая буква кодируется в последнюю, вторая — в предпоследнюю и т.д.

Фраза «ВОЗЬМИ ЕГО В ЭКСЕПШН» превращается при помощи этого шифра в «ЭРЧГТЦ ЪЬР Э ВФНЪПЖС».
Онлайн-калькулятор шифра Атбаш
ROT1
Этот шифр известен многим детям. Ключ прост: каждая буква заменяется на следующую за ней в алфавите. Так, A заменяется на Б, Б на В и т.д., а Я заменяется на А. «ROT1» значит «ROTate 1 letter forward through the alphabet» (англ. «поверните/сдвиньте алфавит на одну букву вперед»). Сообщение «Хрюклокотам хрюклокотамит по ночам» станет «Цсялмплпубн цсялмплпубнйу рп опшбн». ROT1 весело использовать, потому что его легко понять даже ребёнку, и легко применять для шифрования. Но его так же легко и расшифровать.
Онлайн-калькулятор всех русских РОТ-шифров
Шифр Цезаря
Шифр Цезаря — один из древнейших шифров. При шифровании каждая буква заменяется другой, отстоящей от неё в алфавите не на одну, а на большее число позиций. Шифр назван в честь римского императора Гая Юлия Цезаря, использовавшего его для секретной переписки. Он использовал сдвиг на три буквы (ROT3). Шифрование для русского алфавита многие предлагают делать с использованием такого сдвига:

Я всё же считаю, что в русском языке 33 буквы, поэтому предлагаю вот такую кодовую таблицу:
Интересно, что в этом варианте в алфавите замены читается фраза «где ёж?» 🙂
Но сдвиг ведь можно делать на произвольное число букв — от 1 до 33. Поэтому для удобства можно сделать диск, состоящий из двух колец, вращающихся относительно друг друга на одной оси, и написать на кольцах в секторах буквы алфавита. Тогда можно будет иметь под рукой ключ для кода Цезаря с любым смещением. А можно совместить на таком диске шифр Цезаря с атбашем, и получится что-то вроде этого:

Собственно, поэтому такие шифры и называются ROT — от английского слова «rotate» — «вращать».

ROT5
В этом варианте кодируются только цифры, остальной текст остаётся без изменений. Производится 5 замен, поэтому и ROT5: 0↔5, 1↔6, 2↔7, 3↔8, 4↔9.
ROT13
ROT13 — это вариация шифра Цезаря для латинского алфавита со сдвигом на 13 символов. Его часто применяют в интернете в англоязычных форумах как средство для сокрытия спойлеров, основных мыслей, решений загадок и оскорбительных материалов от случайного взгляда.
Латинский алфавит из 26 букв делится на две части. Вторая половина записывается под первой. При кодировании буквы из верхней половины заменяются на буквы из нижней половины и наоборот.
ROT18
Всё просто. ROT18 — это комбинация ROT5 и ROT13 🙂
ROT47
Существует более полный вариант этого шифра — ROT47. Вместо использования алфавитной последовательности A–Z, ROT47 использует больший набор символов, почти все отображаемые символы из первой половины
ASCII-таблицы. При помощи этого шифра можно легко кодировать url, e-mail, и будет непонятно, что это именно url и e-mail 🙂
Например, ссылка на этот текст http://nozdr.ru/games/quest/crypt/cipher/zamena?&#rot47 зашифруется вот так: 9EEAi^^?@K5C]CF^82>6D^BF6DE^4CJAE^4:A96C^K2>6?2nURC@Ecf. Только опытный разгадывальщик по повторяющимся в начале текста двойкам символов сможет додуматься, что 9EEAi^^ может означать HTTP:⁄⁄.
Квадрат Полибия
Полибий — греческий историк, полководец и государственный деятель, живший в III веке до н.э. Он предложил оригинальный код простой замены, который стал известен как «квадрат Полибия» (англ. Polybius square) или шахматная доска Полибия. Данный вид кодирования изначально применялся для греческого алфавита, но затем был распространен на другие языки. Буквы алфавита вписываются в квадрат или подходящий прямоугольник. Если букв для квадрата больше, то их можно объединять в одной ячейке.
Такую таблицу можно использовать как в шифре Цезаря. Для шифрования на квадрате находим букву текста и вставляем в шифровку нижнюю от неё в том же столбце. Если буква в нижней строке, то берём верхнюю из того же столбца. Для кириллицы можно использовать таблицу РОТ11 (аналог шифра Цезаря со сдвигом на 11 символов):
Буквы первой строки кодируются в буквы второй, второй — в третью, а третьей — в первую.
Но лучше, конечно, использовать «фишку» квадрата Полибия — координаты букв:
Под каждой буквой кодируемого текста записываем в столбик две координаты (верхнюю и боковую). Получится две строки. Затем выписываем эти две строки в одну строку, разбиваем её на пары цифр и используя эти пары как координаты, вновь кодируем по квадрату Полибия.
Можно усложнить. Исходные координаты выписываем в строку без разбиений на пары, сдвигаем на нечётное количество шагов, разбиваем полученное на пары и вновь кодируем.
Квадрат Полибия можно создавать и с использованием кодового слова. Сначала в таблицу вписывается кодовое слово, затем остальные буквы. Кодовое слово при этом не должно содержать повторяющихся букв.
Вариант шифра Полибия используют в тюрьмах, выстукивая координаты букв — сначала номер строки, потом номер буквы в строке.
Стихотворный шифр
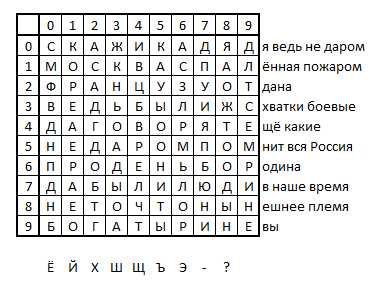
Этот метод шифрования похож на шифр Полибия, только в качестве ключа используется не алфавит, а стихотворение, которое вписывается построчно в квадрат заданного размера (например, 10×10). Если строка не входит, то её «хвост» обрезается. Далее полученный квадрат используется для кодирования текста побуквенно двумя координатами, как в квадрате Полибия. Например, берём хороший стих «Бородино» Лермонтова и заполняем таблицу. Замечаем, что букв Ё, Й, Х, Ш, Щ, Ъ, Э в таблице нет, а значит и зашифровать их мы не сможем. Буквы, конечно, редкие и могут не понадобиться. Но если они всё же будут нужны, придётся выбирать другой стих, в котором есть все буквы.

РУС/LAT
Наверное, самый часто встречающийся шифр 🙂 Если пытаться писать по-русски, забыв переключиться на русскую раскладку, то получится что-то типа этого: Tckb gsnfnmcz gbcfnm gj-heccrb? pf,sd gthtrk.xbnmcz yf heccre. hfcrkflre? nj gjkexbncz xnj-nj nbgf ‘njuj^ Ну чем не шифр? Самый что ни на есть шифр замены. В качестве кодовой таблицы выступает клавиатура.

Таблица перекодировки выглядит вот так:
Литорея
Литорея (от лат. littera — буква) — тайнописание, род шифрованного письма, употреблявшегося в древнерусской рукописной литературе. Известна литорея двух родов: простая и мудрая. Простая, иначе называемая тарабарской грамотой, заключается в следующем. Если «е» и «ё» считать за одну букву, то в русском алфавите остаётся тридцать две буквы, которые можно записать в два ряда — по шестнадцать букв в каждом:
Получится русский аналог шифра ROT13 — РОТ16 🙂 При шифровке верхнюю букву меняют на нижнюю, а нижнюю — на верхнюю. Ещё более простой вариант литореи — оставляют только двадцать согласных букв:
Получается шифр РОТ10. При шифровании меняют только согласные, а гласные и остальные, не попавшие в таблицу, оставляют как есть. Получается что-то типа «словарь → лсошамь» и т.п.
Мудрая литорея предполагает более сложные правила подстановки. В разных дошедших до нас вариантах используются подстановки целых групп букв, а также числовые комбинации: каждой согласной букве ставится в соответствие число, а потом совершаются арифметические действия над получившейся последовательностью чисел.
Шифрование биграммами
Шифр Плейфера
Шифр Плейфера — ручная симметричная техника шифрования, в которой впервые использована замена биграмм. Изобретена в 1854 году Чарльзом Уитстоном. Шифр предусматривает шифрование пар символов (биграмм), вместо одиночных символов, как в шифре подстановки и в более сложных системах шифрования Виженера. Таким образом, шифр Плейфера более устойчив к взлому по сравнению с шифром простой замены, так как затрудняется частотный анализ.
Шифр Плейфера использует таблицу 5х5 (для латинского алфавита, для русского алфавита необходимо увеличить размер таблицы до 6х6), содержащую ключевое слово или фразу. Для создания таблицы и использования шифра достаточно запомнить ключевое слово и четыре простых правила. Чтобы составить ключевую таблицу, в первую очередь нужно заполнить пустые ячейки таблицы буквами ключевого слова (не записывая повторяющиеся символы), потом заполнить оставшиеся ячейки таблицы символами алфавита, не встречающимися в ключевом слове, по порядку (в английских текстах обычно опускается символ «Q», чтобы уменьшить алфавит, в других версиях «I» и «J» объединяются в одну ячейку). Ключевое слово и последующие буквы алфавита можно вносить в таблицу построчно слева-направо, бустрофедоном или по спирали из левого верхнего угла к центру. Ключевое слово, дополненное алфавитом, составляет матрицу 5х5 и является ключом шифра.
Для того, чтобы зашифровать сообщение, необходимо разбить его на биграммы (группы из двух символов), например «Hello World» становится «HE LL OW OR LD», и отыскать эти биграммы в таблице. Два символа биграммы соответствуют углам прямоугольника в ключевой таблице. Определяем положения углов этого прямоугольника относительно друг друга. Затем руководствуясь следующими 4 правилами зашифровываем пары символов исходного текста:
1) Если два символа биграммы совпадают, добавляем после первого символа «Х», зашифровываем новую пару символов и продолжаем. В некоторых вариантах шифра Плейфера вместо «Х» используется «Q».
2) Если символы биграммы исходного текста встречаются в одной строке, то эти символы замещаются на символы, расположенные в ближайших столбцах справа от соответствующих символов. Если символ является последним в строке, то он заменяется на первый символ этой же строки.
3) Если символы биграммы исходного текста встречаются в одном столбце, то они преобразуются в символы того же столбца, находящимися непосредственно под ними. Если символ является нижним в столбце, то он заменяется на первый символ этого же столбца.
4) Если символы биграммы исходного текста находятся в разных столбцах и разных строках, то они заменяются на символы, находящиеся в тех же строках, но соответствующие другим углам прямоугольника.
Для расшифровки необходимо использовать инверсию этих четырёх правил, откидывая символы «Х» (или «Q») , если они не несут смысла в исходном сообщении.
Рассмотрим пример составления шифра. Используем ключ «Playfair example», тогда матрица примет вид:
Зашифруем сообщение «Hide the gold in the tree stump». Разбиваем его на пары, не забывая про правило [1]. Получаем: «HI DE TH EG OL DI NT HE TR EX ES TU MP». Далее применяем правила [2]-[4]:
1. Биграмма HI формирует прямоугольник, заменяем её на BM.
2. Биграмма DE расположена в одном столбце, заменяем её на ND.
3. Биграмма TH формирует прямоугольник, заменяем её на ZB.
4. Биграмма EG формирует прямоугольник, заменяем её на XD.
5. Биграмма OL формирует прямоугольник, заменяем её на KY.
6. Биграмма DI формирует прямоугольник, заменяем её на BE.
7. Биграмма NT формирует прямоугольник, заменяем её на JV.
8. Биграмма HE формирует прямоугольник, заменяем её на DM.
9. Биграмма TR формирует прямоугольник, заменяем её на UI.
10. Биграмма EX находится в одной строке, заменяем её на XM.
11. Биграмма ES формирует прямоугольник, заменяем её на MN.
12. Биграмма TU находится в одной строке, заменяем её на UV.
13. Биграмма MP формирует прямоугольник, заменяем её на IF.
Получаем зашифрованный текст «BM ND ZB XD KY BE JV DM UI XM MN UV IF». Таким образом сообщение «Hide the gold in the tree stump» преобразуется в «BMNDZBXDKYBEJVDMUIXMMNUVIF».
Двойной квадрат Уитстона
Чарльз Уитстон разработал не только шифр Плейфера, но и другой метод шифрования биграммами, который называют «двойным квадратом». Шифр использует сразу две таблицы, размещенные по одной горизонтали, а шифрование идет биграммами, как в шифре Плейфера.
Имеется две таблицы со случайно расположенными в них русскими алфавитами.
Перед шифрованием исходное сообщение разбивают на биграммы. Каждая биграмма шифруется отдельно. Первую букву биграммы находят в левой таблице, а вторую букву — в правой таблице. Затем мысленно строят прямоугольник так, чтобы буквы биграммы лежали в его противоположных вершинах. Другие две вершины этого прямоугольника дают буквы биграммы шифртекста. Предположим, что шифруется биграмма исходного текста ИЛ. Буква И находится в столбце 1 и строке 2 левой таблицы. Буква Л находится в столбце 5 и строке 4 правой таблицы. Это означает, что прямоугольник образован строками 2 и 4, а также столбцами 1 левой таблицы и 5 правой таблицы. Следовательно, в биграмму шифртекста входят буква О, расположенная в столбце 5 и строке 2 правой таблицы, и буква В, расположенная в столбце 1 и строке 4 левой таблицы, т.е. получаем биграмму шифртекста ОВ.
Если обе буквы биграммы сообщения лежат в одной строке, то и буквы шифртекста берут из этой же строки. Первую букву биграммы шифртекста берут из левой таблицы в столбце, соответствующем второй букве биграммы сообщения. Вторая же буква биграммы шифртекста берется из правой таблицы в столбце, соответствующем первой букве биграммы сообщения. Поэтому биграмма сообщения ТО превращается в биграмму шифртекста ЖБ. Аналогичным образом шифруются все биграммы сообщения:
Сообщение ПР ИЛ ЕТ АЮ _Ш ЕС ТО ГО
Шифртекст ПЕ ОВ ЩН ФМ ЕШ РФ БЖ ДЦ
Шифрование методом «двойного квадрата» дает весьма устойчивый к вскрытию и простой в применении шифр. Взламывание шифртекста «двойного квадрата» требует больших усилий, при этом длина сообщения должна быть не менее тридцати строк, а без компьютера вообще не реально.
Полиалфавитные шифры
Шифр Виженера
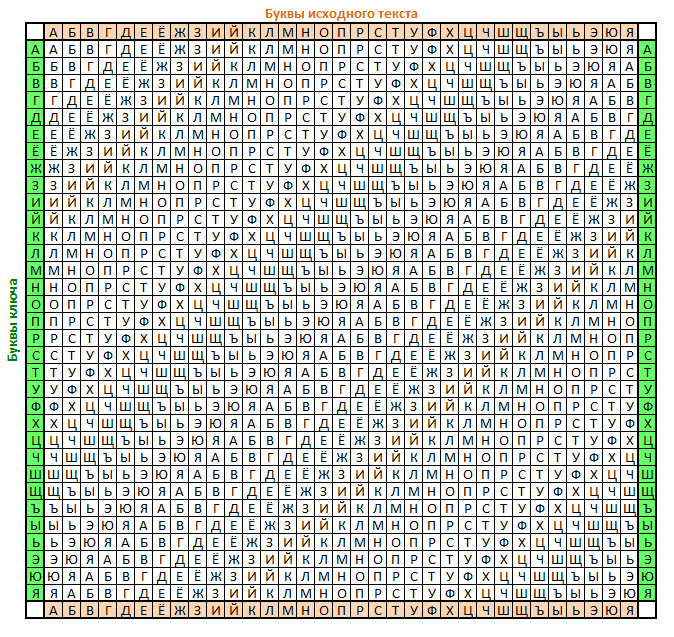
Естественным развитием шифра Цезаря стал шифр Виженера. В отличие от моноалфавитных это уже полиалфавитный шифр. Шифр Виженера состоит из последовательности нескольких шифров Цезаря с различными значениями сдвига. Для зашифровывания может использоваться таблица алфавитов, называемая «tabula recta» или «квадрат (таблица) Виженера». На каждом этапе шифрования используются различные алфавиты, выбираемые в зависимости от буквы ключевого слова.
Для латиницы таблица Виженера может выглядеть вот так:

Для русского алфавита вот так:

Легко заметить, что строки этой таблицы — это ROT-шифры с последовательно увеличивающимся сдвигом.
Шифруют так: под строкой с исходным текстом во вторую строку циклически записывают ключевое слово до тех пор, пока не заполнится вся строка. У каждой буквы исходного текста снизу имеем свою букву ключа. Далее в таблице находим кодируемую букву текста в верхней строке, а букву кодового слова слева. На пересечении столбца с исходной буквой и строки с кодовой буквой будет находиться искомая шифрованная буква текста.
Важным эффектом, достигаемым при использовании полиалфавитного шифра типа шифра Виженера, является маскировка частот появления тех или иных букв в тексте, чего лишены шифры простой замены. Поэтому к такому шифру применить частотный анализ уже не получится.
Для шифрования шифром Виженера можно воспользоваться Онлайн-калькулятором шифра Виженера. Для различных вариантов шифра Виженера со сдвигом вправо или влево, а также с заменой букв на числа можно использовать приведённые ниже таблицы:

Шифр Гронсвельда
Это вариация шифра Виженера, где вместо ключевого слова применяется ключевое число, цифры которого показывают, какой из ROT-шифров применять (на сколько позиций сдвигать букву).
Книжный шифр
Суть метода книжного шифра — это выбор любого текста из книги, и замена каждой буквы шифруемого слова номером слова в выбранном тексте, начинающегося на нужную букву. Можно заменять не на номер слова, а на координату буквы (строка, номер в строке). При этом одной исходной букве может соответствовать несколько разных кодов, ведь одна и та же буква может находиться в разных местах. Для кодирования обычно используют страницу из какой-то заранее оговоренной книги. Без знания кодовой страницы расшифровать такие зашифрованные послания практически невозможно.
Можно использовать не конкретное издание, а какой-то классический текст, который не менялся от одного издания к другому. Например, стихотворную поэму Пушкина «Гавриилиада» или Декларацию независимости США.
Если же в качестве ключа использовать целую книгу (например, словарь), то можно зашифровывать не отдельные буквы, а целые слова и даже фразы. Тогда координатами слова будут номер страницы, номер строки и номер слова в строке. На каждое слово получится три числа. Можно также использовать внутреннюю нотацию книги — главы, абзацы и т.п. Например, в качестве кодовой книги удобно использовать Библию, ведь там есть четкое разделение на главы, и каждый стих имеет свою маркировку, что позволяет легко найти нужную строку текста. Правда, в Библии нет современных слов типа «компьютер» и «интернет», поэтому для современных фраз лучше, конечно, использовать энциклопедический или толковый словарь. Хотя если заранее договориться о некой применяемой фене, например, «смоковница» — это «компьютер», «грех» — это «байт» и т.п., то на основании Библии можно будет шифровать и современные тексты.

Это были шифры замены, в которых буквы заменяются на другие. А ещё бывают перестановочные шифры, в которых буквы не заменяются, а перемешиваются между собой.
Разное

games/quest/crypt/cipher/zamena.txt · Последние изменения: 2019/07/17 14:50 — NoZDR
nozdr.ru
5 интересных систем шифрования. Разгадайте секретные слова | Конкурсы и тесты
В этот день свой профессиональный праздник отмечает Криптографическая служба России.

«Криптография» с древнегреческого означает «тайнопись».
Как раньше прятали слова?

Своеобразный метод передачи тайного письма существовал во времена правления династии египетских фараонов:

выбирали раба. Брили его голову наголо и наносили на неё текст сообщения водостойкой растительной краской. Когда волосы отрастали, его отправляли к адресату.

Шифр — это какая-либо система преобразования текста с секретом (ключом) для обеспечения секретности передаваемой информации.

АиФ.ru сделал подборку интересных фактов из истории шифрования.

Все тайнописи имеют системы

1. Акростих — осмысленный текст (слово, словосочетание или предложение), сложенный из начальных букв каждой строки стихотворения.

Вот, например, стихотворение-загадка с разгадкой в первых буквах:

Довольно именем известна я своим;
Равно клянётся плут и непорочный им,
Утехой в бедствиях всего бываю боле,
Жизнь сладостней при мне и в самой лучшей доле.
Блаженству чистых душ могу служить одна,
А меж злодеями — не быть я создана.
                                               Юрий Нелединский-Мелецкий
Сергей Есенин, Анна Ахматова, Валентин Загорянский часто пользовались акростихами.

2. Литорея — род шифрованного письма, употреблявшегося в древнерусской рукописной литературе. Бывает простая и мудрая. Простую называют тарабарской грамотой, она заключается в следующем: поставив согласные буквы в два ряда в порядке:

употребляют в письме верхние буквы вместо нижних и наоборот, причём гласные остаются без перемены; так, например, токепот = котёнок и т. п.

Мудрая литорея предполагает более сложные правила подстановки.

3. «ROT1» — шифр для детишек?

Возможно, в детстве вы тоже его использовали. Ключ к шифру очень прост: каждая буква алфавита заменяется на последующую букву.

А заменяется на Б, Б заменяется на В и так далее. «ROT1» буквально означает «вращать на 1 букву вперёд по алфавиту». Фраза «Я люблю борщ» превратится в секретную фразу «А мявмя впсъ». Этот шифр предназначен для развлечения, его легко понять и расшифровать, даже если ключ используется в обратном направлении.

4. От перестановки слагаемых…

Во время Первой мировой войны конфиденциальные сообщения отправляли с помощью так называемых перестановочных шрифтов. В них буквы переставляются с использованием некоторых заданных правил или ключей.

Например, слова могут быть записаны в обратном направлении, так что фраза «мама мыла раму» превращается во фразу «амам алым умар». Другой перестановочный ключ заключается в перестановке каждой пары букв, так что предыдущее сообщение становится «ам ам ым ал ар ум».

Возможно, покажется, что сложные правила перестановки могут сделать эти шифры очень трудными. Однако многие зашифрованные сообщения могут быть расшифрованы с использованием анаграмм или современных компьютерных алгоритмов.
Диск с шифром Цезаря. Фото: mr.santak/commons.wikimedia.org
5. Сдвижной шифр Цезаря

Он состоит из 33 различных шифров, по одному на каждую букву алфавита (количество шифров меняется в зависимости от алфавита используемого языка). Человек должен был знать, какой шифр Юлия Цезаря использовать для того, чтобы расшифровать сообщение. Например, если используется шифр Ё, то А становится Ё, Б становится Ж, В становится З и так далее по алфавиту. Если используется шифр Ю, то А становится Ю, Б становится Я, В становится А и так далее. Данный алгоритм является основой для многих более сложных шифров, но сам по себе не обеспечивает надёжную защиту тайны сообщений, поскольку проверка 33-х различных ключей шифра займёт относительно небольшое время.

Никто не смог. Попробуйте вы

Зашифрованные публичные послания дразнят нас своей интригой. Некоторые из них до сих пор остаются неразгаданными. Вот они:
Манускрипт Войнича. «Ботанический» раздел содержит изображения растений. Фото:commons.wikimedia.org
Манускрипт Войнича

Это 240-страничная книга, написанная на абсолютно неизвестном языке с цветными рисунками и странными диаграммами, изображениями невероятных событий и растений, которые не похожи ни на один известный вид.
Криптос у штаба ЦРУ в Лэнгли, штат Вирджиния. Фото: Jim Sanborn/commons.wikimedia.org
Криптос. Скульптура, созданная художником Джимом Санборном, которая расположена перед штаб-квартирой Центрального разведывательного управления в Лэнгли, Вирджиния. Скульптура содержит в себе четыре шифровки, вскрыть код четвёртой не удаётся до сих пор. В 2010 году было раскрыто, что символы 64-69 NYPVTT в четвёртой части означают слово БЕРЛИН.
Криптограмма № 1 — местонахождение тайника. Фото: commons.wikimedia.org
Шифр Бэйла — это комплект из трёх шифровок, которые, предположительно, раскрывают местонахождение одного из величайших захороненных сокровищ в американской истории: многих тысяч фунтов золота, серебра и драгоценных камней.

Теперь, когда вы прочитали статью, то наверняка сможете разгадать три простых шифра.

Свои варианты оставляйте в комментариях к этой статье. Ответ появится в 13:00 13 мая 2014 года.

Ответ:

1) Блюдечко

2) Слоненку все надоело

3) Хорошая погода

Смотрите также:

www.aif.ru
RSA-шифрование на пальцах
RSA-шифрование на пальцах
Вокруг алгоритмов шифрования с отрытым и закрытым ключом существует множество недопониманий и мистификаций. Здесь я хотел бы предельно коротко и наглядно, с конкретными числами и минимумом формул, показать, как это работает.
Я не вдаюсь в теорию (не очень понятно, на какой уровень подготовки читателя следует рассчитывать), но я уверен, что прочитав эту короткую иллюстрацию, любому человеку будет проще разобраться в формулах и строгих доказательствах.
Итак. Допустим, я хочу получить от вас некие данные. Мы с вам не хотим, чтобы эти данные узнал кто-то, кроме нас. И у нас нет никакой уверенности в надёжности канала передачи данных. Приступим.
Шаг первый. Подготовка ключей
Я должен проделать предварительные действия: сгенерировать публичный и приватный ключ.
Выбираю два простых числа. Пусть это будет p=3 и q=7.
Вычисляем модуль — произведение наших p и q: n=p×q=3×7=21.
Вычисляем функцию Эйлера: φ=(p-1)×(q-1)=2×6=12.
Выбираем число e, отвечающее следующим критериям: (i) оно должно быть простое, (ii) оно должно быть меньше φ — остаются варианты: 3, 5, 7, 11, (iii) оно должно быть взаимно простое с φ; остаются варианты 5, 7, 11. Выберем e=5. Это, так называемая, открытая экспонента.
Теперь пара чисел {e, n} — это мой открытый ключ. Я отправляю его вам, чтобы вы зашифровали своё сообщение. Но для меня это ещё не всё. Я должен получить закрытый ключ.
Мне нужно вычислить число d, обратное е по модулю φ. То есть остаток от деления по модулю φ произведения d×e должен быть равен 1. Запишем это в обозначениях, принятых во многих языках программирования: (d×е)%φ=1. Или (d×5)%12=1. d может быть равно 5 ((5×5)%12=25%12=1), но чтобы оно не путалось с e в дальнейшем повествовании, давайте возьмём его равным 17. Можете проверить сами, что (17×5)%12 действительно равно 1 (17×5-12×7=1). Итак d=17. Пара {d, n} — это секретный ключ, его я оставляю у себя. Его нельзя сообщать никому. Только обладатель секретного ключа может расшифровать то, что было зашифровано открытым ключом.
Шаг второй. Шифрование
Теперь пришла ваша очередь шифровать ваше сообщение. Допустим, ваше сообщение это число 19. Обозначим его P=19. Кроме него у вас уже есть мой открытый ключ: {e, n} = {5, 21}. Шифрование выполняется по следующему алгоритму:
Возводите ваше сообщение в степень e по модулю n. То есть, вычисляете 19 в степени 5 (2476099) и берёте остаток от деления на 21. Получается 10 — это ваши закодированные данные.
Строго говоря, вам вовсе незачем вычислять огромное число «19 в степени 5». При каждом умножении достаточно вычислять не полное произведение, а только остаток от деления на 21. Но это уже детали реализации вычислений, давайте не будем в них углубляться.
Полученные данные E=10, вы отправляете мне.
Здесь надо заметить, что сообщение P=19 не должно быть больше n=21. иначе ничего не получится.
Шаг третий. Расшифровка
Я получил ваши данные (E=10), и у меня имеется закрытый ключ {d, n} = {17, 21}.
Обратите внимание на то, что открытый ключ не может расшифровать сообщение. А закрытый ключ я никому не говорил. В этом вся прелесть асимметричного шифрования.
Начинаем раскодировать:
Я делаю операцию, очень похожую на вашу, но вместо e использую d. Возвожу E в степень d: получаю 10 в степень 17 (позвольте, я не буду писать единичку с семнадцатью нулями). Вычисляю остаток от деления на 21 и получаю 19 — ваше сообщение.
Заметьте, никто, кроме меня (даже вы!) не может расшифровать ваше сообщение (E=10), так как ни у кого нет закрытого ключа.
В чём гарантия надёжности шифрования
Надёжность шифрования обеспечивается тем, что третьему лицу (старающемуся взломать шифр) очень трудно вычислить закрытый ключ по открытому. Оба ключа вычисляются из одной пары простых чисел (p и q). То есть ключи связаны между собой. Но установить эту связь очень сложно. Основной загвоздкой является декомпозиция модуля n на простые сомножители p и q. Если число является произведением двух очень больших простых чисел, то его очень трудно разложить на множители.
Постараюсь это показать на примере. Давайте разложим на множители число 360:
сразу ясно. что оно делится на два (получили 2)
оставшееся 180 тоже, очевидно чётное (ещё 2)
90 — тоже чётное (ещё двойка)
45 не делится на 2, но следующая же попытка оказывается успешной — оно делится на три (получили 3)
15 тоже делится на 3
5 — простое.
Мы на каждом шагу, практически без перебора, получали всё новые и новые множители, легко получив полное разложение 360=2×2×2×3×3×5
Давайте теперь возьмём число 361. Тут нам придётся помучиться.
оно не чётное
три — нет, не делится
пять (допустим, мы поступаем умно и перебираем только простые числа, хотя, на практике, поиск больших простых чисел, сам по себе, является сложной задачей) — не подходит
семь? — нет.
…
и только 19 даст нам ответ: 361=19×19.
При использовании больших чисел, задача становится очень сложной. Это позволяет надеяться, что у взломщика просто не хватит вычислительных ресурсов, чтобы сломать ваши шифр за обозримое время.
А как это всё работает на практике?
Многие читатели спрашивают, как всё это применяется на практике. Давайте рассмотрим чуть более приближенный к жизни пример. Зашифруем и расшифруем слово «КРОТ», предложенное одним из читателей. А заодно, бегло рассмотрим, какие проблемы при этом встречаются и как они решаются.
Сперва сгенерируем ключи с чуть бо́льшими числами. Они не так наглядны, но позволят нам шифровать не только числа от нуля до 20.
Оттолкнёмся от пары простых чисел {p, q} = {17, 19}. Пусть наш открытый ключ будет {e, n} = {5, 323}, а закрытый {d, n} = {173, 323}.
Мы готовы к шифрованию. Переведём наше слово в цифровое представление. Мы можем взять просто номера букв в алфавите. У нас получится последовательность чисел: 11, 17, 15, 19.
Мы можем зашифровать каждое из этих чисел открытым ключом {e, n} = {5, 323} и получить шифровку 197, 272, 2, 304. Эти числа можно передать получателю, обладающему закрытым ключом {d, n} = {173, 323} и он всё расшифрует.
Немного о сложностях
На самом деле, изложенный способ шифрования очень слаб и никогда не используется. Причина проста — шифрование по буквам. Одна и та же буква будет шифроваться одним и тем же числом. Если злоумышленник перехватит достаточно большое сообщение, он сможет догадаться о его содержимом. Сперва он обратит внимание на частые коды пробелов и разделит шифровку на слова. Потом он заметит однобуквенные слова и догадается, как кодируются буквы «a», «и», «o», «в», «к»… Путём недолгого перебора, он вычислит дополнительные буквы по коротким словам, типа «но», «не», «по». И по более длинным словам без труда восстановит все оставшиеся буквы.
Таким образом, злоумышленнику не придётся отгадывать ваши секретные ключи. Он взломает ваше сообщение, не зная их.
Чтобы этого не происходило, используются специальные дополнительные алгоритмы, суть которых в том, что каждая предыдущая часть сообщения начинает влиять на следующую.
Упрощённо, это выглядит так. Перед шифрованием, мы применяем к сообщению правило: b := (b + a) % n. Где a — предыдущая часть сообщения, а b — следующая. То есть наше сообщение (11, 17, 15, 19) изменяется. 11 остаётся без изменений. 17 превращается в (11 + 17) % 323 = 28. 15 становится (15 + 28) % 323 = 43. A 19 превращается в 62.
Последовательность (11, 28, 43, 62) получается «запутанной». Все буквы в ней как бы перемешаны, в том смысле, что на каждый код влияет не одна буква, а все предыдущие.
Тот, кто получит ваше сообщение, должен будет проделать обратную операцию, со знаком «минус»: b := (b - a) % n. И только тогда он получит коды букв.
На практике, в исходное сообщение специально добавляются случайные и бессмысленные буквы в начало. Чтобы даже по первому коду было невозможно ничего понять. Получатель просто отбрасывает начало сообщения.
То есть мы можем добавить случайное число в начало и получить (299, 11, 17, 15, 19). После перемешивания получится: 299, 310, 4, 19, 38. После шифрования уже невозможно будет догадаться где была какая буква.
В реальной жизни всё ещё немного сложнее. Блоки, на которые бьётся сообщение длиннее одной буквы. Поэтому, сперва применяются алгоритмы выравнивания, потом алгоритмы разбиения на блоки с перепутыванием, и только потом применяется само RSA-шифрование.
Получатель делает всё в обратном порядке: расшифровывает, «распутывает» блоки и отбрасывает ненужную информацию, добавленную просто для выравнивания (чтобы сообщение можно было разбить на целое число блоков).
Детали и принципы формирования блоков можно почитать тут. Я же в этой заметке хотел рассказать только про RSA. Надесь, удалось.

Отправить
www.michurin.net
Шифрование HTML кода
Что собой представляет шифрование HTML кода страницы?
HTML код это по сути и есть сама ваша страничка, он указывает то, как именно ваш сайт будет строиться и отображаться на дисплее пользователя. Как правило, этот код открытый, то есть любой пользователь может беспрепятственно его увидеть и прочитать. Если же вы по тем или иным причинам не желаете того, чтобы кто-угодно имел доступ к вашему коду, вы можете зашифровать HTML. Это подразумевает собой создание особого алгоритма, который кодирует ваш код, то есть прячет его первичный вид, делая недоступным для пользователей сайта.
Когда и кому это может понадобится?
Сделать такое шифрование может абсолютно любой веб-мастер или владелец сайта. Вопрос в том, на сколько это обоснованно и нужно. К примеру, если у вас обычная лендинг-страничка, сделанная по шаблону, и которая не отличается от других, нету смысла заниматься кодировкой, так как такой шаблон и так является общедоступным. В таком случае вряд ли кто-то будет заниматься копированием и изучением вашего кода. А вот если у вас сайт, который имеет уникальный дизайн, вы долго и кропотливо над ним трудились, или заплатили за это немалые деньги, то о шифровании HTML кода все же стоит подумать. Очень часты случаи, когда владелец имеет сайт, в который было вложено немало сил, времени и денег, и через некоторое время тем или иным образом обнаруживает точно такой же сайт, с таким же дизайном и структурой, но на другом домене и хостинге. Очень часто владельцам сайтов об этом говорят в комментариях сами пользователи. В этом случае можно смело сделать вывод, что кто-то попросту скопировал HTML код вашего сайта и запустил его на своем.
Что же делать чтобы обезопасить себя?
От ситуаций копирования и использования без разрешения чужого HTML кода не так уж и просто себя обезопасить. Да и вообще если человек уже увидел ваш сайт, он даже и без кода сможет его дублировать, при условии наличия определенных знаний в сфере веб-разработки. Но, что касается самого HTML кода, то его можно зашифровать. Работает это на основе специального javascript-скрипта. С помощью нашего инструмента вы шифруете свой HTML код. При этом создается специальный скрипт, который предназначен для расшифровки. Работает это довольно-таки просто: когда посетитель переходит на ваш сайт, загружается зашифрованный код, понять который он не сможет. В этот же момент запускается созданный javascript, который расшифровывает код и отображает сайт на экране пользователя. При этом, сам посетитель не может увидеть настоящий код. Однако, в этом методе есть и небольшой недостаток. Есть пользователи в браузерах которых запрещен запуск javascript на сайте, в таком случае скрипт не запустится, соответственно HTML код не расшифруется и сайт не будет отображен. Но, расстраиваться не стоит, такая настройка браузеров встречается очень редко, можно сказать что на 99% браузерах разрешен запуск javascript.
Как это сделать?
Делается это очень просто, с помощью нашего инструмента. Все что от вас требуется это вставить ваш HTML код в поле на этой страничке, и нажать на кнопку для запуска шифрования. В результате, в другом поле вы получите уже зашифрованный код, который уже можно использовать непосредственно на вашем сайте.
sitespy.ru
Языки, коды, шифры | SOFTMIXER
На свете множество неразгаданных шифров, непонятых языков, загадочных тайнописей и нерасшифрованных карт, но мы остановимся только на 10 из них. Конечно, эти загадки менее известны, чем карта Винланда или рукопись Войнича, зато в их подлинности уже ни у кого не возникает сомнений…
Карты, языки, коды, шифры разгадываются и декодируются каждый день, порой этому предшествуют мучительные годы исследований и расчетов. Последние разработки позволяют расшифровывать ранее непонятные и неразборчивые языки при помощи компьютера.
Одним из последних успехов такой технологии стала расшифровка закодированной немецкой рукописи Copiale cipher. Эта рукопись датировалась 18 веком и принадлежала тайному сообществу окулистов.
Как пишет Нью Йорк Таймс, оказалось, что первые шестнадцать страниц рукописи (весь документ состоит из 105 страниц) посвящены подробному описанию обрядов тайного сообщества, по-видимому, увлекавшегося, глазной хирургией и офтальмологией.
В частности, обряд посвящения нового члена «ордена» проходил так: кандидату выщипывали волос из брови, после чего он приносил клятву верности сообществу.
Интересно? Тогда давайте перейдем к десяти еще более таинственным шифрам, картам и языкам.
Шифр Британской библиотеки
В национальной библиотеке Великобритании вы найдете, по крайней мере, три зашифрованных манускрипта. Первый из них, «Искусство колдовства», был написан Беном Эзразефом в 1657 году.
Вторая книга вышла в свет в 1835 году под очень интересным и длинным названием «Правила поведения у алтаря, древние тайны, которые открыты лишь женщинам: Первая часть секретов, хранившихся в Ассоциации единства девушек, с дополнением».
Третья книга с весьма загадочным названием «Тайны богини Весты» предположительно была издана в 1850 году. В общем, если у вас есть возможность попасть в Британскую библиотеку, вы можете попытать счастья!
Неизвестный древний перуанский язык
Совсем недавно ученые провели подробный анализ 400-летнего письма, написанного неизвестным испанским автором. Оказалось, что в нем содержатся элементы неизвестного ранее древнего перуанского языка.
Само письмо было найдено еще в 2008 году среди руин древней испанской церкви в городе Эль-Брухо на севере Перу, но только теперь лингвисты поняли, что язык этого письма может оказаться ключом к происхождению современного перуанского языка. К тому же, на обратной стороне письма есть небольшие записи, которые оказались переводом неизвестного языка на испанский с использованием арабских цифр.
И хотя новый перуанский язык, на котором говорит все местное население, скорее всего, заимствован у индейского племени Кечуа, все понимают, что он полностью новый и сильно отличается от древнего. Ученые полагают, что неизвестный язык может быть одним из двух языков, упоминающихся в древней литературе – Куангнам или Пескадора (язык рыбаков).
Есть еще одна гипотеза, согласно которой древний язык появился под влиянием культуры инков, потому что в письме используется десятичная система счисления, как и у инков (в культуре Майя использовалась двадцатеричная система счисления).
Конечно, таинственный язык мог возникнуть и из нескольких языков, но все это только догадки, а до настоящего времени филологи и лингвисты всего мира пытаются найти ключ к разгадке в конверте, отправленном неизвестным испанским писателем.
Закодированная карта Птолемея
Историков давно мучает вопрос, где на самом деле были расположены древние поселения и города германцев (в сравнении с современной Германией). Ключ к разгадке этой исторической тайны находится на карте Птолемея. Ведь Птолемей был римским гражданином, а римляне не только знали, где поселения германцев находятся, но и нередко упоминали их в литературных произведениях.
Где же были германцы во времена нашествия римлян? Историки по сей день не могут разгадать этот исторический пазл, потому что никому не удается соотнести 96 древних городов Германии, известных из исторических источников, с современной картой.
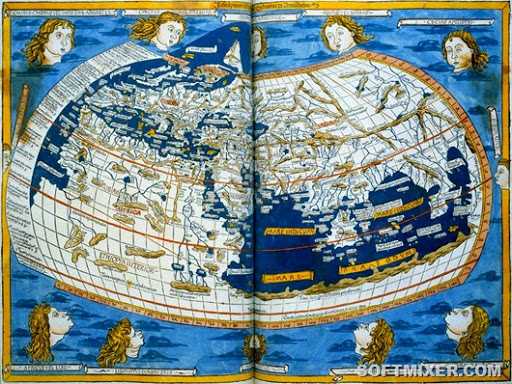
Клавдий Птолемей, известный древнегреческий ученый второго века, включил карту «Великой Германии» в свой труд «География». В 150 году нашей эры Птолемей, немного опередив Google Earth, создал 26 карт, нарисованных цветными чернилами на звериных шкурах.
На этих картах был изображен весь мир, известный на ту пору. И хотя Птолемей никогда не бывал в Германии, он в любом случае должен был сверять свои знания с другими трудами и географическими документами. Есть карта и записи древних римлян, но никто не может понять, как 96 городов, изображенных Птолемеем, превратились в города современной Германии. Во всяком случае, пока.
После шестилетнего исследования берлинская команда ученых-топографов и геодезистов заявили, что знают, как перевести координаты 96 городов птолемеевской карты в общепринятую систему координат. А помогла им в этом невероятная находка. Неожиданно для всех в библиотеке дворца Топкапы города Стамбул (Турция) была найдена более ранняя копия птолемеевской «Географии».
На карте этой копии было изображено множество городов, например, город Йена на востоке Германии (на карте Птолемея город называется Бикургиум). Современный город Эссен был назван «Навалия», а город Фюрстенвальде, как оказалось, существовал еще 2000 лет назад и изначально назывался «Сусудата», что по-немецки означает «грязная свинья». И это все, что на данный момент удалось полностью расшифровать.
Шифр Фейнмана
Это случилось в далеком 1987 году, когда Интернет еще только зарождался, а значительная часть уважаемых читателей еще не появилась на свет. На сайте криптологии (криптология – наука о расшифровке тайнописи) некто, представившийся учеником блестящего физика доктора Ричарда Фейнмана, рассказал интересную историю.
Один знакомый Фейнмана, тоже ученый, предложил великому физику расшифровать три кусочка кода. По словам «ученика», Фейнман показал ему эти шифры, поскольку не смог сам их разгадать. В своем посте молодой человек выложил и эти три шифра, надеясь на то, что кто-нибудь все же сможет в них разобраться.
Надежды оправдались, и вскоре один из трех кодов был разгадан Джоном Моррисоном из Лаборатории реактивных двигателей (США). Оказалось, что под шифром кроются Кентерберийские рассказы автора Джеффри Чосера на среднеанглийском языке. Остальные два кода по сей день остаются неразгаданными.
Транскрипт Энтона
Что это за таинственное слово «Caractors», стоящее в заглавии транскрипта? Ответ на этот вопрос может подтвердить или опровергнуть главный артефакт Мормонской религии. В действительности, транскрипт Энтона – это небольшой клочок бумаги, якобы написанный рукой самого Джозефа Смита младшего, основателя Мормонской религии.
Утверждается, что некоторые «буквы» в этом транскрипте Смит видел в «Золотых Страницах». По легенде, это древняя книга с золотыми страницами, написанная на древнеегипетском языке. Считается, что в 1823 году «Золотые страницы» открылись перед Смитом и легли в основу «Книги Мормона», написанной им же.
Как же транскрипт получил свое название? Дело в том, что в 1828 году он был послан знаменитому эксперту того времени, филологу Чарльзу Энтону, работавшему в Колумбийском университете. Энтон должен был установить подлинность документа и осуществить расшифровку. Некоторые приверженцы религии мормонов утверждают, что Энтон подтвердил подлинность буквенных символов транскрипта, о чем признался в письме Мартину Харрису.
Харрис на тот момент уже был обращен в веру «святых последнего дня» (так мармоны звали самих себя) и, более того, был одним из Трех Свидетелей, которые видели писание «Золотые страницы», с которого, как говорил Джозеф Смит, был сделан перевод «Книга Мормона».
По словам Харрисона, Энтон установил, что транскрипт содержит египетские, халдейские, ассирийские и арабские символы, но опроверг все свои утверждения после того, как узнал, что этот кусочек бумаги был послан Смитом и имеет прямое отношение к мормонской культуре. Сам Энтон все отрицал и заявлял, что никогда не сомневался в том, что трансрипт поддельный.
Что же значит «Caractors»?
Согласно заключению Энтона, «все знаки в этой записи – это всего лишь пародия на буквы из разных алфавитов, а, следовательно, они ни имеют никакого осмысленного значения». Возможно, «caractors» — это просто случайный набор букв, но, по-видимому, это все-таки не так.
Наиболее вероятно, это слово было заимствовано из различных источников, может даже из сокращенной версии Библии, и было перемешано со случайными буквами, чтобы создать видимость настоящего языка. Но не стоит исключать и возможности того, что Джозеф Смит действительно видел это слово. Что из этого правда, а что подделка мы узнаем только после расшифровки.
Тайна корабля «Сидней»
Одна из самых захватывающих нерешенных загадок Второй Мировой Войны – это тайна гибели австралийского корабля ее королевского величества «Сидней». Все, что нам известно из истории, — это то, что легкий крейсер типа «Линдер» Королевского военно-морского флота «Сидней» был потоплен немецким вспомогательным крейсером «Корморан» 19 ноября 1941 года.
В сравнении с «Кормораном» «Сидней» был более мощным и крупным кораблем, вооруженным сверху донизу. Тем не менее, в бою погиб весь экипаж корабля (645 человек), в то время как в команде менее мощного «Корморана» пострадало только несколько человек.
Тот факт, что превосходящее по всем параметрам судно потерпело поражение от немецкого корабля, которое, по сути, являлось переделанным торговым судном, обычно объясняют близостью двух кораблей во время схватки, точными выстрелами немецкого корабля, а также неожиданностью и стремительностью нападения.
Однако, некоторые исследователи считают, что немецкий командир использовал запрещенные приемы, чтобы заманить «Сидней» в ловушку. Есть даже предположения, что в битве участвовала японская подводная лодка. В настоящее время выяснение реальных обстоятельств битвы прикрыли.
Где же здесь шифр, спросите вы? А дело в том, что вскоре «Корморан» был потоплен в сражении, а его главнокомандующий, капитан Детмерс, взят в плен и сослан в австралийский лагерь для военнопленных. Пару лет спустя, в 1945 году, Детмерс попытался сбежать, но его поймали и вернули в лагерь. Когда капитана схватили, при нем обнаружили дневник, написанный шифром Виженера. Некоторые записи были помечены маленькими точками.
Дневник был направлен на криптографический анализ, где исследователи с легкостью распознали шифр Виженера. Из расшифровки австралийских криптологов стало ясно, что Детмерс пытался скрыть в своем дневнике обстоятельства битвы «Сиднея» и «Корморана». Только одно было непонятно австралийским ученым: почему Детмерс использовал код, который был уже давно разгадан и всем известен?
Загадка стала еще более таинственной, когда узнали, что другие австралийские документы подтверждают то, что дневник капитана был написан вовсе не Виженерским шифром, а неизвестным немецким кодом Второй Мировой Войны.
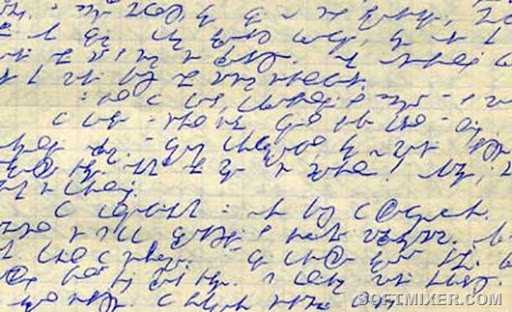
Еще одна расшифровка так называемого дневника Детмерса показала, что автор использовал британскую систему под названием шифр Плейфера, еще один код, который был раскрыт к 1941 году.
Опять-таки, зачем Детмерсу понадобилось использовать английский код, который, возможно, он и не знал вовсе, а если и знал, то неужели он упустил из виду тот факт, что этот код уже со времен начала Второй Мировой не является надежным? Так почему же он использовал его?
Итак, вопросов остается много. Детмерс зашифровал свой дневник Виженерским кодом? Неизвестным немецким кодом? Английским шифром Плейфера?
Можно предположить, что Детмерс вовсе и не кодировал свой дневник, а вместо него это сделали британские или австралийские власти, чтобы только создать видимость. И тогда понятно, почему использовались уже взломанные шифры – чтобы каждый, кто обнаружил дневник, смог с легкостью его прочесть.
Таким образом, «расшифровка» документа рассказала бы миру ту историю, которая была выгодна британцам и австралийцам. Она бы объяснила, как более мощный военный корабль потерпел поражение с полной потерей экипажа от меньшего вражеского суда. Поэтому, в действительности, загадка заключается не в самом шифре, а в том, кто его создал и для чего.
Шифр Белласо
Итальянский криптограф Джованни Батиста Белласо в 1553 году опубликовал свой труд «La Cifra del Sig, Giovan Battista Bellaso», который, по сути, можно было назвать «Криптография для чайников». Позднее, в 1555 и в 1564 году он издал к нему два дополнения. Именно в эти два последних тома Белласо включил несколько задачек для читателей, которые хотели бы попробовать свои силы в расшифровке.
Сам Белласо говорил, что под этими шифрами скрываются прекрасные произведения, которые читателям было бы интересно узнать. Также он обещал лично раскрыть тайну этих заданий ровно через год после их публикации, если к тому моменту никому это не удастся. Свое обещание Белласо так и не выполнил.
Поэтому до недавнего времени оставалось 7 неразгаданных шифров. Но в 2009 году английскому отшельнику Тони Гафни удалось взломать один из них и обнаружить там отрывки из «Астрологической медицины эпохи Возрождения». А если учесть, что Тони не знает итальянского языка, то его достижение становится еще более невероятным.
Но Гафни на этом не остановился и через некоторое время представил расшифровку седьмого задания Белласо, что еще более значимо, потому что этот шифр сильно отличался от предыдущего.
Как вы уже успели подсчитать, оставшиеся пять заданий Белласо еще не выполнены.
Книга дикарей
Французский аббат, миссионер и автор ряда книг Эммануэль-Анри-Дьедонне Домене решил посвятить себя развитию католической церкви в Техасе, для чего в 1846 году покинул родину и направился к берегам Америки. Приехав в Сент-Луис, Домене закончил свое теологическое образование, после чего направился в Кастровилль, штат Техас.
В 1850 году аббат ненадолго вернулся во Францию, где получил аудиенцию Папы Римского, но вскоре вновь отплыл в Америку. В то время шла война с Мексикой и Домене жил в Браунсвилле до 1850 года. Потом опять уехал во Францию, потом в Мексику, потому опять в Европу, в 1880-х – еще одно путешествие в Америку. Последние годы своей жизни Домене провел как своего рода автор духовных произведений о путешествиях.
Может, Атлантический океан так повлиял на аббата (ведь ему пришлось пересечь Атлантику не один раз), может, слишком долгое пребывание в Техасе, но Домене произвел на свет очень странный и таинственный документ, который обнаружили позднее в одной из французских национальных библиотек в Париже.
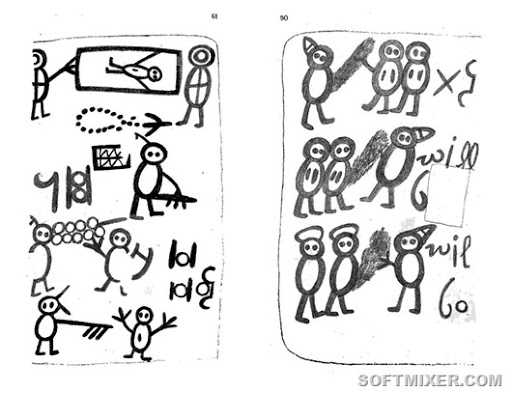
По словам Домене, эта книга, названная «Книгой дикарей» была не его работой, а собранием работ коренных американцев, своего рода любопытным творением аборигенов. Но немецкие критики довольно быстро раскрыли обман, поскольку в тексте «книги» было слишком много немецких слов и символов.
Но привлекает внимание не текст, а странные рисунки. Те же немецкие критики думали, что любопытные рисунки, картинки и непонятные символы – это просто каракули ребенка. Но если вы внимательно посмотрите на картинки, вы поймете, что это дело рук взрослого человека, главным образом, из-за сексуального подтекста рисунков. Они, по меньше мере, странные.
В «Книге дикарей» несколько сотен страниц, однако на них можно заметить некий намек на шифр, который, возможно, отображен и на картинках. Но вряд ли кто-нибудь будет расшифровывать такие неприличные изображения.
Записки Рикки Маккормика
30 июня 1999 года в графстве Сент-Чарльз, штат Миссури на поле было обнаружено тело 41-летнего Рикки Маккормика. Безработный мужчина без высшего образования имел проблемы с сердцем и легкими, и был признан недееспособным задолго до своей смерти, к тому же отсидел в тюрьме за несколько правонарушений.
Тело было найдено в нескольких милях от дома, где Рикки жил со своей матерью. Ни следов преступления, ни каких-либо указаний на причину смерти не было обнаружено.
В кармане убитого были найдены две зашифрованные записки. Может, это ключ к тайне смерти Рикки? Отдел криптоанализа ФБР и Национальная американская Криптографическая ассоциация пытались понять значение этих записок, но не смогли. Дело Рикки Маккормика вошло в список нераскрываемый дел ФБР.

Двенадцать лет спустя власти изменили свое решение и теперь полагают, что Маккормик был убит. Также они считают, что найденные записки могут объяснить смерть мужчины и навести на след убийцы или убийц. 29 марта 2011 года ФБР обратилось ко всем дешифровщикам мира с просьбой установить закодированное послание.
За несколько дней размещения просьбы в интернете сайт ФБР буквально наводнили сообщения с предложениями о помощи и идеями расшифровки. По словам членов семьи Маккормика, Рикки с детства увлекался шифровками, но никто в семье не знал, как их раскодировать. В настоящее время вся общественность пытается помочь ФБР расшифровать эти послания.
Язык близнецов
Это замечательный пример неизвестного языка, который ставит в тупик людей, пытающихся понять его. Он уникален, потому что на нем говорят только два человека.
Криптофазия – это поразительное явление языка для близнецов, который могут понять только два ребенка. Само слово произошло от «крипто» — секрет и «фазия» — нарушение речи. Большинство лингвистов сравнивают криптофазию с идиоглоссией, что, по сути, то же самое, но криптофазия включает в себя еще и зеркальные эффекты, например, схожие походки, манеры. О ней вообще мало что известно.
Раньше думали, что это очень редкое явление, но теперь известно, что криптофазия встречается у 40% близнецов. Эти автономные языки могут быть понятны, разве что, другим близнецам. И хотя криптофазия — явление общее, уникальность языка близнецов постепенно исчезает с возрастом.
Оказывается, близнецы перенимают «взрослый язык» лишь частично. Чаще всего это случается от недостатка общения с родителями. Обычно во время фазы освоения языка братья и сестры постоянно вместе, поэтому принятие модели «взрослого языка» и его использование оказываются не на высоте. Когда носитель взрослой модели речи (а попросту, родитель) отсутствует, дети используют друг друга в качестве этой модели.
Это не значит, что дети придумывают свой собственный язык, они просто создают новые слова. И оказывается, что дети неверно представляют себе модель «взрослого языка», а потому ограничиваются фонологическими возможностями детей младшего возраста. А потому придуманные слова будут трудно узнаваемыми или совершенно непонятными обычным носителям.
Наиболее известный пример такого языка предоставили близнецы Пото и Кабенго – идентичные близнецы (их настоящие имена Грейс и Вирджиния Кеннеди). Они использовали никому неизвестный язык до восьми лет.
В 1979 году режиссер Жан-Пьер Горин даже снял документальный фильм «Пото и Кабенго». Девушки не отличались от своих сверстников умственными способностями, они просто разработали собственный способ коммуникации из-за слабого развития разговорного языка и раннем возрасте.
link
Похожие материалы:
www.softmixer.com
код шифрования — с английского на русский
См. также в других словарях:
код аутентификации сообщения (MAC), получаемый на основе блочного шифрования как функция сжатия ключей — MAC (message authentification code) [http://www.rfcmd.ru/glossword/1.8/index.php?a=index d=23] Тематики защита информации EN block cipher based MAC … Справочник технического переводчика
код Ривеста — KP Общее название серии алгоритмов шифрования, разработанных Ривестом. [http://www.rfcmd.ru/glossword/1.8/index.php?a=index&d=4102] Тематики защита информации Синонимы KP EN Rivest s codeRC … Справочник технического переводчика
Код аутентичности — MAC (имитовставка, англ. message authentication code код аутентичности сообщения) средство обеспечения имитозащиты в протоколах аутентификации сообщений с доверяющими друг другу участниками специальный набор символов, который добавляется к… … Википедия
Код аутентичности сообщения — MAC (имитовставка, англ. message authentication code код аутентичности сообщения) средство обеспечения имитозащиты в протоколах аутентификации сообщений с доверяющими друг другу участниками специальный набор символов, который добавляется к… … Википедия
Теорема Шеннона об источнике шифрования — В теории информатики Теорема Шеннона об источнике шифрования (или теорема бесшумного шифрования) устанавливает предел максимального сжатия данных и числовое значение энтропии Шеннона. Теорема Шеннона об источнике шифрования показывает, что (когда … Википедия
алгоритм шифрования RC2 — Алгоритм шифрования; блочный шифр с переменной длиной ключа, разработанный Роном Райвестом (Ron Rivest). Аббревиатура RC означает «Код Рона» (Ron‘s Code) или «Шифр Райвеста» (Rivest s Cipher).Длина блока 64 бита, длина… … Справочник технического переводчика
Телеграфный банковский код — система условных кодовых обозначений для шифрования текстов телеграфной банковской переписки. Каждый кодовый знак состоит из пяти букв, заменяющих шаблонный трафаретный текст или определенную денежную сумму. В РФ используют два вида кодов:… … Финансовый словарь
Хэш код — Хеширование (иногда хэширование, англ. hashing) преобразование входного массива данных произвольной длины в выходную битовую строку фиксированной длины. Такие преобразования также называются хеш функциями или функциями свёртки, а их результаты… … Википедия
ТЕЛЕГРАФНЫЙ БАНКОВСКИЙ КОД — система условных кодовых обозначений для шифрования текстов телеграфной банковской переписки. Каждый кодовый знак состоит из пяти букв, заменяющих шаблонный трафаретный текст или определенную денежную сумму. В России используют два вида кодов:… … Экономический словарь
ТЕЛЕГРАФНЫЙ БАНКОВСКИЙ КОД — система условных кодовых обозначений для шифрования текстов телеграфной банковской переписки. Каждый кодовый знак состоит из пяти букв, заменяющих шаблонный трафаретный текст или определенную денежную сумму. В России используют два вида кодов:… … Энциклопедический словарь экономики и права
телеграфный банковский код —    система условных кодовых обозначений для шифрования текстов телеграфной банковской переписки. Каждый кодовый знак состоит из пяти букв, заменяющих шаблонный трафаретный текст или определенную денежную сумму. В России используют два вида кодов … Словарь экономических терминов

translate.academic.ru