Не всегда можно определить заранее, сколько раз придется вычислять функцию. Метод золотого сечения почти столь же эффективен при n-2, что и метод Фибоначчи, однако при этом не требуется знать n – количество вычислений функции.
Сущность этого метода заключается в следующем. Интервал неопределенности делится на две неравные части так, что отношение длины большего отрезка к длине всего интервала равно отношению длины меньшего отрезка к длине большего (рис 3).
где τ — «золотое сечение»
Если длина конечного интервала неопределенности равна δ, то для достижения требуемой точности число вычислений значений функции по методу золотого сечения можно найти по условию
Пример.
Методом золотого сечения найти точку минимума x* функции f(x) на отрезке [a;b] с точностью ε и значение целевой функции в этой точке:
f(x)=x4+2x2+4x+1=0, [-1;0], ε=0.1
Решение. Положим a1 = a, b1 = b. Вычислим λ1 = a1 + (1- 0.618)(b1 — a1), μ1 = a1 + 0.618(b1 — a1).
Вычислим f(λ1) = -0.5623, f(μ2) = -0.2149
Итерация №1.
Поскольку f(λ1) 1), то b2 = -0.382, a2 = a1, μ2 = -0.618
μ2 = a2 + 0.618(b2 — a2) = -1 + 0.618(-0.382 +1), f(μ2) = f(-0.618) = -0.2149
Итерация №2.
Поскольку f(λ2) > f(μ2), то a3 = -0.7639, b 3 = b2, λ3 = -0.618
μ3 = a3 + 0.
618(b3 — a3) = -0.7639 + 0.618(-0.382 +0.7639), f(μ3) = f(-0.5279) = -0.5623
Итерация №3.
Поскольку f(λ3) 3), то b4 = -0.5279, a4 = a3, μ4 = -0.618
μ4 = a4 + 0.618(b4 — a4) = -0.7639 + 0.618(-0.5279 +0.7639), f(μ4) = f(-0.618) = -0.4766
Итерация №4.
Поскольку f(λ4) 4), то b5 = -0.618, a5 = a4, μ5 = -0.6738
μ5 = a5 + 0.618(b5 — a5) = -0.7639 + 0.618(-0.618 +0.7639), f(μ5) = f(-0.6738) = -0.5623
Остальные расчеты сведем в таблицу.
| N | an | bn | bn-an | λn | μn | F(λn) | F(μn) |
| 1 | -1 | 0 | 1 | -0. 618 | -0.382 | -0.5623 | -0.2149 |
| 2 | -1 | -0.382 | 0.618 | -0.7639 | -0.618 | -0.548 | -0.5623 |
| 3 | -0.7639 | -0.382 | 0.3819 | -0.618 | -0.5279 | -0.5623 | -0.4766 |
| 4 | -0.7639 | -0.5279 | 0.236 | -0.6738 | -0.618 | -0.5811 | -0.5623 |
| 5 | -0.7639 | -0.618 | 0.1459 | -0.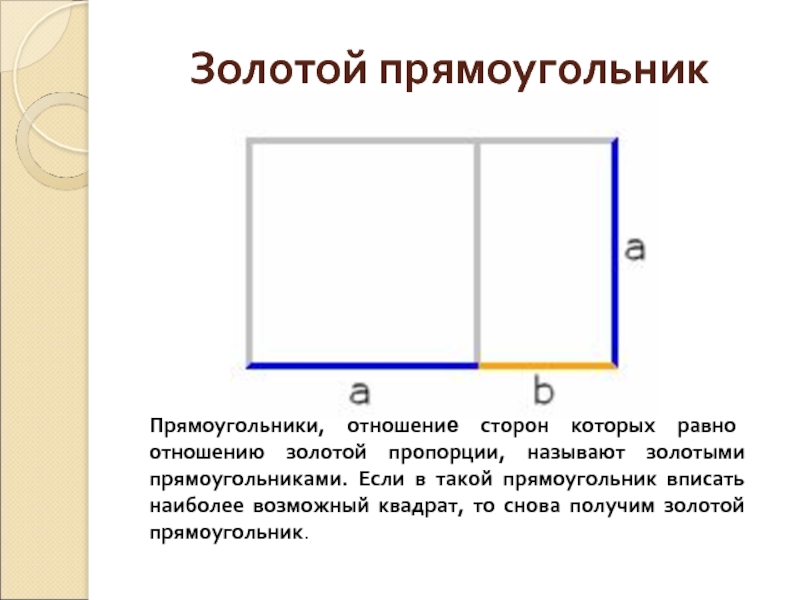 7082 | -0.6738 | -0.5782 | -0.5811 |
| 6 | -0.7082 | -0.618 | 0.09018 | -0.6738 | -0.6524 | -0.5772 |
Ответ: x = -0.66309052; F(x) = -0.57965758
Ширина золотого прямоугольника Калькулятор | Вычислить Ширина золотого прямоугольника
✖Длина золотого прямоугольника — это длина самого длинного края золотого прямоугольника.ⓘ Длина золотого прямоугольника [l] | створаАнгстремарпанастрономическая единицаАттометрAU длиныЯчменное зерноМиллиардный светБор РадиусКабель (международный)Кабель (UK)Кабель (США)калибрсантиметрцепьCubit (греческий)Кубит (Длинный)Cubit (Великобритания)ДекаметрДециметрЗемля Расстояние от ЛуныЗемля Расстояние от СолнцаЭкваториальный радиус ЗемлиПолярный радиус ЗемлиРадиус электрона (классическая)флигельЭкзаметрFamnВникатьFemtometerФермиПалец (ткань)ширина пальцаФутFoot (служба США)ФарлонгГигаметрРукаЛадоньгектометрдюймкругозоркилометркилопарсеккилоярдлигаЛига (Статут)Световой годСсылкаМегаметрМегапарсекметрмикродюйммикрометрмикронмилмилиМиля (Роман)Миля (служба США)МиллиметрМиллион светлого годаNail (ткань)нанометрМорская лига (международная)Морская лига ВеликобританииМорская миля (Международный)Морская миля (Великобритания)парсекОкуньпетаметрцицеропикометраПланка ДлинаТочкаполюскварталРидРид (длинный)прутРоман Actusканатныйрусский АрчинSpan (ткань)Солнечный радиусТераметрТвипVara КастелланаVara ConuqueraVara De ФаареяДворЙоктометрЙоттаметрЗептометрЗеттаметр | +10% -10% |
|
✖Ширина золотого прямоугольника — это длина кратчайшего края золотого прямоугольника. |
|
⎘ копия |
ⓘ Ширина золотого прямоугольника [b]
👎
Формула
сбросить
👍
Ширина золотого прямоугольника Решение
ШАГ 0: Сводка предварительного расчета
ШАГ 1.
Преобразование входов в базовый блок
Длина золотого прямоугольника: 10 метр —> 10 метр Конверсия не требуется
ШАГ 2: Оцените формулу
ШАГ 3: Преобразуйте результат в единицу вывода
6.18033988749895 метр —> Конверсия не требуется
< 4 Ширина золотого прямоугольника Калькуляторы
Ширина золотого прямоугольника формула
Ширина золотого прямоугольника = Длина золотого прямоугольника/[phi]
b = l/[phi]
Что такое Золотой прямоугольник?
В геометрии золотой прямоугольник — это прямоугольник, длина сторон которого находится в золотом сечении, 1: 1 sqrt (5) / 2, что равно 1: phi, примерно 1,618. Золотые прямоугольники демонстрируют особую форму самоподобия: все прямоугольники, созданные путем добавления или удаления квадрата, также являются золотыми прямоугольниками.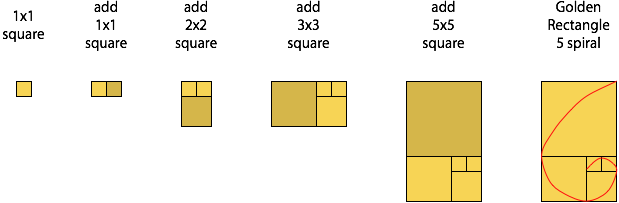
Отличительной особенностью этой формы является то, что при добавлении или удалении квадратной секции продукт представляет собой еще один золотой прямоугольник с тем же соотношением сторон, что и первый. Добавление или удаление квадратов может повторяться бесконечно, и в этом случае соответствующие углы квадратов образуют бесконечную последовательность точек на золотой спирали, уникальной логарифмической спирали с этим свойством. Диагональные линии, проведенные между первыми двумя порядками встроенных золотых прямоугольников, будут определять точку пересечения диагоналей всех встроенных золотых прямоугольников; Клиффорд А. Пиковер называл эту точку «Глазом Бога».
Share
Copied!Калькулятор золотого сечения
Калькулятор золотого сеченияКак работает калькулятор золотого сечения?
Бесплатный калькулятор золотого сечения — Решает 2 из 3 переменных для сегмента, разбитого на 2 части, которые удовлетворяют золотому сечению (золотому сечению).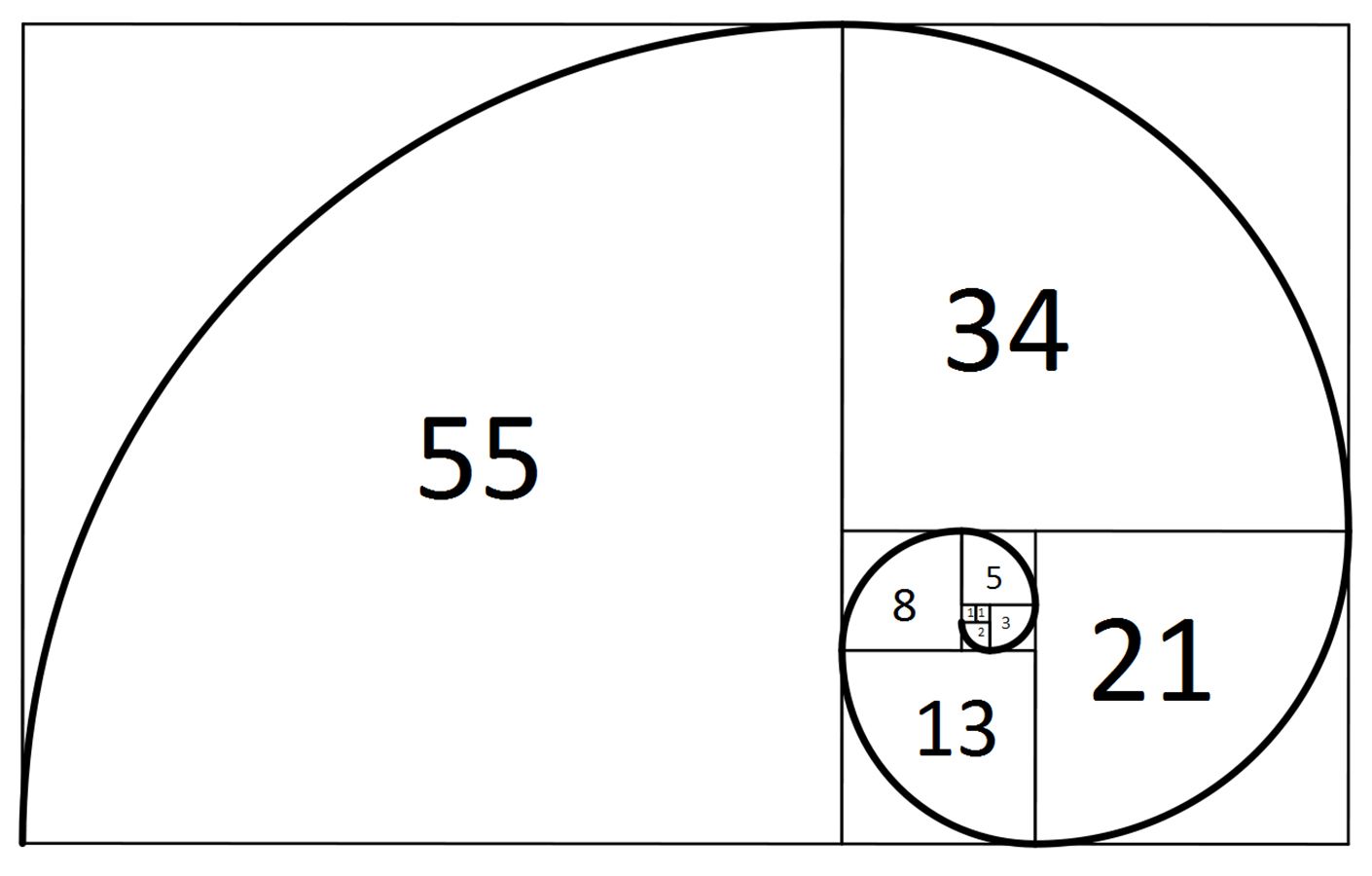
(a) Большой сегмент
(b) Малый сегмент
(a + b) Общий сегмент
Этот калькулятор имеет 3 входа.
Какая 1 формула используется для калькулятора золотого сечения?
- а/б=(а+б)/а
Какие 3 концепции используются в калькуляторе золотого сечения?
- золотое сечение
- Отношение большей стороны к меньшей равно всему отрезку большой стороны
φ = 1,6180339887498948482. - отношение
- показывает, сколько раз одно число содержит другое
- отрезок
- часть прямой линии, которая ограничена двумя различными конечными точками и содержит каждую точку на линии, которая находится между ее конечными точками.
Калькулятор золотого сечения Видео
- Электронная почта: donsevcik@gmail.
com - Тел.: 800-234-2933
com- Математическая тревога
- судоку
- Раздор
- Информационный бюллетень о недобросовестном преимуществе
- Биографии математиков
- Подкаст цены за клик
- Математические Мемы
- Глоссарий по математике
- Предметы
- бейсбольная математика
- Ускорьте удовольствие, свободу и удовлетворение
- Друзья
- Спонсоры
- Связаться с нами
- Вакансии учителя математики
- Политика в отношении файлов cookie
- политика конфиденциальности
- Политика возврата
- СМИ
| iCalculator™
Используйте калькулятор золотого сечения для расчета золотого сечения между двумя числами.
В этом уроке мы объясним, как рассчитать золотое сечение, и подробно объясним концепцию золотого сечения. Знаете ли вы? Многие архитекторы и художники считают, что золотое сечение создает самую красивую и приятную эстетику.
| 🖹 Обычный вид🗖 Полноэкранный просмотр 0102 |
| Числитель отношения (a) |
| Знаменатель отношения (b) |
| Сумма значений отношения a+b (c) |
| Числитель отношения (a) равен | Знаменатель отношения (b) равен |
| Сумма значений отношения a+b (c) равен |
| Формула золотого сечения для расчета числителя отношения |
|---|
| и / б = 1,618 а / = 1,618 а = 1,618 × а = | 901 02
| Золотое сечение Формула для расчета знаменателя отношения |
| а + б / а = 1,618 + б / = 1,618 + b = 1,618 × + b = b = — b = |
Пожалуйста, оцените этот калькулятор коэффициентов.
Если вы новичок в коэффициентах или хотите узнать больше о расчетах коэффициентов, мы предлагаем вам ознакомиться с нашим Введением в коэффициенты с вспомогательным калькулятором коэффициентов.
★ ★ ★ ★ ★ [ 48 голосов ]
Что такое золотое сечение
900 05 Золотое сечение, обозначаемое греческим символом ɸ (фи), представляет собой математическую концепцию, в которой две частиa + b / a = a / b = ɸ
Математически золотое сечение является иррациональным число, которое мы получим после решения следующего квадратного уравнения:
ɸ = x 2 — x — 1 = 0
Используя уравнение золотого сечения, вы получите значение:
ɸ = 1 + √ 5 / 2
ɸ = 1,6180339887
Или
ɸ = 1,62
Золотое сечение также известно как среднее отношение, крайнее отношение, медиальное сечение, Sectio Divina (божественное сечение), золотое число, золотое сечение, золотая пропорция и божественная пропорция.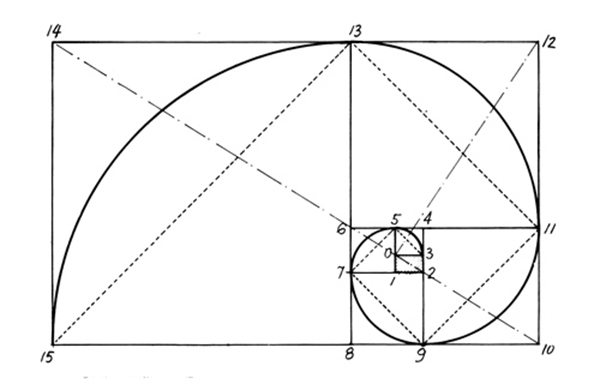
С точки зрения непрофессионала, мы можем представить золотое сечение как линию, разделенную на две части так, что:
- Длинный отрезок, разделенный коротким путем
Равен
- Вся прямая, разделенная на длинную часть
быть 6,12 см, а короткая часть будет 3,82 см в их соответствующих длинах.
В то же время, если вы хотите нарисовать прямоугольник ABCD длиной 10 см, ширина такого прямоугольника будет равна 6,18.
Как рассчитать золотое сечение вручную
В большинстве случаев золотое сечение используется для создания художественных или архитектурных красот, поэтому ключ заключается в знании того, как достичь золотого сечения. Поскольку само число имеет фиксированное значение, все, что нам нужно, это получить одно значение из отношения, либо числитель, либо знаменатель. Другую сторону соотношения можно рассчитать по формуле золотого сечения. Вот как:
Существуют две отдельные формулы для расчета золотого сечения, одна для расчета числителя отношения, а вторая для расчета знаменателя отношения, давайте начнем с того, как рассчитать числитель отношения с помощью формулы золотого сечения.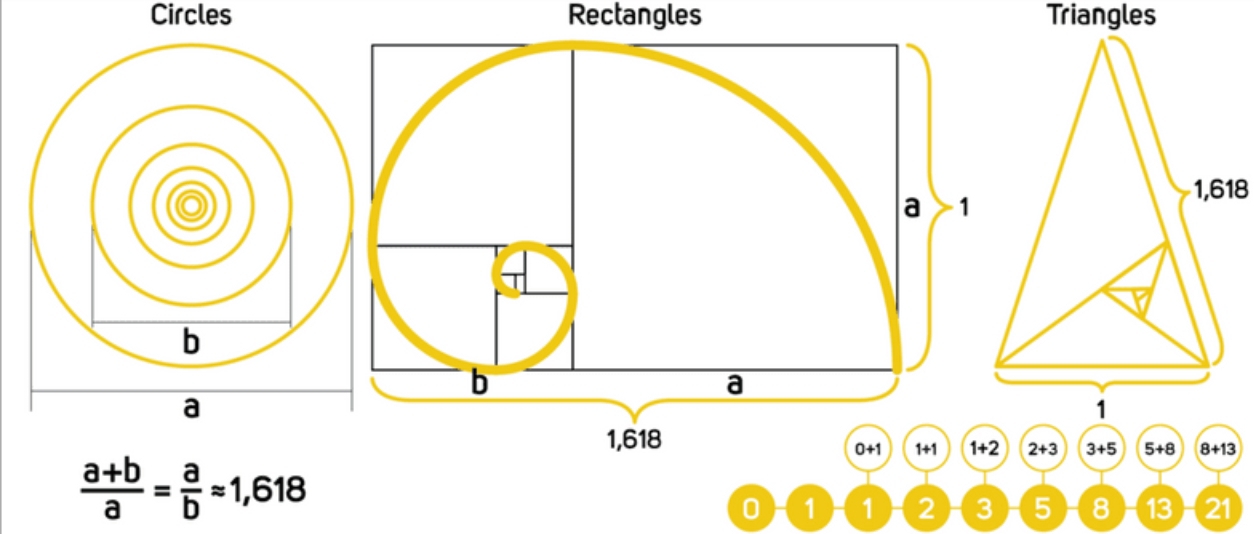
Формула знаменателя золотого сечения
a + b / a = 1,618Расчет знаменателя отношения с использованием thr Golden Rat io Формула знаменателя
Предположим, вы выбрали 3 в качестве числителя отношения.
Если мы рассмотрим нашу формулу, то теперь у нас есть известное значение числителя a = 3, и нам нужно вычислить значение знаменателя отношения b, используя правило золотого сечения,
3 + b / 3 = 1,618
3 + b = 3 x 1,618
3 + b = 4,854
b = 4,854 — 3
b = 1,85 4
a = 3, b = 1,854
Мы знаем есть наш расчет знаменателя отношения с использованием формулы золотого сечения, но что, если нам нужно рассчитать числитель отношения с использованием золотого сечения? Мы просто используем следующую формулу золотого сечения:
Формула числителя золотого сечения
a / b = 1,618 В предыдущем примере мы использовали первый метод, чтобы найти значение b.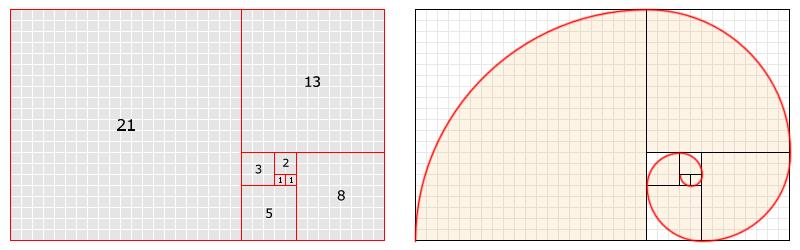
В нашем следующем примере с золотым сечением числитель отношения a неизвестен, а у нас есть значение знаменателя отношения b = 3. Мы будем использовать второе правило золотого сечения для расчета нашего неизвестного значения отношения:
Расчет числителя отношения с использованием thr Golden Формула числителя отношения
a / b = 1,618
a / 3 = 1,618
a = 1,618 x 3
a = 4,854
Две формулы для расчета золотого сечения и приведенные выше примеры позволят вам рассчитать золотое сечение, затем вы можете вручную проверить, выполнили ли вы свои расчеты правильно с помощью калькулятора золотого сечения.
Как пользоваться Калькулятором золотого сечения
Калькулятор золотого сечения, разработанный iCalculator™ ™, представляет собой чрезвычайно простой в использовании онлайн-калькулятор. Этот калькулятор коэффициентов просто требует одно известное значение из пары коэффициентов для расчета неизвестного значения коэффициента с использованием соответствующего уравнения золотого сечения.
Полные расчеты для каждой формулы отображаются рядом, чтобы вы могли понять, как обе части формулы работают рука об руку, кроме того, мы предоставляем сумму двух значений соотношения, отображаем золотое сечение в виде дроби и конвертируем золотое сечение в процент.
В зависимости от того, есть ли у вас значение большей части или меньшей, вам просто нужно ввести данное значение как «a» или «b». После этого все, что вам нужно сделать, это нажать кнопку «Рассчитать».
В двух упомянутых выше примерах, где 3 является большим и меньшим значением, мы использовали калькулятор золотого сечения, чтобы получить правильные результаты. Как и все наши другие цифровые калькуляторы, мы протестировали окончательную версию калькулятора золотого сечения и сравнили его результаты с научным калькулятором.
Использование золотого сечения в реальной жизни
Известный швейцарский архитектор Ле Корбюзье (1887–1965) был известен своей любовью к пропорциям и структурной гармонии.
Он твердо верил, что Вселенная имеет математический порядок, тесно связанный с рядом Фибоначчи и золотым сечением.
В то же время Сальвадор Дали, один из величайших художников в истории, тоже любил работать с концепцией золотого сечения. Почти все его работы в альбомной ориентации созданы на основе золотого прямоугольника, геометрической формы, основанной на золотом сечении.
Золотое сечение также присутствует в природе, вам просто нужно взглянуть на основание сосновых шишек, спиралевидные узоры головок цветочных семян, раковины улиток и наутилусов, примеров множество!
Заключение
Как видно из двух приведенных выше примеров, величайшие архитекторы и художники любили работать с золотым сечением, и многие до сих пор это делают. Золотое сечение придает живописную отделку зданиям и картинам. Хотя вам может понадобиться работать с золотым сечением только для домашней работы или задания, у него также есть много практических применений. И все, что вам нужно, это калькулятор золотого сечения, предоставленный вам iCalculator.