Python модуль числа: 6 способов найти модуль числа в Python 3 — Юрыч BRO на vc.ru

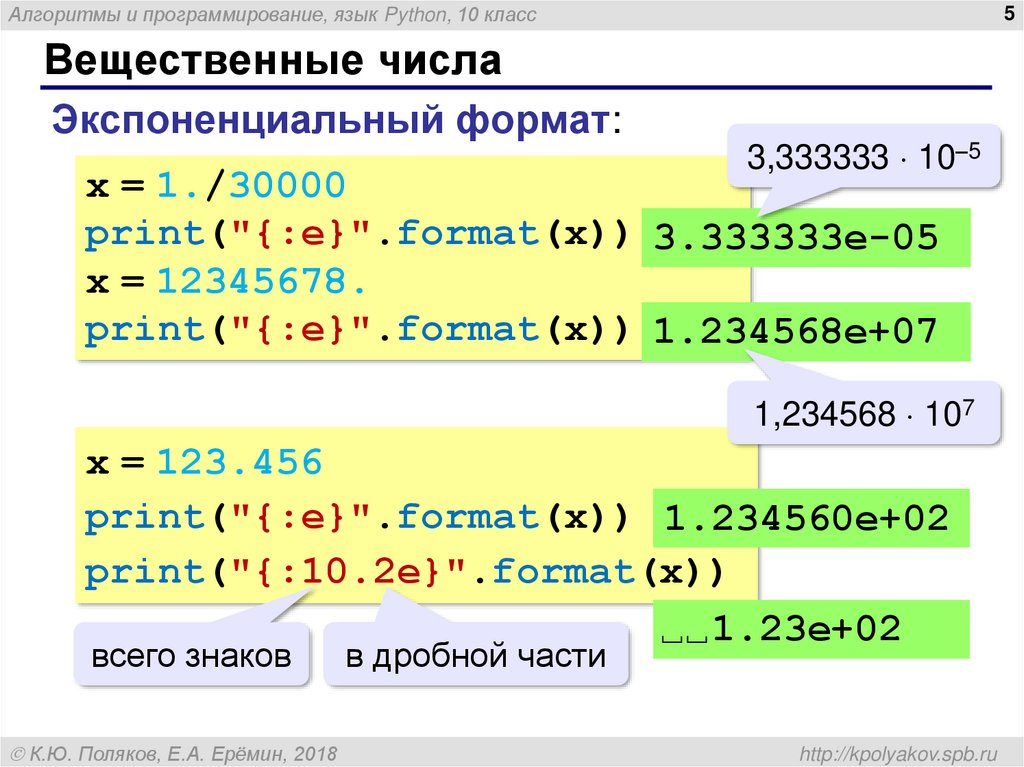
6 способов найти модуль числа в Python 3 — Юрыч BRO на vc.ru

Вступление

5961 просмотров

Всем начинающим кодерам привет!

Модуль числа… Это, казалось бы, простая вещь… да, так оно и есть. Тем не менее — всегда интересно поэкспериментировать и по-новому взглянуть на простое.

Сегодня я покажу вам 6 способов найти модуль числа в Python 3. Я не стал добавлять сюда совсем абсурдные вещи, но немного абсурдности здесь все же будет.

1 способ

Для начала самое очевидное. Проверяем отрицательное число (назовем его x) или положительное, т.е. <0 или нет. В случае отрицательного значения x, его нужно умножить на -1. Можно так:

def abs1(x): if x < 0: return x*(-1) return x

А можно заменить умножение унарным минусом:

def abs1(x): if x < 0: return -x return x

2 способ

Самое короткое решение в нашей статье — найти максимум между x и -x. Таким образом результат всегда будет положительным:

def abs2(x): return max(-x, x)

3 способ

Здесь мы проверяем строку на наличие в ней минуса. Изначально я хотел использовать метод isdigit(), но потом я понял, что метод не считает точку частью числа, поэтому для float в строке метод возвращает False. Поэтому:

​def abs3(x): if ‘-‘ in str(x): return -x return x

4 способ

Этот способ использует условную инструкцию из предыдущей функции, но использует срез, чтобы избавиться от минуса. 3 строка выглядит не очень, приходится дважды менять тип данных результата. По-моему — это ухудшенная версия 3 способа:

def abs4(x): if ‘-‘ in str(x): return float(str(x)[1::]) return x

5 способ

Тут мы будем использовать факт того, что операция квадратного корня в Python всегда возвращает положительный результат. Эту операцию не обязательно брать из библиотеки Math, можно просто возвести число в с степень 0.

def abs5(x): return (x*x)**0.5

6 способ

Здесь мы используем операции со строками, как в 4 способе. Отличие в том, что мы не проверяем строку на наличие минуса. Мы убираем уго, есть он в строке или нет. Метод replace() позволяет убрать все повторения одного символа, что для нас избыточно, но с нулем повторений он тоже работает:

def abs6(x): return float(str(x).replace(‘-‘, »))

Примечание: говоря про положительные значения, правильнее сказать — положительные или нулевые, но я решил не засорять текст такой мелочью.

Статистика быстродействия

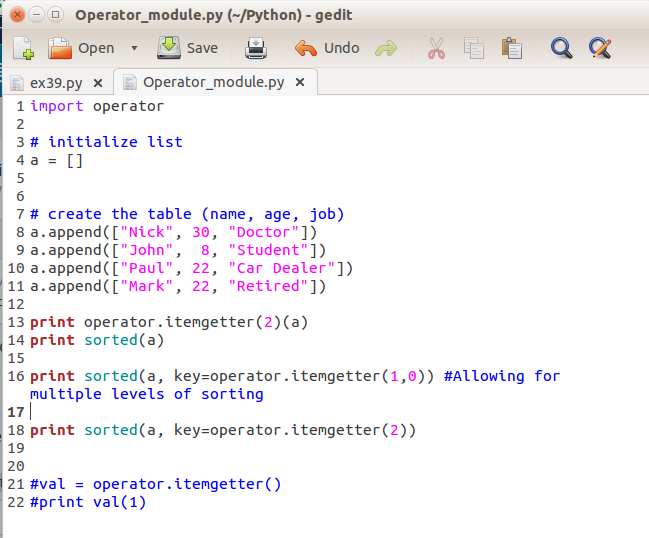
Подведем итоги, узнаем — что же быстрее работает. О том, как замерить время работы программы, я, возможно, расскажу в одной из следующих статей. Ну а пока что приведу статистические данные.

Я измерил время работы данного куска кода, где i — одна из 6 функций.

for j in range(100000): a = (i(1), i(-1), i(1.0), i(-1.0))

И вот что получилось:

Что у нас по итогу? Худший результат показал 4 способ, неудивительно. Самый очевидный способ — первый, на 2 месте. С большим отрывом лидирует 5 вариант, 100000 повторений за 0.79 сек! Математика быстрее логического оператора if и операций со строками.

Заключение

Я надеюсь, что вам была интересна данная статья, и вы разобрались в теме. Если хотите меня дополнить — пишите в комментариях. Удачи в мире IT!

Модуль числа в Python – abs и fabs

Содержание:развернуть

Запускаю китайскую реплику «ТАРДИС», и вот мы в пятом классе. На доске нарисована числовая ось, а на ней выделен отрезок. Его начало в точке 4, а конец — в 8. Учительница говорит, что длину отрезка можно найти путём вычитания координаты начала отрезка из координаты его конца. Вычитаем, получаем 4, и радуемся — мы нашли длину. Ура! 🎉

Перемещаемся на год вперёд, и там происходит странное: учительница выделяет мелом другой отрезок, но делает это в каком-то неправильном месте — левее точки с цифрой «0». Теперь перед нами старая задача, но с новыми числами и даже буквами: A, B, минус 4 и минус 8. Мы начинаем искать длину отрезка AB = [-4;-8]:

Переводим непонимающий взгляд с получившейся отрицательной длины на довольную улыбающуюся учительницу, а затем на доску. Там наверху, рядом с сегодняшней датой, написана тема урока: «Модуль числа».

Что такое модуль числа

Теперь по-взрослому.

Модуль числа называют абсолютной величиной.

Для вещественных чисел модуль определяется так:

Т.е. в любом случае, модуль — число большее или равное 0. Поэтому отрицательная длина в примере хитрой учительницы должна была быть взята по модулю:

Тогда дети бы увидели, что геометрический смысл модуля — есть расстояние. Это справедливо и для комплексных чисел, однако формальное определение для них отличается от вещественного:

, где z — комплексное число: z = x + iy.

В Python для нахождения модуля числа применяются две функции: fabs() из подключаемой библиотеки math и встроенная функция abs().

Abs

В то время как math.fabs() может оперировать только вещественными аргументами, abs() отлично справляется и с комплексными. Для начала покажем, что abs в python работает строго в соответствии с математическим определением.

# для вещественных чисел print(abs(-1)) print(abs(0)) print(abs(1)) > 1 > 0 > 1

Как видно, с вещественными числами всё в порядке. Перейдём к комплексным.

# для комплексных чисел print(complex(-3, 4)) print(abs(complex(-3, 4))) > (-3+4j) > 5.0

Если вспомнить, что комплексное число выглядит так: z = x + iy, а его модуль вычисляется по формуле:

, то можно без труда посчитать, что sqrt(3**2 + 4**2) действительно равно 5.0.

Можно заметить, что abs() возвращает значения разных типов. Это зависит от типа аргумента:

print(type(abs(1))) > <class 'int'> print(type(abs(1. 0))) > <class 'float'> print(type(abs(complex(1.0, 1.0)))) <class 'float'>

В этом кроется ещё одно отличие abs() от fabs(). Функция из модуля math всегда приводит аргумент к вещественному типу, а если это невозможно сделать — выбрасывает ошибку:

print(type(math.fabs(complex(2,3)))) > TypeError: can't convert complex to float

Fabs

Для начала работы с fabs() необходимо импортировать модуль math с помощью следующей инструкции:

import math

Мы уже выяснили, что fabs() не работает с комплексными числами, поэтому проверим работу функции на вещественных:

print(math.fabs(-10)) print(math.fabs(0)) print(math.fabs(10)) > 10.0 > 0.0 > 10.0

Функция производит вычисления в соответствие с математическим определением, однако, в отличие от

print(type(math. fabs(10))) > <class 'float'>

Основные свойства модулей

# Квадрат модуля = квадрату числа print(pow(4, 2) == pow(abs(4), 2)) > True # |x| = |-x| print(abs(-10) == abs(10)) > True # Модуль произведения = произведению модулей: |ab|=|a||b| print(math.fabs(11 * 3) == math.fabs(11) * math.fabs(3)) > True # Аналогично для деления: |a/b|=|a|/|b| print(math.fabs(48/8) == math.fabs(48) / math.fabs(8)) > True # |a ** b| = |a| ** b print(abs(2 ** 10) == abs(2) ** 10) > True

И еще несколько важных неравенств:

• m <= |m|
• -|m| <= m
• |m| >= 0
• |m + n| <= |m| + |n|
• |m – n| <= |m| + |n|
• |m| — |n| <= |m + n|
• |m + n| >= ||m| — |n||
• |m – n| >= ||m| — |n||

чисел — Числовые абстрактные базовые классы — Документация по Python 3.11.1

Исходный код: Lib/numbers.py

Модуль номеров ( PEP 3141 ) определяет иерархию числовых абстрактные базовые классы, которые постепенно определяют больше операций.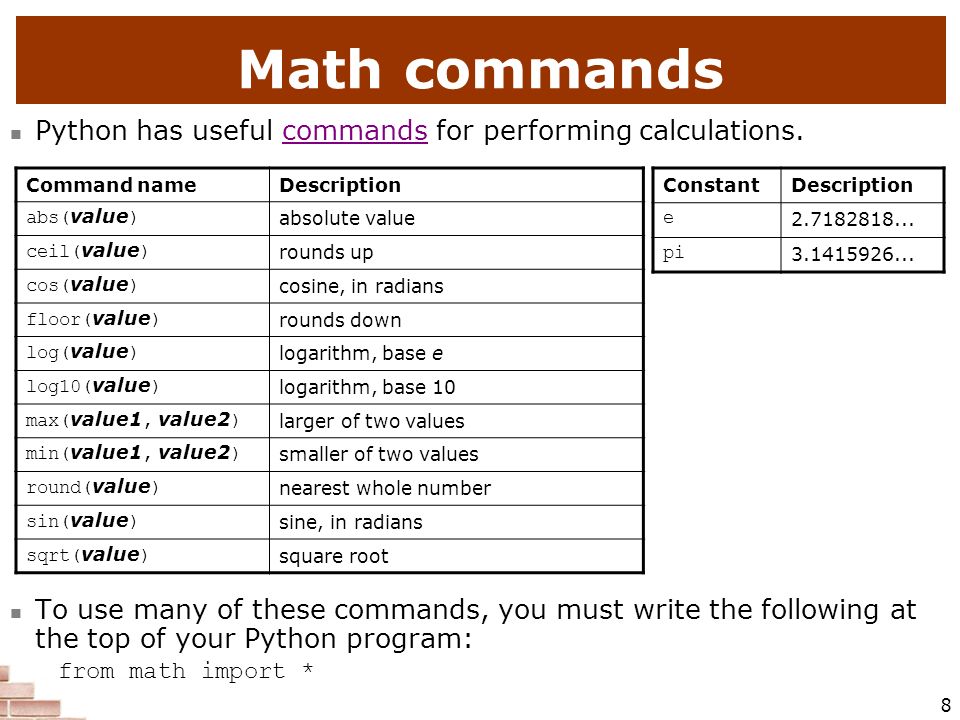 Ни один из типов, определенных в этом модуле, не предназначен для создания экземпляров.

класс номеров.Номер

Корень числовой иерархии. Если вы просто хотите проверить, является ли аргумент x — это число, неважно, какого рода, используйте isinstance(x, Number) .

Числовая башня

класс номеров.Комплекс

Подклассы этого типа описывают комплексные числа и включают операции которые работают на встроенном комплексе типа . Это: преобразования в сложный и

логический , реальный , образ , + , - , *, / , ** , абс() , сопряженное() , == , и != . Все, кроме - и != , являются абстрактными.

настоящий

Реферат. Извлекает действительную составляющую этого числа.

изображение

Реферат. Извлекает мнимую составляющую этого числа.

абстрактный метод сопряженный ()

Реферат. Возвращает комплексное сопряжение. Например, (1+3j).conjugate() == (1-3j) .

класс номеров.Настоящий

К Complex , Real добавляет операции, которые работают с реальными числа.

Короче говоря, это: преобразование в float , math.trunc() , round() , math.floor() , math.ceil() , divmod() , //, % , < , <= , > и >= .

Real также предоставляет значения по умолчанию для complex() , real , imag и conjugate() .

класс номеров. Rational

Подтипы Действительное и добавляет числитель и знаменатель свойств. Он также обеспечивает значение по умолчанию для с плавающей запятой() .

Числитель и знаменатель значений должны быть экземплярами

Integral и должны быть в наименьших условиях с знаменатель положительный.

числитель

Реферат.

знаменатель

Реферат.

класс номеров. Интеграл

Subtypes Rational и добавляет преобразование в 9, | , ~ .

Примечания для разработчиков типа

Разработчики должны быть осторожны, чтобы сделать равные числа равными и хешировать их к одним и тем же значениям. Это может быть тонко, если есть два разных расширения действительных чисел. Например, дроби . Дробь реализует hash() следующим образом:

 по определению __hash__(я):
    если self.знаменатель == 1:
        # Получить целые числа правильно.
        хэш возврата (self.numerator)
    # Дорогая проверка, но точно правильная.
    если я == поплавок (я):
        вернуть хэш (с плавающей запятой (сам))
    еще:
        # Используйте хэш кортежа, чтобы избежать высокой частоты коллизий на
        # простые дроби.
        хеш возврата((self.numerator, self.denominator))
 

Добавление дополнительных числовых ABC

Есть, конечно, и другие возможные азбуки для чисел, и это было бы быть плохой иерархией, если она исключает возможность добавления те. Вы можете добавить MyFoo между Complex и Реальный с:

 класс MyFoo (комплекс): ...
MyFoo.register(Настоящий)
 

Реализация арифметических операций

Мы хотим реализовать арифметические операции так, чтобы смешанный режим операции либо вызывают реализацию, автор которой знал о типы обоих аргументов или преобразовать оба в ближайший встроенный тип и сделать операцию там. Для подтипов Интеграл , это означает, что __add__() и __radd__() должны быть определены как:

 класс MyIntegral(Integral):
    def __add__(я, другой):
        если isinstance (другое, MyIntegral):
            вернуть do_my_adding_stuff(я, другой)
        elif isinstance (другое, OtherTypeIKnowAbout):
            вернуть do_my_other_adding_stuff(я, другой)
        еще:
            вернуть нереализованный
    def __radd__(я, другой):
        если isinstance (другое, MyIntegral):
            вернуть do_my_adding_stuff(другое, себя)
        elif isinstance (другое, OtherTypeIKnowAbout):
            вернуть do_my_other_adding_stuff(другое, себя)
        elif isinstance (другой, интеграл):
            вернуть int(другое) + int(себя)
        elif isinstance (другое, реальное):
            вернуть поплавок (другой) + поплавок (сам)
        elif isinstance (другой, сложный):
            вернуть комплекс (другой) + комплекс (я)
        еще:
            вернуть нереализованный
 

Существует 5 различных случаев для операции смешанного типа над подклассами Комплекс . Я буду ссылаться на весь приведенный выше код, который не см. MyIntegral и OtherTypeIKnowAbout как «шаблон». a будет экземпляром A , который является подтипом Комплекс ( a : A <: Комплекс ) и b : B <: Комплекс . Я рассмотрю a + b :

1. Если А определяет __add__() который принимает b , все хорошо.

2. Если A возвращается к стандартному коду, вернуть значение из __add__() , мы бы упустили возможность что B определяет более интеллектуальный __radd__() , поэтому шаблон должен возвращать NotImplemented из __добавить__() . (Или может не реализовать __add__() в все.)

3. Затем B __radd__() получает шанс. Если он принимает и , все хорошо.

4. Если он возвращается к шаблону, больше нет возможных методы, чтобы попробовать, так что это где реализация по умолчанию должен жить.

5. Если B <: A , Python пытается использовать B.__radd__ до А.__добавить__ . Это нормально, потому что это было реализовано с помощью знание A , поэтому он может обрабатывать эти экземпляры до делегирование Комплекс .

Если A <: Сложные и B <: Действительное без обмена какими-либо другими знаниями, тогда подходящей общей операцией является операция, включающая встроенный в комплексе , и оба __radd__() приземляются там, поэтому a+b == б+а .

Поскольку большинство операций над любым данным типом будут очень похожими, может быть полезно определить вспомогательную функцию, которая генерирует прямые и обратные экземпляры любого заданного оператора. Например, дробей.Дробь использует:

 по определению _operator_fallbacks (мономорфный_оператор, резервный_оператор):
    защита вперед (а, б):
        если isinstance(b, (int, Fraction)):
            вернуть monomorphic_operator(a, b)
        elif isinstance(b, float):
            вернуть fallback_operator (с плавающей запятой (а), б)
        elif isinstance (b, комплекс):
            вернуть fallback_operator (комплекс (а), б)
        еще:
            вернуть нереализованный
    forward.__name__ = '__' + fallback_operator.__name__ + '__'
    вперед.__doc__ = мономорфный_оператор.__doc__
    деф реверс(б, а):
        если isinstance(a, Rational):
            # Включает целые числа.
            вернуть monomorphic_operator(a, b)
        elif isinstance(a, Real):
            return fallback_operator (с плавающей запятой (a), с плавающей запятой (b))
        elif isinstance(a, Комплекс):
            return fallback_operator (комплекс (а), комплекс (б))
        еще:
            вернуть нереализованный
    reverse. __name__ = '__r' + резервный_оператор.__name__ + '__'
    reverse.__doc__ = monomorphic_operator.__doc__
    возврат вперед, назад
определение _add (а, б):
    """а + б"""
    return Fraction (a.числитель * b.знаменатель +
                    б.числитель * а.знаменатель,
                    а.знаменатель * б.знаменатель)
__add__, __radd__ = _operator_fallbacks(_add, operator.add)
# ...
 

Python Numbers — GeeksforGeeks

Числовые типы данных хранят числовые значения. Это неизменяемые типы данных, что означает, что изменение значения числового типа данных приводит к созданию нового выделенного объекта.

Различные типы чисел типов данных:

• INT
• Float
• комплекс

Посмотрите каждый из них:

Int (Integers) . отрицательные числа, но не дроби. В Python нет ограничений на длину целочисленного значения.

Example 1: Creating int and checking type

Python3

Вывод:

 <класс 'int'> 

Пример 2: Выполнение арифметических операций с типом int

a = 5

b = 6

c = a + b

print ( "Дополнение:" , C)

D =

E = 6

6

print ( "Subtraction:" ,f)

g = 8

h = 2

I = G / / H

ПРИНАНИЯ ( "999999 , ( ". 0009

j = 3

k = 5

l = j * k

print ( "Умножение:" , l)

M = 25

N = 5

= 5

= 5

0395 o = m % n

print ( "Modulus:" ,o)

p = 6

q = 2

r = p * * q

print ( "Exponent:" ,r)

Вывод:

 Дополнение: 11
Вычитание: 3
Дивизия: 4
Умножение: 15
Модуль: 0
Показатель степени: 36 

Это действительное число с представлением с плавающей запятой. Он указывается десятичной точкой. Необязательно, символ e или E, за которым следует положительное или отрицательное целое число, может быть добавлен для указания экспоненциального представления. . Некоторые примеры чисел, представленных в виде чисел с плавающей запятой: 0,5 и -7,823457.

Их можно создать напрямую, введя число с десятичной точкой или используя такие операции, как деление целых чисел. Лишние нули в конце числа автоматически игнорируются.

Example 1: Creating float and checking type

Python3

Вывод:

Как мы видели, деление любых двух целых чисел дает число с плавающей запятой.

Число с плавающей запятой также создается путем выполнения операции с двумя числами с плавающей запятой или с числом с плавающей запятой и целым числом.

Python3

Выход:

 <Класс 'Float'> 

Пример 2: . = 5.5

B = 3,2

C = A + B

+ B

+ B

+ B

+ B

+ B

C = A - B

Print ( ". c)

c = a / b

print ( "Division:" , c)

c = A * B

Печать ( "Умножение:" , c)

9918

99918

. Вычитание: 2,3 Подразделение: 1.71875 Умножение: 17,6

Примечание: Точность числа с плавающей запятой только до 15 знаков после запятой, 16-е место может быть неточным.

.  Добавление: (3+8JJ).
Вычитание: (-1+8j)
Подразделение: (1.307692307692308+0.5384615384615384j)
Умножение: (-13+13j) 

 6. 6 

 2.0
5
<класс 'целое число'>
<класс 'плавающий'>
(5+0j)
(6.5+0j) 

 3,30000000000003 

 0.199999999999996 

 1.0011001100110011001100110011001100110011001100110011   

 1.19999999999999995559107
937383830547332763671875 

 3. 3 

• Когда мы хотим определить требуемую точность самостоятельно
• Для финансовых приложений, которым требуются точные десятичные представления Python и функции, предоставляемые этим модулем, см. в разделе Десятичные функции в Python

  Случайные числа в Python

  Python предоставляет модуль random для генерации псевдослучайных чисел. Этот модуль может создавать случайные числа, выбирать случайный элемент из последовательности в Python и т. д.

  Example 1: Creating random value

  Python3

  import random   print (random.random())

  Output

   0. 9867200671824407 

  Пример 2: Выбор случайного элемента из строки или списка0008 random

   

  s = 'geeksforgeeks'

  L = [ 1 , 2 , 3 , 5 , 6 , 7 , 7 , 8 , 0 ]

  (случайный.0009

  печать (случайный.выбор(L))

  Вывод

   f
  0 

  Примечание: Дополнительную информацию о случайных числах см. в нашем руководстве по работе со случайными числами. Пример:

  Python3

  Импорт Математика A = 3,5 ". "") Печать (Math.ceil (a)) Печать ( " ") Печать (math.floor (a)) Печать ( "Значение 3,5 ** 2 IS:" , конец = 9000 «. Печать ( POW (A, 2 )) Print ( "Значение Log2 из 3,5 года. Оставить комментарий Добавить комментарий Отменить ответ Ваш адрес email не будет опубликован. Обязательные поля помечены * Комментарий * Имя * Email * Сайт