Отрицательные и положительные: определение, примеры, какое число больше положительное или отрицательное

Как сложить только положительные или отрицательные числа в Excel

Автор Ivan Excel Admin На чтение 2 мин Просмотров 2.8к. Опубликовано 18.05.2022

Если вы создаете, например, отчеты, то вам может понадобится суммировать только положительные или отрицательные числа.

Это довольно просто можно сделать, с помощью функции СУММ.

Я продемонстрирую вам разные варианты использования этой функции.

Итак, начнём!

Содержание

1. Складываем только положительные значения
2. Складываем положительные числа больше 100
3. Проверяем на критерий отличный от суммирования диапазон
4. Складываем только отрицательные числа

Складываем только положительные значения

Допустим, у нас есть такая табличка:

Наша задача — посчитать сумму только положительных значений

В такой ситуации, формула примет такой вид:

=СУММЕСЛИ(B2:B8;">0";B2:B8)

Мы используем три аргумента:

1. Диапазон, который будет проверяться на критерий;
2. Критерий;
3. Диапазон, который мы суммируем.

Естественно, первый и третий критерии, могут различаться.

Складываем положительные числа больше 100

В прошлом разделе статьи мы сложили только положительные числа, а теперь сложим числа больше 100.

Допустим, у нас есть такая табличка:

Для выполнения такой задачи, формула примет такой вид:

=СУММЕСЛИ(B2:B8;">100";B2:B8)

Готово!

Проверяем на критерий отличный от суммирования диапазон

Ранее я уже говорил, что диапазон, который мы проверяем на критерий, может отличаться от того, который будем суммировать..

Допустим, у нас есть такая табличка.

Наша задача — сложить только те значения из В столбика, для которых значение из С столбика положительно.

Формула принимает такой вид:

=СУММЕСЛИ(C2:C6;">0";B2:B6)

Формула все та же, только мы указали разные диапазоны в 1 и 3 критерии.

Складываем только отрицательные числа

Тут все точно также, как и в первом разделе статьи, только с одним изменением.

Допустим, у нас есть такая табличка:

Наша задача — сложить только отрицательные значения.

Формула принимает такой вид:

=СУММЕСЛИ(B2:B8;"<0";B2:B8)

Критерий отделяет только отрицательные числа, а далее они складываются.

Вы можете изменять критерий, непосредственно, под вашу ситуацию без всяких проблем.

Вот и все! Мы рассмотрели как складывать положительные или отрицательные числа с помощью функции СУММЕСЛИ.

Надеюсь, эта статья оказалась полезной для вас!

Форматирование отрицательных процентных значений для упрощения их поиска

Excel для Microsoft 365 Excel 2021 Excel 2019 Excel 2016 Excel 2013 Еще…Меньше

Отрицательные процентные показатели может быть сложно определить при сканировании. Их можно легко найти, применив специальное форматирование к отрицательным процентным долям или создав правило условного форматирования.

Создание пользовательского формата

Сделайте следующее:

1. Вы можете выбрать ячейки с отрицательными процентами. Чтобы выбрать несколько ячеек, выберем каждую из них, удерживая на клавише CTRL.

2. На вкладке Главная нажмите кнопку Формат >формат ячеек.

3. В окне Формат

   ячеек в списке Категория выберите настраиваемые.

4. org/ListItem»>

   В поле Тип введите следующий формат: 0,00%;[ Красный]-0,00 %.

   Отрицательный процент будет выделен красным цветом.

   Совет: Пользовательские форматы сохраняются вместе с книгой. В следующий раз, когда потребуется применить его, выполните шаги 2 и 3 выше, и вы найдете пользовательский формат в списке Тип. Чтобы использовать пользовательский формат в других книгах, сохраните книгу в качестве шаблона, а затем на его основе будут базироваться будущие книги.

Создание пользовательского правила форматирования

Выполните эти действия, чтобы создать пользовательское правило форматирования, которое будет доступно только на том сайте, на котором оно создается.

org/ItemList»>

1. Вы можете выбрать диапазон ячеек, в который нужно ввести отрицательные проценты.

2. На вкладке Главная нажмите кнопку Условное форматирование и выберите пункт Создать правило. 

3. В окне Новое правило форматирования выберите форматировать только ячейки, содержащие.

4. Во всплывающее окно Изменение описания правила в области Форматирование только ячеек с, выберите меньше.

5. В поле введите число 0.

6. Нажмите кнопку Формат.

7. В окне Формат ячеек выберите шрифт или цвет ячейки, а затем дважды нажмите кнопку ОК.

При введите отрицательное процентное соотношение в выбранном диапазоне, оно автоматически будет отформатировано красным цветом.

Дополнительные сведения

Вы всегда можете задать вопрос специалисту Excel Tech Community или попросить помощи в сообществе Answers community.

Основные правила для положительных и отрицательных чисел.

РАЗРЕШЕНИЕ

Принадлежит YourDictionary, Copyright YourDictionary

Числа больше нуля называются положительными числами, а числа меньше нуля — отрицательными числами. Это означает, что они падают по обе стороны от числовой прямой. Однако то, что они находятся на одной линии, не означает, что они следуют одним и тем же правилам! Продолжайте читать список основных правил использования положительных и отрицательных чисел в математике.

При использовании положительных и отрицательных чисел используются правила для чисел со знаком (числа с положительными или отрицательными знаками перед ними). Эти шаги, также известные как операции над числами со знаком, помогут вам избежать путаницы и решить математические задачи как можно быстрее и правильнее.

Следуйте этим правилам, чтобы определить лучший способ сложения, вычитания, умножения и деления положительных и отрицательных чисел. Помните, что если нет знака + или -, число положительное.

Реклама

Дополнение: одинаковые знаки, добавьте числа

Когда вы складываете два числа вместе, и они имеют одинаковый знак (два положительных или два отрицательных числа), сложите числа и сохраните знак. Например:

• 1 + 1 = 2
• 51 + 32 = 83
• -14 + (-6) = -20
• -196 + (-71) = -267

что уравнения с двумя положительными числами имеют положительные суммы, а уравнения с двумя отрицательными числами имеют отрицательные суммы. Если вы используете числовую прямую для решения задачи, добавление двух положительных чисел приведет к положительной стороне, а добавление двух отрицательных чисел приведет к отрицательной стороне.

Сложение: разные знаки, вычитание чисел

Если вы складываете положительные и отрицательные числа вместе, вычтите меньшее число из большего и используйте знак из большего числа. Например:

• 6 + (-5) = 1
• -17 + 22 = 5
• -100 + 54 = -45
• 299 + (-1) = 298

As как видите, сложение чисел с разными знаками на самом деле является формой вычитания. При использовании числовой прямой ваша сумма будет ближе к нулю.

Реклама

Вычитание: Переключение на сложение

Вычитание положительных и отрицательных чисел означает, что вы складываете противоположные числа или добавите обратное. Замените знак вычитания на сложение, а следующий за ним знак измените на противоположный. Затем следуйте инструкциям по добавлению. Например:

• -3 -(+5) становится -3 + (-5) = -8
• 9 -(-7) становится 9 + (+7) = 16
• -14 -(+8) становится -14 + (-8) = -22
• 25 -(-9).0) становится 25 + (+90) = 115

Хороший совет: всякий раз, когда вы видите знак минус и знак минус вместе, например, в 9 — (-7), немедленно превращайте их в положительные знаки. Отрицательные знаки компенсируют друг друга, и уравнение становится задачей на сложение.

Умножение и деление: один и тот же знак, положительный результат

Кажется, что умножение и деление сложнее, чем сложение и вычитание, но на самом деле они намного проще. Правило умножения положительных и отрицательных чисел с одинаковым знаком (два положительных или два отрицательных) состоит в том, что произведение всегда будет положительным. Например:

• 8 x 4 = 32
• (-8) x (-4) = 32
• 10 x 9 = 90
• (-10) x (-9) = 90

подразделение. При делении числа на другое число с тем же знаком частное (ответ) положительно. Например:

• 12 ÷ 6 = 2
• -12 ÷ (-6) = 2
• 100 ÷ 5 = 20
• -100 ÷ (-5) = 20

9000 4 Почему умножение или деление двух отрицательных чисел всегда дает положительное число? Подобно вычитанию отрицательных чисел, эти операции превращают отрицательные числа в противоположные (обратные). По сути, вы несколько раз вычитаете отрицательное число — и, как показано выше, вычитание отрицательных чисел приводит к положительному уравнению.

Реклама

• ОПИСАНИЕ

  правила умножения и деления двух чисел, положительных и отрицательных

• ИСТОЧНИК

  Created by Karina Goto for YourDictionary 9 0005

• РАЗРЕШЕНИЕ

  Принадлежит YourDictionary, Copyright YourDictionary

Умножение и деление: противоположный знак, отрицательный результат

При умножении положительного и отрицательного числа произведение всегда будет отрицательным. Неважно, в каком порядке стоят знаки. Например:

• 6 х (-7) = -42
• -7 х 6 = -42
• 12 х (-11) = -132
• -11 х 12 = -132

Во всех этих случаях , вам сначала нужно умножить или разделить числа. Затем решите, является ли произведение или частное положительным (два положительных или два отрицательных в уравнении) или отрицательным (один положительный и один отрицательный в уравнении).

Еще один способ подумать о сложении положительных и отрицательных чисел — посмотреть на знаки подряд. Два одинаковых знака подряд (++ или —) означают, что вы складываете числа, а два разных знака подряд (+- или —) означают, что вы вычитаете. Например:

• 7 + (+2) = 9 (++ похожи на знаки, поэтому уравнение является сложением)
• 9 + (-8) = 1 (+- не похожи на знаки, поэтому уравнение представляет собой вычитание)
• 11 — (+13) = 2 (-+ не похожи на знаки, поэтому уравнение представляет собой вычитание)
90 003 15 — (-10) = 25 (— подобны знакам, поэтому уравнение представляет собой сложение)

Этот метод следует тем же правилам, что и выше, но может помочь вам решить проблему быстрее, если вы предпочитаете работать со знаками заранее. Как только вы концептуально поймете положительные и отрицательные числа, вы сможете решить, какой метод лучше всего подходит для вас.

Объявление

Понимание основ математики

Как только вы познакомитесь с основами математики и ее правилами, перед вами откроется весь математический мир. В отличие от других предметов, в математике нет нюансов или интерпретаций — она просто такая, какая есть! Для дополнительной математической практики ознакомьтесь с инструкциями по решению задач на деление в длину (с примерами). Вы также можете просмотреть различные типы чисел в математике перед следующим заданием по математике.

Отрицательные и положительные правила | Сложение, вычитание и примеры

Что такое целые числа?

Целое число — это число, которое можно записать без дробной части. Другими словами, целое число — это целое число, которое может быть положительным, отрицательным или равным нулю. Следовательно, мы можем сказать, что целые числа представляют собой совокупность целых чисел и отрицательных чисел. Набор целых чисел представлен Z и может быть записан как – 

Z = { …….. – 3, – 2, – 1, 0, 1, 2, 3 …….. }

Что такое отрицательные и положительные целые числа?

В соответствии с натуральными числами, 1, 2, 3, 4, 5 …… и т. д., мы создаем новые числа, -1, -2, -3, -4, -5 и так далее. Эти числа называются минус один, минус два, минус три и т. д. такие, что –

1 + ( – 1 ) = 0

2 + ( – 2 ) = 0

3 + ( – 3 ) = 0

Итак, – 1 называется минусом 1, -2 называется отрицательное число 2 и каждое отрицательное число противоположно своему положительному аналогу. Если мы объединим эти отрицательные числа с положительными, вместе мы получим набор чисел, которые мы называем целыми числами.

Числа 1, 2, 3, 4 ….. являются натуральными числами и называются положительными целыми числами, а числа – 1, – 2 , – 3 и т. д. называются отрицательными целыми числами.

Символ для отрицательных целых чисел

Мы используем символ «–» для обозначения отрицательных целых чисел, и тот же символ используется для обозначения вычитания. Однако контекст, в котором используется этот символ, проясняет, хотим ли мы использовать его для отрицательного целого числа или для вычитания. Давайте разберемся на примере.

Предположим, мы запишем число – 5. Это будет означать «минус пять». Точно так же – 17 будет читаться как «минус семнадцать».

Теперь напишем 5 – 3. Здесь мы видим, что «-» находится между двумя числами. Это будет читаться как «пять минус три». Следовательно, здесь символ использовался для вычитания двух чисел.

Символ для положительных целых чисел

Мы используем символ «+» для обозначения положительных целых чисел, и тот же символ используется для обозначения сложения. Однако контекст, в котором используется этот символ, проясняет, хотим ли мы использовать его для положительного целого числа или для сложения. Давайте разберемся на примере.

Предположим, мы пишем число + 5. Это будет читаться как «плюс пять». Точно так же + 17 будет читаться как «плюс семнадцать».

Теперь давайте напишем 5 + 3. Здесь мы видим, что «+» находится между двумя числами. Это будет читаться как «пять плюс три». Следовательно, здесь символ использовался для сложения двух чисел.

Здесь важно отметить, что если с числом не связан ни один знак, оно читается как положительное число. Например, + 5 также можно записать просто как 5. 

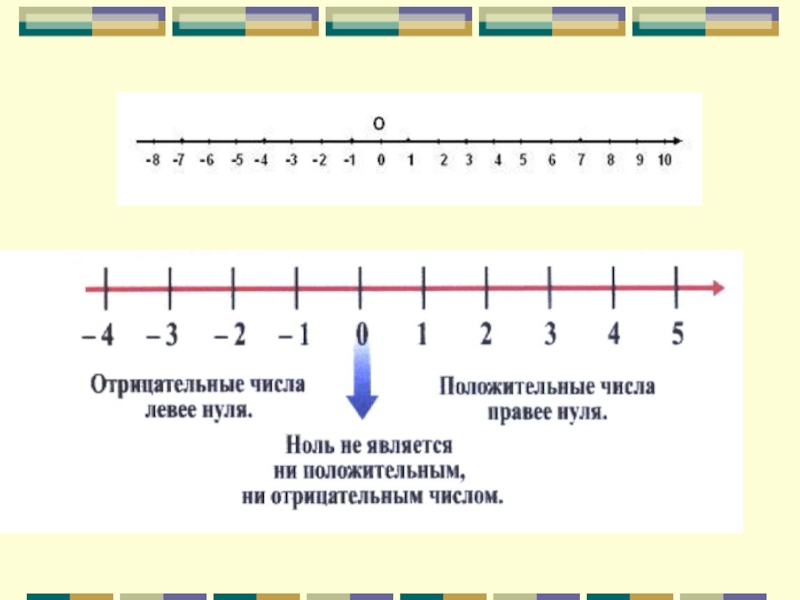
Отрицательные и положительные целые числа в числовой строке

Мы научились представлять целые числа в числовой строке. для представления целых чисел на числовой прямой. Напомним, что числовая линия — это прямая горизонтальная линия с числами, расположенными через равные промежутки, которая обеспечивает визуальное представление чисел. Основные операции, такие как сложение, вычитание, умножение и деление, могут выполняться на числовой прямой. Числа увеличиваются, когда мы движемся к правой стороне числовой линии, и уменьшаются, когда мы движемся влево. Целые числа представлены в числовой строке, как показано ниже – 9.0005

Выше показано визуальное представление стандартной числовой строки для представления целых чисел. Как хорошо видно, при движении слева направо значение целых чисел увеличивается, а при движении справа налево — уменьшается.

Давайте разберемся на примере

Построим 6 и – 6 на числовой прямой.

Правила сложения целых положительных и отрицательных чисел

Мы знаем, как складывать два целых числа. Мы можем складывать целые числа таким же образом, с той лишь разницей, что мы должны выполнять сложение и отрицательных чисел. следующие правила должны соблюдаться для сложения целых чисел –

1. Чтобы сложить два целых положительных или два отрицательных числа, мы складываем их абсолютные значения и присваиваем сумме знак слагаемого.
2. Чтобы сложить положительное или отрицательное целое число, мы определяем разность их абсолютных значений и присваиваем сумму слагаемого, имеющего большее абсолютное значение.

Давайте разберемся на примере.

Пример

Предположим, у нас есть два целых числа, 1258 и 3214, и мы хотим найти их сумму.

Решение

Сначала мы проверим знак обоих чисел. Мы видим, что оба числа одного знака и являются целыми положительными числами. Поэтому по правилам, изложенным выше, мы сложим абсолютное значение обоих чисел и присвоим им положительный знак. У нас будет

1258 + 3214 = 4473

. Рассмотрим другой пример.

Предположим, у нас есть два целых числа — 523 и 937, и мы хотим найти их сумму.

Решение

Мы видим, что складываемые числа имеют разные знаки, поэтому для их сложения находим разность их абсолютных значений и присваиваем знак слагаемого, имеющего большее абсолютное значение. Таким образом, мы будем иметь,

( — 5523 ) + 937 = 937 — 523 = 414

Вышеприведенные правила можно резюмировать как —

Правила вычитания положительных и отрицательных целых чисел

Мы знаем, как вычитать два целые числа. Важно помнить, что в целых числах мы не можем вычесть большее целое число из меньшего целого числа. В случае вычитания целых чисел из целых чисел мы можем вычесть большее целое из меньшего целого. Также важно помнить, что вычитание — это процесс, обратный сложению.

При вычитании целых чисел необходимо соблюдать следующее правило – 

Если a и b два целых числа, то для вычитания b из a меняем знак b и прибавляем его к a, т.е.

Пример

Предположим, мы хотим вычесть – 1235 из 4532

Решение

Чтобы вычесть – 1235 из 4532, мы изменим знак – 1235 и прибавляем к 4532. У нас будет

4532 – ( – 1235 ) = 4532 + 1235 = 5767

Следовательно, 4532 – ( – 1235 ) = 5767

Вышеприведенные правила можно резюмировать как – 

90 174 Правила умножения целых положительных и отрицательных чисел

Мы знаем, что процесс нахождения произведения двух или более чисел называется умножением, а полученный таким образом результат называется произведением . Умножение целых чисел похоже на умножение натуральных чисел и целых чисел, за исключением того факта, что мы также должны позаботиться об умножении отрицательных чисел.

При умножении целых чисел соблюдаются следующие правила – 

Случай 1 – Когда у вас есть два целых числа противоположных знаков – Произведение двух целых чисел противоположных знаков равно аддитивному обратному произведению их абсолютных значений. Это означает, что для того, чтобы найти произведение положительного и отрицательного целых чисел, нам нужно найти произведение абсолютных значений и присвоить произведению знак минус. Давайте разберемся на примере.

Пример

Предположим, у вас есть два числа 7 и -4, и вы хотите найти произведение. Умножение 7 и -4 будет дано как два целых числа с одинаковыми знаками равны произведению их модулей. Это означает, что для того, чтобы найти произведение двух целых чисел, независимо от того, являются ли оба числа положительными или оба отрицательными, нам нужно будет найти произведение их абсолютных значений. Давайте разберемся в этом на примере.

Пример

Предположим, у вас есть два числа 7 и -4, и вы хотите найти произведение. Умножение – 7 и -4 будет равно 

(– 7) x (– 4) = (7 x 4) = 28

Аналогично, (6) x 9 = (6 x 9) = = = 54

Вышеприведенные правила можно резюмировать как –  900 05

Правила деления положительных и отрицательных целых чисел

Мы знаем, что деление — это процесс повторяющегося вычитания. То же самое относится и к делению целых чисел. В делении есть четыре важных члена, а именно делитель, делимое, частное и остаток. Формула для делителя составляет все эти четыре термина. На самом деле именно соотношение этих четырех членов между собой определяет формулу деления. Если мы умножим делитель на частное и прибавим результат к остатку, то получим делимое. Это значит,

Делимое = Делитель x Частное + Остаток

Напомним, что деление целых чисел является обратным процессом умножения. Распространим ту же идею на деление целых чисел. Для деления целых чисел соблюдаются следующие правила: 

Случай 1 – Частное двух целых чисел, как положительных, так и отрицательных, является положительным целым числом, равным частному соответствующих абсолютных значений целых чисел. Это означает, что при делении двух целых чисел с одинаковыми знаками мы делим значения независимо от знака и ставим положительный знак в частном. Давайте разберемся на примере.

Пример

Предположим, у вас есть два числа — 20 и -4, и вы хотите разделить первое целое число на другое. У нас будет

-20 ÷ -4 = $\frac{20}{4}$ = 5

Случай 2 – Частное положительного и отрицательного целых чисел является отрицательным целым числом, и его абсолютное значение равно частному соответствующих абсолютных значений целых чисел. Это означает, что при делении целых чисел с разными знаками мы делим значение независимо от знака и ставим в частное знак минус. Давайте разберемся на примере.

Пример

Предположим, у вас есть два числа — 20 и 4, и вы хотите разделить первое целое число на другое. Мы будем иметь,

-20 ÷ 4 = – $\frac{20}{4}$ = – 5

Приведенные выше правила можно резюмировать как – 

Свойства отрицательных и положительных целых чисел

Давайте теперь обсудим некоторые свойства положительных и отрицательных целых чисел – 

Свойство замыкания

Свойство замыкания указывает, что когда операция выполняется над двумя числами, результат также будет того же типа, что и числа, над которыми была выполнена операция.

Следовательно, сложение, вычитание и умножение как положительных, так и отрицательных целых чисел удовлетворяют свойству замыкания, в то время как деление целых чисел не удовлетворяет свойству замыкания.

Коммутативное свойство 

Коммутативное свойство утверждает, что при выполнении операции над двумя числами порядок, в котором расположены числа, не имеет значения.

Для любых двух целых чисел, a и b,

a + b = b +a

a – b ≠ b – a

a x b = b x a

a ÷ b ≠ b ÷ a

Следовательно, сложение и умножение как положительных, так и отрицательных целых чисел удовлетворяют коммутативному свойству, а вычитание и деление как положительных, так и отрицательных целых чисел не удовлетворяют коммутативному свойству.

Ассоциативное свойство

Ассоциативное свойство утверждает, что когда операция выполняется более чем с двумя числами, порядок, в котором расположены числа, не имеет значения.

Для любых трех целых чисел a, b и c

a + (b + c) = (a + b) + c

a – (b – c) ≠ (a – b) – c

a x (b x c) = (a x b) x c

900 04 a ÷ ( b ÷ c ) ≠ ( a ÷ b ) ÷ c

Следовательно, сложение и умножение положительных и отрицательных чисел удовлетворяют ассоциативному свойству, а вычитание и деление как положительных, так и отрицательных не удовлетворяют ассоциативному свойству.

Распределительное свойство умножения над сложением/вычитанием

Когда два положительных или отрицательных числа складывают или вычитают, а результат умножают на другое число, их можно умножать отдельно.

Следовательно, для любых трех целых чисел, a, b и c, распределительное свойство умножения над сложением утверждает, что

a x (b + c) = (a x b) + (a x c)

Аналогично, для любых трех чисел, a, b и c, распределительное свойство умножения над вычитанием утверждает, что 900 05

а х ( б – в) = (а х б) – (а х в)

Например, давайте сначала рассмотрим 10 x (18 + 12)

Мы будем использовать распределительное свойство умножения над сложением.

У нас есть 10 x (18 + 12)

 = (10 x 18) + (10 x 12)

 = 180 + 120

 = 300

Ключевые факты и Summary

1. Целое число — это число, которое можно записать без дробной части.
2. Числа 1, 2, 3, 4 ….. являются натуральными числами и называются целыми положительными числами, а числа – 1, – 2 , – 3 и т. д. называются целыми отрицательными.
3. Мы используем символ «-» для обозначения отрицательных целых чисел, и тот же символ используется для обозначения вычитания.
4. Мы используем символ «+» для обозначения положительных целых чисел, и тот же символ используется для обозначения сложения.
5. Числа увеличиваются, когда мы движемся вправо по числовой линии, и уменьшаются, когда мы движемся влево.
6. Чтобы сложить два целых положительных или два отрицательных числа, мы складываем их абсолютные значения и присваиваем сумме знак слагаемого.
7. Чтобы сложить положительное или отрицательное целое число, мы определяем разность их абсолютных значений и присваиваем сумму слагаемого, имеющего большее абсолютное значение.
8. Если a и b — два целых числа, то для вычитания b из a меняем знак b и прибавляем его к a, т.е.
9. Произведение двух целых чисел с одинаковыми знаками равно произведению их абсолютных значений.
10. Частное двух целых чисел, как положительных, так и отрицательных, — это положительное целое число, равное частному соответствующих абсолютных значений целых чисел.
11. Частное положительного и отрицательного целых чисел является отрицательным целым числом, и его абсолютное значение равно частному соответствующих абсолютных значений целых чисел.
12. Как положительные, так и отрицательные целые числа удовлетворяют свойству замыкания. Сложение и умножение как положительных, так и отрицательных целых чисел удовлетворяют коммутативным и ассоциативным свойствам. Вычитание и деление как положительных, так и отрицательных целых чисел не удовлетворяют коммутативным и ассоциативным свойствам.

Целые числа (тема Дня мертвых) Рабочие листы по математике
Понимание коммутативного и ассоциативного свойства сложения Рабочие листы по математике для 1-го класса
Распределительное свойство и алгебраические выражения Рабочие листы по математике для 6-го класса

Мы тратим много времени на изучение и сбор информации на этом сайте.