Отрицательные числа определение: Отрицательное число | это… Что такое Отрицательное число?

Отрицательное число | это… Что такое Отрицательное число?

Отрица́тельное число́ — элемент множества отрицательных чисел, которое (вместе с нулём) появилось в математике при расширении множества натуральных чисел. Цель расширения: обеспечить выполнение операции вычитания для любых чисел. В результате расширения получается множество (кольцо) целых чисел, состоящее из положительных (натуральных) чисел, отрицательных чисел и нуля.

Отрицательные числа на числовой оси

Все отрицательные числа, и только они, меньше, чем ноль. На числовой оси отрицательные числа располагаются слева от нуля. Для них, как и для положительных чисел, определено отношение порядка, позволяющее сравнивать одно целое число с другим.

Для каждого натурального числа n существует одно и только одно отрицательное число, обозначаемое -n, которое дополняет n до нуля:

Оба числа называются противоположными друг для друга. Вычитание целого числа a из другого целого числа b равносильно сложению

b с противоположным для a:

При делении с остатком частное может иметь любой знак, но остаток, по соглашению, всегда неотрицателен (иначе он определяется не однозначно). Например, разделим −24 на 5 с остатком:

.

Отрицательные значения на шкале термометра

Содержание 1 Свойства отрицательных чисел 2 Вариации и обобщения 3 Исторический очерк 4 Знаменитые отрицательные числа 5 См. также 6 Литература 7 Примечания

Свойства отрицательных чисел

Отрицательные числа подчиняются практически тем же алгебраическим правилам, что и натуральные, но имеют некоторые особенности.

1. Если любое множество положительных чисел ограничено снизу, то любое множество отрицательных чисел ограничено сверху.
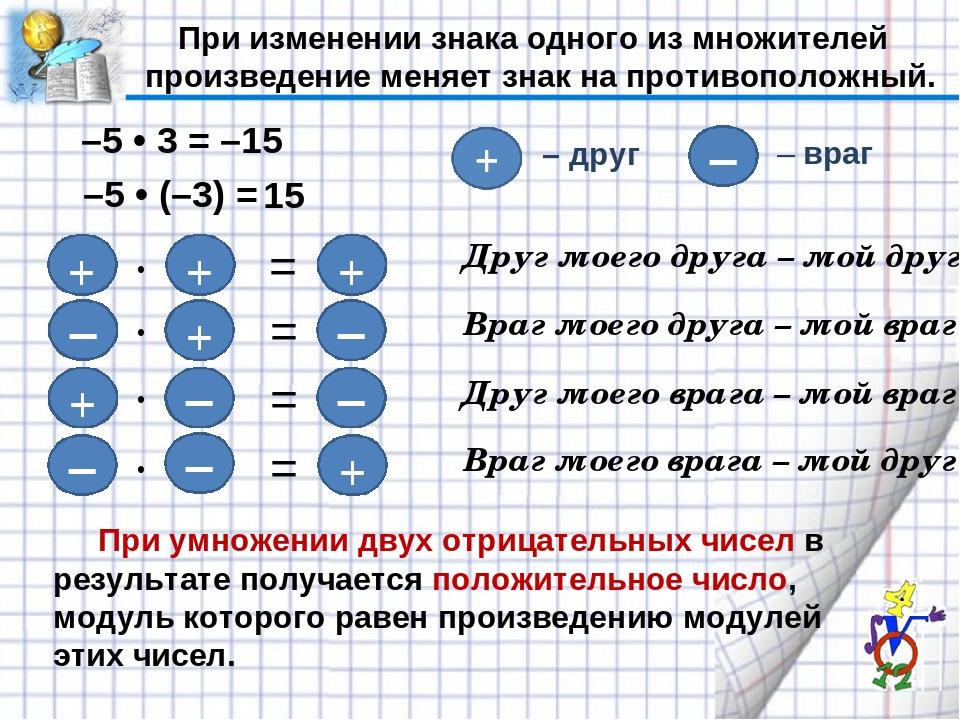
2. При умножении целых чисел действует правило знаков: произведение чисел с разными знаками отрицательно, с одинаковыми — положительно.
3. При умножении обеих частей неравенства на отрицательное число знак неравенства меняется на обратный. Например, умножая неравенство 3 < 5 на −2, мы получаем: −6 > −10.

Вариации и обобщения

Понятия положительных и отрицательных чисел можно определить в любом упорядоченном кольце. Чаще всего эти понятия относятся к одной из следующих числовых систем:

• Целые числа
• Рациональные числа
• Вещественные числа

Приведенные выше свойства 1-3 имеют место и в общем случае. К комплексным числам понятия «положительный» и «отрицательный» неприменимы.

Исторический очерк

Древний Египет, Вавилон и Древняя Греция не использовали отрицательных чисел, а если получались отрицательные корни уравнений (при вычитании), они отвергались как невозможные. Исключение составлял Диофант, который в III веке уже знал правило знаков и умел умножать отрицательные числа. Однако он рассматривал их лишь как промежуточный этап, полезный для вычисления окончательного, положительного результата.

Впервые отрицательные числа были частично узаконены в Китае, а затем (примерно с VII века) и в Индии, где трактовались как долги (недостача), или, как у Диофанта, признавались как временные значения.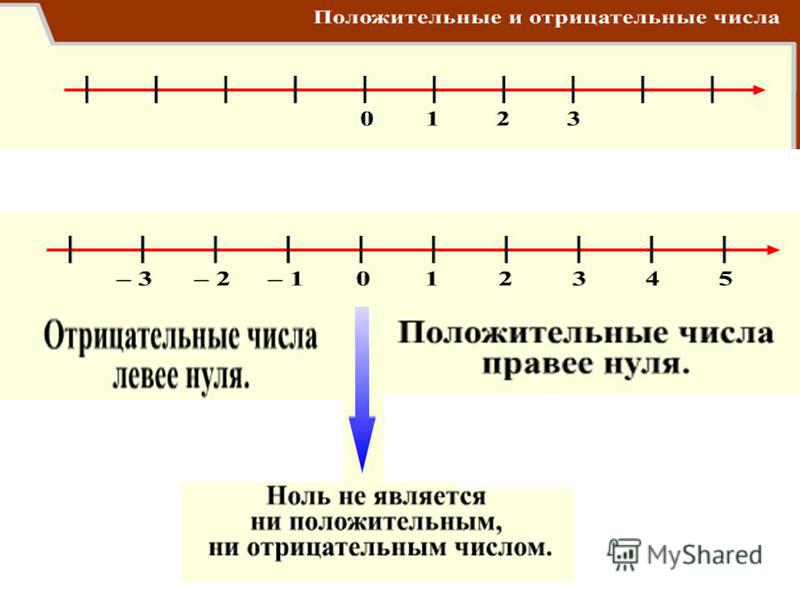 Умножение и деление для отрицательных чисел тогда ещё не были определены. Полезность и законность отрицательных чисел утверждались постепенно. Индийский математик Брахмагупта (VII век) уже рассматривал их наравне с положительными.

В Европе признание наступило на тысячу лет позже, да и то долгое время отрицательные числа называли «ложными», «мнимыми» или «абсурдными». Первое описание их в европейской литературе появилось в «Книге абака» Леонарда Пизанского (1202 год), который трактовал отрицательные числа как долг. Бомбелли и Жирар в своих трудах считали отрицательные числа вполне допустимыми и полезными, в частности, для обозначения нехватки чего-либо. Даже в XVII веке Паскаль считал, что , так как ничто не может быть меньше, чем ничто. Отголоском тех времён является то обстоятельство, что в современной арифметике операция вычитания и знак отрицательных чисел обозначаются одним и тем же символом (минус), хотя алгебраически это совершенно разные понятия.

В XVII веке, с появлением аналитической геометрии, отрицательные числа получили наглядное геометрическое представление на числовой оси. С этого момента наступает их полное равноправие. Тем не менее теория отрицательных чисел долго находилась в стадии становления. Оживлённо обсуждалась, например, странная пропорция 1:(-1) = (-1):1 — в ней первый член слева больше второго, а справа — наоборот, и получается, что большее равно меньшему («парадокс Арно»). Непонятно было также, какой смысл имеет умножение отрицательных чисел, и почему произведение отрицательных положительно; на эту тему проходили жаркие дискуссии. Гаусс в 1831 году считал нужным разъяснить, что отрицательные числа принципиально имеют те же права, что и положительные, а то, что они применимы не ко всем вещам, ничего не означает, потому что дроби тоже применимы не ко всем вещам (например, неприменимы при счёте людей)^[1].

Полная и вполне строгая теория отрицательных чисел была создана только в XIX веке (Уильям Гамильтон и Герман Грассман).

Знаменитые отрицательные числа

Число	Смысл числа	Примечания
−273,15 °C	Абсолютный нуль температуры	Это ноль градусов по шкале Кельвина.
−1,602 176 565·10−19 Кл	Заряд электрона	Элементарный заряд может быть и положительным — у протонов и позитронов.
−13,7 млрд лет	Приблизительный момент Большого взрыва	Начало формирования нашей Вселенной
−2,7·10−9	Константа Де Брюйна — Ньюмэна (англ.)	Числовое значение — по сведениям 2000-го года.

См. также

• Беззнаковое число
• Рациональное число

Литература

• Выгодский М. Я. Справочник по элементарной математике. — М.: АСТ, 2003. — ISBN 5-17-009554-6
• Глейзер Г. И. История математики в школе. — М.: Просвещение, 1964. — 376 с.

Примечания

1. ↑ Александрова Н. В. Математические термины.(справочник). М.: Высшая школа, 1978, стр. 164.

Отрицательное число | это… Что такое Отрицательное число?

Отрица́тельное число́ — элемент множества отрицательных чисел, которое (вместе с нулём) появилось в математике при расширении множества натуральных чисел.

Цель расширения: обеспечить выполнение операции вычитания для любых чисел. В результате расширения получается множество (кольцо) целых чисел, состоящее из положительных (натуральных) чисел, отрицательных чисел и нуля.

Отрицательные числа на числовой оси

Все отрицательные числа, и только они, меньше, чем ноль. На числовой оси отрицательные числа располагаются слева от нуля. Для них, как и для положительных чисел, определено отношение порядка, позволяющее сравнивать одно целое число с другим.

Для каждого натурального числа n существует одно и только одно отрицательное число, обозначаемое -n, которое дополняет n до нуля:

Оба числа называются противоположными друг для друга. Вычитание целого числа a из другого целого числа b равносильно сложению

b с противоположным для a:

При делении с остатком частное может иметь любой знак, но остаток, по соглашению, всегда неотрицателен (иначе он определяется не однозначно). Например, разделим −24 на 5 с остатком:

.

Отрицательные значения на шкале термометра

Содержание 1 Свойства отрицательных чисел 2 Вариации и обобщения 3 Исторический очерк 4 Знаменитые отрицательные числа 5 См. также 6 Литература 7 Примечания

Свойства отрицательных чисел

Отрицательные числа подчиняются практически тем же алгебраическим правилам, что и натуральные, но имеют некоторые особенности.

1. Если любое множество положительных чисел ограничено снизу, то любое множество отрицательных чисел ограничено сверху.
2. При умножении целых чисел действует
   правило знаков: произведение чисел с разными знаками отрицательно, с одинаковыми — положительно.
3. При умножении обеих частей неравенства на отрицательное число знак неравенства меняется на обратный. Например, умножая неравенство 3 < 5 на −2, мы получаем: −6 > −10.

Вариации и обобщения

Понятия положительных и отрицательных чисел можно определить в любом упорядоченном кольце. Чаще всего эти понятия относятся к одной из следующих числовых систем:

• Целые числа
• Рациональные числа
• Вещественные числа

Приведенные выше свойства 1-3 имеют место и в общем случае. К комплексным числам понятия «положительный» и «отрицательный» неприменимы.

Исторический очерк

Древний Египет, Вавилон и Древняя Греция не использовали отрицательных чисел, а если получались отрицательные корни уравнений (при вычитании), они отвергались как невозможные. Исключение составлял Диофант, который в III веке уже знал правило знаков и умел умножать отрицательные числа. Однако он рассматривал их лишь как промежуточный этап, полезный для вычисления окончательного, положительного результата.

Впервые отрицательные числа были частично узаконены в Китае, а затем (примерно с VII века) и в Индии, где трактовались как долги (недостача), или, как у Диофанта, признавались как временные значения. Умножение и деление для отрицательных чисел тогда ещё не были определены. Полезность и законность отрицательных чисел утверждались постепенно. Индийский математик Брахмагупта (VII век) уже рассматривал их наравне с положительными.

В Европе признание наступило на тысячу лет позже, да и то долгое время отрицательные числа называли «ложными», «мнимыми» или «абсурдными». Первое описание их в европейской литературе появилось в «Книге абака» Леонарда Пизанского (1202 год), который трактовал отрицательные числа как долг. Бомбелли и Жирар в своих трудах считали отрицательные числа вполне допустимыми и полезными, в частности, для обозначения нехватки чего-либо. Даже в XVII веке Паскаль считал, что , так как ничто не может быть меньше, чем ничто. Отголоском тех времён является то обстоятельство, что в современной арифметике операция вычитания и знак отрицательных чисел обозначаются одним и тем же символом (минус), хотя алгебраически это совершенно разные понятия.

В XVII веке, с появлением аналитической геометрии, отрицательные числа получили наглядное геометрическое представление на числовой оси.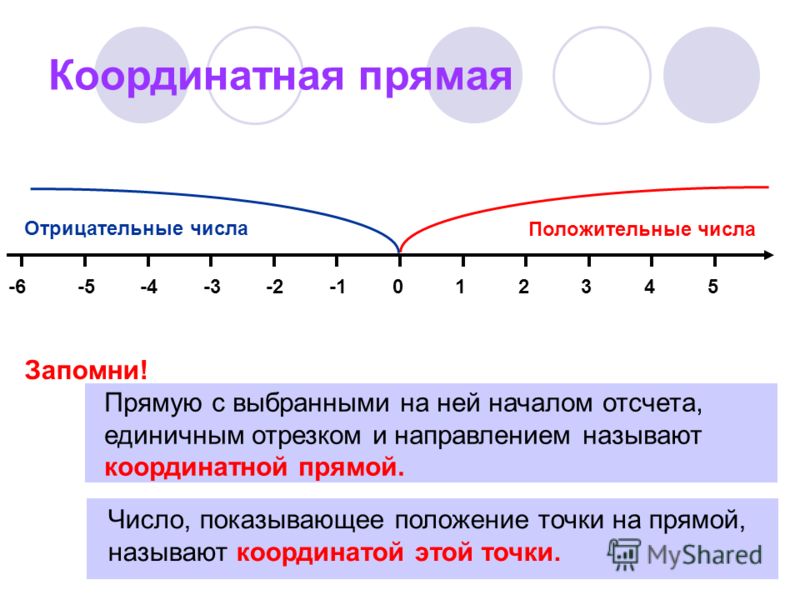 С этого момента наступает их полное равноправие. Тем не менее теория отрицательных чисел долго находилась в стадии становления. Оживлённо обсуждалась, например, странная пропорция 1:(-1) = (-1):1 — в ней первый член слева больше второго, а справа — наоборот, и получается, что большее равно меньшему («парадокс Арно»). Непонятно было также, какой смысл имеет умножение отрицательных чисел, и почему произведение отрицательных положительно; на эту тему проходили жаркие дискуссии. Гаусс в 1831 году считал нужным разъяснить, что отрицательные числа принципиально имеют те же права, что и положительные, а то, что они применимы не ко всем вещам, ничего не означает, потому что дроби тоже применимы не ко всем вещам (например, неприменимы при счёте людей)^[1].

Полная и вполне строгая теория отрицательных чисел была создана только в XIX веке (Уильям Гамильтон и Герман Грассман).

Знаменитые отрицательные числа

Число	Смысл числа	Примечания
−273,15 °C	Абсолютный нуль температуры	Это ноль градусов по шкале Кельвина.
−1,602 176 565·10−19 Кл	Заряд электрона	Элементарный заряд может быть и положительным — у протонов и позитронов.
−13,7 млрд лет	Приблизительный момент Большого взрыва	Начало формирования нашей Вселенной
−2,7·10−9	Константа Де Брюйна — Ньюмэна (англ.)	Числовое значение — по сведениям 2000-го года.

См. также

• Беззнаковое число
• Рациональное число

Литература

• Выгодский М. Я. Справочник по элементарной математике. — М.: АСТ, 2003. — ISBN 5-17-009554-6
• Глейзер Г. И. История математики в школе. — М.: Просвещение, 1964. — 376 с.

Примечания

1. ↑ Александрова Н. В. Математические термины.(справочник). М.: Высшая школа, 1978, стр. 164.

Определение, Использование, Свойства, Операции, Примеры

• Автор Мадхурима дас
• Последнее изменение 29-11-2022

Отрицательные числа: В повседневной жизни мы имеем дело с множеством чисел. Число – это математическое понятие, используемое для выражения количества и подсчета или расчета. Мы можем классифицировать числа по разным типам: целые числа, натуральные числа, целые числа , действительные числа, рациональные, иррациональные числа и т. д.

Чтобы упростить счет, люди изобрели натуральные числа. После этого изобрели ноль, дающий нам представление о целых числах, а затем об отрицательных числах, действительных числах и т. д. Отрицательные числа помогают нам показывать температуру, которая меньше нуля, показывать перерасход на банковском счету и т. д. Давайте см. применение и свойства отрицательных чисел в этой статье.

Что такое числа?

Числа окружают нас повсюду. С утра до ночи мы часто сталкиваемся с множеством чисел. Сейчас мы знаем, как читать и записывать числа, но что было, когда числа вообще не были открыты? В те дни счет производился с использованием доступных тогда физических объектов, таких как камни, кости, палки, листья и так далее. Затем они научились отмечать линии или изгибы на камнях, в пещерах, на глиняной посуде, которую использовали, и так далее.

А потом были введены наши счетные числа. Число — это математическое понятие, которое используется для выражения количества и используется в счетах, вычислениях или любых арифметических операциях и других вертикалях математики.
Например, \(2,3,0,5, – 6, – 100, – 2,3,\sqrt{2,} \) и т. д.

Счетные числа также называются числами и включают в себя положительные целые числа из \( 1\) до бесконечности. Набор натуральных чисел выражается как \(N\) и \(N = \left\{{1,2,3,4,5……} \right\}\)

У всех был преемник и предшественник числа, кроме \(1\) в натуральных числах. Кроме того, изначально не было возможности показать пустоту. Так возникла необходимость демонстрации пустоты, и был введен ноль. Когда к счетным числам добавляется ноль, мы получаем целые числа. Целые числа — это положительные числа от \(0\) до бесконечности и не содержат дробных или десятичных чисел. Набор целых чисел может быть выражен как \(W = \left\{{0,1,2,3,4,5,……} \right\}\)

Знакомство с отрицательными числами

Мы знаем, как выполнять математические операции, такие как сложение, вычитание, умножение и деление над целыми числами. Когда мы вычитаем меньшее целое число из большего целого числа, результатом всегда является целое число. Например, \(30 – 12 = 18,\) результатом является целое число. Но когда мы вычитаем большее целое число из меньшего целого числа, в результате получается не целое число.

Поэтому возникла необходимость иметь набор чисел, включающий числа со знаком минус. Это привело к созданию нового набора чисел, которые называются отрицательными числами. Когда отрицательные числа были добавлены к целым числам, мы получили набор целых чисел.

Набор целых чисел может быть выражен как \(Z = \left\{{… – 5, – 4, – 3, – 2, – 1,0,1,2,3,4,5,….} \right\}\)

Отрицательные числа имеют множество применений в реальной жизни. Например, мы используем его для выражения потерь, декрементов, обесценивания и т. д. Они используются для обозначения температуры (меньше нуля), в банковской системе они используются для представления перерасходованной суммы баланса вашего счета. Они также используются, чтобы показать цену акции и ее взлеты и падения.

Поскольку использование чисел не могло быть ограничено целыми числами, было введено больше наборов чисел, таких как рациональные числа, иррациональные числа, действительные числа и комплексные числа.

1. Рациональные числа: Любое число, которое может быть выражено как отношение одного числа к другому числу, записывается как рациональное число. Его можно записать в виде \(\frac{p}{q}\) формы. Символ \(Q\) обозначает рациональные числа.
Например, \(\frac{3}{4},\frac{{ – 4}}{5},\frac{{ – 6}}{7},\frac{3}{1},\) и т. д. — рациональные числа.

2. Иррациональные числа: Число, которое не может быть представлено как отношение одного числа к другому числу, называется иррациональным числом и обозначается символом \(P. \)
Например, \(\sqrt 3 ,\sqrt 2 ,\sqrt 5 , – \sqrt 7 ,\) и т. д. являются иррациональными числами.

3. Действительные числа: Все наборы положительных и отрицательных целых, дробных и десятичных чисел, за исключением мнимых чисел, известны как действительные числа. Обозначается символом \(R.\). Например, \(1.2,3.2222…,4,5,7, – 8, – 8.2,9.1,\) и т. д. – действительные числа.

Представление отрицательных чисел

Отрицательные числа представляются со знаком минус \(\left( – \right)\) вместе с числом. Эти числа представлены слева от начала координат (нуля) на числовой прямой, и их значения всегда меньше нуля. Это может быть целое, десятичное число, дробь. Их нет в множестве натуральных чисел и целых чисел.

Например, \( – 5.2, – 3.7, – 4, – 5, – 7,3.4,\frac{{ – 5}}{6}, – 9.1, – \sqrt 7 \) и т. д. являются отрицательными числа.

Отрицательные числа в строке чисел

Прямая линия, на которой числа расположены через равные промежутки по ее длине, называется числовой линией. Его можно бесконечно растягивать в любом направлении, и обычно он представлен горизонтально.

Числа могут быть представлены в числовой строке как

В числовой строке положительные числа представлены справа от нуля, а отрицательные числа представлены слева от нуля.

В числовой строке, если числа перемещаются вправо от нуля, значение числа увеличивается, а если числа перемещаются влево в числовой строке от нуля, значение числа уменьшается.

Арифметические операции с отрицательными числами

Существует четыре основных арифметических операции: сложение, вычитание, умножение и деление. Когда мы выполняем эти четыре операции с отрицательными числами, это кажется трудным, но это не так.

Сложение положительного и отрицательного числа

Когда необходимо сложить положительное и отрицательное число, мы должны сначала взять абсолютное значение двух чисел и найти разницу между ними. Ответ будет принимать знак числа, которое имеет большее абсолютное значение.

Например,
1. \(\left({ – 3} \right) + 4\)
Здесь абсолютное значение \( – 3 = 3\) и абсолютное значение \(4 = 4\ ) Таким образом, после получения разности абсолютных значений ответ будет принимать знак числа с большим абсолютным значением.
Следовательно, \( – 3 + 4 = 1\)

2. Аналогично, \( \left({-\frac{2}{7}} \right) + \left({\frac{5}{7 }} \right) = \frac{{ – 2 + 5}}{7} = \frac{3}{7}\)

3. \( – 5 + 1 = – 4\)
Здесь абсолютная значение \( – 5 = 5\) и абсолютное значение \(1 = 1\)
Итак, разность абсолютных значений \( = 5 – 1 = 4\)
Ответ будет принимать знак числа с большим абсолютным значением \( – 5.\)

Аналогично, 4. \(\left({ – 1.5} \right) + \left( 1 \right) = \left({ – 0.5} \right) \)

5. \(\left({\frac{3}{7}} \right) + \left({\frac{{ – 5}}{7}} \right) = \frac{{3 – 5 }}{7} = \frac{{ – 2}}{7}\)

Сложение двух отрицательных чисел

Сложение двух отрицательных чисел выполняется аналогично тому, как мы складываем два положительных числа и единственное меняется знак ответа.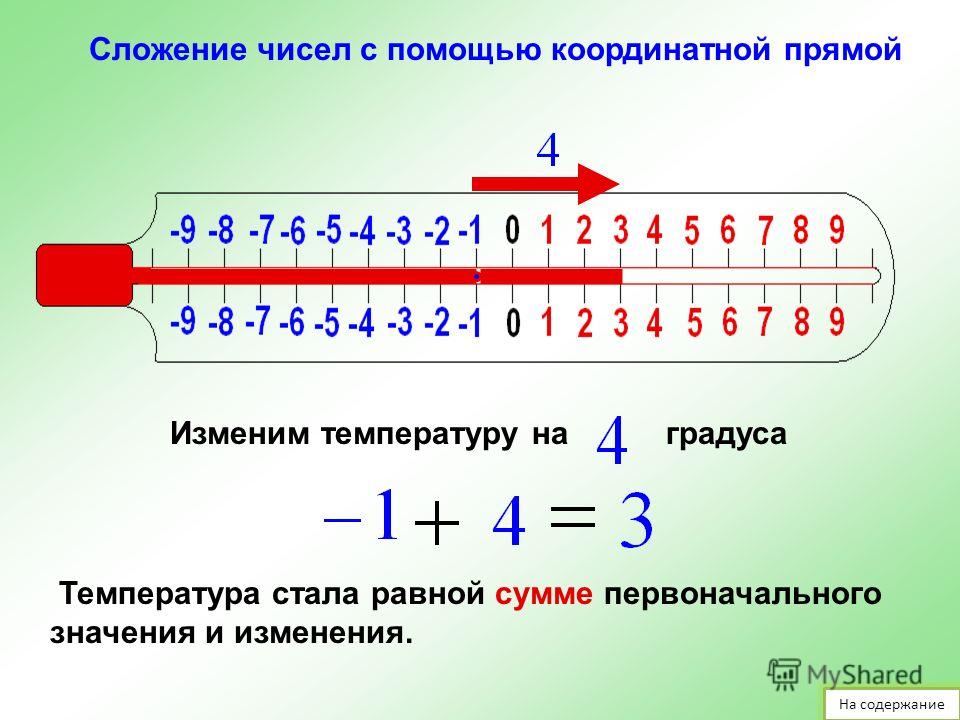 При сложении двух отрицательных чисел результатом будет отрицательное число. Итак, при добавлении двух отрицательных чисел добавьте абсолютное значение обоих чисел и добавьте к ответу знак минус.

Например,
1. \(\влево({ – 3,5} \вправо) + \влево({ – 2} \вправо) = \влево({ – 5,5} \вправо)\)
2. \(\ влево({ – \frac{2}{3}} \right) + \left({ – \frac{5}{3}} \right) = \frac{{ – 2 – 5}}{3} = \ frac{{ – 7}}{3}\)
3. \(\left({ – 5} \right) + \left({ – 2} \right) = – 5 – 2 = \left({ – 7 } \right)\)

Вычитание двух отрицательных чисел

Когда вычитаются два отрицательных числа, получается сложение положительного и отрицательного числа.

Например,
1. \(\влево({ – 4} \вправо) – \влево({ – 3} \вправо) = – 4 + 3 = – 1\)
2. \(\влево({ – 4.2} \вправо ) + \left({ – 2.1} \right) = \left({ – 6.3} \right)\)
3. \(\left({ – \frac{1}{4}} \right) + \left ({ – \frac{3}{4}} \right) = \frac{{ – 1 – 3}}{4} = \frac{{ – 4}}{4} = -1\)

Вычитание Положительные и отрицательные числа

При вычитании положительного и отрицательного числа проверьте, должно ли быть вычтено отрицательное число из положительного числа или положительное число должно быть вычтено из отрицательного числа.

Если положительное число вычитается из отрицательного числа, то сложите оба числа и поставьте знак минус для ответа.

Например,
1. \( – 3 – \влево( 2 \вправо) = – 3 – 2 = -5\)
2. \(\влево({ – 2.2} \вправо) – \влево({ – 2,1} \right) = – 2,2 + 2,1 = – 0,1\)
3. \(\left({ – \frac{1}{4}} \right) – \left({ – \frac{3}{ 4}} \right) = \frac{{ – 1 + 3}}{4} = \frac{2}{4} = \frac{1}{2}\)

Если из Положительное число, затем сложите оба числа и поставьте положительный знак в ответе.

Например,
1. \(3 – \влево({ – 2} \вправо) = 3 + 2 = 5\)
2. \(\влево({2.2} \вправо) – \влево({ – 2.1} \right) = 4.3\)
3. \(\left({\frac{1}{4}} \right) — \left({ — \frac{3}{4}}\right) = \ frac{{1 + 3}}{4} = \frac{4}{4} = 1\)

Умножение двух отрицательных чисел

При умножении двух отрицательных чисел произведение будет положительным числом.

Например,
1. \( – 3 \times – 2 = 6\)
2. \(\left({ – 1,2} \right) \times \left({ – 2} \right) = 2,4\ )
3. \(\left({\frac{{ – 1}}{4}} \right) \times \left({\frac{{ – 3}}{4}} \right) = \frac{{ \left({ – 1} \right) \times \left({ – 3} \right)}}{4} = \frac{3}{4}\)

Умножение положительных и отрицательных чисел

Когда отрицательное и положительное число умножается, произведение будет отрицательным числом.

Например,
1. \( – 3 \times 2 = – 6\)
2. \(\left({ – 1,2} \right) \times \left( 2 \right) = – 2,4\)
3. \(\left({\frac{{ – 1}}{4}} \right) \times \left({\frac{3}{4}} \right) = \frac{{\left({ – 1} \right) \times \left( 3 \right)}}{4} = \frac{{ – 3}}{4}\)

Деление двух отрицательных чисел

При делении двух отрицательных целых чисел в частном получается положительное целое число.

1. \(\влево({ – 3} \вправо) \div \влево({ – 2}\вправо) = \frac{3}{2} = 1,5\)
2. \(\влево({ – 1.2} \right) \div \left({ – 2} \right) = 0.6.\)
3. \(\left({\frac{{ – 1}}{4}} \right) \div \ left({\frac{{ – 3}}{4}} \right) = \frac{1}{3}\)

Деление положительных и отрицательных чисел

При делении положительного и отрицательного числа частное будет отрицательным целым числом.

1. \(\left( 3 \right) \div \left({ – 2} \right) = \frac{{ – 3}}{2} = – 1.5\)
2. \(\left( { – 1.2} \right) \div \left( 2 \right) = – 0.6.\)
3. \(\left({\frac {{ – 1}}{4}} \right) \div \left ({\frac{3}{4}} \right) = \frac{{ – 1}}{3}\)

Деление отрицательного числа на ноль не определено.

Решенные примеры – отрицательные числа

Q.1. Какое изменение температуры испытает путешественник, достигнув отметки 9 градусов над уровнем моря?\circ }{\text{C}}\)

Q.2. Вычтите \(\left({\frac{{ – 20}}{{30}}} \right) – \left({\frac{{ – 9}}{{30}}} \right).\)
Ответ: Дано } \right)\)
Так как обе дроби отрицательны,
\( \Rightarrow \frac{{ – 20}}{{30}} – \frac{{ – 9}}{{30}} = \frac{ { – 20 + 9}}{{30}}\)
\( = \frac{{ – 11}}{{30}}.\)

В.3. Упростить \( – 6 – \ frac{{ – 1}}{2}.\)
Ответ: Дано, \( – 6 – \left({\frac{{ – 1}}{2}} \right)\)
\( – 6,\left({\frac {{ – 1 }}{2}} \right)\) оба принадлежат отрицательным числам
\( – 6 – \left({\frac {{ – 1}}{2}} \right) = – 6 + \frac{1} {2}\)
\( = \frac{{ – 12 + 1}}{2} = \frac{{ – 11}}{2}\)

Q. 4. Найдите предшественника следующих целых чисел.
а) \( – 100\)
б) \( – 16\)
Ответ: Предшественник числа получается вычитанием \(1\) из числа.
а) Предшественником \(-100\) является \(-100-1 = -101\)
б) Предшественником \(-16\) является \(-16-1=-17\)

Q .5. Умножьте \(\left({ – 4} \right)\) и \(\left({ – 1.2} \right).\)
Ответ: Учитывая отрицательные числа \( – 4\) и \( – 1.2.\)
Когда мы умножаем два отрицательных числа, в результате мы получим положительное число.
Таким образом, \( – 4 \times – 1,2 = 4,8\)

Резюме

В этой статье мы узнали определение отрицательных чисел, примеры и их свойства. Мы также обсудили арифметические операции с отрицательными числами, такие как сложение, вычитание, умножение и деление.

Часто задаваемые вопросы (FAQ) – отрицательные номера

Q.1. Объясните отрицательные числа на примерах.
Ответ: Отрицательные числа представляются со знаком минус \(\left( – \right)\) вместе с числом. Эти числа представлены слева от начала координат (нуля) на числовой прямой, и их значения всегда меньше нуля. Это может быть целое число, десятичное число, дробь и т. д. Их нет в множестве натуральных чисел и целых чисел.
Например, \( – 5,2, – 3,7, – 4, – 5, – 7, – 3,4,\frac{{ – 5}}{6}, -9,1, – \sqrt 7 \) и т. д. являются отрицательными числа.

Q.2. Каковы правила для отрицательных чисел?
Ответ:
1. Когда необходимо сложить положительное и отрицательное число, мы должны сначала взять абсолютное значение двух чисел и найти разницу между ними. Ответ будет принимать знак числа, которое имеет большее абсолютное значение.
2. Добавление двух отрицательных чисел добавляет абсолютное значение обоих чисел и добавляет к ответу знак минус.
3. При вычитании двух отрицательных чисел получается сложение положительного и отрицательного числа.
4. Если из отрицательного числа вычитается положительное число, сложите оба числа и поставьте знак минус.
5. При умножении двух отрицательных чисел произведение будет положительным числом.
6. При перемножении отрицательного и положительного числа произведение будет отрицательным числом.
7. При делении двух отрицательных целых чисел частное будет положительным целым числом.
8. При делении положительного и отрицательного числа частное будет отрицательным целым числом.

Q.3. Какое наибольшее отрицательное целое число?
Ответ: Целые числа можно описать как множество натуральных чисел и их аддитивных инверсий, содержащих ноль. Итак, наибольшее отрицательное число равно \( – 1.\)

Q.4. Какое наименьшее отрицательное целое число?
Ответ: Если мы перейдем от нуля к минус бесконечности на числовой прямой, значение уменьшится так, что не будет наименьшего отрицательного числа, так как существует бесконечное количество отрицательных чисел.

Q.5. Каково применение отрицательных чисел?
Ответ: мы используем отрицательные числа для выражения убытков, декрементов, обесценивания и т. д. Они используются для обозначения температуры (меньше нуля), в банковской системе они используются для представления перерасхода суммы баланса вашего счета . Они также используются, чтобы показать цену акции и ее взлеты и падения.

определение — Что такое отрицательное число?

Чтобы ограничить мою ответственность, давайте рассматривать только целые числа, а когда мы начнем говорить о делении, рациональные числа. Во-первых, мы интуитивно понимаем сложение:

 Если у меня есть два яблока и вы дадите мне еще три яблока, то я сейчас
есть 2 + 3 = 5 яблок.
 

Есть два пути, по которым мы можем пойти: 1) мы можем признать существование отрицательных чисел и работать с ними или 2) мы можем принять вычитание как допустимую операцию, которую мы определенно понимаем. Я думаю, что второй подход лучше всего подходит для вашего вопроса (поскольку мы , а не хотим принимать отрицательные числа априори).

Так же, как сложение интуитивно понятно для нас, так же интуитивно понятно и вычитание:

 Если у меня есть 5 яблок, а вы возьмете у меня 3, то у меня останется 2 яблока: 5 - 3 = 2.
 

Нулевое значение теперь становится очень важным, потому что я знаю, что если у меня есть $x$ яблок и вы заберете $x$ яблок, то у меня не останется ни одного, $0$:

$$ х — х = 0 $$

Итак, что происходит, когда у меня есть яблоки по 5$, а вы забираете 6$? Сколько яблок у меня осталось? Очевидно, интуиция теперь дает сбой, потому что у вас , а не есть яблоки по 6$, но математика может остаться:

$$ 5 — 6 = 5 — (5 + 1) = 5 — 5 — 1 = 0 — 1 $$

Мы счастливы в на каждом шаге до последнего, когда я добираюсь до $0 — 1$, для которого у нас нет ценности! Я не понимаю, что $0 — 1$ представляет в именно так же, как я понимаю , а не , понимаю, что представляет $\sqrt{-1} = i$ — это определение ! Теперь я определяю , что $0 — 1 = -1$—$-1$ теперь является символом для этого значения (которое я не совсем понимаю). (и, в конце концов, когда я говорю $-x$, я действительно имею в виду $0-x$)

Теперь, когда у нас есть этот новый символ, что мы можем с ним сделать? Ну, мы можем попробовать и добавить к значениям: $5 + -1 = 5 + (0 — 1) = 5 + 0 — 1 = 5 — 1 = 4$ — мы видим, что $5 + -1$ это тот же как $5 — 1$! А как насчет $5—1$? Это немного сложнее. Теперь, очевидно, мы можем записать $5 — (0 — 1)$, но это не поможет нам, потому что мы не знаем как вычесть отрицательное число (на самом деле приведенное выше выражение просто превращается в $5 — -1$). —оригинальный вопрос)! что мы действительно нужно показать теперь следующее:

$$ 0 — (0 — 1) = 0 — -1 = +1 $$

Таким образом, мы можем сделать это с помощью некоторых алгебраических манипуляций:

$$ 0 — (0 — 1) = х\ 0 = х + (0 — 1) \ 0 = х + 0 — 1 = х — 1 \ 0 + 1 = х + 1 — 1 = х + 0 = х\\ х = 1 $$

Итак, обратите внимание, что я использовал только в дополнение к , чтобы получить этот результат! Это доказывает , что $0 — -1 = +1$, поэтому мы можем переписать :

$$ 5 — -1 = 5 + 0 — -1 = 5 + (0 — -1) = 5 + 1 = 6 $$

На данный момент я надеюсь, что мы оба принимаем отрицательные числа такими, какие они есть. Следующий вопрос на умножение и деление. Если у меня $5*-2$, то какой должен быть результат? Ну, это легко:

$$ 5*-2 = (-2) + (-2) + (-2) + (-2) + (-2) = -10 $$

Что не так просто $-2*5$! Есть два подхода к этому: 1) мы принимаем, что умножение является коммутативным и, таким образом, $-2*5 = 5*-2 = -10$ (как мы уже показали) или 2) отрицательный множитель означает что-то «отличное» от положительный мультипликатор. А 9Положительный множитель 0173 означает, что к прибавляется умножаемая вещь, тогда как отрицательный множитель означает, что вычитается из умножаемой вещи. Последнее определение поможет нам определить , а также как отрицательное число, умноженное на отрицательное.

Так что же такое умножение? Умножение означает взятие значения и добавление его к нулю $x$ раз (каким бы ни был множитель). Если множитель отрицательный, то это означает, что вычитается из нуля . Например:

$$ 5*-2 = 0 + (-2) + (-2) + (-2) + (-2) + (-2) = -10\ -2*5=0-(5)-(5)=-10\ -2*-5 = 0 — (-5) — (-5) = 5 + 5 = +10\ -5*-2 = 0 — (-2) — (-2) — (-2) — (-2) — (-2) = +10 $$

Из приведенного выше определения мы видим, что отрицательное значение, умноженное на положительное, дает отрицательное значение, положительное значение, умноженное на положительное, дает положительное значение, а отрицательное значение, умноженное на отрицательное, дает положительное значение.