Рациональные числа и действия с ними — что это, определение и ответ
Рациональные числа – это числа, представленные в виде отношения \(\frac{m}{n}\), где m – целое число, а n – натуральное.
Они могут быть как положительными, так и отрицательными.
Целые и дробные числа вместе образуют множество рациональных.
Любое целое число является рациональным, потому что его можно записать в виде \(\frac{m}{1}\).
Например:
\(–4 = \frac{- 4}{1}\)
\(2 = \frac{2}{1}\)
\(0 = \frac{0}{1}\)
Сумма, разность и произведение двух рациональных чисел – тоже рациональное число. Частное двух рациональных чисел тоже будет рациональным, если знаменатель не равен 0.
Любое рациональное число можно записать в виде десятичной или периодической дроби.
Периодическая дробь – это десятичная дробь, в записи которой бесконечное количество раз повторяется цифра или несколько цифр.
Например:
\(\frac{1}{3} = 0,33333333..\)
Повторяющиеся цифры периодической дроби записывают в скобках, например:
\(\frac{1}{3} = 0,(3)\)
\(\frac{5}{11} = 0,45454545 = 0,(45)\)
СВОЙСТВА РАЦИОНАЛЬНЫХ ЧИСЕЛ:
Сложение:
Переместительное свойство:
\(a + b = b + a\)
Сочетательное свойство:
\(a + (b + c) = (a + b) + c = (a + c) + b = a + b + c\)
Прибавление нуля не меняет рациональное число, а сумма противоположных чисел равна нулю:
\(a + 0 = a\)
\(a + ( — a) = 0\)
Умножение:
Переместительное свойство:
\(ab = ba\)
Сочетательное свойство:
\(a(bc) = (ab)c = (ac)b = abc\)
Умножение на единицу не меняет рациональное число, а произведение обратных чисел равно единице:
\(a \bullet 1 = a\)
\(a \bullet \frac{1}{a} = 1\)
Если один из множителей равен нулю, то и всё произведение равно 0:
\(a \bullet 0 = 0\)
\(0 \bullet b = 0\)
\(0 \bullet 0 = 0\)
Распределительное свойство:
\((a + b)c = ac + сb\)
ДЕЙСТВИЯ С РАЦИОНАЛЬНЫМИ ЧИСЛАМИ
Так как рациональные числа включают в себя блок целых чисел и блок дробных чисел, действия, пройденные в рамках работы с целыми числами, сохраняются и для рациональных чисел.
Сравнение, умножение, деление, сложение и вычитание происходит так же, как с целыми числами.
СРАВНЕНИЕ РАЦИОНАЛЬНЫХ ЧИСЕЛ:
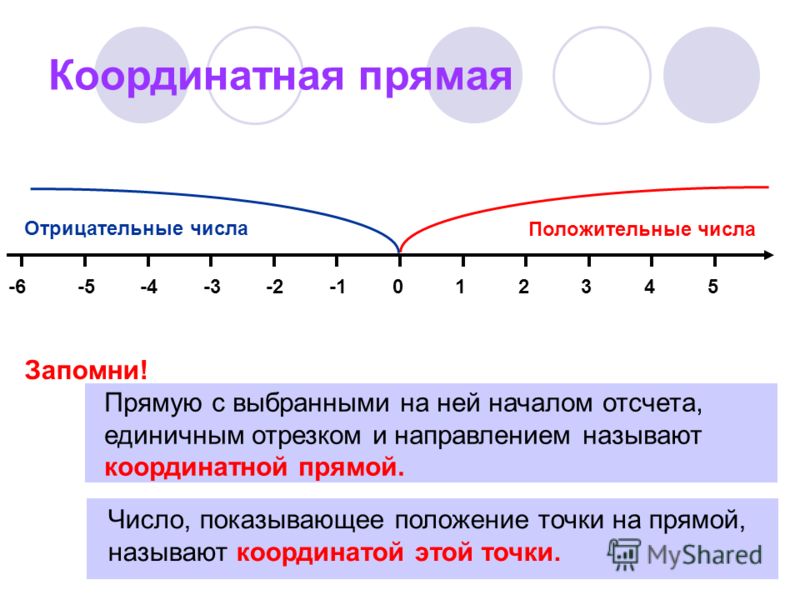
Рациональные числа можно представить на координатной прямой, где справа от нуля находятся положительные числа, а слева от нуля – обратные им, отрицательные:
Числа на такой числовой прямой возрастают слева на право, поэтому глядя на прямую можно сказать, какое числе больше.
Например:
Сравним числа 1,5 и 4:
Мы знаем, что 4 больше, чем 1,5 и еще раз убедились в этом с помощью числовой прямой.
\(4 > 1,5\)
Сравним числа 3,5 и -1:
Если положительные числа справа от нуля, а отрицательные слева, тогда любое положительное числа будет правее отрицательного, а значит будет больше.
\(3,5 > — 1\)
Сравним числа -2,5 и -3:
Конечно, 3 больше 2,5, но, когда мы смотрим на отрицательные числа, получается, что -2,5 правее -3, а значит больше.
\(- 2,5 > — 3\)
СЛОЖЕНИЕ И ВЫЧИТАНИЕ РАЦИОНАЛЬНЫХ ЧИСЕЛ:
Сложение рациональных чисел так же можно представить на числовой прямой. Знак «+» означает, что мы двигаемся в положительном направлении (вправо), знак «–» означает, что мы двигаемся в отрицательном направлении (влево).
Например:
Найдем сумму положительных чисел 1 + 2,5. Значит от координаты 1 пройдем 2 полных отрезка и ещё половину отрезка в положительном направлении:
Видим, что \(1 + 2,5 = 3,5\).
Сумма положительных чисел – положительное число.
Найдем сумму отрицательных чисел -1 + (-2). От координаты -1 пройдем 2 отрезка в отрицательном направлении. При сложении можно опустить знак «+» без изменения знаков слагаемых.
Получилось, что \(- 1 + ( — 2) = — 3.\)
Сумма отрицательных чисел – отрицательное число.
Найдем разность положительных чисел 4 – 1,5.
Можно представить разность чисел как сумму положительного и отрицательного числа: 4 + (-1,5). В любом случае нужно от координаты 4 пройти в отрицательном направлении 1 полный отрезок и ещё половину:
Можно представить разность чисел как сумму положительного и отрицательного числа: 4 + (-1,5). В любом случае нужно от координаты 4 пройти в отрицательном направлении 1 полный отрезок и ещё половину:Получилось, что \(4\ –1,5 = 2,5.\)
Сумма положительного и отрицательного числа – положительное число, если из большего вычитают меньшее.
Найдем сумму 2 + (-4). От координаты 2пройдем 4 отрезка в отрицательном направлении:
Получим, что \(2–4 = — 2.\)
Сумма положительного и отрицательного числа – отрицательное число, если из меньшего вычитают большее.
Найдем разность 1 – (-3). Если нужно пройти в отрицательном направлении дважды, то направление движения станет положительным, то есть 1 – (-3) = 1 + 3:
Чтобы из одного числа вычесть другое, нужно к уменьшаемому прибавить число противоположное вычитаемому.
Найдем сумму двух противоположных чисел 3 + (-3).
От координаты 3 пройдем 3 отрезка в отрицательном направлении:
От координаты 3 пройдем 3 отрезка в отрицательном направлении:Видим, что \(3 + ( — 3) = 0.\)
Сумма двух противоположных чисел \(\mathbf{= 0.}\)
УМНОЖНИЕ И ДЕЛЕНИЕ РАЦИОНАЛЬНЫХ ЧИСЕЛ:
Рациональные числа умножаются и делятся не смотря на знак.
Если перемножались или делились числа с одинаковыми знаками, то в результате получается положительное число. Если перемножались числа с разными знаками, то в результате получается отрицательное число.
Например:
\(3 \bullet 4 = 12\)
\(- 6 \bullet ( — \frac{1}{2}) = 3\)
\(7:( — 2) = — 3,5\)
\(- 12:\frac{1}{3} = — 12 \bullet 3 = — 36\)
Положительные и отрицательные числа. — it-black.ru
Положительные и отрицательные числа. — it-black.ru Перейти к содержимому С предыдущих уроков по языку Assembler мы знаем что процессор работает с двоичными числами, эти числа могут быть положительными или отрицательными.
И сегодня я подробно расскажу какие бывают положительные (без знака) и отрицательные (со знаком) числа.
Положительные числа
Если число положительное, то оно просто представляет собой результат перевода десятичного числа в двоичный вид. Для представления положительных чисел используется специальное кодирование. Старший бит в этом случае обозначает знак числа. Если знаковый бит равен нулю, то число положительное, иначе — отрицательное.
В процессорах семейства Intel основной единицей хранения всех типов данных является байт. Байт, состоит из восьми битов. В таблице представленной ниже приведены диапазоны возможных значений целых положительных чисел, с которыми может работать процессор:
| Тип числа | Диапазон значений | Степени двойки |
| Байт | 0…255 | 0…(28 – 1) |
| Слово | 0…65 535 | 0…(216 – 1) |
| Двойное слово | 0…4 294 967 295 | 0…(232 – 1) |
| Учетверённое слово | 0…18 446 744 073 709 551 615 | 0…(264 – 1) |
При работе с числами не забывайте, что в байт можно записать число со значением не более 255, в слово – со значением не более 65 535 и т.
Переполнение – это когда результат какой-либо операции не помещается в предназначенный для этого результата регистр. Также при переполнении результатом может быть не ноль, а другое число.
Отрицательные числа
Представление отрицательных чисел в вычислительных машинах встречает определенные трудности. Отрицательное число, не имеет числового смысла, оно символизирует, скорее, будущее действие — то, что в дальнейшем из вновь появившихся у нас предметов мы должны вычесть еще несколько.
Отрицательные числа — это числа со знаком минус.
Диапазоны возможных значений отрицательных чисел:
| Тип числа | Диапазон значений | Степени двойки |
| Байт | –128…+127 | -27…(27 – 1) |
| Слово | –32 768…+32 767 | -215…(215 – 1) |
| Двойное слово | –2 147 483 648… +2 147 483 647 | -231…(231 – 1) |
| Учетверённое слово | –9 223 372 036 854 775 808… +9 223 372 036 854 775 807 | -263…(263 – 1) |
Для того чтобы указать знак числа, достаточно одного разряда (бита).
При программировании на ассемблере необходимо учитывать один важный момент «Ограничение диапазона представления чисел».
Например, если размер положительной переменной равен 1 байт, то она может принимать всего 256 различных значений. Это означает, что мы не сможем представить с её помощью число, больше 255 (111111112). Для такой же отрицательной переменной максимальным значением будет 127 (011111112), а минимальным -128 (100000002). Аналогично определяется диапазон для 2- и 4-байтных переменных.
- Виктор Черемных
- 12 августа, 2017
- No Comments
Группа в VK
Обнаружили опечатку?
Сообщите нам об этом, выделите текст с ошибкой и нажмите Ctrl+Enter, будем очень признательны!
Свежие статьи
Облако меток
Похожие статьи
Команды работы с битами.
Работать с отдельными битами операндов можно, используя логические операции и сдвиги. Также в системе команд x86 существуют специальные команды для работы с битами: это команды
Основы создания макросов в Assembler.
Макросы — это шаблоны для генерации кода. Один раз создав макрос, можно использовать его во многих местах в коде программы. Макросы делают процесс программирования на
Синтаксис объявления меток.
Метка в ассемблере – это символьное имя, обозначающее ячейку памяти, которая содержит некоторую команду. Метка может содержать следующие символы: Буквы (от A до Z и
Локальные переменные.
Локальные переменные в Assembler используются для хранения промежуточных результатов во время выполнения процедуры. В отличие от глобальных, эти переменные являются временными и создаются при запуске
Instagram Vk Youtube Telegram OdnoklassnikiПолезно знать
Рубрики
Авторы
отрицательных чисел | Математика ∞ Блог
Понимание отрицательных чисел жизненно важно для того, чтобы учащийся мог получить правильный ответ на вопрос.
Отрицательное число — это в основном число меньше нуля и противоположное положительному числу.
Определение отрицательного числа
Отрицательные числа являются частью действительных чисел и могут быть целыми числами, дробями и т. д. Они просто определяются как числа, которые меньше нуля. Отрицательное число отображается путем проставления тире слева от числа. Например, -3 будет отрицательным числом.
Использование отрицательного числа в математике
Когда кто-то решает уравнение, включающее отрицательное число, он хочет убедиться, что делает уравнение правильно. Если они вычитают большое число из меньшего числа, ответ будет отрицательным, потому что ответ будет меньше нуля. Например, если уравнение 3-5, ответ будет -2. Просматривая числовую строку, человек начнет с 3 и продвинется на 5 позиций влево. Это оставляет им две позиции слева от нуля, что будет равно -2.
Определение вычитания
Понимание вычитания и того, как оно работает, жизненно важно для понимания отрицательных чисел.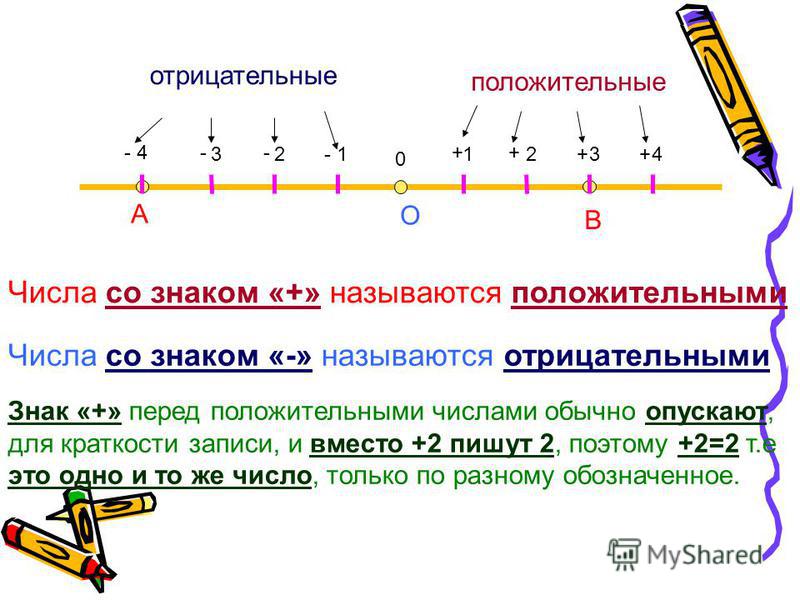
Использование калькулятора для сложения и вычитания отрицательных чисел
Когда учащемуся нужно вычесть большое число, он может использовать для этого калькулятор вычитания. Однако важно быть осторожным при использовании калькулятора. Пока они вводят числа в правильном порядке и знают, должен ли быть ответ положительным или отрицательным, это может помочь им получить правильный ответ.
Методы вычитания, помогающие вычитать положительные и отрицательные числа
Вычитание небольших чисел может быть простым, но когда учащемуся нужно вычесть большие числа, он может использовать один из распространенных методов вычитания. Они могут писать числа друг над другом и, начиная с чисел справа, чертить по одной вертикальной линии, чтобы разбить ее на более мелкие части, которые легче вычитать.
Положительное или отрицательное число влияет на результат уравнения. Независимо от того, использует ли ученик калькулятор, карандаш и бумагу или решает уравнение в уме, понимание того, как работают отрицательные числа, будет иметь жизненно важное значение.
Но в реальной жизни, правда, без них можно было бы обойтись. Большинство людей просто считают удобным немного упростить вещи. Имейте в виду, что в реальной жизни они являются предпочтением, но не необходимостью.
«Посмотрим, у меня четыре числа, я нужно сказать каждый из них про себя. P мазь к каждому целому числу и найдите минус знаки.
I идентифицировать является ли каждое целое число положительным или отрицательным.
E оценка значение каждого целого числа с использованием правил значения. «Посмотрим. Я нарисую числовую линию, чтобы помочь мне оценить. Я поставлю ноль в посередине, и, как и в моей таблице t, поставьте + справа и — справа слева от нуля.» «Правило №1 гласит, что положительные целые числа всегда больше. У меня есть два положительных целых числа, 2,8 и 1,5, поэтому я поместите их в числовую строку первыми. С выбрать целое число наибольшего значения. «Я знаю, что положительные числа больше, и что 2,8 — самое большое из положительных чисел. |
первое число минус три
и шесть десятых, следующий две и восемь десятых, третий отрицательный
одна и две десятых, а последний — одна и пять десятых.
Вы можете захотеть
нарисовать такую диаграмму:
Я знаю, что эти двое будут больше
чем два отрицательных числа, -3,6 и -1,2». Правило №2 гласит, что при положительном
числа, целое число дальше от нуля имеет большую ценность. Для двух положительных целых чисел
если я проведу линию от нуля до каждого из них, 2,8 будет дальше всего от
нуль. Используя это правило, 2,8 является наибольшим из двух положительных чисел.
Для отрицательных чисел это противоположно положительным числам. Правило
# 3 говорит, что с отрицательными числами целое число ближайший до нуля имеет большее значение. Для двух отрицательных целых чисел, если
Я провожу линию от нуля к каждому из них, -1,2 ближе всего к нулю. С использованием
по этому правилу -1,2 больше из двух отрицательных чисел.»