Модули math и numpy — Основы Python
Давайте рассмотрим библиотеки math и numpy для решения математических задач.
Важное уточнение: количество функций и внутренних модулей во многих библиотеках не позволяет рассмотреть их полностью в одной главе. Поэтому при изучении библиотек мы будем рассматривать лишь некоторые их возможности, а более подробную информацию вы сможете найти в документации. Ссылка на документацию будет в конце главы.
Библиотека math является стандартной в Python и содержит много полезных математических функций и констант. Официальная документация Python выделяет следующие виды функций этого модуля:
Функции теории чисел и функции представления. Рассмотрим некоторые из них:
math.comb(n, k)– возвращает количество сочетаний изnэлементов поkэлементам без повторений и без учёта порядка. Определим, сколькими способами можно выбрать 3 объекта из множества в 12 объектов (порядок не важен):import math print(math.
 comb(12, 3)) # 220
comb(12, 3)) # 220
math.factorial(x)– возвращает факториал целого неотрицательного числаx:print(math.factorial(5)) # 120
math.gcd(*integers)– возвращает наибольший общий делитель (НОД) для чисел-аргументов. Возможность определения НОД для более чем двух чисел появилась в Python версии 3.9:print(math.gcd(120, 210, 360)) # 30
math.lcm(*integers)– возвращает наименьшее общее кратное (НОК) для чисел-аргументов. Функция появилась в Python версии 3.9:print(math.lcm(10, 20, 30, 40)) # 120
math.perm(n, k=None)– возвращает количество размещений изnэлементов поkэлементам без повторений и с учётом порядка. Если значение аргументаkне задано, то возвращается количество перестановок множества изnэлементов:print(math.perm(4, 2)) # 12 print(math.perm(4)) # 24
math.– возвращает произведение элементов итерируемого объекта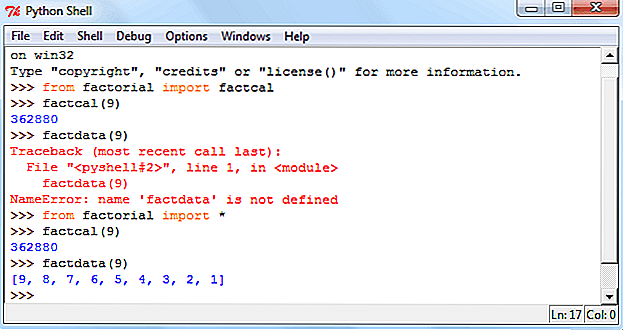 prod(iterable, start=1)
prod(iterable, start=1)iterable. Еслиiterableпустой, то возвращается значение именованного аргументаstart:print(math.prod(range(10, 21))) # 6704425728000
Степенные и логарифмические функции. Некоторые из функций:
math.exp(x)– возвращает значение экспоненциальной функции ex:print(math.exp(3.5)) # 33.11545195869231
math.log(x, base)– возвращает значение логарифма отxпо основаниюbase. Если значение аргументаbaseне задано, то вычисляется натуральный логарифм. Вычисление производится по формулеlog(x) / log(base)print(math.log(10)) # 2.302585092994046 print(math.log(10, 2)) # 3.3219280948873626
math.pow(x, y)– возвращает значениеxв степениy. В отличие от операции**происходит преобразование обоих аргументов в вещественные числа:print(math.
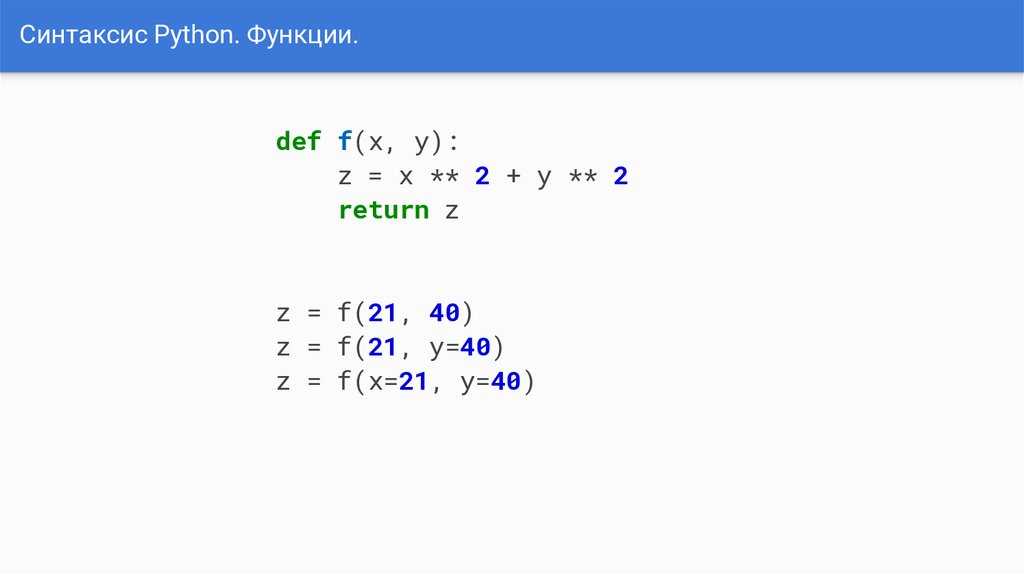 pow(2, 10)) # 1024.0
print(math.pow(4.5, 3.7)) # 261.1477575641718
pow(2, 10)) # 1024.0
print(math.pow(4.5, 3.7)) # 261.1477575641718
Тригонометрические функции. Доступны функции синус (
sin(x)), косинус (cos(x)), тангенс (tan(x)), арксинус (asin(x)), арккосинус (acos(x)), арктангенс (atan(x)). Обратите внимание: угол задаётся и возвращается в радианах. Имеются особенные функции:
, заданными как итерируемые объекты одной длины:math.dist(p, q)– возвращает Евклидово расстояние между точкамиpиqprint(math.dist((0, 0, 0), (1, 1, 1))) # 1.7320508075688772
math.hypot(*coordinates)– возвращает длину многомерного вектора с координатами, заданными в позиционных аргументахcoordinates, и началом в центре системы координат. Для двумерной системы координат функция возвращает длину гипотенузы прямоугольного треугольника по теореме Пифагора:print(math.
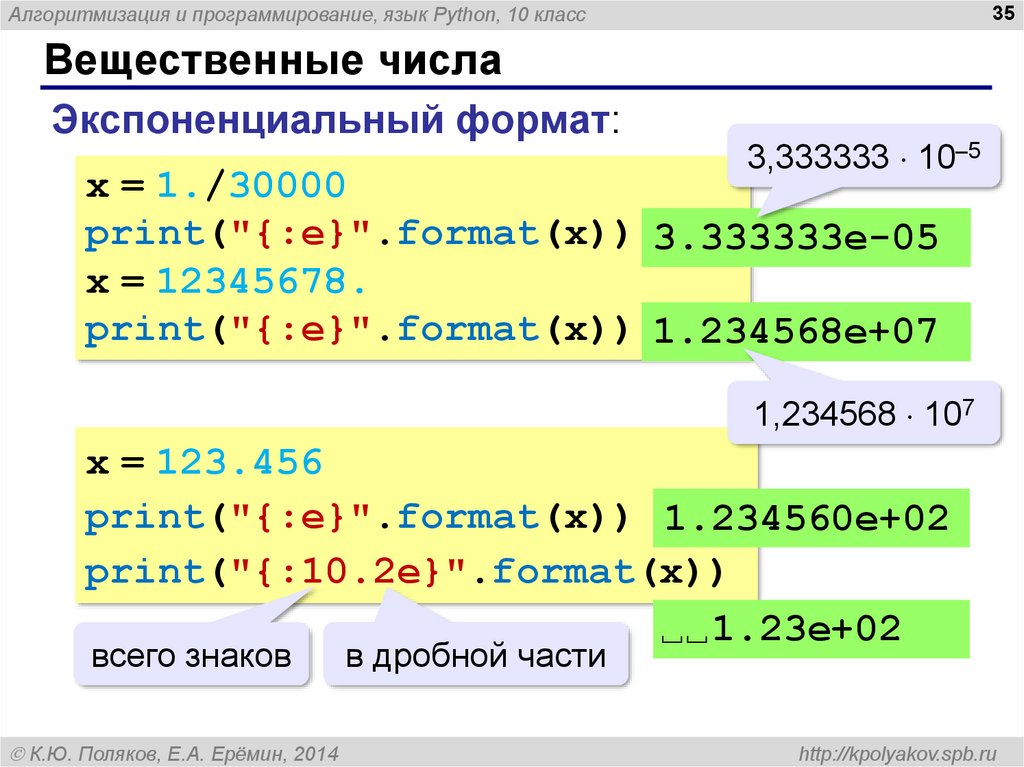 hypot(1, 1, 1)) # 1.7320508075688772
print(math.hypot(3, 4)) # 5.0
hypot(1, 1, 1)) # 1.7320508075688772
print(math.hypot(3, 4)) # 5.0
Функции преобразования угла. Доступны функции:
math.degrees(x)– преобразует угол из радиан в градусы:print(round(math.sin(math.radians(30)), 1)) # 0.5
math.radians(x)– преобразует угол из градусов в радианы.print(round(math.degrees(math.asin(0.5)), 1)) # 30.0
Гиперболические функции. Доступны функции
acosh(x),asinh(x),atanh(x),cosh(x),sinh(x),tanh(x).Специальные функции. Среди специальных функций интерес представляет Гамма-функция. Она описывает гладкую непрерывную функцию f(x) = (x — 1)!, график которой проходит через точки, соответствующие значениям функции факториала для целых чисел. Другими словами, Гамма-функция интерполирует значения факториала для вещественных чисел:
print(math.
 gamma(3)) # 2.0
print(math.gamma(3.5)) # 3.323350970447842
print(math.gamma(4)) # 6.0
gamma(3)) # 2.0
print(math.gamma(3.5)) # 3.323350970447842
print(math.gamma(4)) # 6.0
В библиотеке math можно воспользоваться значениями числа Пи (math.pi) и экспоненты (math.e).
Язык программирования Python удобен для быстрого создания программ с целью проверки какой-либо идеи. Однако зачастую его используют и в решении научных задач, а также при анализе больших данных и машинном обучении. Возникает вопрос: каким образом может быстро обрабатывать много данных интерпретируемая, а не скомпилированная программа? Оказывается, что в решении некоторых математических задач программы на Python могут быть такими же быстрыми, как и программы, созданные на компилируемых языках.
Существенную прибавку в скорости обеспечивает библиотека numpy (Numerical Python, читается как «нампАй»). Библиотека numpy частично написана на языках Си и Фортран, благодаря чему и работает быстро. Таким образом, numpy сочетает в себе вычислительную мощность языков Си и Фортран и простоту синтаксиса Python.
Библиотека numpy является нестандартной библиотекой.
Нестандартные модули можно установить в Python несколькими способами. Мы рассмотрим самый простой – установку из репозитория PyPI (Python Package Index). Репозиторий – коллекция дополнительных библиотек для Python, хранящаяся на сервере. В настоящий момент количество библиотек в репозитории составляет более 400 тысяч.
Для установки библиотек из репозитория необходимо подключение к сети Интернет, а далее выполнить команду в консоли (терминале):
pip install название>
Установим библиотеку numpy командой:
pip install numpy
После ввода команды начнётся загрузка установочного пакета и дополнительных библиотек, от которых зависит numpy. Затем начнётся процесс установки. Если установка пройдёт успешно, то вы увидите вывод в командной строке:
Successfully installed numpy
Для импорта numpy обычно используют следующий код:
import numpy as np
В программе мы сможем обращаться к numpy по новому имени – np. Это упростит чтение кода. Такой импорт широко используется сообществом программистов, поэтому стоит его придерживаться, чтобы ваш код был понятен каждому.
Это упростит чтение кода. Такой импорт широко используется сообществом программистов, поэтому стоит его придерживаться, чтобы ваш код был понятен каждому.
Библиотека numpy работает с объектами-массивами, которые способны хранить много значений и быть многомерными. При этом в отличие от списков массивы могут хранить только значения одного типа. За счёт этого массивы в numpy занимают меньше памяти и работают быстрее, чем списки.
Создать массив можно разными способами. Один из них – использовать функцию array() для преобразования списка в массив. Для доступа к элементам массива необходимо указать индекс элемента в квадратных скобках. Индексация начинается с нуля:
import numpy as np
a = np.array([1, 2, 3, 4])
b = np.array([[1, 2], [3, 4], [5, 6], [7, 8]])
print(f"a[0] = {a[0]}")
print(f"b[0] = {b[0]}")
Вывод программы:
a[0] = 1 b[0] = [1 2]
В нашем примере массив a имеет размерность равную 1. Размерность массива b равна 2. В терминологии
В терминологии numpy массив a имеет одну ось (термин «axis» из документации) длиной 4 элемента, а массив b имеет 2 оси: первая имеет длину 4, а длина второй оси равна 2.
Массивы numpy являются объектами класса ndarray. Наиболее важными атрибутами класса ndarray являются:
ndarray.ndim– размерность (количество осей) массива;ndarray.shape– кортеж, значения которого содержат количество элементов по каждой из осей массива;ndarray.size– общее количество элементов массива;ndarray.dtype– объект, описывающий тип данных элементов массива;ndarray.itemsize– размер памяти в байтах, занимаемый одним элементом массива.
import numpy as np
a = np.array([[1, 2], [3, 4], [5, 6], [7, 8]])
print(f"a.ndim = {a.ndim}, a.shape = {a.shape}, a.size = {a.size}, a.dtype = {a.dtype}")
Вывод программы:
a.ndim = 2, a.shape = (4, 2), a.size = 8, a.dtype = int32
Встроенные в numpy типы данных аналогичны типам данных в языке программирования Си. Например, в предыдущем примере мы создали массив со значениями типа int32, то есть целые числа со знаком (отрицательные и положительные) и размером занимаемой памяти 32 бита. Из ограничения в размере памяти для типов данных в numpy следует то, что массивы каждого типа данных могут хранить значения из определённого диапазона. Например, для
Покажем на примере, что произойдёт, если попытаться записать значение не из диапазона для типа данных. Для этого создадим массив типа uint8 – целые числа без знака размером 8 бит. Диапазон значений для этого типа от 0 до 255. Тип данных можно указать через именованный аргумент dtype при создании массива:
import numpy as np a = np.array([1, 2, 3], dtype="uint8") a[0] = 256 print(a)
Вывод программы:
[0 2 3]
Значение элемента не вышло за пределы диапазона, а было взято с его начала.
В numpy существуют и другие встроенные типы данных. С ними можно ознакомиться в документации.
При создании массива без указания его типа в аргументе dtype библиотека numpy попытается привести его к тому типу данных, который сможет хранить все значения исходной коллекции.
Рассмотрим пример:
import numpy as np a = np.array([1, 2.5, 3]) print(a) print(a.dtype) b = np.array(['text', 1, 2.5]) print(b) print(b.dtype)
Вывод программы:
[1. 2.5 3. ] float64 ['text' '1' '2.5'] <U32
В примере для массива a был выбран тип данных float64, так как исходный список содержит вещественное число. Для массива b был выбран тип данных <U32, который может хранить строки в кодировке Unicode длиной 32 символа. Такой тип данных был выбран, поскольку в исходной коллекции есть элемент-строка.
Для создания массива из нулей используется функция np.zeros(), который принимает кортеж с количеством чисел, соответствующим количеству осей массива, а значения в кортеже – количество элементов по каждой из осей.
import numpy as np a = np.zeros((4, 3)) print(a) print() a = np.zeros((4, 3), dtype="int32") print(a)
Вывод программы:
[[0. 0. 0.] [0. 0. 0.] [0. 0. 0.] [0. 0. 0.]] [[0 0 0] [0 0 0] [0 0 0] [0 0 0]]
Функция np.ones() создаёт массив аналогично функции np.zeros(), только из элементов-единиц.
import numpy as np a = np.ones((4, 3)) print(a)
Вывод программы:
[[1. 1. 1.] [1. 1. 1.] [1. 1. 1.] [1. 1. 1.]]
Для создания массива, заполненного значениями из диапазона, используется функция np.arange(). Эта функция похожа на стандартную функцию range(), но возвращает массив и может создавать диапазон значений из вещественных чисел.
import numpy as np a = np.arange(1, 10) print(a) print() a = np.arange(1, 5, 0.4) print(a)
Вывод программы:
[1 2 3 4 5 6 7 8 9] [1. 1.4 1.8 2.2 2.6 3. 3.4 3.8 4.2 4.6]
Функция np.linspace() создаёт массив из заданного количества вещественных равномерно-распределённых значений из указанного диапазона.
import numpy as np a = np.linspace(1, 5, 10) # задаётся начало, конец диапазона и количество значений print(a)
Вывод программы:
[1. 1.44444444 1.88888889 2.33333333 2.77777778 3.22222222 3.66666667 4.11111111 4.55555556 5. ]
Для изменения размерности массива используется функция reshape(). Она принимает кортеж, значения которого задают новые размеры массива по осям. Функция reshape() возвращает новый массив. Обратите внимание: при изменении размерности количество элементов в массиве не должно измениться.
import numpy as np a = np.zeros((4, 3), dtype="uint8") print(a) print() a = a.reshape((2, 6)) print(a)
Вывод программы:
[[0 0 0] [0 0 0] [0 0 0] [0 0 0]] [[0 0 0 0 0 0] [0 0 0 0 0 0]]
Метод resize() меняет размерность исходного массива:
import numpy as np a = np.zeros((4, 3), dtype="uint8") print(a) print() a.resize((2, 2, 3)) print(a)
Вывод программы:
[[0 0 0] [0 0 0] [0 0 0] [0 0 0]] [[[0 0 0] [0 0 0]] [[0 0 0] [0 0 0]]]
Если при изменении размерности в функции reshape() указать значение -1 по одной или нескольким осям, то значения размерности рассчитаются автоматически:
import numpy as np a = np.zeros((4, 3), dtype="uint8") print(a) print() a = a.reshape((2, 3, -1)) print(a)
Вывод программы:
[[0 0 0] [0 0 0] [0 0 0] [0 0 0]] [[[0 0] [0 0] [0 0]] [[0 0] [0 0] [0 0]]]
Для работы с массивами доступны все стандартные арифметические операции, а также тригонометрические, экспоненциальная и другие функции. Выполнение математических операций над массивами происходит поэлементно. Размерность массивов должна совпадать при выполнении этих операций. Применение некоторых из операций приведено в примере:
import numpy as np a = np.array([9, 8, 7]) b = np.array([1, 2, 3]) print(a + b) print(a - b) print(a * b) print(a / b)
Вывод программы:
[10 10 10] [8 6 4] [ 9 16 21] [9. 4. 2.33333333]
Для умножения матриц используется операция @ или функция dot:
import numpy as np
a = np.array([[1, 2, 3],
[4, 5, 6],
[7, 8, 9]])
b = np.array([[0, 0, 1],
[0, 1, 0],
[1, 0, 0]])
print(a @ b)
Вывод программы:
[[3 2 1] [6 5 4] [9 8 7]]
Матрицы можно транспонировать функцией transpose() и поворачивать функцией rot90(). При повороте можно указать направление поворота вторым аргументом:
При повороте можно указать направление поворота вторым аргументом:
import numpy as np
a = np.arange(1, 13).reshape(4, 3)
print(a)
print("Транспонирование")
print(a.transpose())
print("Поворот вправо")
print(np.rot90(a))
print("Поворот влево")
print(np.rot90(a, -1))
Вывод программы:
[[ 1 2 3] [ 4 5 6] [ 7 8 9] [10 11 12]] Транспонирование [[ 1 4 7 10] [ 2 5 8 11] [ 3 6 9 12]] Поворот вправо [[ 3 6 9 12] [ 2 5 8 11] [ 1 4 7 10]] Поворот влево [[10 7 4 1] [11 8 5 2] [12 9 6 3]]
Функции вычисления суммы элементов массива, поиска минимального и максимального элементов и многие другие по умолчанию работают для всех элементов массива, не учитывая размерность:
import numpy as np
a = np.array([[1, 2, 3],
[4, 5, 6],
[7, 8, 9]])
print(a.sum())
print(a.min())
print(a.max())
Вывод программы:
45 1 9
Дополнительно в указанных функциях можно указать номер оси (индексация с 0), на которой будет работать функция:
import numpy as np a = np.array([[1, 2, 3], [4, 5, 6], [7, 8, 9]]) print(a.sum(axis=0)) # сумма чисел в каждом столбце print(a.sum(axis=1)) # сумма чисел в каждой строке print(a.min(axis=0)) # минимум по столбцам print(a.max(axis=1)) # максимум по строкам
Вывод программы:
[12 15 18] [ 6 15 24] [1 2 3] [3 6 9]
В массивах можно брать срез. Для одномерных массивов эта операция аналогична стандартному срезу в Python. Для многомерного массива можно задавать диапазон среза отдельно для каждой оси. Таким образом, можно взять срез отдельной части матрицы, указав какие строки и столбцы должны попасть в срез:
import numpy as np a = np.arange(1, 13).reshape(3, 4) print(a) print() print(a[:2, 2:]) print() print(a[:, ::2])
Вывод программы:
[[ 1 2 3 4] [ 5 6 7 8] [ 9 10 11 12]] [[3 4] [7 8]] [[ 1 3] [ 5 7] [ 9 11]]
В цикле for можно пройти по элементам первой оси массива:
import numpy as np a = np.arange(1, 13).reshape(3, 4) print(a) for row in a: print(row)
Вывод программы:
[[ 1 2 3 4] [ 5 6 7 8] [ 9 10 11 12]] [1 2 3 4] [5 6 7 8] [ 9 10 11 12]
Для линеаризации многомерного массива можно использовать атрибут flat, который является итератором, возвращающим последовательно значения массива:
import numpy as np
a = np.arange(1, 13).reshape(3, 4)
print(a)
print()
print("; ".join(str(el) for el in a.flat))
Вывод программы:
[[ 1 2 3 4] [ 5 6 7 8] [ 9 10 11 12]] 1; 2; 3; 4; 5; 6; 7; 8; 9; 10; 11; 12
Покажем на примере различие в скорости работы массивов и списков. Посчитаем сумму квадратных корней первых 107 чисел.
import numpy as np
from time import time
t = time()
print(f"Результат итератора: {sum(x ** 0.5 for x in range(10 ** 7))}.")
print(f"{time() - t} с.")
t = time()
print(f"Результат numpy: {np.sqrt(np.arange(10 ** 7)).sum()}.")
print(f"{time() - t} с.")
Вывод программы:
Результат итератора: 21081849486.439312. 1.7823209762573242 с. Результат numpy: 21081849486.442448. 0.05197310447692871 с.
Библиотека numpy решила задачу в 30 раз быстрее, чем итератор.
За счёт скорости работы и удобной обработки массивов библиотека numpy используется для расчётов во многих других библиотеках. С одной из них мы поработаем в следующей главе.
Для более детального изучения библиотеки numpy рекомендуем почитать документацию.
Числа ⚡️ Python 3 с примерами кода
Числа в Python 3 — целые, вещественные, комплексные. Работа с числами и операции над ними.
Целые числа (int)
Числа в Python 3 ничем не отличаются от обычных чисел. Они поддерживают набор самых обычных математических операций:
| Синтаксис | Описание |
|---|---|
x + y | Сложение |
x - y | Вычитание |
x * y | Умножение |
x / y | Деление |
x // y | Получение целой части от деления |
x % y | Остаток от деления |
-x | Смена знака числа |
abs(x) | Модуль числа |
divmod(x, y) | Пара (x // y, x % y) |
x ** y | Возведение в степень |
pow(x, y[, z]) | xy по модулю (если модуль задан) |
Также нужно отметить, что целые числа в python 3, в отличие от многих других языков, поддерживают длинную арифметику (однако, это требует больше памяти). y
y
x & yx << nx >> y~xДополнительные методы
int.bit_length()- количество бит, необходимых для представления числа в двоичном виде, без учёта знака и лидирующих нулей.
>>> n = -37 >>> bin(n) '-0b100101' >>> n.bit_length() 6
int.to_bytes(length, byteorder, *, signed=False)- возвращает строку байтов, представляющих это число.
>>> (1024).to_bytes(2, byteorder='big') b'\x04\x00' >>> (1024).to_bytes(10, byteorder='big') b'\x00\x00\x00\x00\x00\x00\x00\x00\x04\x00' >>> (-1024).to_bytes(10, byteorder='big', signed=True) b'\xff\xff\xff\xff\xff\xff\xff\xff\xfc\x00' >>> x = 1000 >>> x.to_bytes((x.bit_length() // 8) + 1, byteorder='little') b'\xe8\x03'
classmethod int.from_bytes(bytes, byteorder, *, signed=False)- возвращает число из данной строки байтов.
>>> int.from_bytes(b'\x00\x10', byteorder='big') 16 >>> int.from_bytes(b'\x00\x10', byteorder='little') 4096 >>> int.from_bytes(b'\xfc\x00', byteorder='big', signed=True) -1024 >>> int.from_bytes(b'\xfc\x00', byteorder='big', signed=False) 64512 >>> int.from_bytes([255, 0, 0], byteorder='big') 16711680
Системы счисления
Те, у кого в школе была информатика, знают, что числа могут быть представлены не только в десятичной системе счисления. К примеру, в компьютере используется двоичный код, и, к примеру, число 19 в двоичной системе счисления будет выглядеть как 10011. Также иногда нужно переводить числа из одной системы счисления в другую. Python для этого предоставляет несколько функций:
int([object], [основание системы счисления])- преобразование к целому числу в десятичной системе счисления.
 По умолчанию система счисления десятичная, но можно задать любое основание от
По умолчанию система счисления десятичная, но можно задать любое основание от 2до36включительно. bin(x)- преобразование целого числа в двоичную строку.
hex(х)- преобразование целого числа в шестнадцатеричную строку.
oct(х)- преобразование целого числа в восьмеричную строку.
Примеры:
>>> a = int('19') # Переводим строку в число
>>> b = int('19.5') # Строка не является целым числом
Traceback (most recent call last):
File "", line 1, in
ValueError: invalid literal for int() with base 10: '19.5'
>>> c = int(19.5) # Применённая к числу с плавающей точкой,
# отсекает дробную часть
>>> print(a, c)
19 19
>>> bin(19)
'0b10011'
>>> oct(19)
'0o23'
>>> hex(19)
'0x13'
>>> 0b10011 # Так тоже можно записывать числовые константы
19
>>> int('10011', 2)
19
>>> int('0b10011', 2)
19
Вещественные числа (float)
Вещественные числа поддерживают те же операции, что и целые. Однако (из-за представления чисел в компьютере) вещественные числа неточны, и это может привести к ошибкам:
Однако (из-за представления чисел в компьютере) вещественные числа неточны, и это может привести к ошибкам:
>>> 0.1 + 0.1 + 0.1 + 0.1 + 0.1 + 0.1 + 0.1 + 0.1 + 0.1 + 0.1 0.9999999999999999
Для высокой точности используют другие объекты (например Decimal и Fraction)).
Также вещественные числа не поддерживают длинную арифметику:
>>> a = 3 ** 1000 >>> a + 0.1 Traceback (most recent call last): File "", line 1, in OverflowError: int too large to convert to float
Простенькие примеры работы с числами:
>>> c = 150 >>> d = 12.9 >>> c + d 162.9 >>> p = abs(d - c) # Модуль числа >>> print(p) 137.1 >>> round(p) # Округление 137
Дополнительные методы
float.as_integer_ratio()- пара целых чисел, чьё отношение равно этому числу.
float.is_integer()- является ли значение целым числом.

float.hex()- переводит
floatвhex(шестнадцатеричную систему счисления). classmethod float.fromhex(s)floatиз шестнадцатеричной строки.
>>> (10.5).hex()
'0x1.5000000000000p+3'
>>> float.fromhex('0x1.5000000000000p+3')
10.5
Помимо стандартных выражений для работы с числами (а в Python их не так уж и много), в составе Python есть несколько полезных модулей.
Модуль math предоставляет более сложные математические функции.
>>> import math >>> math.pi 3.141592653589793 >>> math.sqrt(85) 9.219544457292887
Модуль random реализует генератор случайных чисел и функции случайного выбора.
>>> import random >>> random.random() 0.15651968855132303
Комплексные числа (complex)
В Python встроены также и комплексные числа:
>>> x = complex(1, 2) >>> print(x) (1+2j) >>> y = complex(3, 4) >>> print(y) (3+4j) >>> z = x + y >>> print(x) (1+2j) >>> print(z) (4+6j) >>> z = x * y >>> print(z) (-5+10j) >>> z = x / y >>> print(z) (0.44+0.08j) >>> print(x.conjugate()) # Сопряжённое число (1-2j) >>> print(x.imag) # Мнимая часть 2.0 >>> print(x.real) # Действительная часть 1.0 >>> print(x > y) # Комплексные числа нельзя сравнить Traceback (most recent call last): File "", line 1, in TypeError: unorderable types: complex() > complex() >>> print(x == y) # Но можно проверить на равенство False >>> abs(3 + 4j) # Модуль комплексного числа 5.0 >>> pow(3 + 4j, 2) # Возведение в степень (-7+24j)
Для работы с комплексными числами используется также модуль cmath.
Что такое модульный оператор (%) в Python?
Когда мы видим «%», первое, что приходит нам на ум, это «знак процента», но когда мы думаем об этом с точки зрения компьютерного языка, этот знак на самом деле имеет другое имя и значение. В вычислениях операция по модулю (%) находит остаток или знаковый остаток после деления одного числа на другое (называемый модулем операции).
Даны два положительных числа, a и n, по модулю n (a % n, сокращенно a mod n) — это остаток от евклидова деления числа a на n, где a — делимое, а n — делитель.
По сути, операция Python по модулю используется для получения остатка от деления. Оператор по модулю (% ) считается арифметической операцией, наряду с +, — , /, *, **, //. В большинстве языков оба операнда этого оператора по модулю должны быть целыми числами. Но Python Modulo в этом случае универсален. Операнды могут быть либо целое число или число с плавающей запятой .
Синтаксис:
а % б
Здесь a делится на b, и возвращается остаток от этого деления.
Code:
Python3
|
Выход:
13 mod 5 = 3 15,0 по модулю 7,0 = 1,0
Это был простой пример, показывающий использование синтаксиса и базовую операцию, выполняемую оператором по модулю. Предположим, мы хотим вычислить остаток от каждого числа от 1 до n при делении на фиксированное число k.
Предположим, мы хотим вычислить остаток от каждого числа от 1 до n при делении на фиксированное число k.
Python3
. ) |
Вывод:
1 mod 3 = 1 2 по модулю 3 = 2 3 мод 3 = 0 4 по модулю 3 = 1 5 мод 3 = 2
Исключения
Единственное исключение, которое вы получаете с операцией по модулю python, равно ZeroDivisionError . Это происходит, если операнд делителя оператора по модулю становится равным ноль . Это означает, что правый операнд не может быть равен нулю . Давайте посмотрим на следующий код, чтобы узнать об этом исключении Python.
Это происходит, если операнд делителя оператора по модулю становится равным ноль . Это означает, что правый операнд не может быть равен нулю . Давайте посмотрим на следующий код, чтобы узнать об этом исключении Python.
Python3
|
Вывод:
Нельзя делить на ноль! Изменить значение правого операнда.
Оператор модуля Python — Javatpoint
следующий → ← предыдущая Как и в других языках программирования, оператор модуля Python выполняет ту же работу, чтобы найти модуль заданного числа. Оператор — это математический символ, используемый для выполнения различных операций, таких как (+, -, * /) сложение, вычитание, умножение и деление с заданными двумя числами, чтобы вернуть результат в виде целого числа, а также числа с плавающей запятой. . Оператор указывает компилятору выполнять определенные действия на основе переданного символа оператора для заданного числа. Python Modulus Operator — это встроенный оператор, который возвращает оставшиеся числа путем деления первого числа на второе. Он также известен как Python по модулю . В Python символ модуля представлен как символ процента ( % ). Синтаксис Ниже приведен синтаксис для получения остатка путем деления первого числа на второе. Rem = X % Y Здесь X и Y — два целых числа, а модуль (%) используется для получения остатка от деления первого числа (X) на второе число (Y). Например, у нас есть два числа, 24 и 5. И мы можем получить остаток, используя модуль или оператор по модулю между числами 24 % 5. Здесь 24 делится на 5, что возвращает 4 в качестве остатка и 4 в качестве остатка. частное. Когда первое число полностью делится на другое число без остатка, результат будет 0, Получить модуль двух целых чисел с помощью цикла whileДавайте напишем программу для получения остатка от двух чисел, используя цикл while и оператор модуля (%) в Python. Get_rem.py while True: # если условие while истинно, если блок выполняется
a = input('Вы хотите продолжить или нет (Да/Нет)?')
if a. Вывод: Вы хотите продолжить или нет (Да/Нет)? Д Первое число: 37 Второе число: 5 37 % 5 = 2 5 % 37 = 5 Вы хотите продолжить или нет (Да/Нет)? Д Первое число: 37 Второе число: 5 24 % 5 = 4 5 % 24 = 5 Вы хотите продолжить или нет (Да/Нет)? Д Первое число: 37 Второе число: 5 28 % 5 = 3 5 % 28 = 5 Получить модуль двух чисел с плавающей запятойДавайте напишем программу для нахождения остатка от двух целых чисел с помощью оператора модуля в Python. Мод.py x = float(input('Первое число:')) y = float (ввод ('Второе число:')) res = x % y # сохраняем остаток в переменной res print("Модуль двух чисел с плавающей запятой: ", x, "%", y, " = ", res, sep = " ") Вывод: Первое число: 40,5 Второй номер: 20,5 Модуль двух чисел с плавающей запятой: 40,5% 20,5 = 20,0 Получить модуль отрицательного числа Давайте напишем программу для получения остатка от двух отрицательных чисел, используя цикл while и оператор модуля (%) в Python. Мод.py пока верно: x = input(' Вы хотите продолжить (Y/N)?') если x.upper() != 'Y': перерыв # введите два целых числа и сохраните их в x и y x = int (ввод (' Первое число: ')) y = int (ввод (' Второе число: ')) print("Модуль отрицательного числа: ", x, "%", y, " = ", x % y, sep = " ") print("Модуль отрицательного числа: ", y, "%", x, " = ", y % x, sep = " ") Вывод: Первое число: -10 Второе число: 3 Модуль отрицательного числа: -10 % 3 = 2 Модуль отрицательного числа: 3 % -10 = -7 Вы хотите продолжить (Да/Нет)? Н Получить модуль двух чисел с помощью функции fmod()Давайте напишем программу для получения остатка от двух чисел с плавающей запятой, используя функцию fmod() в Python. Fmod.py import math # импортировать математический пакет для использования функции fmod().
res = math.fmod(25. Вывод: Модуль с использованием fmod(): 3,5 Модуль с использованием fmod(): 13,5 Первое число 24 Второе число 5 Модуль двух чисел с использованием функции fmod() равен 24 % 5 = 4,0. Получить модуль n чисел с помощью функцииДавайте напишем программу на Python, чтобы найти модуль числа n, используя функцию и цикл for. getRemainder.py def getRemainder(n, k):
для i в диапазоне (1, n + 1):
# Сохраняем остаток в переменной rem, когда i делится на число k
рем = я % к
print(i, "%", k, "=", rem, sep = "") # использовать код драйвера _name_
если __name__ == "__main__": # определить первое число для отображения числа до желаемого числа. Вывод: Определите число, до которого вы хотите отобразить остаток 7 Введите второе число 5 1 % 5 = 1 2 % 5 = 2 3 % 5 = 3 4 % 5 = 4 5 % 5 = 0 6 % 5 = 1 7 % 5 = 2 Получить модуль заданного массива с помощью функции mod()Давайте напишем программу для демонстрации функции mod() в Python. Mod_fun.py импортировать numpy как np # импортировать пакет numpy x = np.array([40, -25, 28, 35]) # определяем первый массив y = np.array([20, 4, 6, 8]) # определяем второй массив # вызвать функцию mod() и передать x и y в качестве параметра print("Модуль данного массива равен ", np.mod (x, y)) Вывод: Модуль данного массива равен [0 3 4 3] Как видно из приведенной выше программы, переменные x и y содержат массивы. Получить модуль двух чисел с помощью numpy.Давайте рассмотрим программу, которая импортирует пакет numpy из библиотеки Python, а затем использует функцию остатка для получения модуля в Python. Число.py импортировать пакет numpy как np # импортировать пакет numpy как np # объявление переменных с их значениями число = 38 число2 = 8 res = np.remainder(num, num2) # используем функцию np.remainder() print("Модуль равен", num, "%", num2, "=", res) # отображение модуля num % num2 Вывод: Модуль равен 38 % 8 = 6 Исключения в операторе Python Modulus В Python, когда число делится на ноль, возникает исключение, и это исключение называется ZeroDivisionError . Давайте напишем программу для демонстрации оператора Python Exception in Modulus. За исключением.py x = int(input('Первое число: ')) y = int(input(' Второе число равно: ')) # отображаем обработку исключений try: # определить попытку напечатать (х, '%', у, '=', х% у) кроме ZeroDivisionError as err: # определить исключение print('Невозможно разделить число на ноль!' + 'Итак, измените значение правого операнда.') Вывод: Первое число: 24 Второе число: 0 Нельзя делить число на ноль! Итак, измените значение правого операнда. Как видно из приведенного выше результата, он отображает: « Невозможно разделить число на ноль! Итак, измените значение правого операнда ». Оставить комментарий
|

 comb(12, 3)) # 220
comb(12, 3)) # 220


 '
'  Следовательно, он называется оператором остатка.
Следовательно, он называется оператором остатка. upper() != 'Y': # Если пользователь передает 'Y', выполняется следующий оператор.
перерыв a = int(input(' Первое число равно: ')) # первое число
b = int(input(' Второе число равно: ')) # второе число
print(a, ' % ', b, ' = ', a % b) # выполнить a % b
print(b, ' % ', a, ' = ', b % a) # выполнить b % a
upper() != 'Y': # Если пользователь передает 'Y', выполняется следующий оператор.
перерыв a = int(input(' Первое число равно: ')) # первое число
b = int(input(' Второе число равно: ')) # второе число
print(a, ' % ', b, ' = ', a % b) # выполнить a % b
print(b, ' % ', a, ' = ', b % a) # выполнить b % a
 5, 5.5) # передать параметры
print ("Модуль с использованием fmod() равен:", res)
ft = math.fmod(75,5, 15,5)
print ("Модуль с использованием fmod() равен:", ft)
# взять два целых числа от пользователя
x = int(input("Первое число равно"))
y = int (ввод ("Второе число"))
out = math.fmod(x, y) # передать параметры
print("Модуль двух чисел с использованием функции fmod() равен", x, "%", y, "=", out)
5, 5.5) # передать параметры
print ("Модуль с использованием fmod() равен:", res)
ft = math.fmod(75,5, 15,5)
print ("Модуль с использованием fmod() равен:", ft)
# взять два целых числа от пользователя
x = int(input("Первое число равно"))
y = int (ввод ("Второе число"))
out = math.fmod(x, y) # передать параметры
print("Модуль двух чисел с использованием функции fmod() равен", x, "%", y, "=", out) n = int(input ("Определите число, до которого вы хотите отобразить остаток"))
k = int( input ("Введите второе число")) # определяем делитель # вызов функции определения
получить остаток (n, k)
n = int(input ("Определите число, до которого вы хотите отобразить остаток"))
k = int( input ("Введите второе число")) # определяем делитель # вызов функции определения
получить остаток (n, k) После этого мы используем функцию mod() для передачи x и y в качестве параметра массива, который делит первый массив (x) на второй массив (y), а затем возвращает оставшиеся числа.
После этого мы используем функцию mod() для передачи x и y в качестве параметра массива, который делит первый массив (x) на второй массив (y), а затем возвращает оставшиеся числа. Другими словами, он возвращает исключение, когда число делится на делитель, равный нулю. Поэтому, если мы хотим удалить исключение из оператора модуля Python, делитель не должен быть равен нулю.
Другими словами, он возвращает исключение, когда число делится на делитель, равный нулю. Поэтому, если мы хотим удалить исключение из оператора модуля Python, делитель не должен быть равен нулю.