Какие числа отрицательные: § Отрицательные числа. Координатная прямая

какие так называют, что такое в математике, чем отличаются

Содержание:

• Какие числа называются положительными и отрицательными
• Сравнение положительных и отрицательных чисел
• Правила действий с отрицательными и положительными числами
• Примеры задач с решением

Содержание

• Какие числа называются положительными и отрицательными
• Сравнение положительных и отрицательных чисел
• Правила действий с отрицательными и положительными числами
• Примеры задач с решением

Какие числа называются положительными и отрицательными

Отрицательными числами в алгебре являются числа со знаком минус (-). Например, к таким числам относят -1, -2, -3. Прочитать запись можно, как минус один, минус два, минус три.

Отрицательное число — это какое-либо число меньше нуля, перед которым ставится знак минус.

Положительные числа — числа, состоящее в множестве положительных чисел, являются числами без знака минус в обозначении и не являются нулем.

Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.

В системе отрицательных чисел так же, как и среди положительных есть дроби: обыкновенные и десятичные, целые числа, корни и так далее. Почти все подвиды чисел, которые встречаются среди положительных чисел, есть и среди отрицательных. Стоит отметить, что, согласно понятию, число 0 не является ни положительным, ни отрицательным числом.

Положительные числа — это числа, соответствующие точкам в той части координатной прямой, которая лежит с правой стороны относительно начала отсчета.

Отрицательные числа — являются числами, соотносящимися с точками в части координатной прямой, которая расположена с левой стороны относительно начала отсчета (нуля).

Наглядным примером использования отрицательных чисел является термометр. Прибор демонстрирует температуру тела, воздуха, почвы, воды. Зимой при холодной погоде температура воздуха снижается до отрицательных значений. К примеру, -10 градусов мороза:

 

Обычные числа, в том числе, 1, 2, 3 называют положительными. Данные числа имеют знак (+). Обычно, его не записывают.

Координатная прямая — является прямой линией, на которой размещены все числа, включая отрицательные и положительные.

Координатная прямая имеет следующий вид:

 

В данном случае отмечены только числа от −5 до 5. В действительности координатная прямая бесконечна. На изображении можно увидеть только фрагмент этой прямой. Для того чтобы отметить на координатной прямой числа, использую точки. Началом отсчета является нуль. С левой стороны от нуля отмечают отрицательные числа, а с правой — положительные.

Координатная прямая продолжается бесконечно по обе стороны. Бесконечность в математике обозначается символом   \(\infty\). Отрицательное направление будет обозначаться символом −\(\infty\), а положительное — символом +\(\infty\). Таким образом, координатная прямая содержит все числа от минус бесконечности до плюс бесконечности:

\((−\infty; +\infty)\)

Каждая точка на координатной прямой обладает определенным именем и координатой. Именем является какая-либо латинская буква. Координата представляет собой число, указывающее на положение точки на прямой. Таким образом, координатой является то число, которое требуется отметить на координатной прямой. К примеру, точка А(2) читается, как «точка А с координатой 2» и обозначается на координатной прямой таким образом:

 

При рассмотрении изображения координатной прямой можно заметить, что отрицательные числа лежат левее относительно начала отсчета, а положительные числа — правее. С каждым шагом в левую сторону число будет уменьшаться в меньшую сторону. При каждом шаге в правом направлении число будет увеличиваться.

Сравнение положительных и отрицательных чисел

Положительные числа, то есть те, которые больше 0, можно рассматривать в качестве прибыли, прибавки, увеличения количества чего-либо. Отрицательные числа можно представить, как недостаток, убыток, расход, долг. Предположим, что имеется 55 неких предметов, например, яблок. Цифра 55 является положительной. В том случае, когда требуется отдать кому-то 5 яблок, данной действие можно обозначить, как -5. На градуснике рост температуры на 4,5 значений можно описать как +4,5, а снижение, в свою очередь, как −4,5. В приборах, которые используют для измерений, часто применяют положительные и отрицательные числа. Это объясняется удобством отображения изменения величин.

Любое отрицательное число меньше, чем любое положительное число. К примеру, если сравнить -5 и 3, то минус пять меньше трех.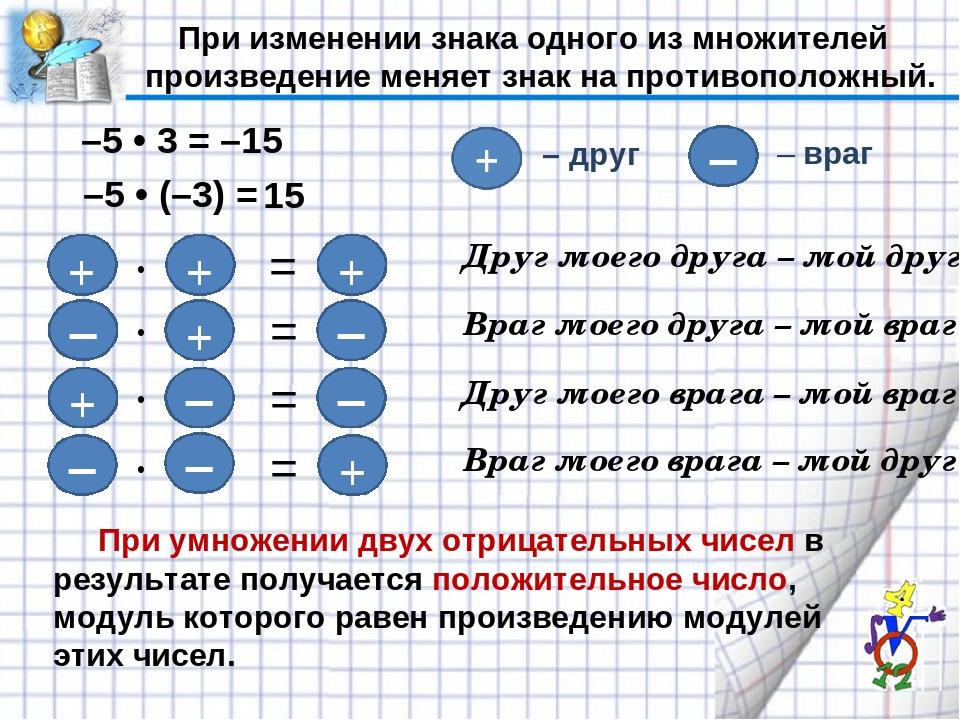

Это объясняется тем, что -5 представляет собой отрицательное число, а 3 является положительным числом. С помощью координатной прямой достаточно просто определить положение данных чисел.

 

На прямой -5 расположено левее относительно числа 3. Согласно правилу, любое отрицательное число меньше любого положительного числа. Отсюда следует, что:

−5 < 3

Из двух отрицательных чисел меньше то, которое располагается левее на координатной прямой. К примеру, при сравнении чисел -4 и -1 можно сделать вывод, что минус четыре меньше, чем минус единица. Причина заключается в том, что на координатной прямой -4 располагается левее, чем -1.

 

Видно, что -4 лежит левее, а -1 правее. Из двух отрицательных чисел меньше то, которое располагается левее на координатной прямой. Таким образом:

-4 < -1

Ноль больше, чем любое отрицательное число. К примеру, при сравнении 0 и -3 можно сделать вывод, что ноль больше, чем минус три. Это объясняется тем, что на координатной прямой 0 располагается правее, чем -3.

 

При рассмотрении координатной прямой можно заметить, что 0 лежит правее, а -3 левее. Согласно правилу, нуль больше любого отрицательного числа. Таким образом:

0 > -3

Нуль меньше любого положительного числа. К примеру, можно сравнить 0 и 4. Ноль меньше, чем 4.

 

На координатной прямой 0 располагается левее, а 4 правее. Исходя из правила, ноль меньше, чем какое-либо положительное число. Таким образом:

0 < 4

Правила действий с отрицательными и положительными числами

Существуют следующие правила знаков при умножении и делении отрицательных чисел:

1. Умножение или деление отрицательного числа на отрицательное приводит в результате к получению положительного числа.
2. При умножении или делении положительного числа на отрицательное число результатом является отрицательное число.
3. Если требуется умножить или разделить отрицательное число на положительное, то получится отрицательное число.

В процессе сложения отрицательных чисел следует руководствоваться аналогичными правилами знаков в несколько ином виде. По общей формулировке правило знаков звучит так: «Плюс на минус дает минус, минус на минус дает плюс и плюс на плюс дает плюс». В таком случае, при сложении отрицательного числа с другим, получится:

-а+(-в)=-а-в — то есть из отрицательного числа вычитается положительное.

Аналогичное правило применимо для примеров с вычитанием отрицательных чисел:

-а-(-в)=-а+в — к отрицательному числу в итоге прибавляется положительное.

В том случае, когда требуется сложить два отрицательных числа, следует сложить два числа и поставить знак минус. К примеру:

(−2)+(−3)=−5(−2)+(−3)=−5

Если первое число положительное, а второе отрицательное, требуется определить, какое число по модулю больше. Далее нужно отнять от большего меньшее число и поставим знак большего числа. Например:

(−8)+4=4−8=−4

9+(−4)=9−4=5

Каждое число, за исключением 0, соответствует противоположному элементу. В сумме с ним число дает 0. Например:

−9+9=0

7,1+(−7,1)=0

При вычитании двух отрицательных чисел следует руководствоваться правилом: минус на минус дает плюс. Таким образом, когда стоят рядом два минуса, в сумме получается плюс. К примеру:

(−7)−(−6)=(−7)+6=(−1)

В том случае, когда первое число положительное, а второе число является отрицательным, вычитание выполняют по тому же принципу, что и сложение. Нужно определить, какое число по модулю больше. Далее следует отнять от большего меньшее число и поставить знак большего числа.

7−9=−2

так как 9>7

Одним из ключевых свойств является то, что минус на минус дает плюс:

7−(−9)=7+9=16

Примеры задач с решением

Задача 1

Задача

Нужно решить: (+3) + (+4)

Решение:

(+3) + (+4) = +7

Ответ: 7

Задача 2

Задача

Требуется решить: (-4) + (-3)

Решение:

(-4) + (-3) = -7

Ответ: -7

Задача 3

Задача

Необходимо выполнить сложение: (+15) + (-7)

Решение:

(+15) + (-7) = 15 — 7 = 8

Ответ: 8

Задача 4

Задача

Нужно выполнить вычитание: (+7) — (+4)

Решение:

(+7) — (+4) = +3

Ответ: 3

Задача 5

Задача

Требуется найти разность чисел: -17 — (-14)

Решение:

-17 — (-14) = -17 + 14 = -3

Ответ: -3

Задача 6

Задача

Необходимо решить пример: (+5) ⋅ (-8)

Решение:

(+5) ⋅ (-8) = -40

Ответ: -40

Задача 7

Задача

Нужно найти произведение двух чисел: -9 ⋅ (-9)

Решение:

-9 ⋅ (-9) = 81

Ответ: 81

Задача 8

Задача

Требуется решить пример: -6 ⋅ 5

Решение:

-6 ⋅ 5 = -30

Ответ: -30

Задача 9

Задача

Нужно выполнить деление двух чисел: 40 : (-8)

Решение:

40 : (-8) = -5

Ответ: -5

Задача 10

Задача

Требуется найти разность: (-6) — (+6) — (-8)

Решение:

(-6) — (+6) — (-8) = -12 — (-8) = -12 + 8 = -4

Ответ: -4

Задача 11

Задача

Необходимо решить пример:  (-5) ⋅ (-4) + (+3) ⋅ (-2)

Решение:

(-5) ⋅ (-4) + (+3) ⋅ (-2) = 20 + (-6) = 14

Ответ: 14

Задача 12

Задача

Нужно найти ответ: (-15) ⋅ [-3 + (-15)] : (+5)

Решение:

(-15) ⋅ [-3 + (-15)] : (+5) = -15 ⋅ (-18) : 5 = (-15 : 5) ⋅ (-18) = -3 ⋅ (-18) = 54

Ответ: 54

Задача 13

Задача

Требуется выполнить деление: -18 : [-20 — (30 — 56)]

Решение:

-18 : [-20 — (30 — 56)] = -18 : [-20 — (-26)] = -18 : (-20 + 26) = -18 : 6 = -3

Ответ: -3

Задача 14

Задача

Нужно найти значение выражения:

(−1)−(−512)⋅(+411)=(−1)−(−521)⋅(+114)

Решение:

(−1)−(−512)⋅411=−1−(−112)⋅411=(−1)−(−521)⋅114=−1−(−211)⋅114=−1−(−2)=−1+2=1−1−(−2)=−1+2=1

Ответ: 1

Задача 15

Задача

Необходимо вычислить:

Вычислить |a| — |b| + |c|

при a = -8, b = -5, c = 1

Решение:

|-8| — |-5| + |1| = 8 — 5 + 1 = 4

Ответ: 4

Задача 16

Задача

Требуется решить пример:

[2,4−(0,3−0,21)⋅2+0,44:(−2)]:45=[2,4−(0,3−0,21)⋅2+0,44:(−2)]:54

Решение:

[2,4−(0,3−0,21)⋅2+0,44:(−2)]:45=[2,4−(0,3−0,21)⋅2+0,44:(−2)]:54=

[2,4−0,09⋅2+(−0,22)]:45=[2,4−0,09⋅2+(−0,22)]:54= (2,4−0,18−0,22):25=

2:45=52=2,5(2,4−0,18−0,22):52=2:54=25=2,5

Ответ: 2,5

 

Насколько полезной была для вас статья?

У этой статьи пока нет оценок.

Отрицательные числа – примеры, правила знаков

4

Средняя оценка: 4

Всего получено оценок: 286.

4

Средняя оценка: 4

Всего получено оценок: 286.

Отрицательные числа тяжело воспринимаются учениками 6 класса математики, поскольку долгое время их учат том, что все результаты вычислений, которые меньше нуля неверны. Приходится переучиваться, привыкать к новым правилам. Но на самом деле, если разобраться в отрицательных числах, ничего сложного в них нет.

Отрицательные числа

Отрицательным числом называется любое число меньше нуля. Чтобы обозначить, что число меньше нуля, перед ним ставится знак минус.

Среди отрицательных чисел так же, как и среди положительных есть дроби: обыкновенные и десятичные, целые числа, корни и так далее. Практически все подвиды чисел, которые встречаются среди положительных чисел, есть и среди отрицательных. Так же важно помнить, что число 0 не относится ни к положительным, ни к отрицательным числам.

Числовая прямая

Числовая прямая это прямая, которая имеет обозначение 0 и единичных отрезков. На числовой прямой все отрицательные числа лежат левее нуля.

Числовую прямую очень удобно использовать для сравнения отрицательных чисел. Чем ближе отрицательное число на числовой прямой к нулю, тем большим значением оно является.

Правило знаков

Умножение и деление отрицательных чисел происходит согласно правилу знаков:

• При умножении или делении отрицательного числа на отрицательное, в результате получится положительное число.
• При умножении или делении положительного числа на отрицательное в результате получится отрицательное число.
• При умножении или делении отрицательного числа на положительное, получится отрицательное число.

Сложение отрицательных чисел

При сложении отрицательных чисел действует все то же правило знаков, только в несколько ином виде. Общая формулировка правила знаков звучит так: «Плюс на минус дает минус, минус на минус дает плюс и плюс на плюс дает плюс». Тогда если к одному отрицательному числу прибавить другое, то получится:

-а+(-в)=-а-в – то есть из отрицательного числа вычитается положительное.

Так же работает правило при примерах на вычитание отрицательных чисел:

-а-(-в)=-а+в – к отрицательному числу в итоге прибавляется положительное.

Что мы узнали?

Мы поговорили об отрицательных числах. Рассказали, как удобнее сравнивать отрицательные целые числа, а также как правильно подобные числа перемножать между собой, делить, складывать и вычитать.

Тест по теме

Доска почёта

Чтобы попасть сюда — пройдите тест.

• Ярослав Перфильев

  5/5

• Георгий Григорьев

  4/5

• Sveta Sveta

  4/5

Оценка статьи

4

Средняя оценка: 4

Всего получено оценок: 286.

---

А какая ваша оценка?

Основные правила для положительных и отрицательных чисел

Числа больше нуля называются положительными числами, а числа меньше нуля — отрицательными числами. Это означает, что они падают по обе стороны от числовой прямой. Однако то, что они находятся на одной линии, не означает, что они следуют одним и тем же правилам! Продолжайте читать список основных правил использования положительных и отрицательных чисел в математике.

правила сложения и вычитания двух положительных и отрицательных чисел

Реклама

Правила для чисел со знаком

При использовании положительных и отрицательных чисел вы используете правила для чисел со знаком (числа с положительными или отрицательными знаками перед ними). Эти шаги, также известные как операции над числами со знаком, помогут вам избежать путаницы и решить математические задачи как можно быстрее и правильнее.

Следуйте этим правилам, чтобы определить лучший способ сложения, вычитания, умножения и деления положительных и отрицательных чисел. Помните, что если нет знака + или -, число положительное.

Сложение: одинаковые знаки, сложите числа

Когда вы складываете два числа вместе, и они имеют одинаковый знак (два положительных или два отрицательных числа), сложите числа и сохраните знак. Например:

• 1 + 1 = 2
• 51 + 32 = 83
• -14 + (-6) = -20
• -196 + (-71) = -267

Обратите внимание, что уравнения с двумя положительные суммы имеют положительные суммы, а уравнения с двумя отрицательными числами имеют отрицательные суммы. Если вы используете числовую прямую для решения задачи, добавление двух положительных чисел приведет к положительной стороне, а добавление двух отрицательных чисел приведет к отрицательной стороне.

Сложение: разные знаки, вычитание чисел

Если вы складываете положительные и отрицательные числа вместе, вычтите меньшее число из большего и используйте знак из большего числа. Например:

• 6 + (-5) = 1
• -17 + 22 = 5
• -100 + 54 = -45
• 299 + (-1) = 298

Как видите, сложение числа с разными знаками на самом деле является формой вычитания. При использовании числовой прямой ваша сумма будет ближе к нулю.

Вычитание: Переключиться на сложение

Вычитание положительных и отрицательных чисел означает сложение противоположных чисел или аддитивное обратное. Замените знак вычитания на сложение, а следующий за ним знак измените на противоположный. Затем следуйте инструкциям по добавлению. Например:

• -3 — (+5) становится -3 + (-5) = -8
• 9 — (-7) становится 9 + (+7) = 16
• -14 — (+8) становится -14 + (-8) = -22
• 25 — (-90) становится 25 + (+90) = 115

Хороший совет: всякий раз, когда вы видите знак минус и знак минус вместе, например, в 9 — (-7), немедленно делайте их положительными. Отрицательные знаки компенсируют друг друга, и уравнение становится задачей на сложение.

Реклама

Умножение и деление: один и тот же знак, положительный результат

Кажется, что умножение и деление сложнее, чем сложение и вычитание, но на самом деле они намного проще. Правило умножения положительных и отрицательных чисел с одинаковым знаком (два положительных или два отрицательных) состоит в том, что произведение всегда будет положительным. Например:

• 8 x 4 = 32
• (-8) x (-4) = 32
• 10 x 9 = 90
• (-10) x (-9) = 90

То же правило применяется для деления . При делении числа на другое число с тем же знаком частное (ответ) положительно. Например:

• 12 ÷ 6 = 2
• -12 ÷ (-6) = 2
• 100 ÷ 5 = 20
• -100 ÷ (-5) = 20

числа всегда равны положительному числу? Подобно вычитанию отрицательных чисел, эти операции превращают отрицательные числа в противоположные (обратные). По сути, вы вычитаете отрицательное число несколько раз — и, как показано выше, вычитание отрицательных чисел приводит к положительному уравнению.

Реклама

Умножение и деление: обратный знак, отрицательный результат

При умножении положительного и отрицательного числа произведение всегда будет отрицательным. Неважно, в каком порядке стоят знаки. Например:

• 6 х (-7) = -42
• -7 х 6 = -42
• 12 х (-11) = -132
• — 11 x 12 = -132

Во всех этих случаях сначала нужно умножить или разделить числа. Затем решите, является ли произведение или частное положительным (два положительных или два отрицательных в уравнении) или отрицательным (один положительный и один отрицательный в уравнении).

Знаки сходства и отличия в сложении и вычитании

Еще один способ подумать о сложении положительных и отрицательных чисел — посмотреть на знаки в ряду. Два одинаковых знака подряд (++ или —) означают, что вы складываете числа, а два разных знака подряд (+- или —) означают, что вы вычитаете. Например:

• 7 + (+2) = 9 (++ похожи на знаки, поэтому уравнение представляет собой сложение)
• 9 + (-8) = 1 (+- не похожи на знаки, поэтому уравнение представляет собой вычитание)
• 11 — (+13) = 2 (-+ разные знаки, поэтому уравнение представляет собой вычитание)
• 15 — (-10) = 25 (— подобны знакам, поэтому уравнение представляет собой сложение)

Этот метод следует тем же правилам, что и выше, но может помочь вам решить проблему быстрее, если вы предпочитаете работать с знаки заранее. Как только вы концептуально поймете положительные и отрицательные числа, вы сможете решить, какой метод лучше всего подходит для вас.

Понимание основ математики

Как только вы познакомитесь с основами математики и ее правилами, перед вами откроется весь математический мир. В отличие от других предметов, в математике нет нюансов или интерпретаций — она просто такая, какая есть! Для дополнительной математической практики ознакомьтесь с инструкциями по решению задач на деление в длину (с примерами). Вы также можете просмотреть различные типы чисел в математике перед следующим заданием по математике.

Штатный писатель

Отрицательные числа

Что такое отрицательное число? Это достаточно сложный вопрос сам по себе, но он тесно связан с другим действительно сложным вопросом.

Этот другой вопрос смущает и расстраивает очень многих учеников средней школы, не говоря уже о большинстве взрослых. Вот:

Что означает вычитание отрицательного числа?

Чтобы ответить на этот вопрос, нам нужно прояснить некоторые распространенные заблуждения о вычитании вообще и о том, что такое отрицательное число.

В более ранних статьях я указывал на некоторые вещи, необходимые для ответа на этот вопрос.

В одном я определил вычитание как поиск недостающего слагаемого в операторе сложения. В другом я проиллюстрировал, как это можно представить на числовой прямой.

Здесь я рассмотрю третий вопрос выше: что такое отрицательное число? Так что же такое отрицательное число? Разве не все знают?

Если вы спросите наугад 100 выпускников средней школы, по крайней мере 99 из них, вероятно, скажут, что отрицательное число — это число, которое «меньше нуля» (если, конечно, они хоть что-то понимают в математике).

Но что это на самом деле «значит».

Удивительно, но это оставалось загадкой даже для лучших математиков еще долгое время после того, как они решили гораздо более сложные проблемы математики.

Только в середине 1500-х годов математики, наконец, начали принимать отрицательные числа как «настоящие» (то есть не поддельные) числа, и этот процесс не был завершен до 1800-х годов.

Вот критическая проблема, из-за которой их было так трудно принять, даже в столь позднее время. Ниже приводится парафраз вопроса, заданного де Морганом, выдающимся английским математиком, в 1800-х годах:

Как у вас может быть минус 5 яблок
(или любой другой объект, который вы можете придумать)?

Довольно странная идея, не правда ли?

Что ж, получается, у вас не может быть с отрицательным числом яблок. (Но для более подробной информации придется подождать позже.)

Большой прорыв в размышлениях по этому вопросу на самом деле был связан с использованием числовой прямой для представления чисел. Многие люди считают, что Джон Уоллис, английский математик, был первым, кто использовал графическую диаграмму числовой прямой в конце 1600-х годов.

Используя числовую прямую, он представил положительные числа как числа справа от нуля, а отрицательные числа как числа слева от нуля следующим образом:

Это представление позже помогло устранить большую часть беспокойства по поводу отрицательных чисел.

И, конечно же, когда вы показываете отрицательные числа на такой числовой прямой, как эта, 90 172 и 90 173, вы считаете их от нуля, отрицательное число действительно лежит слева от нуля.

Проблема в том, что это не то, чем «на самом деле является» отрицательное число. Другими словами, это не настоящее определение отрицательного числа.

Одна из причин этого заключается в том, что вам не нужно считать числа, начиная с 0. Числа можно считать, начиная с любой точки на числовой прямой. (В противном случае вы не могли бы, среди прочего, показать сложение или вычитание на числовой прямой.)

Это фундаментальный момент, который почти никогда не учитывается при обучении математике в начальной школе. Но это критично.

Вот почему.

На самом деле математики не определяют напрямую, что такое «отрицательное число». Они определяют отрицательное число в терминах «аддитивной инверсии» числа.

Аддитивное обратное число X определяется как число, которое вы добавляете к X, чтобы получить ноль. Вот как это выглядит на числовой прямой.

Предположим, что X равно 5, поэтому мы поместим 5 на числовую прямую.

Чтобы прибавить число к 5, мы начинаем считать с 5 для второго числа.

Где мы должны закончить, согласно определению аддитивной инверсии, это 0.

Если мы начнем считать с 5 и хотим закончить на 0, в каком направлении мы должны считать?

Мы должны считать налево. Когда мы это делаем, это выглядит так.

Число, показанное красным, отрицательное 5… по определению.

Лежит ли -5 левее нуля?

Нет, не в этом случае.

Действительно ли это отрицательное число?

Да. Так определяется отрицательное число. Отрицательное число является обратным положительному числу.

И что является обратным 5?

Это число, которое вам нужно добавить, когда вы начинаете считать с 5 и хотите закончить на 0. Но теперь давайте посмотрим на другую ситуацию.

Допустим, мы хотим добавить обратное число 5, которое, как мы теперь знаем, равно -5, к 0, а не к 5. Как это будет выглядеть?

Начинаем считать с 0…

… и мы считаем обратное число 5, то есть -5.

Точка, в которой мы заканчиваем, представляет собой -5. Красная стрелка показывает минус 5 ниже.

Обратите внимание, что -5, красная стрелка, указывающая влево, точно такое же число, как -5 в приведенном выше примере, который также является красной стрелкой, указывающей влево.

Тот факт, что две красные стрелки начинаются в разных местах на числовой прямой и заканчиваются в разных местах, не влияет на то, что это за число.

В каждом случае вы считаете одинаковое количество единиц. Разница только в том, где вы начинаете считать.

Конечно, другим важным моментом является направление, в котором вы считаете. В каждом случае 5 единиц считаются влево .

Вот почему это отрицательное число.

Итак, чтобы назвать отрицательное число, нам нужно знать две вещи:

• Количество учитываемых единиц
• Направление подсчета единиц

И неважно, с чего начать отсчет.

Итак, вот разница в положительном числе и отрицательном числе:

• Положительное число — это число, отсчитываемое справа на числовой прямой.
• Отрицательное число — это число, отсчитываемое слева на числовой прямой.

Вот и все.

Вот почему мы описываем отрицательное число как «противоположное» положительному числу. Он считается в обратном направлении.

Фактическое направление подсчета каждого типа чисел не имеет абсолютного значения. Мы могли бы решить, как культура, считать положительные числа слева и отрицательные числа справа. это просто историческая случайность, что мы считаем положительные числа справа.

Как только был принят счет положительных чисел справа, «противоположный» стал считать слева.