Как записываются арифметические выражения в информатике: 7.20. Как записываются арифметические выражения?

7.20. Как записываются арифметические выражения?

Главная  > Справочник по образованию  > Энциклопедия де-факто  > Математика и компьютерные дисциплины  > Информатика  > Электронная версия учебника по информатике 10-11  > Глава 1.7. Алгоритмы. Алгоритмизация. Алгоритмические языки   > 7.20. Как записываются арифметические выражения?

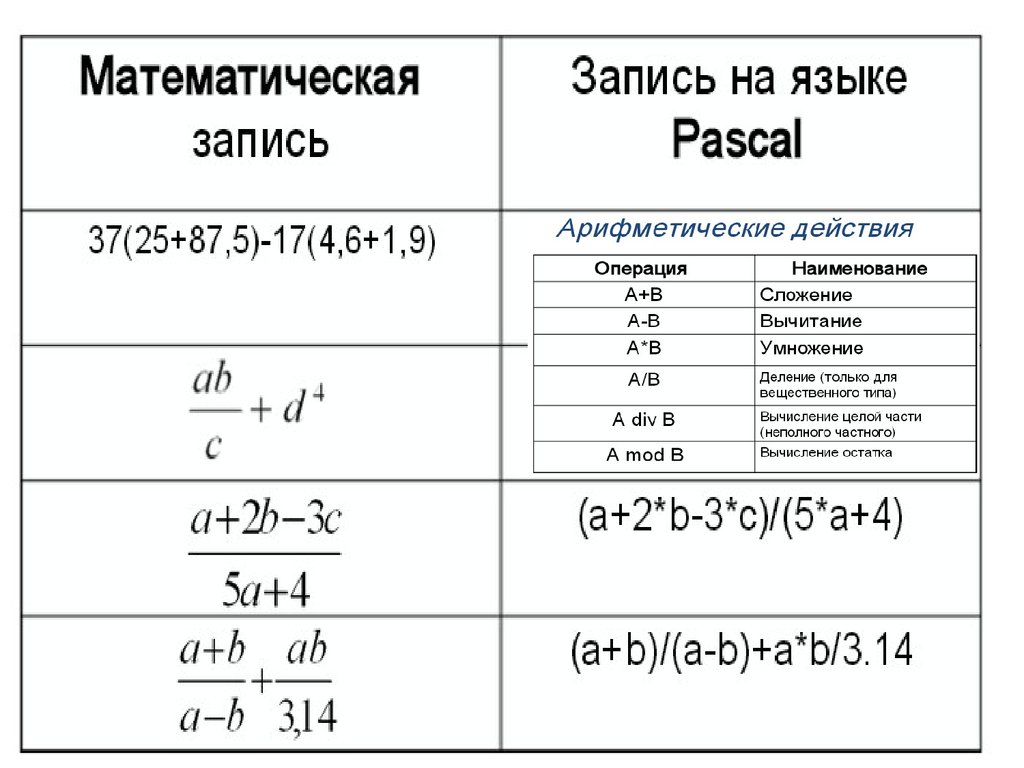
Арифметические выражения записываются по следующим правилам:

•  
  • Нельзя опускать знак умножения между сомножителями и ставить рядом два знака операций.
  • Индексы элементов массивов записываются в квадратных (школьный АЯ, Pascal) или круглых (Basic) скобках.
  • Для обозначения переменных используются буквы латинского алфавита.
  • Операции выполняются в порядке старшинства: сначала вычисление функций, затем возведение в степень, потом умножение и деление и в последнюю очередь — сложение и вычитание.
  • Операции одного старшинства выполняются слева направо . z как exp(exp(z*ln(y))*ln(x)).

Примеры записи арифметических выражений

Математическая запись	Запись на школьном алгоритмическом языке
	x*y/z
	x/(y*z) или x/y/z
	(a**3+b**3)/(b*c)
	(a[i+1]+b[i-1])/(2*x*y)
	(-b+sqrt(b*b-4*a*c))/(2*a)
(x<0)	sign(x)*abs(x)**(1/5)
	0.49*exp(a*a-b*b)+ln(cos(a*a))**3
	x/(1+x*x/(3+(2*x)**3))

Типичные ошибки в записи выражений:

5x+1 a+sin x ((a+b)/c**3

Пропущен знак умножения между 5 и х Аргумент x функции sin x не заключен в скобки Не хватает закрывающей скобки

Другие записи

10. 06.2016. 7.11. Что такое вложенные циклы?

Возможны случаи, когда внутри тела цикла необходимо повторять некоторую последовательность операторов, т. е. организовать внутренний цикл. Такая структура получила название цикла в цикле или вложенных…

10.06.2016. 7.12. Чем отличается программный способ записи алгоритмов от других? 7.13.Что такое уровень языка программирования?

7.12. Чем отличается программный способ записи алгоритмов от других? При записи алгоритма в словесной форме, в виде блок-схемы или на псевдокоде допускается определенный произвол при изображении команд.…

10.06.2016. 7.14. Какие у машинных языков достоинства и недостатки? 7.15. Что такое язык ассемблера? 7.16. В чем преимущества алгоритмических языков перед машинными?

7.14. Какие у машинных языков достоинства и недостатки? Каждый компьютер имеет свой машинный язык, то есть свою совокупность машинных команд, которая отличается количеством адресов в команде, назначением…

10.

06.2016. 7.17. Какие компоненты образуют алгоритмический язык? 7.18. Какие понятия используют алгоритмические языки?

7.17. Какие компоненты образуют алгоритмический язык? Алгоритмический язык (как и любой другой язык) образуют три его составляющие: алфавит, синтаксис и семантика. Алфавит — это фиксированный…

10.06.2016. 7.19. Что такое стандартная функция?

При решении различных задач с помощью компьютера бывает необходимо вычислить логарифм или модуль числа, синус угла и т.д. Вычисления часто употребляемых функций осуществляются посредством подпрограмм,…

значение, примеры / Справочник :: Бингоскул

Арифметические строковые и логические выражения: значение, примеры

добавить в закладки удалить из закладок

Содержание:

Логический пример – выражение, состоящее из логических переменных, значений, операций и операторов, сравнивающих числа, строки. Арифметический конструктив всегда приводится к одному из двух значений – правда или ложь. Часто используется обозначение на английском языке – true, false.

Информатика использует конструкции логических операций из языков программирования. Для умножения необходимо указать And, сложение обозначается Or, операция отрицания – Not. Если структура сложная, разрешается пользоваться скобками. Пример логической конструкции:

5>3Anda=b=ложь;
5 Not5>3=ложь.

Что такое арифметическое выражение – теория, примеры

Арифметическая последовательность может включать ряд числовых переменных, число, символ, знак, алгебраические операции, арифметические элементы. Чтобы вычислить значение арифметической конструкции, следует руководствоваться общими правилами решения математических примеров. Переменные, числа могут возводиться в степень, делиться, умножаться, складываться, вычитаться. Изменить порядок выполнения действий помогут скобки.

Как записываются арифметические выражения в информатике

В таблице представлены основные условия и форма их записи на языке алгоритма

Условия	Принцип записи на языке алгоритма
Значение дробной доли вещественного аргумента С=0	int(с) = 0
Переменная является целым, четным числом	mod(с,2) = 0
Переменная – целая, нечетная цифра	mod(с,2) = 1
Значение числа С кратное 6	mod(с,6) = 0
Присутствуют положительные аргументы а, с	а>0, (с>0)
Положительный аргумент а, с – отрицательное или равно 0	((a>0) и (с
Один из показателей а,б,с – отрицательный	а
Числовое значение у находится между 2,5	у≥2, (у
Коэффициент б соответствует а	(б>=а), (б
Для цельных чисел а, с характерна идентичная четность	((mod(a,2)=0),(mod(с,2)=0) или ((mod(a,2)=1), (mod(с,2)=1))
Координаты точки (б,к) соответствуют центру круга, имеющего радиус Р в точке (а,с)	(б-a)**2+(к-с)**2*r

Правильная строковая запись выражения – что значит составить выражение

Арифметические строковые и логические выражения записываются в соответствии с рядом правил. Строковый пример предполагает использование строковых данных для определения операндов. В состав могут входить:

• Переменные;
• Константы;
• Операционные обозначения;
• Указатели функций.

Доступные операции – сложение, соотношение. Сложение позволяет объединить строки. Есть ограничение длины выражения – 255 символов. Сцепление является приоритетным перед операндами соотношения. 

Например, необходимо решить задачу. Выберите арифметическое выражение, значение которого максимально:

• 318 + 1000002
• 168 + 1011002
• 418 + 11112
• 448 + 110002 

Для расчета считаем сумму каждой конструкции: 

• 318 + 1000002 = 1000320;
• 168 + 1011002 = 1011170;
• 418 + 11112 = 11530;
• 448 + 110002 = 110450.

Ответ: максимальное значение второго выражения.

Поделитесь в социальных сетях:

27 мая 2021, 14:43

Информатика

Could not load xLike class!

Вычисление арифметического выражения — темы масштабирования

Обзор

Арифметические выражения могут быть записаны в 3 различных нотациях — инфиксной, префиксной и постфиксной. В префиксной нотации оператор записывается перед операндом в выражении. С другой стороны, в нотации Postfix оператор пишется после операнда. Выражения оцениваются с использованием стека.

Область применения

• Порядок вычисления арифметических операторов.
• Польская (префиксная) и обратная польская (постфиксная) нотации.
• Преобразование из инфиксной нотации в префиксную и постфиксную.

Введение

Выражение, которое содержит только арифметические операнды и операторы, называется арифметическим выражением. Результаты этих выражений всегда представлены числовыми значениями. Арифметические выражения обычно представляются в так называемой инфиксной нотации. В этих обозначениях оператор находится между двумя операндами (пример: X + Y, где X и Y являются арифметическими операндами). Мы даже можем использовать круглые скобки в арифметических выражениях.

Любое арифметическое выражение, записанное в инфиксной нотации, оценивается по следующим правилам приоритета операторов.

Однако, если мы хотим оценить выражение без учета приоритета оператора, мы можем использовать польских (или префиксных) нотаций или обратных польских (или постфиксных) нотаций.

Типы вычисления выражения в C

В языке программирования C существует четыре типа вычисления выражения:

1. Вычисление арифметических выражений — Арифметические выражения возвращают числовые значения. Например: 30/630/630/6.
2. Вычисление реляционных выражений — Реляционные выражения используются для сравнения двух операндов. Например: (a+b)>=(c∗d)(a + b) >= (c * d)(a+b)>=(c∗d).
3. Оценка логических выражений — Логические выражения возвращают значения true или false. Например: (a
4. Вычисление условных выражений — Если условное выражение истинно, оно возвращает определенный оператор/выражение. Но если оно ложно, оно возвращает другой оператор/выражение. Например: (10 > 3)? «выражение истинно» : «выражение ложно». В этом примере, поскольку 10 > 3 истинно, будет возвращено утверждение «* выражение истинно». Если бы это было не так, то было бы напечатано утверждение «выражение ложно».

В этой статье мы узнаем об вычислении арифметических выражений.

Порядок вычисления арифметических выражений

Для вычисления арифметических выражений компилятор имеет предопределенный порядок, в котором он вычисляет любое выражение. Порядок оценки, которому следует компилятор:

• Сначала вычисляются выражения со скобками. Если в выражении есть две или более круглых скобок, скобки оцениваются слева направо. В случае вложенных скобок самые внутренние скобки оцениваются первыми, а самые внешние — последними.

• Если круглые скобки отсутствуют, порядок вычисления выражения основан на приоритете оператора и ассоциативности:

  Precedence	Operator	Associativity
  1	Unary plus, Unary minus	Left to Right
  1	Built-in functions	Left to Right
  2	Умножение и деление	Слева направо
  3	Сложение и вычитание	Слева направо

Предположим, что круглые скобки не определяют последовательность выполнения выражения, а два или более оператора имеют одинаковый приоритет.

В этом случае порядок оценки слева направо.

Давайте разберемся в этой теме на примере инфиксной записи:

 
 8 * sqrt(25) - -3
 

Ответ:

Шаги для вычисления приведенного выше выражения:

1. В приведенном выше выражении унарный минус имеет наивысший приоритет. Значит, она будет решена в первую очередь. Выражение упростится до: 8 * sqrt(25) + 3.
2. Поскольку sqrt(25) является встроенной функцией, она будет оцениваться следующей. Теперь выражение примет вид: 8∗5+38 * 5 + 38∗5+3.
3. Далее будет выполнено умножение. Выражение станет 40 + 3.
4. Наконец, будет выполнено добавление. Итак, ответ будет 43.

Возьмем другой пример:

 
 7 * (5 + 15) / (2 * 5) - 3;
 

Ответ:

Шаги для вычисления приведенного выше выражения:

1. Скобки имеют наивысший приоритет. Таким образом, выражения внутри круглых скобок будут оцениваться первыми. После решения все выражение упрощается до: 7*20/10-37 * 20/10 — 37*20/10-3.
2. Теперь умножение и деление имеют одинаковый приоритет. Поскольку умножение и деление имеют ассоциативность слева направо, умножение будет выполняться первым. Выражение теперь принимает вид: 140/10-3140 / 10 — 3140/10-3.
3. Далее, подразделение имеет более высокий приоритет. Таким образом, выражение примет вид 14−314 — 314−3.
4. Наконец, мы вычтем 3 из 14, чтобы получить 11 на выходе.

Польская (или префиксная) нотация

В польской или префиксной нотации оператор записывается перед операндом в выражении. Это обозначение не требует круглых скобок, потому что вычисление выражения выполняется в стеке. Таким образом, нам не нужно указывать порядок выполнения для вычисления арифметических выражений. Компилятор может обрабатывать префиксную нотацию быстрее, чем инфиксную, потому что ему не нужно обрабатывать какие-либо круглые скобки или следовать правилам приоритета.

Выражение в польской записи выглядит так:

Приведенное выше выражение эквивалентно X * Y в инфиксной нотации, где X и Y — два арифметических операнда, а * — оператор.

Шаги для вычисления префиксного выражения отличаются от шагов, которые мы обычно выполняем для вычисления инфиксного выражения. Мы можем вычислить значение арифметических операций, используя стек. Вот шагов для вычисления значения префиксного выражения:

1. Поместите переменную var в последний элемент выражения.
2. Если переменная var указывает на:
   • Операнд, поместите этот элемент в стек.
   • Оператор X извлекает два элемента (операнда) из стека и обрабатывает извлеченные операнды с помощью оператора X . После выполнения операции поместите вычисленное значение обратно в стек.
3. Уменьшить значение переменной на 1.
4. Повторять шаги 2 и 3 до тех пор, пока не будут пройдены все элементы.
5. Возвращает единственное значение, присутствующее в стеке в конце.

Давайте теперь возьмем пример, чтобы понять, как вычисляются арифметические выражения с использованием префиксной записи.

 
 * / + 9 7 8 2
 

Ответ:

Используя описанные выше шаги, мы вычислим значение этого выражения.

Шаг 1: Поместите указатель на последний элемент, т. е. на 2 в этом примере.

Шаг 2: Поскольку 2 является операндом, мы поместим его в стек. Стек будет выглядеть так:

Шаг 3: Теперь мы уменьшаем значение указателя на 1, чтобы он указывал на последнее число, равное 8. И снова 8 является операндом, поэтому мы помещаем его в стек. Подобным образом эти шаги будут повторяться до тех пор, пока стек не станет таким:

Шаг 4: Еще раз уменьшая значение указателя на 1, мы столкнемся с оператором, т. е. +. Итак, мы удалим из стека два верхних элемента (9и 7) и добавьте их. 16 ( 9 + 7 ) будет добавлено в стек. Теперь стек выглядит так:

Шаг 5: Еще раз уменьшите значение указателя и повторите шаги. В итоге, проведя все расчеты, получим:

Шаг 6: Верните значение, присутствующее в стеке, чтобы получить окончательный ответ. Следовательно, ответ равен 4.

Обратная польская (или постфиксная) нотация

В обратной польской или постфиксной нотации оператор записывается после операнда в выражении. В этой нотации скобки не нужны, потому что порядок выполнения выражения уже определен в стеке. Выражение в постфиксной записи выглядит так:

Приведенное выше выражение эквивалентно X + Y , где X и Y — два арифметических операнда, а + — оператор.

Вычисление арифметических выражений в постфиксной записи аналогично вычислению арифметических выражений в префиксной записи. Мы также можем вычислить значение арифметических операций, используя стек. Вот шагов для вычисления значения постфиксного выражения:

1. Поместите указатель на первый элемент строки.
2. Если указатель указывает на:

• Оператор X извлекает два верхних элемента (операнда) из стека и работает с оператором X .
• Операнд, поместите этот элемент в стек.

3. Увеличить значение указателя на 1.
4. Перейти к шагу 2, если в выражении остались элементы для сканирования.
5. Вернуть результат, хранящийся в стеке.

Давайте рассмотрим пример, чтобы понять, как вычислять арифметические выражения:

 
 5 3 7 * + 4 -
 

Ответ:

Используя шаги, описанные выше, вычислим значение этого выражения.

Шаг 1: Поместите указатель на первый элемент, 5.

Шаг 2: Поскольку 5 является операндом, поместите его в стек. Стек теперь содержит — [5].

Шаг 3: Теперь увеличьте значение указателя на 1. Теперь указатель будет указывать на второй элемент, 3. Опять же, поскольку 3 является операндом, поместите его в стек. Стек теперь содержит — [5 3] (снизу вверх).

Шаг 4: Повторите процесс шага 3. Теперь стек содержит — [5 3 7]

Шаг 5: Еще раз увеличьте значение указателя. Указатель теперь указывает на оператора * . Итак, вынимаем из стека два верхних операнда (7, 3) и выполняем над ними операцию умножения. Затем поместите вычисленное значение обратно в стек. Стек теперь содержит — [5 21].

Шаг 6: Повторите вышеуказанные шаги, чтобы стек содержал — [4 26].

Шаг 7 : Увеличьте значение указателя для выполнения последней операции. Теперь в выражении больше не осталось элементов, и [22] — единственный элемент, оставшийся в стеке. Следовательно, ответ 22.

Таблица для преобразования инфиксной нотации в префиксную и постфиксную нотацию

Хотя инфиксная нотация является наиболее распространенной нотацией, используемой нами, компьютеры предпочитают префиксную или постфиксную нотацию для вычисления арифметических выражений, потому что они быстрее выполняются, чем инфиксные нотации.

Поскольку префиксная и постфиксная нотации необходимы для программирования, мы должны знать типичные выражения в инфиксной нотации и их преобразование в префиксную и постфиксную нотации. Таблица, содержащая стандартные выражения для преобразования инфиксной нотации в префиксную или постфиксную нотацию , приведена ниже.

9007 4 9. 9. 9. 9007 4 9. 9. 9007 4 9. 9007 4 9. 9007 4 9. 9

Серийный номер	Инфиксная нотация	Префиксная нотация	Постфиксная нотация
1	m + n	+ m n	m n +
2	m ∗ (n + o)	∗ m + n o	m n o + ∗
3	(m + N) ∗ o	∗ + M N O	M N + O ∗
4	(M + N) ∗ (O + P)	∗ + M N + O P	M N + O P + ∗
5	м/н + о/р	+/м н/о р	м н/о р/+
Left to Right
2	Division and Multiplication	/ \*	Left to Right
3	Addition and Subtraction	+ —	Left to Right

The В приведенной выше таблице показано поведение бинарных операторов по умолчанию. Порядок вычисления арифметических операторов можно изменить с помощью круглых скобок. Вычислить значение этих арифметических операций с помощью стека

Резюме

• Арифметические выражения могут быть записаны в 3-х различных нотациях — инфиксной, префиксной и постфиксной.
• В префиксной нотации оператор записывается перед операндом в выражении. С другой стороны, в нотации Postfix оператор пишется после операнда.
• Префиксные и постфиксные нотации быстрее, чем инфиксные.
• Мы можем преобразовывать инфиксные нотации в префиксные или постфиксные и наоборот.

3.4 Основные арифметические операторы — Основы компьютерного программирования в Ruby [книга]

Теперь, когда некоторые классы, определяющие различные типы данных, были введены, что вы можете сделать с ними? Как и все остальное программирование языков, Ruby может выполнять множество математических операций. В Таблице 3-1 показано, как использовать Ruby в качестве Калькулятор.

Таблица 3-1. Основные арифметические операторы

Символ	Операция	Пример
+	Дополнение	х = 6 + 2 8
-	Вычитание	х = 3 - 2 1
*	Умножение	х = 5 * 2 10
/	Отдел	х = 16/8 2
%	Модуль	х = 5 % 3 2
**	Мощность	х = 2 ** 4 16

Все перечисленные операторы являются бинарными, т. е. оператор имеет два операнда. Например, команда A + B — это бинарная операция, где A и B — это два операнда и + является оператором.

При вводе математических операций в интерпретаторе Ruby учитывается порядок действий. Чтобы изменить порядок операции, используйте круглые скобки. Попробуйте ввести в команду следующее line:

 irb  (    main    ):    001    :    0    >     x     =     10     +     4     /     2   

Какой результат вы получили? Теперь попробуйте ввести следующее в подсказка:

 irb  (    main    ):    001    :    0    >     x     =     (    10     +     4    )     /     2  

Большинство операторов должны выглядеть знакомыми.