Функции в си: Функции в языке Си : вызов функции, возвращаемое значение

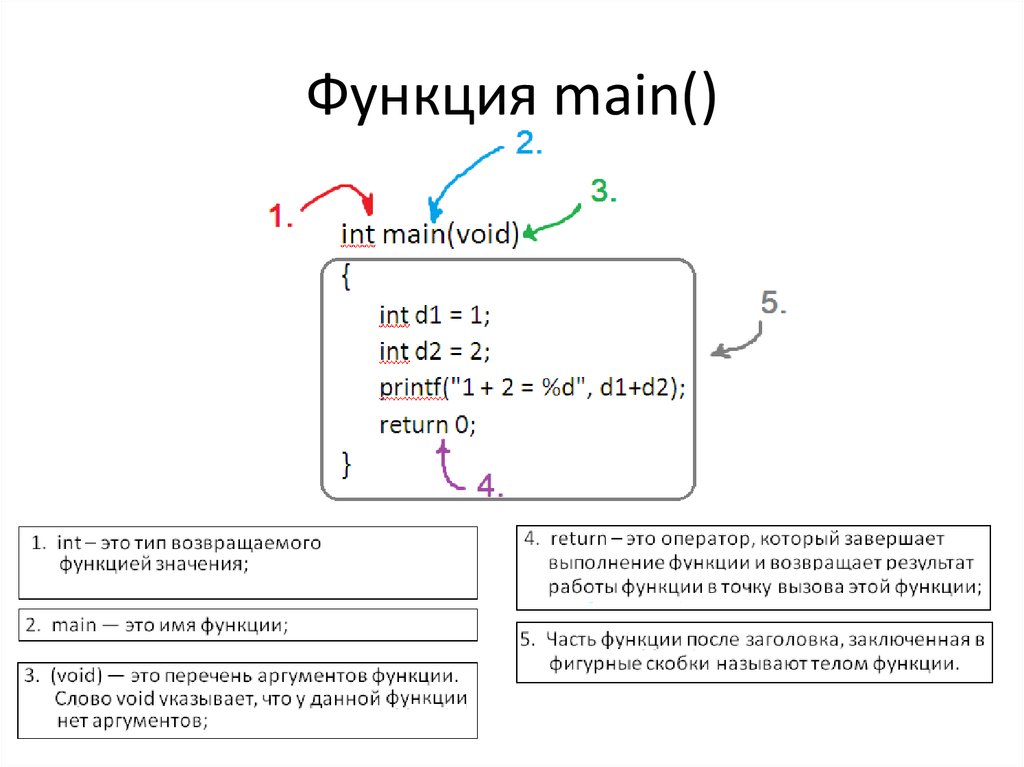
Макросы vs функции в Си

Когда C-разработчик достигает определенного уровня квалификации, он обязательно сталкиваются с макросами. Во многих других языках программирования аналога макросов нет, причем неспроста, ведь их применение может оказаться небезопасным. Все дело в том, что макросы в Си имеют ряд особенностей и нюансов, которые не всегда понятны на первый взгляд.

Когда программист только знакомится с макросами, они могут показаться ему самыми, что ни на есть обычными вызовами функций. Да, с немного странным синтаксисом, но все-таки функциями, да и ведут они себя, как функции. Так в чем же разница?

Если говорить условно, то макрос — это функция обработки и замены программного кода. После того, как будет выполнена сборка программы, макросы меняются на макроопределения. Как это выглядит, лучше рассмотреть на примере:

При этом данный код преобразуется в другой (отработавший код опустим):

В процессе вызова функции, под нее выделяется новый стековый кадр, и функция выполняется самостоятельно, то есть она не зависит от места в программном коде, откуда была вызвана. В результате переменные с одинаковыми именами в различных функциях ошибку не вызовут даже в том случае, если вызывать лишь одну функцию из другой.

Однако если попытаться выполнить тот же трюк с помощью макроса, то в процессе компиляции будет выброшена ошибка. Дело в том, что обе переменные по итогу станут находиться в одной функции:

Мало того, функции ведь выполняют проверку типов: если функция ожидает строку на входе, но получает число, то будет выброшена ошибка (либо, в крайнем случае, предупреждение, что уже зависит от компилятора). Макросы же просто меняют аргумент, который им передан.

Вдобавок к этому, макросы не подлежат отладке. К примеру, в отладчике мы можем войти в функцию и пройтись по программному коду функции, а вот с макросами этот номер не пройдет. В результате если макрос по каким-то причинам сбоит, то существует лишь единственный способ обнаружить проблему — перейти к определению макроса, разбираясь уже там.

Однако нельзя не выделить явное преимущество макросов перед функциями — это производительность. Макрос быстрее функции. Мы уже упоминали, что под функцию выделяются допресурсы. Используя макросы, эти ресурсы можно сэкономить. Данный плюс порой играет значительную роль, особенно когда речь идет о системах, имеющих ограниченные ресурсы (достаточно вспомнить очень старые микроконтроллеры). При этом даже в современных системах разработчики выполняют оптимизацию, применяя для небольших процедур макросы.

Однако в C99 и C++ есть альтернатива макросам — встраиваемые (inline) функции. Если добавить перед функцией ключевое слово inline, компилятор получит указание включить тело функции непосредственно в место вызова функции (как и в случае с макросом). Причем встраиваемые функции могут быть отлажены, плюс у них существует проверка типов.

Но ключевое слово inline — это лишь подсказка для компилятора, то есть это не строгое правило, в результате чего компилятор может и проигнорировать данную подсказку. Дабы так не случилось, в gcc существует атрибут always_inline, заставляющий компилятор встраивать функцию. Конечно, встраиваемые функции — вещь неплохая, поэтому может возникнуть мысль, что применение макросов становится нецелесообразным. Но на деле это не совсем так. Однако о том, как лучше использовать макросы в Си, мы поговорим в следующий раз, поэтому следите за новостями!

По материалам статьи «How to properly use macros in C»

Как найти область определения функции?

Понятие области определения функции

Впервые школьники знакомятся с термином «функция» на алгебре в 7 классе, и с каждой четвертью, с каждой новой темой это понятие раскрывается с новых сторон. И, конечно же, усложняются задачки. Сейчас дадим определения ключевым словам и будем находить область определения функции заданной формулой и по графику.

Если каждому значению x из некоторого множества соответствует число y, значит, на этом множестве задана функция. При этом х называют независимой переменной или аргументом, а у — зависимой переменной или функцией.

Зависимость переменной у от переменной х называют функциональной зависимостью. Записывают так:

y = f(x).

Функция — это соответствие между двумя множествами, причем каждому элементу первого множества соответствует один элемент второго множества.

Из понятия функции сформулируем определение области определения функции.

Область определения функции — это множество всех значений аргумента (переменной x). Геометрически — это проекция графика функции на ось Ох. Чтобы обозначить область определения некоторой функции y, используют запись D(y).

Множество значений функции — множество всех значений, которые функция принимает на области определения. Геометрически — это проекция графика функции на ось Оy.

• Например, область значений функции y = x2 — это все числа больше либо равные нулю. Это можно записать так: Е (у): у ≥ 0.

Область определения можно описывать словами, но часто ответ получается громоздким. Поэтому используют специальные обозначения.

Если мы хотим указать на множество чисел, которые лежат в некотором промежутке, то делаем так:   Через точку с запятой указываем два числа: левую и правую границы промежутка. Если граница входит в промежуток, ставим возле нее квадратную скобку, если не входит — круглую. Если у промежутка нет правой границы, записываем так: +∞. Если нет левой границы, пишем -∞. Если нужно описать множество, состоящее из нескольких промежутков, ставим между ними знак объединения: ∪.

Например, все действительные числа от 2 до 5 включительно можно записать так:

• [2; 5].

Все положительные числа можно описать так:

• (0; +∞).

Ноль не положительное число, поэтому скобка возле него круглая.

Демо урок по математике

Узнайте, какие темы у вас «хромают», а после — разбирайте их без зубрежки формул и скучных лекций.

Области определения основных элементарных функций

Область определения функции — неотъемлемая часть самой функции. Когда мы вводим какую-либо функцию, то сразу указываем ее область определения.

На уроках алгебры мы последовательно знакомимся с каждой функцией: прямая пропорциональность, линейная функция, функция y = x² и другие. А области их определения изучаем, как свойства.

Рассмотрим области определения основных элементарных функций.

Область определения постоянной функции

Постоянная функция задается формулой y = C, то есть f(x) = C, где C — некоторое действительное число. Ее еще называют константа. 

Смысл функции — в том, что каждому значению аргумента соответствует значение функции, которое равно C. Поэтому, область определения этой функции — множество всех действительных чисел R.

Например:

• Область определения постоянной функции y = -3 — это множество всех действительных чисел: D(y) = (−∞, +∞) или D(y) = R.
   
• Областью определения функции y = ³√9 является множество R.

Для тех, кто учится в 7 классе, материала выше достаточно, чтобы подготовиться к контрольной работе. А вот старшеклассникам нужно разбираться в теме несколько глубже — поэтому продолжаем.

Еще больше наглядных примеров и практики — на курсах по математике в онлайн-школе Skysmart!

Бесплатные занятия по английскому с носителем

Занимайтесь по 15 минут в день. Осваивайте английскую грамматику и лексику. Сделайте язык частью жизни.

Область определения функции с корнем

Функцию с корнем можно определить так: y = ⁿ√x, где n — натуральное число больше единицы.

Рассмотрим две вариации такой функции.

Область определения корня зависит от четности или нечетности показателя:

• Если n — четное число, то есть, n = 2m, где m ∈ N, то ее область определения есть множество всех неотрицательных действительных чисел:
  
• Если показатель корня нечетное число больше единицы, то есть n = 2m+1, при этом m принадлежит к N, то область определения корня — множество всех действительных чисел:
  

Значит, область определения каждой из функций y = √x, y = ⁴√x, y = ⁶√x,… есть числовое множество [0, +∞). А область определения функций y = ³√x, y = ⁵√x, y = ⁷√x,… — множество (−∞, +∞).

Пример 

Найти область определения функции:

Как решаем:

Подкоренное выражение должно быть неотрицательным, но поскольку оно стоит в знаменателе, то равняться нулю не может. Следовательно, для нахождения области определения необходимо решить неравенство x

2 + 4x + 3 > 0.

Для этого решим квадратное уравнение x² + 4x + 3 = 0. Находим дискриминант:

D = 16 — 12 = 4 > 0

Дискриминант положительный. Ищем корни:

Значит парабола f(x) = x² + 4x + 3 пересекает ось абсцисс в двух точках. Часть параболы расположена ниже оси (неравенство x² + 4x + 3 < 0), а другая часть — выше оси (неравенство x² + 4x + 3 > 0).

Поскольку коэффициент a = 1 > 0, то ветви параболы смотрят вверх.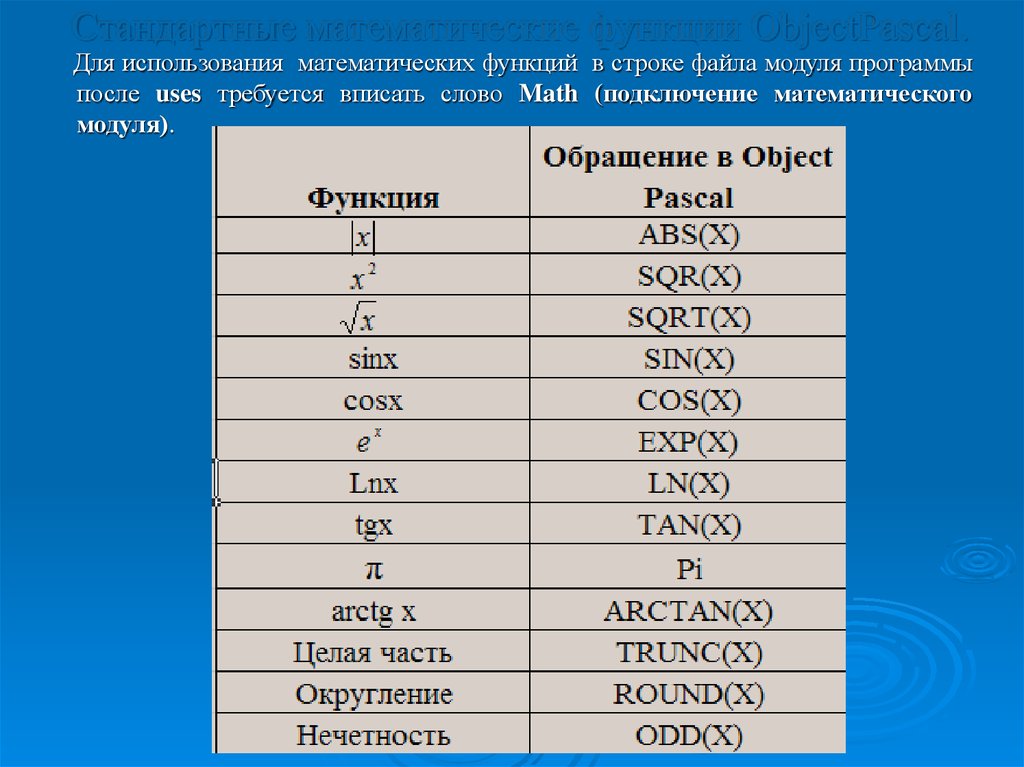 Можно сделать вывод, что на интервалах (−∞, -3) ∪ (−1, +∞) выполнено неравенство x² + 4x + 3 > 0 (ветви параболы уходят вверх на бесконечность), а вершина параболы расположена на промежутке (-3; -1) ниже оси абсцисс, что соответствует неравенству x

2 + 4x + 3 < 0.

Ответ: область определения: D(f) = (−∞, -3) ∪ (−1, +∞).

Если в знаменателе функции стоит выражение, зависящее от х, то для того, чтобы найти область определения данной функции, нам нужно исключить точки, которые обращают знаменатель в ноль.

Область определения степенной функции

Степенная функция выглядит так: y = x^a, то есть, f(x) = x^a, где x — переменная в основании степени, a — некоторое число в показателе степени.

Область определения степенной функции зависит от значения показателя степени.

Перечислим возможные случаи:

• Если a — положительное целое число, то область определения функции есть множество действительных чисел: (−∞, +∞).
• Для нецелых действительных положительных показателей степени: D(f) = [0, +∞).
• Если a — отрицательное целое число, то область определения функции представляет собой множество (−∞, 0) ∪ (0, +∞).
• Для остальных действительных отрицательных a область определения степенной функции — числовой промежуток (0, +∞).

При a = 0 степенная функция y = x^a определена для всех действительных значений x, кроме x = 0. Это связано с тем, что мы не определяли 0⁰. А любое отличное от нуля число в нулевой степени равно единице. То есть, при a = 0 функция приобретает вид y = x⁰ = 1 на области определения (−∞, 0) ∪ (0, +∞).

Рассмотрим несколько примеров.

 

1. Область определения функций y = x
   5, y = x¹² — множество R, так как показатели степени целые положительные.


2. Степенные функции определены на интервале [0, +∞), так как их показатели положительные, но не целые.


3. Область определения функции y = x⁻², как и функции y = x⁻⁵ — это множество (−∞, 0) ∪ (0, +∞), так как показатели степени целые отрицательные.


4. Область определения степенных функций y = x^-√19, y = x^-3e, — открытый числовой луч (0, +∞), так как их показатели не целые и отрицательные.

Область определения показательной функции

Показательную функцию можно задать формулой y = a^x, где переменная x — показатель степени, а — больше нуля и не равно единице.

Область определения показательной функции — это множество R.

Примеры показательных функций:

• y = e^x
• y = (√15)^x
• y = 13^x.

Область определения каждой из них (−∞, +∞).

Область определения логарифмической функции

Логарифмическая функция выглядит так: y = log_ax, где где число a > 0 и a ≠ 1. Она определена на множестве всех положительных действительных чисел.

Область определения логарифмической функции или область определения логарифма — это множество всех положительных действительных чисел. То есть, D (loga) = (0, +∞).
Например:

• D (ln) = (0, +∞) и D (lg) = (0, +∞).

Рассмотрим примеры логарифмических функций: 

• y = log₇x
• y = lnx

Область определения этих функций есть множество (0, +∞).

Пример

Укажите, какова область определения функции:

Как решаем:

Составим и решим систему:

Графическое решение:

Ответ: область определения: D(f) = (−3, -2) ∪ (−2, +∞).

Область определения тригонометрических функций

Сначала вспомним, как задавать тригонометрические функции и как увидеть их области определения.

• Функция, которая задается формулой y = sinx, называется синусом, обозначается sin и определяется на множестве всех действительных чисел. Область определения синуса — это множество всех действительных чисел, то есть, D(sin) = R.
• Функция, которая задана формулой y = cosx, называется косинусом, обозначается cos и определяется на множестве R. Область определения функции косинус — множество всех действительных чисел: D(cos) = R.
• Функции, которые заданы формулами y = tgx и y = ctgx, называются тангенсом и котангенсом и обозначаются tg и ctg. Область определения тангенса — это множество всех действительных чисел, кроме чисел . Область определения котангенса — это множество всех действительных чисел, кроме чисел πk, k ∈ Z.

Поэтому, если x — аргумент функций тангенс и котангенс, то области определения тангенса и котангенса состоят из всех таких чисел x, что и x ∈ r, x ≠ πk, k ∈ Z соответственно.

Пример

Найдите область определения функции f(x) = tg2x.

Как решаем:

Так как a(x) = 2x, то в область определения не войдут следующие точки:

Перенесем 2 из левой части в знаменатель правой части:

В результате . Отразим графически:

Ответ: область определения: .

Область определения обратных тригонометрических функций

Вспомним обратные тригонометрические функции: арксинус, арккосинус, арктангенс и арккотангенс.

• Функция, которая задается формулой y = arcsinx и рассматривается на отрезке [−1, 1], называется арксинусом и обозначается arcsin.

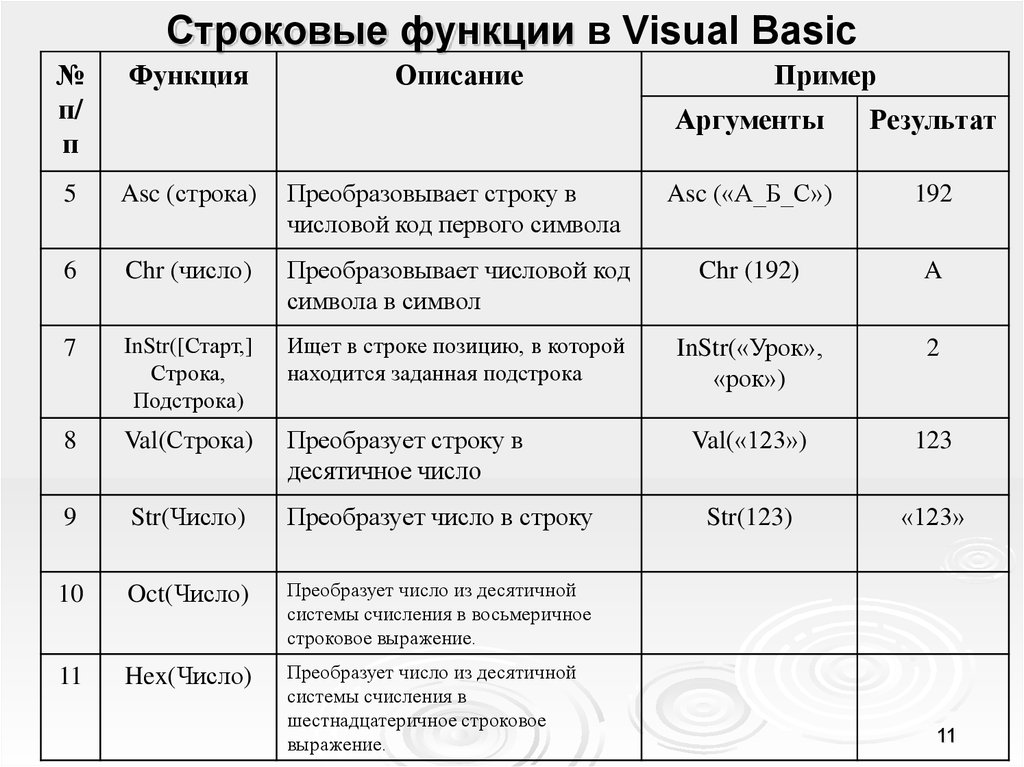
  Область определения арксинуса — это множество [−1, 1], то есть, D(arcsin) = [−1, 1].

• Функция, которая задается формулой y = arccosx и рассматривается на отрезке [−1, 1], называется арккосинусом и обозначается arccos.

  Область определения функции арккосинус — отрезок [−1, 1], то есть, D(arccos) = [−1, 1].

• Функции, которые задаются формулами вида y = arctgx и y = arcctgx и рассматриваются на множестве всех действительных чисел, называются арктангенсом и арккотангенсом и обозначаются arctg и arcctg.

  Область определения арктангенса и арккотангенса — все множество действительных чисел R. То есть, D(arctg) = R и D(arcctg) = R.

Таблица областей определения функций

Области определения основных функций в табличном виде можно распечатать и использовать на уроках, чтобы быстрее решать задачки.

И, помните: чем чаще вы практикуетесь в решении задач — тем быстрее все запомните. 

Функция	Область определения функции
Постоянная y = C	R
Корень y = n√x	[0 ; +∞) , если n — четное; (-∞; +∞) , если n  — нечетное.
Степенная y = xa	(-∞; +∞) , если a > 0, a ∈ Z; [0 ; +∞), если a > 0, a ∈ R, a ∉ Z; (-∞; 0) ∪ (0; +∞) , если a < 0, a ∈ Z; (0; +∞), если a ∈ R, a ≠ Z; (-∞; 0) ∪ (0, +∞), если a = 0.
Показательная y = ax	R
Логарифмическая y = lognx	(0; +∞)
Тригонометрические y = sin(x) y = cos(x) y = tg(x) y = ctg(x)	R R x ∈ R, x ≠ π/2 + πk, k ∈ Z x ∈ R, x ≠ πk, k ∈ Z
Обратные тригонометрические y = arcsin(x) y = arccos(x) y = arctg(x) y = arcctg(x)	[-1; 1] [-1; 1] R R

Что такое интровертное восприятие?

Интровертное восприятие (SI) является доминирующей когнитивной функцией, определяющей способ, которым определенные типы личности воспринимают и понимают окружающий мир. Все типы используют некоторые вариации функции зондирования, и примерно половина населения функционирует как пользователь Si. Вы сможете идентифицировать их, как только ознакомитесь с их методами обработки.

Давайте предположим, что вы уже знакомы с четырьмя буквами вашего профиля типа личности Майерса и Бриггса и знаете, действуете ли вы как Сенсор или предпочитаете использовать Интуицию. Этот аспект вашего типа личности говорит вам, как ваш мозг обрабатывает поступающую информацию. Все Сенсоры предпочитают использовать свои чувства (обоняние, осязание, зрение, вкус, звук) в очень физическом, практическом способе обучения.

Не знаете свой тип личности? Пройдите тест Typefinder здесь.

Однако, независимо от того, являетесь ли вы Сенсором или Интуитивом, вы будете использовать Сенсорику в большей или меньшей степени. Например, для ESTP предпочтительна функция Sensing. ENTP, с другой стороны, не будут уделять столько внимания информации, поступающей через их чувства, но они все равно могут использовать эти навыки, когда они им нужны. Все аспекты личности существуют в спектре — они не абсолютны.

Итак, теперь мы объяснили букву «S» в слове Si. Откуда взялась буква «i» в этом символе? В этом письме рассказывается о том, как вы используете свое ощущение — независимо от того, обрабатывается ли оно внутри (интровертное ощущение или Си) или гордо выставляется на всеобщее обозрение (экстравертное ощущение или Си). Подробнее об этом ниже.

Последняя часть головоломки решает, использует ли ваша личность Si как доминирующую функцию или вспомогательную, второстепенную или поддерживающую функцию. У ISJ доминирующая когнитивная функция — Si, а у ESJ — вспомогательная когнитивная функция.

Для сравнения, эти типы личности используют функцию Si или Se:

(Si) Интровертная сенсорика как доминантная функция: ISFJ, ISTJ

(Si) Интровертная сенсорика как вспомогательная функция: ESFJ, ESTJ

(Se) Экстравертная сенсорика как доминантная функция: ESTP, ESFP

(Se) Экстравертная сенсорика как вспомогательная функция: ISTP, ISFP

Другие типы имеют Si как третью или четвертую функцию. Это означает, что они могут обращаться к нему в случае необходимости, но он совсем не используется в их повседневных процессах.

Подробнее: Руководство для начинающих по пониманию когнитивной функции

Си и Се заходят в бар

Сенсоры используют пять чувств в качестве системы отсчета для восприятия поступающей информации, но не все Сенсоры обрабатывают ее одинаково. В этом отличие экстравертного восприятия от интровертного.

Экстравертные Сенсоры воспринимают данные через конкретные физические и внешние факты. Вам нужны факты, которые ваши чувства представляют вам, чтобы понять, на что вы смотрите, и это несколько быстрее преобразуется в решения. Прямая связь пользователя Se с органами чувств позволяет ему быстрее реагировать и направлять больше энергии на выполнение поставленной задачи, а также обеспечивать обратную связь в режиме реального времени.

Интровертные сенсоры фильтруют данные и переживания через заранее организованный набор внутренних воспоминаний и ощущений, таких как боль или голод, сравнивая и противопоставляя то, что происходит, всему, что мы испытывали раньше. Это позволяет нам формировать субъективные мнения и принимать решения, но для их принятия требуется немного больше времени.

Еще один способ увидеть эти различия — заметить, что пользователи Se работают преимущественно с кратковременной памятью. Пользователи Si работают с долговременной памятью. Пользователи Se будут воспринимать информацию и избавляться от старых воспоминаний, освобождая для них место. Пользователи Si будут принимать информацию и обдумывать ее. Подумайте об этом. Задержитесь на этом.

Хороший способ думать об этом как о ящике воспоминаний.

Нам нужно убедиться, что новые данные попадают в нужное поле и должным образом связаны со всем, что мы уже знаем. Это много мелких корректировок. Но в результате мы закрепляем его в долговременной памяти, и старые воспоминания теперь поддерживают его. Все наши воспоминания остаются основанными на связях, которые мы установили между ними.

Пользователи Si хранят свои данные в ящиках и складывают их глубоко и широко. Вы узнаете их по тому, о чем они обычно говорят. Если кто-то рассказывает историю 20-летней давности (а вы уже слышали ее раньше!), скорее всего, это Си. Если кто-то предпочитает болтать о том, что происходит здесь и сейчас, скорее всего, это Se.

Нестандартная работа

Мы справляемся с неизвестным, сравнивая, противопоставляя и экстраполируя его с чем-то уже знакомым нам. Как еще мы собираемся положить его в правильную коробку? По мере того, как входящие данные представляются, мы ищем ссылку, с которой можно их связать. Все взаимосвязано, все является шаблоном, и мы соответствующим образом упорядочиваем наш мир.

Вы найдете меня на новой работе, сгорбившись над своим столом, просто наслаждаясь всеми поступающими данными. Дать перевариться. Переставляя кусочки снова и снова, пока не сформируется узор, расцветает рутина, и из хаоса возникает внезапная гармония. Я нашел нужные коробки, выровнял их по новой системе, и теперь мы можем выходить и доминировать на работе.

Интроверты обращаются к своему внутреннему миру, когда они переживают жизнь. Постоянно собирая и упорядочивая новые данные в текущем наборе ящиков, мы будем расширять и иногда реорганизовывать ящики по мере того, как узнаем что-то новое. Небо не всегда голубое. Мы добавляем каждый новый цвет по мере того, как мы его воспринимаем, а ящик на небе соответствующим образом перестраивает и маркирует свои файлы.

Однако, если мы точно знаем, потому что так говорит наш ящик, что на небе всегда бывает только одно солнце, и мы просыпаемся с двойным восходом солнца, наш основной ящик трескается. Мы в основном обездвижены до тех пор, пока эти новые данные не могут быть либо выровнены с коробкой, либо мы не создадим совершенно новую коробку для их хранения.

Пакет льгот

Si — это терпеливая и щедрая функция. Си-личности умеют распознавать несоответствия или изменения. Как упоминалось ранее, внутренняя обработка создает у пользователя Si долговременные и точные воспоминания. Это означает, что они учатся на своих ошибках и редко их повторяют.

Пользователи Si лояльны, ответственны и традиционны. Они высоко ценят авторитет и предпочитают системы ценностей, поддерживающие его. Пользователи Si могут быть материально бережливыми и утверждать, что «если это не сломано, не чините это». Как правило, это люди с низким уровнем обслуживания, которые избегают драмы.

Пользователи Healthy Si могут сознательно обращаться к своим более счастливым воспоминаниям, решая, что может означать новая информация. Они лучше создают и адаптируют новые традиции и опыт, когда благоприятная среда стабильна и предсказуема. Их навыки планирования и организации в сочетании с минималистским отношением создают желанное открытое пространство для новых данных и не дают им перегружаться.

После того, как пользователи Si приведут свои ящики в порядок, они смогут легко достичь состояния потока, помещая их «в зону» в режиме реального времени. Это похоже на глубокое счастливое рождественское утро или явное плавное выполнение задачи на работе.

Понимание того, как функционируют наши личности, и связи, которая поддерживает и направляет наше восприятие мира, поддается многим моментам «ага». Если вашей доминирующей когнитивной функцией является Si, вы стареете с достоинством, опираясь на историю, чтобы сделать будущее лучше.

8 юнгианских функций: роли, образы и характеристики

Содержание

I. Аналитический подход к 8 функциям

II. Целостный подход: «Функциональные роли»

Fi: «Оценка»

Fe: «Соединение»

Ti: «Рассуждение»

Te: «Структурирование»

Ni: «Знание»

Ne: «Представление»

Si: «Стабилизация»

Se:

Доктор А.Дж. Drenth

В своем посте «Типология 101» я представил обзор восьми предпочтений Майерс-Бриггс (E, I, S, N, T, F, J, P). Хотя предпочтения могут быть полезны для определения вашего типа личности и получения общего представления о типах, они не дают нам всей истории. Также очень важно развить понимание восьми функций.

Примерно до 2018 года я использовал исключительно концепции Карла Юнга (например, «Интровертная интуиция») при работе с функциями. Однако в какой-то момент я начал видеть потенциальные преимущества понимания функций с точки зрения их первичных ролей , которые я с тех пор называю «функциональными ролями».

Преимущество функциональных ролей в том, что они предоставляют информацию о богатстве в единой концепции (например, Fi как «оценка»). Их также можно сочетать с символическими изображениями, которые ускоряют и помогают пониманию:

Однако этот подход не лишен недостатков. Если имя, назначенное функциональной роли, не находит отклика, люди могут потерять интерес или ассоциировать себя с неправильным типом или функцией. Исключительное использование функциональных ролей может также привести к игнорированию важных деталей и нюансов, связанных с концепциями Юнга.

По сути, мы имеем дело с компромиссом между логической структурой юнговской терминологии и непосредственным целостным впечатлением от функциональных ролей; это дилемма левого и правого полушарий. Но поскольку оба подхода имеют свои достоинства, я готов предоставить каждому место за столом.

В этом посте мы рассмотрим основные особенности функций как с аналитической, так и с целостной точки зрения. Надеемся, что это обеспечит более полное и осмысленное понимание функций, чем любой подход сам по себе.

I. Аналитический подход к 8 функциям

Мое понимание функций было в значительной степени основано на интенсивном изучении аналитической работы и работ Юнга, Майерс-Бриггс и их предшественников. Итак, я хотел бы начать с краткого обзора того, что я считаю ключевыми концептуальными категориями, которые отличают восемь функций. Хотя это обсуждение ценно само по себе, оно также послужит необходимой теоретической базой для понимания функциональных ролей, которые мы обсудим позже в этом посте.

Скрытое или явное?

Скрытые/интровертные функции : Ni, Si, Ti, Fi

Выраженные/экстравертные функции : Ne, Se, Te, Fe

Это различие достаточно очевидно и легко для понимания. Экстравертные (Э) функции по определению направлены наружу , тогда как интровертные (I) функции направлены внутрь . Экстравертные функции более явно выражены и их легче наблюдать. Интровертные функции, будучи в значительной степени скрытыми, труднее различить извне.

Как я уже отмечал в другом месте, это может привести к неправильному пониманию интровертов, поскольку их доминирующая функция, которая является интровертной по своей природе, не сразу обнаруживается или распознается. Вместо этого люди обычно сталкиваются с экстравертной вспомогательной функцией интровертов, которая не является ни самой сильной, ни самой предпочтительной функцией. В любом случае, это важно понимать, когда общаешься с интровертами и печатаешь их.

Суждение или восприятие?

Судейские функции : Ti, Fi, Te, Fe

Функции восприятия : Ni, Si, Ne, Se

Функции суждения помогают нам принимать решения и делать выводы. Они связаны с желанием контролировать, предсказывать, упорядочивать или иным образом формировать ход вещей. При использовании функции суждения мы можем закрыться от новой информации (т. е. перестать воспринимать) в надежде продвинуться к цели, ответу или решению.

Функции восприятия отвечают за получение или извлечение информации. Наблюдение за птицами, обоняние цветов, чтение романов и припоминание чего-либо по памяти являются примерами деятельности восприятия. Воспринимающие функции менее заинтересованы в активном формировании или контроле и, таким образом, могут рассматриваться как более пассивные, чем их оценочные аналоги.

Функции суждения и восприятия могут быть скрытыми (I) или выраженными (E). Типы с предпочтением суждения (J) внешне выражают суждение через Fe или Te и поэтому могут казаться более твердыми, серьезными и прямолинейными. Типы с предпочтением восприятия (P) демонстрируют Se или Ne и часто кажутся более непринужденными, открытыми и гибкими.

Автономный или общий?

Автономный : Fi, Ti

Общий : Fe, Te

Эта категория обсуждается реже, чем первые две, но связана с вековым различием между индивидуумом и коллективом. Хотя особенности будут различаться в зависимости от того, обсуждаем ли мы мышление или чувство, основная структура остается неизменной.

Fi и Ti, используемые главным образом FP ​​и TP соответственно, являются автономными функциями, поскольку их причины (Ti), ценности (Fi) и методы выводятся изнутри. Следовательно, их суждения могут временами казаться более своеобразными или неортодоксальными, чем суждения Fe или Te.

Будучи экстравертными функциями, Fe и Te, используемые в основном ФД и ТД, ориентированы на общие или коллективные нормы. Fe согласуется с нормами F, такими как социальные обычаи, манеры, жесты и т. д. Его суждения также имеют более сильную межличностную направленность, чем суждения Fi. Суждения направляются и основываются на заранее установленных технических, научных, юридических или организационных стандартах. В то время как Ti склонен изобретать свои собственные стандарты и методы, Te обычно верит, что стандартные процедуры существуют не просто так, а именно потому, что они доказали свою фундаментальную надежность и надежность.

Читая это, можно подумать, что Ti и Fi немного бунтарские, а Te и Fe более послушные. Я не думаю, что это совсем неправильно, особенно если мы тщательно очерчиваем контекст, в котором это верно (например, Ти более бунтарский или «свободомыслящий» в вопросах T, Fi в вопросах F). Тем не менее, когда дело доходит до идей, интуиция (N) тесно связана с оригинальностью и нестандартностью, а это означает, что NJ также склонны к неортодоксальности, даже если они не носят ее на рукаве.

Наконец, хотя и могут быть некоторые способы, которыми функции S и N можно классифицировать как автономные или общие, это различие, на мой взгляд, более применимо к функциям суждения. Воспринимающие функции лучше описываются в терминах конвергенции и дивергенции, которые мы сейчас обсудим.

Конвергентность или дивергенция?

Конвергентное : Ni, Si

Дивергентное : Ne, Se

Эта категория сосредоточена на объеме и продолжительности восприятия. Юнг иногда описывал интровертный подход как интенсивный и экстравертный подход как экстенсивный . Другими словами, интроверты, как правило, проводят больше времени, сосредотачиваясь на чем-то одном, в то время как экстраверты фокусируются на более коротком и разнообразном.

Как Ni, так и Si преуспели в извлечении из опыта, чтобы сформировать последовательное и надежное мировоззрение. Они просеивают свое восприятие, чтобы достичь согласованного и конвергентного понимания. Затем это понимание служит как ориентиром для жизни, так и линзой для интерпретации нового опыта. Сходящиеся операции Ni и Si могут в некоторых отношениях сделать их похожими на оценивающие функции. Но это только в том случае, если мы заходим слишком далеко в идее «закрытия равного суждения» и не в состоянии признать, что лежащий в основе метод Ni и Si остается перцептивным по своей природе.

С другой стороны, Ne и Se хорошо рассматриваются как расходящиеся функции. Они тонко распределяются по разнообразным сенсорным переживаниям (Se) или абстрактным идеям/возможностям (Ne). В отличие от Ni и Si, они меньше озабочены или умеют отсеивать свое восприятие. Вместо этого их привлекает новизна, они постоянно расширяют свой список впечатлений или воображаемых возможностей.

II. Целостный подход: «Функциональные роли»

Аналитические критерии функций, которые мы только что обсуждали, являются основой, на которой возникло мое понимание функциональных ролей. Кроме того, я использовал следующие критерии при выборе дескрипторов для каждой функции:

• Дескриптор должен представлять собой легко узнаваемую человеческую роль или деятельность.
• В целях экономии каждой функции будет назначен только один дескриптор.
• Дескриптор должен отражать наиболее существенные, значимые или отличительные особенности каждой функции.

Важно понимать, что функции не работают изолированно. Каждый тип личности регулярно использует все четыре свои функции. Из-за этих взаимодействий мы часто видим сходство между типами, даже если они используют разные группы функций. Две (или более) функции могут комбинироваться для создания эффекта, напоминающего эффект другой функции (например, Ni и Se объединяются таким образом, что имитирует Ne).

Следующие снимки функциональных ролей не следует рассматривать как исчерпывающее описание функций. По этой причине я разместил под каждым описанием ссылки на страницы, содержащие дополнительную информацию. Моя основная задача здесь — помочь читателям понять смысл дескрипторов и изображений.

Интровертная интуиция (Ni): «Знание»

Интуитивные (N) суждения (J) используют интровертную интуицию (Ni) в качестве своей доминирующей или вспомогательной функции. Малкольм Гладуэлл удачно описал интуицию как процесс «знания без знания», то есть ощущения, что мы что-то знаем, но без полного понимания того, как мы это узнали. Таков опыт типов NJ, которых Ни постоянно наполняет чувством «знания» и понимания вещей.

Как мы обсуждали ранее, Ni действует конвергентно, а не дивергентно. Вместо того, чтобы создавать постоянно расширяющуюся сеть связей, как Ne, он извлекает основные идеи и разрабатывает конвергентные объяснительные модели. Это процесс дистилляции, различения того, что прочно и важно, от того, что произвольно, мимолетно или аномально.

В ответ на конвергентную работу Ни, NJ обычно сообщают о сильном чувстве интуитивного знания и убежденности. В то время как их коллеги из НП склонны рассматривать идеи Не как потенциально или условно верные, НС воспринимают идеи Ни как самоочевидно верные и заслуживающие доверия.

«Умственное око» — популярный символ интуитивного познания и проницательности , поэтому я выбрал глаз для обозначения Ни.

Знание Ni способствует эффективности NJ в качестве идейных лидеров, теоретиков, руководителей, советников, советников, консультантов и т.п.

Подробнее об интровертной интуиции (Ni)→

Интуитивные (N) воспринимающие (P) типы используют экстравертную интуицию (Ne) в качестве своей доминирующей или вспомогательной функции. Как мы уже обсуждали выше, Ne — это дивергентная форма интуиции, специализирующаяся на генерировании множества идей, связей и возможностей. Вынужденные исследовать все доступные варианты и возможности, принятие твердых и окончательных решений может быть особенно сложным для НП.

Согласно Википедии, дивергентное мышление — это «мыслительный процесс или метод, используемый для генерации творческих идей путем изучения множества возможных решений». Из-за способности Ne колоссально создавать новые и беспрецедентные связи, NP превосходят другие типы по нескольким показателям креативности.

Merriam-Webster определяет «идеирование» как «формирование идеи или концепции». В искусстве идея относится к ранним стадиям творческого процесса, который исследуется посредством набросков, прототипирования или мозгового штурма. Кажется, это идеально отражает роль Ne, заключающуюся в генерации идей и концептуальных возможностей.

Вербальное выражение Не часто напоминает мозговой штурм вслух. Во время выступления НП не всегда может показаться, что они «имеют смысл», поскольку они блуждают от одной идеи к другой. Другим типам Нэ может показаться случайным, отвлекающим, причудливым или взбалмошным.

Нэ также любит представлять и размышлять о , что могло бы быть . Его интерес к предвидению будущих возможностей дает НП хорошее чутье в таких областях, как искусство, дизайн, маркетинг, изобретательство и предпринимательство.

Подробнее об экстравертной интуиции (Ne)→

Интровертное чувство (Fi): «Оценивание»

Чувствующие (F) воспринимающие (P) типы используют интровертное чувство (Fi) в качестве своей доминирующей или вспомогательной функции. Как мы обсуждали ранее, Fi направлен внутрь себя, ориентируясь и управляя личными чувствами и ценностями на независимой основе. В то время как Fe полагается на других в плане эмоциональной поддержки и родства, Фай более автономен в решении эмоциональных вопросов. Когда ПЛ все же решают выразить свои чувства и ценности, они часто делают это косвенно, будь то через активные (S), творческие (N) или рациональные (T) каналы.

Как подробно описано в моей книге My True Type , каждая из восьми функций может рассматриваться как имеющая собственный набор значений. Тем не менее, я решил описать Fi как «ценный» по нескольким причинам. Во-первых, Fi больше, чем любая другая функция, имеет естественную оценку самой жизни, особенно таких вещей, как природа, дети и животные. Никому не нужно учить FP о ценности и святости жизни, потому что они уже чувствуют это на глубоком, врожденном уровне. В самом деле, многие распространенные причины FP — благополучие детей, защита окружающей среды, вегетарианство, права животных и т. д. — являются просто расширениями их основных ценностей Fi.

FP также используют свои личные ценности в качестве компаса для навигации по жизни. Хотя ценности Fi могут пересекаться с коллективными ценностями Fe, FP будут противоречить культурному зерну, если с ними что-то не так. Признавая важность свободы следовать своим собственным ценностям, ПС, как правило, рады предоставить такую ​​же свободу другим. Они также склонны ценить разнообразные выражения и образы жизни, возникающие, когда люди (и культуры) маршируют в такт своему собственному барабанщику.

Подробнее об Интровертном Чувстве (Fi) →

Чувствующие (F) осуждающие (J) типы используют Экстравертное Чувство (Fe) в качестве доминирующей или вспомогательной функции. Экстравертная природа Fe иллюстрируется тем фактом, что FJ являются наиболее эмоционально экспрессивными и коммуникативными из всех типов.

Как мы уже упоминали ранее, Fe менее эмоционально автономен, чем Fi. Это верно в двух смыслах. Во-первых, Fe быстрее обращается к другим за эмоциональной поддержкой. Во многих отношениях простой разговор о своих эмоциональных проблемах кажется терапевтическим для FJ. Во-вторых, Фе всегда внимательно следит за социальными нормами, чтобы определить «социально приемлемые» слова или эмоции для данной ситуации. Они часто отодвигают свои собственные эмоции на второй план (при условии, что знают о них), чтобы убедиться, что они сливаются с социальным контекстом. Хотя это может показаться недостоверным или неискренним для типов Fi, это помогает установить социальную сплоченность и связи, которые важны для FJ.

Помимо того, что Fe приспосабливается к социальному контексту, он отлично умеет читать и отражать эмоции других. Это делает его мощным инструментом для достижения главной цели Фе: установления эмоционального взаимопонимания с другими. Без прочной межличностной связи остальная часть программы Fe — консультирование других, повышение морального духа, достижение консенсуса и т. д. — может оказаться неэффективной.

Fe также вдохновляет FJ замечать и удовлетворять потребности других. FJ хотят знать, что все ладят и относятся к ним гуманно и гостеприимно. Им также нравится давать советы и советы, особенно по духовным, личным или межличностным вопросам 9.0003

Подробнее об Экстравертном Чувстве (Fe) →

Интровертное Мышление (Ti): «Рассуждение»

Мыслящие (T) воспринимающие (P) типы используют Ti в качестве своей доминирующей или вспомогательной функции. Полезно думать о Ti как о врожденной склонности к логическим рассуждениям — будь то пространственные, математические или другие. Читатели, которые являются школьными учителями, вероятно, знакомы с понятием «чувство чисел» и с тем, что у одних учеников оно естественно сильнее, чем у других. Точно так же логическое мышление является второй натурой для TP, позволяя им самостоятельно решать логические задачи. TP (особенно ITP) — это ваш типичный тип «сделай сам» или «действуй в одиночку», поэтому в нашем предыдущем обсуждении я классифицировал Ti как 9.0095 автономная функция по отношению к Te.

«Рассуждение», согласно Оксфордскому словарю, включает в себя «мышление, понимание и формирование суждений посредством логического процесса». Более того, термин «разум» долгое время ассоциировался с философской дисциплиной, и многие известные философы, вероятно, были INTP. Философия также служила убежищем для «свободомыслящих», для тех, кто был достаточно смел, чтобы тщательно исследовать предположения даже самых широко распространенных верований или парадигм. Это подчеркивает критический и исследовательский характер мышления Ти (особенно в партнерстве с Не), который я подробно обсуждаю в двух своих книгах INTP.

Тем не менее, мы должны быть осторожны, чтобы не слишком склонить наш взгляд на Ti в сторону абстракции NTP. Правда в том, что Ti так же актуален и полезен для решения практических (S) задач, как и для абстрактных (N); STP, как правило, больше внимания уделяют первому, а NTP — второму. Спортсмены STP, хирурги и механики, например, используют рассуждения Ti для принятия решений о конкретной ситуации, стоящей перед ними. НПТ применяют Ti более абстрактно — воздействуя на идеи, теории, проекты и т. д.

Подробнее об интровертном мышлении (Ti) →

Мыслящие (T) и оценивающие (J) типы используют экстравертное мышление (Te) в качестве своей доминирующей или вспомогательной функции. В межличностном плане Te включает внешнее выражение рациональных суждений и утверждений; TJ буквально «думают вслух». Выражаясь твердо и откровенно, они ваши типичные «прямострелы».

Te направлен на рациональное понимание внешних систем/структур, диагностику их недостатков, а также на то, чтобы сделать их более эффективными и действенными. Дома Те может контролировать такие действия, как планирование, маркировка, организация и финансы. На рабочем месте его можно использовать для упорядочения и оптимизации процессов или даже для реструктуризации всей организации. Чтобы сделать это эффективно, Те опирается на эмпирические данные и установленные методы и процедуры.

В отличие от TP, TJ предпочитают не импровизировать, а использовать проверенные способы ведения дел. Тем не менее, NTJ, в частности, будут отказываться от существующих стандартов или работать над их пересмотром, когда это необходимо, но обычно это скорее продукт их интуиции, чем Te.

Умение Te «структурировать» деятельность способствует успеху TJ в работе, которая включает планирование, организацию, картографирование или количественную оценку. Это может включать в себя карьеру в широком спектре областей, таких как право, бизнес, финансы, наука, менеджмент, технологии и т. д.

Подробнее об экстравертном мышлении (Te) →

Интровертное восприятие (Si): «Стабилизация»

Сенсорное (S) и оценивающее (J) типы используют интровертное восприятие (Si) в качестве доминирующей или вспомогательной функции. Si доверяет тому, что знает. А то, что он знает, это то, что он вспоминает из прошлого опыта — из воспоминаний, традиций, связей, установившихся порядков и т. д. В отличие от ориентации Не на будущее, ценности и решения Си руководствуются прошлым. Вместо того, чтобы пробовать что-то новое, Си предпочитает не рисковать, придерживаясь устоявшихся убеждений и моделей поведения. Больше, чем другие типы, SJ находят утешение и удовольствие в известном и знакомом. Как я заметил в Мой Истинный Тип :

Растущая привязанность к рутине, привычному и ожидаемому, повторение играет заметную роль в Si. Чем больше SJ повторяют что-то — едят определенную еду, слушают определенную песню и т. д. — тем более симпатичным (или терпимым) это становится… SJ также придерживаются консервативного подхода к своим убеждениям и мировоззрению. Став взрослыми, они часто упорствуют в убеждениях, представлениях и традициях своего детства.

Знакомство дает SJ чувство безопасности и защищенности. Если они могут увековечить прошлое в настоящем и будущем, они знают, чего ожидать, и могут соответствующим образом планировать. Их предпочтение стабильности и предсказуемости способствует лояльности и надежности SJ во всех аспектах жизни — будь то друзья, супруги, родители или сотрудники. На рабочем месте Si помогает с вниманием к деталям, соблюдением установленных правил и процедур и контролем качества. Это особенно полезно в юридических, канцелярских, административных и смежных областях.

Подробнее об интровертном восприятии (Si) →

Чувствительные (S) воспринимающие (P) используют экстравертное восприятие (Se) в качестве своей доминирующей или вспомогательной функции. Обычно ассоциируемый с «пятью чувствами», Se опосредует наши отношения с нашим физическим окружением. С его вниманием к деталям и быстрой интуицией он, несомненно, был (и буквально) спасателем жизни в наши дни охотников-собирателей.

SP-типы чувственны, инстинктивны и обладают аппетитом. Они наслаждаются новыми чувственными переживаниями, материальными удовольствиями и азартом действия. Se стимулируется постоянно меняющимися обстоятельствами и вызовами окружающей среды. Вот почему многим ПЛ нравятся спортивные занятия, которые обеспечивают постоянный поток новых и непредсказуемых вызовов, которые нужно воспринимать и реагировать на них. ПЛ также могут задействовать свою СЭ с помощью практических задач и проектов, а также экспериментируя с новыми вещами (например, рецептами, расстановкой мебели, модой) и опытом (например, путешествуя).

Эстетические предпочтения Се часто отражают то, что популярно или модно. Некоторые ПЛ развивают дорогой вкус, будь то еда, вино, автомобили или жилье. Эти вещи не только доставляют удовольствие сами по себе, они также могут служить символами статуса, что, как правило, ценят ПЛ.

Благодаря своей способности наблюдать и быстро реагировать на изменения в непосредственной окружающей среде, ПЛ, как правило, получают удовольствие и преуспевают в практической работе: приготовлении пищи, столярных работах, ремонте автомобилей, хирургии, реагировании на чрезвычайные ситуации, личном обучении, косметологии и т. д.

Узнать больше об экстравертном восприятии (Se) →

Узнать больше:

Подробно ознакомиться с каждой из 8 функций можно в нашей последней книге:

Мой истинный тип: уточнение вашего типа личности, Настройки и функции

Похожие сообщения:

Типология 101: Настройки

«Функциональный стек» (Типология 301)

Основная страница функций

5.