Функции в c: Функции в языке Си : вызов функции, возвращаемое значение

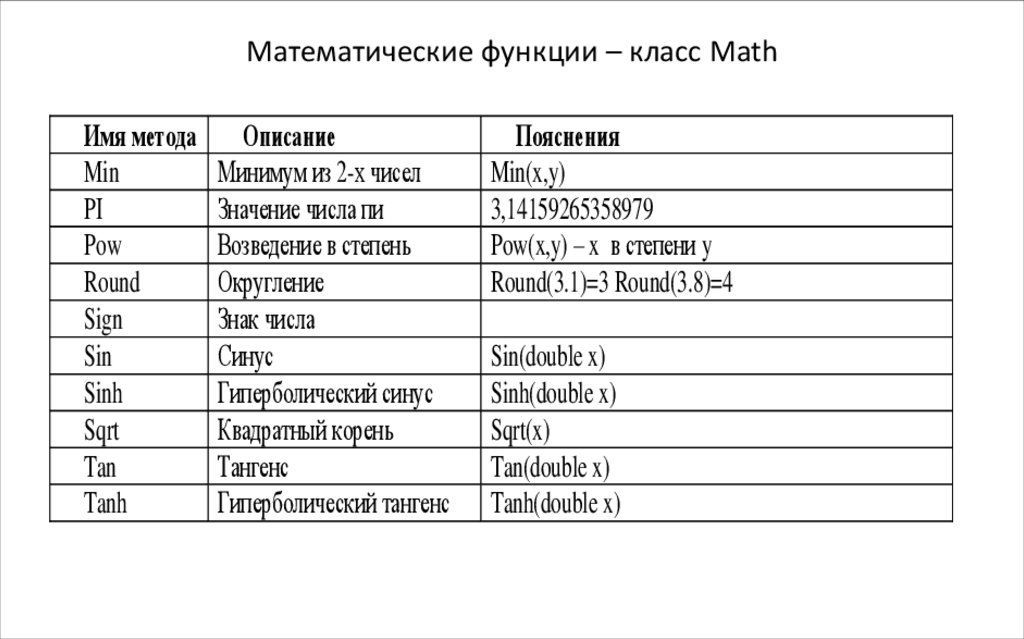
Встроенные функции в C++

Когда в C ++ вызывается обычная функция, некоторые из них подслушиваются только за вызов функции. Фактически, для вызова функции требуется время, прежде чем она действительно начнет выполняться. Это время между вызовом функции и ее фактическим запуском называется временем переключения. Если обычная функция велика, то есть ее выполнение займет много времени, тогда время переключения относительно невелико, и пользователь может его игнорировать. Однако, если обычная функция мала, как и многие функции, то время переключения, примерно одинаковое для больших и малых функций, не следует игнорировать. Во многих ситуациях время переключения больше, чем время, необходимое для реального выполнения небольшой функции; в некоторых случаях намного дольше.

Для решения этой проблемы C ++ использует макрос и встроенную функцию. Макрос похож на небольшую функцию, но обычно он короче типичной небольшой функции. Самый длинный макрос — это одно «утверждение». В теле функции может быть несколько операторов. Небольшая встроенная функция имеет преимущества перед обычной небольшой функцией.

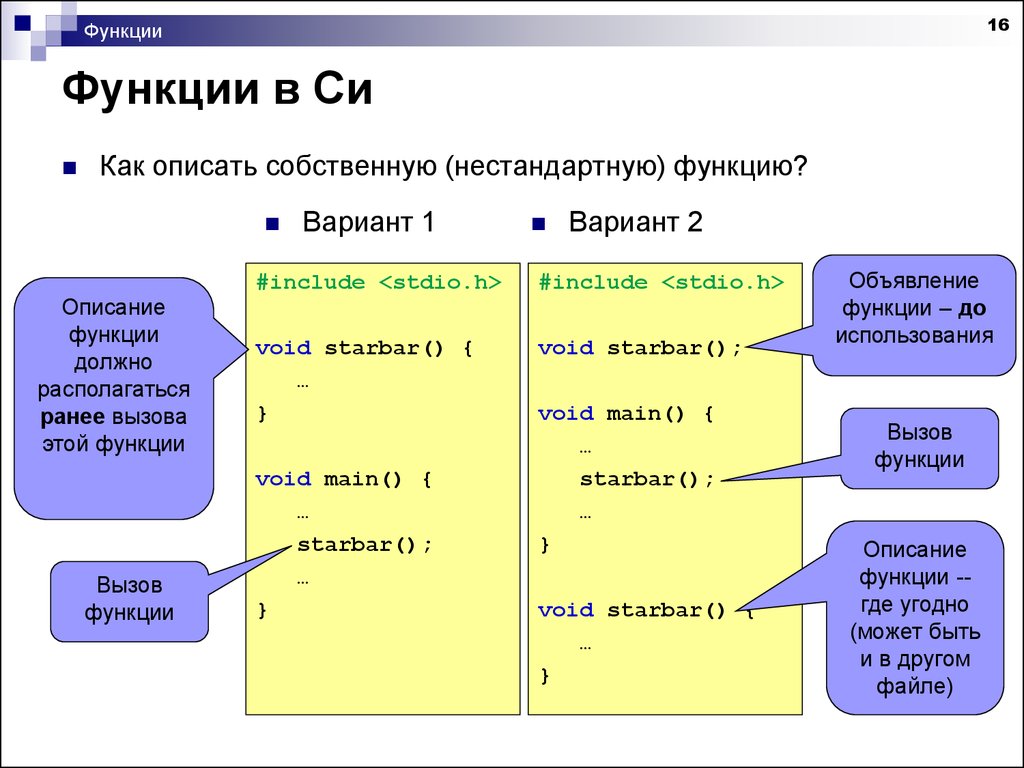
Когда макрос определен, он вызывается позже в программе. Встроенная функция также определяется, а затем вызывается позже в программе. Обычная функция определяется, а затем вызывается позже в программе. Все эти три типа определены и вызываются позже в программе. Любой из них может быть вызван более одного раза.

Макро- и небольшие встроенные функции отличаются от нормальной функции подхода, когда они позже отключаются в программе. Компилятор C ++ размещает определенный код макроса или определенный небольшой встроенный код функции (тело) везде, где он вызывается в программе. Когда компилятор делает это, считается, что компилятор расширил макрос или встроенную функцию. Это не относится к нормальному функционированию. Обычная функция не раскрывается там, где она вызывается.

Хотя для вызова нормальной функции требуется время переключения, для того, чтобы функция была правильно утверждена перед ее выполнением, макрос или небольшая встроенная функция начинает выполнение всякий раз, когда она вызывается, и нет потери времени переключения.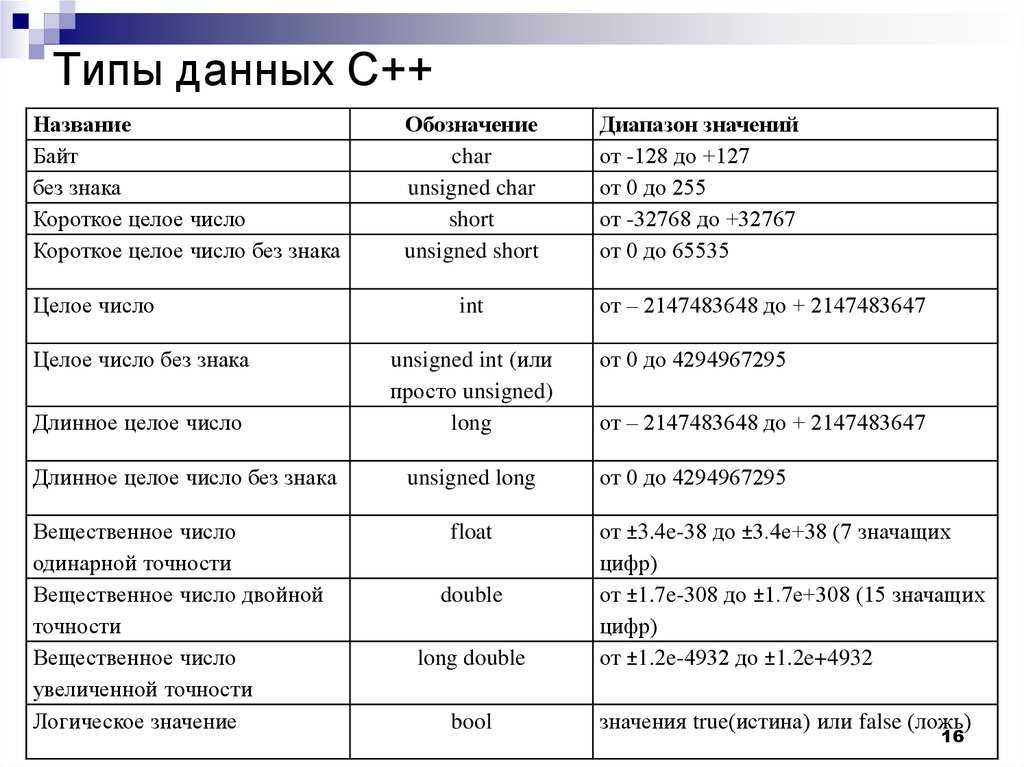 Это главное преимущество макроса и небольшой встроенной функции по сравнению с обычной функцией, т. Е. Время переключения не учитывается.

В этой статье объясняется сравнение встроенных функций в C ++ с макросами. Дается объяснение макроса. Сравнение встроенной функции и нормальной функции проводится в конце статьи.

Примечание. Вызов макроса в программе называется вызовом макроса.

Содержание

1. Определение макросов и встроенных функций
2. Функционально-подобный макрос и встроенная функция
3. Встроенная функция и компилятор
4. Сравнение макросов и встроенных функций
5. Сравнение встроенных и обычных функций
6. Заключение

Определение макросов и встроенных функций

Макрос, подобный объекту, и встроенная переменная.
Существует макрос, подобный объекту, и макрос, подобный функции. Соответственно, есть встроенные переменные и встроенные функции. Рассмотрим следующую программу на C ++:

#include
using namespace std;

#define var1 «E»

inline char var2 = ‘E’;

int main()
{
cout << var1 << endl;
cout << var2 << endl;

return ;
}

Результат:

E
E

Эта программа имеет объектно-подобный макрос и встроенную переменную. Каждый содержит значение «E». Макрос, подобный объекту, начинается с #define и не имеет индикатора типа. Встроенная переменная начинается со слова «встроенная», а за ней следует индикатор типа. У макросов есть недостаток по сравнению со встроенными типами, поскольку они не указывают тип. Это может привести к проблемам с несоответствием типов в программе. В функции main () var1 и var2 — это код определения различных переменных соответственно.

Примечание: неясно, содержит ли var1 символ или буквальную строку. Также обратите внимание, что макрос, как объектный, так и функциональный, не заканчивается точкой с запятой. Он заканчивается нажатием клавиши Enter. Встроенная переменная или встроенная функция заканчиваются своим обычным образом.

Функционально-подобный макрос и встроенная функция

Функциональный макрос — это макрос, который принимает аргументы. Подобно объектно-подобному макросу, везде, где функциональный макрос вызывается в программе, компилятор заменяет вызов определением кода и устраняет время переключения (накладные расходы на вызов функции) во время выполнения.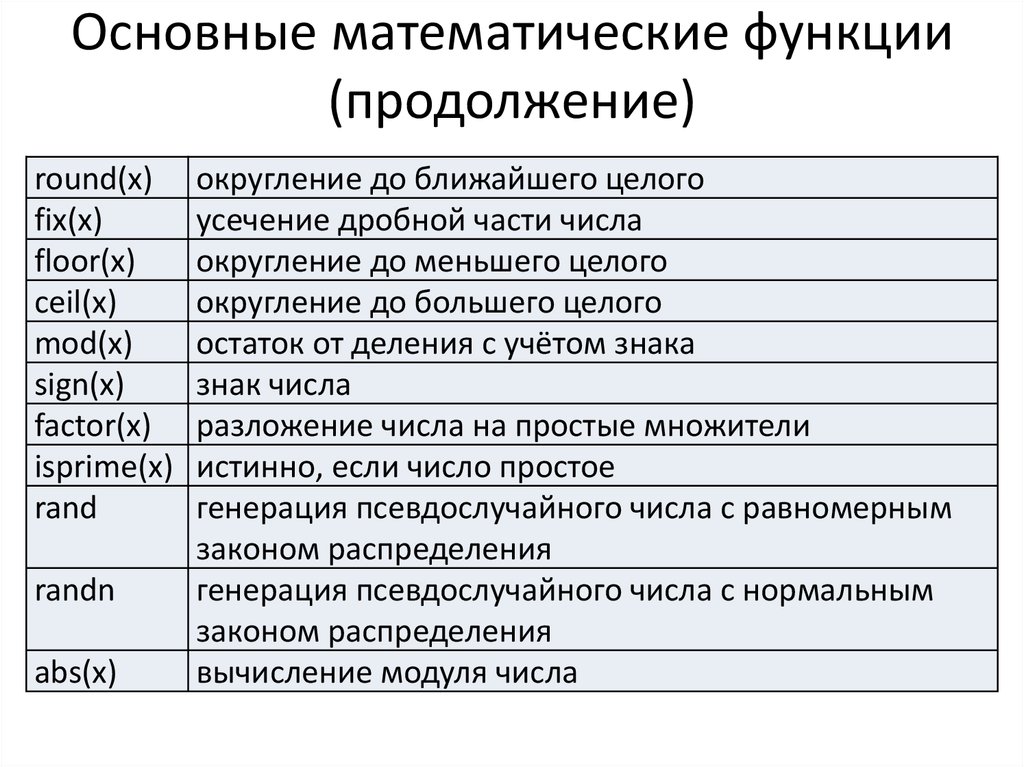

Встроенная функция — это функция, которая начинается со слова «встроенная». Он имеет преимущество перед функционально-подобным макросом с его типом возвращаемого значения и типами аргументов. Макрос, подобный функции, не имеет типов аргументов или возвращаемых типов. Его возвращаемый тип — это последнее значение имени макроса.

Следующая программа на C ++ имеет макрос, похожий на функцию, и встроенную функцию, каждая из которых ищет максимальное значение из двух аргументов. Встроенная функция сравнивает два целых числа и возвращает большее целое число. Возвращаемое значение встроенной функции может быть присвоено новой переменной типа int. С другой стороны, окончательное значение макроса становится значением макроса.

#include
using namespace std;

#define maxM(a, b) ((a) > (b) ? (a): (b))

inline int maxI(int a, int b) {
if (a > b)
return a;
if (a < b)
return b;
if (a == b)
return a;
}

int main()
{
cout << maxM(2. 5, 6) << endl;
cout << maxI(3, 7) << endl;

return ;
}

Результат:

6
7

В макросе аргументы должны быть совместимого типа. Это дает макросу своего рода преимущество перед встроенной функцией, типы аргументов которой в этом случае должны быть одинаковыми.

Имя макроса — maxM. Аргументы — а и б. Остальное — это своего рода тело функции, ограниченное круглыми скобками. Он говорит, что если (a)> (b) истинно, то a становится значением макроса; в противном случае b становится значением макроса.

Встроенная функция и компилятор

После того, как компилятор заменяет встроенный вызов функции кодом определения функции, программа все равно должна выполняться. Компиляция не выполняется или не выполняется программа. При нормальной функции накладные расходы (время переключения) возникают, когда программа запускается (выполняется). Макро- или встроенная замена происходит во время компиляции, то есть перед выполнением (перед отправкой программы заказчику или пользователю).

В конце концов, время переключения опускается или увеличивается для макросов и небольших встроенных функций. Однако, если встроенная функция велика, компилятор решит, объявить ли функцию встроенной, встроенной или нет. Если функция, объявленная как встроенная, имеет большой размер, замена любого из ее вызовов телом кода функции может не принести существенного выигрыша. О критериях решения компилятора — см. Ниже.

Примечание. Функция, определенная в определении класса, является встроенной функцией, которой предшествует встроенный спецификатор.

Сравнение макросов и встроенных функций

Макрос может работать с разными типами, если они совместимы. Это преимущество. Однако это также приводит к побочным эффектам, что в свою очередь делает его недостатком. Встроенная функция проверяет допустимость своих типов аргументов перед использованием аргументов, что предотвращает побочные эффекты.

Сравнение встроенных и обычных функций

Преимущества встроенной функции

• Нет накладных расходов на вызов функций (нет времени переключения).
• При возврате из нормальной функции возникают также накладные расходы. При использовании встроенной функции накладные расходы на обратный вызов отсутствуют.
• Возможна контекстно-зависимая оптимизация тела функции с помощью встроенной функции.

Недостатки встроенной функции

• Для каждого вызова встроенной функции код определения функции (тела) повторяется (был повторно набран компилятором). Это может привести к получению очень большого двоичного (скомпилированного) файла.
• Компилятору требуется много времени для компиляции, поскольку он повторяет один и тот же код для всех вызовов.

Встроенные функции могут не понадобиться для многих встроенных систем, потому что меньший размер программы предпочтительнее более высокой скорости.

Заключение

Встроенная функция похожа на макрос. Они служат той же цели. Код определения заменяет каждый вызов или вызов функции. Однако встроенная функция имеет больше преимуществ перед макросом. Есть объектный макрос и, соответственно, встроенная переменная. Есть макрос, подобный функции, и, соответственно, встроенная функция. Функция, определенная в определении класса, является встроенной функцией, независимо от того, предшествует ли ей встроенный спецификатор или нет.

Чтобы определить макрос, подобный объекту, или макрос, подобный функции, поставьте перед ним #define, за которым следует имя макроса. Макрос не указывает тип значения или типы аргументов. Чтобы определить встроенную переменную или встроенную функцию, поставьте перед ней спецификатор inline, за которым следует тип возвращаемого значения, а затем имя. Для встроенной функции как возвращаемый тип, так и типы аргументов являются точными. Побочные эффекты предотвращены.

Встроенная функция имеет общие преимущества перед макросом. Когда встроенная функция сравнивается с нормальной функцией, есть свои плюсы и минусы.

Как найти область определения функции?

Понятие области определения функции

Впервые школьники знакомятся с термином «функция» на алгебре в 7 классе, и с каждой четвертью, с каждой новой темой это понятие раскрывается с новых сторон. И, конечно же, усложняются задачки. Сейчас дадим определения ключевым словам и будем находить область определения функции заданной формулой и по графику.

Если каждому значению x из некоторого множества соответствует число y, значит, на этом множестве задана функция. При этом х называют независимой переменной или аргументом, а у — зависимой переменной или функцией.

Зависимость переменной у от переменной х называют функциональной зависимостью. Записывают так:

y = f(x).

Функция — это соответствие между двумя множествами, причем каждому элементу первого множества соответствует один элемент второго множества.

Из понятия функции сформулируем определение области определения функции.

Область определения функции — это множество всех значений аргумента (переменной x). Геометрически — это проекция графика функции на ось Ох. Чтобы обозначить область определения некоторой функции y, используют запись D(y).

Множество значений функции — множество всех значений, которые функция принимает на области определения. Геометрически — это проекция графика функции на ось Оy.

• Например, область значений функции y = x2 — это все числа больше либо равные нулю. Это можно записать так: Е (у): у ≥ 0.

Область определения можно описывать словами, но часто ответ получается громоздким. Поэтому используют специальные обозначения.

Если мы хотим указать на множество чисел, которые лежат в некотором промежутке, то делаем так:   Через точку с запятой указываем два числа: левую и правую границы промежутка. Если граница входит в промежуток, ставим возле нее квадратную скобку, если не входит — круглую. Если у промежутка нет правой границы, записываем так: +∞. Если нет левой границы, пишем -∞. Если нужно описать множество, состоящее из нескольких промежутков, ставим между ними знак объединения: ∪.

Например, все действительные числа от 2 до 5 включительно можно записать так:

• [2; 5].

Все положительные числа можно описать так:

• (0; +∞).

Ноль не положительное число, поэтому скобка возле него круглая.

Демо урок по математике

Узнайте, какие темы у вас «хромают», а после — разбирайте их без зубрежки формул и скучных лекций.

Области определения основных элементарных функций

Область определения функции — неотъемлемая часть самой функции.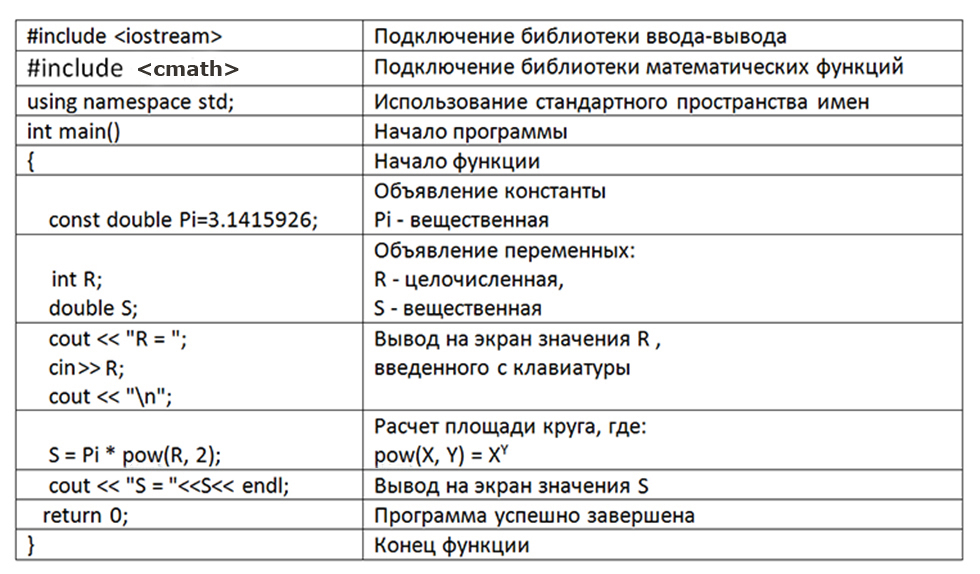 Когда мы вводим какую-либо функцию, то сразу указываем ее область определения.

На уроках алгебры мы последовательно знакомимся с каждой функцией: прямая пропорциональность, линейная функция, функция y = x

2 и другие. А области их определения изучаем, как свойства.

Рассмотрим области определения основных элементарных функций.

Область определения постоянной функции

Постоянная функция задается формулой y = C, то есть f(x) = C, где C — некоторое действительное число. Ее еще называют константа. 

Смысл функции — в том, что каждому значению аргумента соответствует значение функции, которое равно C. Поэтому, область определения этой функции — множество всех действительных чисел R.

Например:

• Область определения постоянной функции y = -3 — это множество всех действительных чисел: D(y) = (−∞, +∞) или D(y) = R.
   
• Областью определения функции y = ³√9 является множество R.

Для тех, кто учится в 7 классе, материала выше достаточно, чтобы подготовиться к контрольной работе. А вот старшеклассникам нужно разбираться в теме несколько глубже — поэтому продолжаем.

Еще больше наглядных примеров и практики — на курсах по математике в онлайн-школе Skysmart!

Бесплатные занятия по английскому с носителем

Занимайтесь по 15 минут в день. Осваивайте английскую грамматику и лексику. Сделайте язык частью жизни.

Область определения функции с корнем

Функцию с корнем можно определить так: y = ⁿ√x, где n — натуральное число больше единицы.

Рассмотрим две вариации такой функции.

Область определения корня зависит от четности или нечетности показателя:

• Если n — четное число, то есть, n = 2m, где m ∈ N, то ее область определения есть множество всех неотрицательных действительных чисел:
  
• Если показатель корня нечетное число больше единицы, то есть n = 2m+1, при этом m принадлежит к N, то область определения корня — множество всех действительных чисел:
  

Значит, область определения каждой из функций y = √x, y = ⁴√x, y = ⁶√x,… есть числовое множество [0, +∞).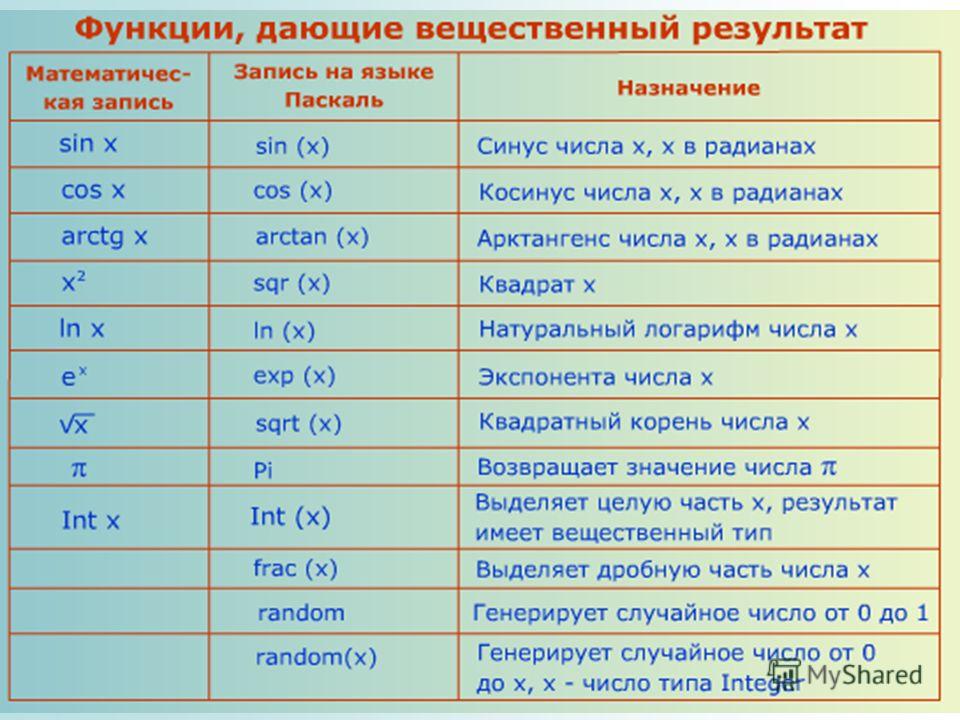 А область определения функций y = ³√x, y = ⁵√x, y = ⁷√x,… — множество (−∞, +∞).

Пример 

Найти область определения функции:

Как решаем:

Подкоренное выражение должно быть неотрицательным, но поскольку оно стоит в знаменателе, то равняться нулю не может. Следовательно, для нахождения области определения необходимо решить неравенство x

2 + 4x + 3 > 0.

Для этого решим квадратное уравнение x² + 4x + 3 = 0. Находим дискриминант:

D = 16 — 12 = 4 > 0

Дискриминант положительный. Ищем корни:

Значит парабола f(x) = x² + 4x + 3 пересекает ось абсцисс в двух точках. Часть параболы расположена ниже оси (неравенство x² + 4x + 3 < 0), а другая часть — выше оси (неравенство x² + 4x + 3 > 0).

Поскольку коэффициент a = 1 > 0, то ветви параболы смотрят вверх. Можно сделать вывод, что на интервалах (−∞, -3) ∪ (−1, +∞) выполнено неравенство x² + 4x + 3 > 0 (ветви параболы уходят вверх на бесконечность), а вершина параболы расположена на промежутке (-3; -1) ниже оси абсцисс, что соответствует неравенству x

2 + 4x + 3 < 0.

Ответ: область определения: D(f) = (−∞, -3) ∪ (−1, +∞).

Если в знаменателе функции стоит выражение, зависящее от х, то для того, чтобы найти область определения данной функции, нам нужно исключить точки, которые обращают знаменатель в ноль.

Область определения степенной функции

Степенная функция выглядит так: y = x^a, то есть, f(x) = x^a, где x — переменная в основании степени, a — некоторое число в показателе степени.

Область определения степенной функции зависит от значения показателя степени.

Перечислим возможные случаи:

• Если a — положительное целое число, то область определения функции есть множество действительных чисел: (−∞, +∞).
• Для нецелых действительных положительных показателей степени: D(f) = [0, +∞).
• Если a — отрицательное целое число, то область определения функции представляет собой множество (−∞, 0) ∪ (0, +∞).
• Для остальных действительных отрицательных a область определения степенной функции — числовой промежуток (0, +∞).

При a = 0 степенная функция y = x^a определена для всех действительных значений x, кроме x = 0. Это связано с тем, что мы не определяли 0⁰. А любое отличное от нуля число в нулевой степени равно единице. То есть, при a = 0 функция приобретает вид y = x⁰ = 1 на области определения (−∞, 0) ∪ (0, +∞).

Рассмотрим несколько примеров.

 

1. Область определения функций y = x⁵, y = x¹² — множество R, так как показатели степени целые положительные.


2. Степенные функции определены на интервале [0, +∞), так как их показатели положительные, но не целые.


3. Область определения функции y = x⁻², как и функции y = x⁻⁵ — это множество (−∞, 0) ∪ (0, +∞), так как показатели степени целые отрицательные.


4. Область определения степенных функций y = x^-√19, y = x^-3e, — открытый числовой луч (0, +∞), так как их показатели не целые и отрицательные.

Область определения показательной функции

Показательную функцию можно задать формулой y = a^x, где переменная x — показатель степени, а — больше нуля и не равно единице.

Область определения показательной функции — это множество R.

Примеры показательных функций:

• y = e^x
• y = (√15)^x
• y = 13^x.

Область определения каждой из них (−∞, +∞).

Область определения логарифмической функции

Логарифмическая функция выглядит так: y = log_ax, где где число a > 0 и a ≠ 1. Она определена на множестве всех положительных действительных чисел.

Область определения логарифмической функции или область определения логарифма — это множество всех положительных действительных чисел. То есть, D (loga) = (0, +∞).
Например:

• D (ln) = (0, +∞) и D (lg) = (0, +∞).

Рассмотрим примеры логарифмических функций: 

• y = log₇x
• y = lnx

Область определения этих функций есть множество (0, +∞).

Пример

Укажите, какова область определения функции:

Как решаем:

Составим и решим систему:

Графическое решение:

Ответ: область определения: D(f) = (−3, -2) ∪ (−2, +∞).

Область определения тригонометрических функций

Сначала вспомним, как задавать тригонометрические функции и как увидеть их области определения.

• Функция, которая задается формулой y = sinx, называется синусом, обозначается sin и определяется на множестве всех действительных чисел. Область определения синуса — это множество всех действительных чисел, то есть, D(sin) = R.
• Функция, которая задана формулой y = cosx, называется косинусом, обозначается cos и определяется на множестве R. Область определения функции косинус — множество всех действительных чисел: D(cos) = R.
• Функции, которые заданы формулами y = tgx и y = ctgx, называются тангенсом и котангенсом и обозначаются tg и ctg. Область определения тангенса — это множество всех действительных чисел, кроме чисел . Область определения котангенса — это множество всех действительных чисел, кроме чисел πk, k ∈ Z.

Поэтому, если x — аргумент функций тангенс и котангенс, то области определения тангенса и котангенса состоят из всех таких чисел x, что и x ∈ r, x ≠ πk, k ∈ Z соответственно.

Пример

Найдите область определения функции f(x) = tg2x.

Как решаем:

Так как a(x) = 2x, то в область определения не войдут следующие точки:

Перенесем 2 из левой части в знаменатель правой части:

В результате . Отразим графически:

Ответ: область определения: .

Область определения обратных тригонометрических функций

Вспомним обратные тригонометрические функции: арксинус, арккосинус, арктангенс и арккотангенс.

• Функция, которая задается формулой y = arcsinx и рассматривается на отрезке [−1, 1], называется арксинусом и обозначается arcsin.

  Область определения арксинуса — это множество [−1, 1], то есть, D(arcsin) = [−1, 1].

• Функция, которая задается формулой y = arccosx и рассматривается на отрезке [−1, 1], называется арккосинусом и обозначается arccos.

  Область определения функции арккосинус — отрезок [−1, 1], то есть, D(arccos) = [−1, 1].

• Функции, которые задаются формулами вида y = arctgx и y = arcctgx и рассматриваются на множестве всех действительных чисел, называются арктангенсом и арккотангенсом и обозначаются arctg и arcctg.

  Область определения арктангенса и арккотангенса — все множество действительных чисел R. То есть, D(arctg) = R и D(arcctg) = R.

Таблица областей определения функций

Области определения основных функций в табличном виде можно распечатать и использовать на уроках, чтобы быстрее решать задачки.

И, помните: чем чаще вы практикуетесь в решении задач — тем быстрее все запомните. 

Функция	Область определения функции
Постоянная y = C	R
Корень y = n√x	[0 ; +∞) , если n — четное; (-∞; +∞) , если n  — нечетное.
Степенная y = xa	(-∞; +∞) , если a > 0, a ∈ Z; [0 ; +∞), если a > 0, a ∈ R, a ∉ Z; (-∞; 0) ∪ (0; +∞) , если a < 0, a ∈ Z; (0; +∞), если a ∈ R, a ≠ Z; (-∞; 0) ∪ (0, +∞), если a = 0.
Показательная y = ax	R
Логарифмическая y = lognx	(0; +∞)
Тригонометрические y = sin(x) y = cos(x) y = tg(x) y = ctg(x)	R R x ∈ R, x ≠ π/2 + πk, k ∈ Z x ∈ R, x ≠ πk, k ∈ Z
Обратные тригонометрические y = arcsin(x) y = arccos(x) y = arctg(x) y = arcctg(x)	[-1; 1] [-1; 1] R R

функций в C: Учебное пособие по C на хинди #19

Зачем изучать язык программирования C? : Учебное пособие по C на хинди #1

Что такое кодирование и язык программирования C? : Учебное пособие по C на хинди #2

Установка и настройка кода VS с помощью компилятора C: Учебное пособие по C на хинди #3

Базовая структура программы на языке C на хинди: Учебное пособие по C на хинди #4

Основной синтаксис программы на языке C: C Учебник на хинди #5

Переменные и типы данных в C: Учебник на хинди #6

Операторы в C: Учебное пособие по C на хинди #7

Упражнение по программированию на C 1. Таблицы умножения: Учебное пособие по C на хинди #8

Спецификаторы формата C и управляющие последовательности с примерами: Учебное пособие по C на хинди #9

Операторы управления If Else In C: Учебное пособие по C на хинди #10

Switch Операторы управления регистром In C: Учебное пособие по C на хинди #11

Циклы In C: Учебное пособие по C на хинди #12

Do While Loop In C: Учебное пособие по C на хинди #13

Цикл в то время как в C: Учебное пособие по C на хинди # 14

Цикл For In C: Учебник C на хинди #15

Операторы Break and Continue на C: Учебник C на хинди #16

Оператор Goto на C: Учебник C на хинди #17

Приведение типов на C: Учебник C In Hindi #18

Функции на C: Учебник по C на хинди #19

C Упражнение 1: Решение таблицы умножения + Shoutouts: Учебник по C на хинди #20

Рекурсивные функции: Рекурсия на C: Учебник по C на хинди #21

C Упражнение 2: Единицы и преобразования: Учебное пособие по C на хинди #22

Массивы в C: Учебник по C на хинди #23

Упражнение 2: Решение + Shoutouts: Учебник по C на хинди #24

Упражнение 3 Рекурсии: Учебник по C на хинди #25

Указатели на C: Учебник по C на хинди #26

Массивы и арифметика указателей в C: Учебное пособие по C на хинди #27

Упражнение 3 О рекурсиях: решение + выкрики: Учебное пособие по C на хинди #28

Всегда ли рекурсия хороша? : Учебное пособие по C на хинди #29

Упражнение 4. Печать узоров звезд на языке C: Учебное пособие по C на хинди #30

Вызов по значению и вызов по ссылке на языке C: Учебное пособие по C на хинди #31

Передача массивов в качестве аргументов функции: Учебное пособие по C на хинди #32

Образец звезды на языке C. Упражнение 4 Решение: Учебное пособие по C на хинди #33

Строки в C: Учебное пособие по C на хинди #34

Строковые функции на C и библиотека string.h: Учебное пособие по C на хинди #35

Обращение массива на C. Упражнение 5: Учебное пособие по C на хинди #36

Структуры на C : Учебное пособие по C на хинди #37

Typedef на языке C: Учебное пособие по C на хинди #38

Unions In C: Учебное пособие по C на хинди #39

Обращение массива в языке C Упражнение 5: Решение: Учебное пособие по C на хинди #40

Язык C HTML Parser Упражнение 6: Учебное пособие по C на хинди #41

Статические переменные в C : Учебное пособие по C на хинди #42

Учебное пособие по C. Упражнение 6: Решения и ответы: Учебное пособие по C на хинди #43

Менеджер туристического агентства C Language. Упражнение 7: Учебное пособие по C на хинди #44

Структура памяти программ на языке C — динамическая Распределение памяти: Учебное пособие по C на хинди #45

C Language Менеджер туристического агентства Упражнение 7 Решение: Учебное пособие по C на хинди #46

Динамическое выделение памяти Malloc Calloc Realloc & Free(): Учебное пособие по C на хинди #47

C Language Менеджер сотрудников Упражнение 8: Учебное пособие по C на хинди # 48

Классы хранения на языке C Auto, Extern Static и Register Storage Classes: Учебное пособие по C на хинди #49

Менеджер сотрудников на языке C — Упражнение 8 Решение: Учебное пособие по C на языке хинди #50

Камень, бумага, ножницы для кодирования Упражнение на языке C 9: Учебное пособие по C на хинди #51

Пустой указатель на языке C: Учебное пособие по C на хинди #52

NULL Указатель на языке C: Учебное пособие по C на хинди #53

Висячий указатель на языке C: Учебное пособие по C на хинди #54

Дикий указатель на языке C: Учебное пособие по C на хинди #55

Камень, бумага и ножницы на языке C — Упражнение 9 Решение: Учебное пособие по C на хинди №56

Умножение матриц на языке C — Упражнение 10: Учебное пособие по C на хинди # 57

Введение и работа с препроцессором C: Учебное пособие по C на хинди #58

#define и #include Директивы препроцессора: Учебное пособие по C на хинди #59

Предопределенные макросы и другие директивы препроцессора: Учебное пособие по C на хинди #60

Умножение матриц в C — упражнение 10 Решение: Учебное пособие по C на хинди #61

Файловый ввод-вывод на C: Учебное пособие по C на хинди #62

Проверка палиндрома на языке C — Упражнение 11: Учебное пособие по C на хинди #63

Функции для файлового ввода-вывода на языке C: Учебное пособие по C на хинди #64

Числовой палиндром Программа на языке C: Упражнение 11 Решение: Учебное пособие по C на хинди #65

Автоматический генератор квитанций на языке C. Упражнение 12. Учебное пособие по языку C на хинди #66

Режимы файлов, fgets, fputs, fgetc, fputc и многое другое по работе с файлами C: Учебное пособие по языку C на хинди #67

Аргументы командной строки на языке C: Учебное пособие по C на хинди #68

Автоматический генератор счетов на C (решение) — Упражнение 12: Учебное пособие по C на хинди #69

Калькулятор командной строки на C — Упражнение 13: Учебное пособие по C на хинди #70

[Решено] Командная строка Калькулятор на C Упр.13 : Учебник по C на хинди #71

Указатели функций в C: Учебное пособие по C на хинди #72

Функции обратного вызова с использованием указателей на функции в C: Учебное пособие по C на хинди #73

Упражнение 13 Область круга с использованием указателей на функции: Учебное пособие по C на хинди #74

Память Утечка на C: Учебное пособие по C на хинди #75

Площадь круга на C Упражнение 14 Решение: Учебное пособие по C на хинди #76

Настройка сгенерированного интерфейса функции C для функций точки входа модели — MATLAB & Simulink

Настройка интерфейса сгенерированной функции C для функций точки входа модели

Что такое функция точки входа?

Точка входа — это место в коде, где происходит передача управления программой (выполнение) имеет место. Основная функция ( main() ) является точкой входа в программу C/C++. и вызывается, когда приложение начинает выполняться. Вызовы других функций, например из основной функции укажите точки входа в функциональный код. Программа управление передается вызываемой функции. Код функции выполняется, и когда он завершен, возвращает управление основная или другая вызывающая функция.

При создании кода для модели генератор кода определяет набор функций точки входа который вы можете вызвать для выполнения сгенерированного кода. Вы можете вызывать сгенерированные функции из внешний код или из версии сгенерированной основной функции, которую вы модифицируете.

В разделе отчета об интерфейсе кода отчета о генерации кода указана точка входа функции, которые генератор кода производит для модели. Дополнительные сведения см. в разделе Анализ интерфейса кода сгенерированных данных (встроенный кодер).

Типы сгенерированных функций точки входа

Генератор кода создает функции точки входа для этих типов моделей функции.

Type of Model Function	Model Source Name	Default Generated Function Name	Description
Exported function (requires Embedded Coder ® )	ExportedFunction: slIdentifier , где slIdentifier имя function-call Inport block в модели	function-call-inport-block-name или signal-label (если указано)	Для модели с экспортируемой функцией — экспортированная функция для подсистемы.
Функция инициализации	Инициализация	модель _initialize	Код инициализации для модели. В начале кода приложения вызовите функция один раз . Не используйте эту функцию для сброса структура данных модели реального времени ( rtM ).
Функция разделения	Раздел: slIdentifier , где slIdentifier — это раздел, который был создан явно из блока в модели и показан в Simulink® Schedule Редактор (например, P1) или имя задачи в диалоговом окне «Параллельное выполнение»	модель _step n , где n однозначно идентифицирует функцию формируется для одного из периодов выборки модели	Для модельного раздела код вывода и обновления. Параметр конфигурации модели Одноместный Выбрана функция вывода/обновления (по умолчанию).
Функция обновления раздела	PartitionUpdate: slIdentifier , где slIdentifier — это раздел, который был создан явно из блока в модели и показан в Simulink® Schedule Редактор (например, P1) или имя задачи в диалоговом окне Concurrent Execution	модель _выход n и модель _update n , где n однозначно идентифицирует функцию создан для одного из периодов выборки модели	Для раздела модели вывод и обновление кода в отдельных функциях. Модель параметр конфигурации Одиночный функция вывода/обновления очищается.
Функция периодической многозадачности	Periodic: slIdentifier , где slIdentifier — это аннотация, соответствует периоду выборки для периодической или непрерывной скорости многозадачная модель (например, D1)	модель _step n , где n однозначно идентифицирует функцию генерируется для одного из периодов выборки модели	Для блоков в модели на основе скорости, сконфигурированной для многозадачности, вывода и обновления код. Генератор кода создает функцию для каждого периода выборки. Модель параметр конфигурации Одиночный Выбрана функция вывода/обновления (по умолчанию).
Функция периодического многозадачного обновления	PeriodicUpdate: slIdentifier , где slIdentifier — это аннотация, соответствует периоду выборки для периодической или непрерывной скорости многозадачная модель (например, D1)	модель _output n и модель _update n , где n однозначно идентифицирует функцию генерируется для одного из периодов выборки модели	Для блоков в модели на основе скорости, сконфигурированной для многозадачности, вывода и обновления код в отдельных функциях. Генератор кода производит функции вывода и обновления за каждый период выборки. Параметр конфигурации модели Один выход/обновление функция очищается.
Периодическая однозадачная функция	Периодическая	модель _step	код. Параметр конфигурации модели Один выход/обновление выбрана функция (по умолчанию).
Функция периодического однозадачного обновления	PeriodicUpdate	модель _output и модель _update	Для блоков в модели на основе скорости, настроенной для однозадачности, вывода и обновления код в отдельных функциях. Параметр конфигурации модели Один выход/обновление функция очищается.
Функция сброса	Сброс: slIdentifier , где slIdentifier имя функция сброса в модели	модель _ имя-функции-сброса	Если модель включает функциональный блок сброса, код сброса сгенерировано. Чтобы сбросить условия или состояние, вызовите функцию из приложения код.
Функция Simulink	Функция Simulink: slIdentifier , где slIdentifier имя Функциональный блок Simulink в модели	имя-функции для глобального Функциональный блок Simulink или модель _ имя-функции для функционального блока Simulink с заданной областью действия	Для модели с экспортируемой функцией экспортированная функция для Simulink Функциональный блок.
Функция завершения	Завершение	модель _terminate	Код для выключения системы. Для моделей на основе ERT можно подавить генерация этой функции путем очистки параметра конфигурации модели Завершить функцию требуется (встроенный кодер) (устанавливается по умолчанию).

Если у вас есть программное обеспечение Embedded Coder, чтобы упростить интеграцию внешнего и сгенерированного кода и достичь соответствие стандартам и руководствам по коду, вы можете настроить, как генератор кода создает функциональные интерфейсы из модели или подсистемы.

Настройка возможности повторного использования функций точки входа

По умолчанию для топовых моделей генератор кода создает код, который нельзя использовать повторно или повторно входящий. Функции точки входа имеют интерфейс void-void . Код взаимодействует с другим кодом, напрямую обращаясь к глобальным структурам данных, которые находятся в Общая память.

Если вашему приложению требуется повторно используемый многоэкземплярный код функции точки входа, вы можете настроить генератор кода для вызова каждой функции (экземпляра) с уникальными данными. В таком случае, код реентерабельный.

Вы настраиваете возможность повторного использования функций точки входа в конфигурации модели параметр Интерфейс кода упаковка и сопутствующие параметры. Настройки параметров, которые вы выбираете зависит от таких факторов, как выбор конфигурации для целевого файла системы, программирование язык и интерфейс аргументов.

Конфигурации по умолчанию для функций точки входа C с одним экземпляром

По умолчанию для целевых файлов системы на основе GRT и ERT генератор кода создает одноэкземплярные функции точки входа C. Сгенерированный код:

Параметры конфигурации модели по умолчанию для настройки одного экземпляра Код функции точки входа:

Генерация многоразовых многоэкземплярных функций точки входа C

Вы можете настроить генератор кода для создания многократно используемых функций точки входа на языке C системный целевой файл на основе GRT или ERT. Однако функциональные интерфейсы, которые Генератор кода выдает по умолчанию разные. Предполагая, что параметр конфигурации модели Язык установлен на C и Код упаковки интерфейса установлен на Повторно используемая функция , генератор кода производит это код функции точки входа для каждого сценария системного целевого файла.

Целевой файл системы	Интерфейс
На основе GRT	Повторно используемые многоэкземплярные функции точки входа C, которые являются реентерабельными. Упаковывает значения блоков Inport корневого уровня модели и Блоки вывода в структуру данных модели реального времени. Передает эту структуру функции выполнения в качестве аргумента ссылка. Динамически выделяет память во время выполнения для данных экземпляра модели. Выделяет память, вызывая функцию, например маллок .
на базе ERT	Повторно используемые многоэкземплярные функции точки входа C, которые повторно входящий. Передает значение каждого блока Inport корневого уровня модели и блока Outport в функцию выполнения в качестве отдельного аргумента. Статическое выделение памяти для структур данных модели.

Если вы используете системный целевой файл на основе ERT и хотите создать повторно используемый, многоэкземплярные функции точки входа C, которые являются реентерабельными, рассмотрите:

• Использование динамического выделения памяти для инициализации структур данных модели. Выберите Использовать динамический выделение памяти для инициализации модели (Embedded Coder).

• Упаковка значений блоков Inport корневого уровня модели в структуру, упаковка значений блоков Outport корневого уровня во вторую структуру и передача структур исполнительной функции в качестве аргументов по ссылке. Набор Передать ввод-вывод корневого уровня как (встроенный кодер) в структуру ссылка .

• Значения упаковки блоков Inport корневого уровня модели и Блоки вывода в структуру данных модели реального времени и передача этого структуру функции выполнения в качестве аргумента по ссылке. Установите Передача ввода-вывода корневого уровня как (встроенный кодер) на Часть модели структура данных .

Как взаимодействовать со сгенерированными функциями точки входа

1. После создания кода для модели используйте представление Code для просмотра сгенерированные функции точки входа и, если применимо, переменные, представляющие внешние входные и выходные порты.

2. Добавьте операторы #include во внешний код, которые включают сгенерированные файлы заголовков, которые объявляют функции точки входа модели.

3. Добавьте инструкцию #include , которая включает сгенерированный файл rtwtypes.h . Этот файл содержит определения типов, #define инструкции и перечисления.

4. Инициализация целевых структур данных и оборудования, таких как АЦП или ЦАП.

5. Если применимо, инициализируйте данные для каждого экземпляра повторно используемой модели.

6. Если применимо, запишите входные данные в сгенерированные переменные, которые представляют модель Ввод блоки.

7. Вызов сгенерированных функций точки входа или настройка использования Функция rt_OneStep .

8. Если применимо, считать данные из сгенерированных переменных, которые представляют модель Outport блоки.

Дополнительные сведения см. в разделе Развертывание приложений на целевом оборудовании (встроенный кодер).

Ограничения настройки интерфейса функций C

Эти ограничения применяются к настройкам для сгенерированных интерфейсов функций C:

• Необходимо выбрать параметр конфигурации модели Один выход/обновление функция .

• Поддерживаются многоскоростные модели, но вы должны настроить модели для односкоростного режима. постановка задач.

• Для использования Класс хранения по умолчанию .

• Если вы решите настроить функциональный интерфейс, вы должны предоставить свой собственный основная программа . Вы не можете настроить функциональный интерфейс с статический rt_main.c , который предоставляет MathWorks ^® . Указание конфигурации функционального интерфейса, отличной от default создает несоответствие между сгенерированным кодом и статическим по умолчанию rt_main.c .

• Генератор кода удаляет структуру данных для корневых портов модели, если подсистема, реализованная одноразовой функцией, использует значение одного или нескольких импорт.

• Генератор кода удаляет структуру данных для корневых портов модели за исключением случаев, когда вы включаете ведение журнала MAT-файла или если шаг расчета одного или нескольких outports не является фундаментальной базовой ставкой (включая постоянную ставку).

• Если вы копируете блок подсистемы для создания блока в новой модели или той же модели, информация о функциональном интерфейсе из исходного блока подсистемы не копируется в новый блок подсистемы.

• Если у вас есть Stateflow ^® , для диаграммы Stateflow, которая использует входное значение корня модели или вызывает подсистему, которая использует значение входа корня модели, выполните одно из следующих действий для создания кода:

  • Очистите Выполнить (ввести) Диаграмму при инициализации флажок на диаграмме Stateflow.

  • Сделайте функцию Stateflow функцией, не допускающей повторного использования.

  • Вставка Simulink ^® Блок преобразования сигнала сразу после корневого входа. в Диалоговое окно параметров блока преобразования сигнала, выберите Исключить этот блок из оптимизации «Сокращение блоков» .

• Если значение входа корня модели соединяется с блоком преобразования Simscape™, вставьте Simulink Блок преобразования сигнала между корневым входом и блоком преобразования Simscape. В параметрах блока Signal Conversion диалоговом окне выберите Исключить этот блок из «Уменьшение блока» оптимизация .

• При построении ссылочной модели, настроенной с функциональным интерфейсом, не использовать виртуальные шины в качестве входных или выходных данных для модели, на которую ссылаются. Используйте невиртуальные автобусы вместо.

• Если интерфейс функции C не используется по умолчанию, значение для модели игнорируется. параметр конфигурации. Дополнительные сведения см. в разделе Передайте входные данные скалярного корня фиксированного размера по значению для генерации кода.

См. также

Функция Simulink | Вызывающий функцию

См.