Комментарии к ячейке в формуле в Excel — TutorExcel.Ru
Поговорим про комментарии в формулах к ячейкам в Excel, которые помогают дать текстовое описание или разъяснение для числовых формул.
Приветствую всех, уважаемые читатели блога TutorExcel.Ru!
Как часто мы разбираясь в чужой или хорошо забытой своей формуле пытаемся вспомнить как она вообще считалась и что значат отдельные ее элементы? Лично мне в этот момент очень не хватает комментария, который бы мог дать короткие пояснения что и откуда берется.
Поэтому сегодня у нас не совсем обычная тема, потому что добавлять комментарии в ячейку на первый взгляд может показаться странной затеей. Ведь можно добавить примечание к ячейке или написать комментарий где-то рядом в соседней ячейке.
Однако и у этих способов есть ряд недостатков, например, структура книги может быть такой, что нет возможности или попросту неудобно добавить комментарий рядом с формулой, а примечание неудобно смотреть в режиме редактирования ячейки. К тому же вышеуказанные способы могут дать комментарии в целом к формуле, но не к отдельным ее частям, что тоже время от времени бывает необходимо.
В общем давайте переходить к делу и на конкретном примере посмотрим как можно вставить комментарий в ячейке к формуле, а заодно сделаем формулу гораздо более читаемой.
Как добавить комментарий к ячейке в Excel?
Давайте для примера рассмотрим небольшую таблицу, где участникам проставлены оценки за соревнования и рассчитывается средняя оценка за выступление:
Но при этом, как на практике часто бывает, средняя оценка будет считаться не как среднее арифметическое всех чисел, а как среднее за вычетом минимального и максимального значения. Давайте вот эту формулу и возьмем за пример для разбора инструмента:
При этом нам вообще не так важно какая именно формула записана в ячейке, она может быть любой сложности.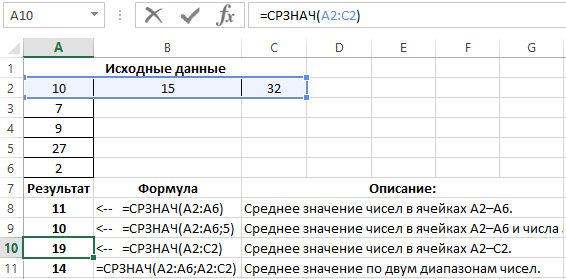
Взглянув на формулу с большим количеством скобок не всегда понятно где какая часть начинается, а где какая заканчивается, что зачастую мешает грамотному редактированию формулы, как нам, так и любому другому человеку, работающему с этим файлом.
Поэтому первым делом приведем формулу в более читаемый вид.
Как сделать формулу в Excel более читаемой?
Давайте немного задумаемся что вообще такое читаемый и удобный вид для формулы.
Обычно мы ее пишем в одну строчку, без пробелов, но с точки зрения читаемости иногда это выглядит как чтение книги в которой нет абзацев — один сплошной текст. Как только мы видим абзацы и красные строки, то текст преобразуется и его гораздо легче воспринимать. Аналогичного эффекта можно достичь и с формулами в Excel.
В режиме редактирования нам на самом деле доступно много возможностей для настройки внешнего вида формулы без фактического изменения значения формулы.
Например, мы прекрасно понимаем что запись вида «2+3» и «2 + 3» это одно и тоже, хоть они записаны немного по разному.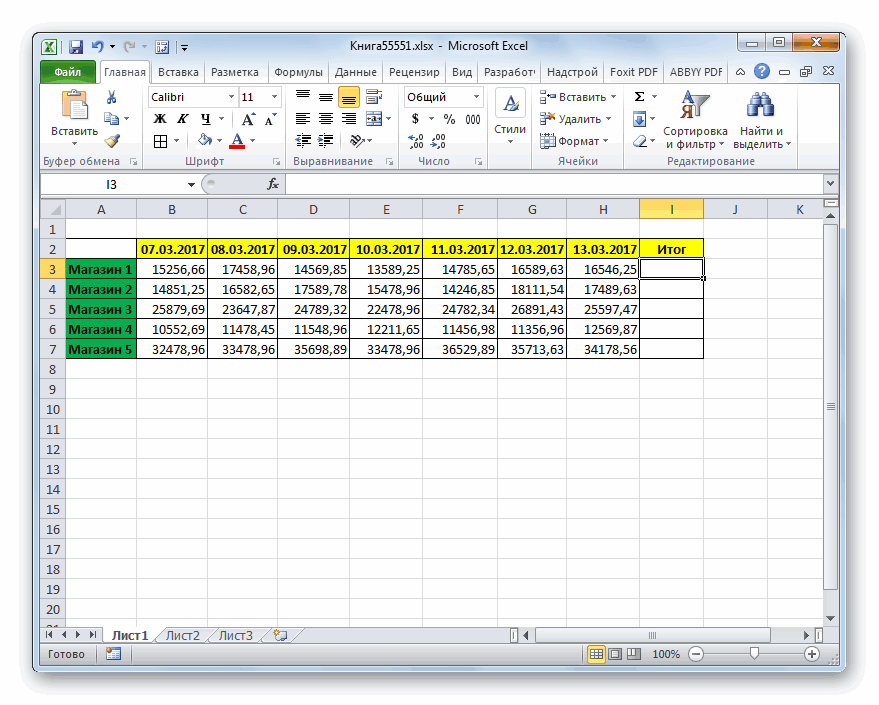
Excel тоже так умеет, поэтому мы можем ставить пробелы и переносить часть формулы на следующие строки, в тех случаях когда не нарушается логика чтения синтаксиса формулы.
Давайте перенесем каждую из функций в формуле на отдельную строку, чтобы наглядно показать как эта формула считается, проставив пробелы и переносы строк в соответствующих местах:
Напомню, что перенос строки в Excel делается с помощью горячих клавиш — в режиме редактирования нужно воспользоваться сочетанием клавиш Alt + Enter.
Вставка комментария в формуле к ячейке в Excel
Теперь давайте перейдем непосредственно к добавлению комментария. Для этого нам понадобится стандартная функция Ч в Excel, которая преобразует данные в числовые значения:
Ч (значение)
Преобразует нечисловые значения в числа, даты — в даты, представленные числами, значения ИСТИНА в 1, все остальные значения — в 0 (ноль).
Полезная особенность этой функции заключается в том, что текстовые значения она преобразует в 0, таким образом добавляя в формулу эту функцию с текстовым комментарием мы никак не изменяем значение формулы — фактически мы к значению формулы прибавляем 0:
В результате мы получаем весьма понятный для чтения вид формулы, после просмотра которого наверняка большинство вопросов по расчету формулы наверняка отпадут и тем самым сэкономят много времени.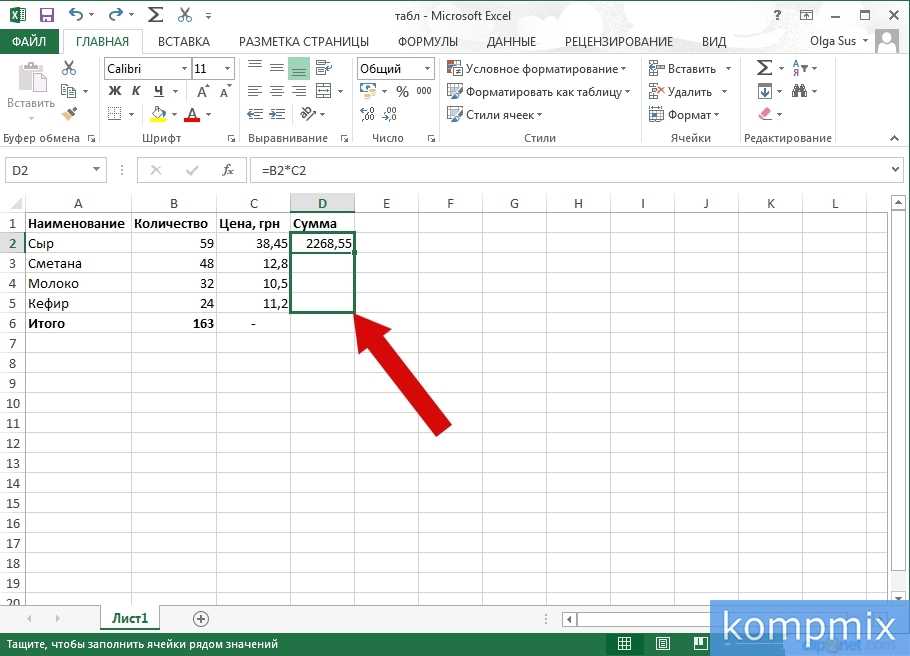
И при этом, конечно, значение ячейки осталось точно таким же, чего мы и добивались.
Скачать файл с примером.
Спасибо за внимание!
Если у вас есть вопросы по теме статьи — заходите, спрашивайте и делитесь мыслями в комментариях.
Удачи вам и до скорых встреч на страницах блога TutorExcel.Ru!
Поделиться с друзьями:
Поиск по сайту:
Формулы Excel для анализа данных: базовый и расширенный
Давайте будем честными, мы все в какой-то момент своей жизни боролись с Microsoft Excel. Чтобы максимально использовать Microsoft Excel, нам необходимо хорошо разбираться в формулах Excel для анализа данных. И давайте не будем забывать, что Microsoft Excel — важный инструмент для анализа данных.
Если вы один из тех, кто стремится к анализу данных, тогда вы должны владеть формулами Microsoft Excel для анализа данных. Если вы хотите хорошо разбираться в формулах Excel для анализа данных, то вы попали в нужное место.
Формулы, которые мы будем обсуждать, работают со значениями внутри ячейки или ячеек. Ниже вы можете найти формулы Excel для анализа данных, которые вам очень помогут и помогут понять основные функции Excel.
Упомянутые формулы могут использоваться каждым, что может помочь вам улучшить вашу способность анализировать данные.
Формулы Microsoft Excel для анализа данных
СЦЕПИТЬ
Это одна из основных и самых популярных формул Excel, которая используется при анализе данных. Формула позволяет пользователям комбинировать числа, тексты, даты и т. Д. Из ячейки или ячеек. Формула конкатенации полезна, когда вы хотите объединить данные из разных ячеек в одну.
В приведенном выше примере мы использовали формулу конкатенации, чтобы объединить ячейки месяца и продаж в один столбец.
ФОРМУЛА
= Объединить (ячейка1, ячейка2)
LEN
Это просто еще одна функция для анализа данных, которая используется для расчета количества символов в данной ячейке.
Эта формула пригодится, когда вы пытаетесь создать тексты с ограничениями на количество символов и при попытке определить различия между различными уникальными идентификаторами (UID).
= Лен (ячейка)
COUNTA
Если вы стремитесь стать аналитиком данных, вам необходимо знать, что в своей карьере вы почти ежедневно будете сталкиваться с неполными наборами данных. Чтобы решить эту проблему, вам пригодится формула COUNTA in excel. Формула определяет, пуста ячейка или нет. Это позволяет пользователю оценивать пробелы в наборе данных без реорганизации данных.
ФОРМУЛА
= COUNTA (ячейка)
ВПР
Формула ВПР используется для сопоставления данных из таблицы с входными данными. ВПР предлагает два режима сопоставления: точное и приблизительное. Эти два режима контролируются диапазоном поиска.
Теперь вам может быть интересно, какая роль является точным и приблизительным предложением.
Что ж, если вы установите для диапазона значение ИСТИНА, тогда он будет искать приблизительное совпадение, но если вы установите диапазон в значение ЛОЖЬ, тогда он будет искать точное совпадение.
ФОРМУЛА
= ВПР (ПРОСМОТР-ЗНАЧЕНИЕ; ТАБЛИЦА_ARRAY; COL_INDEX_NUM; [RANGE_LOOKUP])
MINIFS / MAXIFS
MINIFS и MAXIFS аналогичны знанию минимального и максимального значения. Вам просто нужно установить критерии и дать им набор значений для работы. Затем он ищет минимальное и максимальное значения и сопоставляет их с установленными критериями.
ФОРМУЛА
= MINIFS (мин-диапазон, диапазон-критериев1, критерии1,…)
= МАКСЕСЛИМН (макс-диапазон, диапазон-критериев1, критерии1,…)
СРЕДНИЙ
Как следует из названия, функция используется для вычисления или поиска среднего значения для набора данных на основе одного или нескольких критериев. Среднее значение может быть разным для каждого критерия и набора значений.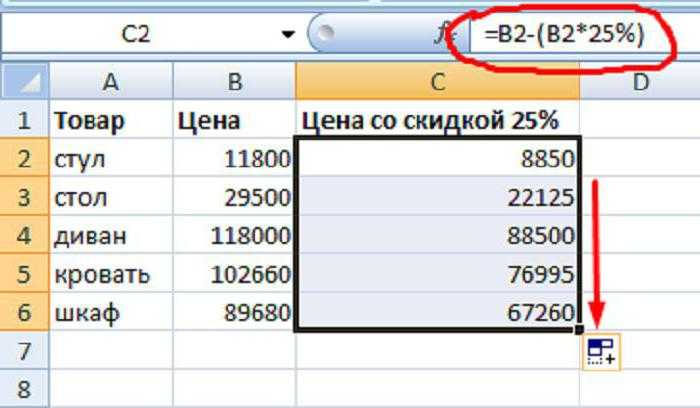
ФОРМУЛА
= СРЕДНЕЛИМН (средн_диапазон, диапазон-критериев1, критерий1,…)
СЧЁТЕСЛИМН
Функция СЧЁТЕСЛИМН может использоваться для подсчета количества экземпляров набора данных, соответствующих определенным критериям. Функция позволяет добавлять в запрос неограниченные критерии.
ФОРМУЛА
= СЧЁТЕСЛИМН (ДИАПАЗОН; КРИТЕРИИ1;….)
СУММПРОИЗВ
С помощью этой формулы вы можете умножать диапазоны или массивы, а затем возвращать сумму произведений. С помощью этой формулы вы можете рассчитать среднюю доходность, ценовые ориентиры и маржу.
ФОРМУЛА
= СУММПРОИЗВ (ДИАПАЗОН1; ДИАПАЗОН2) / ВЫБРАТЬ ЯЧЕЙКУ
НАЙТИ / ПОИСК
Если вы хотите изолировать определенный текст в наборе данных, можно использовать функцию НАЙТИ / ПОИСК. Обе функции одинаковы, но между ними есть одно существенное различие.
ФОРМУЛА
= НАЙТИ (ТЕКСТ; ВНУТРИ ТЕКСТА;[START-NUMBER])
= ПОИСК (ТЕКСТ; ВНУТРИ ТЕКСТА; [START-NUMBER])
ИНДЕКС / МАТЧ
Функция ИНДЕКС / ПОИСКПОЗ может использоваться для поиска конкретных данных на основе входных данных. Функцию ИНДЕКС / ПОИСКПОЗ можно использовать вместе, чтобы преодолеть ограничение, которое имеет ВПР. Когда вы используете ИНДЕКС / ПОИСКПОЗ вместе, они будут точно определять ссылку на данные и искать значение в одномерном массиве.
ФОРМУЛА
= ИНДЕКС (столбец данных, которые вы хотите вернуть)
= ПОИСКПОЗ (общая точка данных, которую вы пытаетесь сопоставить, столбец другого источника данных, имеющий общую точку данных, 0))
СУММЕСЛИМН
СУММЕСЛИМН — одна из известных формул Excel для анализа данных. Функция используется для вычисления суммы значений на основе нескольких критериев.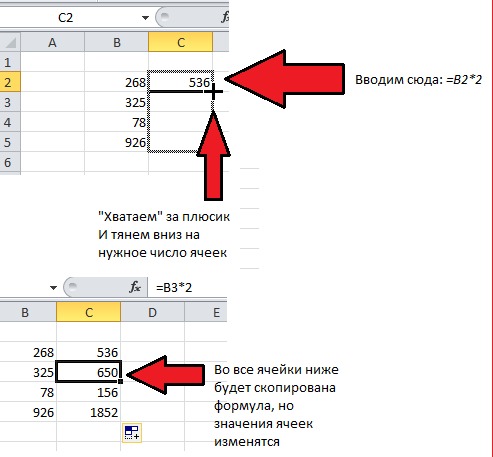
ФОРМУЛА
= СУММЕСЛИ (ДИАПАЗОН; КРИТЕРИИ;[SUM_RANGE])
КЛАССИФИЦИРОВАТЬ
Функция RANK используется для обозначения ранжирования значений в наборе данных в порядке возрастания или убывания.
ФОРМУЛА
= РАНГ (ЯЧЕЙКА; ДИАПАЗОН-ПРОТИВ;[ORDER])
Получив базовое представление о формулах Excel для анализа данных, теперь давайте сосредоточимся на некоторых расширенных формулах Excel для анализа данных.
ИМЕТЬ В ВИДУ()
ФОРМУЛА
= СРЕДНИЙ (число1;[num2],…)
МЕДИАНА ()
ФОРМУЛА
= МЕДИАНА (число1;[num2],…)
РЕЖИМ()
ФОРМУЛА
= РЕЖИМ (число1;[num2],…)
НИЖЕ()
Функция LOWER заменяет символы верхнего регистра на символы нижнего регистра.
ФОРМУЛА
= НИЖНИЙ (текст)
ВЕРХНИЙ ()
Функция UPPER заменяет символы нижнего регистра на символы верхнего регистра.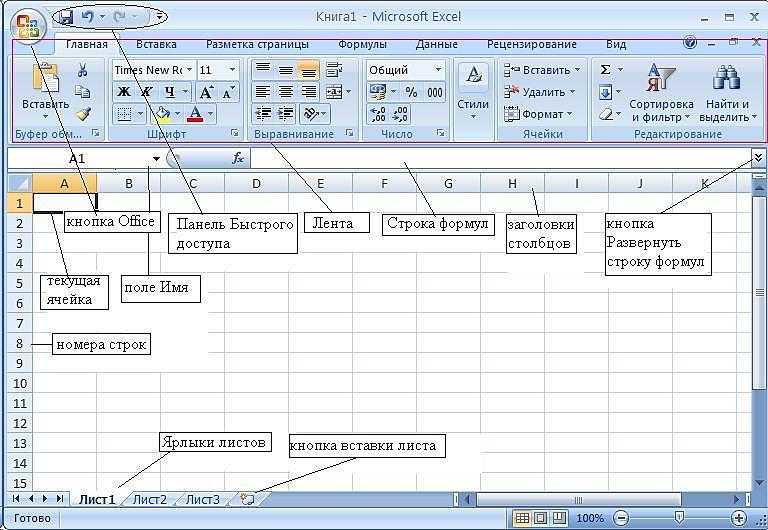
ФОРМУЛА
= ВЕРХНИЙ (текст)
ПРАВИЛЬНЫЙ()
Правильная функция делает первый символ буквы или слова заглавным или прописным, а остальную часть символа — строчными.
ФОРМУЛА
= PROPER (текст)
ПОДРЕЗАТЬ()
Функция TRIM удаляет ненужные пробелы между словами в строке.
ФОРМУЛА
= ОБРЕЗАТЬ (текст)
WEEKNUM ()
Функция WEEKNUM используется для извлечения определенного числа недели в конкретную дату.
ФОРМУЛА
= WEEKNUM (s.no,[return-type])
РАБОЧИЙ ДЕНЬ()
Функция РАБДЕНЬ используется для вывода даты рабочего дня, только если указано количество дней.
ФОРМУЛА
= РАБДЕНЬ (s.no,[return-type])
NETWORKDAYS ()
Функция ЧИСТРАБДНИ дает количество рабочих дней, если указаны два предоставленных дня. Он рассчитывает рабочие дни между этими двумя предоставленными днями, исключая выходные и праздничные дни, если таковые имеются.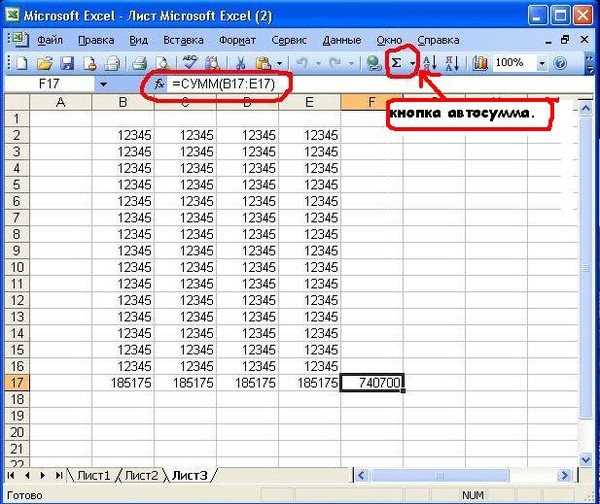
ФОРМУЛА
= ЧИСТРАБДНИ (дата начала, дата окончания, [holiday])
YEARFRAC ()
YEARFRAC — это функция, которая позволяет пользователю узнать долю года, только если указаны две даты.
ФОРМУЛА
= ГОД (дата начала, дата окончания, [basis])
ДАТА ()
Он дает конкретную еду только тогда, когда вы указываете или упоминаете количество дней после определенной даты.
= ДАТА (дата начала, месяцы)
ТИП()
Функция TYPE дает числовой код в качестве вывода, когда вы передаете тип данных внутри этой функции.
ФОРМУЛА
= ТИП (значение)
ЗАКЛЮЧЕНИЕ
Эти формулы Excel для анализа данных очень вам помогут. Хотя это некоторые основные формулы, но они сделают свою работу. Некоторые более сложные формулы помогут вам в серьезном анализе данных. Но упомянутые выше функции помогут вам выполнить большую часть вашей работы.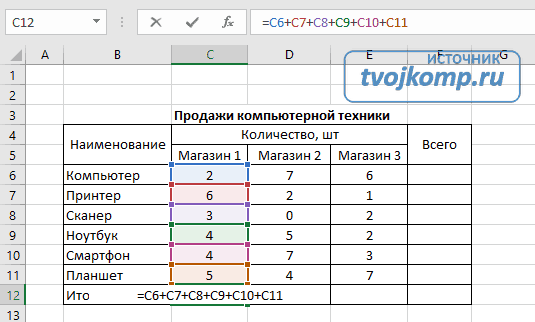
Выберите верное утверждение
a) Chl a представляет собой сине-зеленый пигмент с
Если вы видите это сообщение, это означает, что JavaScript отключен в вашем браузере , включите JS , чтобы это приложение заработало.Получение изображения
Пожалуйста, подождите…
Вопрос:
Решение:
Ответ:(b)
Связанный ответ
Связанный ответ
Хл b и фикоцианин
(b) Chl a, Chl c, фикоцианин и фукоксантин
(c) Chl a, Chl b, каротины и ксантофиллы
(г) Хл а и фукоксантин
More Related Question & Answers
3.0k LIKES
3.0k VIEWS
1.5k SHARES
3.0k LIKES
3.
0k VIEWS1.5k SHARES
3.0k LIKES
3.0k VIEWS
1.5 K Акции
3,0K Like
3,0K просмотр
1,5K Акции
3.0K Like
3,0K просмотр
1,5K Акции
3,0K Likes
3,01K
3,0K Likes
3,0KS
3,0K. k НРАВИТСЯ
3,0K Просмотр
1,5K Акции
3,0K, как
3,0K Просмотр
1,5K Акции
3.0K Like
1.5K Шарес.
1,5K Акции
3,0K Like
3,0K просмотр
1,5K Акции
3,0K Like
3,0K VIVERS
1,5K SHARES
3,0K Like
1,5K SHARES
3,0K Like
1.
01.01.01.01.5.0101.014 9001,014.3.0k НРАВИТСЯ
3,0K Просмотр
1,5K Акции
3,0K Нравится
3,0K Просмотр
1,5K Акции
3,0K Like
3,0K VIEW
1.5k SHARES
3.0k LIKES
3.0k VIEWS
1.5k SHARES
3.0k LIKES
3.0k VIEWS
1.5k SHARES
Disclaimer
The questions posted on the site are solely user generated , Doubtnut не владеет и не контролирует характер и содержание этих вопросов. Doubtnut не несет ответственности за какие-либо расхождения относительно дублирования контента по этим вопросам.
Похожие вопросы пользователей
Выберите правильное утверждение
а) Chl a – сине-зеленый пигмент с формулой C55H70O6N4Mg
б) Chl a is .
..
Растение обладает уникальным фотосинтетическим пигментом. Листья этого растения кажутся красновато-желтыми. …
Криптохром — это … …. [ Odisha 2006 ] а) поглощает желтый свет б) Пигмент криптогамов в) Красный …
В сине-зеленых водорослях Фотосистема II содержит важный пигмент, необходимый для фотолиза воды …
Что из следующего верно для хлорофилла цианобактерий ‘ Что из следующего вер…
Какого цвета фитохромный пигмент ‘ Какого цвета фитохромный пигмент ? а) Красный б) …
После проведения хроматографического разделения листа растения экспериментатор обнаружил ярко-синий …
Норман Борлоуг связан с … [ CBSE 2005 ] а) Белая революция б) Зеленая революция c) Blu…
Старые корни бобовых зеленеют из-за ….. ….. [C.P.M.T.1998]
а) Преобразование леггемоглобина .
..
Цветение зависит от … … [BHU 1990] а) Влажность почвы б) Кислотность почвы в) Фотопери…
Фотосинтетический пигмент, способный поглощать зеленый свет, это ? [БХУ 1997] а) фикоцианин б) Каротино…
Зеленый цвет Hydra viridis (Chlorohydra viridisima) обусловлен а) хлоропласты б) пигмент …
C55H70O6N4 Мг а) вспомогательный пигмент фотосинтеза б) Присутствует в PS-II в) Присутствует во всех…
Пигменты, присутствующие в Улотриксе: ? [РПМТ 2002] а) Хл а, Хл b и фикоцианин б) Chl a, Chl c, тел…
Гемоглобин (CB.S.E.1999) а) кровеносительство б) витамин в) Пигмент кожи г) дыхательный пигмент
Какой пигмент защищает растения от повреждения ультрафиолетом? Какой пигмент защищает растения от повреждения ультрафиолетом? …. …..
Водоросли с фотосинтезирующим пигментом обладают питанием ? .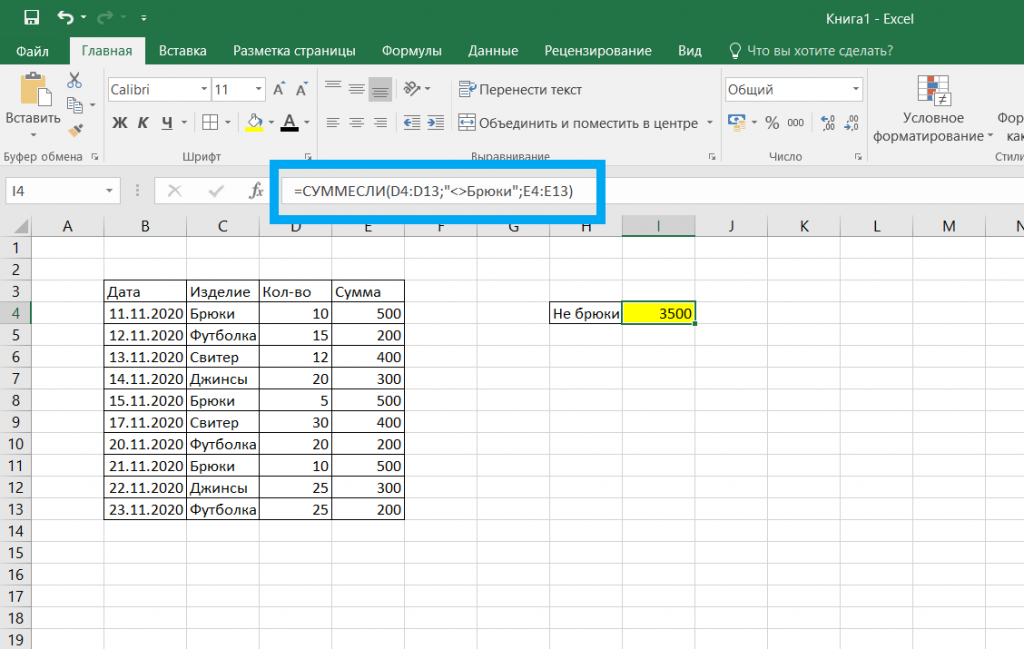
. [АМУ 1997]
а) голозой
б) сапрофитный
в)…
Большинство гликогенов при смешивании с йодом дает окраску, которая синий б) красный в) зеленый г) розовый
Рассмотрим следующие утверждения относительно молекулы хлорофилла а: (i) Молекулярная формула хлора…
Какое из следующих описаний неверно относительно хризофитов? Какое из следующих описаний…
Модели эквивалентности и прогнозирования НХЛ: Построение модели эквивалентности НХЛ (Часть 2) | Патрик Бэкон
Несколько незначительных обновлений устоявшейся концепции
В первой части книги «Эквивалентность НХЛ и модели прогнозирования перспектив» я сделал несколько ссылок на подсчет очков за пределами НХЛ. Это было бы легко измерить, если бы все проспекты играли в одной лиге. Было бы даже хорошо, если бы все они играли в небольшой горстке лиг, которые были бы достаточно похожи, чтобы сравнивать игроков в каждой из них, например, в трех лигах, составляющих КХЛ.
Анализ, на который я ссылался ранее, сравнивал результативность защитников во всех трех лигах КХЛ и рассматривал эти результативности как равные, и у меня не было особых проблем с этим, потому что все они довольно похожи.
Однако не все проспекты поступают из КХЛ или сопоставимых лиг. Возьмем, к примеру, Томаса Хертля, игрока первого раунда «Сан-Хосе» за год до Мирко Мюллера: Хертл провел весь свой год драфта в Чешской экстралиге, высшей мужской лиге Чехии, и набрал 25 очков в 38 играх ( 0,66 P/GP). Нападающий, который забивал с такой скоростью в любой из лиг КХЛ в свой драфт-год, может оказаться под угрозой полного исключения из драфта или, по крайней мере, ждать до следующего раунда, чтобы услышать свое имя. Но Хертл был выбран 17-м в общем зачете. И, в отличие от Мюллера, выбор Hertl заставил Сан-Хосе выглядеть очень умным; его карьера в НХЛ занимает 2-е место в WAR и 3-е место по очкам среди его драфт-класса, и он, безусловно, поднялся бы намного выше, чем 17-е место в повторном драфте.
Высокий отбор Хертла на драфте и последующий успех на уровне НХЛ не должны никого удивлять, потому что его результативность в год драфта была на самом деле лучше, чем у кого-либо еще в его драфтовой когорте. Его исходные показатели очков просто не отражали этого, потому что он играл в лиге, где было значительно сложнее забивать.
Откуда я знаю, что Хертл играл в лиге, где было сложнее забивать? Одного того факта, что он играл против взрослых мужчин, а не подростков, недостаточно, чтобы это подтвердить. В конце концов, в моей пивной лиге полно взрослых мужчин, но команда, полная худших подростков в ОХЛ, все равно зажжет нашу лучшую команду, если они сойдутся лицом к лицу. И хотя здравого смысла может быть достаточно, чтобы сказать нам, что Чешской Экстралиге лучше , чем в любой лиге КХЛ, и что результативность Хертла на драфте лучше, чем у форварда КХЛ, который забил с той же скоростью, мы не можем точно сказать, насколько лучше, или сравнить с игроками.
которые забили с разной скоростью в других лигах без измерения того, насколько хороша Чешская Экстралига и другие лиги.
Это подчеркивает необходимость модели эквивалентности: такой, которая определяет стоимость очка в любой данной лиге по всему миру. Я построил свою модель как эквивалент НХЛ (NHLe) по шкале 1 очка НХЛ, что означает, что если лига имеет значение NHLe 0,5, одно очко в этой лиге стоит 0,5 очка НХЛ.
«Классическая» модель НХЛ рассчитывает стоимость очка в одной лиге путем прямого сравнения того, как группа игроков набрала очки в одной лиге, с тем, как те же игроки набрали очки в НХЛ, как правило, в том же году или в следующем году. В «Эквивалентности лиг», одной из первых опубликованных работ на эту тему, Габриэль Дежарден изложил свой метод:
Изображение из «Эквивалентности лиг» Габриэля ДежарденаЧтобы определить качество АХЛ (или любой другой лиги), мы можем просто посмотреть на каждого игрока, который провел год один в низшей лиге и второй год в НХЛ и сравните их средние PPG. Другими словами, качество лиги по отношению к НХЛ составляет:
Эта методология сама по себе очень эффективна, но имеет три проблемы: что искажает его в пользу лиг с более молодыми игроками.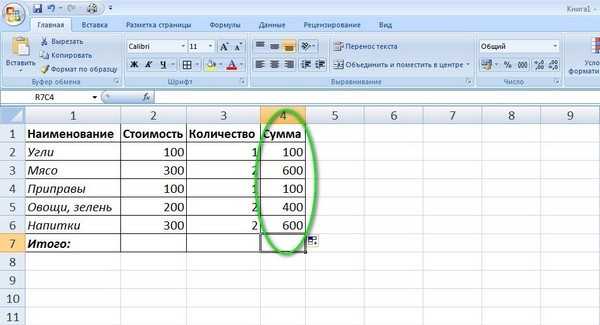
Если Лига А точно такая же, как Лига Б во всех отношениях, за исключением того, что Лига А полна более молодых игроков, то само собой разумеется, что импорт НХЛ из Лиги А претерпит большее развитие в период между 1 и 2 годами, чем импорт из Лиги Б, и таким образом, забить больше в год 2. Это приведет к тому, что модель ошибочно заявит, что в Лиге А сложнее забить гол, хотя на самом деле в ней есть более молодые игроки, которые лучше развиваются до того, как увидят НХЛ.
Кроме того, в то время как горстка лиг выпускает игроков НХЛ в следующем сезоне, многие из них производят настолько мало, что один выброс в любом направлении может сильно повлиять на окончательную оценку.Все три проблемы были решены в одном месте, когда CJ Turtoro опубликовал Network NHLe, превосходную статью, которую я рекомендую вам прочитать. ( В качестве примечания, я не могу отблагодарить CJ за все усилия, которые он приложил для публикации своей первоначальной работы, и за помощь, которую он оказал мне в моей. Такие люди, как CJ, которые не только обладают интеллектом и знаниями в предметной области, чтобы помогать другим, но кроме того, доброта и искренняя страсть, необходимые для этого, делают сообщество хоккейных аналитиков непобедимой армией ботаников, которые реже ошибаются.)
CJ решил первую проблему, используя только переходы между игроками, которые играли в двух лигах в том же году. (Я тоже так делал и никогда серьезно не рассматривал возможность многолетних переходов.
)
Он решил вторую задачу, разделив общую сумму очков в лиге на общую сумму сыгранных игр.
С третьей проблемой — которую я считаю самой большой из трех — он справился с помощью сетевого подхода, используя непрямые пути между лигами для определения относительной силы каждой из них. В следующем примере используются вымышленные данные с красивыми круглыми числами, чтобы объяснить, как рассчитывается один непрямой путь:
- 100 игроков играли в Лиге А и Лиге В в одном и том же году. Они набрали в общей сложности 1000 очков в 1000 играх в Лиге А (1,0 P/GP) и 500 очков в 1000 играх в Лиге B (0,5 P/GP). Чтобы определить «эквивалент Лиге B» лиги A, мы делим очки за игру в лиге B на очки за игру в лиге A, что дает
0,5/1,0 = 0,5. - 500 игроков играли в Лиге B и НХЛ за один и тот же год. Они набрали в общей сложности 1000 очков в 1000 играх в Лиге B (1,0 P/GP) и 200 очков в 1000 играх в НХЛ (0,2 P/GP). Мы следуем той же методологии, изложенной выше, для расчета эквивалентности Лиги B в НХЛ:
0,2/1,0 = 0,2.
- Мы знаем, что Лига А имеет «Эквивалентность Лиге B» 0,5, а Лига B имеет эквивалентность НХЛ 0,2. Чтобы определить эквивалент Лиги А в НХЛ, мы просто умножаем эти два значения друг на друга:
0,5*0,2 = 0,1. В этом пути указано, что очко в Лиге А стоит 0,1 очка НХЛ.
Чтобы эта методология работала, игрокам не нужно играть в лиге А и НХЛ в одном сезоне. Пока между ними есть связующая лига, значение NHLe может быть рассчитано для лиги A.
Вот пример реальной дорожки, которая начинается с КХЛ и использует АХЛ как связующее звено:
В данном случае игроки, игравшие в КХЛ и АХЛ в один и тот же год, набрали в сумме 1,63 очка. выше в АХЛ, чем в КХЛ. Это означает, что коэффициент «эквивалентности АХЛ» для КХЛ здесь будет равен 1,63. Между тем, игроки АХЛ, которые играли в НХЛ в том же году, забили в НХЛ в 0,38 раза больше, чем в АХЛ. Перемножив эти два значения вместе, мы получим значение 0,63, которое является «NHLe» для КХЛ для этого конкретного пути.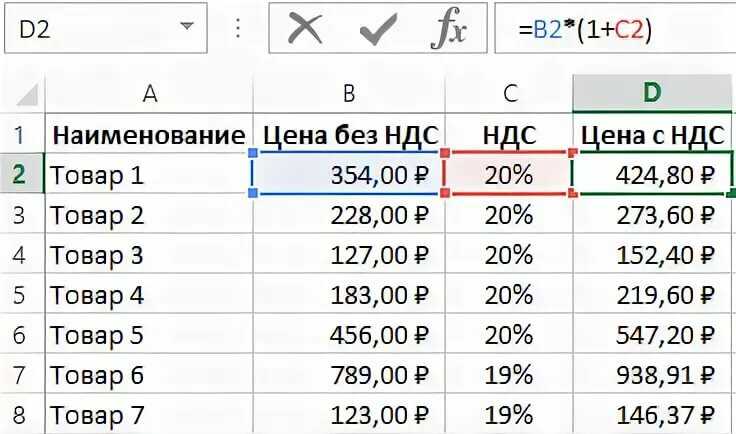
Однако не на всех путях есть ровно одна соединительная лига. В некоторых путях их нет, и они по-прежнему полностью действительны, например, путь из КХЛ напрямую в НХЛ:
Некоторые, например путь от J18 Allsvenskan в НХЛ, включают более одной связующей лиги:
Методология лиг с более чем одним разъемом остается прежним: рассчитайте коэффициент преобразования для каждой лиги в следующую, а затем умножьте значения друг на друга. В этом случае коэффициент преобразования между J18 Allsvenskan и Дивизионом-1 (теперь известным как HockeyEttan) составляет 0,34, коэффициент преобразования между Дивизионом-1 и SHL составляет 0,1, а коэффициент преобразования между SHL и NHL составляет 0,33. Умножьте эти 3 значения, выполнив 0,34 * 0,1 * 0,33 = 0,012 , и результат показывает, что ценность очка в J18 Allsvenskan составляет около 0,012 очка в НХЛ. (Обратите внимание, что эти значения округлены, и если вы вручную выполните эти расчеты с округленными значениями, вы получите немного другой результат.
)
То, что я показал до сих пор, — это просто методология расчета один путь. Но в отличие от классического NHLe, где единственным путем является единственный путь без соединителей, в Network NHLe могут быть десятки, если не сотни путей! Это вызывает больше вопросов:
- Как мы определяем верхний путь для использования?
- Как только мы определили верхний путь, должны ли мы использовать только его или несколько? Если больше, то сколько?
- Все ли пути действительны, или мы должны исключить пути с незначительным размером выборки переходящих игроков?
- Присваиваем ли мы разные веса разным показателям эквивалентности, полученным на каждом пути, или просто усредняем их все?
В ответах на (некоторые из) этих вопросов мой NHLe отличается от ответа Турторо, который дал следующие ответы на каждый из них: 9(Подключения) * MinimumInstances
Где Connections — это количество подключений (включая последнее подключение к NHL), которые составляют путь, а MinimumInstances — это минимальное количество переходных игроков, которые составляют экземпляр внутри пути.
.
Это может показаться немного сложным, поэтому вот пример взвешивания трех путей для КХЛ:
- Первый путь здесь КХЛ->АХЛ->НХЛ. Этот путь имеет 2 соединения. Соединение КХЛ->АХЛ имеет 65 случаев перехода, а соединение АХЛ->НХЛ — 2876. Это означает, что наименьшее количество экземпляров в любом соединении для этого пути равно 65, а вычисление веса этого пути равно 9.(3) * 56 = 7 .
Со значениями и весами NHLe для каждого пути процесс расчета окончательного значения лиги становится довольно простым: умножьте каждое значение NHLe на вес его пути, возьмите сумму этих выходных данных, а затем разделите их на сумму веса. В этом случае расчет равен ((0,63*16,25)+(0,83*13)+(0,85*7))/(16,25 + 13 + 7) = 26,98/36,25 = 0,74 . Если бы мы использовали только эти 3 пути, итоговый НХЛ для КХЛ был бы 0,74.
Я думаю, что каждый ответ, который CJ дал на эти вопросы, подкреплен веским обоснованием. Я мог бы ответить на эти проблемы по-другому, если бы начинал с нуля, но моя цель здесь заключалась не просто в том, чтобы скопировать процесс CJ и принять несколько произвольных решений, чтобы изменить то, что мне не нравилось.
Моя цель состояла в том, чтобы собрать воедино набор возможных ответов на эти вопросы, которые все имели для меня смысл, а затем проверить каждый из этих ответов друг на друга и на CJ в надежде определить оптимальный набор параметров моделирования для построения сети NHLe. модель. Вот различные наборы параметров, которые я решил протестировать в качестве ответа на каждый вопрос:
Для определения лучшего(их) пути(ов):
- Выберите путь, который будет иметь наибольший вес в соответствии с весовым уравнением, изложенным выше.
- Выберите путь с наименьшим количеством соединяющихся лиг, используя наибольший вес в соответствии с уравнением взвешивания в качестве тай-брейка.
- Выберите путь с наибольшим минимальным количеством экземпляров среди всех подключений.
Для определения количества используемых путей:
- Протестируйте выбор только одного лучшего пути путем выбора до 15 лучших путей.
Для исключения путей на основе размера выборки:
- Протестируйте выбор путей с минимум 1 экземпляром путем выбора путей с минимум 15 экземплярами.
Для взвешивания каждого пути:
- Здесь я просто использовал формулу взвешивания CJ. Я ненадолго опробовал несколько разных методов, но его результаты оказались лучше в предварительных тестах и просто имели слишком много смысла.
Кроме того, я решил проверить еще 3 параметра:
- Включая чемпионаты мира среди юниоров до 20 и 18 лет.
- Изменение метода расчета коэффициента преобразования между двумя лигами. Я проверил метод CJ по использованию полной суммы очков в каждой лиге, метод Дежардена по использованию среднего значения очков за игру в каждой лиге и мой собственный метод (предложенный CJ) по использованию медианы очков за игру в каждой лиге. .
- Удаление первой соединительной лиги на одном пути перед созданием нового пути для этой лиги. Например, если используется путь КХЛ->АХЛ->НХЛ, все остальные пути для КХЛ с этого момента не могут использовать АХЛ в качестве первого соединения. (Первоначальная реализация этого правила была на самом деле несчастным случаем, вызванным тем, что я неверно истолковал методологию CJ, но в итоге я оставил его в качестве тестового параметра, потому что подумал, что может быть предпочтительнее не придавать слишком большое значение каким-либо прямым отношениям для данной лиги. )
)С набором параметров, которые я все счел подходящими для построения окончательной модели, пришло время протестировать каждый из них и определить лучший. Я решил, что целью моих тестов будет минимизация средней абсолютной ошибки между прогнозируемыми очками за игру и фактическими очками за игру для всех игроков, перешедших из одной лиги в другую. Прогнозируемые очки за игру рассчитывались на основе значения NHLe для каждой лиги и количества очков за игру в первой из двух лиг, причем значения NHLe были получены после построения модели с заданным набором параметров.
Я знаю, что только что бросил вам словесный салат, но процесс тестирования на самом деле довольно прост; Расскажу на примере Мелькера Карлссона в 2010 году:
- В этом сезоне Мелькер набрал 35 очков в 27 играх (1,3 Б/ГП) в суперэлите и 2 очка в 36 играх в ВХЛ (0,06 Б/ГП). ГП).
- Если бы модель NHLe, полученная из заданного набора тестовых параметров, утверждала, что значение NHLe для SHL равно 0,53, а значение для суперэлиты равно 0,08, то мы могли бы получить коэффициент преобразования из суперэлиты в SHL, выполнив
0,08/0,53 = 0,15. - Затем мы умножаем коэффициент пересчета на его результативность в суперэлите и выполняем
0,15*1,3 = 0,2, что дает нам прогнозируемую результативность в SHL. Его фактическая результативность в SHL составила 0,06, а абсолютное значение разницы между 0,06 и прогнозируемой результативностью 0,2 равно 0,14, что и является ошибкой, полученной для данного конкретного перехода. - Затем мы повторим этот процесс, используя его результаты в SHL, чтобы предсказать его результат в суперэлите, выполнив
0,53/0,08 = 6,625, чтобы получить коэффициент пересчета из SHL в суперэлиту, а затем выполнить6,625 * 0,06 = 0,4, чтобы получить прогнозируемый коэффициент результативности в суперэлите. - Поскольку его фактическая результативность в суперэлите составляла 1,3 P/GP, ошибка между этим значением и его прогнозируемой результативностью 0,4 составила бы 0,9. В заключение, этот один переход даст нам два значения ошибки: 0,14 и 0,9.
- Средняя абсолютная ошибка для данной модели NHLe — это среднее значение всех значений ошибок, полученных от игроков, перешедших из одной лиги в другую.
Набор данных, который я использовал для проведения этих тестов и построения моей модели, включал всех фигуристов, сыгравших не менее 5 игр в любых двух или более из 124 лиг, которые я использовал в любом отдельном сезоне с 2005–2006 по 2019–2020 годы. за исключением 2012–2013 гг. (2012–2013 годы были полностью удалены из-за изменения глобального качества конкуренции, вызванного локаутом НХЛ.) Я не мог просто обучить свою модель NHLe, используя эти наборы параметров на всем наборе данных, один раз, а затем протестировать ее на том же самом наборе данных. данные, поскольку моей целью не было найти точный набор параметров, которые могли бы наилучшим образом предсказать то, что уже произошло; Моя цель состояла в том, чтобы построить модель, которая могла бы наилучшим образом предсказать оценку вне выборки. Способ обучить его этому заключался в том, чтобы «попрактиковаться» в прогнозировании результатов за пределами выборки. Я сделал это к случайным образом разделил мой набор данных на пятые части и выполнил 5-кратную перекрестную проверку.
5-кратная перекрестная проверка может показаться пугающей, но это не так уж и страшно. Вы начинаете с тренировочного набора, который состоит из 4/5 пар лиг в наборе данных, и тестового набора, который содержит другую 1/5 часть пар игроков. Для каждого отдельного набора параметров модель NHLe строится на обучающем наборе, а затем тестируется на тестовом наборе. Затем этот процесс повторяется еще четыре раза с использованием других групп обучающих наборов и тестовых наборов, в результате чего для каждого набора параметров получаются пять разных тестовых значений. (Обратите внимание, что ни один из наборов тестов/поездов не перекрывается; каждая пара отдельных игроков появляется ровно один раз в одном тестовом наборе и ни в одном из четырех других тестовых наборов, и та же самая пара игроков появляется один раз в других 4 наборах поездов, для которых она не используется. появляются в соответствующем тестовом наборе.) Вот пример того, как будет выглядеть перекрестная проверка с пятью поддельными игроками, где красная подсветка указывает на тестовый набор, а зеленая — на набор поездов:
Перекрестная проверка для каждой складки выполняется с использованием каждого возможного набора параметров для построения модели на обучающем наборе и проверки ее на тестовом наборе.
После завершения перекрестной проверки для всех 5 кратностей среднее значение теста получается для каждого набора параметров. Набор параметров с лучшим средним тестовым значением (в данном случае с наименьшей средней абсолютной ошибкой) считается оптимальным набором параметров для построения модели NHLe.
Результаты моей 5-кратной перекрестной проверки определили следующий набор параметров как наиболее оптимальный:
- Верхним доступным путем будет тот, у которого наименьшее количество ребер, а общий вес используется для разрешения конфликтов, если два пути имеют одинаковое количество ребер.
- До 11 лучших путей будут использоваться для лиги.
- Действительны пути с минимум 8 переходами игроков; все остальные будут отброшены.
- Будут использоваться юниоры мира (как U18, так и U20).
- Полная сумма очков будет разделена на полную сумму игр, сыгранных в каждой лиге, чтобы определить коэффициент пересчета между двумя лигами.
- Первая соединительная лига будет навсегда удалена, прежде чем будут созданы какие-либо дальнейшие пути.
Среднее значение средней абсолютной ошибки по этим пяти кратностям составило 0,33. (Я также вычислил R², который также был равен 0,33, но решил не использовать его в качестве целевого параметра в обучении.)
После установки этих параметров пришло время построить модель, используя весь набор данных на этот раз. Это оценки эквивалентности для каждой лиги для окончательной модели NHLe:
╔══════════════════╦═══════╗
║ Лига ║ nhle ║
╠═════════════ ═════╬═══════╣
║ nhl ║ 1 ║
║ Khl ║ 0,772 ║
║ Чехия ║ 0,583 ║
║ SHL ║ 0,566 ║
║ NLA ║ 0,459 ║
║ Liiga ║ 0,441 ║ ║ 0,459 ║
║ ahl ║ 0,389 ║
║ del ║ 0,352 ║
║ allsvenskan ║ 0,351 ║
║ VHL ║ 0,328 ║
║ Словакия ║ 0,295 ║
║ rebel ║ 0,26999 ║ 0,295 ║
║ 0,269 ║ 0,295 ║
║ 0,269 ║ 0,295 ║
.║
║ WJC-20 ║ 0,269 ║
║ Франция ║ 0,250 ║
║ Беларусь ║ 0,242 ║
║ Czech3 ║ 0,240 ║
║ ║
║ 0,20 ║ 9040 ║ 0,20 ║
║
║
║
║
║ 0,235 ║
║
║
║
║
║
║
║
║
║
║
║
║
║
║
.
║ NCAA ║ 0,194 ║
║ Дания ║ 0,190 ║
║ MESTIS ║ 0,178 ║
║ NLB ║ 0,176 ║
║ Италия ║ 0,176 ║
║ 907333 3 ║
║ 0,173333 3 904 ║ ║ 9043 ║ 9043 ║ 9043 ║ 9043 ║ 9043 ║ ║ 9043 ║ ║ ║ 9043 ║
║
║ 9043 ║
║ 0,173 3
║
║ 9043 ║
║
║
║ 0,173 3
0419 ║ OHL ║ 0.144 ║
║ MHL ║ 0.143 ║
║ USHL ║ 0.143 ║
║ WHL ║ 0.141 ║
║ Poland ║ 0.135 ║
║ WJC-18 ║ 0.135 ║
║ Russia3 ║ 0.135 ║
║ Usports ║ 0.125 ║
║ USDP ║ 0,121 ║
║ Qmjhl ║ 0,113 ║
║ Дивизион 1 ║ 0,109 ║
║ Чех4 ║ 0,104 ║
║ ERSTE-LIGA ║ 0,103 ║
║ Slovakia2 ║ 0,1019 ║
║
║ 0,1019 ║
║ 0,1019 ║
║ 0,1019 ║
║ 0,1019 ║ 0,1019 ║
║
║
║
.9 ║
║ Superelit ║ 0.091 ║
║ NAHL ║ 0.087 ║
║ Germany3 ║ 0.085 ║
║ ALPSHL ║ 0.
║ U20 SM-Liiga ║ 0.083 ║
║ BCHL ║ 0.080 ║
║ NMHL ║ 0.076 ║
║ Czech -U20 ║ 0,074 ║
║ AJHL ║ 0,062 ║
║ EJHL ║ 0,060 ║
║ Чеш U19 ║ 0,059 ║
║ Swissdiv1 ║ 0,054 ║
║
║ Swissdiv1 ║ 0,054 ║
║
. 0,049║
║ CCHL ║ 0,048 ║
║ MJHL ║ 0,046 ║
║ USPHL-PREMIER ║ 0,046 ║
║ Slovakia-U20 ║ 0,044 ║
║ russia-u17 ║ 0,044444 ║
║ 9044 ║
║ 9044 ║
. Sarja ║ 0,040 ║
║ naphl-18U ║ 0,039 ║
║ Чехия U18 ║ 0,038 ║
║ J18 allsvenskan ║ 0,038 ║
║ 0,038 ║
║
║ 0,038 ║
║
║ 0,038 ║
║
║ 0,038 ║
. 0,035 ║
║ ОЖХЛ ║ 0,034 ║
║ HPHL-16U ║ 0.034 ║
║ Slovenia ║ 0.033 ║
║ Russia-U18 ║ 0.032 ║
║ 16U-AAA ║ 0.031 ║
║ J18-Elit ║ 0.029 ║
║ USHS-Prep ║ 0.028 ║
║ QMAAA ║ 0,028 ║
║ CISAA ║ 0,027 ║
║ Норвегия2 ║ 0,027 ║
║ USPHL-16U ║ 0,027 ║
║ GOJHL ║ 0,027 ║
║ AYHL-10 ║ 0,026 ║ 0,027 ║
║ yhl-25 0,024 ║
║ УШС-МН ║ 0,024 ║
║ DNL ║ 0,024 ║
║ Дамания2 ║ 0,023 ║
║ Vijhl ║ 0,021 ║
║ NOJHL ║ 0,021 ║
║ Slovakia-U18 ║ 0,020 ║
║
║ 0,020 ║
║
║
║ 0,020 ║
║ 0,020 ║ 0,021 ║
║ 0,021 ║ 0,021 ║
║ 0,021 ║ 0,021 ║
║ 0,021.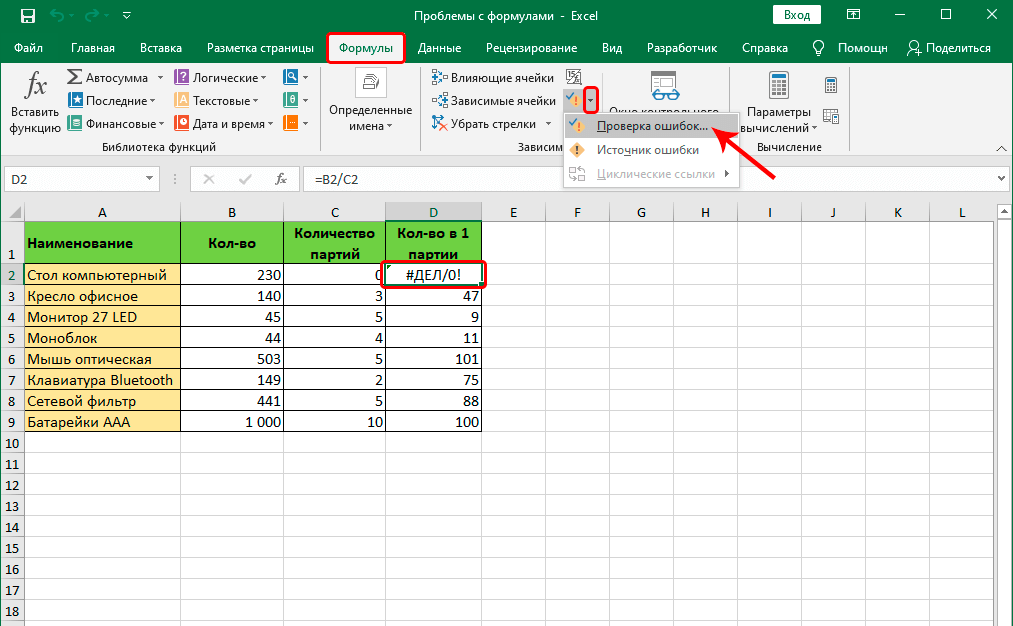
║ kijhl ║ 0,020 ║
║ u17-elit ║ 0,018 ║
║ II-дивизиона ║ 0,018 ║
║ U20-Top ║ 0,017 ║
║ 0,0119.019.019.0119.019.019.019.019.019.019.019.019.019.019.019.019.019.019.019.019.019.019.019.019.019.019.019.019.019.019.019.019.019.019.019.019.019.019.019.019.019.019.019 ║
. ║
║ Czech U16 ║ 0.014 ║
║ Denmark-U20 ║ 0.013 ║
║ MMHL ║ 0.013 ║
║ U16 SM-Sarja-Q ║ 0.012 ║
║ GTHL-U16 ║ 0.012 ║
║ J20-Div.1 ║ 0.011 ║
║ U16-SM ║ 0,011 ║
║ U16-ELIT ║ 0,010 ║
║ Alliance-U16 ║ 0,009 ║
║ GTHL-U18 ║ 0,008 ║
║ J18-DIV.1 ║ 0,008 ║
║ 40419 ║ J18-DIV.1 ║ 0,008 ║
║
.
║ QMEAA ║ 0,007 ║
║ J20-Div.2 ║ 0,007 ║
║ Дания-U17 ║ 0,006 ║
║ U16-Div.1 ║ 0,005 ║
║ J18-Div.2 ║ 0,005 ║
║ etahl U18 ║ 0,005 ║
║ AMMHL ║ 0,005 ║
║ QBAAA ║ 0,004 ║
║
║ QBAAA ║ 0,004 ║
║
. .2 ║ 0,002 ║
╚══════════════════╩═══════╝
║ 
084 ║ 
Обратите внимание, что некоторые из этих лиг объединены с другими лигами.
Например, до появления КХЛ в базе данных EliteProspects была лига, известная как «Россия», которая фактически называлась КХЛ; Я просто объединил эти два понятия в КХЛ. То же самое касается и «России2», и ВХЛ, и еще одной-двух лиг.
Я упоминал об этом ранее, когда упомянул, что никогда не видел игры Мирко Мюллера, когда «Шаркс» выбрали его в 2013 году, но позвольте мне быть предельно ясным: я не перспективный человек . Я болею за «Шаркс» всю свою жизнь и более десяти лет внимательно слежу за НХЛ, но я никогда не обращал пристального внимания ни на какую другую лигу, а это значит, что у меня нет четкого представления о том, как это положено смотреть. Недостаток моего опыта работы с потенциальными клиентами имеет несколько плюсов и минусов:
- Pro: У меня нет предвзятых мнений об определенных лигах, поэтому я не пытаюсь подтвердить какие-либо предубеждения при построении модели.
- Против: Без представления о том, как все должно выглядеть, мне гораздо сложнее выявлять баги и ошибки в моем коде, а затем устранять и исправлять их, когда мне это удается. Эта проблема в основном связана со временем, потраченным на мою сторону, поскольку окончательная модель, насколько мне известно, не содержит ошибок и ошибок.
- Pro: Знание того, что модель может быть не только очень плохой, но и то, что я не смог бы идентифицировать ее невооруженным глазом, если бы это было так, побудило меня применить очень надежный математический подход, чтобы убедиться, что модель действительно хороша. .
- Con: Мне сложнее понять и выразить ограничения моей работы, особенно с практической точки зрения. Например, я могу посмотреть на результаты моей модели WAR и сказать: «Это переоценивает Микко Рантанена и недооценивает Натана Маккиннона, потому что обычно переоценивает финишера в таких дуэтах, а я достаточно их посмотрел, чтобы понять, что Маккиннон намного лучше. ” Мне гораздо труднее выразить (или даже понять), почему моя модель NHLe переоценивает европейские мужские лиги и недооценивает юношеские лиги, хотя это мое общее впечатление.
Эта проблема в основном связана со временем, потраченным на мою сторону, поскольку окончательная модель, насколько мне известно, не содержит ошибок и ошибок.