Динамический массив это: Динамический массив данных: что это, как создать

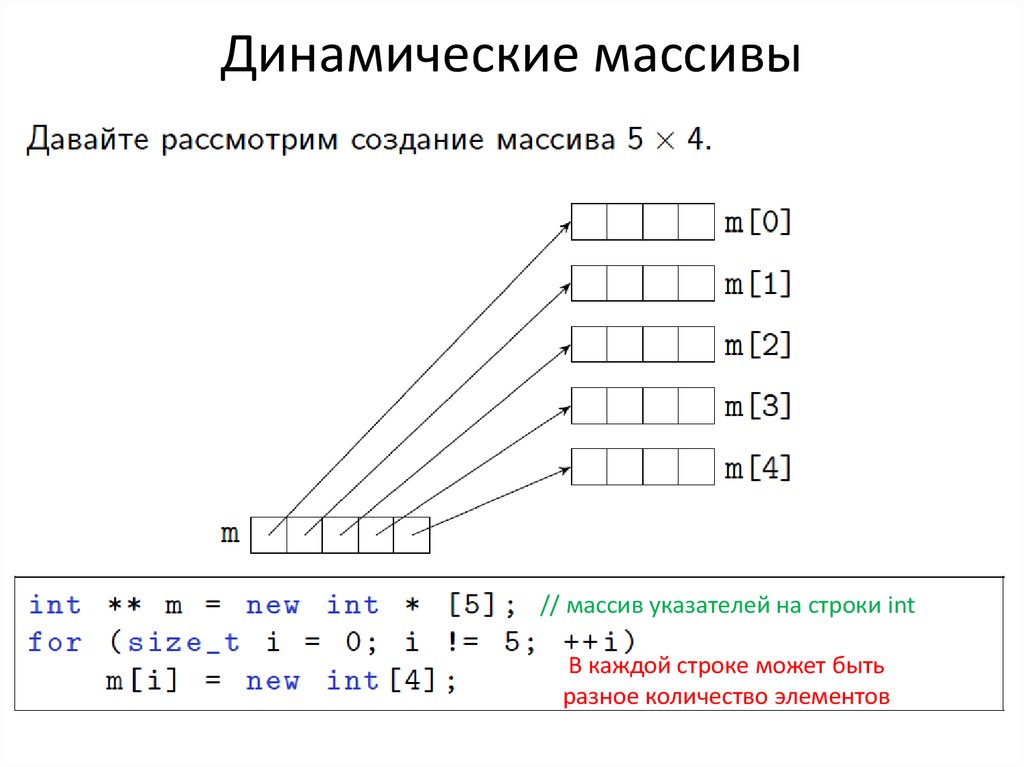
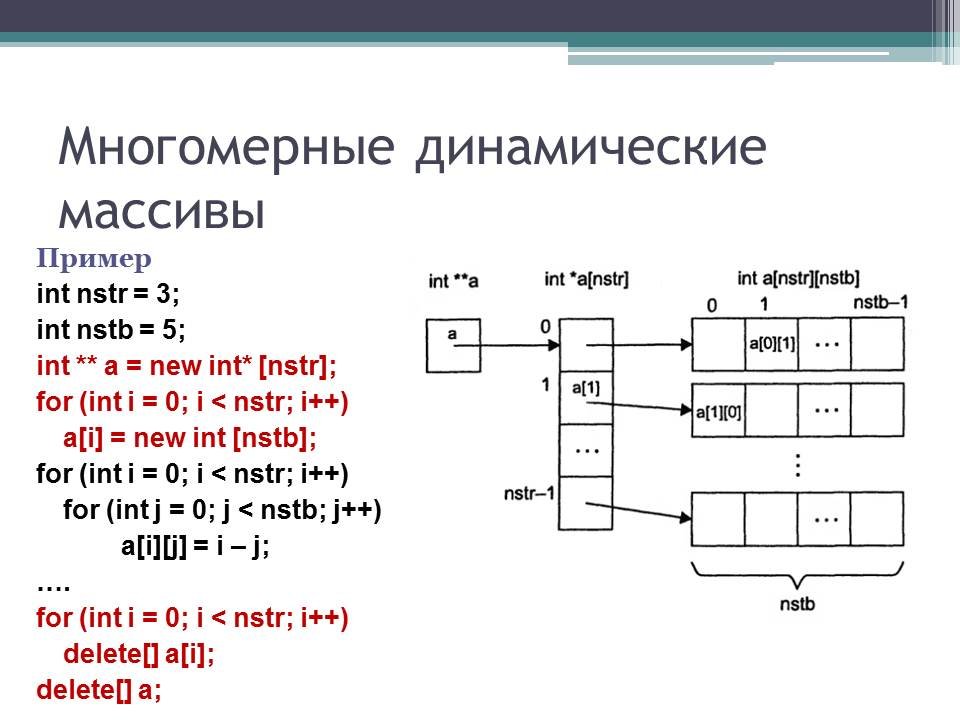
теория веб-разработки – Skillfactory media

Статья посвящена одной из основных структур данных в веб-разработке — динамическим массивам данных (dynamic arrays). В отличие от…

Статья посвящена одной из основных структур данных в веб-разработке — динамическим массивам данных (dynamic arrays). В отличие от простых массивов, их размер определяется при выполнении кода, что избавляет программиста от утомительной необходимости планировать распределение памяти (языки C, мы смотрим в вашу сторону).

Мы расскажем, для чего используется эта структура данных и как она реализована в Python с технической точки зрения. Эти знания помогут всем желающим выбрать оптимальный инструмент для решения множества типичных проблем и изучить (самостоятельно или на нашем курсе) программирование на Python.

Введение в динамические массивы

Динамические массивы применяются в ситуациях, когда разработчик не знает точно, сколько памяти ему потребуется в тот или иной момент.

Они позволяют гибко менять используемый объем ресурсов и освобождать ненужные ячейки. Эти процессы происходят автоматически, поэтому такие массивы и называются динамическими.

Благодаря этой структуре данных программа может занимает в памяти ровно тот объем, который ей необходим для хранения конкретных данных. Представим, что вам нужно сгенерировать список пользователей, которые соответствуют каким-то критериям. Вы не знаете, сколько их будет — 10, 50, 100? Если ошибиться в меньшую сторону, код не будет работать. Если перестраховаться и зарезервировать избыточное место (например, сразу на 1000 пользователей), без ресурсов могут остаться приложения, которым они действительно нужны. Однако с использованием динамических массивов вы забываете обо всех трудностях.

Курс

Python для веб-разработки

Авторская программа от эксперта-практика. После обучения вы сможете в одиночку создавать и поддерживать сайты. Скидка по промокоду BLOG 5%.

Узнать больше

Еще одна проблема, которую решается таким образом — это фрагментация памяти. В своей работе веб-разработчики нередко сталкиваются с ситуацией, когда ресурсов вроде бы должно быть достаточно, однако программа начинает сбоить. Причина в том, что в какой-то момент ей нужен один большой кластер памяти, а свободные ячейки оказываются распределены по нескольким участкам. При использовании динамических массивов система оптимально формирует блоки и эффективно освобождает ненужные площади.

Вопросы производительности

Функционально динамический массив соответствует статистическому, открывая при этом ряд удобных возможностей. Время уточнения или изменения значения любого элемента массива не зависит от его расположения. При последовательном переборе элементов,  время операции возрастает в линейной прогрессии, а ресурсы кеша расходуются максимально эффективно. То же самое справедливо для добавления или удаления элементов в середине массива. На проведение этих же операций с элементами в конце массива уходит постоянное амортизированное время, то есть в отдельные моменты скорость падает, однако общая производительность остается на уровне константы.

Если вы уже проштудировали руководство по веб-разработке, вы наверняка сравните динамические массивы со связными списками — они также позволяют менять содержимое без лишних затрат ресурсов. Однако массивы обеспечивают лучшие показатели индексирования и перебора элементов. С другой стороны, они несколько проигрывают в скорости добавления данных — если в списке достаточно изменить внутренние ссылки, то содержимое массива приходится двигать в памяти целиком. Для решения этих проблем применяются буферные окна (gap buffers) и многоуровневые векторы (tiered vectors).

Взгляд за кулисы

Теперь рассмотрим, какая механика стоит за всеми этими операциями — как именно Python создает динамические массивы и как меняет их размер. Для начала практическая демонстрация этого механизма.

import sys # этот модуль позволит нам использовать функцию для определения точного объема, который программа занимает в памяти

n = 10 # задаем пороговое значение

data = [] # создаем пустой список

for i in range(n): 

a = len(data) # количество элементов

b = sys. getsizeof(data) # объем памяти

print (‘Length:{0:3d}; Size of bytes:{1:4d}’.format(a, b))

data.append(n) # увеличиваем размер на единицу

После выполнения кода мы видим следующую картину (рамками обозначены границы выделенных блоков памяти):

По этой таблице можно понять принцип, которому Python следует при выделении ресурсов. Первые два дополнительных блока содержат по четыре ячейки. После того, как программа последовательно занимает эти пространства, интерпретатор делает вывод о ее ресурсоемкости и сразу предоставляет в два раза больше места. В дальнейшем он будет поступать так же — каждый новый блок будет вдвое превышать предыдущий.

Помните, мы говорили про постоянное амортизированное время при добавлении элементов в конец массива? Падение производительности происходит как раз в тот момент, когда нужно выделить новый, в два раза больший блок памяти. Остальные операции занимают одинаковый период.

Этот принцип позволяет программе быстро добрать небольшое количество ресурсов, которых ей не хватает в начале работы. Если же ее аппетиты продолжают расти, она обращается за помощью все реже.

Алгоритм, который позволяет переносить данные из блока A в блок B, выглядит следующим образом:

1. Выделить участок B с нужным объемом памяти, в соответствии с описанным выше методом.
2. Установить, что B[i] = A[i], i=0,….,n-1, где n — это текущий номер последнего элемента.
3. Установить, что A = B.
4. Добавить элементы в новый массив.

Другими словами, с того момента, как Python создает новый массив B и копирует в него данные, он считает его массивом A. Именно такая элегантная эффективность и снискала этому языку признание тысяч и тысяч программистов по всему миру.

Перламутровые пуговицы

Что ещё можно делать с массивами? Например, структура под названием “куча” (heap) позволяет программисту в любой момент определить в ряду значений минимальное.

Функционально “куча” представляет собой бинарное дерево, где каждый родитель больше   двух своих наследников.

Таким образом, верхний узел (heap[0]) всегда оказывается самым меньшим из всего массива.

_{Пример “кучи” из технического описания модуля heapq. heap[k] <= heap[2*k+1] и heap[k] <= heap[2*k+2] для всех k, начиная с нуля.}

Список доступных в Python операций с “кучей” включает определение наименьшего элемента, его добавление или удаление, слияние нескольких массивов и др. С помощью “кучи”  вы можете, например, выстроить приоритетную очередь для нескольких равноправных процессов, объединить записи двух журналов и выставить их в хронологическом порядке.

Как и другие бинарные деревья, “кучу” может быть сохранить в массиве, но при этом она оказывается компактнее. Дело в том, что в этом случае не требуется пространство для указателей — родителя и его наследников можно найти арифметически по индексам.

Одни и те же данные в виде “кучи” и массива.

Ещё одна вариация структуры на основе массива — двухсторонняя очередь (double-ended queue, deque).

Она объединяет в себе функции стека и, собственно, очереди. Как вы помните, главное отличие между этими двумя структурами — порядок получения сохранённых данных. В очереди первыми предоставляются те данные, которые были раньше в ней сохранены (принцип First-In-First-Out). В стеке — наоборот, как в стопке книг или тарелок, сверху оказываются самые новые элементы (First-In-Last-Out).

Двусторонняя очередь позволяет работать с данными с обеих сторон массива — добавлять и удалять элементы как в начале, так и в конце. Классический пример практического применения — планировщик задач для параллельных вычислений. Для каждого участвующего процессора формируется отдельная deque, в которую потоки сохраняются по принципу FIFO. Освободившийся процессор забирает первую задачу в своей очереди. Если она пуста, он обращается к deque другого процессора и забирает себе задачу, которая стоит там последней.

На этом сегодняшний теоретический экскурс окончен. Надеемся, что эти знания помогут вам в изучении Python и покорении новых вершин веб-разработки.

Курс

Python для веб-разработки

Авторская программа от эксперта-практика. После обучения вы сможете в одиночку создавать и поддерживать сайты. Скидка по промокоду BLOG 5%.

Узнать больше

_{текст: Помогаев Дмитрий}

#5. Динамический массив. Принцип работы

Смотреть материал на видео

Мы продолжаем курс по структурам данных. На этом занятии речь пойдет о динамических массивах. Что это такое? На данный момент мы с вами уже хорошо знаем, что из себя представляет и как работает статический массив. Но у него есть один существенный недостаток – неизменяемое число элементов. Поэтому, когда создается статический массив, программист должен как то решить, сколько элементов он должен иметь. Далеко не всегда можно указать разумное значение. Чтобы как то выйти из этой ситуации в мире программирования появилась более гибкая структура данных тоже в виде массива, но с изменяемым (увеличивающимся) числом элементов.

Такие массивы получили название динамические.

Приведу один простой пример их использования. Предположим, мы просматриваем файловую систему и сохраняем имена файлов в каждом каталоге. Очевидно, число файлов может варьироваться от нескольких десятков до нескольких тысяч. Если воспользоваться статическим массивом, то придется задавать число элементов, скажем, в 10 000. И это приведет к неоправданному расходу памяти. Гораздо лучше взять динамические массивы с начальным размером в 100 элементов. А, затем, по мере необходимости, увеличивать этот размер. Тогда память будет расходоваться куда экономнее.

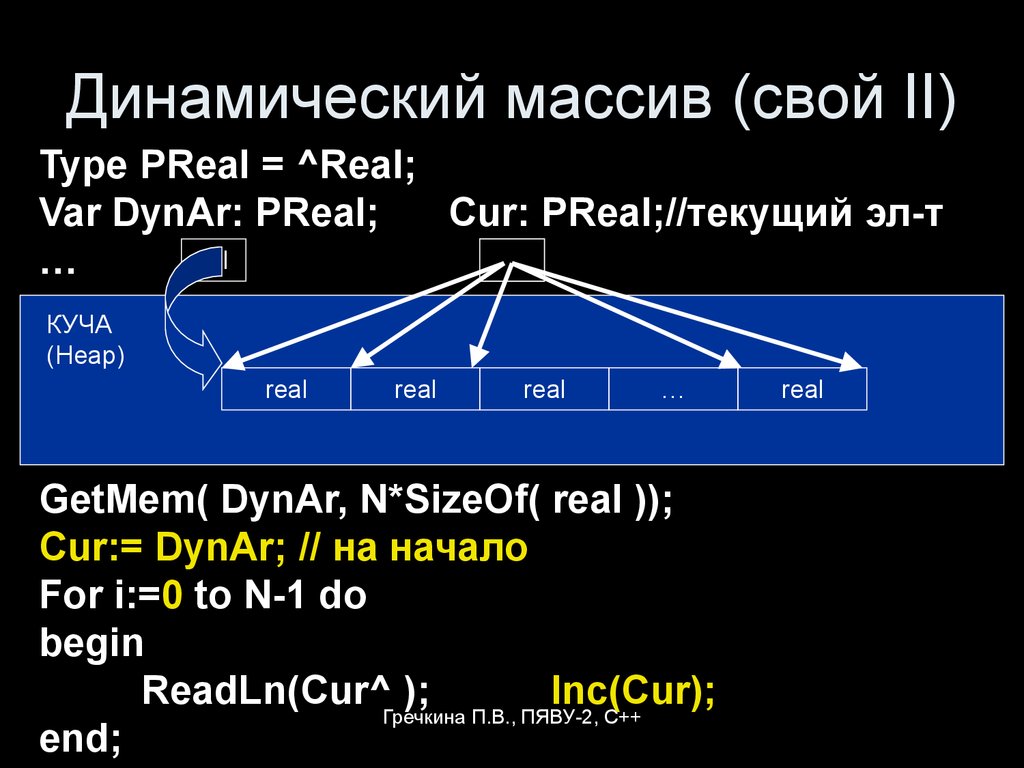
Структура динамического массива

Давайте теперь посмотрим, как можно организовать массив с изменяемым числом элементов. Для этого воспользуемся обычным массивом с некоторым начальным размером, допустим, в 10 элементов:

Реальный размер массива называют физическим, а число записанных в него данных – логическим. Чтобы программно оперировать этими величинами вводят две вспомогательные переменные, например:

currentLength = 7
maxCapacity = 10

Переменная currentLength содержит индекс следующего добавляемого в массив значения, а также определяет число уже записанных данных. Переменная maxCapacity равна максимальному числу элементов, который имеет массив dar.

Добавление и вставка элементов в массив

Теперь предположим, что мы хотим добавить новое значение в конец этого массива. Так как все элементы в массивах должны следовать строго друг за другом с самого начала без каких-либо пропусков, то новое значение нам следует записать в ячейку с индексом currentLength:

dar[currentLength] = 8

и увеличить значение currentLength на единицу:

currentLength += 1

С точки зрения О большого скорость этой операции составляет O(1).

Но это добавление в конец. А что если нам нужно вставить новое значение, скажем, после пятерки. Как в этом случае будет выглядеть алгоритм? В действительности, так же, как и в обычном статическом массиве. Необходимо сдвинуть значения 6, 7, 8 вправо на один элемент и на прежнее место шестерки записать вставляемое значение. Переменная currentLength увеличивается на единицу:

Вычислительная сложность этой операции с точки зрения О большого составляет O(n), где n – физический размер динамического массива.

Изменение физического размера динамического массива

Я думаю эти простые операции добавления и вставки новых значений в массив, пока есть свободное место, вы себе хорошо представляете. Но что делать, когда все элементы заняты, а мы хотим добавить еще один?

Было бы неплохо выделить следующие несколько байт под новый элемент массива и записать туда требуемое значение.

При этом вся выделенная под массив область памяти должна быть непрерывной. К сожалению, в общем случае, такую операцию выполнить не получится, т.к. следующие ячейки памяти могут быть заняты другими процессами. Поэтому приходится идти несколько более сложным, но более надежным путем. Выделяется память под новый статический массив длиной в два, три раза больший первоначального (чаще всего удваивают физический размер). В этот новый массив копируют все значения из прежнего массива, записывают новое значение и увеличивают переменную currentLength:

Вычислительная сложность этой операции с позиции О большого составляет O(n), где n – физический размер динамического массива.

Далее, если все новые элементы также будут заполнены, то операция удвоения физического размера массива повторяется. Это принцип работы динамического массива.

Здесь у вас может возникнуть вопрос, зачем под новый массив выделять в несколько раз больше элементов, чем в прежнем? Почему бы не увеличить его просто на один элемент (или требуемое число элементов)? Зачем удваивать? Ответ прост. Если нам не хватило физического размера прошлого массива, то скорее всего не хватит и для нового массива с одним дополнительным элементов. А, значит, операцию выделения памяти и копирования всех прежних значений в новый массив снова придется повторять. Это приводит к неоправданному расходу процессорного времени. Логичнее сделать размер массива сразу в два раза больше и минимизировать вероятность создания новых массивов с большими размерами.

Удаление элементов в динамическом массиве

Итак, с добавлением новых значений и изменением физического размера динамического массива мы с вами разобрались. Осталось сказать пару слов про удаление значений. Здесь все намного проще, т.к. физический размер массива при этом не меняется. Поэтому здесь все абсолютно так же, как и в случае со статическими массивами.

Предположим, нам нужно исключить последнее значение. Нет ничего проще. Достаточно уменьшить значение currentLength на единицу и все. Последнего значения теперь как бы нет. Вычислительная сложность этой операции составляет O(1).

Немного сложнее выполняется удаление остальных значений (не последнего). В этом случае нам нужно сдвинуть все элементы правее удаляемого влево на одну позицию и не забыть уменьшить значение currentLength на единицу:

Сложность этой операции составляет O(n). Еще раз отмечу, что при удалении значений физический размер массива не меняется, даже если ранее он увеличивался.

Заключение

Давайте подведем итог этого занятия.

Динамический массив – это массив, который может менять число своих элементов в процессе работы программы.

Динамические массивы реализуются на основе обычных статических массивов и хранят данные в непрерывной области памяти. Благодаря этому доступ к произвольному элементу выполняется за фиксированное время с вычислительной сложностью O(1).

Если начального физического размера динамического массива недостаточно, то создается новый массив размером в несколько раз больше предыдущего с копированием всех прежних значений. Часто делают удвоение размеров.

Операции добавления и удаления значений элементов в динамическом массиве выполняются почти так же, как и в статических массивах. Разница только в том, что при добавлении новых значений может дополнительно происходить увеличение физического размера массива. При этом вычислительная сложность операций вставки/удаления составляет O(n), где n – общий размер динамического массива.

На следующем занятии мы продолжим эту тему и увидим, как реализуются динамические массивы на языках Python и С++.

Видео по теме

#1. О большое (Big O) — верхняя оценка сложности алгоритмов

#2. О большое (Big O). Случаи логарифмической и факториальной сложности

#3. Статический массив. Структура, его преимущества и недостатки

#4. Примеры реализации статических массивов на C++

#5. Динамический массив. Принцип работы

#6. Реализация динамического массива на Python

#7. Реализация динамического массива на С++ с помощью std::vector

#8. Односвязный список. Структура и основные операции

#9. Делаем односвязный список на С++

#10. Двусвязный список. Структура и основные операции

#11. Делаем двусвязный список на С++

#12. Двусвязный список (list) в STL на С++

#13. Очереди типов FIFO и LIFO

#14. Очередь collections.deque на Python

#15. Очередь deque библиотеки STL языка C++

#16. Стек. Структура и принцип работы

#17. Реализация стека на Python и C++

#18. Бинарные деревья. Начало

#19. Бинарное дерево. Способы обхода и удаления вершин

#20. Реализация бинарного дерева на Python

#21. Множества (set). Операции над множествами

#22. Множества set и multiset в C++

#23. Контейнер map библиотеки STL в C++

#24. Префиксное (нагруженное, Trie) дерево. Ассоциативные массивы

#25. Хэш-таблицы. Что это такое и как работают

#26. Хэш-функции. Универсальное хэширование

#27. Метод открытой адресации. Двойное хэширование

#28. Использование хэш-таблиц в Python и С++

Структура данных динамического массива в программировании

Что такое динамический массив?

Недостаток обычных массивов в том, что мы не можем изменить их размер в процессе выполнения кода. Другими словами, он не сможет добавить (n + 1)-й элемент, если мы выделим размер массива, равный n. Одна из идей состоит в том, чтобы выделить большой массив, что может привести к трате значительного объема памяти. Итак, что является подходящим решением этой проблемы? Думать! Мы решаем эту проблему, используя идею динамического массива, где мы можем динамически увеличивать размер массива по мере необходимости.

Как работает динамический массив?

Предположим, мы начинаем с массива размером 1 и удваиваем его каждый раз, когда заканчивается место. Этот процесс включает в себя выделение нового массива двойного размера, копирование данных старого массива в нижнюю половину нового и удаление пространства, используемого старым массивом. Дополнительные затраты, связанные с этим процессом, связаны с повторным копированием старых данных в новый массив при каждом удвоении. Важнейший вопрос: сколько раз нужно перекопировать элемент после n вставок? Давайте визуализируем.

• После первой вставки мы удваиваем размер массива и копируем первый элемент в новый массив. Теперь размер массива равен 2, а в массиве один элемент. Итак, после второй вставки нам нужно удвоить размер массива до 4 и скопировать два элемента в новый массив.
• Теперь размер массива равен 4, а элементов в массиве два, поэтому нет необходимости изменять размер массива после 3-й вставки. Но после 4-й вставки массив будет заполнен, и нам нужно удвоить размер массива до 8 и скопировать четыре элемента в новый массив. 9я = п => я = logn. Итак, после n операций вставки нам нужно удвоить размер массива logn раз. Думать! Таким образом, общее количество операций копирования после logn количество удвоений = 1 + 2 + 4 + ….. n/4 + n/2 + n

  = n + n/2 + n/4 + … .. + 4 + 2 + 1

  = n (1 + 1/2 + 1/4 + ….. + 4/n + 2/n + 1/n)

  ≤ n (1 + 1/ 2 + 1/4 + ….. + 4/n + 2/n + 1/n + …. до бесконечности)

  ≤ n * 1/(1 — 1/2) ≤ 2n

  Примечание: 94 + . .. до бесконечности = 1/(1 — r)

  Таким образом, для logn количества вставок (в каждой точке удвоения) нам нужно выполнить не более 2n операций копирования. С другой стороны, нет необходимости выполнять операции копирования оставшихся n — logn вставок. Всего операций копирования на вставку = 2n / n = 2. Таким образом, в среднем каждый элемент n перемещается только два раза, что является постоянным.

  • Увеличение размера массива в 2 раза гарантирует, что вставка n элементов займет в целом O(n) времени, а это означает, что каждая вставка занимает O(1) среднего постоянного времени, что почти эквивалентно обычной ситуации с массивом.
  • Почти все запросы на вставку будут быстрыми, за исключением logn запросов, которые вызывают удвоение массива. Другими словами, частота наилучшего сценария очень высока (n — logn), а частота наихудшего сценария будет очень низкой (logn). Вот почему средний случай ближе к лучшему. Думать!

  Для реализации динамического массива как абстрактного типа данных на C++ или Java или каком-либо другом языке программирования нам необходимо определить следующие вещи:

  • A[] : Указатель на массив
  • currSize : Количество элементов в динамическом массиве A[]. Он инициализируется значением 0 в начале.
  • capacity : Общее количество элементов, которое динамический массив A[] может содержать до изменения размера. Он инициализируется значением 1 в начале.
  • Конструктор динамического массива : вызывается, когда мы создаем объект динамического массива в нашем коде. Он инициализирует значение указателя массива A[], currSize и емкость.
  Операции с динамическим массивом

  Теперь мы определяем и реализуем операции с динамическим массивом для работы с данными. Мы также можем определить некоторые другие операции в зависимости от необходимости.

  • void insertAtEnd(int x): Вставить элемент в конец индекса
  • void reSizeArray(): Увеличить емкость массива вдвое
  • void rejectArray(): Уменьшить емкость массива наполовину
  • недействительным вставитьAtMiddle (индекс int, int x): Вставить элемент в некоторый средний индекс
  • void deleteAtEnd(): Удалить элемент из конечного индекса
  • void deleteAtMiddle(int index): Удалить элемент из некоторого среднего индекса

  Для работы с принципами oops мы объявляем указатель массива A, currSize и емкость как частный  член класса. Это инкапсуляция, когда мы скрываем внутренние детали объекта. Точно так же мы объявляем конструктор и операции как общедоступных  членов класса. Это абстракция, в которой мы раскрываем только важные детали для внешнего мира.

  Примечание. Для лучшей абстракции мы можем объявить методы reSizeArray() и shrinkArray() как закрытые члены класса, поскольку обе операции будут использоваться внутри методов вставки и удаления. Поэтому нет необходимости предоставлять публичный доступ к этим методам. Думать!

  Псевдокод: Структура класса DynamicArray

   открытый класс DynamicArray
  {
  Частный
      интервал А[]
      int currSize
      внутренняя емкость
      недействительным reSizeArray()
      {
          //Код реализации
      }
      
       недействительный сжимаемый массив ()
      {
          // Код реализации
      }
     
  публичный:
      Динамический массив ()
      {
          A = новый интервал [1]
          курсрсайз = 0
          емкость = 1
      }
      пустота insertAtEnd (целое число x)
      {
          // Код реализации
      }
    
      пустота insertAtMiddle (индекс int, int x)
      {
          // Код реализации
      }
      аннулировать deleteAtEnd()
      {
          // Код реализации
      }
    
      недействительным deleteAtMiddle (индекс int)
      {
          // Код реализации
      }
      
      ...//Другие операции с динамическими массивами...
  } 

  операция resizeArray()

  Эта операция требуется, когда выделенное пространство массива заполняется с определенной емкостью после некоторой последовательности вставки. Поэтому мы вызываем этот метод, когда currSize == емкость во время вставки.

  • Мы удваиваем емкость массива и объявляем новый массив temp[] размером 2*емкость.
  • Мы запускаем цикл от i = 0 до емкости — 1 и копируем все элементы из исходного массива A[] в новый массив temp[].
  • Мы освобождаем пространство, используемое A[], и инициализируем его с помощью temp[].
  • Наконец, мы удваиваем значение емкости.

  Реализация псевдокода

   void resizeArray()
  {
      если (currSize == мощность)
      {
          интервал времени [2 * емкость]
          for (int i = 0; i < вместимость; i = i + 1)
              темп[я] = А[я]
          бесплатно(А)
          А = температура
          вместимость = 2 * вместимость
      }
  } 

  операция insertAtEnd(int x)

  Если (currSize < вместимость), , то мы легко вставляем элемент с индексом A[currSize] и увеличиваем currSize на 1. В противном случае массив заполняется своей емкостью. Поэтому мы вызываем операцию resizeArray(), чтобы удвоить его размер, добавить элемент x по индексу A[currSize] и увеличить currSize на 1.

  Реализация псевдокода

   void insertAtEnd(int x)
  {
      если (currSize == мощность)
          изменить размер массива ()
      A[currSize] = х
      размер_курса = размер_курса + 1
  } 

  операция insertAtMiddle(int index, int x)

  If(currSize == вместимость) , то мы изменяем размер массива в два раза и перемещаем элементы из index в currSize - 1 на единицу вверх. Этот процесс создаст пространство для вновь прибывшего элемента x. Теперь мы вставляем элемент x в A[index] и увеличиваем currSize на 1. Примечание. Если (currSize < емкости), нам не нужно изменять размер массива.

  Реализация псевдокода

   void insertAtMiddle(int index, int x)
  {
      если (currSize == мощность)
          изменить размер массива ()
              
      for (int i = currSize; i > index; i = i - 1)
          А [я] = А [я - 1]
              
      А [индекс] = х
      размер_курса = размер_курса + 1
  } 

  операция сжатия()

  После некоторой последовательности удаления currSize массива может быть значительно меньше по сравнению с текущей емкостью . Таким образом, динамический массив также может освободить часть пространства, если его размер упадет ниже определенного порога, например 1/4 текущей емкости. Это поможет сократить потери дополнительного пространства.

  Выполняем эту операцию, когда currSize == capacity/4 при удалении.

  • Мы объявляем новый массив temp[] размера вместимость/2.
  • Теперь мы запускаем цикл от i = 0 до currSize -1 и копируем все элементы из исходного массива A[] в массив temp[].
  • Мы обновляем новую емкость, равную емкости/2, и освобождаем пространство, используемое A[].
  • Наконец, мы инициализируем A[] новым массивом temp[].

  Реализация псевдокода

   void сжимаемый массив ()
  {
      если (currSize == емкость/4)
      {
          инт темп[емкость/2]
          for (int i = 0; i < currSize; i = i + 1)
              темп[я] = А[я]
          мощность = мощность/2
          бесплатно(А)
          А = температура
      }
  } 

  операция deleteAtEnd()

  Нам нужно проверить текущий размер массива. if(currSize == 0) , то массив пуст или в массиве не будет элементов. В противном случае мы удаляем элемент с индексом currSize - 1 и уменьшаем currSize на 1. Во время этого процесса if (currSize == capacity/4) , затем мы вызываем метод shrinkArray(), чтобы уменьшить размер динамического массива вдвое.

  Реализация псевдокода

   void deleteAtEnd()
  {
      если (currSize == 0)
          print("динамический массив пуст!")
      еще
      {
          A[currSize - 1] = INT_MIN
          размер_курса = размер_курса - 1
          если (currSize == емкость/4)
              уменьшитьмассив()
      }
  } 

  deleteAtMiddle(int index) операция

  Нам нужно проверить текущий размер массива. if(currSize == 0) , массив пуст или в нем не будет элементов. В противном случае мы перемещаем все элементы из currSize - 1 в индекс на 1 вниз, устанавливаем значение в A[currSize - 1] равным 0 и уменьшаем currSize на 1. В ходе этого процесса if (currSize == capacity/4 ) , затем мы вызываем метод shrinkArray(), чтобы уменьшить размер динамического массива вдвое.

  Реализация псевдокода

   void deleteAtMiddle(int index)
  {
      если (currSize == 0)
          print("динамический массив пуст!")
      еще
      {
          for (int i = index; i < currSize - 1; i = i + 1)
              А [я] = А [я + 1]
          A[currSize - 1] = INT_MIN
          размер_курса = размер_курса - 1
          если (currSize == емкость/4)
              уменьшитьмассив()
      }
      
  } 

  Критические понятия для размышления в динамическом массиве!

  • Проанализируйте и сравните временные сложности операций динамического массива выше с обычным массивом.
  Динамический массив
  • поставляется со стандартными библиотеками многих современных языков программирования. В C++ он называется вектором, а в Java имеет две реализации: ArrayList и Vector.
  • Коэффициент роста для динамического массива зависит от нескольких факторов, таких как компромисс времени и памяти, алгоритмы, используемые внутри распределителя памяти и т. д.
  • Для коэффициента роста k среднее время на операцию вставки составляет около k/(k−1), где максимальное количество потерянного пространства составит (k−1)n.
  • Для простоты анализа мы использовали коэффициент роста k = 2. Но если распределитель памяти использует алгоритм распределения по первому совпадению, то такие значения коэффициента роста, как k = 2, могут привести к нехватке памяти при динамическом расширении массива. хотя значительный объем памяти все еще может быть доступен.
  • Было несколько дискуссий об идеальных значениях фактора роста. Некоторые эксперты предлагают значение золотого сечения в качестве фактора роста, но библиотечная реализация разных языков программирования использует разные значения. Исследуй и думай!

  Наслаждайтесь обучением, наслаждайтесь алгоритмами!

  Динамические массивы, функции и формулы Excel

  Благодаря революционному обновлению механизма вычислений Excel 365 формулы массивов стали очень простыми и понятными для всех, а не только для опытных пользователей. В учебнике объясняется концепция новых динамических массивов Excel и показано, как они могут сделать ваши рабочие листы более эффективными и намного проще в настройке.

  Формулы массива Excel всегда считались прерогативой гуру и экспертов по формулам. Если кто-то скажет: «Это можно сделать с помощью формулы массива», многие пользователи немедленно отреагируют: «А нет ли другого способа?».

  Введение динамических массивов — долгожданное и долгожданное изменение. Благодаря своей способности работать с несколькими значениями простым способом, без каких-либо уловок и причуд, формулы динамического массива — это то, что каждый пользователь Excel может понять и получить удовольствие от создания.

  Динамические массивы Excel

  Динамические массивы — это массивы с изменяемым размером, которые автоматически вычисляют и возвращают значения в несколько ячеек на основе формулы, введенной в одну ячейку.

  За более чем 30-летнюю историю Microsoft Excel претерпел множество изменений, но одно осталось неизменным — одна формула, одна ячейка. Даже с традиционными формулами массива необходимо было вводить формулу в каждую ячейку, где должен появиться результат. С динамическими массивами это правило больше не выполняется. Теперь любая формула, возвращающая массив значений, автоматически переносится в соседние ячейки, и вам не нужно нажимать Ctrl + Shift + Enter или выполнять какие-либо другие действия. Другими словами, работать с динамическими массивами становится так же просто, как с одной ячейкой.

  Позвольте мне проиллюстрировать концепцию очень простым примером. Допустим, вам нужно перемножить две группы чисел, например, для вычисления разных процентов.

  В преддинамических версиях Excel приведенная ниже формула будет работать только для первой ячейки, если вы не введете ее в несколько ячеек и не нажмете Ctrl + Shift + Enter, чтобы явно сделать ее формулой массива:

  =A3:A5*B2:D2
  

  Теперь посмотрите, что происходит, когда та же формула используется в Excel 365. Вы вводите ее всего в одну ячейку (в нашем случае B3), нажимаете клавишу Enter… и вся ярость сразу заполняется результатами:
  

  Заполнение нескольких ячеек одной формулой называется разливом , а заполненный диапазон ячеек называется диапазоном разброса.

  Важно отметить, что недавнее обновление — это не просто новый способ обработки массивов в Excel. По сути, это революционное изменение всего механизма расчета. Благодаря динамическим массивам в библиотеку функций Excel было добавлено множество новых функций, а существующие стали работать быстрее и эффективнее. В конечном итоге предполагается, что новые динамические массивы полностью заменят устаревшие формулы массивов, которые вводятся с помощью сочетания клавиш Ctrl + Shift + Enter.
  

  Доступность динамических массивов Excel

  Динамические массивы были представлены на конференции Microsoft Ignite в 2018 г. и выпущены для подписчиков Office 365 в январе 2020 г. В настоящее время они доступны в подписках Microsoft 365 и Excel 2021.

  Динамические массивы поддерживаются в следующих версиях:

  • Excel 365 для Windows
  • Excel 365 для Mac
  • Excel 2021
  • Excel 2021 для Mac
  • Excel для iPad
  • Excel для iPhone
  • Excel для планшетов Android
  • Excel для телефонов Android
  • Excel для Интернета

  Функции динамического массива Excel

  В рамках новой функциональности в Excel 365 было введено 6 новых функций, которые обрабатывают массивы и выводят данные в диапазон ячеек. Вывод всегда динамичен — когда в исходных данных происходит какое-либо изменение, результаты обновляются автоматически. Отсюда и название группы - функции динамического массива .

  Эти новые функции легко справляются с рядом задач, которые традиционно считаются крепкими орешками. Например, они могут удалять дубликаты, извлекать и подсчитывать уникальные значения, отфильтровывать пробелы, генерировать случайные целые и десятичные числа, сортировать по возрастанию или убыванию и многое другое.

  Ниже вы найдете краткое описание того, что делает каждая функция, а также ссылки на подробные руководства:

  1. UNIQUE - извлекает уникальные элементы из ряда ячеек.
  2. ФИЛЬТР — фильтрует данные на основе заданных вами критериев.
  3. SORT — сортирует диапазон ячеек по указанному столбцу.
  4. SORTBY — сортирует диапазон ячеек по другому диапазону или массиву.
  5. RANDARRAY — генерирует массив случайных чисел.
  6. ПОСЛЕДОВАТЕЛЬНОСТЬ - генерирует список порядковых номеров.
  7. TEXTSPLIT - разбивает строки по указанному разделителю между столбцами и/или строками.
  8. TOCOL — преобразовать массив или диапазон в один столбец.
  9. TOROW - преобразовать диапазон или массив в одну строку.
  10. WRAPCOLS — преобразует строку или столбец в двумерный массив на основе указанного количества значений в строке.
  11. WRAPROWS — преобразует строку или столбец в двумерный массив на основе указанного количества значений в столбце.
  12. TAKE — извлекает указанное количество смежных строк или столбцов из начала или конца массива.
  13. DROP — удаляет определенное количество строк или столбцов из массива.
  14. EXPAND - увеличить массив до указанного количества строк и столбцов.
  15. CHOOSECOLS — возвращает указанные столбцы из массива.
  16. CHOOSEROWS — извлекает указанные строки из массива.

  Кроме того, есть две современные замены популярных функций Excel, которые официально не входят в группу, но используют все преимущества динамических массивов:

  XLOOKUP — это более мощный преемник функций VLOOKUP, HLOOKUP и LOOKUP, который может выполнять поиск как в столбцах, так и в строках и возвращать несколько значений.

  XMATCH — это более универсальный преемник функции MATCH, который может выполнять вертикальный и горизонтальный поиск и возвращать относительное положение указанного элемента.
  

  Формулы динамического массива Excel

  В современных версиях Excel поведение динамического массива глубоко интегрировано и становится родным для всех функций , даже тех, которые изначально не были предназначены для работы с массивами. Проще говоря, для любой формулы, которая возвращает более одного значения, Excel автоматически создает диапазон с изменяемым размером, в который выводятся результаты. Благодаря этой способности существующие функции теперь могут творить чудеса!

  В приведенных ниже примерах показаны новые формулы динамических массивов в действии, а также влияние динамических массивов на существующие функции.

  Пример 1. Новая функция динамического массива

  Этот пример демонстрирует, насколько быстрее и проще решение может быть выполнено с помощью функций динамического массива Excel.

  Чтобы извлечь список уникальных значений из столбца, вы обычно используете сложную формулу CSE, подобную этой. В динамическом Excel все, что вам нужно, это УНИКАЛЬНАЯ формула в ее базовой форме:

  =УНИКАЛЬНЫЙ(B2:B10)

  Вы вводите формулу в любую пустую ячейку и нажимаете Enter. Excel немедленно извлекает все разные значения из списка и выводит их в диапазон ячеек, начиная с ячейки, в которую вы ввели формулу (в нашем случае D2). При изменении исходных данных результаты автоматически пересчитываются и обновляются.
  
  

  Пример 2. Объединение нескольких функций динамического массива в одну формулу

  Если нет возможности выполнить задачу с помощью одной функции, соедините несколько вместе! Например, чтобы отфильтровать данные по условию и упорядочить результаты в алфавитном порядке, оберните функцию SORT вокруг FILTER следующим образом:

  =СОРТИРОВКА(ФИЛЬТР(A2:C13, B2:B13=F1, "Нет результатов"))

  Где A2:C13 — исходные данные, B2:B13 — значения для проверки, а F1 — критерий.
  
  

  Пример 3. Использование новых функций динамического массива вместе с существующими

  Поскольку новый механизм вычислений, реализованный в Excel 365, может легко преобразовывать обычные формулы в массивы, ничто не мешает вам комбинировать новые и старые функции вместе.

  Например, чтобы подсчитать количество уникальных значений в определенном диапазоне, вложите функцию динамического массива UNIQUE в старый добрый COUNTA:

  =COUNTA(UNIQUE(B2:B10))
  
  

  Пример 4. Существующие функции поддерживают динамические массивы

  Если вы укажете диапазон ячеек для функции TRIM в более старой версии, такой как Excel 2016 или Excel 2019, она вернет один результат для первой ячейки:

  =ОТРЕЗКА(A2:A6)

  В динамическом Excel одна и та же формула обрабатывает все ячейки и возвращает несколько результатов, как показано ниже:
  
  

  Пример 5. Формула ВПР для возврата нескольких значений

  Как всем известно, функция ВПР предназначена для возврата одного значения на основе указанного вами индекса столбца. Однако в Excel 365 вы можете указать массив номеров столбцов, чтобы получить совпадения из нескольких столбцов:

  .

  =ВПР(F1, A2:C6, {1,2,3}, ЛОЖЬ)
  
  

  Пример 6. Формула ТРАНСПОНС стала проще

  В более ранних версиях Excel синтаксис функции ТРАНСП не оставлял места для ошибок. Чтобы повернуть данные на вашем листе, вам нужно было подсчитать исходные столбцы и строки, выбрать такое же количество пустых ячеек, но изменить ориентацию (невероятная операция в огромных рабочих листах!), ввести формулу ТРАНСП в выбранном диапазоне и нажмите Ctrl + Shift + Enter, чтобы завершить его правильно. Фу!

  В динамическом Excel вы просто вводите формулу в крайнюю левую ячейку выходного диапазона и нажимаете Enter:

  =ТРАНСП(A1:B6)

  Готово!
  
  

  Диапазон заполнения — одна формула, несколько ячеек

  Диапазон разлива — это диапазон ячеек, который содержит значения, возвращаемые формулой динамического массива.

  При выборе любой ячейки в диапазоне разливов появляется синяя рамка, показывающая, что все внутри нее рассчитывается по формуле в верхней левой ячейке. Если вы удалите формулу в первой ячейке, все результаты исчезнут.
  

  Диапазон разброса — действительно замечательная вещь, которая значительно облегчает жизнь пользователям Excel. Раньше при работе с формулами массива СПП нам приходилось угадывать, во сколько ячеек их копировать. Теперь вы просто вводите формулу в первую ячейку, а Excel позаботится обо всем остальном.

  Примечание. Если какие-то другие данные блокируют диапазон разлива, возникает ошибка #SPILL. Как только мешающие данные будут удалены, ошибка исчезнет.

  Дополнительные сведения см. в разделе Диапазон сброса Excel.
  

  Ссылка на диапазон разлива (символ #)

  Чтобы сослаться на весь диапазон сброса, возвращаемый формулой динамического массива, поместите хэш-тег или символ решетки (#) после адреса верхней левой ячейки диапазона.

  Например, чтобы узнать, сколько случайных чисел сгенерировано формулой СЛУЧАЙ в A2, укажите ссылку на диапазон разброса для функции СЧЕТЧИК:

  =СЧЕТЧИК(A2#)

  Чтобы сложить значения в диапазоне разливов, используйте:

  =СУММ(A2#)
  

  Советы:

  • Чтобы быстро перейти к диапазону разлива, просто выберите все ячейки внутри синего поля с помощью мыши, и Excel создаст для вас ссылку разлива.
  • В отличие от обычной ссылки на диапазон, ссылка на диапазон разлива является динамической и автоматически реагирует на изменение размера диапазона.

  Подробнее см. Оператор диапазона разлива.
  

  Неявное пересечение и символ @

  В динамическом массиве Excel есть еще одно существенное изменение в языке формул - введение символа @, известного как оператор неявного пересечения .

  В Microsoft Excel неявное пересечение — это поведение формулы, сводящее множество значений к одному значению. В старом Excel ячейка могла содержать только одно значение, так что это было поведение по умолчанию, и для него не требовался специальный оператор.

  В новом Excel все формулы по умолчанию рассматриваются как формулы массива. Неявный оператор пересечения используется для предотвращения поведения массива, если вы не хотите его использовать в конкретной формуле. Другими словами, если вы хотите, чтобы формула возвращала только одно значение, поставьте @ перед именем функции, и она будет вести себя как формула без массива в традиционном Excel.

  Чтобы увидеть, как это работает на практике, взгляните на скриншот ниже.

  В C2 есть формула динамического массива, которая распределяет результаты по многим ячейкам:

  =УНИКАЛЬНЫЙ(A2:A9)

  В E2 перед функцией стоит символ @, который вызывает неявное пересечение. В результате возвращается только первое уникальное значение:

  .

  =@УНИКАЛЬНЫЙ(A2:A9)
  

  Дополнительные сведения см. в разделе Неявное пересечение в Excel.
  

  Преимущества динамических массивов Excel

  Несомненно, динамические массивы — одно из лучших усовершенствований Excel за последние годы. Как и у любой новой функции, у них есть сильные и слабые стороны. К счастью для нас, сильные стороны новых формул динамических массивов Excel просто огромны!

  Простой и более мощный

  Динамические массивы позволяют создавать более мощные формулы гораздо более простым способом. Вот пара примеров:

  • Извлечение уникальных значений: традиционные формулы | функции динамического массива
  • Подсчет уникальных и различных значений: традиционные формулы | функции динамического массива
  • Сортировка столбцов по алфавиту: традиционные формулы | функции динамического массива

  Родной для всех формул

  В динамическом Excel не нужно заморачиваться, какие функции поддерживают массивы, а какие нет. Если формула может возвращать несколько значений, она будет делать это по умолчанию. Это также относится к арифметическим операциям и устаревшим функциям, как показано в этом примере.
  

  Вложенные функции динамического массива

  Для решения более сложных задач вы можете комбинировать новые функции динамических массивов Excel или использовать их вместе со старыми, как показано здесь и здесь.
  

  Относительные и абсолютные ссылки менее важны

  Благодаря подходу "одна формула, много значений" нет необходимости блокировать диапазоны знаком $, поскольку технически формула находится только в одной ячейке. Таким образом, по большей части не имеет значения, использовать ли абсолютные, относительные или смешанные ссылки на ячейки (что всегда было источником путаницы для неопытных пользователей) - формула динамического массива в любом случае будет давать правильные результаты!
  

  Ограничения динамических массивов

  Новые динамические массивы — это здорово, но, как и в случае с любой новой функцией, есть несколько предостережений и соображений, о которых вам следует знать.
  

  Результаты не могут быть отсортированы обычным способом

  Диапазон разброса, возвращаемый формулой динамического массива, не может быть отсортирован с помощью функции сортировки Excel. Любая такая попытка приведет к ошибке « Вы не можете изменить часть массива ». Чтобы упорядочить результаты от меньшего к большему или наоборот, оберните текущую формулу функцией СОРТИРОВКИ. Например, так вы можете одновременно фильтровать и сортировать.
  

  Невозможно удалить любое значение в диапазоне разлива

  Ни одно из значений в диапазоне разлива не может быть удалено по той же причине: вы не можете изменить часть массива. Такое поведение ожидаемо и логично. Традиционные формулы массива CSE также работают таким же образом.
  

  Не поддерживаются в таблицах Excel

  Эта функция (или ошибка?) довольно неожиданная. Формулы динамического массива не работают в таблицах Excel, только в пределах обычных диапазонов. Если вы попытаетесь преобразовать диапазон разброса в таблицу, Excel сделает это. Но вместо результатов вы увидите только #РАЗЛИВ! ошибка.
  

  Не работает с Excel Power Query

  Результаты формул динамического массива не могут быть загружены в Power Query. Скажем, если вы попытаетесь объединить два или более диапазонов сброса вместе с помощью Power Query, это не сработает.
  

  Динамические массивы и традиционные формулы массивов CSE

  С введением динамических массивов мы можем говорить о двух типах Excel:

  1. Dynamic Excel , который полностью поддерживает динамические массивы, функции и формулы. В настоящее время это только Excel 365 и Excel 2021.
  2. Устаревший Excel , также известный как традиционный или преддинамический Excel, где поддерживаются только формулы массива Ctrl + Shift + Enter. Это Excel 2019, Excel 2016, Excel 2013 и более ранние версии.

  Само собой разумеется, что динамические массивы превосходят формулы массивов CSE во всех отношениях. Хотя традиционные формулы массива сохранены из соображений совместимости, в дальнейшем рекомендуется использовать новые.

  Вот самые существенные отличия:

  • Формула динамического массива вводится в одну ячейку и завершается обычным нажатием клавиши Enter. Чтобы завершить старомодную формулу массива, вам нужно нажать Ctrl + Shift + Enter.
  • Новые формулы массива автоматически распределяются по многим ячейкам. Формулы СПП должны быть скопированы в диапазон ячеек, чтобы возвращать несколько результатов.
  • Размер вывода формул динамического массива автоматически изменяется при изменении данных в исходном диапазоне. Формулы CSE усекают выходные данные, если возвращаемая область слишком мала, и возвращают ошибки в дополнительных ячейках, если возвращаемая область слишком велика.
  • Формулу динамического массива можно легко редактировать в одной ячейке. Чтобы изменить формулу СПП, необходимо выделить и отредактировать весь диапазон.
  • Невозможно удалять и вставлять строки в диапазон формул СПП — сначала необходимо удалить все существующие формулы. С динамическими массивами вставка или удаление строк не является проблемой.

  Обратная совместимость: динамические массивы в прежних версиях Excel

  Когда вы открываете книгу, содержащую формулу динамического массива в старом Excel, она автоматически преобразуется в обычную формулу массива, заключенную в {фигурные скобки}. Когда вы снова откроете лист в новом Excel, фигурные скобки будут удалены.

  В прежних версиях Excel новые функции динамического массива и ссылки на диапазоны разлива получают префикс _xlfn, чтобы указать, что эта функция не поддерживается. Знак ссылки диапазона разброса (#) заменяется функцией ANCHORARRAY.

  Например, вот как выглядит УНИКАЛЬНАЯ формула в Excel 2013 :
  

  Большинство формул динамического массива (но не все!) будут продолжать отображать свои результаты в прежней версии Excel, пока вы не внесете в них какие-либо изменения. Редактирование формулы немедленно прерывает ее и отображает одно или несколько слов #ИМЯ? значения ошибок.
  

  Формулы динамического массива Excel не работают

  В зависимости от функции могут возникнуть различные ошибки, если вы используете неверный синтаксис или недопустимые аргументы. Ниже приведены 3 наиболее распространенные ошибки, с которыми вы можете столкнуться при использовании любой формулы динамического массива.

  #РАЗЛИВ! ошибка

  Когда динамический массив возвращает несколько результатов, но что-то блокирует диапазон разлива, #SPILL! возникает ошибка.

  Чтобы исправить ошибку, вам просто нужно очистить или удалить все ячейки в диапазоне разлива, которые не полностью пусты. Чтобы быстро определить все мешающие ячейки, щелкните индикатор ошибки, а затем нажмите 9.0291 Выберите мешающие ячейки .
  

  Помимо непустого диапазона разлива, эта ошибка может быть вызвана еще несколькими причинами. Для получения дополнительной информации см.:

  • Ошибка Excel #SPILL — причины и исправления
  • Как исправить ошибку #РАЗЛИВ! ошибка с ВПР, ПОИСКПОЗ ИНДЕКС, СУММЕСЛИ

  #ССЫЛКА! ошибка

  Из-за ограниченной поддержки внешних ссылок между книгами динамические массивы требуют, чтобы оба файла были открыты.