C++ | Математические константы и операции
Последнее обновление: 13.02.2023
Математические константы
Начиная со стандарта C++20 стандартная библиотека предоставляет модуль numbers, который содержит ряд встроенных математических констант. Некоторые наиболее распростраенные:
std::numbers::e: число 2.71828 (основание натурального алгоритма)std::numbers::pi: число π —3.14159...std::numbers::sqrt2: квадратный корень числа 2 —1.41421...std::numbers::phi: золотое сечение (число Фидия) φ —1.618...
Все эти числа представляют тип double
Математические функции
Заголовочный файл <cmath> стандартной библиотеки C++ определяет набор математических функций. которые можно использовать в программах. Перечислю наиболее распространенные:
abs(arg): вычисляет абсолютное значение arg.
В отличие от большинства функций , abs() возвращает
целочисленный тип, если arg является целым числом.ceil(arg): вычисляет ближайшее целое число, большее или равное arg, и возвращает его в виде числа с плавающей точкой. Например, выражениеstd::ceil(2.5)возвращает3.0, аstd::ceil(-2.5)—-2.0. (дробная часть округляется до единицы)floor(arg): вычисляет ближайшее целое число, меньшее или равное arg, и возвращает его в виде числа с плавающей точкой. Например, выражениеstd::floor(2.5)возвращает 2.0, аstd::floor(-2.5)— число -3.0. (дробная часть округляется до нуля)exp(arg): вычисляет выражениеearg.log(arg): вычисляет натуральный логарифм (по основанию e) числа arg.log10(arg): вычисляет логарифм по основанию 10 от arg.pow(arg1, arg2): вычисляет значение arg1, возведенное в степень arg2, то естьarg1arg2. Числа arg1 и arg2 могут быть целочисленными или с плавающей запятой. Так, результатstd::pow(2, 3)равен 8.0, аstd::pow(4, 0,5)равно 2,0.sqrt(arg): вычисляет квадратный корень из arg.round(arg),lround (arg)иllround (arg)округляют число до ближайщего целого. Разница между ними состоит в типа возвращаемого результата:round()возвращает число с плавающей точкой,lround (arg)— числоlong, аllround (arg)—long long.Половинные значения округляются до нуля:
std::lround(0.5)возвращает1L, тогда какstd::round(-1.5f)sin(arg): вычисляет синус угла, при этом arg представляет значение в радианах.cod(arg): вычисляет косинус угла.tan(arg): вычисляет тангенс угла.isinf(arg): возвращаетtrue, если аргумент представляет +-бесконечность.isnan(arg): возвращаетtrue, если аргумент представляет NaN.
В отличие от большинства функций , abs() возвращает
целочисленный тип, если arg является целым числом.
Пример применения некоторых функций:
#include <iostream>
#include <math.h> // подключаем заголовочный файл math.h
int main()
{
std::cout << "abs(-3) = " << std::abs(-3)<< "\n";
std::cout << "pow(-3, 2) = " << std::pow(-3, 2)<< "\n";
std::cout << "round(-3.4) = " << std::round(-3.2)<< "\n";
std::cout << "ceil(3.2) = " << std::ceil(3.2)<< "\n";
std::cout << "floor(3.2) = " << std::floor(3.2)<< "\n";
std::cout << "ceil(-3. 2) = " << std::ceil(-3.2)<< "\n";
std::cout << "floor(-3.2) = " << std::floor(-3.2)<< "\n";
}
2) = " << std::ceil(-3.2)<< "\n";
std::cout << "floor(-3.2) = " << std::floor(-3.2)<< "\n";
}
Консольный вывод:
abs(-3) = 3 pow(-3, 2) = 9 round(-3.4) = -3 ceil(3.2) = 4 floor(3.2) = 3 ceil(-3.2) = -3 floor(-3.2) = -4
Проверка результата арифметических операций на NaN и бесконечность:
#include <iostream>
#include <math.h>
int main()
{
double a{ 1.5 }, b{-1.5}, c{}, d {};
std::cout << a << "/" << b << " is Infinity? " << std::isinf(a / b) << std::endl;
std::cout << a << "/" << b << " is Nan? " << std::isnan(a / b) << std::endl;
std::cout << a << "/" << c << " is Infinity? " << std::isinf(a / c) << std::endl;
std::cout << c << "/" << d << " is NaN? " << std::isnan(c / d) << std::endl;
}
Консольный вывод:
1.
5/-1.5 is Infinity? 0
1.5/-1.5 is Nan? 0
1.5/0 is Infinity? 1
0/0 is NaN? 1
НазадСодержаниеВперед
Стандартный заголовок библиотеки Этот заголовок изначально был стандартной библиотекой C .
Types | |
float_t (C++11) | самый эффективный тип с плавающей точкой, по крайней мере такой же ширины, как и число с float (typedef) |
double_t (C++11) | самый эффективный тип с плавающей точкой, по крайней мере, такой же ширины, как double (typedef) |
Macros | |
HUGE_VALFHUGE_VALHUGE_VALL (C++11)(C++11) | указывает значение переполнения для float , double и long double соответственно(macro constant) |
INFINITY (C++11) | оценивается как положительная бесконечность или значение, гарантирующее переполнение числа с float (macro constant) |
NAN (C++11) | оценивает тихий NaN типа float (macro constant) |
math_errhandlingMATH_ERRNOMATH_ERREXCEPT (C++11)(C++11)(C++11) | определяет механизм обработки ошибок,используемый обычными математическими функциями (macro constant) |
Classification | |
FP_NORMALFP_SUBNORMALFP_ZEROFP_INFINITEFP_NAN (C++11)(C++11)(C++11)(C++11)(C++11) | указывает на категорию с плавающей запятой (macro constant) |
Functions | |
Basic operations | |
abs(float)fabsfabsffabsl (C++11)(C++11) | абсолютное значение значения с плавающей точкой (\(\small{|x|}\)|x|) (function) |
fmodfmodffmodl (C++11)(C++11) | остаток операции с плавающей запятой (function) |
remainderremainderfremainderl (C++11)(C++11)(C++11) | подписанный остаток операции дивизиона (function) |
remquoremquofremquol (C++11)(C++11)(C++11) | подписанный остаток,а также три последних бита операции дивизиона (function) |
fmafmaffmal (C++11)(C++11)(C++11) | плавленая операция умножения (function) |
| fmaxfmaxffmaxl (C++11)(C++11)(C++11) | большее из двух значений с плавающей точкой (function) |
fminfminffminl (C++11)(C++11)(C++11) | меньшее из двух значений с плавающей запятой (function) |
fdimfdimffdiml (C++11)(C++11)(C++11) | положительная разность двух значений с плавающей точкой (\({\small\max{(0,x-y)}}\)max(0,x-y)) (function) |
nannanfnanl (C++11)(C++11)(C++11) | not-a-number (NaN) (function) |
Linear interpolation | |
lerp (C++20) | линейная интерполяционная функция (function) |
Exponential functions | |
expexpfexpl (C++11)(C++11) | returnseвозведенный в заданную степень (\ ({\ small e ^ x} \) e x ) (function) |
exp2exp2fexp2l (C++11)(C++11)(C++11) | returns2возводится в заданную степень (\({\small 2^x}\)2 x ) (function) |
expm1expm1fexpm1l (C++11)(C++11)(C++11) | returnseв данной степени минус один (\({\ small e^x-1}\)e x -1) (function) |
loglogflogl (C++11)(C++11) | вычисляет естественный (базовыйe) логарифм (\ ({\ small \ ln {x}} \) ln (x)) (function) |
log10log10flog10l (C++11)(C++11) | общие (базовые)расчёты10) логарифм (\ ({\ small \ log_ {10} {x}} \) log 10 (x)) (function) |
log2log2flog2l (C++11)(C++11)(C++11) | логарифм по основанию 2 заданного числа (\ ({\ small \ log_ {2} {x}} \) log 2 (x)) (function) |
log1plog1pflog1pl (C++11)(C++11)(C++11) | натуральный логарифм (к основаниюe) из 1 плюс заданное число (\({\ small \ln{(1+x)}}\)ln(1+x)) (function) |
Power functions | |
powpowfpowl (C++11)(C++11) | возводит число в заданную степень (\(\small{x^y}\)x y ) (function) |
sqrtsqrtfsqrtl (C++11)(C++11) | вычисляет квадратный корень (\(\small{\sqrt{x}}\)√x) (function) |
cbrtcbrtfcbrtl (C++11)(C++11)(C++11) | вычисляет кубический корень (\(\small{\sqrt[3]{x}}\)3√x) (function) |
hypothypotfhypotl (C++11)(C++11)(C++11) | вычисляет квадратный корень из суммы квадратов двух или трех (C++17)заданных чисел (\(\scriptsize{\sqrt{x^2+y^2}}\)√x2 +y2 ), (\(\scriptsize{\sqrt{x^2+y^2+z^2} }\)√x2 +y2 +z2 ) (function) |
Trigonometric functions | |
sinsinfsinl (C++11)(C++11) | вычисляет синус (\({\small\sin{x}}\)sin(x)) (function) |
coscosfcosl (C++11)(C++11) | вычисляет косинус (\({\small\cos{x}}\)cos(x)) (function) |
tantanftanl (C++11)(C++11) | вычисляет тангенс (\({\small\tan{x}}\)tan(x)).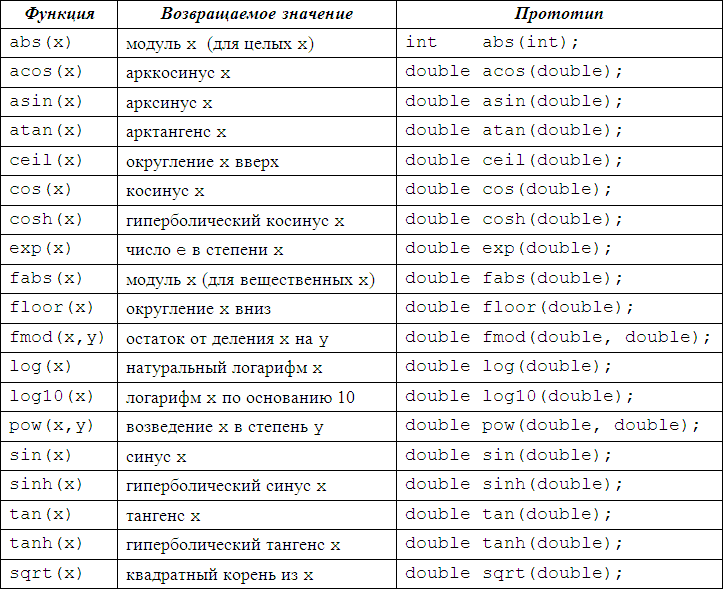 (function) |
asinasinfasinl (C++11)(C++11) | вычисляет синус дуги (\({\small\arcsin{x}}\)arcsin(x)) (function) |
acosacosfacosl (C++11)(C++11) | вычисляет косинус дуги (\({\small\arccos{x}}\)arccos(x)) (function) |
atanatanfatanl (C++11)(C++11) | вычисляет тангенс дуги (\({\small\arctan{x}}\)arctan(x)) (function) |
atan2atan2fatan2l (C++11)(C++11) | тангенс дуги,используя знаки для определения квадранта (function) |
Hyperbolic functions | |
sinhsinhfsinhl (C++11)(C++11) | вычисляет гиперболический синус (\({\small\sinh{x}}\)sinh(x)). (function) |
coshcoshfcoshl (C++11)(C++11) | вычисляет гиперболический косинус (\({\small\cosh{x}}\)cosh(x)). (function) |
tanhtanhftanhl (C++11)(C++11) | вычисляет гиперболический тангенс (\({\small\tanh{x}}\)tanh(x)).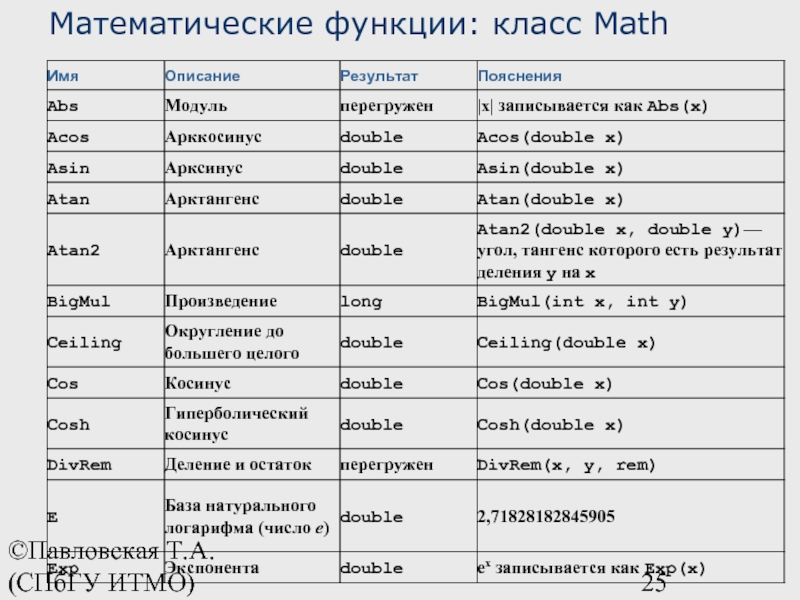 (function) |
asinhasinhfasinhl (C++11)(C++11)(C++11) | вычисляет обратный гиперболический синус (\({\small\operatorname{arsinh}{x}}\)arsinh(x)). (function) |
acoshacoshfacoshl (C++11)(C++11)(C++11) | вычисляет обратный гиперболический косинус (\({\small\operatorname{arcosh}{x}}\)arcosh(x)). (function) |
atanhatanhfatanhl (C++11)(C++11)(C++11) | вычисляет обратный гиперболический тангенс (\({\small\operatorname{artanh}{x}}\)artanh(x)). (function) |
Функции ошибок и гамма-функции | |
erferfferfl (C++11)(C++11)(C++11) | error function (function) |
erfcerfcferfcl (C++11)(C++11)(C++11) | дополнительная функция погрешности (function) |
tgammatgammaftgammal (C++11)(C++11)(C++11) | gamma function (function) |
lgammalgammaflgammal (C++11)(C++11)(C++11) | естественный логарифм гамма-функции (function) |
Ближайшие целочисленные операции с плавающей точкой | |
ceilceilfceill (C++11)(C++11) | ближайшее целое число не менее заданного значения (function) |
floorfloorffloorl (C++11)(C++11) | ближайшее целое число не больше заданного значения (function) |
trunctruncftruncl (C++11)(C++11)(C++11) | ближайшее целое число не больше заданного значения (function) |
roundroundfroundllroundlroundflroundlllroundllroundfllroundl (C++11)(C++11)(C++11)(C++11)(C++11)(C++11)(C++11)(C++11)(C++11) | ближайшее целое число,округляя от нуля в половине случаев. (function) |
nearbyintnearbyintfnearbyintl (C++11)(C++11)(C++11) | ближайшее целое число с использованием текущего округления (function) |
rintrintfrintllrintlrintflrintlllrintllrintfllrintl (C++11)(C++11)(C++11)(C++11)(C++11)(C++11)(C++11)(C++11)(C++11) | ближайшее целое число,использующее текущий режим округления с исключение,если результат отличается (function) |
Функции манипуляции с плавающей точкой | |
frexpfrexpffrexpl (C++11)(C++11) | разлагает число на значимое и степень 2 (function) |
ldexpldexpfldexpl (C++11)(C++11) | умножает число на 2 , возведенное в степень(function) |
modfmodffmodfl (C++11)(C++11) | разбивает число на целые и дробные части (function) |
scalbnscalbnfscalbnlscalblnscalblnfscalblnl (C++11)(C++11)(C++11)(C++11)(C++11)(C++11) | умножает число на FLT_RADIX , возведенное в степень(function) |
ilogbilogbfilogbl (C++11)(C++11)(C++11) | выдержка экспонат номера (function) |
logblogbflogbl (C++11)(C++11)(C++11) | выдержка экспонат номера (function) |
nextafternextafterfnextafterlnexttowardnexttowardfnexttowardl (C++11)(C++11)(C++11)(C++11)(C++11)(C++11) | следующее репрезентативное значение с плавающей точкой по отношению к заданному значению (function) |
copysigncopysignfcopysignl (C++11)(C++11)(C++11) | копирует знак плавающей запятой (function) |
Классификация и сравнение | |
fpclassify (C++11) | классифицирует данное значение с плавающей точкой (function) |
isfinite (C++11) | проверяет,имеет ли данное число конечное значение (function) |
isinf (C++11) | проверяет,не бесконечно ли заданное число (function) |
isnan (C++11) | проверяет,является ли данное число NaN (function) |
isnormal (C++11) | проверяет,является ли данное число нормальным (function) |
signbit (C++11) | проверяет,не является ли данное число отрицательным (function) |
isgreater (C++11) | проверяет,не превышает ли первый аргумент с плавающей точкой больше второго. (function) |
isgreaterequal (C++11) | проверяет,что первый аргумент с плавающей точкой больше или равен второму (function) |
isless (C++11) | проверяет,что первый аргумент с плавающей точкой меньше второго (function) |
islessequal (C++11) | проверяет,меньше или равно ли первый аргумент с плавающей точкой,чем второй (function) |
islessgreater (C++11) | проверяет,меньше или больше ли первый аргумент с плавающей точкой,чем второй (function) |
isunordered (C++11) | проверяет,не упорядочены ли два значения с плавающей запятой (function) |
Математические специальные функции | |
assoc_laguerreassoc_laguerrefassoc_laguerrel (C++17)(C++17)(C++17) | ассоциированные лагуерские полиномы (function) |
assoc_legendreassoc_legendrefassoc_legendrel (C++17)(C++17)(C++17) | связанные полиномы Легенды (function) |
betabetafbetal (C++17)(C++17)(C++17) | beta function (function) |
comp_ellint_1comp_ellint_1fcomp_ellint_1l (C++17)(C++17)(C++17) | (полный) эллиптический интеграл первого рода (function) |
comp_ellint_2comp_ellint_2fcomp_ellint_2l (C++17)(C++17)(C++17) | (полный) эллиптический интеграл второго рода (function) |
comp_ellint_3comp_ellint_3fcomp_ellint_3l (C++17)(C++17)(C++17) | (полный) эллиптический интеграл третьего рода (function) |
cyl_bessel_icyl_bessel_ifcyl_bessel_il (C++17)(C++17)(C++17) | обычные модифицированные цилиндрические функции Бесселя (function) |
cyl_bessel_jcyl_bessel_jfcyl_bessel_jl (C++17)(C++17)(C++17) | цилиндрические функции Бесселя (первого рода) (function) |
cyl_bessel_kcyl_bessel_kfcyl_bessel_kl (C++17)(C++17)(C++17) | неравномерные изменения цилиндрических функций Бесселя (function) |
cyl_neumanncyl_neumannfcyl_neumannl (C++17)(C++17)(C++17) | цилиндрические функции Неймана (function) |
ellint_1ellint_1fellint_1l (C++17)(C++17)(C++17) | (неполный) эллиптический интеграл первого рода |
ellint_2ellint_2fellint_2l (C++17)(C++17)(C++17) | (неполный) эллиптический интеграл второго рода (function) |
ellint_3ellint_3fellint_3l (C++17)(C++17)(C++17) | (неполный) эллиптический интеграл третьего рода (function) |
expintexpintfexpintl (C++17)(C++17)(C++17) | exponential integral (function) |
hermitehermitefhermitel (C++17)(C++17)(C++17) | Hermite polynomials (function) |
legendrelegendreflegendrel (C++17)(C++17)(C++17) | Legendre polynomials (function) |
laguerrelaguerreflaguerrel (C++17)(C++17)(C++17) | Laguerre polynomials (function) |
riemann_zetariemann_zetafriemann_zetal (C++17)(C++17)(C++17) | дзета-функция Римана (function) |
sph_besselsph_besselfsph_bessell (C++17)(C++17)(C++17) | сферические функции Бесселя (первого рода) (function) |
sph_legendresph_legendrefsph_legendrel (C++17)(C++17)(C++17) | сферические связанные функции Легенды (function) |
sph_neumannsph_neumannfsph_neumannl (C++17)(C++17)(C++17) | сферические функции Неймана (function) |
С++ cmath
КОДИРОВАНИЕ
PRO
СКИДКА 36%
Попробуйте на практике C++ с Programiz PRO
Получите скидку сейчас
C++ acos()
Возвращает арккосинус числа
C++ acosh()
возвращает гиперболический косинус числа
C++ asin()
Возвращает арксинус числа
C++ asinh()
возвращает гиперболическую дугу синус числа
C++ atan()
Возвращает арктангенс числа
C++ atan2()
Возвращает арктангенс координаты
C++ atanh()
возвращает аркгиперболический тангенс числа
C++ cbrt()
Вычисляет кубический корень числа 9 0005
С++ ceil()
Возвращает максимальное значение числа
C++ cmath abs()
Возвращает абсолютное значение аргумента
C++ copysign()
возвращает num со значением первого и знаком второго
C++ cos()
Возвращает Cos из Аргумент
C++ cosh()
Возвращает гиперболический косинус угла.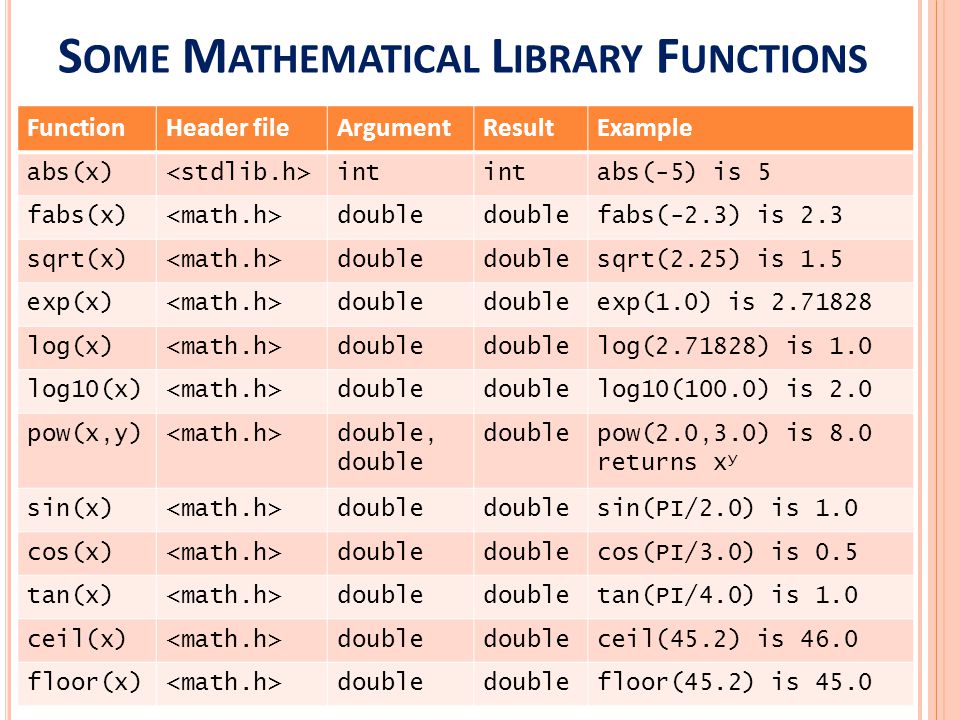
05
C++ expm1( )
Возвращает значение e в степени минус 1
C++ fabs()
Возвращает абсолютное значение аргумента
C++ fdim()
Возвращает положительное значение Различное между аргументами
C++ floor()
9 0002 Возвращает минимальное значение десятичного числаC++ fma()
Возвращает объединенное умножение-накопление
C++ fmax()
возвращает наибольший из двух переданных аргументов
C++ fmin()
возвращает наименьший из двух заданных аргументов
C++ fmod()
Вычисления остаток от деления с плавающей запятой
C++ frexp()
разбивает число с плавающей запятой на его двоичную мантиссу
C++ hypot()
Возвращает квадратный корень из суммы квадратов аргументов
C++ ilogb()
возвращает целую часть логарифма |x|
C++ ldexp()
возвращает произведение x и 2, возведенное в степень e
C++ llrint()
Округляет аргумент, используя текущий режим округления
C++ log()
Возвращает натуральный логарифм числа
C++ log10()
Возвращает логарифм числа по основанию 10
C++ log1p()
возвращает натуральный логарифм x+1.
C++ log2()
возвращает логарифм числа по основанию 2
C++ logb()
возвращает логарифм |x|
C++ lrint()
Округление аргумента с использованием текущего режима округления
C++ lround()
Возвращает значение типа long int, ближайшее к аргументу
С++ нано ()
возвращает тихое значение NaN
C++ nearint()
Округляет аргумент до использования текущего режима округления
C++ nextafter()
возвращает следующее значение после x в направлении y
C++ nexttoward()
возвращает следующее значение после x в направлении y
C++ pow()
Вычисляет мощность числа
90 010 С++ остаток ()Возвращает остаток x/y
C++ remquo()
Компьютерный остаток и сохраняет частное x/y
C++ rint()
Округляет аргумент, используя текущий режим округления
C++ round() 900 11
Возврат целочисленное значение, ближайшее к аргументу
C++ scalbln()
Масштабирует x с помощью FLT_RADIX в степень n
C++ scalbn()
Масштабирует x с помощью FLT_RADIX в степень n
C++ sin()
Возвращает S ine of the Argument
C++ sinh(
Возвращает гиперболический синус угла 11
возвращает гиперболический тангенс угла
C++ trunc()
Усекает кратную часть числа
cmath — Математические функции для комплексных чисел — Документация Python 3.
11.3 Этот модуль обеспечивает доступ к математическим функциям для комплексных чисел.
функции в этом модуле принимают целые числа, числа с плавающей запятой или комплексные
числа в качестве аргументов. Они также будут принимать любой объект Python, который имеет либо __complex__() или метод __float__() : эти методы используются для
преобразовать объект в комплексное число или число с плавающей запятой, соответственно, и
затем функция применяется к результату преобразования.
Примечание
Для функций, включающих обрезку ветвей, возникает проблема принятия решения о том, как
определите эти функции на самом разрезе. Вслед за Каханом «Срезание ветвей для
сложные элементарные функции», а также Приложение G документа C99 и более поздних версий C
стандартов, мы используем знак нуля, чтобы отличить одну сторону среза ответвления
от другого: для ветки, срезанной вдоль (участка) действительной оси, мы смотрим
по знаку мнимой части, а для ветви, срезанной по
мнимой оси смотрим на знак действительной части.
Например, функция cmath.sqrt() имеет ветвь, срезанную вдоль
отрицательная действительная ось. Аргумент complex(-2.0, -0.0) обрабатывается как
правда лежит ниже ветка срезана, а так дает результат на минус
мнимая ось:
>>> cmath.sqrt (complex (-2.0, -0.0)) -1,4142135623730951j
Но аргумент комплекс (-2.0, 0.0) обрабатывается так, как будто он лежит выше
вырез ветки:
>>> cmath.sqrt(complex(-2.0, 0.0)) 1.4142135623730951j
Преобразование в полярные координаты и обратно
Комплексный номер Python z хранится внутри с использованием прямоугольного или декартовых координат . Он полностью определяется его реальными
часть z.real и его мнимая часть z.imag . В других
слов:
z == z.real + z.imag*1j
Полярные координаты дают альтернативный способ представления комплекса
число.
В полярных координатах комплексное число z определяется
модуль r и фазовый угол фи . Модуль r — это расстояние
от z до начала координат, а фаза фи против часовой стрелки
угол, измеренный в радианах, от положительной оси x до линии
сегмент, соединяющий начало координат с z .
Следующие функции можно использовать для преобразования из собственного прямоугольных координат в полярные координаты и обратно.
- cmath.фаза( х )
Возвращает фазу x (также известную как аргумент из x ) в виде числа с плавающей запятой.
Phase(x)эквивалентноmath.atan2(x.imag, x.real). Результат лежит в диапазоне [- π , π ], а ветвь, разрезаемая для этой операции, лежит вдоль отрицательной действительной оси. Знак результата тот же, что и знакx.imag, даже еслиx.imagравен нулю:>>> фаза (комплекс (-1,0, 0,0)) 3.
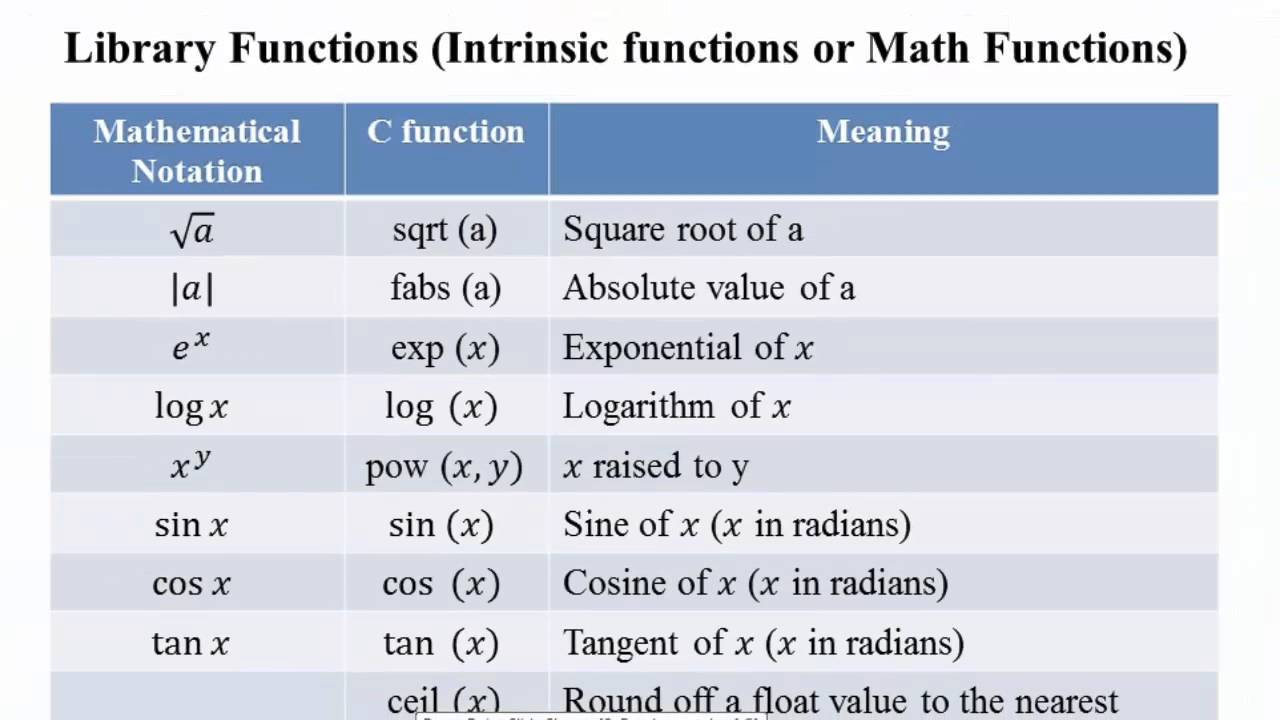141592653589793
>>> фаза (комплекс (-1.0, -0.0))
-3,141592653589793
141592653589793
>>> фаза (комплекс (-1.0, -0.0))
-3,141592653589793
Примечание
Модуль (абсолютное значение) комплексного числа x может быть
вычисляется с помощью встроенной функции abs() . Здесь нет
отдельная функция модуля cmath для этой операции.
- cmath.polar( x )
Возвращает представление x в полярных координатах. Возвращает пара
(r, phi), где r — это модуль x , а фи — это фаза x .polar(x)эквивалентно(abs(x), фаза(х)).
- cmath.rect( r , фи )
Возвращает комплексное число x с полярными координатами r и phi . Эквивалентно
r * (math.cos(phi) + math.sin(phi)*1j).
Степенные и логарифмические функции
- cmath.exp( x )
Возврат e в степени x , где e — основание натурального логарифмы.
- cmath.log( x [ база ])
Возвращает логарифм x по заданному основанию . Если база не указанный, возвращает натуральный логарифм x . Там одна ветка срезана, от 0 вдоль отрицательной вещественной оси до -∞.
- cmath.log10( x )
Возвращает логарифм по основанию 10 от x . У него такая же ветвь срезана, как
лог().
- cmath.sqrt( x )
Возвращает квадратный корень из x . Это имеет ту же ветку, что и
log().
Тригонометрические функции
- cmath.acos( x )
Возвращает арккосинус числа х . Есть два разреза ветвей: один проходит вправо от 1 вдоль вещественной оси до ∞. Другой простирается влево от -1 вдоль реальная ось до -∞.
- cmath.asin( x )
Возвращает арксинус x .
У него те же ветвления, что и у acos().
У него те же ветвления, что и у - cmath.atan( x )
Возвращает арктангенс x . Есть два разреза ветвей: один проходит от
1jпо мнимой оси до∞j. Другой простирается от-1jвдоль мнимой оси до-∞j.
- cmath.cos( x )
Возвращает косинус x .
- cmath.sin( x )
Возврат синуса x .
- cmath.tan( x )
Возврат касательной x .
Гиперболические функции
- cmath.acosh( x )
Возвращает гиперболический арккосинус x . Там одна ветка срезана, простираясь влево от 1 вдоль действительной оси до -∞.
- cmath.asinh( x )
Возврат обратного гиперболического синуса x .
Есть два разреза ветвей:
Один простирается от 1jвдоль мнимой оси до∞j. Другой простирается от-1jвдоль мнимой оси до-∞j.
Есть два разреза ветвей:
Один простирается от - cmath.atanh( x )
Возвращает гиперболический арктангенс x . Есть два разреза ветвей: один простирается от
1вдоль вещественной оси до∞. Другой простирается от-1по действительной оси до-∞.
- cmath.cosh( x )
Возвращает гиперболический косинус числа х .
- cmath.sinh( x )
Возвращает гиперболический синус x .
- cmath.tanh( x )
Возвращает гиперболический тангенс x .
Функции классификации
- cmath.isfinite( x )
Вернуть
Истинно, если и действительная, и мнимая части x конечны, иЛожьв противном случае.Новое в версии 3.2.
- cmath.isinf( x )
Возврат
Истинно, если действительная или мнимая часть x является бесконечность иFalseв противном случае.
- cmath.isnan( x )
Возврат
True, если действительная или мнимая часть x является NaN, иFalseв противном случае.
- cmath.isclose( a , b , * , rel_tol=1e-09 , abs_tol=0.0 )
Вернуть
True, если значения a и b близки друг к другу иFalseв противном случае.Считаются ли два значения близкими, определяется в соответствии с заданы абсолютные и относительные допуски.
rel_tol — относительный допуск — максимально допустимая разница между a и b относительно большего абсолютного значения a или b .
Например, чтобы установить допуск 5%, введите rel_tol=0,05. По умолчанию допуск равен1e-09, что гарантирует, что два значения совпадают. примерно с точностью до 9 знаков после запятой. rel_tol должен быть больше нуля.abs_tol — минимальный абсолютный допуск — полезно для сравнений вблизи нуль. abs_tol должен быть не меньше нуля.
Если ошибок нет, результат будет таким:
абс(а-б) <= макс(отн_допуск * макс(абс(а), абс(б)), абс_доп).Специальные значения IEEE 754
NaN,infи-infбудут обрабатывается в соответствии с правилами IEEE. В частности,NaNне считается близко к любому другому значению, включаяNaN.infи-infтолько считают близкими себе.Новое в версии 3.5.
См. также
PEP 485 — Функция проверки приблизительного равенства
Например, чтобы установить допуск 5%, введите Константы
- cmath. pi
Математическая константа π в виде числа с плавающей запятой.
pi- cmath.e
Математическая константа e в виде числа с плавающей запятой.
- cmath.тау
Математическая константа τ , как число с плавающей запятой.
Новое в версии 3.6.
- cmath.inf
Положительная бесконечность с плавающей запятой. Эквивалентно
float('inf').Новое в версии 3.6.
- cmath.infj
Комплексное число с нулевой действительной частью и положительной бесконечностью мнимой часть. Эквивалентно
complex(0.0, float('inf')).Новое в версии 3.6.
- cmath.нан
Значение с плавающей запятой «не число» (NaN). Эквивалентно
поплавок('нан').Новое в версии 3.6.
- cmath.nanj
Комплексное число с нулевой действительной частью и NaN мнимой частью.
Эквивалентно комплекс(0.0, число с плавающей запятой('нан')).Новое в версии 3.6.
Эквивалентно Обратите внимание, что выбор функций подобен, но не идентичен выбору в
модуль математика . Причина наличия двух модулей в том, что некоторые пользователи не
интересуются комплексными числами и, возможно, даже не знают, что они собой представляют. Они
лучше бы math.sqrt(-1) вызывает исключение, чем возвращает комплекс
число. Также обратите внимание, что функции, определенные в cmath , всегда возвращают
комплексное число, даже если ответ может быть выражен действительным числом (в котором
если комплексное число имеет мнимую часть нуля).
Замечание о ветвях: это кривые, вдоль которых данная функция не работает.
быть непрерывным. Они являются необходимым элементом многих сложных функций. Это
предполагается, что если вам нужно выполнять вычисления со сложными функциями, вы поймете
о обрезке веток. Проконсультируйтесь практически с любой (не слишком элементарной) книгой по сложным
переменные для просветления.