Циклический сдвиг си: массивы — Циклический сдвиг массива

5.4. Циклический сдвиг элементов массива

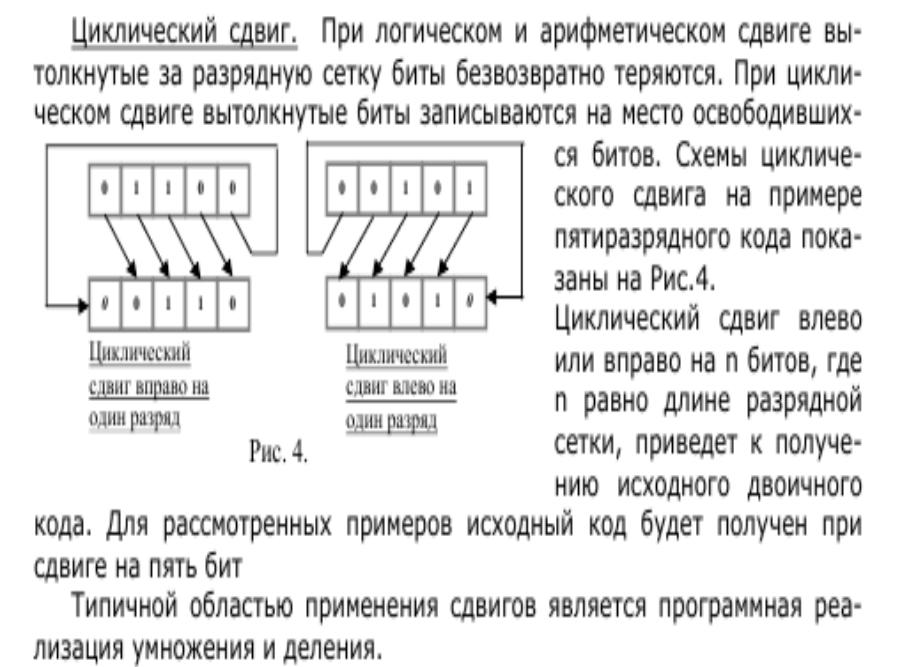
Под циклическим сдвигом понимается перестановка значений всех элементов массива на одну или несколько позиций влево или вправо. При этом значение первого (последнего) элемента массива заносится в последний (первый) элемент массива в зависимости от направления сдвига.

Схематичное изображение циклического сдвига элементов массива вправо на одну позицию, выполняемого в три этапа, показано на рис. 5.4.1. Блок-схема алгоритма, выполняющего такой сдвиг, показана на рис. 5.4.2.

На 1-м этапе значение последнего элемента массива X_N заносится в дополнительную переменную А (блок 1). На 2-м этапе организовывается цикл «Для» на основе блока модификации (блок 2), который перебирает элементы массива Х в обратном порядке, т.е. с правого края (шаг -1), начиная с N-го и заканчивая 2-м элементом. На каждом шаге цикла текущему элементу X

i присваивается значение предыдущего элемента X_i-1 (блок 3). В результате выполнения 2-го этапа значение предварительно сохраненного последнего элемента массива будет удалено. Значения остальных элементов массива будут смещены на одну позицию вправо. Значение первого элемента массива будет продублировано во втором элементе. На 3-м этапе алгоритма значение дополнительной переменной А, в которой хранится последний элемент исходного массива, будет занесено в первый элемент массива X₁. В итоге будет выполнен циклический сдвиг элементов массива Х на одну позицию вправо.

Следует обратить внимание на граничные значения параметра цикла i, который изменяется от N до 2. При подстановке этих значений в формулу сдвига не должно происходить обращение к несуществующим элементам массива. При i

=N формула сдвига принимает вид X_N =X_{N —1}, при i =2 – X₂ =X₁. В случае если бы правая граница параметра i была равна 1, то в формуле сдвига происходило бы обращение к несуществующему элементу массива с индексом 0: X₁=X₀, что недопустимо.

Схематичное изображение циклического сдвига элементов массива влево на одну позицию, также выполняемого в три этапа, показано на рис. 5.4.3. Блок-схема алгоритма, выполняющего такой сдвиг, показана на рис. 5.4.4.

На 1-м этапе значение первого элемента массива X₁ заносится в дополнительную переменную А (блок 1). На 2-м этапе организовывается цикл «Для» (блок 2), который перебирает элементы массива Х в прямом порядке, т.е. с левого края (шаг +1), начиная с 1-го и заканчивая N-1-м элементом. На каждом шаге цикла текущему элементу X_i присваивается значение последующего элемента массива X_i+1 (блок 3). В результате выполнения 2-го этапа значение предварительно сохраненного первого элемента массива будет удалено. Значения остальных элементов массива будут смещены на одну позицию влево. Значение последнего элемента массива будет продублировано в предпоследнем элементе. На 3-м этапе алгоритма значение дополнительной переменной А, в которой хранится первый элемент исходного массива, будет занесено в последний элемент массива

X_N. В итоге будет выполнен циклический сдвиг элементов массива Х на одну позицию влево.

Для выполнения циклического сдвига элементов массива на k позиций достаточно k раз выполнить алгоритм сдвига на одну позицию, т.е. добавить внешний цикл, который будет требуемое количество раз повторять сдвиг на одну позицию. Пример блок-схемы алгоритма, выполняющего циклический сдвиг элементов массива на k позиций влево, представлен на рис. 5.4.5.

Сдвиг элементов массива находит применение при удалении или добавлении элементов в массив, а также в других задачах.

Циклический сдвиг элементов массива — Студопедия

Поделись с друзьями: 

Под циклическим сдвигом понимается перестановка значений всех элементов массива на одну или несколько позиций влево или вправо. При этом значение первого (последнего) элемента массива заносится в последний (первый) элемент массива в зависимости от направления сдвига.

Схематичное изображение циклического сдвига элементов массива вправо на одну позицию, выполняемого в три этапа, показано на рис. 5.4.1. Блок-схема алгоритма, выполняющего такой сдвиг, показана на рис. 5.4.2.

На 1-м этапе значение последнего элемента массива X_N заносится в дополнительную переменную А (блок 1). На 2-м этапе организовывается цикл «Для» на основе блока модификации (блок 2), который перебирает элементы массива Х в обратном порядке, т.е. с правого края (шаг -1), начиная с N -го и заканчивая 2-м элементом. На каждом шаге цикла текущему элементу X_i присваивается значение предыдущего элемента X_{i -1}

(блок 3).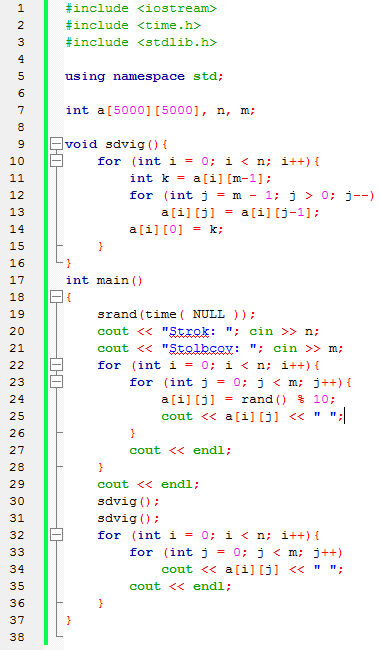 В результате выполнения 2-го этапа значение предварительно сохраненного последнего элемента массива будет удалено. Значения остальных элементов массива будут смещены на одну позицию вправо. Значение первого элемента массива будет продублировано во втором элементе. На 3-м этапе алгоритма значение дополнительной переменной А, в которой хранится последний элемент исходного массива, будет занесено в первый элемент массива X ₁. В итоге будет выполнен циклический сдвиг элементов массива Х на одну позицию вправо.

Следует обратить внимание на граничные значения параметра цикла i, который изменяется от N до 2. При подстановке этих значений в формулу сдвига не должно происходить обращение к несуществующим элементам массива. При i =N

формула сдвига принимает вид X_N = X_{N — 1}, при i =2 – X ₂ = X ₁. В случае если бы правая граница параметра i была равна 1, то в формуле сдвига происходило бы обращение к несуществующему элементу массива с индексом 0: X ₁ = X ₀, что недопустимо.

Схематичное изображение циклического сдвига элементов массива влево на одну позицию, также выполняемого в три этапа, показано на рис. 5.4.3. Блок-схема алгоритма, выполняющего такой сдвиг, показана на рис. 5.4.4.

На 1-м этапе значение первого элемента массива X ₁ заносится в дополнительную переменную

А (блок 1). На 2-м этапе организовывается цикл «Для» (блок 2), который перебирает элементы массива Х в прямом порядке, т.е. с левого края (шаг +1), начиная с 1-го и заканчивая N -1-м элементом. На каждом шаге цикла текущему элементу X_i присваивается значение последующего элемента массива X_{i +1} (блок 3). В результате выполнения 2-го этапа значение предварительно сохраненного первого элемента массива будет удалено. Значения остальных элементов массива будут смещены на одну позицию влево. Значение последнего элемента массива будет продублировано в предпоследнем элементе. На 3-м этапе алгоритма значение дополнительной переменной А, в которой хранится первый элемент исходного массива, будет занесено в последний элемент массива X_N. В итоге будет выполнен циклический сдвиг элементов массива Х на одну позицию влево.

Для выполнения циклического сдвига элементов массива на k позиций достаточно k раз выполнить алгоритм сдвига на одну позицию, т.е. добавить внешний цикл, который будет требуемое количество раз повторять сдвиг на одну позицию. Пример блок-схемы алгоритма, выполняющего циклический сдвиг элементов массива на k позиций влево, представлен на рис. 5.4.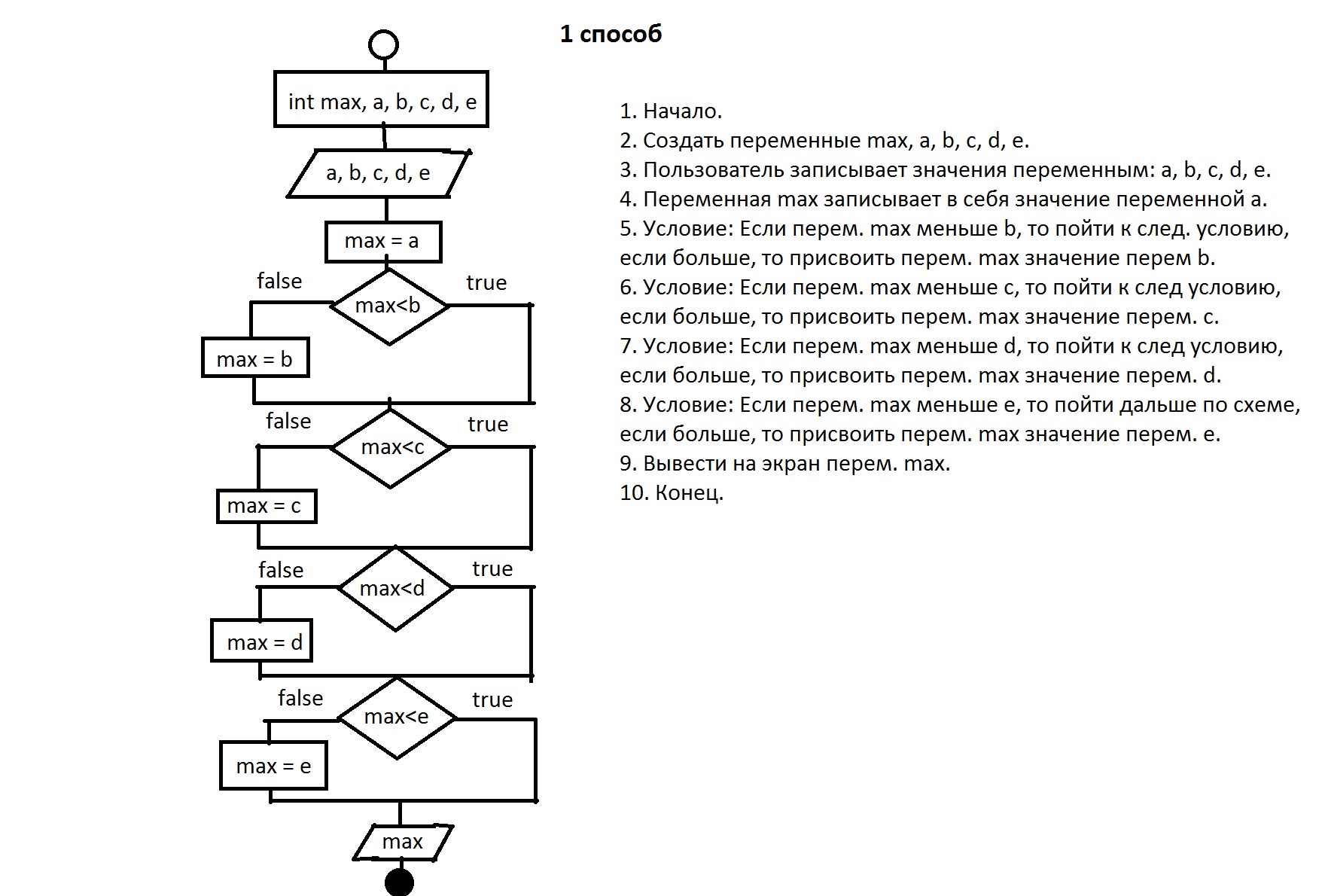 5.

Сдвиг элементов массива находит применение при удалении или добавлении элементов в массив, а также в других задачах.

---

Понравилась статья? Добавь ее в закладку (CTRL+D) и не забудь поделиться с друзьями:  

---



Оценка циклического сдвига с отсроченной корреляцией и совпадающей фильтрацией во временной области циклическая-SLM для снижения PAPR

на этой стр.

AbstractIntroductionsystem ModelConclisionsReferencescopyrightrelated Статьи

Циклосное отображение TDC-SLM). коэффициент мощности (PAPR) в системах OFDM, в то время как количество циклических сдвигов требуется для восстановления переданного сигнала в приемнике. Одной из критических проблем схемы SLM является отправка дополнительной информации (SI), которая снижает пропускную способность в беспроводных системах OFDM. Предлагаемая схема реализует корреляцию с задержкой и согласованную фильтрацию (DC-MF) для оценки количества циклических сдвигов в приемнике. В предложенной схеме DC-MF размещается после выравнивания в частотной области (FDE) для повышения точности оценки циклического сдвига. Точность предложенной схемы достигает 100% при = 5 дБ, а частота ошибок по битам (BER) улучшается на 0,2 дБ по сравнению с обычным TDC-SLM. Показатели BER предложенной схемы также лучше, чем у обычного TDC-SLM, даже несмотря на то, что предполагается нелинейный усилитель высокой мощности.

1. Введение

Мультиплексирование с ортогональным частотным разделением каналов (OFDM) — это модуляция с несколькими несущими, которая обеспечивает надежную высокоскоростную скорость передачи данных благодаря высокой спектральной эффективности и устойчивости к каналам с многолучевым замиранием. Одной из существенных проблем сигнала OFDM является его высокое отношение пиковой мощности к средней мощности (PAPR), которое требует линейности широкого диапазона в усилителе мощности (PA). Высокий PAPR может вывести усилитель мощности в область насыщения, создать помехи между поднесущими и исказить спектр сигнала [1–3]. Были доступны некоторые схемы уменьшения PAPR, например, кодирование, фильтрация и отсечение, а также фазовая манипуляция (выборочное отображение и частичные последовательности передачи).

Selective mapping (SLM) — одна из популярных схем снижения PAPR без искажения сигнала. SLM — это вероятностная схема, в которой сигналы-кандидаты (SC) генерируются путем умножения исходной последовательности сигналов и последовательности фаз. Для передачи выбирается SC с наименьшим PAPR. В SLM дополнительная информация (SI) необходима на стороне получателя для восстановления переданного сигнала. SI обычно передается как набор битов для каждого символа OFDM, и для его защиты от жесткого канала требуется кодирование канала. Это связано с уменьшением пропускной способности в беспроводных системах OFDM. Кроме того, SLM имеет большую вычислительную сложность, поскольку требует нескольких операций обратного дискретного преобразования Фурье (IDFT) и накладывает ограничения на реализацию. Для решения этой проблемы также была предложена менее сложная схема SLM [4–15].

Для исключения SI было предложено множество схем [9–16]. Схема в [9] делает разницу между средними энергиями расширенных и нерасширенных символов для восстановления SI в приемнике. Как следствие, символы модуляции более высокого порядка будут влиять на точность обнаружения SI. Схема в [10] реализует полуслепое обнаружение SI в SLM. Однако эта схема требует внедрения SI в символы передачи. В схеме, представленной в [11], циклический SLM во временной области с задержкой корреляции (DC) применяется для уменьшения PAPR и оценки величины циклического сдвига в приемнике без передачи SI. Тем не менее, существует компромисс между степенью снижения PAPR и BER. Метод в [12] был предложен для дальнейшего снижения PAPR вышеупомянутой схемы. Он использует согласованную фильтрацию (MF) с последовательностью Баркера для оценки количества циклических сдвигов. Одной из причин ошибки оценки являются многолучевые компоненты. Эти компоненты вводят в заблуждение выходные данные DC-MF.

В этой статье предлагается циклический SLM во временной области (TDC-SLM) без передачи SI. Предлагаемый циклический SLM во временной области (TDC-SLM) помещает DC-MF после коррекции в частотной области (FDE) для удаления компонентов многолучевого распространения в принимаемом сигнале. На стороне передатчика сигнал передачи генерируется путем суммирования исходного сигнала и сигналов с циклическими сдвигами. На стороне приемника количество циклических сдвигов определяется с помощью DC-MF. В предлагаемой схеме интервалы между циклическими сдвигами рассчитаны таким образом, чтобы приемник мог различать циклические сдвиги и многолучевые задержки при использовании MF. Однако компоненты многолучевости все еще ухудшают точность оценки циклического сдвига, поскольку они генерируют дополнительные пики на выходах DC-MF. При использовании предложенной схемы повышается точность, а частота ошибок по битам (BER) снижается по сравнению с обычными TDC-SLM и DC-MF в [12].

Остальная часть этого документа организована следующим образом. Раздел 1 содержит введение. В разделе 2 объясняются системные модели, включая структуру символов OFDM, циклически-избирательное отображение во временной области, оценку канала и выравнивание в частотной области, а также предлагаемую схему оценки циклического сдвига. В Разделе 3 представлены результаты работы предложенной схемы, и, наконец, Раздел 4 завершает эту статью.

2. Модель системы

2.1. Символ OFDM

Дискретный сигнал OFDM во временной области может быть записан следующим образом: где — индекс времени, — символ данных на й поднесущей, обозначает индекс поднесущей и — количество поднесущих. Сигнал OFDM также может быть определен как вектор.

Для уменьшения межсимвольной интерференции необходим защитный интервал (GI). GI можно получить, скопировав последнюю часть сигнала OFDM и добавив ее в начало сигнала, где — длина GI.

2.2. Циклически-селективное отображение во временной области

В схеме TDC-SLM сигнал на каждой ветви генерируется путем применения циклического сдвига к исходному сигналу. Блок-схема схемы TDC-SLM показана на рисунке 1. Циклически сдвинутый сигнал в TDC-SLM представлен как где – сигнал OFDM во временной области с временным индексом , – длина GI, – SC, который генерируется путем циклического сдвига сигнала OFDM на , является величиной циклического сдвига для th SC, и , где является целым числом [11, 12].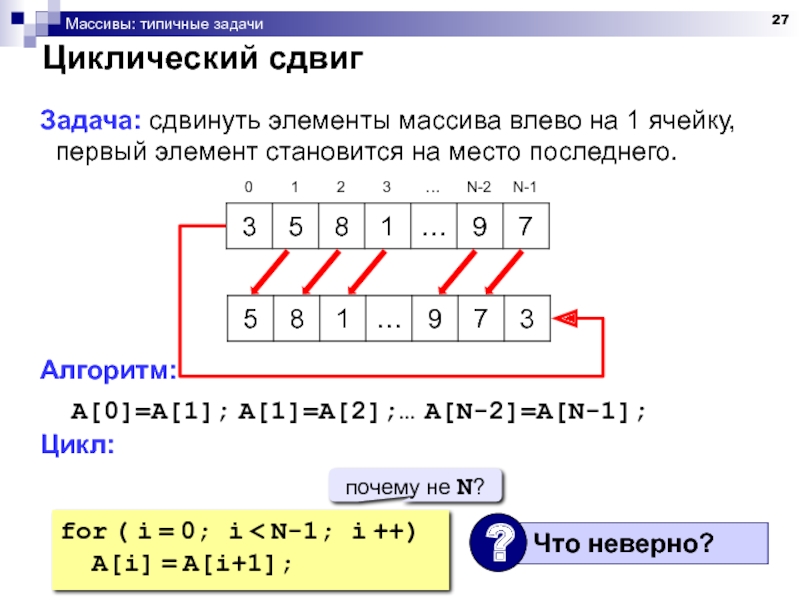 Разрешение циклических сдвигов должно быть достаточно большим для точной оценки циклических сдвигов в приемнике.

Передатчик объединяет SC с исходным сигналом во временной области следующим образом: где — сигнал передачи, — количество ветвей, — й коэффициент в фазовой последовательности, — исходный сигнал с GI. Один и тот же набор применяется к нескольким символам, поскольку соответствующие выходные данные DC-MF усредняются для повышения точности оценки циклического сдвига. Таким образом, набор выбирается таким образом, чтобы максимальное PAPR по символам для усреднения было минимальным. Здесь PAPR вычисляется для каждого периода символа OFDM, где обозначает операцию ожидания.

2.3. Оценка канала и выравнивание частотной области

Частотная характеристика и приблизительная синхронизация символов могут быть получены путем отправки символов преамбулы в начале передаваемого сигнала. Принятый сигнал преамбулы указывается где и является переданным и принятым сигналами преамбулы во временной области соответственно. В приемнике сигнал преамбулы на й поднесущей демодулируется с помощью дискретного преобразования Фурье (ДПФ) как

. Оценка частотной характеристики канала на й поднесущей в частотной области дается следующим образом: где передаваемые символы преамбулы на й поднесущей. Из-за TDC-SLM во временной области частотная характеристика канала должна быть изменена в течение периода данных. Наложение последовательности данных работает подобно искусственному многолучевому отклику канала. Чтобы вычислить частотную характеристику канала в периоде данных, предполагаемая характеристика канала преобразуется в импульсную характеристику в области задержки следующим образом: где — th импульсная характеристика канала, и обозначает транспонирование.

Коэффициенты коррекции в частотной области (FDE) с минимальной среднеквадратичной ошибкой (MMSE-) для th поднесущей, где обозначает сопряженную частотную характеристику канала, полученную из (8), и представляет собой дисперсию шум оценивается в приемнике. Затем демодулированный сигнал на й поднесущей обозначает сигнал на й поднесущей в приемнике.

2.4. Схема оценки циклического сдвига

DC-MF применяется к сигналу во временной области после MMSE-FDE для оценки количества циклических сдвигов в приемнике. Принятый сигнал во временной области может быть записан как где – частотная характеристика канала, – составляющая сигнала, – гауссовский шум на й поднесущей. Кроме того, — принятый сигнал, — отношение сигнал-шум на выборку, — размер ДПФ, и обозначает сопряженный. Процесс DC-MF состоит из DC и MF, как показано на рисунке 2. На стороне передатчика TDC-SLM генерирует несколько SC, применяя циклические сдвиги к исходному сигналу после обратного DFT (IDFT) и генерирует сигнал передачи через суммирование исходного сигнала и СК. DC-MF используется для оценки количества циклических сдвигов, поскольку они необходимы для восстановления передаваемого сигнала.

В основном процесс DC умножает полученный сигнал во временной области на сопряженную последовательность GI.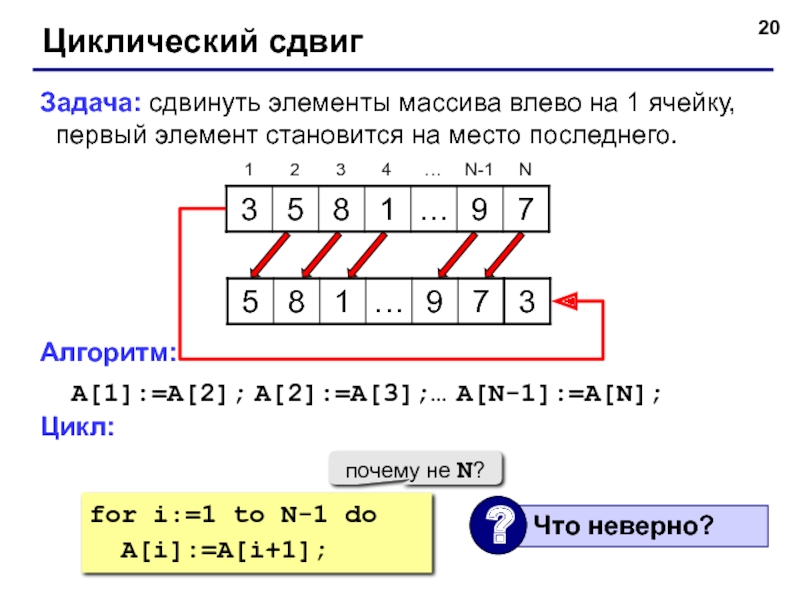 Самый большой пик появляется, когда последняя часть символа OFDM умножается на сопряженный GI. Выходной сигнал DC помещается в MF для оценки набора циклических сдвигов путем обнаружения второго по величине пикового выходного сигнала. Процессы DC-MF с 3 ветвями показаны на рисунке 3. DC определяется следующим образом: где и и — компоненты сигнала и шума на й поднесущей, выходящие из задержанной ветви DC, соответственно. После суммирования выходы ДК усредняются следующим образом: где — количество символов, использованных в процессе усреднения. Первый пик обусловлен GI и находится путем максимизации as Кроме того, DC производит корреляцию между последовательностью GI и принятым сигналом с задержкой , то есть . Передаваемый сигнал в GI состоит из последней части исходного сигнала OFDM, а также последней части последовательности SC, . Следовательно, если , DC выводит другой пик следующим образом:где кандидат на величину циклического сдвига на й ветви. Уравнение (16) можно переписать в виде Следовательно, пиковый выход ДК задается как

Затем выходные данные DC передаются в MF для оценки количества циклических сдвигов. На рис. 4 представлена ​​структура МФ. Для уменьшения количества комбинаций здесь величины циклических сдвигов выбираются из каждой выборки как . В составе СЧ есть линия задержки, в которой все задержки установлены на . Выход MF выражается следующим образом:где выход MF.

Циклический сдвиг первой ветви, , оценивается посредством максимизации как, где — расчетная величина циклического сдвига для первой ветви, . Импульсная характеристика канала в (9) сдвигается на расчетные циклические сдвиги и суммируется с исходной импульсной характеристикой следующим образом: Принятый сигнал в частотной области после компенсации канала задается следующим образом: где характеристика канала на й поднесущей в периоде данных равна

3 Численные результаты

3.1. Условия моделирования

В таблице 1 показаны параметры моделирования предлагаемой схемы, которые взяты из параметров LTE. Количество поднесущих данных равно 128, и каждая поднесущая модулируется с помощью QPSK. Размер DFT равен 256, а длина GI установлена ​​равной 64 выборкам.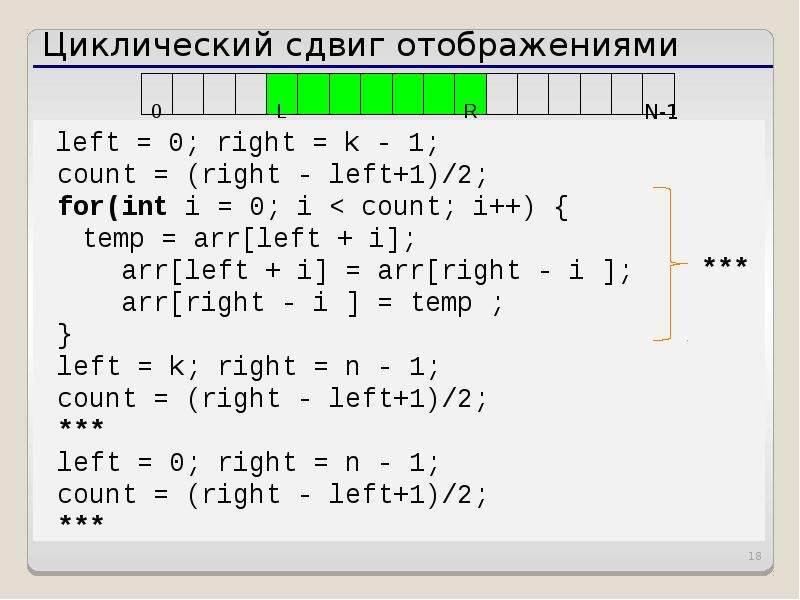 Количество символов для усреднения устанавливается равным 1, 2, 4 или 8, а диапазон циклического сдвига () ограничивается от 60 до 124 с разрешением каждые 4 отсчета (), что означает 16 СК. Применяется сверточный код со скоростью 1/2 и длиной ограничения 7 с полиномиальным генератором. Применяется блочный перемежитель размером . Количество ветвей равно 3, и в качестве фазовой последовательности используется последовательность Баркера длиной 3 (). Однородный профиль задержки с 6 путями предполагается в качестве модели канала при компьютерном моделировании. В качестве нелинейного усилителя высокой мощности (HPA) предполагается модель твердотельного усилителя мощности (SSPA) Раппа с коэффициентом колена 3. Входной откат (IBO) для HPA установлен на 0, 2 и 4 дБ.

3.2. Снижение PAPR

Кривые характеристик PAPR оцениваются с точки зрения дополнительных кумулятивных функций распределения (CCDF). TDC-SLM предполагает переходы с разрешением циклического сдвига , а количество символов для усреднения выбирается из 1, 2, 4 или 8. Из рисунка 5 видно, что по сравнению с исходным сигналом Величина снижения PAPR в TDC-SLM для 1, 2, 4 или 8 символов для усреднения составляет 2,8 дБ, 2,7 дБ, 2,6 дБ и 2,5 дБ соответственно при CCDF . Когда количество символов для усреднения равно 1, каждый символ OFDM имеет различный набор циклических сдвигов, и достигается наилучшее снижение PAPR. С другой стороны, наименьшее уменьшение PAPR реализуется, когда 8 символов OFDM имеют одинаковый набор циклических сдвигов для усреднения соответствующих выходных сигналов постоянного тока. Тем не менее, разница в величине снижения PAPR для 1 и 8 символов для усреднения составляет всего 0,3 дБ при CCDF .

3.3. Коэффициент точности и производительность BER

Коэффициент точности представляет собой отношение правильной оценки с точки зрения количества циклических сдвигов на стороне приемника. Степень точности оценки циклического сдвига показана на рисунке 6. Здесь предполагается канал с равномерным профилем задержки. На рисунке 6 точность предлагаемой схемы для 1, 2, 4 или 8 символов для усреднения составляет около 57,04%, 87,80%, 98,28% и 100% соответственно при  дБ.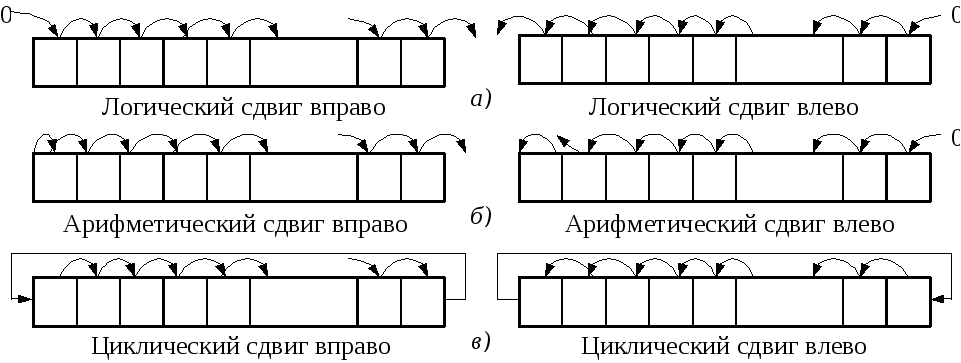 Многолучевой канал влияет на степень точности оценки циклического сдвига. Отмечено, что показатели точности предложенной схемы с 8 символами для усреднения самые высокие по сравнению с другими. Показатели точности предложенной схемы и традиционной TDC-SLM с 8 символами для усреднения достигают 100% при и  dB, для 8 символов для усреднения соответственно. Показатели точности на 2 дБ лучше, чем у обычной схемы TDC-SLM.

Коэффициент точности влияет на производительность BER. Показатели BER предложенной схемы и традиционной схемы TDC-SLM с 8 символами для усреднения представлены на рисунке 7 на канале с равномерным профилем задержки. Разница между BER при идеальной оценке и предложенной схемой с 8 символами для усреднения составляет 0,6 дБ, что на 0,2 дБ лучше, чем у традиционной схемы TDC-SLM.

Также оцениваются BER и коэффициент точности HPA. На рисунке 8 представлено сравнение показателей точности между предложенной схемой и обычной TDC-SLM. Количество символов для усреднения установлено равным 8. Точность предлагаемой схемы достигает 100% при = 10 дБ, 11 дБ и 13 дБ для IBO 4 дБ, 2 дБ и 0 дБ соответственно. С другой стороны, уровень точности обычного TDC-SLM достигает 100 % при = 11 дБ, 12 дБ и 14 дБ для IBO 4 дБ, 2 дБ и 0 дБ соответственно. Это показывает, что уровень точности предложенной схемы улучшается, когда DC-MF помещается после FDE-MMSE, даже если предполагается нелинейность HPA. Показатели точности на 1 дБ лучше по сравнению с обычной схемой TDC-SLM.

BER для различных значений IBO также оцениваются, как показано на рисунке 9. В обычном TDC-SLM требуемые значения BER составляют 13 дБ, 13,3 дБ и 13,8 дБ, для IBO 4 дБ , 2 дБ и 0 дБ соответственно. С другой стороны, при предложенной схеме это 12,8 дБ, 13,1 дБ и 13,3 дБ для IBO 4 дБ, 2 дБ и 0 дБ соответственно. Замечено, что BER улучшается за счет увеличения IBO. Различия BER между обычной TDC-SLM и предложенной схемой составляют 0,4 дБ, 0,3 дБ и 0,4 дБ при BER для IBO, равном 4 дБ, 2 дБ и 0 дБ соответственно. Доказано, что предложенная схема улучшает уровень точности и производительность BER, поскольку они приближаются к значениям с идеальной оценкой.

4. Выводы

В этой статье была предложена схема обнаружения SI для TDC-SLM. DC-MF реализуется после обнаружения MMSE для устранения эффекта многолучевого канала. Величина снижения PAPR с TDC-SLM составляет около 2,5 дБ по сравнению с исходным сигналом для 8 символов для усреднения, когда разрешение циклического сдвига равно выборкам. Точность предложенной схемы достигает 100% при = 5 дБ, а разница BER с 8 символами для усреднения составляет около 0,6 дБ по сравнению с идеальной оценкой SI. BER на 0,2 дБ лучше, чем у обычной схемы TDC-SLM. При нелинейности HPA предложенная схема по-прежнему улучшает характеристики BER примерно на 0,4 дБ при BER для IBO, равном 4 дБ, 2 дБ и 0 дБ.

Конкурирующие интересы

Авторы заявляют, что у них нет конкурирующих интересов.

Ссылки

1. Y. Rahmatallah и S. Mohan, «Уменьшение отношения пиковой мощности к средней в системах OFDM: обзор и таксономия», IEEE Communications Surveys and Tutorials , vol. 15, нет. 4, стр. 1567–1592, 2013.

   Посмотреть по адресу:
   Сайт издателя | Google Scholar

2. К. Бае, К. Шин и Э. Дж. Пауэрс, «Анализ производительности систем OFDM с выбранным отображением при наличии нелинейности», IEEE Transactions on Wireless Communications , vol. 12, нет. 5, стр. 2314–2322, 2013.

   Посмотреть по адресу:
   Сайт издателя | Google Scholar

3. Т. Цзян и Ю. Ву, «Обзор: методы снижения отношения пиковой мощности к средней для сигналов OFDM», IEEE Transactions on Broadcasting , vol. 54, нет. 2, стр. 257–268, 2008 г.

   Посмотреть по адресу:
   Сайт издателя | Google Scholar

4. C.-L. Ван и Ю. Оуян, «Выбранные схемы отображения низкой сложности для снижения отношения пиковой мощности к средней мощности в системах OFDM», IEEE Transactions on Signal Processing , vol. 53, нет. 12, стр. 4652–4660, 2005.

   Посмотреть по адресу:
   Сайт издателя | ученый Google | MathSciNet

5. Л. Ян, К. К. Су, Ю. М. Сиу и С. К. Ли, «Выбранная схема отображения низкой сложности с использованием метода наложения последовательностей во временной области для уменьшения PAPR в системе OFDM», IEEE Transactions on Broadcasting , vol. . 54, нет. 4, стр. 821–824, 2008 г.

   Посмотреть по адресу:
   Сайт издателя | Академия Google

6. Дж. С. Ван, С. Хванг, С. Дж. Ким и Ю. Х. Ким, «Объединение сигналов во временной области с циклической задержкой и фазовым сдвигом для уменьшения PAPR в системах OFDM», в Proceedings of the IEEE International Conference on Consumer Electronics (ICCE). ’11) , стр. 449–450, январь 2011 г.

   Посмотреть по адресу:
   Сайт издателя | Google Scholar

7. С.-Дж. Хео, Х.-С. Но, Ж.-С. Нет, и Д.-Ж. Шин, «Модифицированная схема SLM с низкой сложностью для снижения PAPR в системах OFDM», IEEE Transactions on Broadcasting , vol. 53, нет. 4, стр. 804–808, 2007 г.

   Посмотреть по адресу:
   Сайт издателя | Google Scholar

8. Х. -Б. Чон, Дж.-С. Нет, и Д.-Ж. Шин, «Схема SLM низкой сложности, использующая аддитивные последовательности отображения для уменьшения PAPR сигналов OFDM», IEEE Transactions on Broadcasting , vol. 57, нет. 4, стр. 866–875, 2011.

   Посмотреть по адресу:
   Сайт издателя | Google Scholar

9. С. Ю. Ле Гофф, С. С. Аль-Самахи, Б. К. Ху, К. С. Цименидис и Б. С. Шариф, «Выбранное сопоставление без дополнительной информации для уменьшения PAPR в OFDM», IEEE Transactions on Wireless Communications , vol. 8, нет. 7, стр. 3320–3325, 2009.

   Посмотреть по адресу:
   Сайт издателя | Google Scholar

10. Э. Ф. Бадран и А. М. Эль-Хелв, «Новый полуслепой выбранный метод отображения для уменьшения PAPR в OFDM», IEEE Signal Processing Letters , vol. 18, нет. 9, стр. 493–496, 2011.

    Посмотреть по адресу:
    Сайт издателя | Google Scholar

11. П. Д. Памунгкасари и Ю. Санада, «Уменьшение PAPR с использованием циклически-селективного отображения с отложенной корреляцией во временной области», в Труды 81-й конференции IEEE по автомобильным технологиям (VTC ’15) , стр. 1–5, IEEE, Глазго, Великобритания, май 2015 г.

    Посмотреть по адресу:
    Сайт издателя | Google Scholar

12. П. Д. Памунгкасари и Ю. Санада, «Циклично-селективное отображение во временной области для уменьшения PAPR с использованием корреляции с задержкой и согласованным фильтром в системе OFDM», в Трудах 22-й Международной конференции по телекоммуникациям (ICT ’15) , стр. 373–377, IEEE, Сидней, Австралия, апрель 2015 г.

    Посмотреть по адресу:
    Сайт издателя | Google Scholar

13. П. Д. Памунгкасари и Ю. Санада, «Оценка циклического сдвига с корреляцией с задержкой и согласованной фильтрацией в циклическом снижении PAPR с помощью SLM», Технический отчет IEICE , том. 114, нет. 402, стр. CS2014–CS2090, 2015.

    Просмотр по адресу:
    Google Scholar

14. Дж. Парк, Э. Хонг и Д. Хар, «Декодирование данных низкой сложности для систем OFDM на основе SLM без дополнительной информации », IEEE Communications Letters , vol. 15, нет. 6, стр. 611–613, 2011.

    Посмотреть по адресу:
    Сайт издателя | Google Scholar

15. Э. Хонг, Х. Ким, К. Ян и Д. С. Хар, «Обнаружение дополнительной информации с помощью пилота в системах OFDM на основе SLM», IEEE Transactions on Wireless Communications , vol. 12, нет. 7, стр. 3140–3147, 2013.

    Посмотреть по адресу:
    Сайт издателя | Google Scholar

16. С.-С. Эом, Х. Нам и Ю.-К. Ко, «Схема снижения PAPR низкой сложности без дополнительной информации для систем OFDM», IEEE Transactions on Signal Processing , vol. 60, нет. 7, стр. 3657–3669, 2012.

    Посмотреть по адресу:
    Сайт издателя | ученый Google | MathSciNet

Copyright

Copyright © 2016 Panca Dewi Pamungkasari и Yukitoshi Sanada. Это статья с открытым доступом, распространяемая в соответствии с лицензией Creative Commons Attribution License, которая разрешает неограниченное использование, распространение и воспроизведение на любом носителе при условии надлежащего цитирования оригинальной работы.

Оценка циклического сдвига с корреляцией с задержкой и согласованной фильтрацией в циклическом SLM во временной области для уменьшения PAPR

. 2016 26 сентября; 2016:8506986.

дои: 10.1155/2016/8506986. Электронная коллекция 2016.

Панча Деви Памунгкасари ¹ , Юкитоши Санада ¹

принадлежность

• ¹ Факультет электроники и электротехники, Университет Кэйо, 3-14-1 Хиёси, Кохоку, Иокогама, Канагава 223-8522, Япония.

• PMID: 27752539
• PMCID: PMC5056534
• DOI: 10. 1155/2016/8506986

Бесплатная статья ЧВК

Панча Деви Памунгкасари и др. Уведомления Int Sch Res. 2016 .

Бесплатная статья ЧВК

. 2016 26 сентября; 2016:8506986.

дои: 10.1155/2016/8506986. Электронная коллекция 2016.

Авторы

Панча Деви Памунгкасари ¹ , Юкитоши Санада ¹

принадлежность

• ¹ Факультет электроники и электротехники, Университет Кэйо, 3-14-1 Хиёси, Кохоку, Иокогама, Канагава 223-8522, Япония.

• PMID: 27752539
• PMCID: PMC5056534
• DOI: 10. 1155/2016/8506986

Абстрактный

Циклически-избирательное отображение во временной области (TDC-SLM) снижает отношение пиковой мощности к средней мощности (PAPR) в системах OFDM, в то время как количество циклических сдвигов требуется для восстановления передаваемого сигнала в приемнике. Одной из критических проблем схемы SLM является отправка дополнительной информации (SI), которая снижает пропускную способность в беспроводных системах OFDM. Предлагаемая схема реализует корреляцию с задержкой и согласованную фильтрацию (DC-MF) для оценки количества циклических сдвигов в приемнике. В предложенной схеме DC-MF размещается после выравнивания в частотной области (FDE) для повышения точности оценки циклического сдвига. Точность предлагаемой схемы достигает 100% при E _b / N ₀ = 5 дБ, а коэффициент битовых ошибок (BER) улучшается на 0,2 дБ по сравнению с обычным TDC-SLM. Показатели BER предложенной схемы также лучше, чем у обычного TDC-SLM, даже несмотря на то, что предполагается нелинейный усилитель высокой мощности.

Заявление о конфликте интересов

Авторы заявляют, что у них нет конкурирующих интересов.

Цифры

Рисунок 1

TDC-SLM с ( D =…

Рисунок 1

TDC-SLM с ( D = 3) кандидатами сигналов.

Рисунок 1

TDC-SLM с ( D = 3) сигнальными кандидатами.

Рисунок 2

Блок-схема предлагаемой схемы.

Рисунок 2

Блок-схема предлагаемой схемы.

фигура 2

Блок-схема предлагаемой схемы.

Рисунок 3

Процесс DC-MF ( D =…

Рисунок 3

Процесс DC-MF ( D = 3).

Рисунок 3

Процесс DC-MF ( D = 3).

Рисунок 4

Соответствующий фильтр.

Рисунок 4

Соответствующий фильтр.

Рисунок 4

Соответствующий фильтр.

Рисунок 5

Уменьшение PAPR.

Рисунок 5

Уменьшение PAPR.

Рисунок 5

Снижение PAPR.

Рисунок 6

Показатель точности при равномерной задержке…

Рисунок 6

Показатель точности на канале с единым профилем задержки.

Рисунок 6

Точность на канале с единым профилем задержки.

Рисунок 7

BER на едином профиле задержки…

Рисунок 7

BER на канале с единым профилем задержки.

Рисунок 7

BER на канале с единым профилем задержки.

Рисунок 8

Показатель точности с HPA на…

Рисунок 8

Показатель точности с HPA на канале с единым профилем задержки.

Рисунок 8

Показатель точности с HPA на канале с единым профилем задержки.

Рисунок 9

BER с HPA на униформе…

Рисунок 9

BER с HPA на канале с единым профилем задержки.

Рисунок 9

BER с HPA на канале с единым профилем задержки.

См. это изображение и информацию об авторских правах в PMC

Похожие статьи

• Об исследовании взаимосвязи между линейным/нелинейным снижением PAPR и производительностью передачи для систем VLC на основе OFDM.

  Лу Х., Хун Ю., Чен Л.К., Ван Дж. Лу Х и др. Выбрать Экспресс. 2018 28 мая; 26 (11): 13891-13901. doi: 10.1364/OE.26.013891. Выбрать Экспресс. 2018. PMID: 29877435

• Несложная рекомбинированная схема SLM для снижения PAPR в оптических системах OFDM с IM/DD.

  У И, Хе С, Чжан Ц, Сунь И, Ван Т. Ву Ю и др. Выбрать Экспресс. 2018 26 ноября; 26 (24): 32237-32247. doi: 10.1364/OE.26.032237. Выбрать Экспресс. 2018. PMID: 30650687

• Новая двухступенчатая схема резервирования тона низкой сложности для уменьшения PAPR в системах OFDM.

  Ту Ю.П., Чанг К.С. Ту Ю.П. и др. Датчики (Базель). 2023 13 января; 23 (2): 950. дои: 10.3390/s23020950. Датчики (Базель). 2023. PMID: 36679746 Бесплатная статья ЧВК.

• Модифицированный метод изменения формы созвездия для уменьшения PAPR PDM CO-OFDM на основе алгоритма SLM.

  Цзоу В., Хуан Т., Юань Дж., Ван Д., Ли С., Ченг З. Цзоу В. и др. Прил. опт. 20191 марта 58(7):1800-1807. doi: 10.1364/AO.58.001800. Прил. опт. 2019. PMID: 30874214

• Повышение безопасности для OFDM-PON с использованием броуновского движения и хаоса в ячейке.

  Ву Т, Чжан С, Чен С, Хоу Х, Вэй Х, Ху С, Цю К. Ву Т и др. Выбрать Экспресс. 3 сентября 2018 г .; 26 (18): 22857-22865. doi: 10.1364/OE.26.022857. Выбрать Экспресс. 2018. PMID: 30184943 Обзор.

Посмотреть все похожие статьи

Рекомендации

1. 1. Rahmatallah Y. , Mohan S. Снижение отношения пиковой мощности к средней в системах OFDM: обзор и таксономия. Обзоры и учебные пособия IEEE по коммуникациям. 2013;15(4):1567–1592. doi: 10.1109/surv.2013.021313.00164. — DOI
2. 1. Бэ К., Шин С., Пауэрс Э. Дж. Анализ производительности систем OFDM с выбранным отображением при наличии нелинейности. Транзакции IEEE в беспроводной связи. 2013;12(5):2314–2322. doi: 10.1109/twc.2013.040213.120968. — DOI
3. 1. Цзян Т., Ву Ю. Обзор: методы снижения отношения пиковой мощности к средней для сигналов OFDM. IEEE Transactions on Broadcasting. 2008;54(2):257–268. doi: 10.1109/tbc.2008.915770. — DOI
4. 1. Wang C.-L., Ouyang Y. Выбранные схемы отображения низкой сложности для снижения отношения пиковой мощности к средней в системах OFDM. Транзакции IEEE при обработке сигналов. 2005;53(12):4652–4660. doi: 10.1109/tsp.2005.859327. — DOI
5. 1. Ян Л., Су К.К., Сиу Ю.М., Ли С.К. Выбранная схема отображения низкой сложности с использованием метода наложения последовательностей во временной области для уменьшения PAPR в системе OFDM.