Что такое отрицательные числа: ОТРИЦАТЕЛЬНОЕ ЧИСЛО | это... Что такое ОТРИЦАТЕЛЬНОЕ ЧИСЛО?

Содержание

Метавселенная. Нуля не существует. Отрицательная площадь и объем. Мнимые числа — Timur Akhmetyanov на vc.ru

Откуда появились отрицательные числа?

666 просмотров

В древнем Египте если получались отрицательные значения, то они отвергались как невозможные. Диофант в 3 веке первым использовал отрицательные числа.

Впервые отрицательные числа были узаконены в Китае 2 век до н.э. и трактовались как долги.

В 1202 году в Европе появилось описание минус чисел для определения долга. Их сформулировал Леонардо Пизанский или Фибонначи.

Многие годы математики спорили о смысле отрицательных чисел. В мире принято считать, что -1 меньше 0. Но на самом деле чисел меньше 0 нет. Они появились благодаря возникновению долгов. А для комплексных чисел понятие «отрицательное число» и вовсе не существует.

В 17 веке отрицательные числа получили наглядное геометрическое представление, когда в 1637 г. Рене Декартом создал прямоугольную систему координат.

Технологии продвинулись вперед и сегодня я разоблачу систему координат Рене Декарта и докажу, что 0 не может являться началом координат.

Предлагаю:

Новую прямоугольную систему координат, где (-1;1) – точка начала отсчета.

Квадрат со стороной 0.5, больше не будет иметь площадь 0.25. Площадь не может быть меньше стороны! И что может быть меньше, чем площадь 1?

(-1;1) – это квадрат с площадью -1 или по модулю 1. Этот квадрат является точкой. Это новое определение точки. Его сторона является равной площади. Можем площадь этой точки для удобства называть i или -i.

Спасибо, дедушка Эйлер. Вот новая система координат (Рисунок 1):

Рисунок 1. Новая система координат.

Дальше расскажу, как на ней считать площадь пустоты и полноты.

А теперь начнем непростой путь к самой сути! Погнали!

Что такое 0?

«0» является временным недостижимым состоянием между полнотой и пустотой.

Положительные числа определяют объем полноты, а отрицательные числа являются величиной описывающие объем пустоты.

Так образуются невидимые отрицательные объемы денежных средств (пузыри), когда денежный долг может быть больше объема всех напечатанных денежных средств.

Почему нет 0?

Бытовой пример:

Мы ошибаемся, когда говорим, что бутылка пустая: в ней -1 или -5 литров воды, который потенциально можно заполнить.

Рассмотрим на примере:

Возьмем две бутылки с объемами 1 литр и 5 литров. Если из обоих вылить воду, то обе бутылки будут пустыми, но они не будут при этом равно пустыми с объемами равными 0, так как потенциал стать полными у них разный.

Их величины объема воды: -1 и -5 литров воды соответственно. В итоге -5 литров больше, чем -1 литр воды.

Что означает этот пример?

Все числа уменьшаются в направлении 0, но не достигают 0, они уменьшаются до 1, а дальше становятся отрицательными. Точки 1 и -1 являются началом координат и лежат в центре всего.

Отрицательные числа растут с увеличением и отрицательные площади являются мнимыми(рис. 2), а их стороны а и b cо значениями например: —5 и 5.

Мнимое число i существует и является параметром измерения отрицательного объема в невидимом измерении. Видимые и мнимые предметы. Видимые предметы имеют положительный объем пустоты или полноты.

А еще существует отрицательный объем в мнимом пространстве. (Рисунок 2):

Рисунок 2. Координаты предметов мнимого пространства и реальных на системе координат двух измерений.

Существует единичный отрицательный объем и отрицательная площадь, квадрат которого равен sqrt(-1).

· i – является характеристикой пустоты.

· 0 – промежуточное недостижимое состояние между полнотой и пустотой.

Поэтому существуют:

1. Пространство полноты – положительные числа.

2. Пространство пустоты – отрицательные числа.

3. 0 является суммой пространств полноты и пустоты и не может быть достигнут, он характеризует отношения равенства между полнотой и пустотой.

4. 0 является законом о том, что без пустоты невозможно наличие полноты.

Почему 0 не может быть достижим?

Потому что существует бесконечно малое положительные и отрицательные числа: (-1/∞) и (1/ ∞).

Соответственно, можем представить две числовые плоскости со значениями {-∞; -1/∞} и {∞; 1/∞}

Отрицательных и положительных чисел бесконечное множество, но их бесконечные плоскости не пересекаются в точке «0» и являются параллельными (Рисунок 3):

Рисунок 3. Параллельные плоскости чисел.

В сумме две эти бесконечные плоскости равны 0 и открывают принцип тождественности для теории чисел. Пример: +5 тождественно -5.

При этом две бесконечные плоскости (+ и -) являются одновременно мнимой бесконечной плоскостью 0, то есть нулевая бесконечная плоскость включает в себя бесконечные положительную и отрицательную плоскости и наоборот.

Если разделить абсолютную числовую плоскость на 3 уровня, то увидим следующую теорию чисел в метапространстве (Рисунок 4):

Рисунок 4. Метапространство чисел.

Отрицательных чисел не существует, но мы используем отрицание для удобного расчета потенциала для создания полноты.

В астрономии:

В феврале 1987 года произошла вспышка Сверхновой. В Большом Магеллановом Облаке, в 167644 св. годах от Земли массивная звезда взорвалась сверхновой (Рисунок 5).

Рисунок 5. После вспышки Сверхновой в 1987 году.

Как мы видим, звезда распалась на 2 положительных кольца. Я вынес гипотезу, что 2 кольца тождественны друг другу и несут в себе равную энергию.

0 – мнимое пространство и состояние. Например, когда звезда достигает состояние 0, то переходит в новую форму и делится на 2 части. Звезда не была в состоянии 0 никакое время, она прошла через него и переродилась в новые формы.

0 – это портал в новое состояние!

Времени нет?

Бесконечность есть?

Даже звезды не умирают. Они меняют форму.

Что думаете об этом?

Какие вопросы и идеи в продолжении темы?

отрицательное число

Отрицательное число — это число, указывающее на противоположное. Если положительное число — это расстояние вверх, то отрицательное — это расстояние вниз. Если положительное число — это расстояние справа, то отрицательное — это расстояние слева. Если положительное число — это депозит на банковский счет, то отрицательное число — это снятие средств с этого банковского счета. Если положительное число — это количество минут в будущем, то отрицательное число — это количество минут в прошлом. Если положительное число означает сложение, то отрицательное — вычитание.

Счетные числа (1, 2, 3 и т.д.) — это все положительные числа. Положительные числа, отрицательные числа и вместе взятое нулевое число называются «знаковыми числами» или целыми числами.

Число ноль не является ни положительным, ни отрицательным. Ноль — это его собственная противоположность, то есть +0 = -0. То есть нулевой шаг вправо — это то же самое, что нулевой шаг влево.

Отрицательное число всегда меньше нуля.

Отрицательное число записывается путем проставления знака минуса «-» перед положительным числом.

Например, 3 — положительное число, а -3 — отрицательное. Оно читается как «отрицательная тройка» или «минус тройка»; это означает противоположность знаку 3.

Отрицательные числа в числовой строке оставляют ноль. Число и его противоположность всегда находятся на одном и том же расстоянии от нуля. Отрицательное число -3 находится слева от нуля, а 3 справа от нуля:

Иногда для выделения мы пишем пару противоположных чисел как -3 и +3.

Число и его противоположность всегда складываются к нулю. Таким образом, сумма -3 и +3 равна 0. Можно записать это либо как -3 + 3 = 0, либо как 3 + (- 3) = 0. Кроме того, число и его противоположность говорят, что «аннулируют друг друга».

арифметика с отрицательными числами

Добавление отрицательного числа к чему-то — это то же самое, что и вычитание положительного числа из него. Например, прибавление отрицательного числа «-1» к числу «9» равнозначно вычитанию одного из девяти. В символах:

9 + (−1) = 9 − 1 = 8

Вычитание отрицательного числа из чего-то — то же самое, что и добавление к нему положительного числа. Например, вычитание отрицательного числа «-8» из числа «6» равнозначно сложению числа «6» и числа «8». В символах:

6 − (−8) = 6 + 8 = 14

Отрицательное число, умноженное на другое отрицательное число, дает положительное число. Например, умножить отрицательное число «-3» на отрицательное число «-2» то же самое, что умножить число «3» на число «2». В символах:

(−3) × (−2) = 3 × 2 = 6

Отрицательное число, умноженное на положительное, дает отрицательное число. Например, умножение отрицательного числа «-4» на положительное число «5» аналогично умножению числа «4» на число «5», но ответ отрицательный. В символах:

(−4) × 5 = −(4 × 5) = −20

Использование отрицательных чисел

Когда человек беден, люди иногда говорят, что у него отрицательная сумма денег. Отрицательные числа используются в бухгалтерии и науке.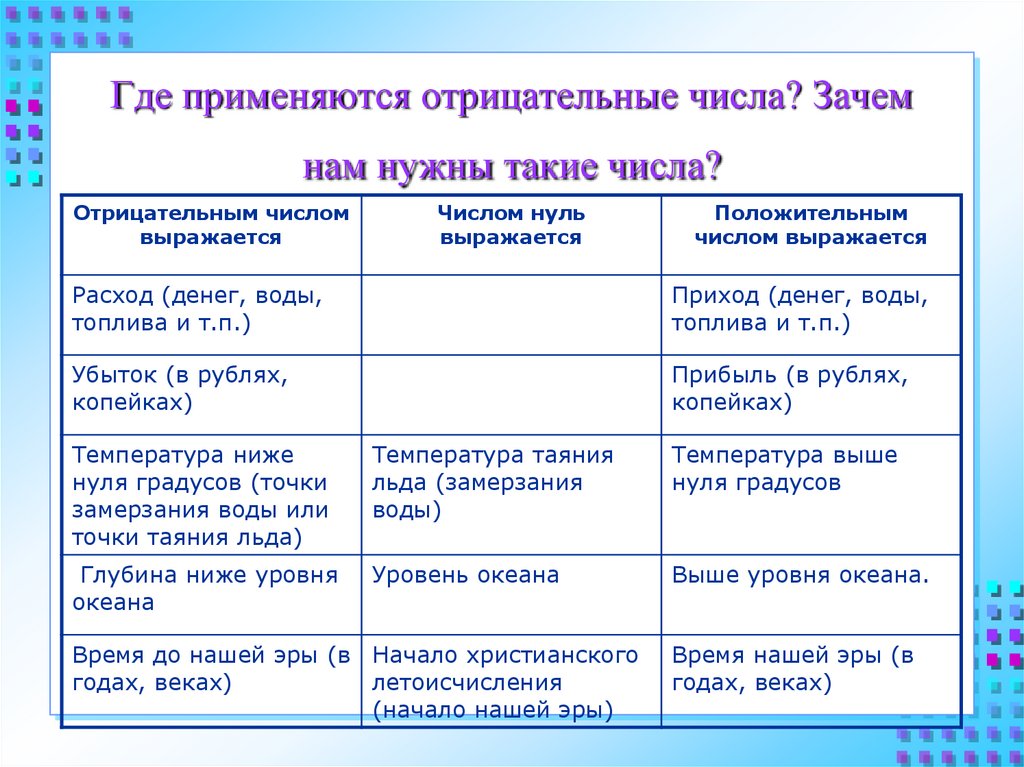

Вопросы и ответы

В: Что такое отрицательное число?
О: Отрицательное число — это число, которое указывает на противоположное. Например, если положительное число означает расстояние вверх, то отрицательное число означает расстояние вниз. Если положительное число означает сложение, то отрицательное число означает вычитание.

В: Как записывается отрицательное число?
О: Отрицательное число записывается путем постановки знака минус, «-«, перед положительной версией того же числа. Например, 3 — это положительное число, а -3 — его соответствующая отрицательная версия.

В: Что такое знаковые числа?
О: Знаковые числа или целые числа — это множество всех положительных чисел, отрицательных чисел и нуля вместе взятых. Сам ноль не имеет определенного знака, так как его можно рассматривать как свою противоположность; поэтому +0 = -0.

В: Где мы находим отрицательные числа на вещественной прямой?
О: Отрицательные числа находятся слева от нуля на вещественной прямой.

В: Что происходит, когда Вы складываете два противоположных знаковых числа вместе?
О: Когда Вы складываете два противоположных знаковых числа вместе, они всегда аннулируют друг друга и дают в результате 0; например, -3 + 3 = 0 или 3 + (-3) = 0.

В: Есть ли другой способ представить все отрицательные действительные числа?
О: Да, все отрицательные действительные числа можно также представить в виде R-{\displaystyle \mathbb {R} _{-}}. .

Автор

Alegsaonline.com — отрицательное число — Leandro Alegsa — 2020-11-19 00:36:32 — url: https://ru.alegsaonline.com/art/69018

Библиографические ссылки

— www.mathleague.com — Math league website discussion of negative numbers- www.purplemath.com — Purple Math website about negative numbers

Отрицательные числа

Что такое отрицательное число? Это достаточно сложный вопрос сам по себе, но он тесно связан с другим действительно сложным вопросом.

Этот другой вопрос смущает и расстраивает очень многих учеников средней школы, не говоря уже о большинстве взрослых. Вот:

Что означает вычитание отрицательного числа?

Чтобы ответить на этот вопрос, нам нужно прояснить некоторые распространенные заблуждения о вычитании вообще и о том, что такое отрицательное число.

В более ранних статьях я указывал на некоторые вещи, необходимые для ответа на этот вопрос.

В одном я определил вычитание как поиск недостающего слагаемого в операторе сложения. В другом я проиллюстрировал, как это можно представить на числовой прямой.

Здесь я рассмотрю третий вопрос выше: что такое отрицательное число? Так что же такое отрицательное число? Разве не все знают?

Если вы спросите наугад 100 выпускников средней школы, по крайней мере 99 из них, вероятно, скажут, что отрицательное число — это число, которое «меньше нуля» (если, конечно, они хоть что-то понимают в математике).

Но что это на самом деле «значит».

Удивительно, но это оставалось загадкой даже для лучших математиков еще долгое время после того, как они решили гораздо более сложные проблемы математики.

Только в середине 1500-х годов математики, наконец, начали принимать отрицательные числа как «настоящие» (то есть не поддельные) числа, и этот процесс не был завершен до 1800-х годов.

Вот критическая проблема, из-за которой их было так трудно принять, даже в столь позднее время. Ниже приводится парафраз вопроса, заданного де Морганом, выдающимся английским математиком, в 1800-х годах:

Как у вас могут быть отрицательные 5 яблок
(или любой другой объект, который вы можете придумать)?

Довольно странная идея, не правда ли?

ну получается тебе не может иметь отрицательное количество яблок. (Но для более подробной информации придется подождать позже.)

Большой прорыв в размышлениях по этому вопросу на самом деле был связан с использованием числовой прямой для представления чисел. Многие люди считают, что Джон Уоллис, английский математик, был первым, кто использовал графическую диаграмму числовой прямой в конце 1600-х годов.

Используя числовую прямую, он представил положительные числа как числа справа от нуля, а отрицательные числа как числа слева от нуля следующим образом:

Это представление позже помогло устранить большую часть беспокойства по поводу отрицательных чисел.

И, конечно же, когда вы показываете отрицательные числа на такой числовой прямой, как эта, и , вы считаете их от нуля, отрицательное число действительно лежит слева от нуля.

Проблема в том, что это не то, чем «на самом деле является» отрицательное число. Другими словами, это не настоящее определение отрицательного числа.

Одна из причин этого заключается в том, что вам не нужно считать числа, начиная с 0. Числа можно считать, начиная с любой точки на числовой прямой. (В противном случае вы не могли бы, среди прочего, показать сложение или вычитание на числовой прямой.)

Это фундаментальный момент, который почти никогда не учитывается при обучении математике в начальной школе. Но это критично.

Вот почему.

На самом деле математики не определяют напрямую, что такое «отрицательное число». Они определяют отрицательное число в терминах «аддитивной инверсии» числа.

Аддитивное обратное число X определяется как число, которое вы добавляете к X, чтобы получить ноль. Вот как это выглядит на числовой прямой.

Предположим, что X равно 5, поэтому мы поместим 5 на числовую прямую.

Чтобы прибавить число к 5, мы начинаем считать с 5 для второго числа.

Где мы должны закончить, согласно определению аддитивной инверсии, это 0.

Если мы начнем считать с 5 и хотим закончить на 0, в каком направлении мы должны считать?

Мы должны считать налево. Когда мы это делаем, это выглядит так.

Число, показанное красным, отрицательное 5… по определению.

Лежит ли -5 левее нуля?

Нет, не в этом случае.

Действительно ли это отрицательное число?

Да. Так определяется отрицательное число. Отрицательное число является обратным положительному числу.

И что является обратным 5?

Это число, которое вам нужно добавить, когда вы начинаете считать с 5 и хотите закончить на 0. Но теперь давайте посмотрим на другую ситуацию.

Допустим, мы хотим добавить обратное число 5, которое, как мы теперь знаем, равно -5, к 0, а не к 5. Как это будет выглядеть?

Начинаем считать с 0…

… и мы считаем обратное число 5, то есть -5.

Точка, в которой мы заканчиваем, представляет собой -5. Красная стрелка показывает минус 5 ниже.

Обратите внимание, что -5, красная стрелка, указывающая влево, точно такое же число, как -5 в приведенном выше примере, который также является красной стрелкой, указывающей влево.

Тот факт, что две красные стрелки начинаются в разных местах на числовой прямой и заканчиваются в разных местах, не влияет на то, что это за число.

В каждом случае вы считаете одинаковое количество единиц. Разница только в том, где вы начинаете считать.

Конечно, другим важным моментом является направление, в котором вы считаете. В каждом случае 5 единиц считаются на слева 9.0035 .

Вот почему это отрицательное число.

Итак, чтобы назвать отрицательное число, нам нужно знать две вещи:

Количество подсчитанных единиц
Направление подсчета единиц

И неважно, с чего начать отсчет.

Итак, вот разница в положительном числе и отрицательном числе:

Положительное число — это число, отсчитываемое справа на числовой прямой.
Отрицательное число — это число, отсчитываемое слева на числовой прямой.

Вот и все.

Вот почему мы описываем отрицательное число как «противоположное» положительному числу. Он считается в обратном направлении.

Фактическое направление подсчета каждого типа чисел не имеет абсолютного значения.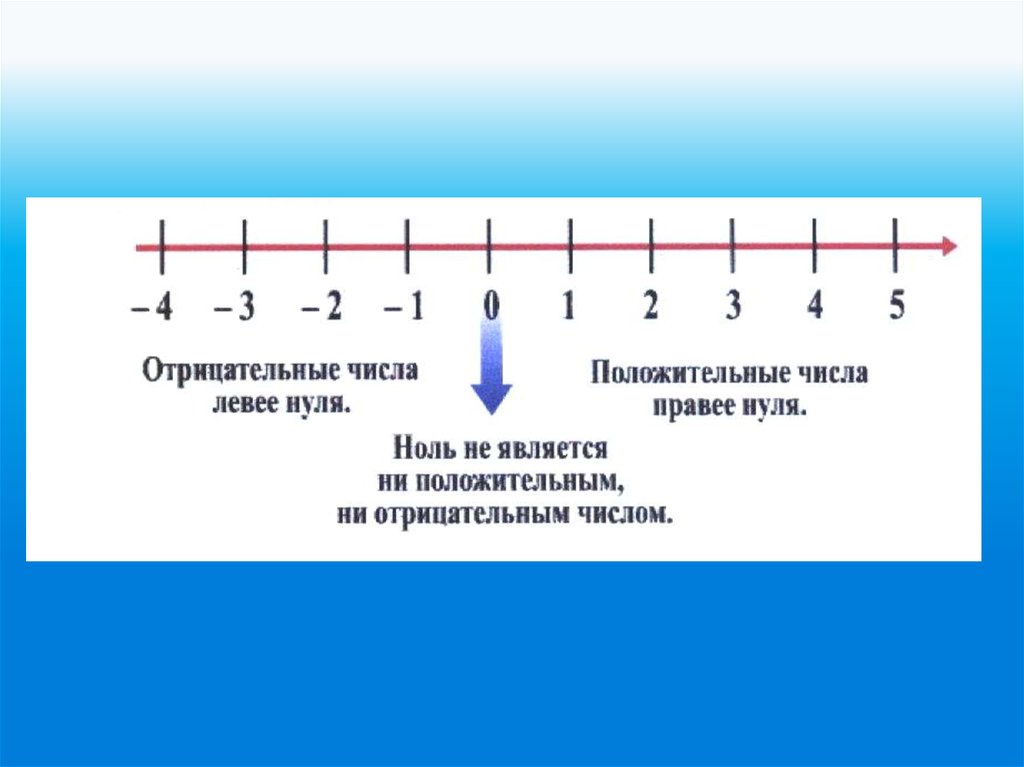 Мы могли бы решить, как культура, считать положительные числа слева и отрицательные числа справа. это просто историческая случайность, что мы считаем положительные числа справа.

Как только был принят счет положительных чисел справа, «противоположный» стал считать слева. Настоящая разница в том, что направления разные .

И, наконец, конечно, отрицательные числа по-прежнему «ложатся левее 0», но — это всего лишь , если мы считаем их, начиная с 0, что не является требованием отрицательного числа или положительного числа, если уж на то пошло.

Смотрите другие из этой серии:

Вычитание не означает «вычитание»
Что такое вычитание?
Обучение вычитанию из числовой строки
Что такое отрицательное число?

Нажмите ниже для просмотра других ресурсов

Исследовать

Белые бумаги

Истории успеха

Математические темы

Другие источники

Что такое отрицательные числа? | TheSchoolRun

Мы объясняем, что такое отрицательные числа и как можно научить детей этому понятию с помощью числовой прямой, а также рассмотрим типы вопросов, которые детям могут задавать с отрицательными числами.

или Зарегистрируйтесь, чтобы добавить к своим сохраненным ресурсам