Арифметические выражения
В этой главе показано, каким образом Пролог выполняет арифметические операции. Будут описаны арифметические операторы и их использование в выражениях, а также рассмотрены встроенные предикаты, служащие для вычисления и сравнения арифметических выражений.
Введение
Язык Пролог не предназначен для программирования задач с большим количеством арифметических операций. Для этого используются процедурные языки программирования. Однако в любую Пролог-систему включаются все обычные арифметические операторы:
+ сложение
— вычитание
* умножение
/ деление
mod остаток от деления целых чисел
div целочисленное деление
В некоторых реализациях языка Пролог присутствует более широкий набор встроенных арифметических операторов.
Пролог позволяет также сравнивать арифметические выражения, используя следующие встроенные предикаты:
Диапазоны чисел, входящих в арифметические
выражения, зависят от реализации
Пролога.
–8388606 … 8388607
Арифметические выражения
Арифметическое выражение является числом или структурой. В структуру может входить одна или более компонент, таких, как числа, арифметические операторы, арифметические списковые выражения, переменная, конкретизированная арифметическим выражением, унарные функторы, функторы преобразования и арифметические функторы.
Числа. Числа и их диапазоны определяются в конкретной реализации Пролога.
Арифметические операторы. + — * / mod div
Арифметические списковые выражения. Если Х — арифметическое выражение, то список [X ] также является арифметическим выражением, например [1,2,3]. Первый элемент списка используется как операнд в выражении. Скажем,
X is ([l,2,3]+5)
имеет значение 6.
Арифметические списковые выражения
полезны и при обработке символов,
поскольку последние могут рассматриваться
как небольшие целые числа.
Переменная, конкретизированная арифметическим выражением. Примеры:
Х-5+2 и У-3*(2+А)
Унарные функторы. Примеры:
+(Х) и -(У)
Функторы преобразования. В некоторых реализациях Пролога имеется арифметика с плавающей точкой, а следовательно, и функторы преобразования. Например:
float (X) преобразует целое число Х в число с плавающей точкой.
Математические функторы. Пример: квадрат(Х) объявлен как оператор и эквивалентен арифметическому выражению (Х*Х).
Арифметические операторы
Атомы +, -, *, /, mod и div — обычные атомы Пролога
и могут использоваться почти в любом
контексте. Указанные атомы — не встроенные
предикаты, а функторы, имеющие силу
только в пределах арифметических
выражений. Они определены как инфиксные
операторы. Эти атомы являются главными
функторами в структуре, а сама структура
может принимать только описанные выше
формы.
но Пролог выдаст сообщение об ошибке, если встретит выражение Z is X среднее Y.
Это произойдет потому, что Х среднее Y не образует арифметического выражения, а среднее не является арифметическим оператором, определенным в системе.
Арифметические выражения в математике и информатике | Учебно-методический материал (9 класс) по теме:
МБОУ «Новопавловская СОШ №2» |
Тема: «Арифметические выражения в математике и информатике». |
Семинар учителей математики Кировского района |
Реферат
Составил учитель математики
МБОУ СОШ №2
Лийка Владимир Владимирович.
Н о в о п а в л о в с к
2010
Арифметические выражения в математике и информатике
Как известно, при изучении математики сначала изучается математический алфавит, затем, используя алфавит, составляются математические «слова» т.
е. выражения. Что же такое выражение?
Выражение – синтаксическая единица языка, определяющая способ вычисления некоторого значения.
А арифметическое выражение — это совокупность чисел, скобок, объединенных знаками арифметических действий, так, чтобы оно имело определенное числовое значение. Для вычисления значения арифметического выражения существуют определенные правила, требующие безукоснительного их выполнения.
При дальнейшем изучении математики в арифметическое выражение добавили буквы и стали говорить уже о выражении как об алгебраическом. Итак с появлением новых понятий в математике круг названий выражений расширяется: рациональные, иррациональные, тригонометрические, степенные, логарифмические и т. д.
В информатике же арифметическое выражение приобретает смысл общего определения выражения. Так в языке программирования Паскаль выражения формируются в соответствии с рядом правил из констант, переменных, компонент массивов, полей записей, полей объектов, функций, знаков операций и круглых скобок.
Переменные – параметры программы, значения которых могут изменяться в процессе выполнения её.
Константы – параметры программы, значения которых в процессе выполнения её не меняются.
Стандартные функции – заранее разработанные подпрограммы-функции, которые могут использоваться как готовые объекты.
Знаки операций:
арифметические
№пп | Знак операции | Действия |
1. | + | сложение |
2. | — | вычитание |
3. | * | умножение |
4. | / | деление |
5. | DIV | целочисленное деление |
6. | MOD | остаток от деления |
логические
Х | У | Х или У | Х и У | Х искл. | не Х |
Истина | Истина | Истина | Истина | Ложь | Ложь |
Истина | Ложь | Истина | Ложь | Истина | Ложь |
Ложь | Истина | Истина | Ложь | Истина | Истина |
Ложь | Ложь | Ложь | Ложь | Ложь | Истина |
или У
и другие.
Действия выполняются в соответствии с их приоритетом:
a) Действия в скобках;
б) Вычисление функций;
в) Умножение, деление, DIV, MOD;
г) Сложение, вычитание.
В математике арифметические выражения могут записываться многоэтажными дробями, могут пропускаться, например, операция умножения, что не допустимо в информатике.
В информатике арифметические выражения записываются в строку, и все действия прописываются обязательно.
Например:
Видно, что в функции требуется обязательное заключение аргумента в скобки и т. д.
Первичные выражения. Арифметические выражения строятся из элементов – так называемых первичных выражений, которые с помощью знаков операций и скобок объединяются в более сложные арифметические выражения. Сами первичные выражения представляют собой частные случаи арифметического выражения. К первичным выражениям относятся: число, переменная, функция, арифметическое выражение в круглых скобках.
Например: 135, В, cos(x), (a + c/z), (…).
Многоточие означает произвольное арифметическое выражение (возможно громоздкое), которое, будучи заключенное в скобки, представляет собой первичное выражение.
Заключенное в круглые скобки арифметическое выражение любой сложности, становится первичным выражением, в частности, числом, переменной, функцией.
Рассмотрим еще несколько аспектов работы с арифметическими выражениями в математике и информатике.
С к о б о ч н ы е в ы р а ж е н и я. К таким выражениям относятся так называемые «пустые скобки». Например: {[(a+b)*c+e/(k-m)]*p+[(x+y)*a+b]/a}*c.
Опустив буквы и знаки операций, оставит только скобки, получим:
{[( ) ( ) ] [( ) ] } — «пустые скобки».
Запишем этот набор скобок в более сжатом виде:
{[()()][()]} — скобочное выражение.
Но так как скобок разной конфигурации на клавиатуре ограничено, то используют только круглые скобки (редко используют другие) при этом наше выражение примет вид ((()())(())).
При такой записи выражений можно допустить описки, а для контроля можно указывать уровни скобок. Номера уровней запишем под скобками. Каждая открывающая скобка должна иметь закрывающую скобку соответствующего уровня.
( ( ( ) ( ) ) ( ( ) ) )
1 2 3 3 3 3 2 2 3 3 2 1
Контроль за правильностью скобочного выражения представляет собой необходимый этап проверки записи арифметического выражения, как в математике, так и в информатике.
В математике правильность записи может проверить сам ученик или учитель, но в информатике строгость контроля должна быть усилена, так как компьютер реагирует на любую ошибку, включая очевидную описку. Машинный контроль правильности всей программы осуществляется транслятором. Он выявляет ошибки и выдает сообщение об ошибке.
Б е с к о н е ч н а я з а п и с ь а р и ф м е т и ч е с к и х в ы р а ж е н и й. В информатике имеются способы записи арифметических выражений без использования скобок. Существует несколько способов такой записи.
Префиксная запись. В этом способе сначала записывается символ операции, а затем по порядку слева направо – операнды. Если же операнд содержит действие, то к нему применяется то же правило. Например. Исходное выражение (a+b)*(c-a), запишется
* +ab –ca — польская бесконечная запись.
Подчеркнуты два операнда операции умножения «*». Каждый операнд содержит одну операцию, за которой следует так же два операнда +ab и -ca.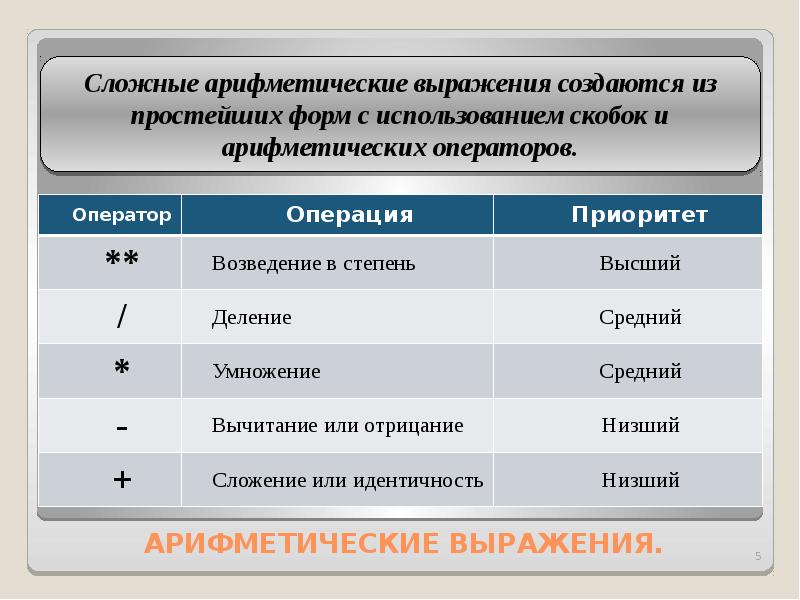
Операнды друг от друга отделены пробелами.
Постфиксная запись. В этом виде записи символ операции располагается после списка операндов. Рассмотрим только польскую инверсную запись постфиксной записи.
Исходное выражение
(a+b)*(c-a) представится в виде:
ab+ ca- *, где ab+ и ca- первый и второй операнды операции «*».
Такую запись арифметических выражений можно наблюдать при работе с микрокалькуляторами.
Первый элемент с индикатора микрокалькулятора отсылается в рабочий регистр, а далее набирается второй аргумент и так далее.
Представление арифметических выражений в виде дерева.
Для того чтобы представить арифметическое выражение в виде дерева, введем условные обозначения, с помощью которых будем строить дерево:
Корень — соответствует главной операции.
Узлы — изображают операции промежуточного уровня.
Листья — ссылки на данные или константы.
Корень и узлы изображаются кружками и овалами, а листья — квадратиками и прямоугольниками.
Рассмотрим несколько примеров:
Пример 1. х*у — одна главная операция
Пример 2. –х — унарная операция,
иногда её обозначают буквой «М».
Пример 3. — унарная операция обозначают SQRT – во многих языках
программирования.
Пример 4. x*y*z — здесь в качестве главной операции
можно взять первую и них. Пунктиром
выделены по одному из операндов для главной операции.
Сам операнд (в пунктирном прямоугольнике) является
сложным, и он раскрывается в нем.
Пример 5. ((a+b)*c)+e представляет следующее дерево, где главная операция взята после последней операции «+»:
Анализ записи арифметических выражений, их представление в бесконечном виде, изображение структуры с помощью деревьев, контроль за правильностью записей и
его машинная реализация, а также разработка алгоритмов соответствующих задач могли бы способствовать реализации связей математики и информатики.
Список используемой литературы:
- Журнал «Математика в школе» №3 1998г. И.Н. Антипов, О.А. Боковнев «Арифметические выражения в математике и информатике», с. 43 – 46.
- А.Епанешников, В. Епанешников Программирование в среде TURBO PASCAL 7.0 М.: «ДИАЛОГ – МИФИ», 1993г.
- Арифметические выражения. htm, сайт: http://mukfrn.narod.ru
- Арифметические выражения. htm, сайт: http://kurs-vb.narod.ru
- Г.В.Дорофеев, Л.Г.Петерсон Математика учебник для 5 класса I часть. «Ювента» 2006.
Определение арифметического выражения | ПКМаг
(1) Один или несколько символов, связанных с арифметикой, например, 1+2=3 или 8*6 .
(2) В программировании арифметическое выражение, результатом которого является 10 % значения, может выглядеть так: результат=0,10*всего .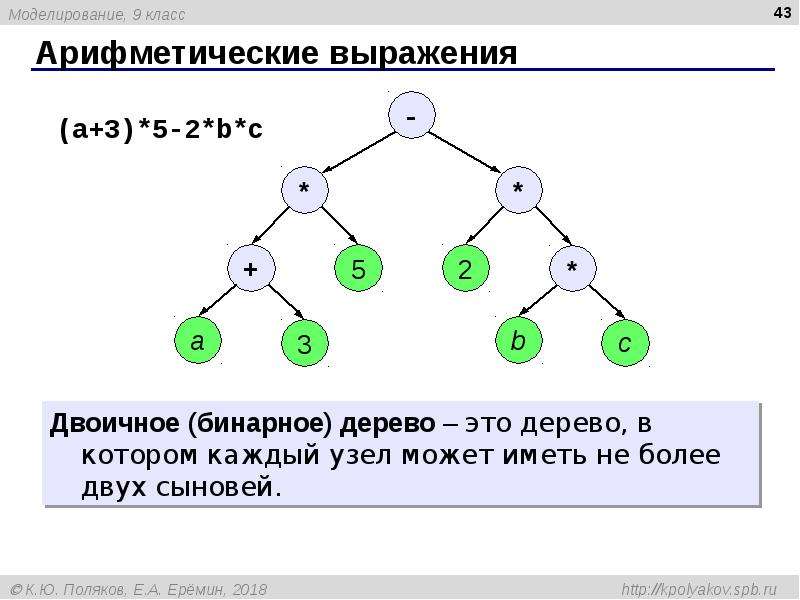
Числовые значения определяются как целые числа (целые числа) или числа с плавающей запятой (с десятичной точкой). Два других типа программных выражений — это «символьные» (текст в кавычках) или логические значения «да/нет» (0 или 1). См. целое число и число с плавающей запятой.
Реклама
Истории PCMag, которые вам понравятся
{X-html заменен}
Выбор редакции
ЭТО ОПРЕДЕЛЕНИЕ ПРЕДНАЗНАЧЕНО ТОЛЬКО ДЛЯ ЛИЧНОГО ИСПОЛЬЗОВАНИЯ. Любое другое воспроизведение требует разрешения.Copyright © 1981-2023. The Computer Language(Opens in a new window) Co Inc. Все права защищены. Информационные бюллетени PCMag
Информационные бюллетени PCMag
Наши лучшие истории в вашем почтовом ящикеСледите за новостями PCMag
- Фейсбук (Открывается в новом окне)
- Твиттер (Откроется в новом окне)
- Флипборд (Открывается в новом окне)
- Гугл (откроется в новом окне)
- Инстаграм (откроется в новом окне)
- Pinterest (Открывается в новом окне)
PCMag.
com является ведущим авторитетом в области технологий, предоставляющим независимые лабораторные обзоры новейших продуктов и услуг. Наш экспертный отраслевой анализ и практические решения помогут вам принимать более обоснованные решения о покупке и получать больше от технологий.
- (Открывается в новом окне) Логотип Зиффмедиа
- (Открывается в новом окне) Логотип Аскмен
- (Открывается в новом окне) Логотип Экстримтек
- (Открывается в новом окне) Логотип ИНГ
- (Открывается в новом окне) Лайфхакер Логотип
- (Открывается в новом окне) Логотип Mashable
- (Открывается в новом окне) Предлагает логотип
- (Открывается в новом окне) Логотип RetailMeNot
- (Открывается в новом окне) Логотип Speedtest
PCMag поддерживает Group Black и ее миссию по увеличению разнообразия голосов в СМИ и владельцев СМИ.
© 1996-2023 Ziff Davis, LLC., компания Ziff Davis. Все права защищены.
PCMag, PCMag.com и PC Magazine входят в число зарегистрированных на федеральном уровне товарных знаков Ziff Davis и не могут использоваться третьими лицами без явного разрешения. Отображение сторонних товарных знаков и торговых наименований на этом сайте не обязательно указывает на какую-либо принадлежность или поддержку PCMag. Если вы нажмете на партнерскую ссылку и купите продукт или услугу, этот продавец может заплатить нам комиссию.
- О Ziff Davis(Открывается в новом окне)
- Политика конфиденциальности(Открывается в новом окне)
- Условия использования(Открывается в новом окне)
- Реклама(Открывается в новом окне)
- Специальные возможности(Открывается в новом окне)
- Не продавать мою личную информацию (откроется в новом окне)
- (Открывается в новом окне) доверительный логотип
- (Открывается в новом окне)
операций в выражениях — основная арифметика
Все основные арифметические ресурсы
6 Диагностические тесты 75 практических тестов Вопрос дня Карточки Learn by Concept
← Предыдущая 1 2 Следующая →
Справка по основам арифметики » Действия в выражениях
Решить:
Возможные ответы: Правильный ответ: Объяснение: Используйте порядок операций: PEMDAS (круглые скобки, возведение в степень, умножение, деление, сложение, вычитание).
Сначала мы хотим решить, что в скобках.
Теперь выполните деление и умножение.
Следовательно, наше уравнение принимает следующий вид:
Наконец, вычитаем.
Сообщить об ошибке
Решить:
Возможные ответы: Правильный ответ: Объяснение:Для решения используйте порядок операций PEMDAS (круглые скобки, показатели степени, умножение, деление, сложение, вычитание).
Поскольку здесь нет ни скобок, ни степеней, мы можем сразу перейти к умножению и делению.
и
Следовательно, получается следующее:
Затем сложите и вычтите.
Сообщить об ошибке
Используя порядок операций, нам нужно сначала решить то, что находится в скобках.
Далее делаем умножение и деление.
Наконец, сложите и вычтите.
Сообщить об ошибке
Упростить
Возможные ответы: Правильный ответ: Объяснение:Начнем с того, что в скобках, поэтому становится .
Далее мы позаботимся обо всех экспонентах, которые нам дают.
Далее мы позаботимся об умножении/делении, что даст нам или .
Наконец, мы выполняем сложение/вычитание, оставляя нам .
Сообщить об ошибке
Решить:
Возможные ответы: Правильный ответ: Объяснение:Используя PEMDAS, мы сначала делаем бит в скобках:
Теперь мы делаем умножение и деление:
Наконец, вычитаем.
Сообщить об ошибке
Возможные ответы: Правильный ответ: Объяснение:Это классический вопрос о порядке действий, и если вы не будете осторожны, вы можете получить неправильный ответ!
Помните, порядок операций говорит о том, что вы должны действовать в следующем порядке: Скобки, Экспоненты, Умножение, Деление, Сложение, Вычитание (также известное как PEMDAS).
В этом уравнении вы начнете со скобок. В скобках у нас
.
Но в скобках вам все равно нужно следовать PEMDAS. Сначала мы решим показатель степени, а квадрат 2 равен 4. Затем мы разделим 16 на 4, что даст нам 4, поэтому мы можем переписать исходное уравнение как 9.0009
Теперь мы можем разделить на , что дает нам
.
Последний шаг — сложение и вычитание приведенных выше чисел, обращая особое внимание на отрицательные знаки. В конце концов, мы получаем потому что прибавлено к равно и минус равно равно .
Сообщить об ошибке
При вычислении выражения
,
в каком порядке вы должны выполнять три операции?
Возможные ответы:Вычитание, сложение, умножение
Умножение, вычитание, сложение
Умножение, сложение, вычитание
Вычитание, умножение, сложение
Сложение, вычитание, умножение дополнение
Объяснение: По порядку операций, при отсутствии группирующих символов, перед сложением или вычитанием необходимо отработать умножение.
Затем сложение и вычитание должны выполняться слева направо; вычитание находится слева, поэтому затем выполняется вычитание, а затем сложение.
Сообщить об ошибке
При вычислении выражения
,
какую из пяти операций нужно выполнить третьей?
Возможные ответы:Возведение в квадрат
Деление
Сложение
Умножение
Вычитание
Правильный ответ: 90 004Возведение в квадрат
Объяснение:По порядку операций любые операции в круглых скобках должны выполняться первыми; здесь их два, сложение и вычитание. После того, как это будет сделано, показатель степени или возведение в квадрат должен быть обработан перед другими операциями. Таким образом, правильным ответом является возведение в квадрат, третья операция.
Сообщить об ошибке
При вычислении выражения
,
в каком порядке вы должны выполнять три операции?
Возможные ответы:Кубирование, вычитание, умножение
Вычитание, умножение, кубирование
Кубирование, умножение, вычитание
Умножение, кубирование, вычитание
Вычитание, возведение в куб, умножение
Правильный ответ:Возведение в куб, умножение, вычитание
Объяснение: По порядку операций, при отсутствии группирующих символов, показатель степени (представленный здесь в кубе) должен быть обработан первым.