Арифметические выражения: Выражения — урок. Информатика, 8 класс.

Арифметические выражения

Арифметические выражения используются для программирования правых частей равенств.

Арифметическое выражение – совокупность операндов, соединенных знаками арифметических действий и разделенных, в случае необходимости, круглыми скобками.

В качестве операндов используются простейшие конструкции (данные) – константы, переменные, вызовы функций.

Под операциями подразумеваются арифметические действия.

В Си/Си++ существует большой набор операций, классифицируемых в большинстве случаев на унарные и бинарные.

Унарная – операция для обработки одного операнда.

Например, унарные операции используют для формирования знаковых констант (разд. 3.5.2.2).

Бинарная – операция с использованием двух операндов.

В арифметических выражениях используются унарные и бинарные операции.

К бинарным операциям относятся арифметические действия:

+ сложение;

— вычитание;

* умножение;

/ деление;

% взятие остатка (деление по модулю).

По способу машинного выполнения две первые операции называются аддитивными, три остальные – мультипликативными.

Результат вычисления любого арифметического выражения – константа. Поэтому, в языке Си/Си++ арифметическое выражение называется константным.

1. Арифметические выражения записываются одноэтажно. Например, 0.35+а*2-cos(b)/(PI+2).

2. Все знаки арифметических операций указываются явно. Например, А+В+С не равно АВ+С, так как во втором случае подразумевается переменная с именем АВ, а не две переменные.

3. Запись подряд двух знаков операций, как правило, запрещается (исключение см. разд. 6.2.1). Обойти это правило можно с помощью круглых скобок. Например, a*(-b).

4. Арифметическое выражение может быть любой сложности. Минимально может состоять из одного операнда. Реально определяется математической моделью задачи. Если зависимости математической модели относительно громоздки, рекомендуется представлять одну сложную зависимость несколькими простыми, – содержащими не более 5–7 операций в каждой.

5. Последовательность выполнения операций в арифметическом выражении соответствует принятой в математике:

Например, выражение 0.2-cos(0.5)*pow(v,3) выполняется в следующем порядке: вычисление косинуса, возведение v в куб, умножение первого результата на второй и, наконец, вычитание из константы 0.2 константы, полученной после умножения.

6. Одноранговые операции выполняются слева направо. Например, выражение А*В/С*3 будет выполняться в порядке записи.

7. При необходимости нарушить последовательность выполнения действий используют скобки. Например, А+В/(С+D) или (0.2-v)*cos(0.5).

8. При делении целого операнда на целый от частного используется только целая часть. Так, результатом вычисления 5/2 будет целая константа 2, а выражения 2/5 – ноль. Для получения истинного результата необходимо сделать вещественными оба операнда или один из них. Например, 5./2. или 5./2 (5/2.).

9. Возведение в степень (pow(a,x)), если показатель (х) целочисленный, выполняется методом последовательного умножения. Если показатель степени вещественный, возведение осуществляется по формуле a^x = е^xlna. Использование функций (экспоненты и логарифма) приводит к получению приближенного значения результата.

10. В арифметическом выражении желательно использовать операнды одного типа. Например, i+23*k, если переменные i, k – целые или x*2.-0.36/cos(y), если переменные x, y – вещественные. В первом случае результатом будет целая константа, во втором – вещественная константа двойной точности (перед использованием автоматически все вещественные операнды приводятся к типу double).

11. Допускается применение смешанных арифметических выражений. При этом наличие хотя бы одного вещественного операнда приводит к получению результата (константы) с двойной точностью. Например, при вычислении выражения 4/z+i*k-0.07*sin(3./b) результатом будет вещественная константа двойной точности, если переменные i, k – целые, а z, b – вещественные. Аналогично, возможно получение дробного результата деления целых переменных использованием дополнительного операнда в виде вещественной константы (1. ). Так, если переменные i и k описаны как целые, то результат выражения i/k есть целая константа (целая часть частного), а результат выражения i*1./k есть вещественная константа двойной точности. Следует помнить, что наличие операции деления двух целых операндов в смешанном выражении может привести к неверному результату. Например, вычисление выражения 0.02 + 3/5 — 0.01 дает неверный результат (0.01), так как второе слагаемое (частное от деления целой константы 3 на целую константу 5) равно нулю.

12. Деление по модулю % используют в целочисленной арифметике. Результат операции– остаток от деления целого операнда, записанного слева от знака операции, на операнд справа от него. Например, выражение 13%5 дает результат 3, поскольку 13=5*2+3, где 3 – остаток от деления.

13. Вычисление корня n-ой степени при n>2 требует предварительного преобразования его к виду , а затем использование функции возведения в степень. Например, зависимость должна быть преобразована к виду , а затем сформирована как вызов функции pow(x,1.

    /3.) Попытка вычисления функции вида pow(x,1/3) приведет к получению неверного результата – единицы, так как показатель степени (1/3) после деления станет равен нулю.

• Внимание! Сообщения об ошибках, возможных при выполнении арифметических выражений (например, переполнение разрядной сетки), как правило, не выдаются.

Изучение выражений завершает рассмотрение простейших и промежуточных конструкций языка.

4. Основные конструкции Си/Си++

Оператор – основная конструкция большинства языков высокого уровня.

Оператор соответствует предложению в разговорном языке.

Каждый блок схемы алгоритма реализуется одним или несколькими операторами. Следовательно, совокупность операторов образует программу.

Программа на языке высокого уровня – последовательность операторов, выполняемых в порядке их записи.

В языке Си/Си++ базовой конструкцией является функция (разд. 3.5.2.4), что позволяет представлять любые участки вычислений структурировано (блочно). Поэтому некоторые операторы языка Си/Си++ есть функции, оформленные специальным образом.

По критерию значимость все операторы можно классифицировать схемой рис. 3.7.

Рис. 3.7. Классификация операторов

Неисполняемые – операторы-описатели не вызывающие действий в программе.

Исполняемые – операторы, предписывающие конкретные действия обработки информации в программе.

Неисполняемые операторы – вспомогательные конструкции алгоритмических языков.

Большинство из них – описатели типов операндов-переменных, участвующих в задаче.

Классификация операторов описателей представлена на рис. 3.8.

Рис. 3.8. Классификация операторов описателей

Назначение, структура, правила использования описателей изложены выше (разд. 3.5.2.3).

Исполняемые операторы – основные конструкции, формирующие программу.

Каждый из них при выполнении программы предписывает полную (частичную) реализацию указаний, соответствующего блока схемы алгоритма. Такими блоками являются ввод исходных данных, вывод результатов, вычисления по формулам, проверка условий, формирование циклов и т.п.

Укрупненно по критерию назначение исполняемые операторы классифицируются схемой (рис. 3.9).

Операторы присваивания – программные аналоги формульных вычислений алгоритма.

Операторы ввода-вывода – программные аналоги предписаний соответствующих блоков схем алгоритма. Их разнообразие обусловлено значительным диапазоном внешних устройств, используемых для обмена данными между пользователем и

Рис. 3.9. Классификация исполняемых операторов

ЭВМ (ручной ввод с клавиатуры, вывод на экран дисплея, в поток и т.п.).

Операторы управления – программные аналоги предписаний соответствующих блоков схем алгоритмов (решение, начало и конец цикла, модификация, предопределенный процесс и т. п.).

Операторы присваивания, ввода-вывода информации – обязательный элемент конструкции практически любого вычислительного процесса, начиная с простейшего – линейного. Операторы управления – специфические конструкции, организующие основные операции ветвящихся, циклических, смешанных процессов. Значительное разнообразие операторов управления обусловлено конкретными особенностями этих процессов. Назначение, структуры, правила записи и использования различных операторов управления рассматриваются в соответствующих разделах (гл. 4, 5).

Рассмотрим операторы, используемые в программировании линейных вычислительных процессов.

Практика: Арифметические выражения и калькуляторы

Стеки

В этой лабораторной работе многократно будет использоваться стек, поэтому для начала предлагается освежить в памяти, как эта структура обычно выглядит на языке python.

Упражнение №1

Напишите программу, которая последовательно кладет в стек произвольный массив чисел, а затем распечатывает их , последовательно доставая, пока стек не пуст (например, набор (1,. ..,10)).

Правильные скобочные структуры

Известно, что скобочные выражения могут быть корректными и некорректными. Корректные — это такие, которые можно вычислить по правилам, если расставить между ними числа и знаки бинарных операций. Иными словами, интуитивно, такие. где зоны действия скобок разных типов не пересекаются(если есть скобки разных типов).

Упражнение №2

Написать программу, определяющую правильность введенного скобочного выражения, в котором используются скобки 3 видов: (), {}, /.

Арифметические выражения. Инфиксная, постфиксная и префиксная нотации

Рассмотрим арифметическое выражение

\begin{equation*} (2-3)*(12-10)+4/2 \end{equation*}

Его значение легко вычисляется и оказывается даже целым — это 0(не забываем правила приоритета операций!). Это привычная для нас форма записи арифметических выражений, в которой если операция бинарная (т.е. требует 2 аргументов, например, сложение, деление), то один аргумент пишется перед знаком операции, а другой — после неё.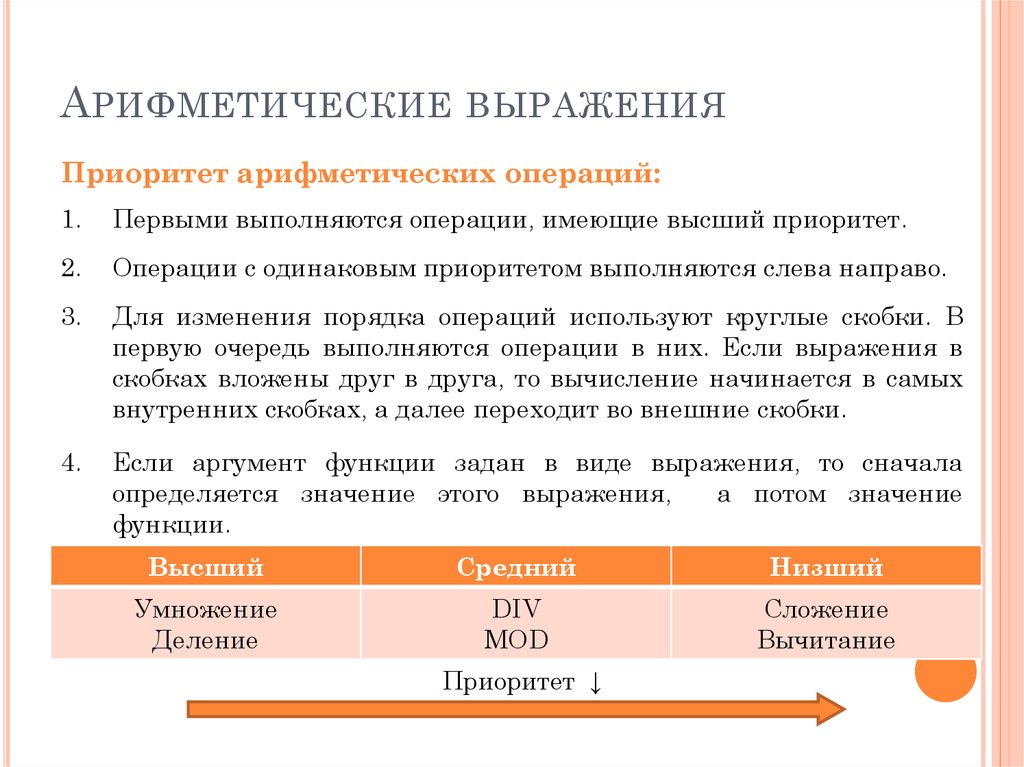 Такая форма записи называется инфиксной.

Нотация (способ записи), в которой операнды пишутся перед знаком операции — называется постфиксной или обратной польской.

Нотация. в которой операнды пишутся после знака операции — прямой польской или префиксной.

Например, уже рассмотренное выражение в обратной польской записи будет выглядеть как

\begin{equation*} 2 3 — 12 10 — * 4 2 / + \end{equation*}

После пары 2 и 3 стоит знак вычитания. После пары 12 и 10 — тоже. Далее стоит знак перемножения, потому что результаты этих двух операций надо умножить. Далее стоят 4 и 2 и после них знак деления. А после — знак сложения, показывающий, что результат предыдущего нужно сложить с результатом деления 4 на 2.

а в прямой польской как

\begin{equation*} + * — 2 3 — 12 10 / 4 2 \end{equation*}

Аналогичным образом, только теперь знак операции стоит перед операндами (или их описаниями в виде выражений в той же форме записи).

Упражнение №3

Перевести выражение

\begin{equation*} (3+4*(2-1))/5 \end{equation*}

в прямую и обратную польские записи.

В общем и целом, любое выражение можно представить в виде структуры, называемой деревом(синтаксическим деревом в данном случае, поскольку оно отражает структуру выражения). Например, для разобранного выражения синтаксическое дерево будет выглядеть так:

Его конечные вершины, листья (из которых стрелки никуда не идут) — это операнды, а промежуточные (из которых идут стрелки)- операции. Прямая польская запись (префиксная) получается, если читать это дерево сверху вниз. Обратная (постфиксная) — если читать снизу вверх.

Стековый калькулятор

Стековый калькулятор — это устройство (реальное или виртуальное), которрое вычисляет значения арифметических выражений , записанный в постфиксной форме. Стековым он называется по понятным причинам: если нам встречается число — мы должны поместить его в стек; если знак опренрации — мы должны достать из стека столько чиссел, скольок необходимо для выполнения данной операции. Именно так и работает т.н. математический сопроцессор (например, в INtel8086+AMD64)- часть ЦП, отвечающая за операции над числами с плавающей запятой.

Упражнение №4

Реализовать стековый калькулятор на python. Написать программу, которая читает выражение в обратной польской нотации и считает его значение или пишет, что выражение составлено не корректно (если оно некорректно).

Сортировочная станция Дейкстры

Как нетрудно видеть: выражения в обратной польской записи удобны для чтения компьютером , но неудобны для чтения и составления людьми. Поэтому хотелось бы доверить труд составления постфиксной формы выражений по их привычной инфиксной форме компьютеру. Это можно сделать с помощью так называемого алгоритма сортировочной станции (Shunting Yard algorithm , придуман Э. Дейкстрой в 1961 году, см https://en.wikipedia.org/wiki/Shunting-yard_algorithm для трансляторов языка Algol60 https://ir.cwi.nl/pub/9251).

В следующем примере, взятом как раз из википедии, разбирается преобразование выражения

\begin{equation*} a+b*c-d \end{equation*}

Есть сортировочная станция с 3 путями: 2 подъездных и 1 тупик.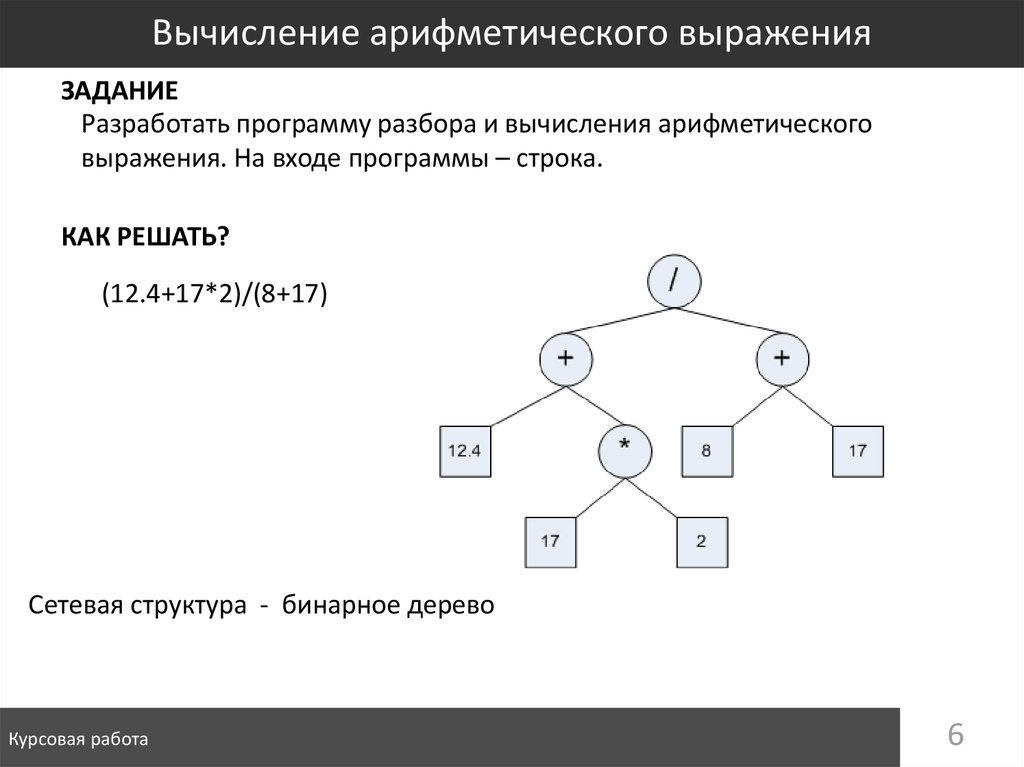 С правоого подъездного пути едут выражения: в каждом «вагоне» или операнд или знак операции. Операнды свободно проезжают в левый путь (образуя очередь), а операторы заезжают в тупик.

By Salix alba — Own work, CC BY-SA 3.0, https://commons.wikimedia.org/w/index.php?curid=10960619

Если приоритет входящего оператора ниже приоритета того, что навершине стека (на входе в тупик), то из стека достаётся оператор с большим приоритетом (на шаге g это умножение). То же самое происходит, если приооритет приходящего оператора равен приоритету такового на вершине стека, но тот, что на вершине — ассоциативен. В данном случае после отъезда умножения остаётся сложение, приоритет которого равен приоритету вычитания, но сложение в отличие от вычитания ассоциативно:

\begin{equation*} (a+b)+с=a+(b+c) (a-b)-c!=a-(b-c)=a-b+c \end{equation*}

Упражнение №5

Реализовать на python алгоритм сортировочной станции для преобразования произвольных арифметических выражений с 4 действиями (+,-,*,/) из инфиксной записи в обратную польскую.

Упражнение №6(*)

Добавить в предыдущую реализацию поддержку выражений со скобками.

Арифметические выражения в C — Разделы масштабирования

Аннотация

Арифметические выражения представляют собой комбинацию операндов, соединенных между собой арифметическими операторами. В конечном итоге они оцениваются как одно значение. Мы, люди, используем метод под названием BODMAS для вычисления арифметических выражений в нашей реальной жизни, но компьютеры и язык программирования C используют похожий, но другой метод. Они используют приоритет и ассоциативность.

Объем статьи

Эта статья поможет вам понять разницу между выражением и уравнением. Это также поможет вам ответить на такие вопросы, как

• Какие типы выражений доступны в языке C?
• Что такое арифметические выражения в C?
• Некоторые примеры допустимых и недопустимых арифметических выражений.
• Как они оцениваются?
• Приоритет и ассоциативность различных арифметических операторов.
• Влияние типов данных операндов, участвующих в арифметическом выражении, на результат арифметического выражения.
• Сложный пример, отслеживающий вычисление арифметического выражения в C

Арифметические выражения на C

Большинство людей, слыша слова «выражения», думают об уравнениях. Некоторые из вас могут задать себе вопрос: «Разве они не одинаковы?». Позвольте мне прояснить это для вас.

Возможно, вы оказывались в такой ситуации один или несколько раз. Вы стоите в столовой вашего колледжа или школы или выражения. Кто-то подходит рядом и просит конкретный продукт, скажем, как Магги у продавца. Владелец магазина обнаруживает, что Магги нет в наличии, и он просто дает другую лапшу быстрого приготовления, а покупатель просто берет ее и платит наличными. Вот и все. Никаких вопросов не было задано. 🤨

В таких ситуациях покупатель на самом деле имел в виду лапшу быстрого приготовления, а не Maggi от Nestle. Название Maggi было настолько глубоким, что оно заменило название «Лапша быстрого приготовления».

То же самое и с уравнениями и выражениями: когда люди слышат слово «выражение», их ум обычно думает об уравнениях, а не о выражениях. Одна вещь, которую нужно понять и принять к сведению, это то, что выражение является жизненно важной частью уравнения, но не единственной .

Чтобы двигаться дальше по этому пути, нам нужно немного выучить жаргон. Не бойтесь, это всего лишь простые термины, и весьма вероятно, что вы их уже знаете.

Операнд

Переменная или константа, над которой должна быть выполнена операция

Оператор

Символ указывает, какая операция должна быть выполнена.

Выражение

Комбинация операндов, соединенных с операторами, которые имеют логический смысл.

Уравнение

Уравнение состоит из трех частей: переменной, оператора присваивания — равно и выражения.

Типы выражений в языке C

Теперь, когда вы знаете, что такое выражение, давайте продолжим изучение различных типов выражений в языке программирования C. В языке программирования C есть четыре вида выражений.

Они

• Арифметические выражения
• Реляционные выражения
• Логические выражения
• Условные выражения

Эти выражения классифицируются по входным данным, которые они принимают, и выходным данным, которые они производят. В этой статье мы сосредоточимся на арифметических выражениях. Арифметические выражения языка C аналогичны выражениям большинства других языков программирования.

Что такое арифметическое выражение в C?

Арифметическое выражение представляет собой комбинацию операндов и арифметических операций, таких как сложение, вычитание и т. д. Эти комбинации операндов и операторов должны быть математически осмысленными, иначе их нельзя рассматривать как арифметическое выражение в C.

В таблице ниже перечислены различные арифметические операторы, доступные в языке программирования C, вместе с небольшим описанием.

900 94 означает, что число является положительным целым числом.

Символ	Унарный / Двоичный	Описание
+	Унарный
—	Унарный	означает, что число является отрицательным целым числом.
++	Унарный	Увеличивает значение переменной на 1
—	Унарный	Уменьшает значение переменной на 1
+	Двоичный	выполняет математическое сложение двух данных операнды.
—	Двоичный	выполняет математическое вычитание двух заданных операндов.
*	Двоичный	выполняет математическое умножение двух заданных операндов.
\	Двоичный	выполняет математическое деление двух заданных операндов и возвращает частное.
%	Двоичный	выполняет математическое деление двух заданных операндов и возвращает остаток как результат.

В таблице ниже приведены некоторые допустимые и недопустимые арифметические выражения на языке C с объяснением всех недопустимых выражений.

Арифметическое выражение	Действительный или недействительный	Объяснение
6,4%5,0	Недействительный	оператор по модулю работает только с целыми значениями.
a-	Недействительно	Если минус является унарным оператором, он должен стоять перед операндом. Если минус является бинарным оператором, то второй операнд отсутствует. Так что, в любом случае, выражение недействительно.
-a	Действительный	За унарным минусом следует операнд
a-b	Действительный	Двоичный минус имеет два допустимых операнда, поэтому это допустимое арифметическое выражение.
5%2	Действительно	Оператор по модулю имеет два целочисленных операнда.

Вычисление арифметических выражений в C

Вычисление арифметического выражения основано на трех разных вещах; приоритет, ассоциативность арифметических операторов и типы данных операндов, над которыми выполняется арифметическая операция.
Это больше похоже на правило BODMAS, которое вы выучили в школьные годы, но может ощущаться немного по-другому. Итак, давайте сначала начнем с двух незнакомых терминов и попробуем их понять.

Приоритет

Арифметическое выражение может содержать более одного арифметического оператора. Тогда как вы можете определить, в каком порядке вы будете их выполнять? Допустим, у вас есть арифметическое выражение для вычисления, такое как 2+3*5 , поэтому, если вы сначала выполните умножение, вы получите ответ как 17, а если вы сначала выполните сложение, а затем выполните умножение, вы получите получите ответ как 25. Итак, я надеюсь, вы получили потребность в общепринятом порядке приоритета, когда дело доходит до выполнения различных арифметических операторов в выражении. Потому что другой порядок выполнения операторов дал бы нам другой результат.

Ниже приведена таблица, содержащая список приоритетов всех арифметических операторов в языке программирования Си.

90 094 1

Приоритет	Оператор
0	круглая скобка ()
Унарный плюс (+), Унарный минус (-), Приращение (++), Декремент (— )
2	умножение (*), деление (/), модуль (%)
3	сложение (+), вычитание (-)

В приведенной выше таблице перечислены только приоритеты арифметических операторов, следует отметить, что в языке программирования C есть и другие операторы. Читатель должен узнать о других операторах и их приоритете, если он этого хочет.

Оператор с наименьшим приоритетом выполняется первым, если выражение имеет более одного оператора с одинаковым приоритетом, а затем порядок, в котором операция основана на ассоциативности операторов, участвующих в выражении.

Ассоциативность

Свойство Ассоциативность языка программирования C указывает направление, в котором будет выполняться операция. Помимо указания направления операции, которая должна быть выполнена, свойство Ассоциативность также помогает нам решить проблему, какую операцию выполнять, когда две операции имеют одинаковый приоритет.

В таблице ниже показана ассоциативность всех арифметических операторов.

Оператор	Ассоциативность
Унарный плюс (+)	Справа налево
Унарный минус (-)	Справа налево 900 95
Приращение (++)	Зависит от использования
Уменьшение (—)	Зависит от использования
Сложение (+)	Слева направо
Вычитание (-)	Влево вправо
Умножение (*)	Слева направо
Деление (/)	Слева направо
Модуль (%)	Слева направо

В случае инкремента и декремента оператора, ассоциативность оператора зависит от его использования. Ассоциативность операторов слева направо в случае префиксной операции и справа налево в случае постфиксной операции.

Я упомянул, что свойство Ассоциативность используется для определения того, какая операция должна выполняться, когда два или более оператора имеют одинаковый приоритет. Теперь давайте рассмотрим пример, демонстрирующий вышеупомянутый сценарий.

Рассмотрим выражение: -++a*2, где a = 5 .

В этом выражении и унарный минус (-), и оператор приращения (++) имеют одинаковый приоритет, поэтому какую операцию следует выполнить первой. Ассоциативность унарного минуса — справа налево, а правая часть оператора имеет выражение. Следовательно, мы должны оценить выражение.

Выражение справа от унарного минуса (-) равно ++a*2 , значение an равно 5, поэтому выражение становится равным ++5*2 , оператор приращения имеет более высокий приоритет по сравнению с оператором умножения. Таким образом, компилятор выполнит операцию приращения и заменит ее в выражении результатом, то есть 6.

Теперь вернемся к исходному выражению, выражение -6*2 , все еще правая часть унарного минус — это выражение, поэтому компилятор сначала оценит умножение перед выполнением унарного минуса. Итак, после умножения выражение равно -12, теперь вычисляется унарный минус, и окончательный ответ равен -12.

Вывод

Помимо этих двух вещей, типы данных задействованных операндов также влияют на результат арифметического выражения в языке программирования C.

Типы данных

Типы данных операндов также влияют на результат арифметического выражения. Как вы могли заметить, большинство арифметических операторов являются бинарными операторами, и для выполнения их функций им нужны операнды.

Как вы думаете, каким будет результат этого выражения: 5/2,5?

Можно подумать, что результат будет 2, но, к сожалению, это не так. Когда вы оцениваете выражение 5/2.5 стандартным компилятором C, в результате вы получите 2. 0. Позвольте мне объяснить причину ПОЧЕМУ.

Арифметический оператор всегда выбирает типы данных, которые более эффективны для хранения результирующего значения арифметического выражения. Большинство арифметических операторов являются бинарными, и их может быть три.

• Оба операнда имеют целочисленный тип данных. Тогда результат также будет иметь целочисленный тип данных.
• Оба операнда имеют тип данных float. Тогда результат также будет того же типа данных, что и число с плавающей запятой.
• Когда один операнд имеет тип данных integer, а другой — тип данных float. Онлайн-компилятор C вернет результат в виде значения с плавающей запятой, потому что тип данных float в таких случаях более точен для хранения вывода, чем целые числа.

Оператор приведения типа

В программировании на C вы можете преобразовать значение из одного типа данных в другой тип данных с помощью оператора приведения типа. Целое число при преобразовании в число с плавающей запятой будет иметь десятичные значения с точностью до шести знаков, а число в плавающем состоянии при преобразовании в целое число будет иметь усеченные десятичные значения. Оператор приведения типа имеет приоритет над операторами умножения, деления и по модулю.

Синтаксис: (type_name) выражение

Пример:

Преобразование числа с плавающей запятой в целое

Код:

Вывод:

Целое число в Flo при преобразовании

Код:

Вывод:

Пример Арифметическое выражение в C

Достаточно теории. Теперь давайте возьмем арифметическое выражение в C и проследим его выполнение.

Рассмотрим арифметическое выражение: -7*5/(3+2*3/12+8)+15*( (float)10 / 5)

Первый приоритет отдается скобкам, но здесь в этом выражении две скобки, поэтому начнем с первого слева.

• Шаг 1:
  • Мы должны вычислить выражение в первой скобке, то есть 3+2*3/12+8 .
  • В этом выражении есть и умножение, и деление. Оба этих оператора имеют одинаковый приоритет, поэтому нам придется сначала выполнить умножение, а затем деление, потому что оба оператора имеют ассоциативность слева направо.
  • После выполнения 2*3 и изменения выражения на 3+6/12+8
  • Теперь нам нужно выполнить деление. Деление 6 на 12 обычно дает 0,5, но поскольку оба операнда здесь являются целыми числами, результат также будет преобразован в тип данных целого числа. Поэтому, когда значение с плавающей запятой преобразуется в целое число, десятичные значения усекаются и приводят к 0
  .
  • Теперь выражение имеет вид 3+0+8
  • После сложения 3 и 0 выражение становится 3+8
  • И после выполнения этого последнего сложения мы получим 11.
  • Теперь замените результат этого выражения исходным выражением.
• Шаг 2:
  • Теперь у нас есть выражение: -7*5/11+15*( (float)10/5) . Таким образом, мы должны оценить вторую скобку и заменить ее результатом в этом выражении. Оцените выражение: (с плавающей запятой)10 / 5
  • Оператор приведения типа имеет максимальный приоритет, поэтому после преобразования 10 из целого числа в число с плавающей запятой выражение становится 10,0/5.
  • Деление 10 на 5 дает нам частное 2, полное целое число, но, поскольку один из операндов является числом с плавающей запятой, результат также должен иметь тип данных с плавающей запятой. Итак, результат 2.0
  .
  • Теперь заменив результат этого выражения в исходное выражение, получим -7*5/11+15*2.0
• Шаг 3:
  • Теперь рядом с 7 стоит унарный минус, поэтому мы должны выполнить его следующим.
• Шаг 4:
  • Затем мы выполняем умножение -7 и 5 и заменяем их положение в исходном выражении на результат -35.
  • У нас есть -35/11+15*2.0
• Шаг 5:
  • Теперь выполните деление -35 и 11, поскольку оба значения имеют целочисленный тип данных, результатом будет -3, а не -3,181.
  • Заменив -35/11 на -3, выражение станет -3+15*2,0
• Шаг 6:
  • Теперь нам нужно выполнить умножение 15 на 2.0, результатом будет 30.0, так как один из операндов является числом с плавающей запятой.
• Шаг 7:
  • Теперь у нас есть выражение -3+30.0, поэтому результат 27.0

Таким образом вычисляется арифметическое выражение, и любой другой ответ, кроме 27.0, неверен.

Заключение:

В этой статье мы узнали о том, что представляют собой различные арифметические операторы в языке программирования C, их приоритет и ассоциативность, что такое выражения в целом и арифметические выражения в C, а также о том, как используются типы данных операндов. в арифметическом выражении влияет на результат арифметического выражения в C.

Затем мы взяли пример арифметического выражения на языке C и проследили его внутреннюю работу, т. е. то, как выражение вычисляется на языке программирования C.

Надеюсь, вы узнали что-то новое из этой статьи.

Спасибо.

Арифметические выражения | Документация Mendix

Mendix 10 в настоящее время находится в стадии бета-тестирования. Подробнее о Mendix 9.24 LTS см. в Руководстве по Studio Pro 9.

Последнее изменение: 20 апреля 2023 г.

1 Введение

В этом документе описаны арифметические операторы, которые поддерживаются в выражениях. Все они работают с числовыми типами данных (Integer/Long и Decimal).

2 Умножение

Умножает два числа.

2.1 Входные параметры

Входные параметры описаны в таблице ниже:

Значение	Тип
Первый номер	Целое/длинное, десятичное
Второй номер	Целое/длинное, десятичное

2.2 Выход

Если оба входа имеют тип Integer/Long, результат будет типа Integer/Long.

Если любой из двух входных данных имеет тип Decimal, результат будет иметь тип Decimal.

2.3 Пример

Если вы используете следующий ввод:

Вывод:

3 Деление

Делит два числа. Вы можете использовать синтаксис div или двоеточие ( : ), как показано ниже в примерах. двоеточие ( :) синтаксис основан на символе деления ÷ . Мы не можем использовать более традиционный синтаксис косой черты (/), потому что это будет противоречить косой черте, которая используется для разделения объектов и элементов.

3.1 Входные параметры

Входные параметры описаны в таблице ниже:

Значение	Тип
Первый номер	Целое/длинное, десятичное
Второй номер	Целое/длинное, десятичное

3.2 Выходные данные

Результат всегда имеет тип Decimal, независимо от типов входных данных.

3.3 Пример

Найдите пример использования ниже:

Результат деления является приблизительным, если он имеет бесконечное десятичное разложение. Два приведенных ниже примера иллюстрируют это приближение:

• Если вы используете следующий ввод:

  вывод:

  0,4285714285714285714285714285714286
   

  Если продолжить вычисления с результатами деления, результаты могут оказаться неожиданными. Следующий ввод:

   (3 : 7) * 7
   

  приводит к выводу ниже:

   3.00000000000000000000000000000000002
   

• Если вы используете следующий ввод:

   ячейка((3 : 7) * 7)
   

  вывод:

Поэтому операции деления рекомендуется выполнять в последнюю очередь.

4 Модуль

Вычисляет остаток от деления одного числа на другое. Другими словами, м по модулю n соответствует: м = p + k*n , где p является результатом операции м по модулю n .

4.1 Входные параметры

Входные параметры описаны в таблице ниже:

Значение	Тип
Первый номер	Целое/длинное, десятичное
Второй номер	Целое/длинное, десятичное

4.2 Выход

Если оба входа имеют тип Integer/Long, результат будет типа Integer/Long.

Если любой из двух входных данных имеет тип Decimal, результат будет иметь тип Decimal.

4.3 Пример

Если вы используете следующий ввод:

 23 mod 5
 

вывод:

5 Дополнение

Добавляет два числа.

Сведения об использовании символа сложения для объединения строк см. в разделе Вызовы строковых функций.

5.1 Входные параметры

Входные параметры описаны в таблице ниже:

Значение	Тип
Первый номер	Целое/длинное, десятичное
Второй номер	Целое/длинное, десятичное

5.