Отрицательные числа примеры: Сложение Чисел с Разными Знаками

Вычитание отрицательного числа, правило, примеры, как вычесть два отрицательных числа, как из отрицательного числа вычесть положительное

Данная статья посвящена разбору такой темы, как выполнение вычитания отрицательных чисел. Материал представляет собой полезную информацию о правиле вычитания отрицательных чисел и других определениях. Для закрепления сути параграфа мы детально разберем примеры типичных упражнений и задач.

Правило вычитания отрицательных чисел

Для того, чтобы разобраться в данной теме, следует узнать основные определения и понятия.

Определение 1

Правило вычитания отрицательных чисел формулируется так: чтобы из числа a вычесть число b со знаком минус, необходимо к уменьшаемому a прибавить число −b, которое является противоположным вычитаемому b.

Если представить данное правило вычитания отрицательного числа b из произвольного числа a в буквенном виде, то оно будет выглядеть так: a−b=a+(−b).

Для того, чтобы использовать данное правило, необходимо доказать его справедливость.

Возьмем числа a и b. Чтобы вычесть из числа a число b, необходимо найти такое число с, которое в сумме с числом b будет равняться числу a. Другими словами, если найдено такое число c, что c+b=a, то разность a−b равна c.

Для того, чтобы доказать правило вычитания, необходимо показать, что сложение суммы

a+(−b) с числом b – это есть число a. Необходимо вспомнить о свойствах действий с действительными числами. Так как в этом случае работает сочетательное свойство сложения, то равенство (a+(−b)) +b=a+((−b) +b) будет верным.

Так, как сумма чисел с противоположными знаками равняется нулю, то a+((−b) +b) =a+0, а сумма a+0= а (если к числу прибавить нуль, то оно не изменится). Равенство a−b=a+(−b)считается доказанным, значит, доказана и справедливость приведенного правила вычитания чисел со знаком минус.

Мы рассмотрели, как работает данное правило для действительных чисел a и b. Но оно также считается справедливым для любых рациональных и целых чисел a и b. Действия с рациональными и целыми числами также обладают свойствами, использованными при доказательстве. Следует добавить, что с помощью разобранного правила можно выполнять действия числа со знаком минус как из положительного числа, так и из отрицательного или нуля.

Рассмотрим разобранное правило на типичных примерах.

Примеры использования правила вычитания

Рассмотрим примеры с вычитанием чисел. Для начала рассмотрим простой пример, который поможет легко разобраться со всеми тонкостями процесса.

Пример 1

Необходимо отнять от числа −13 число −7.

Возьмем число, противоположное вычитаемому −7. Это число 7. Тогда по правилу вычитания отрицательных чисел имеем (−13) −(−7) =(−13) +7. Выполняем сложение. Теперь получаем: (−13) +7=−(13−7) =−6.

Вот все решение: (−13) −(−7) =(−13) +7=−(13−7) =−6. (−13)−(−7)=−6. Вычитание дробных отрицательных чисел также можно выполнять. Необходимо перейти к обыкновенным дробям, смешанным числам или десятичным дробям. Выбор числа зависит от того, с каким вариантом вам удобнее работать.

Пример 2

Необходимо выполнить вычитание из числа 3,4 числа -2323.

Применяем описанное выше правило вычитания, получаем 3,4—2323=3,4+2323. Заменяем дробь на десятичное число: 3,4=3410=175=325 (как переводить дроби, можно посмотреть в материале по теме), получаем 3,4+2323=325+2323. Выполняем сложение. На этом вычитание отрицательного числа -2323 из числа 3,4 завершено.

Приведем краткую запись решения: 3,4—2323=27115.

Пример 3

Необходимо выполнить вычитание числа −0,(326) от нуля.

По правилу вычитания, которое мы изучили выше, 0−(−0,(326))=0+0,(326)=0,(326).

Последний переход верен, так как здесь работает свойство сложения числа с нулем: 0−(−0,(326))=0,(326).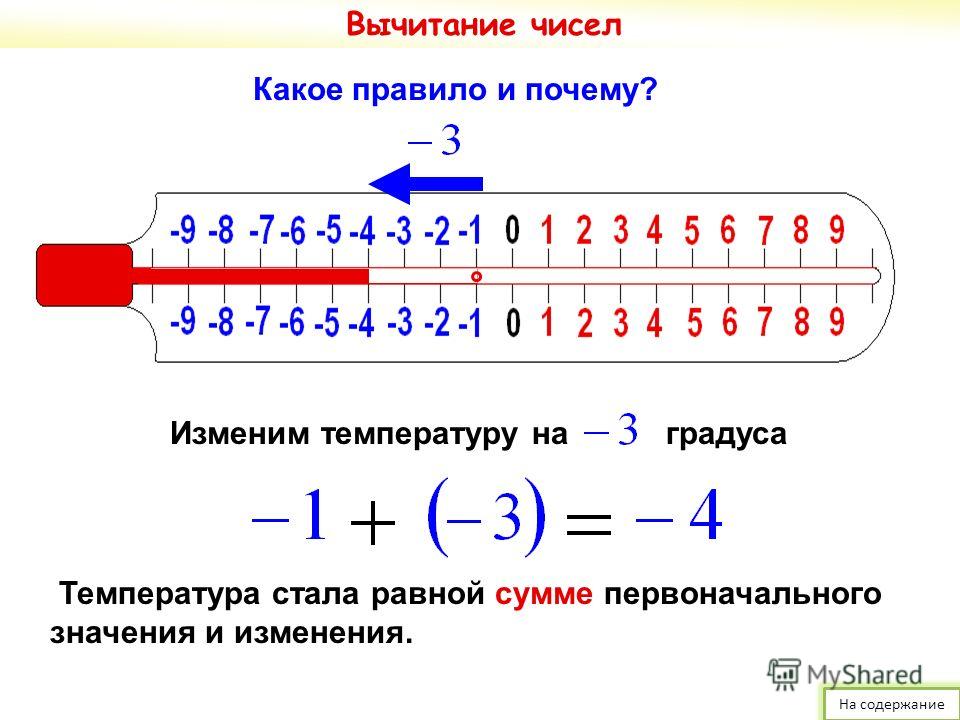

Из рассмотренных примеров видно, что при вычитании отрицательного числа может получиться как положительное, так и отрицательное число. Вычитание отрицательного числа может в результате дать и число

0, это происходит, когда уменьшаемое равно вычитаемому.

Пример 4

Необходимо вычислить разность отрицательных чисел -5—5.

По правилу вычитания мы получаем -5—5=-5+5.

Мы пришли к сумме противоположных чисел, которая всегда равна нулю: -5—5=-5+5=0 

Итак,-5—5=0.

В некоторых случаях результат вычитания необходимо записать в виде числового выражения. Это справедливо в тех случаях, когда уменьшаемое или вычитаемое является иррациональным числом. К примеру, вычитание из отрицательного числа −2 отрицательного числа –π проводится так: (−2)−(−π)=(−2)+π=π−2. Значение полученного выражения может быть вычислено максимально точно только в том случае, если это необходимо. Для подробной информации можно изучить другие разделы, связанные с данной темой.

Решение задач от 1 дня / от 150 р. Курсовая работа от 5 дней / от 1800 р. Реферат от 1 дня / от 700 р.

Автор: Ирина Мальцевская

Преподаватель математики и информатики. Кафедра бизнес-информатики Российского университета транспорта

Пример отрицательного числа? – Обзоры Вики

Отрицательные числа могут быть целыми, дробными или десятичными. Например, — 2,- 3,- 4, -5, -2/3, -5/7, -3/4, -0.5, -0.7. и т.д являются примерами отрицательных чисел.

Точно так же, каковы четыре правила негативов? Правила:

	Правило	Пример
+ (+)	Два подобных знака становятся положительным знаком	3 + (+ 2) = 3 + 2 = 5
— (-)	6 — (- 3) = 6 + 3 = 9
+ (-)	Два непохожих знака становятся отрицательным знаком	7 + (- 2) = 7 — 2 = 5
— (+)	8 — (+ 2) = 8-2 = 6

Как написать отрицательное число словами? Это зависит от контекста. Если вы перечисляете балансы, вы можете указать баланс Тома как — $ 10. Если вы пишете ОЧЕНЬ небрежно, вы могли бы написать: «Баланс на счете Тома упал на десять долларов». Я также видел суммы, записанные в формате $-10 или ($10) или даже $10-.

Как научить ребенка отрицательным числам? Ответ на вопрос: как научить ребенка отрицательным числам? Учить отрицательные числа как «направленные» числа в строке действительных чисел. Полезным примером может быть использование карты мира Меркатора. Широты к северу и югу от экватора направлены как положительные, так и отрицательные градусы.

Во-вторых, каковы некоторые примеры отрицательных чисел в реальной жизни? Отрицательные числа обычно используются для описания температура ниже точки замерзания, денежный кредит, высота ниже уровня моря, уровень лифта, когда он ниже уровня земли, отрицательные оценки на экзаменах, как штраф в викторинах / играх и т. д.

Как читать отрицательное число?

Отрицательное число написано со знаком минус, «-», перед положительным числом. Например, 3 — положительное число, а −3 — отрицательное число. Читается «минус три» или «минус три»; это означает противоположность 3. Иногда для большей выразительности мы пишем пару противоположных чисел как −3 и +3.

Как написать отрицательное число на письме?

Стандартный способ учета — всегда показывать отрицательные числа. в скобках. Если вы хотите обратиться в первую очередь к финансистам, это общепринятая практика.

Почему бухгалтеры используют скобки для отрицательных чисел? Балансы счетов на самом деле не имеют отрицательных значений, они просто другой баланс. Например, «отрицательный» баланс на счете расходов будет кредитовым балансом. Когда это происходит, кредитовый баланс может отображаться в квадратных скобках, чтобы обозначить переключение между дебетовым/кредитным статусом.

Как заключить в скобки отрицательное число?

В учебниках по математике отрицательное число, которое вы вычитаете, часто заключают в круглые скобки, чтобы знаки не совпадали, поэтому 3 – –5 равно 3 – (–5). При взятии отрицательного числа минус положительное число, отбросьте оба знака минус и добавьте два числа, как если бы они оба были положительными; затем прикрепите к результату знак минус.

Как учащиеся понимают отрицательные числа? Чтобы помочь моим ученикам лучше понять, я предлагаю им думать об отрицательных числах следующим образом:

1. Отрицательный знак говорит вам, насколько далеко число от нуля.
2. Таким образом, -3 означает, что вы находитесь в 3 шагах от 0, а -5 означает, что вы находитесь в 5 шагах от нуля.
3. Следовательно, -5 меньше, чем -3, потому что вы дальше от нуля.

Как объяснить ребенку негатив?

6 советов, как помочь вашему негативно настроенному ребенку

1. Перестаньте жаловаться на себя. Часто дети, мыслящие негативно, имеют негативно мыслящих родителей. …
2. Помогите ребенку поменять фильтр. …
3. Развивайте отношение благодарности. …
4. Мысли «проверка реальности». …
5. Сопереживайте и помогайте им понять их эмоции. …
6. Помогите им решить их собственные проблемы.

Как объяснить детям отрицательные числа?

Отрицательное число — это число что указывает на обратное. Например: если положительное число соответствует расстоянию вверх, то отрицательное число соответствует расстоянию вниз. Если положительное число — это расстояние вправо, то отрицательное число — это расстояние влево.

Как вы можете использовать отрицательные числа для представления реальных проблем? Отрицательные числа используются во многих различных ситуациях. Вы читали об отрицательных числах в сводки погоды и на упаковке пищевых продуктов. Температура -5°C означает «минус пять градусов» и означает 5 градусов ниже нуля. Узнайте больше об отрицательных числах на упаковке пищевых продуктов в информационном бюллетене Хранение замороженных продуктов.

Какое самое большое отрицательное число? Так, -1 является наибольшим из всех отрицательных чисел. Таким образом, в заключение мы можем сказать, что −1 является самым большим отрицательным числом.

Как научить ребенка отрицательным числам?

Это минус 1 или минус 1? В математике −1 (также известный как отрицательный или минус один) является аддитивным, обратным 1, то есть числом, которое при добавлении к 1 дает аддитивный элемент идентичности, 0. Это отрицательное целое число больше отрицательного числа два (-2) и меньше 0.

Как объяснить отрицательные числа на числовой прямой?

Какая связь между 7 и отрицательной 7? Любое число без знака минус перед ним считается положительным числом, то есть числом, которое больше нуля. Итак, пока -7 минус семь, 7 плюс семь, или просто семь.

Как вы вводите негативы?

Вы узнаете отрицательные числа по маленькому минусу или знаку минуса перед ними. Вы можете думать об этом отрицательном знаке как о том, что вы смотрите на число, которое намного меньше 0. Итак, -7 на 7 меньше 0. Любое число со знаком минус впереди является отрицательным числом.

Как знакомить детей с отрицательными числами?

Отрицательные числа – Объяснение и примеры

Некоторым людям изучение отрицательных чисел может показаться немного скучным.

У этих людей возникают вопросы, например, зачем изучать отрицательные числа?

Как отрицательные числа связаны с их повседневной жизнью?

Итак, в этой статье мы узнаем, что такое отрицательные числа, их действия и как числа связаны в реальной жизни.

История отрицательных чисел началась тысячу лет назад, когда их начали использовать математики с Индийского субконтинента. Позже европейцы проявили интерес к отрицательным числам, но очень неохотно их принимали.

Египтяне также пренебрежительно относились к отрицательному числу и в какой-то момент считали отрицательное число смешным. Это потому, что математика, которую они использовали в то время, основывалась только на геометрических понятиях, таких как длина окружности и площадь. Позже европейцы начали догонять отрицательные числа, когда ученые начали переводить арабские тексты, полученные из Северной Африки.

Из этой краткой истории мы узнали, что, тем не менее, этим поколениям блестящих и умных людей изначально было трудно принять концепцию отрицательных чисел.

Они, наконец, приняли эту идею после того, как открыли значение отрицательных чисел.

Что такое отрицательное число?

Отрицательное число — это число, значение которого меньше нуля. Отрицательные числа обозначаются знаком минус или тире (-) перед числом.

Они представлены на числовой строке слева от начала координат. Отрицательные числа могут быть целыми, дробными или десятичными. Например, – 2, – 3, – 4, – 5, -2/3, -5/7, -3/4, -0,5, -0,7. и т. д. являются примерами отрицательных чисел. В этом случае эти числа произносятся как минус два, минус три, минус четыре и так далее.

Отрицательное число имеет несколько различных интерпретаций. А это:

• Отрицательное число — это число меньше нуля
• Числа слева от нуля на числовой прямой
• Число, противоположное положительному числу
• Отрицательное число означает утрату или отсутствие чего-либо.
• Величина, имеющая направление

Что такое отрицательное целое число?

Отрицательное целое число — это целое число, значение которого меньше нуля. Отрицательные целые числа обычно представляют собой целые числа, например, -3, -5, -8, -10 и т. д.

Операции с отрицательными целыми числами

Отрицательные целые числа имеют правила для выполнения различных вычислений. Это:

• Сложение отрицательного и положительного целых чисел

При сложении отрицательного и положительного целых чисел вычтите целые числа и запишите знак большего абсолютного значения. Другими словами, когда небольшое отрицательное целое число прибавляется к большему положительному целому, целые числа вычитаются и получают положительный знак. Например,

8 + (- 2) = 6. Точно так же при сложении небольшого положительного и большого отрицательного целых чисел сумма всегда будет отрицательной. Например, – 5 + 3 = – 2.

• Добавление отрицательных целых чисел

При добавлении отрицательных целых чисел числа складываются, и сумма принимает знак исходных целых чисел.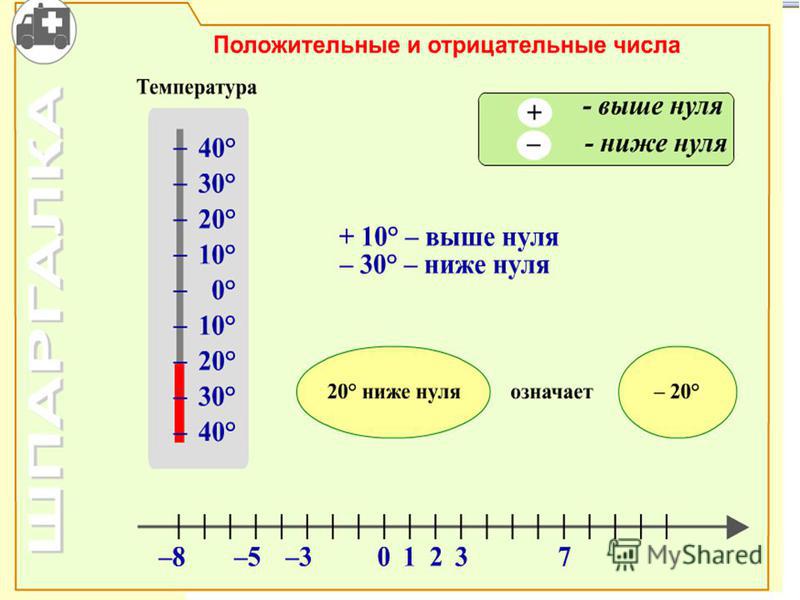 Например, – 5 + (-1) = – 6.

• Вычитание целых чисел со знаком

Вычитание положительного целого числа из отрицательного числа эквивалентно прибавлению отрицательного числа этого целого числа. Например, -10 – 15 = -10 + (-15) = -25.

Вычитание отрицательного целого числа из другого отрицательного числа равносильно добавлению положительного числа этого целого числа. Например, 13 – (-14) = 13 + 14 = 27.

• Умножение и деление отрицательных целых чисел

Когда отрицательное целое число умножается на другое отрицательное целое число, произведение положительное. Пример: -4 x -4 = 16. Точно так же деление отрицательного целого числа на другое отрицательное целое число дает положительное частное.

Умножение положительного целого числа на другое отрицательное число дает отрицательное произведение. Например, -2 х 5 = -10. А деление положительного целого числа на отрицательное дает отрицательное частное.

Применение отрицательных целых чисел в реальной жизни

Независимо от их значения, отрицательные целые числа широко применяются в различных сферах жизни. Следующие примеры применения отрицательных чисел в реальной жизни побудят вас увидеть преимущества их изучения.

• Банковско-финансовый сектор.

Банки и финансовые учреждения связаны с дебетом, кредитом и деньгами. По этой причине необходимо иметь номера, которые различают кредитную и дебетовую транзакцию. Прибыли и убытки также определяются положительным и отрицательным числом соответственно. Еще одна область, где используются отрицательные числа, — это фондовый рынок. Положительные и отрицательные числа используются для обозначения взлетов и падений цены акций.

Депозиты обычно обозначаются положительным знаком, тогда как снятие средств обозначается отрицательным знаком.

• Наука, техника и медицина

Отрицательные числа используются в прогнозах погоды для отображения температуры в регионе. Отрицательные целые числа используются для отображения температуры по шкале Фаренгейта и Цельсия.

В технике, например, в таких приборах, как котлы и паровые двигатели, используются манометры и термометры, калиброванные от отрицательных до положительных целых чисел.

Приборы для измерения артериального давления, массы тела и тестирования на наркотики работают на концепте отрицательной или положительной шкалы.

• Другие применения отрицательных целых чисел в реальной жизни

Разница голов в таких видах спорта, как футбол, хоккей и баскетбол, обозначается отрицательными целыми числами.

Лифты, спидометры и Alco-blow используют отрицательные и положительные значения.

 

Отрицательные числа — математика GCSE

Введение

Что такое отрицательные числа?

Сложение и вычитание отрицательных чисел

Умножение и деление отрицательных чисел

Как складывать и вычитать отрицательные числа

Как умножать и делить отрицательные числа

Рабочий лист отрицательных чисел

Распространенные заблуждения

Практикуйте вопросы с отрицательными числами

Отрицательные числа Вопросы GCSE

Контрольный список обучения

Следующие уроки

Все еще застряли?

Индивидуальные занятия по математике, созданные для успеха KS4

Теперь доступны еженедельные онлайн-уроки повторения математики GCSE

Узнать больше

Введение

Что такое отрицательные числа?

Сложение и вычитание отрицательных чисел

Умножение и деление отрицательных чисел

Как складывать и вычитать отрицательные числа

Как умножать и делить отрицательные числа

Рабочий лист отрицательных чисел

Распространенные заблуждения

Практикуйте вопросы с отрицательными числами

Отрицательные числа Вопросы GCSE

Контрольный список обучения

Следующие уроки

Все еще застряли?

Здесь мы узнаем о отрицательных числах , в том числе о том, как складывать, вычитать, умножать и делить отрицательные числа.

Существуют также рабочие листы с отрицательными числами, основанные на экзаменационных вопросах Edexcel, AQA и OCR, а также дополнительные рекомендации о том, что делать дальше, если вы все еще застряли.

Что такое отрицательные числа?

Отрицательные числа — это любые числа меньше нуля, перед которыми стоит знак минус или минус (-).

Числа больше нуля называются положительными числами . Если перед числом нет знака, то число положительное.

В числовой строке ниже мы можем видеть некоторые положительные и отрицательные целые числа (целые числа):

Числа оранжевого цвета являются отрицательными значениями, а числа синего цвета — положительными значениями. Ноль не является ни положительным, ни отрицательным.

Точно так же, как вы можете складывать, вычитать, умножать и делить положительные числа, вы можете делать то же самое с отрицательными числами, будь то целые числа, десятичные числа или дроби.

Что такое отрицательные числа?

Сложение и вычитание отрицательных чисел

При сложении и вычитании отрицательных чисел используйте числовую строку:

При сложении перемещайтесь вправо от числовой строки.

При вычитании переместитесь влево от числовой строки .

Иногда вопрос может иметь две операции, расположенные рядом друг с другом:

Напр. 4 + (−2)

Если знаки одинаковые, замените на положительный знак .

Если знаки разные, замените знаком минус.

Таблица ниже суммирует это:

Как правило: одинаковые знаки складываются, разные знаки вычитаются.

Пошаговое руководство: Сложение и вычитание отрицательных чисел

Что нужно помнить при сложении и вычитании отрицательных чисел?

Умножение и деление отрицательных чисел

Аналогичные правила применяются для умножения и деления отрицательных чисел:

Если знаки совпадают, ответ положительный.

Если знаки разные, ответ отрицательный.

При умножении отрицательных чисел:

Те же правила применяются и при делении отрицательных чисел:

Пошаговое руководство: Умножение и деление отрицательных чисел

Что нужно помнить при умножении и делении отрицательных чисел ?

Арифметика отрицательных чисел

Существуют правила вычисления с отрицательными числами.

При сложении и вычитании чисел важно учитывать положительные и отрицательные значения. Если число не имеет знака, это означает, что это положительное число, например, 5 на самом деле +5.

Когда два знака пишутся рядом друг с другом, мы должны помнить эти правила.

Когда мы складываем и вычитаем отрицательные числа, мы можем использовать числовую прямую, чтобы понять, в каком направлении нам нужно двигаться.

Выработка -2-4

-2-4 = -6

Выработка -4+13

-4+13=9

Напр.

Работа 4+-7

Два различных знака написаны рядом друг с другом. Они становятся отрицательными .

Таким образом,  4+-7 = 4-7

4-7= -3

При умножении и делении отрицательных чисел часто бывает полезно сначала завершить вычисление, используя положительные числа. Тогда помните правила

• Умножение или деление двух чисел с одинаковыми знаками даст положительный ответ
• Умножение или деление двух чисел с разными знаками даст отрицательный ответ

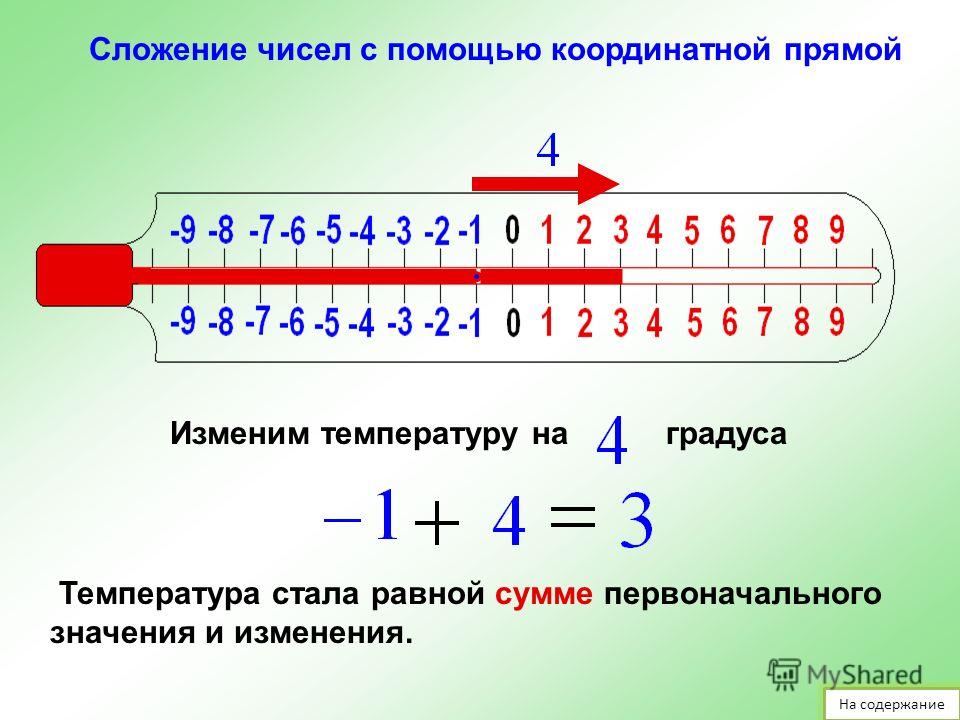
3 E.g.

Вычислить -4 × -3

4×3 = 12

Оба числа имеют один и тот же знак , поэтому ответ будет положительным .

-4 × -3 = 12

Тренировка 12 ÷-2

12÷2=6

Числа имеют различных знаков, поэтому ответ будет отрицательным .

12 ÷-2 = -6

Порядок целых чисел


Целые числа (целые числа) упорядочиваются в числовой строке на основе положительных целых чисел и отрицательных целых чисел. Центр числовой строки отмечен как 0. Целые числа, которые на больше, чем 0, являются положительными

целыми числами. Целые числа, которые на меньше 0 — это отрицательных целых чисел.

Чем больше целое число отрицательное , тем меньше значение. Чем больше целое число положительное , тем больше значение.

Расположите эти числа в порядке возрастания.

4,-2,0, 3,-3,-5, 1, 2

Помните: возрастание означает от меньшего к большему.

-5 — это наибольшее отрицательное число, поэтому это наименьшее значение.

4 самый позитивный число, так что это самое большое значение.

Итак, расставив их в порядке возрастания, мы получим -5,-3,-2, 0, 1, 2, 3, 4

Например.

Расположите эти числа в порядке убывания.

-1, -6, -12, -4, -3, -8

Помните, что убывание означает от большего к меньшему.

-1 — это наименьшее отрицательное число , поэтому это самое большое значение.

-12 — это самое отрицательное число , поэтому это наименьшее значение.

Итак, расположив их в порядке убывания, мы получим -1, -3, -4, -6, -8, -12

Как складывать и вычитать отрицательные числа

Чтобы складывать и вычитать отрицательные числа:

1. Если у вас есть два знака рядом друг с другом, замените их одним знаком.
         Если знаки совпадают, замените их положительным знаком (+).
         Если знаки разные, замените их знаком минус (-).
   
2. Обведите первое число в числовой строке.
3. Используйте числовую строку для сложения или вычитания чисел:
        При добавлении переместитесь вправо от числа на шаге 2 (→).
        При вычитании переместитесь влево от числа на шаге 2 ( ←).
4. Напишите свой окончательный ответ.

Объясните, как складывать и вычитать отрицательные числа за 4 шага

Как умножать и делить отрицательные числа

Чтобы умножать и делить отрицательные числа:

1. Умножать или делить числа как обычно.
2. При необходимости измените знак, используя правила умножения и деления отрицательных чисел:
        Если знаки совпадают, ответ положительный.
        Если знаки разные, ответ отрицательный.

Объясните, как умножать и делить отрицательные числа в 2 шага

Рабочий лист с отрицательными числами

Получите бесплатный рабочий лист с отрицательными числами, содержащий более 20 вопросов и ответов. Включает рассуждения и прикладные вопросы.

СКАЧАТЬ БЕСПЛАТНО

Икс

Рабочий лист с отрицательными числами

Получите бесплатный рабочий лист с отрицательными числами, содержащий более 20 вопросов и ответов. Включает рассуждения и прикладные вопросы.

СКАЧАТЬ БЕСПЛАТНО

Примеры отрицательных чисел

Пример 1: добавление положительного числа

\[ −5 + 8 \]

1. I Если у вас есть два знака рядом друг с другом, замените их одним знаком.

Если в середине вычисления знаки совпадают, замените их положительным знаком (+).

Если знаки разные, замените знаком минус (-).

В этом случае у вас нет двух знаков рядом друг с другом.

2 Обведите первое число в числовой строке.

Первое число в вопросе (−5)

3 Используйте числовую строку для сложения или вычитания ваших чисел.

При добавлении переместитесь вправо от числа на шаге 2 (→).

При вычитании переместитесь влево от числа на шаге 2 ( ←).

В этом случае мы добавляем 8, поэтому переместите 8 пробелов прямо от (-5) в числовой строке:

4Запишите свой окончательный ответ.

\[-5 + 8 = 3\]

Пример 2: вычитание отрицательного числа (две операции)

\[ −7 − (−5) \]

Если у вас есть два знака рядом друг с другом , измените их на один знак.

В этом случае у вас есть минус и минус рядом друг с другом.


Поскольку знаки одинаковые, замените их знаком плюс (+).

\[-7 \color{violet}+ 5\]

Обведите первое число в числовой строке.

Первое число в вопросе (-7)

Используйте числовую строку для сложения или вычитания ваших чисел.

В этом случае мы прибавляем 5, поэтому переместите 5 пробелов справа от (-7) в числовой строке:

Напишите свой окончательный ответ.

\[-7 – (-5) = -2\]

Пример 3: умножение отрицательных чисел

\[ −6 × (−7) \]

Обычное умножение или деление чисел.

\[ 6 × 7 = 42\]

Измените знак, используя правила умножения и деления отрицательных чисел:

\[\color{orange}{-6} × \color{orange}{- 7}\]


В этом случае у нас есть число, которое умножается на отрицательное число.


Знаки одинаковые, поэтому ответ должен быть положительным.

\[= 42\]

Пример 4: деление отрицательных чисел

\[ -25 ÷ 5 \]

Нормальное умножение или деление чисел.

\[ 25 ÷ 5 = 5\]

Измените знак, используя правила умножения и деления отрицательных чисел:

\[\color{orange}{-25} ÷ \color{blue}5\ ]


В этом случае у нас есть отрицательное число, деленное на положительное число.


Знаки одинаковые, поэтому у нас должно быть отрицательное частное.

\[= -5\]

Пример 5: смешанные операции (Порядок операций) 92=\]

Начните с индексов

В этом случае мы имеем дело с тремя разными операциями (+, × и ÷) и индексом. Нам нужно использовать BIDMAS, чтобы определить порядок расчета.


Первое, что мы вычисляем, это индексы: B I DMAS


(−2) ² равно −2 × (−2)


Мы знаем, что 2 × 2 = 4

2

2

3

3
Если знаки одинаковые ((−2 × (−2)) , то ответ положительный. 92 =4\]

Умножить или разделить числа как обычно.

Для первой части 18 ÷ 6 = 3


Для второй части 3 × 4 = 12

Измените знак, используя правила умножения и деления отрицательных чисел:

Для первой части −18 ÷ (−6),
знаки одинаковые, поэтому ответ положительный 3.


Для второй части -3 × 4,
знаки разные, поэтому ответ отрицательный (−12).


Осталось:

\[3-12\]

Обведите первое число в числовой строке.

Первое число в вопросе — 3.

Используйте числовую строку, чтобы сложить или вычесть числа и написать окончательный ответ.

В этом случае мы вычитаем 12, поэтому переместим 12 делений влево от 3 в числовой строке:

Окончательный ответ:

\[3 – 12 = -9\]

Пример 6: задача со словами из реальной жизни

В таблице ниже показаны температуры, зарегистрированные в Лестере в разное время дня. 9{\circ}C )

−8

−5

3

−1

Для расчета а) :

запишите самые высокие и самые низкие температуры.

Максимальная температура 3ºC.

Самая низкая температура -8ºC.

Обычное умножение или деление чисел.

\[ 8 × 3 = 24\]

Изменить знак, используя правила умножения и деления отрицательных чисел:

9{\circ}C\]

Чтобы рассчитать b):

Если у вас есть два знака рядом друг с другом, замените их одним знаком.


Температура в 2 часа ночи была -8°C, а в 13 часов 3°C.

Чтобы найти разницу, мы должны вычислить -8 – 3.

В этом случае у вас нет двух знаков рядом друг с другом.

Обведите первое число в числовой строке.

Первое число в вопросе (-8):

Используйте числовую строку для сложения или вычитания чисел :
Если вы добавляете, переместитесь вправо от числа на шаге 2 (→) .
При вычитании переместитесь влево от числа на шаге 2 ( ←) .

В этом случае мы вычитаем 3, поэтому переместите 3 пробела справа от (-8) в числовой строке:

Напишите свой окончательный ответ.

\[-8 – 3 = -11\]

Распространенные заблуждения

• Большее отрицательное число означает большее число

Студенты иногда предполагают, что чем больше отрицательное число, тем оно больше. Например, учащиеся могут ошибочно предположить, что -3 больше 2, потому что 3 — большее число.

• Возведение отрицательного числа в степень больше единицы

Помните, что при возведении отрицательного числа в степень больше 1 результат может быть положительным или отрицательным. Когда вы возводите отрицательное число в нечетную степень, в результате получается отрицательный ответ, когда вы возводите отрицательное число в четную степень, в результате получается положительный ответ.

• Изменение знаков при сложении и вычитании
  При сложении или вычитании отрицательных чисел знаки меняются только в том случае, если они находятся рядом друг с другом в середине вычисления и различны

Практические вопросы по отрицательным числам

– \; – вместе, поэтому измените его на + .

 

-11+8 = -3

 

8 х 9 = 72

  9{\circ}C

Расчет, который нам нужно сделать здесь, это 2 – – 9. Существует – \; – вместе, так что это становится +.

 

2–9 = 2 + 9 = 11

Отрицательные числа Вопросы GCSE

1. У Тилли есть следующие 6 карточек:

Она собирается выбрать 3 карточки и умножить их.

(a)   Какое максимально возможное число она может составить?

(b)   Какое наименьшее число она может составить?

(6 баллов)

Показать ответ

(a)

Для определения 2 из следующих: -9 или -8 или 7 .

(1)

Умножьте -9 и -8, чтобы получить 72.

(1)

Правильное умножение -9, -8 и 7 или 504 видно.

(1)

(b)

Для определения 2 из следующих: -9 или 7 или 3 .

(1)

Показывает, как умножать.

(1)

Правильное умножение -9, 7 и 3 или -189 видно.

(1)

2. На банковском счете мистера и миссис Браун было 198,78 фунтов стерлингов. В конце месяца они должны были оплатить 4 счета


Они заплатили за телевизионную лицензию на 57,20 фунтов стерлингов, коммунальные услуги на 134,78 фунтов стерлингов, страховку автомобиля на 38,25 фунтов стерлингов и счет по кредитной карте на 94 фунта стерлингов.


Как сколько Брауны перерасходовали?

 

(3 балла)

Показать ответ

Нахождение суммы 4 купюр.

(1)

 

Вычитание стоимости четырех банкнот из остатка на банковском счете.

(1)

CAO

-\ Фундс 125,45

(1)

3. Ниже приведен список городов и их возвышения:

Элева.0002 Helsinki 25M

Новый Орлеан -2M

Buenos Aires 10M

Амстердам -7M

Baku -28M

(A), какие города находятся ниже уровня моря?

 

(b)   В чем разница между высотами Буэнос-Айреса и Баку?

 

(5 баллов)

Показать ответ

(a)

 

Баку

(1)

 

Amsterdam

(1)

 

New Orleans

(1)

 

(b)

 

10 – (-28)  

(1)

38M

(1)

Контрольный список обучения

Вы узнали, как:

• Добавить и выбирать целые числа и негативные
• .