Вычитание отрицательного числа, правило, примеры, как вычесть два отрицательных числа, как из отрицательного числа вычесть положительное
Данная статья посвящена разбору такой темы, как выполнение вычитания отрицательных чисел. Материал представляет собой полезную информацию о правиле вычитания отрицательных чисел и других определениях. Для закрепления сути параграфа мы детально разберем примеры типичных упражнений и задач.
Правило вычитания отрицательных чисел
Для того, чтобы разобраться в данной теме, следует узнать основные определения и понятия.
Определение 1Правило вычитания отрицательных чисел формулируется так: чтобы из числа a вычесть число b со знаком минус, необходимо к уменьшаемому a прибавить число −b, которое является противоположным вычитаемому b.
Если представить данное правило вычитания отрицательного числа b из произвольного числа a в буквенном виде, то оно будет выглядеть так: a−b=a+(−b).
Для того, чтобы использовать данное правило, необходимо доказать его справедливость.
Возьмем числа a и b. Чтобы вычесть из числа a число b, необходимо найти такое число с, которое в сумме с числом b будет равняться числу a. Другими словами, если найдено такое число c, что c+b=a, то разность a−b равна c.
Для того, чтобы доказать правило вычитания, необходимо показать, что сложение суммы
Так, как сумма чисел с противоположными знаками равняется нулю, то a+((−b) +b) =a+0, а сумма a+0= а (если к числу прибавить нуль, то оно не изменится). Равенство a−b=a+(−b)считается доказанным, значит, доказана и справедливость приведенного правила вычитания чисел со знаком минус.
Мы рассмотрели, как работает данное правило для действительных чисел a и b. Но оно также считается справедливым для любых рациональных и целых чисел a и b. Действия с рациональными и целыми числами также обладают свойствами, использованными при доказательстве. Следует добавить, что с помощью разобранного правила можно выполнять действия числа со знаком минус как из положительного числа, так и из отрицательного или нуля.
Рассмотрим разобранное правило на типичных примерах.
Примеры использования правила вычитания
Рассмотрим примеры с вычитанием чисел. Для начала рассмотрим простой пример, который поможет легко разобраться со всеми тонкостями процесса.
Пример 1Необходимо отнять от числа −13 число −7.
Возьмем число, противоположное вычитаемому −7. Это число 7. Тогда по правилу вычитания отрицательных чисел имеем (−13) −(−7) =(−13) +7. Выполняем сложение. Теперь получаем: (−13) +7=−(13−7) =−6.
Вот все решение: (−13) −(−7) =(−13) +7=−(13−7) =−6. (−13)−(−7)=−6. Вычитание дробных отрицательных чисел также можно выполнять. Необходимо перейти к обыкновенным дробям, смешанным числам или десятичным дробям. Выбор числа зависит от того, с каким вариантом вам удобнее работать.
Необходимо выполнить вычитание из числа 3,4 числа -2323.
Применяем описанное выше правило вычитания, получаем 3,4—2323=3,4+2323. Заменяем дробь на десятичное число: 3,4=3410=175=325 (как переводить дроби, можно посмотреть в материале по теме), получаем 3,4+2323=325+2323. Выполняем сложение. На этом вычитание отрицательного числа -2323 из числа 3,4 завершено.
Приведем краткую запись решения: 3,4—2323=27115.
Пример 3Необходимо выполнить вычитание числа −0,(326) от нуля.
По правилу вычитания, которое мы изучили выше, 0−(−0,(326))=0+0,(326)=0,(326).
Последний переход верен, так как здесь работает свойство сложения числа с нулем: 0−(−0,(326))=0,(326).
Из рассмотренных примеров видно, что при вычитании отрицательного числа может получиться как положительное, так и отрицательное число. Вычитание отрицательного числа может в результате дать и число 0, это происходит, когда уменьшаемое равно вычитаемому.
Пример 4Необходимо вычислить разность отрицательных чисел -5—5.
По правилу вычитания мы получаем -5—5=-5+5.
Мы пришли к сумме противоположных чисел, которая всегда равна нулю: -5—5=-5+5=0
Итак,-5—5=0.
В некоторых случаях результат вычитания необходимо записать в виде числового выражения. Это справедливо в тех случаях, когда уменьшаемое или вычитаемое является иррациональным числом. К примеру, вычитание из отрицательного числа −2 отрицательного числа –π проводится так: (−2)−(−π)=(−2)+π=π−2. Значение полученного выражения может быть вычислено максимально точно только в том случае, если это необходимо. Для подробной информации можно изучить другие разделы, связанные с данной темой.
Автор: Ирина Мальцевская
Преподаватель математики и информатики. Кафедра бизнес-информатики Российского университета транспорта
Отрицательные числа (сложение и вычитание)
80,00 ₽
В каждой карточке 3 вида заданий: 1) Сложение и вычитание положительных и отрицательных чисел в одно действие, 2) Примеры в 2 действия без скобок, 3) Примеры в 2 действия со скобками. С ответами. Для печати А4.
Количество товара Отрицательные числа (сложение и вычитание)
Артикул: i-9383 Категория: Для учебы Метка: Разные задания по математике
- Описание
- Детали
- Отзывы (0)
Описание
Программа «Отрицательные числа: сложение и вычитание» формирует примеры для закрепления соответствующей темы. Практика счета таких примеров поможет повторить и систематизировать изученный материал, а также развить внимательность и закрепить навыки устного счета положительных и отрицательных чисел.
Практика счета таких примеров поможет повторить и систематизировать изученный материал, а также развить внимательность и закрепить навыки устного счета положительных и отрицательных чисел.
Программа представляет собой тренажер для счета положительных и отрицательных чисел в пределах 100. Она написана в Excel с помощью макросов. С помощью генератора примеров можно создать и распечатать готовые примеры в пределах 100.
В каждой карточке формируется 3 вида заданий:
- Сложение и вычитание положительных и отрицательных чисел в одно действие — 10 примеров,
- Примеры в 2 действия без скобок — 10 примеров,
- Примеры в 2 действия со скобками — 10 примеров.
Задания генерируются случайным образом, количество генераций не ограничено. Генератор примеров по математике будет очень удобен как для родителей, так и для учителей. Не нужно заранее покупать задачники и пособия по математике с примерами. Можно скачать файл и сгенерировать карточки в любое время независимо от подключения к интернету и распечатать.
Можно скачать файл и сгенерировать карточки в любое время независимо от подключения к интернету и распечатать.
Для ознакомления с программой «Отрицательные числа: сложение и вычитание» можно бесплатно скачать примеры из описания. Для получения новой карточки примеров достаточно скачать, нажать на кнопку генерации и распечатать.
На сайте представлен каталог программ, в котором все программы распределены по группам с указанием различий в программах внутри каждой группы. С помощью каталога Вы можете выбрать те программы, которые подходят именно Вам.
Вам также будет интересно…
Дроби смешанные
100,00 ₽В корзинуРаскрыть скобки в примерах
Оценка 5.00 из 5
120,00 ₽В корзинуПростые проценты
Оценка 5.00 из 5
80,00 ₽В корзинуСложение и вычитание десятичных дробей в столбик
80,00 ₽В корзинуДроби обыкновенные
80,00 ₽В корзинуКорни квадратные
80,00 ₽В корзину
Определение, Использование, Свойства, Операции, Примеры
- Автор Мадхурима дас
- Последнее изменение 28-01-2023
Отрицательные числа: В повседневной жизни мы имеем дело с множеством чисел.
Чтобы упростить счет, люди изобрели натуральные числа. После этого изобрели ноль, дающий нам представление о целых числах, а затем об отрицательных числах, действительных числах и т. д. Отрицательные числа помогают нам показывать температуру, которая меньше нуля, показывать перерасход на банковском счету и т. д. Давайте см. применение и свойства отрицательных чисел в этой статье.
Что такое числа?
Числа окружают нас повсюду. С утра до ночи мы часто сталкиваемся с множеством цифр. Сейчас мы знаем, как читать и записывать числа, но что было, когда числа вообще не были открыты? В те дни счет производился с использованием доступных тогда физических объектов, таких как камни, кости, палки, листья и так далее. Затем они научились отмечать линии или изгибы на камнях, в пещерах, на глиняной посуде, которую использовали, и так далее.
Затем они научились отмечать линии или изгибы на камнях, в пещерах, на глиняной посуде, которую использовали, и так далее.
А потом были введены наши счетные числа. Число — это математическое понятие, которое используется для выражения количества и используется в счетах, вычислениях или любых арифметических операциях и других вертикалях математики.
Например, \(2,3,0,5, – 6, – 100, – 2,3,\sqrt{2,} \) и т. д.
Счетные числа также называются числами и включают в себя положительные целые числа из \( 1\) до бесконечности. Набор натуральных чисел выражается как \(N\) и \(N = \left\{{1,2,3,4,5……} \right\}\)
У всех был преемник и предшественник числа, кроме \(1\) в натуральных числах. Кроме того, изначально не было возможности показать пустоту. Так возникла необходимость демонстрации пустоты, и был введен ноль. Когда к счетным числам добавляется ноль, мы получаем целые числа. Целые числа — это положительные числа от \(0\) до бесконечности и не содержат дробных или десятичных чисел.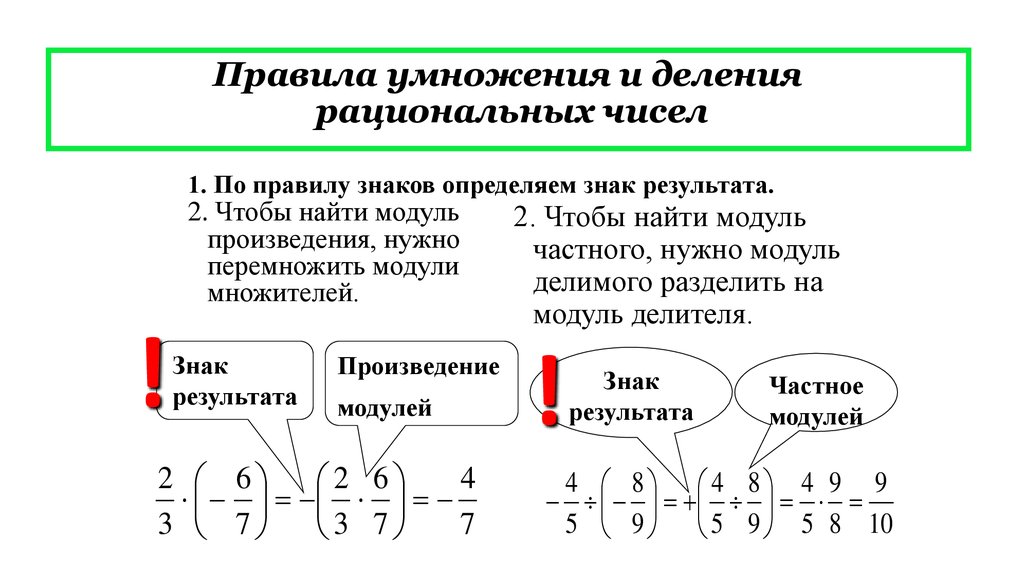 Набор целых чисел может быть выражен как \(W = \left\{{0,1,2,3,4,5,……} \right\}\)
Набор целых чисел может быть выражен как \(W = \left\{{0,1,2,3,4,5,……} \right\}\)
Знакомство с отрицательными числами
Мы знаем, как выполнять математические операции, такие как сложение, вычитание, умножение и деление над целыми числами. Когда мы вычитаем меньшее целое число из большего целого числа, результатом всегда является целое число. Например, \(30 – 12 = 18,\) результатом является целое число. Но когда мы вычитаем большее целое число из меньшего целого числа, в результате получается не целое число.
Поэтому возникла необходимость иметь набор чисел, включающий числа со знаком минус. Это привело к созданию нового набора чисел, которые называются отрицательными числами. Когда отрицательные числа были добавлены к целым числам, мы получили набор целых чисел.
Набор целых чисел может быть выражен как \(Z = \left\{{… – 5, – 4, – 3, – 2, – 1,0,1,2,3,4,5,….} \right\}\)
Отрицательные числа имеют множество применений в реальной жизни. Например, мы используем его для выражения потерь, декрементов, обесценивания и т. д. Они используются для обозначения температуры (меньше нуля), в банковской системе они используются для представления перерасходованной суммы баланса вашего счета. Они также используются, чтобы показать цену акции и ее взлеты и падения.
д. Они используются для обозначения температуры (меньше нуля), в банковской системе они используются для представления перерасходованной суммы баланса вашего счета. Они также используются, чтобы показать цену акции и ее взлеты и падения.
Поскольку использование чисел не могло быть ограничено целыми числами, было введено больше наборов чисел, таких как рациональные числа, иррациональные числа, действительные числа и комплексные числа.
1. Рациональные числа: Любое число, которое может быть выражено как отношение одного числа к другому числу, записывается как рациональное число. Его можно записать в виде \(\frac{p}{q}\) формы. Символ \(Q\) обозначает рациональные числа.
Например, \(\frac{3}{4},\frac{{ – 4}}{5},\frac{{ – 6}}{7},\frac{3}{1},\) и т. д. — рациональные числа.
2. Иррациональные числа: Число, которое не может быть представлено как отношение одного числа к другому числу, называется иррациональным числом и обозначается символом \(P. \)
\)
Например, \(\sqrt 3 ,\sqrt 2 ,\sqrt 5 , – \sqrt 7 ,\) и т. д. являются иррациональными числами.
3. Действительные числа: Все наборы положительных и отрицательных целых, дробных и десятичных чисел, за исключением мнимых чисел, известны как действительные числа. Обозначается символом \(R.\). Например, \(1.2,3.2222…,4,5,7, – 8, – 8.2,9.1,\) и т. д. – действительные числа.
Представление отрицательных чисел
Отрицательные числа представляются со знаком минус \(\left( – \right)\) вместе с числом. Эти числа представлены слева от начала координат (нуля) на числовой прямой, и их значения всегда меньше нуля. Это может быть целое, десятичное число, дробь. Их нет в множестве натуральных чисел и целых чисел.
Например, \( – 5.2, – 3.7, – 4, – 5, – 7,3.4,\frac{{ – 5}}{6}, – 9.1, – \sqrt 7 \) и т. д. являются отрицательными числа.
Отрицательные числа в строке чисел
Прямая линия, на которой числа расположены через равные промежутки по ее длине, называется числовой линией. Его можно бесконечно растягивать в любом направлении, и обычно он представлен горизонтально.
Его можно бесконечно растягивать в любом направлении, и обычно он представлен горизонтально.
Числа могут быть представлены в числовой строке как
В числовой строке положительные числа представлены справа от нуля, а отрицательные числа представлены слева от нуля.
В числовой строке, если числа перемещаются вправо от нуля, значение числа увеличивается, а если числа перемещаются влево в числовой строке от нуля, значение числа уменьшается.
Арифметические операции с отрицательными числами
Существует четыре основных арифметических операции: сложение, вычитание, умножение и деление. Когда мы выполняем эти четыре операции с отрицательными числами, это кажется трудным, но это не так.
Сложение положительного и отрицательного числа
Когда необходимо сложить положительное и отрицательное число, мы должны сначала взять абсолютное значение двух чисел и найти разницу между ними. Ответ будет принимать знак числа, которое имеет большее абсолютное значение.
Например,
1. \(\left({ – 3} \right) + 4\)
Здесь абсолютное значение \( – 3 = 3\) и абсолютное значение \(4 = 4\ ) Таким образом, после получения разности абсолютных значений ответ будет принимать знак числа с большим абсолютным значением.
Следовательно, \( – 3 + 4 = 1\)
2. Аналогично, \( \left({-\frac{2}{7}} \right) + \left({\frac{5}{7 }} \right) = \frac{{ – 2 + 5}}{7} = \frac{3}{7}\)
3. \( – 5 + 1 = – 4\)
Здесь абсолютная значение \( – 5 = 5\) и абсолютное значение \(1 = 1\)
Итак, разность абсолютных значений \( = 5 – 1 = 4\)
Ответ будет принимать знак числа с большим абсолютным значением \( – 5.\)
Аналогично, 4. \(\left({ – 1.5} \right) + \left( 1 \right) = \left({ – 0.5} \right) \)
5. \(\left({\frac{3}{7}} \right) + \left({\frac{{ – 5}}{7}} \right) = \frac{{3 – 5 }}{7} = \frac{{ – 2}}{7}\)
Сложение двух отрицательных чисел
Сложение двух отрицательных чисел выполняется аналогично тому, как мы складываем два положительных числа и единственное меняется знак ответа. При сложении двух отрицательных чисел результатом будет отрицательное число. Итак, при добавлении двух отрицательных чисел добавьте абсолютное значение обоих чисел и добавьте к ответу знак минус.
При сложении двух отрицательных чисел результатом будет отрицательное число. Итак, при добавлении двух отрицательных чисел добавьте абсолютное значение обоих чисел и добавьте к ответу знак минус.
Например,
1. \(\влево({ – 3,5} \вправо) + \влево({ – 2} \вправо) = \влево({ – 5,5} \вправо)\)
2. \(\ влево({ – \frac{2}{3}} \right) + \left({ – \frac{5}{3}} \right) = \frac{{ – 2 – 5}}{3} = \ frac{{ – 7}}{3}\)
3. \(\left({ – 5} \right) + \left({ – 2} \right) = – 5 – 2 = \left({ – 7 } \right)\)
Вычитание двух отрицательных чисел
Когда вычитаются два отрицательных числа, получается сложение положительного и отрицательного числа.
Например,
1. \(\влево({ – 4} \вправо) – \влево({ – 3} \вправо) = – 4 + 3 = – 1\)
2. \(\влево({ – 4.2} \вправо ) + \left({ – 2.1} \right) = \left({ – 6.3} \right)\)
3. \(\left({ – \frac{1}{4}} \right) + \left ({ – \frac{3}{4}} \right) = \frac{{ – 1 – 3}}{4} = \frac{{ – 4}}{4} = -1\)
Вычитание Положительные и отрицательные числа
При вычитании положительного и отрицательного числа проверьте, должно ли быть вычтено отрицательное число из положительного числа или положительное число должно быть вычтено из отрицательного числа.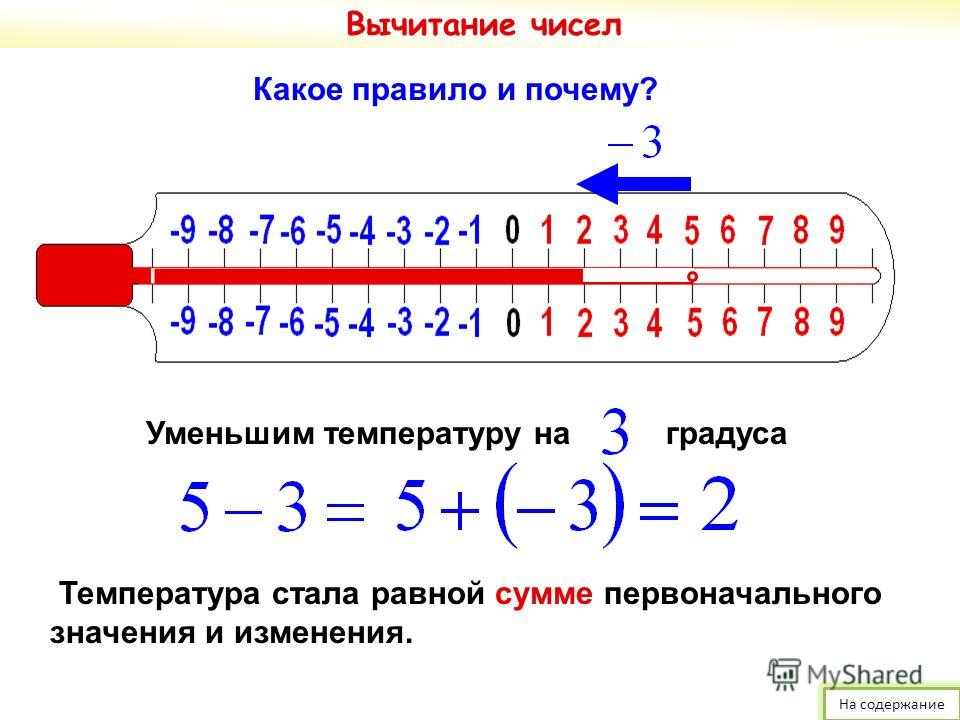
Если положительное число вычитается из отрицательного числа, то сложите оба числа и поставьте знак минус для ответа.
Например,
1. \( – 3 – \влево( 2 \вправо) = – 3 – 2 = -5\)
2. \(\влево({ – 2.2} \вправо) – \влево({ – 2,1} \right) = – 2,2 + 2,1 = – 0,1\)
3. \(\left({ – \frac{1}{4}} \right) – \left({ – \frac{3}{ 4}} \right) = \frac{{ – 1 + 3}}{4} = \frac{2}{4} = \frac{1}{2}\)
Если из Положительное число, затем сложите оба числа и поставьте положительный знак в ответе.
Например,
1. \(3 – \влево({ – 2} \вправо) = 3 + 2 = 5\)
2. \(\влево({2.2} \вправо) – \влево({ – 2.1} \right) = 4.3\)
3. \(\left({\frac{1}{4}} \right) — \left({ — \frac{3}{4}}\right) = \ frac{{1 + 3}}{4} = \frac{4}{4} = 1\)
Умножение двух отрицательных чисел
При умножении двух отрицательных чисел произведение будет положительным числом.
Например,
1. \( – 3 \times – 2 = 6\)
2. \(\left({ – 1,2} \right) \times \left({ – 2} \right) = 2,4\ )
3. \(\left({\frac{{ – 1}}{4}} \right) \times \left({\frac{{ – 3}}{4}} \right) = \frac{{ \left({ – 1} \right) \times \left({ – 3} \right)}}{4} = \frac{3}{4}\)
\(\left({\frac{{ – 1}}{4}} \right) \times \left({\frac{{ – 3}}{4}} \right) = \frac{{ \left({ – 1} \right) \times \left({ – 3} \right)}}{4} = \frac{3}{4}\)
Умножение положительных и отрицательных чисел
Когда отрицательное и положительное число умножается, произведение будет отрицательным числом.
Например,
1. \( – 3 \times 2 = – 6\)
2. \(\left({ – 1,2} \right) \times \left( 2 \right) = – 2,4\)
3. \(\left({\frac{{ – 1}}{4}} \right) \times \left({\frac{3}{4}} \right) = \frac{{\left({ – 1} \right) \times \left( 3 \right)}}{4} = \frac{{ – 3}}{4}\)
Деление двух отрицательных чисел
При делении двух отрицательных целых чисел в частном получается положительное целое число.
1. \(\влево({ – 3} \вправо) \div \влево({ – 2}\вправо) = \frac{3}{2} = 1,5\)
2. \(\влево({ – 1.2} \right) \div \left({ – 2} \right) = 0.6.\)
3. \(\left({\frac{{ – 1}}{4}} \right) \div \ left({\frac{{ – 3}}{4}} \right) = \frac{1}{3}\)
Деление положительных и отрицательных чисел
При делении положительного и отрицательного числа частное будет отрицательным целым числом.
1. \(\left( 3 \right) \div \left({ – 2} \right) = \frac{{ – 3}}{2} = – 1.5\)
2. \(\left( { – 1.2} \right) \div \left( 2 \right) = – 0.6.\)
3. \(\left({\frac {{ – 1}}{4}} \right) \div \left ({\frac{3}{4}} \right) = \frac{{ – 1}}{3}\)
Деление отрицательного числа на ноль не определено.
Решенные примеры – отрицательные числаQ.1. Какое изменение температуры испытает путешественник, достигнув отметки 9 градусов над уровнем моря?\circ }{\text{C}}\)
Q.2. Вычтите \(\left({\frac{{ – 20}}{{30}}} \right) – \left({\frac{{ – 9}}{{30}}} \right).\)
Ответ: Дано } \right)\)
Так как обе дроби отрицательны,
\( \Rightarrow \frac{{ – 20}}{{30}} – \frac{{ – 9}}{{30}} = \frac{ { – 20 + 9}}{{30}}\)
\( = \frac{{ – 11}}{{30}}.\)
В.3. Упростить \( – 6 – \ frac{{ – 1}}{2}.\)
Ответ: Дано, \( – 6 – \left({\frac{{ – 1}}{2}} \right)\)
\( – 6,\left({\frac {{ – 1 }}{2}} \right)\) оба принадлежат отрицательным числам
\( – 6 – \left({\frac {{ – 1}}{2}} \right) = – 6 + \frac{1} {2}\)
\( = \frac{{ – 12 + 1}}{2} = \frac{{ – 11}}{2}\)
Q. 4. Найдите предшественника следующих целых чисел.
4. Найдите предшественника следующих целых чисел.
а) \( – 100\)
б) \( – 16\)
Ответ: Предшественник числа получается вычитанием \(1\) из числа.
а) Предшественником \(-100\) является \(-100-1 = -101\)
б) Предшественником \(-16\) является \(-16-1=-17\)
Q .5. Умножьте \(\left({ – 4} \right)\) и \(\left({ – 1.2} \right).\)
Ответ: Учитывая отрицательные числа \( – 4\) и \( – 1.2.\)
Когда мы умножаем два отрицательных числа, в результате мы получим положительное число.
Таким образом, \( – 4 \times – 1,2 = 4,8\)
Резюме
В этой статье мы узнали определение отрицательных чисел, примеры и их свойства. Мы также обсудили арифметические операции с отрицательными числами, такие как сложение, вычитание, умножение и деление.
Часто задаваемые вопросы (FAQ) – отрицательные номера
Q.1. Объясните отрицательные числа на примерах.
Ответ: Отрицательные числа представляются со знаком минус \(\left( – \right)\) вместе с числом. Эти числа представлены слева от начала координат (нуля) на числовой прямой, и их значения всегда меньше нуля. Это может быть целое число, десятичное число, дробь и т. д. Их нет в множестве натуральных чисел и целых чисел.
Например, \( – 5,2, – 3,7, – 4, – 5, – 7, – 3,4,\frac{{ – 5}}{6}, -9,1, – \sqrt 7 \) и т. д. являются отрицательными числа.
Q.2. Каковы правила для отрицательных чисел?
Ответ:
1. Когда необходимо сложить положительное и отрицательное число, мы должны сначала взять абсолютное значение двух чисел и найти разницу между ними. Ответ будет принимать знак числа, которое имеет большее абсолютное значение.
2. Добавление двух отрицательных чисел добавляет абсолютное значение обоих чисел и добавляет к ответу знак минус.
3. При вычитании двух отрицательных чисел получается сложение положительного и отрицательного числа.
4. Если из отрицательного числа вычитается положительное число, сложите оба числа и поставьте знак минус.
5. При умножении двух отрицательных чисел произведение будет положительным числом.
6. При перемножении отрицательного и положительного числа произведение будет отрицательным числом.
7. При делении двух отрицательных целых чисел частное будет положительным целым числом.
8. При делении положительного и отрицательного числа частное будет отрицательным целым числом.
Q.3. Какое наибольшее отрицательное целое число?
Ответ: Целые числа можно описать как множество натуральных чисел и их аддитивных инверсий, содержащих ноль. Итак, наибольшее отрицательное число равно \( – 1.\)
Q.4. Какое наименьшее отрицательное целое число?
Ответ: Если мы отодвинемся от нуля к минус бесконечности на числовой прямой, значение уменьшится так, что не будет наименьшего отрицательного числа, так как существует бесконечное количество отрицательных чисел.
Q.5. Каково применение отрицательных чисел?
Ответ: мы используем отрицательные числа для выражения потерь, декрементов, обесценивания и т. д. Они используются для обозначения температуры (меньше нуля), в банковской системе они используются для представления перерасхода суммы баланса вашего счета . Они также используются, чтобы показать цену акции и ее взлеты и падения.
Сложение и вычитание отрицательных чисел
Введение
Что такое отрицательные числа?
Как складывать и вычитать отрицательные числа
Лист сложения и вычитания отрицательных чисел
Распространенные заблуждения
Похожие уроки
Практика сложения и вычитания отрицательных чисел вопросы
Сложение и вычитание отрицательных чисел Вопросы GCSE
Контрольный список обучения
Следующие уроки
Все еще застряли?
Индивидуальные занятия по математике, созданные для успеха KS4
Теперь доступны еженедельные онлайн-уроки повторения математики GCSE
Узнать больше
Введение
Что такое отрицательные числа?
Как складывать и вычитать отрицательные числа
Лист сложения и вычитания отрицательных чисел
Распространенные заблуждения
Похожие уроки
Практика сложения и вычитания отрицательных чисел вопросы
Сложение и вычитание отрицательных чисел Вопросы GCSE
Контрольный список обучения
Все еще застряли?
Здесь мы узнаем о сложении и вычитании отрицательных чисел включая то, что такое отрицательные числа и как их складывать и вычитать.
На рабочих листах также есть рабочие листы с отрицательными числами и экзаменационные вопросы, основанные на экзаменационных вопросах Edexcel, AQA и OCR, а также дополнительные указания о том, что делать дальше, если вы все еще застряли.
Что такое отрицательные числа?
Отрицательные числа — это любые числа меньше нуля, перед которыми стоит знак минус (-).
Числа больше нуля называются положительными числами . Если перед числом нет знака, то число положительное.
В числовой строке ниже числа, выделенные оранжевым цветом, являются отрицательными значениями, а синие числа — положительными значениями:
Точно так же, как вы можете складывать и вычитать положительные числа, вы можете делать то же самое с отрицательными числами.
При сложении и вычитании отрицательных чисел используйте числовую строку:
При сложении перемещайтесь вправо от числовой строки.
При вычитании переместитесь влево от числовой строки .
Когда у вас есть два знака рядом друг с другом:
Если знаки одинаковые, замените на положительный знак .
Если знаки разные, замените знаком минус.
Что нужно помнить при сложении и вычитании отрицательных чисел?
Как складывать и вычитать отрицательные числа
Чтобы складывать и вычитать отрицательные числа:
- Если у вас есть два знака рядом друг с другом, замените их одним знаком.
Если знаки одинаковые, заменить на положительный знак (+) .
Если знаки разные, замените знаком минус (-) . - Обведите первое число в числовой строке.
- Используйте числовую строку, чтобы складывать или вычитать числа.
При добавлении переместитесь вправо от числа на шаге 2 (→) .
При вычитании переместитесь влево от числа на шаге 2 ( ←) . - Напишите свой окончательный ответ.

Объясните, как складывать и вычитать отрицательные числа за 4 шага
Рабочий лист сложения и вычитания отрицательных чисел
Получите бесплатный рабочий лист сложения и вычитания отрицательных чисел, содержащий более 20 вопросов и ответов. Включает рассуждения и прикладные вопросы.
СКАЧАТЬ БЕСПЛАТНО
ИксРабочий лист сложения и вычитания отрицательных чисел
Получите бесплатный рабочий лист сложения и вычитания отрицательных чисел, содержащий более 20 вопросов и ответов. Включает рассуждения и прикладные вопросы.
СКАЧАТЬ БЕСПЛАТНО
Примеры сложения и вычитания отрицательных чисел
Пример 1: сложение положительного числа
\[ -4+7 \]
- Если у вас есть два знака рядом друг с другом, замените их одним знаком.
Если знаки одинаковые, замените их положительным знаком (+) .
Если знаки разные, замените знаком минус (-) .
В этом случае у вас нет двух знаков рядом друг с другом.
2 Обведите первое число в числовой строке .
Первое число в вопросе (−4)
3 Используйте числовую строку, чтобы сложить или вычесть числа .
При добавлении переместитесь вправо от числа на шаге 2 (→) .
При вычитании переместитесь влево от числа на шаге 2 ( ←) .
В этом случае мы прибавляем 7, поэтому переместите 7 делений справа от (−4) в числовой строке:
4 Напишите свой окончательный ответ .
\[-4 + 7 = 3\]
Пример 2: добавление отрицательного числа
\[ -2+(-3 )\]
Если у вас есть два знака рядом друг с другом, измените их на единый знак.
Если знаки одинаковые, замените знаком плюс (+) .
Если знаки разные, замените знаком минус (-) .
В этом случае у вас есть плюс и минус рядом друг с другом.
Поскольку знаки разные, замените знаком минус (-):
\[-2 -3\]
Обведите первое число в числовой строке .
Первое число в вопросе: (−2)
Используйте числовую строку для сложения или вычитания чисел .
При добавлении переместитесь вправо от числа на шаге 2 (→) .
При вычитании переместитесь влево от числа на шаге 2 ( ←) .
В этом случае мы вычитаем 3, поэтому переместите 3 пробела слева от -2 в числовой строке:
Напишите свой окончательный ответ .
\[-2 + (-3) = -5\]
Пример 3: вычитание положительного числа
\[ -5-2 \]
Если у вас есть два знака рядом друг с другом, измените их к единому знаку.
Если знаки одинаковые, замените знаком плюс (+) .
Если знаки разные, замените знаком минус (-) .
В этом случае у вас нет двух знаков рядом друг с другом.
Обведите первое число в числовой строке .
Первое число в вопросе (−5)
Используйте числовую строку, чтобы сложить или вычесть числа .
При добавлении переместитесь вправо от числа на шаге 2 (→) .
При вычитании переместитесь влево от числа в шаге 2 (←) .
В этом случае мы вычитаем 2, поэтому переместите 2 пробела слева от (−5) в числовой строке:
Напишите свой окончательный ответ .
\[-5 – 2 = -7\]
Пример 4: вычитание отрицательного числа
\[ -8-(-10) \]
Если у вас есть два знака рядом друг с другом, измените их к единому знаку.
Если знаки одинаковые, заменить знаком плюс (+)
Если знаки разные, заменить знаком минус (-)
В этом случае у вас есть минус и минус рядом друг с другом.
Поскольку знаки одинаковые, замените знаком плюс (+)
\[-8 + 10\]
Обведите первое число в числовой строке .
Первое число в вопросе (−8)
Используйте числовую строку, чтобы сложить или вычесть числа .
При добавлении переместитесь вправо от числа на шаге 2 (→) .
При вычитании переместитесь влево от числа в шаге 2 (←) .
В этом случае мы прибавляем 10, поэтому переместите 10 делений справа от (−8) в числовой строке:
Напишите свой окончательный ответ .
\[-8 – (-10) = 2\]
Пример 5: смешанные операции
\[ 7-8 – (-5) \]
Если у вас есть два знака рядом друг с другом, измените их к одному знаку.
Если знаки одинаковые, замените на положительный знак (+) .
Если знаки разные, заменить знаком минус (-) .
В этом случае у вас есть минус и минус рядом друг с другом.
Поскольку знаки одинаковые, замените знаком плюс (+)
\[7 – 8 + 5\]
Обведите первое число в числовой строке .
Первое число в вопросе: (7)
Используйте числовую строку для сложения или вычитания чисел .
При добавлении переместитесь вправо от числа на шаге 2 (→) .
При вычитании переместитесь влево от числа в шаге 2 (←) .
В этом случае мы вычитаем положительную цифру 8, поэтому переместите 8 делений влево от 7 в числовой строке:
Теперь мы добавляем 5, поэтому переместите 5 делений вправо от (−1) в числовой строке:
Напишите ваш окончательный ответ .
\[7 – 8 – (-5) = 4\]
Пример 6: сформулированный вопрос
У Алины на банковском счету было 12 фунтов стерлингов. Она купила пальто стоимостью 20 фунтов стерлингов. На сколько она перерасходовала?
Начнем с 12 в качестве первого числа уравнения. Поскольку она потратила 20, деньги списываются с ее банковского счета, поэтому вам придется их вычесть.
Поскольку она потратила 20, деньги списываются с ее банковского счета, поэтому вам придется их вычесть.
\[12 – 20 \]
Если у вас есть два знака рядом друг с другом, измените их на один знак.
Если знаки одинаковые, замените на положительный знак (+) .
Если знаки разные, замените знаком минус (-) .
В этом случае у вас нет двух знаков рядом друг с другом.
Обведите первое число в числовой строке .
Первое число в вопросе (12)
Используйте числовую строку, чтобы сложить или вычесть числа .
При добавлении переместитесь вправо от числа на шаге 2 (→) .
При вычитании переместитесь влево от числа на шаге 2 ( ←) .
В этом случае мы вычитаем 20.
Поскольку шкала в числовой строке ниже равна 2, переместите 10 делений влево (20 ÷ 2 = 10) от 12 в числовой строке:
Напишите свой окончательный ответ .
\[12 – 20 = -8\]
У нее превышен лимит на 8 фунтов стерлингов.
Распространенные заблуждения
- Большее отрицательное число не означает большее число
Распространенной ошибкой является предположение, что чем больше отрицательное число, тем больше число.
напр.
−3 меньше, чем 2
Сложение и вычитание отрицательных чисел — часть нашей серии уроков, посвященных пересмотру отрицательных чисел. Возможно, вам будет полезно начать с основного урока по отрицательным числам, чтобы получить краткое изложение того, чего ожидать, или использовать пошаговые руководства ниже для получения дополнительной информации по отдельным темам. Другие уроки в этой серии включают в себя: 9{\circ}\text{C}
Расчет, который нам нужно сделать, это -9+11
Сложение и вычитание отрицательных чисел Вопросы GCSE
В таблице показана температура в Уотфорде в разное время суток.
| Время суток | Температура (℃) |
| 2 часа ночи | -3 |
| 4 утра | 0 |
| 6 утра | 2 |
| 8:00 | 6 |
(a) Запишите самую низкую температуру.
(b) Найдите разницу между показаниями самой высокой и самой низкой температуры.
(3 оценки)
Показать ответ
−3
(1)
Идентификация самых теплых и самых холодных температур, 6 и -3
(1)
6 -3 =
(1)
6 -3 =
(1)
6 -3
(1)
6 -3
(1)
6 -3
(1)
6 -3
(1)
2. У Сары есть следующие 6 карт:
Она собирается выбрать 2 карты и вычесть их.
(a) Какое максимально возможное число она может составить?
(б) Теперь Сара решила складывать числа, а не вычитать их. Какое наименьшее число она может составить?
(4 балла)
Показать ответ
а) для определения 3 или -8 или 3- (-8)
(1)
правильное вычитание двух чисел 9 (9000 8 9000 900) 1)
b) для определения -7 или -8
(1)
правильное добавление двух чисел или -15 видно
(1)
их банковский счет. В конце месяца они должны были оплатить 4 счета. Они оплатили телефонный счет в размере 67,20 фунтов стерлингов, коммунальные услуги в размере 34,78 фунтов стерлингов, страховку автомобиля в размере 78,24 фунтов стерлингов и счет по кредитной карте в размере 144 фунтов стерлингов. Насколько перерасходовали Смиты?
(3 балла)
Показать ответ
Нахождение суммы 4 купюр
(324,22 фунта стерлингов)
(1)
Вычитание стоимости четырех купюр из остатка на банковском счете
(156,78-324,22 фунта стерлингов)
98 (
9) )
£ 167,44
(1)
Контрольный список для обучения
Теперь вы научились:0004
Все еще зависает?
Подготовьте своих учеников KS4 к успешной сдаче выпускных экзаменов по математике с помощью программы Third Space Learning.