Золотое сечение пример: Правило золотого сечения в живописи

Правило золотого сечения в живописи

Вероятно, вы часто встречали упоминание о «правиле золотого сечения» и его важности для художника. Что же это за правило и как его применять, расскажет этот материал.

ЧТО ТАКОЕ ЗОЛОТОЕ СЕЧЕНИЕ

Золотое сечение — это пропорциональное соотношение двух величин.

В численном выражении это бесконечное число, которое округляют до 1,618 и обозначают число золотого сечения греческой буквой Ф (фи). 

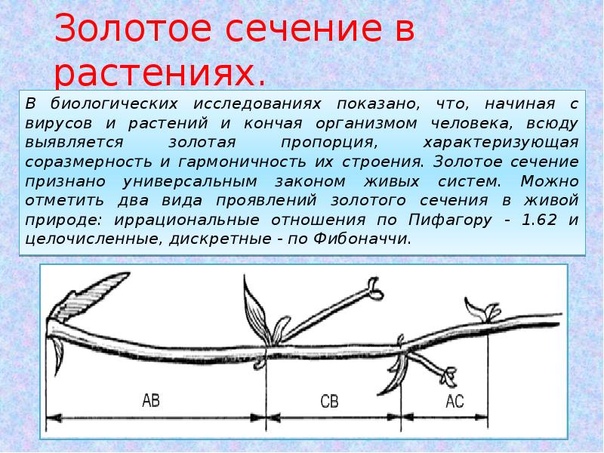
Если взять отрезок АВ и поделить его точкой С, то золотым сечением будет, когда меньший отрезок относится к большему так, как больший отрезок относится к целому.

Т.е. это пропорция, продолжающая саму себя.

Если вы посмотрите на изображение ракушки, то увидите наглядный пример этого правила — каждое последующее деление меньше предыдущего в соотношении золотой пропорции:

Мы можем найти подобные примеры во многих формах жизни: моллюски и земноводные, семечки у подсолнуха или шишки,  паутина, а также строение частей тела человека).  

Именно поэтому пропорция получила название «создающая жизнь».

Также золотое сечение называют пропорцией божественной гармонии. Это и понятно — природа столетиями оттачивала свои формы для того, чтобы получить жизнеспособные организмы в итоге пришла к этой пропорции с выражением 1,618. 

Вот еще несколько примеров правила золотого сечения:

• направление ветра в урагане
• распределение веток и листьев на деревьях
• пропорции туловища ящериц
• строение морских раковин
• основы иконографии
• строение молекулы ДНК
• конфигурация уха
• объем вдыхаемого и выдыхаемого воздуха в процессе дыхания
• соотношение длины фаланг пальцев и кисти руки в целом

ИСПОЛЬЗОВАНИЕ ПРАВИЛА ЗОЛОТОГО СЕЧЕНИЯ

Человек в своей деятельности и искусстве многое берет от природы. Зачем изобретать велосипед, когда природа уже создала гармоничный и жизнеспособный аналог?

Золотое сечение в искусстве встречается во многих произведениях мировой архитектуры, дизайна и живописи.

Египетские пирамиды, собор Парижской Богоматери, Парфенон — все это образцы использования пропорции Золотого сечения в архитектуре.

ПрОПОРЦИЯ золотого сечения в живописи

Как же использовать эту гармоничную пропорцию в живописи и графике, в изображение на плоском листе?

Правило золотого сечения в картине проявляется делением ее на части четырьмя линиями — две из них горизонтальные,  и две вертикальные. Расположены они согласно пропорции 1,618.

ЧЕМ ВАЖНО ПРАВИЛО ЗОЛОТОГО СЕЧЕНИЯ?

То, что находится на этих линиях, наиболее важно для нашего глаза. 

Картину, построенную с использование золотого сечения мы воспринимаем как правильную и красивую.

Найдя эти линии у себя в картине, мы можем расположить значимые элементы так, чтобы работа в целом производила гармоничное впечатление.

Кроме того, на пересечении линий золотого сечения находятся особые зрительные центры. Они  расположены на расстоянии примерно 3/8 и 5/8 от краев изображения. Подмечено, что человек всегда концентрирует на них свое внимание.

Если вы посмотрите на картину И.Левитана, то очень четко видно, что в ней использовано правило золотого сечения.

Луна и ее отражение стоят на линии золотого сечения. Полоса леса в центре также помещается в пропорции золотого сечения.

Еще один пример. В картине Н.Ге «Александр Сергеевич Пушкин в селе Михайловском»  фигура главного героя также расположена на одной из линий золотого сечения.

Таким образом математические закономерности помогают выстраивать картину так, чтобы она выглядела гармонично и красиво, а зритель сразу обращал внимание на главное.

Выбрав формат листа или холста, расчертите его в пропорции золотого сечения. Используйте эти линии, чтобы разместить на них значимые элементы композиции. Это придаст вашей картине гармоничную структуру и упорядоченность.

ПрИНЦИП золотого сечения:

как построить линии в картине

1) Математический вариант

Для такого просчета удобно использовать онлайн калькуляторы.

Достаточно задать один из параметров, нажать кнопку «рассчитать», и система предоставит результат.

Вот пример удобного сервиса:

— https://planetcalc.ru/1061/

Берем размер ширины или высоты картины, вводим в калькулятор и получаем размер, на каком расстоянии от края будут проходить линии золотого сечения.

Очень просто!

2) Геометрический вариант

Точки зрительных центров здесь находятся путем геометрических построений. Посмотрите фрагмент ВИДЕО из встречи в Перископе, где я наглядно показываю, как это делать:

3) Использование шаблона

Если вы делаете много небольших эскизов, то оптимальным для построения линий золотого сечения будет использование специальной линейки.

Если взять за основу 100, то линии золотого сечения будут проходить на отметках 38 и 62. Изготовьте такую линейку самостоятельно, отметив также делениями 10, 14, 24. Эти размеры составляют продолжение золотой пропорции, их можно использовать для размеров объектов или расстояний между ними, чтобы продолжить принцип гармоничных соотношений. 

А как правильно пользоваться линейкой, посмотрите в этом фрагменте из видео:

Выбирайте любой удобный способ и обязательно опробуйте его в создании собственных композиций.

А еще рекомендую рассмотреть работы разных художников и проанализировать, как они используют линии золотого сечения. Полагаю, вы найдете массу достойных примеров.

Если вам интересна эта тема, и вы хотите узнать больше о правиле золотого сечения и его практическом применении, то обратите внимание на книгу

Ф.В. Ковалева «Золотое сечение в живописи»

Это очень полезное издание по композиции!

Если статья была вам полезна, нажмите на кнопочку и поделитесь ей в соцсетях.

Спасибо!

Больше полезных статей:

Золотое сечение в архитектуре: принцип проектирования зданий

Почему нас так привлекают строения древней архитектуры, при виде которых мы испытываем гармонию и умиротворение? Все они были построены на основе золотого сечения, данная зависимость прослеживается и в средневековье, и в современном мире. Математическая пропорция встречается повсеместно: это и ракушки моллюсков, и знаменитые картины художников, и строение человеческого тела, и даже египетские пирамиды. Сегодня об обзоре редакции Homius.ru расскажем простыми словами, как и, самое главное, зачем нужно использовать божественную гармонию чисел, и как она поможет в строительстве собственного дома и оформлении интерьера.

Винтовая лестница построена по принципу золотого сечения

Содержание статьи

Просто о сложном: что это такое – правило золотого сечения

Золотое сечение –это правило общей пропорции, которая создает универсальную композицию. Математики называют её формулой божественной гармонии или асимметричной симметрией.

Это интересно! Общее определение правила ЗС –меньшая величина относится к большей, как большая к целому. Было рассчитано приблизительное число, равное 1,6180339887, это и есть коэффициент золотого сечения. Если смотреть в процентном соотношении, то в одном целом меньшая величина занимает 38%, большая – 62%.

Признано считать, что ЗС пришло к нам еще с древней Греции, но есть и такое мнение, что его греки подсмотрели у египтян. Если проанализировать архитектуру Египта того времени, можно чётко проследить соблюдение математической гармонии. Необычные свойства числовой зависимости стали причиной мистического отношения к золотому сечению:

• практически все живые организмы можно привести к принципу числовой зависимости. Например, тело человека, количество семечек в подсолнухе, структуру ДНК, произведения искусства и вирусную бактерию;
• данная зависимость чисел характерна только для биологических существ и кристаллов, все остальные неживые объекты природы крайне редко обладают золотой пропорцией;
• именно математическая пропорция в строении биологических объектов оказалась оптимальной для выживания.

Идеальный пример ЗС в природе — раковина морского моллюска

Экскурс в историю: кто придумал золотое сечение

Представление о золотой пропорции имели и древние греки, и египтяне, известно было о ней и на Руси. Но впервые ещё в 1509 году в книге «Божественная Пропорция», иллюстрации к которой принадлежат Леонардо да Винчи, монах Лука Пачоли дал научное определение правилу. Он видел в золотом сечении божественное единство:

• маленький отрезок – это сын;
• большой – отец;
• весь отрезок – это святой дух.

Это интересно! Историки присваивают Леонардо да Винчи определение термина ЗС, поскольку он долгое время изучал божественную закономерность и воплощал её принцип в своих творениях.

Вторую жизнь ЗС получило в 1855 году благодаря философу Адольфу Цейзингу. Он доработал теорию до абсолютного идеала, и она стала универсальной для всех проявлений. Все это он описал в своей книге «Математическое Эстетство», на которое в свое время обрушилось много негатива и критики.

Золотое сечение в божественной пропорции

Принцип расчета и построения золотого сечения

Примеры пропорции золотого сечения можно видеть при строительстве многих архитектурных сооружений, только нужно знать, как правильно его увидеть. Для этого достаточно посмотреть на строение всего 5 минут.

Как определить число золотого сечения

С пропорцией ЗС связывают астронома из Италии Фибоначчи, он вывел ряд чисел, в котором значение каждого последующего равно сумме двух предыдущих. Сегодня эта закономерность известна как ряд Фибоначчи:

• 0, 1,1 (0+1), 2 (1+1), 3 (1+2), 5 (2+3), 8 (3+5), 13 (5+8), 21 (8+13), 34 (13+21), 55 (21+34), 89 (34+55) и так до бесконечности;
• если выполнить деление последующего числа на предыдущее – получится коэффициент ЗС.

Данную формулу применяют для расчета пропорций золотого сечения в любой отрасли, на практике чаще всего используют округленные значения 0,62 и 0,38.

Ряд Фибоначчи в церкви Покрова на Нерли

Как рассчитать золотое сечение на простейшем примере

Проще всего объяснить гармонию ЗС можно на примере обычного куриного яйца, точнее на удалении всех точек скорлупы от центра тяжести. Именно форма оболочки, а не её прочность, обеспечила выживаемость птиц столь долгое время и в любых условиях.

Если взять обычный отрезок, который состоит из нескольких маленьких, их длины относятся к большей величине как 0,62. Это показывает, как можно разбить целую линию для получения идеальной пропорции.

Простой пример золотого сечения в курином яйце

Как построить золотое сечение на примере прямоугольника и спирали

Если построить золотой прямоугольник, используя ряд Фибоначчи, он будет выглядеть как единое целое. Рассмотрим зависимость на примере:

• нужно нарисовать квадрат со стороной 1 и рядом ещё один аналогичный;
• над ними разместить квадрат со стороной 2;
• слева гармонично помещается квадрат с гранью 3;
• ниже – квадрат со стороной 5;
• справа пространство займет квадрат с гранью 8;
• площадь прямоугольника 8×13, в котором 13 — это следующее число ряда;
• если разделить на калькуляторе следующее число на предыдущее, получится значение золотого сечения 1,62, причём, чем больше числа, тем меньшая погрешность в их отношении;
• если по этому принципу построить спираль, каждую четверть витка она будет расширяться именно на значение ЗС.

Принцип золотого сечения в прямоугольникеПостроение золотой спирали из прямоугольника

На видео можно более подробно узнать про магию чисел Фибоначчи:

Божественная гармония золотого сечения в архитектуре: фото древних построек и примеры современного строительства

Многие древние здания, которые сохранились до наших времен, подтверждают мнение, что они были построены по правилам идеальной пропорции. Это резиденции королей, церкви, общественные сооружения. Рассмотрим на примерах принцип золотого сечения в разных странах.

Тайны древнеегипетской архитектуры

В архитектуре Древнего Египта по правилам золотой пропорции была построена пирамида Хеопса. Глядя на творение строителей, можно увидеть треугольник с прямым углом, один катет которого является высотой, второй – половиной длины основания. Если взять отношение гипотенузы к меньшей стороне, получим идеальное значение 1,61950 или 1,62.

Это интересно! Форма пирамиды имеет ещё одно неоспоримое свойство. В нём сталь становится прочнее, вода дольше сохраняет свежий вкус, и быстрее растут живые растения. Много лет ученые пытаются разгадать этот феномен, но пока его научное решение не найдено.

Было замечено, что пирамида улучшает психоэмоциональное состояние человека, в её области уменьшаются вредоносные излучения, пропадают геопатогенные зоны.

Идеальная пропорция золотого сечения в пирамиде

Идеальные пропорции в древней Греции

Идеальная пропорциональность делает архитектурные объекты запоминающимися. Яркий представитель ЗС из древней Греции – Парфенон, который возведен в 5 веке до нашей эры. Если взять отношение его высоты к ширине, получится практически идеальное число 0,618.

Ученые определили, что для абсолютного золотого числа нужно отнять от высоты 14 см и прибавить их к ширине. Учитывая строение сооружения, очень похоже, что это было сделано древними архитекторами Иктином и Калликратом намеренно, поскольку фасад немного сужается в верхней части и отклоняется от золотого прямоугольника. Но общие пропорции ЗС соблюдены.

Принцип идеальной пропорции в древнегреческом Парфеноне:

Памятники архитектуры средневековья

Прекрасным памятником истории архитектуры средневековья, сохранившимся до нашего времени, является собор Парижской Богоматери или Нотр-Дам де Пари.

В здании очень заметно желание архитектора соблюсти гармонию и целостностьАнализируя строение, принцип ЗС можно видеть на нескольких участках

Архитектура России

Ряд Фибоначчи – это своеобразная матрица, с помощью которой анализируют любое архитектурное сооружение. Чтобы было проще ориентироваться, можно построить на принципе золотого сечения циркуль Фибоначчи.

Разметчик Фибоначчи построен по правилу золотого сеченияИспользовать циркуль можно практически на любом архитектурном сооруженииЧтобы исследовать большие объекты, нужно отойти на некоторое расстояние и приложить циркуль

Золотое сечение в архитектуре Москвы

Выдающееся здание МГУ на Воробьевых горах было построено в послевоенное время. В те годы это было самое высокое строение, состоящее из пяти композиционных групп, которые венчает центральная башня. Здесь чётко прослеживается треугольник с прямым углом, гипотенуза которого захватывает пристройки и проходит через угол здания.

В МГУ золотому сечению подчиняются высоты

Золотые пропорции прослеживаются и в работах русского зодчего Матвея Казакова.

Кремлевское здание сенатаПречистенский дворецГолицынская больницаДом союзов — благородное собрание

Использовал это прием и архитектор Василий Баженов, его здания причислены к историческим памятникам

Дом Пашкова

Архитектура в Санкт-Петербурге

Живым примером золотого сечения является Исаакиевский собор.

ЗС в Исаакиевском соборе

В первую очередь можно проанализировать его ширину, равную 400 единицам:

• при делении числа 400 на значение золотого сечения получим приблизительно 248;
• при дальнейшем делении 248/1,618=153;
• основная часть собора вписывается в золотой прямоугольник, длинная сторона которого равна 400, ширина – 248.

По высоте здания ЗС можно видеть у купола, благодаря этому внешнее восприятие памятника архитектуры становится гармоничным.

На фото чётко прослеживаются золотой треугольник и прямоугольник в Исаакиевском соборе

Приведем ещё несколько примеров золотого сечения в архитектуре Санкт-Петербурга.

Кунсткамера

Кунсткамера была построена ещё в 1718 году, руководил строительством немецкий архитектор Георг Маттарнови. Она представляет собой 2 корпуса по 3 этажа, между ними возведена куполообразная многоярусная конструкция в виде башни.Золотое сечение в соотношении сторон можно наблюдать в длине корпусов и в высотах разных уровней.

В башне по всей высоте четко прослеживается равнобедренный треугольник, а это значит, что Кунсткамера построена по общему принципу ЗС

Торговый дом Эсдерс и Схейфальс

ЗС в здании, возведенном в 1907 году, наблюдается в следующих размерах:

• 671, 414, 256, 98, 60, 37 и 23.

Композиция смотрится гармонично благодаря золотому соблюдению высотных величин.

Основной элемент здания — шпиль

Дом Советов

Дом Советов был возведен по проекту Троцкого в 1941 году, основной акцент выполняют портик по центру с 14 колоннами и скульптурный ансамбль. По обе стороны расположены два корпуса высотой в 5 этажей. Длина здания – 1472 единицы, если разделить его на значение Ф = 1,618, получим размерный ряд:

• 1472, 909, 562, 347, 214, 132, 81, 50. К ним относятся высота входа, всего сооружения, различных элементов.

Анализ длин и высот Дома Советов

Золотой прямоугольный треугольник идеально вписывается в центр здания, его вершина совпадает с вершиной Дома Советов, а гипотенуза заканчивается в конце бокового крыла. Если построить равнобедренный золотой треугольник, его грани будут проходить через точки в верхней части основного входа.

Очевидная пропорциональность Дома Советов

Примеры золотого сечения в современной архитектуре

В современной архитектуре формула расчёта золотого сечения позволяет проектировать уникальные формы, которые несут прочность, спокойствие и красоту.

Правило золотого сечения при строительстве частного дома

Многие архитекторы, которые разрабатывают проекты частных домов, используют правило золотого сечения. У клиентов создается ощущение, что все детали проработаны для максимально комфортного проживания. При грамотном выборе площадей жильцы на психологическом уровне ощущают умиротворение и успокоение.

Что нужно знать при проектировании фасада

В современном строительстве при проектировании домов кроме ряда Фибоначчи используют ещё один метод, основоположником которого был архитектор из Франции Ле Корбюзье. Он принимал за основу рост будущих владельцев усадьбы и, исходя их этого, рассчитывал параметры строения и комнат. Благодаря такому подходу дом получался не только гармоничный, но и максимально комфортный с индивидуальными чертами хозяев.

Идеальные пропорции частного дома

Золотое сечение в оформлении интерьера

Даже если дом возведен по типовому проекту, можно внутри его создать интерьер, максимально приближенный к идеальной пропорции 1:1,62. Например, благодаря дополнительным перегородкам или расположению мебельных групп, а также можно изменить дверные или оконные проемы, чтобы соотношение ширины к высоте было в золотом сечении.

Аналогичная ситуация и с цветовым оформлением интерьера, здесь действует упрощенное правило:

• 60% — основная палитра;
• 30% — дополнительный оттенок;
• 10% — близкий тон, который усиливает восприятие основного и дополнительного.

Правило 1/1,62 в интерьере должно сопровождаться во всем: в соотношении мебели к общей площади, в ее высоте по отношению к параметрам комнаты.

Заключение

Принцип золотого сечения не является новым в архитектуре, поскольку в прежние времена здания строились не по типовым проектам, а с учетом индивидуальных особенностей будущих владельцев. Такие строения выглядят даже спустя многие года гармоничными и привлекательными. Интерьер, оформленный по правилам идеальной пропорции, позволяет грамотно использовать все площади.

Теперь вы сможете самостоятельно и правильно применить божественную гармонию математических цифр, планируя строительство дома или оформляя свой интерьер. Более того, интересную комбинацию цифр можно использовать и в экономике, и в расчете инвестиций и во всех деталях, с которыми соприкасается человек ежедневно.

Если у вас ещё остались вопросы, предлагаем посмотреть видео, в котором простыми словами разъяснен принцип действия золотого сечения:

 

Предыдущая

Новинки рынкаОт теории к практике: самостоятельная регулировка окон к зиме

Следующая

Новинки рынкаБалкон и лоджия: в чём разница, о каких нюансах стоит знать, если вы решились на переделку?

Понравилась статья? Сохраните, чтобы не потерять!

ТОЖЕ ИНТЕРЕСНО:

ВОЗМОЖНО ВАМ ТАКЖЕ БУДЕТ ИНТЕРЕСНО:

ОСНОВЫ КОМПОЗИЦИИ: Золотое сечение — PhotoDzen.com

15 Апреля 2015

Композиция — это распределение предметов и фигур в пространстве, установление соотношения объёмов, света и тени, цвета и т. п. Существуют разные способы и правила для создания гармоничной композиции. Когда мы смотрим вокруг невооруженным глазом, наш мозг быстро выхватывает интересные сюжеты, объекты. Камера же фиксирует все подряд. Поэтому это ваша задача выбрать основной объект, сделать центром внимания в кадре, а окружающие его другие объекты превратить в фон или сделать частью истории, которую Вы хотите «рассказать» своим снимком.

Фотографии с правильно выбранной композицией заставляют задержать на них взгляд и рассмотреть детали. Они рассказывают историю, создают настроение и заставляют задуматься.

Золотое сечение в фотографии — основной и мощный инструмент для получения динамичных, интересных снимков. Правило золотого сечения встречается и в природе, причем повсеместно. О нем знали еще в древнем Египте. Пропорции пирамиды Хеопса, храмов, барельефов, предметов быта и украшений из гробницы Тутанхамона свидетельствуют, что египетские мастера пользовались соотношениями золотого сечения при их создании.

В фасаде древнегреческого храма Парфенона также присутствуют золотые пропорции. Этот феномен изучил и стал применять на практике известный ученый, художник и скульптор Леонардо Да Винчи.

Для желающих узнать больше — видео:

Мы затронем только практическую часть применения золотого сечения в фотографии. Кадр условно делиться на три части по горизонтали и вертикали:

При пересечении горизонтальной и вертикальной линии образуется особая точка –

«точка силы» или «узел внимания». Их четыре – именно в этих точках лучше располагать главные объекты кадра, именно на них останавливается взгляд в независимости от формата кадра или картины.

Практические советы:

• Если расположитьлинию горизонта по одной из горизонтальных линий, то кадр будет смотреться гармоничней. Но на какой из линий, на верхней или нижней?
• Если вы хотите сконцентрировать внимание зрителя на земле или воде – то лучше на верхней.
• Если же вы делаете акцент на интересном, выразительном небе – то на нижней.
• Если вы снимаете портрет, то лучше размещать глаза на верхней горизонтальной линии.
• Если вы снимаете человека в полный рост, то лучше размещать его на правой или левой вертикальной линии.
• Очень важно следить за тем, в какую сторону направляется человек, или куда направлен его взгляд. Например, если человек смотрит влево, то его соответственно необходимо разместить на правой горизонтальной линии, что бы перед ним оставалось пространство.

В современных фотоаппаратах уже есть функция-подсказка, которая отображает линии правила третей на мониторе или в видоискателе.

Размещайте важные части композиции вдоль линий, а самое главное — на их пересечении.

Золотое сечение может прослеживаться не только в прямоугольной сетке, но и в диагоналях или спирали. Принцип расположения предметов – тот же, по основным линиям и в точках их пересечений.

 Фото: Steve McCurry

 Фото: Joe McNally

Фото: Richard Barnabe

ДИАГОНАЛЬНОЕ ЗОЛОТОЕ СЕЧЕНИЕ

Применяя правило золотого сечения проводим диагонали и получаем прямоугольник состоящий из трех секторов. Этот прямоугольник можно поворачивать как угодно Если скомпонуете свой кадр так, чтобы три разных объекта примерно располагались в этих секторах, а главные объекты в более крупных секциях — то композиция будет выглядеть очень гармонично.

Это правило используется, если у вас в кадре есть несколько областей, различающихся по смыслу.

СПИРАЛЬНОЕ ЗОЛОТОЕ СЕЧЕНИЕ

Спирали очень распространены в природе. Форма спирально завитой раковины привлекла внимание Архимеда. Он изучал ее и вывел уравнение спирали. Спираль, вычерченная по этому уравнению, называется его именем. Увеличение ее шага всегда равномерно. В настоящее время спираль Архимеда широко применяется в технике. Гёте называл спираль — «кривой жизни».

Используя эту спираль при построении композиции в кадре (ее можно перевернуть вверх ногами или в другую сторону), мы получим кадр с четко выраженным предметом в центре спирали.

Фото: Джона Лемьё (John Lemieux)

 Фото: Анри Картье-Брессон

Больше фотографируйте и экспериментируйте. Удачи!

Другие статьи о композиции в фотографии:

Золотое сечение в фотографии

Сила линий в фотографии

Формат кадра в фотографии

Контраст в фотографии (Часть 1)

Контраст в фотографии (Часть 2)

Точка съемки и выбор плана

Ракурс

Геометрия в фотографии

Равновесие

 

Золотое сечение в дизайне

Говорят, что “божественная пропорция” заложена в природе, и во многих вещах вокруг нас. Вы можете найти ее в цветах, ульях, морских раковинах, и даже нашем теле.

Эта божественная пропорция, также известная как золотое сечение, божественное сечение, или золотая пропорция может быть применена к различным видам искусства и обучения. Ученые утверждают, что чем ближе объект к золотому сечению, тем лучше человеческий мозг воспринимает его.

С тех пор как это соотношение было открыто, многие художники и архитекторы применяли его в своих работах. Вы можете найти золотое сечение в нескольких шедеврах эпохи Возрождения, архитектуре, живописи, и многом другом. В результате – красивый и эстетически приятный шедевр.

Немногие знают, в чем заключается тайна золотого сечения, что так радует наши глаза. Многие полагают, что то, что она появляется везде и является “универсальной” пропорцией, заставляет нас принять ее как что-то логическое, гармоничное и органичное. Другими словами, оно просто “чувствует” то, что нам нужно.

Итак, что такое золотое сечение?

Золотое сечение, также известное как “фи” по-гречески, это математическая константа. Оно может быть выражено уравнением a/b=a+b/a=1,618033987, где a больше, чем b. Это также можно объяснить последовательностью Фибоначчи, другой божественной пропорцией. Последовательность Фибоначчи начинается с 1 (некоторые говорят с 0) и добавляет к нему предыдущее число, чтобы получить последующее (т.е. 1, 1, 2, 3, 5, 8, 13, 21 …)

Если вы попытаетесь найти частное от деления двух последующих чисел Фибоначчи (т.е. 8/5 или 5/3), результат очень близок к золотому сечению 1,6 или φ (фи).

Золотая спираль создается с помощью золотого прямоугольника. Если у вас есть прямоугольник из квадратов 1, 1, 2, 3, 5 и 8 соответственно, как показано на рисунке выше, вы можете приступить к строительству золотого прямоугольника. Используя сторону квадрата, как радиус, вы создаете дугу, которая касается точек квадрата по диагонали. Повторите эту процедуру с каждым квадратом в золотом треугольнике, и в конечном итоге вы получите золотую спираль.

Где мы можем увидеть его в природе

Золотое сечение и последовательность Фибоначчи можно найти в лепестках цветов. У большинства цветков количество лепестков сводится к двум, трем, пяти или больше, что походит на золотое сечение. Например, у лилий 3 лепестка, у лютиков 5, у цветков цикория 21, а у ромашек 34. Вероятно, семена цветков также следуют золотому сечению. Например, семена подсолнечника прорастают из центра и растут к внешней стороне, заполняя головку семени. Обычно они спиралевидные и имеют сходство с золотой спиралью. Более того, количество семян, как правило, сводится к числам Фибоначчи.

Руки и пальцы также являются примером золотого сечения. Посмотрите ближе! Основание ладони и кончик пальца разделен частями (костьми). Соотношение одной части в сравнении к другой всегда 1,618! Даже предплечья с руками находятся в таком же соотношении. И пальцы, и лицо, и можно продолжать список…

Применение в искусстве и архитектуре

Парфенон в Греции, как утверждается, был построен с использованием золотых пропорций. Считается, что размерные соотношения высоты, ширины, колонн, расстояния между столбами, и даже размер портика близки к золотому сечению.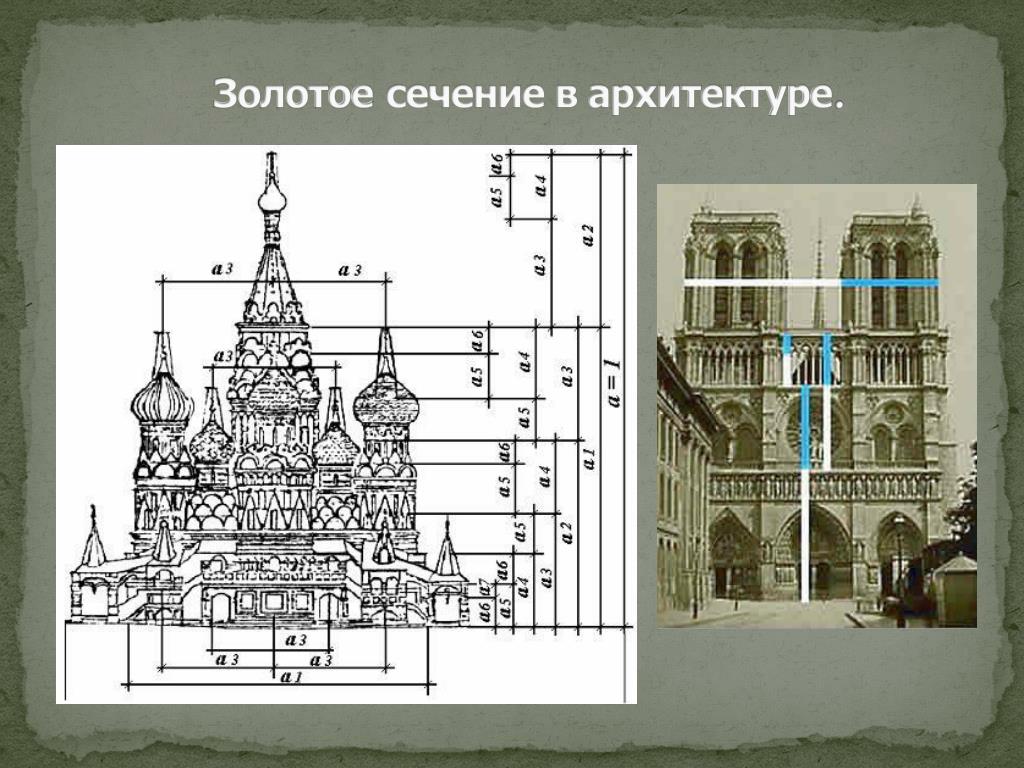 Это возможно потому, что здание выглядит пропорционально идеально, и оно было таким с древних времен.

Леонардо Да Винчи был также поклонником золотого сечения (и многих других любопытных предметов, собственно говоря!). Дивная красота Мона Лизы может быть связана с тем, что ее лицо и тело представляют собой золотое сечение, как и реальные человеческие лица в жизни. Кроме того, цифры в картине “Тайная вечеря” Леонардо Да Винчи расположены в порядке, который используется в золотом сечении. Если начертить золотые прямоугольники на холсте, Иисус окажется как раз в центральной доле.

Применение в дизайне логотипов

Неудивительно, что вы также можете найти использование золотого сечения во многих современных проектах, в частности, дизайне. Сейчас давайте сосредоточимся на том, как это может быть использовано в дизайне логотипа. Во-первых, рассмотрим некоторые из самых известных в мире брендов, которые использовали золотое сечение для совершенствования своих логотипов.

Видимо, Apple использовал круги из чисел Фибоначчи, соединив и обрезав формы для получения логотипа Apple. Неизвестно, было ли это сделано намеренно или нет. Тем не менее, в результате получился идеальный и визуально эстетичный дизайн логотипа.

Логотип Toyota использует соотношение a и b, формируя сетку, в которой образуются три кольца. Обратите внимание, как этот логотип использует прямоугольники вместо кругов для создания золотого сечения.

Логотип Pepsi создан двумя пересекающимися кругами, один больше другого. Как показано на рисунке выше, больший круг пропорционален в соотношении к меньшему – вы уже догадались! Их последний нерельефный логотип – простой, эффектный и красивый!

Кроме Toyota и Apple, логотипы некоторых других компаний, таких как, BP, iCloud, Twitter, и Grupo Boticario, как полагают, также использовали золотое сечение. И мы все знаем, насколько известны эти логотипы – все потому, что изображение сразу всплывает в памяти!

Как вы можете применить его в своих проектах?

Создайте эскиз золотого прямоугольника, как показано выше желтым цветом. Этого можно достичь путем построения квадратов с высотой и шириной из чисел, принадлежащих золотому сечению. Начните с одного блока и поместите другой рядом с ним. А другой квадрат, чья площадь равна тем двум, поместите над ними. Вы автоматически получите сторону из 3 блоков. После построения этой конструкции из трех блоков, в конечном итоге у вас будет сторона из 5 четырехугольников, из которой можно сделать другую (площадью в 5 блоков) коробку. Это может продолжаться сколько угодно, пока вы не найдете тот размер, который вам нужен!

Прямоугольник может перемещаться в любом направлении. Выделите мелкие прямоугольники и используйте каждый из них, чтобы собрать макет, который будет служить в качестве сетки дизайна логотипа.

Если логотип более округлый, то вам потребуется круговая версия золотого прямоугольника. Вы можете добиться этого начертанием кругов, пропорциональных числам Фибоначчи. Создайте золотой прямоугольник, используя только круги (это означает, что самый большой круг будет иметь диаметр 8, а у круга поменьше будет диаметр 5, и так далее).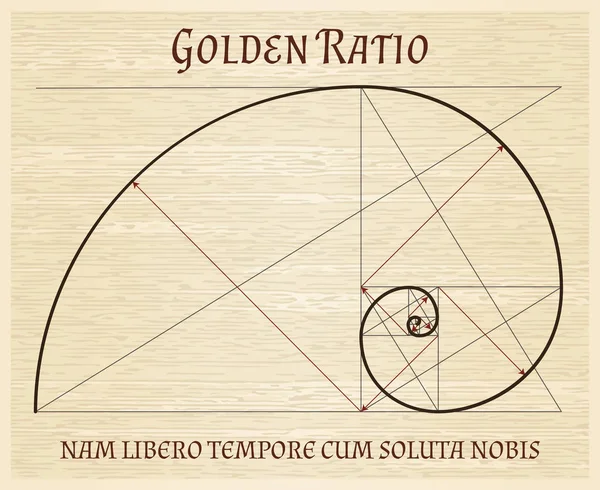 Теперь разделите эти круги и разместите их так, чтобы вы могли сформировать основную схему для вашего логотипа. Вот пример логотипа Twitter:

Примечание: Вам не обязательно чертить все круги или прямоугольники золотого сечения. Вы также можете использовать один размер неоднократно.

Как применять его в дизайне текста

Это проще, чем проектирование логотипа. Простое правило для применения золотого сечения в тексте заключается в том, что последующий больший или меньший текст должен соответствовать Фи. Давайте разберем этот пример:

Если размер моего шрифта – 11, то подзаголовок должен быть написан в более крупном шрифте. Умножаю шрифт текста на число золотого сечения, чтобы получить большее число (11*1,6=17). Значит подзаголовок должен быть написан в 17 размере шрифта. А теперь заголовок или название. Умножу подзаголовок на пропорцию и получу 27 (1*1,6=27). Вот так! Ваш текст теперь пропорционален золотому сечению.

Как применить его в веб-дизайне

А здесь немного сложнее. Вы можете оставаться верными золотому сечению даже в веб-дизайне. Если вы опытный веб-дизайнер, вы уже догадались, где и как ее можно применить. Да, мы можем эффективно использовать золотое сечение и применить его к сеткам наших веб-страниц и макетам пользовательского интерфейса.

Возьмите общее число сетки пикселей за ширину или высоту и используйте его для построения золотого прямоугольника. Разделите наибольшую ширину или длину для получения меньших чисел. Это может быть шириной или высотой вашего основного контента. То, что осталось, может быть боковой панелью (или нижней панелью, если вы применили его к высоте). Теперь продолжайте использовать золотой прямоугольник для дальнейшего применения его к окнам, кнопкам, панелям, изображениям и тексту. Вы также можете построить полную сетку, основанную на маленьких версиях золотого прямоугольника расположенных как горизонтально, так и вертикально для создания более маленьких объектов интерфейса, которые пропорциональны золотому прямоугольнику. Для получения пропорций вы можете использовать этот калькулятор.

Спираль

Вы также можете использовать золотую спираль, чтобы определить, где разместить контент на вашем сайте. Если ваша домашняя страница загружается с графическим контентом, как, например, на веб-сайте онлайн магазина или блога фотографий, вы можете воспользоваться золотым методом спирали, который используют многие художники в своих работах. Задумка в том, чтобы поместить наиболее ценный контент в центре спирали.

Контент со сгруппированным материалом тоже может быть размещен при помощи золотого прямоугольника. Это означает, что чем ближе спираль движется к центральным квадратам (к одному квадратному блоку), тем “плотнее” там содержимое.

Вы можете использовать эту технику, чтобы обозначить расположение вашего заголовка, изображений, меню, панели инструментов, окна поиска и других элементов. Twitter славится не только использованием золотого прямоугольника в дизайн логотипа, но и задействовал его в веб-дизайне. Как? Благодаря использованию золотого прямоугольника, или, другими словами концепцией золотой спирали, в странице профиля пользователей.

Но нелегко будет проделать такое на платформах CMS, где автор материала определяет расположение вместо веб-дизайнера. Золотое сечение подходит WordPress и другим дизайнам блога. Это, вероятно, потому, что боковая панель почти всегда присутствует в дизайне блога, который хорошо вписывается в золотой прямоугольник.

Правило третей

Для тех, кто не очень понимает язык математики, есть более простой способ. Он известен как правило третей. Оно не включает в себя точные математические вычисления, но помогает достигнуть правильных пропорций.

Все, что требуется – это разделить первоначальный эскиз на девять равных частей: 

Точки, где встречаются линии в сетке, будут основными точками вашего дизайна, от которых вы будете в дальнейшем отталкиваться. Вы можете поместить ключевую тему или основные элементы на одну или все точки пересечения.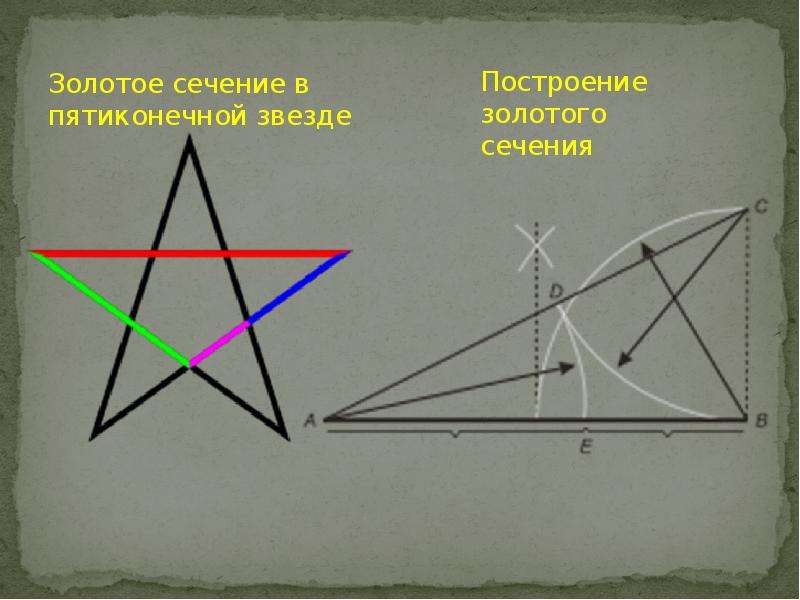 Фотографы также используют эту концепцию.

Если Вы разделите каждую колонку в сетке так, чтобы получились две равные половины, то Вы получите сетку для работы с дизайном сайта. Например, Вы можете разместить эмблему или логотип в верхнем правом квадрате в левой части. Менее важная информация, которая будет располагаться вертикально сверху вниз, может брать свое начало верхнем правом квадрате.

Чем ближе прямоугольники к соотношению 1:1,6, тем приятнее воспринимается картина человеческим мозгом (так как это ближе к золотому сечению). Если вы не любите математику и не хотите считать, то достаточно использовать отношение 3:5 при расчете золотого отношения. Результат будет не таким точным, но он будет близок к пропорциям, которые применяются в работе с дизайном.

Пример того, как можно использовать сечение в веб-дизайне, описан ниже. 

Золотое сечение на примере

Ширина вашего макета может быть фиксированная или гибкая, но прежде чем применить золотое отношение, вам нужно определить число, чтобы начать с ним работать. Для веб-дизайна это число будет равно числу пикселей в ширине лэйаута.

Если вы, например, работаете на лэйауте в 1200 пикселей, то нужно разделить это число на Phi. Для упрощения задачи, число Phi можно сократить до 1.62. При делении 1200 на 1.62, Вы получаете ширину основной колонны, что в нашем случае составит 740 пикселей.

Чтобы определить ширину второй колонки, просто вычтите ширину главной колонки от общей ширины. В этом примере получается 460 пикселей.

Теперь у вас есть две колонки в 740 пикселей и 460. При помощи этого простого вычисления, вы всегда сможете определить идеальные пропорции для колонок вашего сайта.

Для гибкого лэйаута нужно брать расчеты в процентах. Делим 100% на 1.62 и получаем основную колонку, которая займет 62%, а вторая – 38% соответственно. Далее вы сможете работать исходя из этого соотношения.

Золотое отношение может эффективно использоваться, при создании маленьких прямоугольников в пределах общего дизайна. Это пространство может быть использовано для кнопок навигации, заголовков изображений, пространства для объявлений или для текста, который располагается вокруг изображения. Как бы их не использовали, эти мини золотые прямоугольники будут пропорциональны и законченный вид дизайна, будет приятным завершением работы.

Золотое сечение – не панацея

Использование золотого сечения в дизайне не гарантирует успех вашего лендинга.

В то же время изображения, блоки текста и врезок могут быть хорошо представлены в маленьких золотых прямоугольниках, которые формируют красивый, сбалансированный вид, но число прямоугольников на каждой странице должно быть ограниченным. Ничто в веб-дизайне не должно быть в слишком большом количестве.

Также важно помнить о том, что есть много других факторов, которые нужно учитывать при создании дизайна, и которые будут соответствовать общей цели проекта.

Инструменты для дизайнеров

Калькулятор Phi

Когда вы вводите число в этот веб-инструмент, он рассчитывает результат, необходимый для золотого сечения. Этот сервис бесплатный и очень простой в использовании.

Типографический калькулятор Pearsonified

Это онлайн инструмент с кнопкой ‘Set My Type’. Вы просто нажимаете на нее после того, как введете ширину контента и/или размер шрифта, и сервис сам подберет лучшее типографическое решение. У Вас также есть возможность ввести значение CPL. Он оптимизирует размер знаков по линиям.

Сервис золотого отношения UX Triggers

Вы можете проверить любой сайт с помощью этого бесплатного сервиса и быстро определить использована ли последовательность Фибоначчи в дизайне.

Заключительные мысли

Веб-страницы выглядят более гармонично, когда они сделаны с использованием принципов золотого сечения. Это единственное соотношение, которое использовалось еще две тысячи лет назад, для тех же целей, что и сегодня. Посетителя интуитивно будут чувствовать комфорт гармоничного интерфейса, потому что им уже знакомы классические пропорции архитектурных строений и других произведений искусства.

Использование золотых прямоугольников дает чувство упорядоченности вашему лендингу. Но вы должны быть аккуратны, и избегать злоупотребления ими. Слишком большое их количество произведет обратный эффект и сделает дизайн приторным и менее привлекательным.

Сочетание математических вычислений и органической структуры в веб-дизайне может дать отличный результат. Необязательно, чтобы весь дизайн опирался на все упомянутые принципы, иногда достаточно правила третей, которое поможет вам правильно соблюсти пропорции и расположить элементы на свои места.

Готовы проверить полученные знания на лендинге? Вы можете выбрать подходящий шаблон и настроить его под себя в конструкторе LPgenerator, или, если у вас нет времени разбираться в тонкостях лендостроения, но при этом вам нужна уникальная страница с гарантированно высокой конверсией, подать заявку на индивидуальный дизайн. 

Он будет выполнен с учетом всех ваших пожеланий, подчеркнет особенности оффера и позиционирование бренда, а еще — легко масштабируется по мере необходимости.

Высоких конверсий!

12-03-2016

Золотое сечение: Самый раздутый миф в дизайне

Золотое сечение – это полный нонсенс в дизайне. И вот почему.

В мире искусства, архитектуры и дизайна золотое сечение завоевало потрясающую репутацию. Великие гении, включая Корбюзье и Сальвадора Дали, использовали эту пропорцию в своих работах. Парфенон, Пирамиды в Гизе, полотна Микелянджело, Мона Лиза и даже логотип Apple якобы построены на его основе.

Это бред. Эстетика золотого сечения – это просто современная байка, миф. Многие дизайнеры им пренебрегают, а если и используют, то не стесняются преуменьшать его значение. Кроме того, у этой пропорции нет никакой научной подоплеки. Те, кто верят, что за красотой золотого сечения кроется математика, попались на крючок 150-летней давности.

Пользователь FlickrSébastien Bertrand

Что такое золотое сечение?

Изначально описанный в Элементах Эвклида 2300 лет назад, этот термин гласит: два объекта находятся в золотой пропорции, если соотношение между ними идентично отношению их суммы к большему из двух элементов. Обычно эта пропорция составляет 1.6180. Самое известное применение золотого сечения – так называемый золотой прямоугольник, который может быть разделен на идеальный квадрат и меньший прямоугольник тех же пропорций, что и “родительский” прямоугольник. Вы можете применить эту теорию к большему разнообразию объектов, также разделяя их на компоненты.

Золотое сечение всегда немного неточное.

Простым языком: если у вас есть два объекта (или один объект, который можно разделить на два, по аналогии с золотым прямоугольником), и если после вышеописанной математики, вы получите число 1.6180, обычно считается, что два объекта демонстрируют золотое сечение. Но есть одна проблема. Когда вы все-таки посчитаете, то сама пропорция не равна 1.6180. Она равна 1.6180339887… И десятичная часть уходит в бесконечность.

“Собственно говоря, невозможно подобрать примеры золотого сечения в реальном мире, потому что это иррациональное число”, – заявляет Кит Девлин, профессор математики Стэнфордского университета. Вы можете только приблизиться к более стандартным пропорциям. Стороны экрана iPad соотносятся как 3:2, пропорция HDTV составляет 16:9, и все это “вокруг да около”, по словам Девлина. Но само золотое сечение – это как число “пи”. Как нельзя найти идеальный круг в реальном мире, так и нельзя применить точное золотое сечение к любому объекту в реальном мире. Оно всегда будет немного смещаться.

Золотое сечение – это как эффект Моцарта

Конечно, это педантизм. Неужели 1.6180 – недостаточно точно? Возможно, и достаточно, если бы было какое-то научное обоснование того, что именно золотое сечение позволяет нам считать объекты вроде Парфенона или Моны Лизы эстетически приятными.

Но это не так. Девлин считает, что сама идея, будто золотое сечение имеет какое-то отношение к эстетике, исходит от двух людей, один из которых был неправильно истолкован, а второй это толкование и обнародовал.

Первый человек – Лука Пачоли, францисканский монах, который написал книгу под названием De Divina Proportione в далком 1509 году, и она была названа в честь золотого сечения. Примечательно то, что в своей книге Пачоли не отстаивал теорию эстетики этого сечения в отношении к искусству, архитектуре и дизайну: вместо этого он поддерживал Витрувианскую систему рациональных пропорций, основанную римским архитектором первого века, Витрувием. Золотое сечение ошибочно было приписано Пачоли в 1799 году, согласно Марио Ливио, который буквально написал книгу по золотому сечению. Но Пачоли был близким другом Леонардо да Винчи, чьи работы получили огромное признание и популярность в 19 веке. Так как Да Винчи проиллюстрировал De Divina Proportione, вскоре начали говорить, что и сам Да Винчи применил золотое сечение как секретную математику в своих восхитительно красивых творениях.

Адольф Цейзинг был тем, кто в это поверил. “Это человек, который хотел сжечь себя на костре во имя репутации золотого сечения” – шутит Девлин. Цейзинг был немецким психологом, который отстаивал идею, что золотое сечение является универсальным законом, описывающим “красоту и завершенность в природе и в искусстве… оно проходит красной нитью как первостепенный духовный идеал во всех структурах, формах и пропорциях, космических и индивидуальных, органических и неорганических, акустических или оптических”.

Он был очень многословным. Единственной проблемой Цейзинга было то, что он видел закономерности там, где их не было. Например, Цейзинг доказывал, что золотое сечение можно применить к человеческому телу, взяв рост человека от пупка до пальцев ног, поделив его на полный рост. По словам Девлина, это всего лишь произвольные части тела, слепленные в формулу. Он говорит: “При замерах чего-то столь сложного, как человеческое тело, очень легко найти примеры разных пропорций, близких к 1.6”.

В моей собственной работе я даже не найду примера использования золотого сечения.

Но это не имеет никакого значения. Теории Цейзинга стали невероятно популярны, и Девлин называет их “эквивалентом эффекта Моцарта 19-го века”. Эффект Моцарта гласит, что прослушивание классической музыки повышает интеллект. В 20 веке известный швейцарско-французский архитектор Ле Корбузье положил золотое сечение в основу своей системы антропометрических пропорций “Модулора”. Дали нарисовал свой шедевр “Тайная вечеря” на холсте в форме золотого прямоугольника. Тем временем историки искусства начали просматривать и другие шедевры, пытаясь отыскать золотое сечение в Стоунхендже, полотнах Рембранта, Шартрском соборе и работах Сёра. Связь между золотым сечением и красотой превратилась в самую раздутую утку в мире искусства, архитектуры и дизайна.

Ian Yen на Yanko Design

На самом деле, вы не очень-то и предпочитаете золотое сечение

В реальном мире людям не особо необходимо золотое сечение.

Девлин совместно с кафедрой психологии Стенфордского университета в течение многих лет опрашивал сотни студентов, какой прямоугольник их любимый. Он показывал разные прямоугольники студентам, а затем просил их выбрать наиболее понравившийся. Если бы оды золотому сечению были оправданы, студенты бы выбирали прямоугольники, близкие к золотому. Но это было не так. Они выбирают их произвольно. И если вы попросите их повторить свой выбор, они выберут другие прямоугольники. “Это очень полезный пример для демонстрации сложности человеческого восприятия”. Кроме того, это отличная демонстрация того, что золотое сечение не является более приятным для людей с эстетической точки зрения.

Эксперименты Девлина не единственные в исследовании золотого сечение. Исследование, проведенное специалистами Школы бизнеса имени Уолтера Хааса в Беркли, показало, что в среднем потребители предпочитают прямоугольники, пропорция которых между 1.414 и 1.732. Золотое сечение входит в этот диапазон, но не является явным “любимчиком” публики.

Многие современные дизайнеры не считают его полезным

Дизайнеры, с которыми мы обсуждали золотое сечение, не видят в нем особой пользы.

Ричард Мейер, легендарный архитектор, автор Центра Гетти и Музея современного искусства в Барселоне, отмечает, что в начале своей карьеры у него был архитекторский треугольник, который соответствовал золотому сечению, но он никогда не создавал свои здания по золотому сечению. “В мире такое множество других чисел и формул, которые важнее при проектировании зданий”, – говорит Мейер, ссылаясь на формулы по расчету максимальных допустимых размеров пространств зданий, или на формулы расчета структурной нагрузки.

Алиса Андрасек, дизайнер из Biothing, онлайн-репозитория машинного проектирования, соглашается с этим: “В своей работе я даже не найду примера использования золотого сечения. Я могу представить, что эту пропорцию можно встроить в разные системы в качестве ‘изюминки’, но мне сложно вообразить, чтобы весь дизайн был построен именно на золотом сечении, как это случалось в истории… это слишком уж упрощенно”.

Джорджия Лупи из Accurat, итальянской дизайн-фирмы, говорит, что в лучшем случае золотое сечение так же важно для дизайнеров, как и любое другое композиционное правило, например, правило третей: отличное распространенное правило, которое хорошие дизайнеры могут с таким же успехом проигнорировать. “Я не знаю, сколько дизайнеров на практике специально внедряют золотое сечение в свои работы. Лично я никогда не работала с этой пропорцией в своих проектах”.

Из всех опрошенных дизайнеров, индустриальный дизайнер Ив Бехар из Fuseproject теплее всех относится к золотому сечению: “Иногда я действительно вижу золотое сечение в пропорциях продуктов и графики, которую мы создаем, но это скорее просто случайность, чем догма. Это важный инструмент, но не правило”.

Даже дизайнеры, которые по совместительству являются математиками, скептически относятся к использованию золотой пропорции в дизайне. Эдмуд Харрис – клинический доцент кафедры математики в Университете Арканзаса, который использует множество формул для создания новых произведений искусства. Но и Харрис говорит, что золотое сечение, в лучшем случае, всего лишь один из множества инструментов в руках дизайнеров, склонных к математике: “Во многих смыслах это просто число, и оно, как и другие числа, часто встречается в разных местах… [Но] это точно не универсальная формула эстетической красоты”.

Тайная вечеря, 1955, Сальвадор Дали

Почему этот миф так популярен?

Если ценность золотого сечения так незначительна, почему же этот миф процветает?

Девлин поясняет это просто: “Мы создания, генетически запрограммированные видеть паттерны и искать смысл. В нашей ДНК не зашифрована способность мириться с условными вещами вроде эстетики, поэтому мы пытаемся доказать их с помощью нашего часто ограниченного математического видения. Большая часть людей не понимает математику, и даже не может понять, как формула вроде золотого сечения применяется к сложной системе, так что и проверить себя они не могут. Люди думают, что повсюду видят золотое сечение, в природе и в любимых объектах, но они не могут это обосновать. Они – жертвы своего природного желания найти смысл в разных объектах вселенной, но из-за недостаточной математической грамотности они не могут понять, что обнаруживаемые закономерности иллюзорны”.

Золотое сечение в дизайне интерфейсов

Золотое сечение в природе, человеке, искусстве

Когда смотрим на красивый пейзаж, мы охватываемых все вокруг. Потом уделяем внимание деталям. Речке журчащей или дереву величественному. Видим поле зеленое. Замечаем, как ветер его обнимает нежно и журя шатает со стороны в сторону траву. Можем почувствовать аромат природы и услышать пение птиц…Все гармонично, все взаимосвязано и даёт чувство умиротворения, чувство прекрасного. Восприятие идёт поэтапно чуть меньшими долями.Куда вы сядете на скамье: на край, на середину или в любое место? Большинство ответит, что чуть дальше от середины. Приблизительное число в пропорции скамьи от вашего тела до края будет 1,62. Так и в кинотеатре, в библиотеке,- везде. Инстинктивно создаём гармонию красоту, которую во всем мире называю “Золотым сечением”.

Золотое сечение в математике

Вы задумывались, можно  ли определить меру красоте? Оказывается, с математической точки зрения возможно. Простая арифметика даёт понятие об абсолютной гармонии, которая и отображается в безупречной красоте, благодаря принципу Золотого сечения. Архитектурные сооружения др. Египта и Вавилона первыми начали соответствовать данному принципу. Но сформулировал принцип первым Пифагор. В математике это деление отрезка чуть больше половины, а точнее 1,628. Данное соотношение представляется как φ =0,618= 5/8. Маленький отрезок = 0,382 = 3/8, а полностью отрезок принимаем за единицу.

А:B=B:C  и C:B=B:A

От принципа золотого сечения отталкивались и великие писатели, архитекторы, скульпторы, музыканты, – люди искусства, и христиане, рисующие пиктограммы (пятиконечные звезды и т.д.) с его элементами в храмах, спасаясь от нечисти, и люди, изучающие точные науки, решающая проблемы кибернетики.

Золотое сечение в природе и явлениях.

Все на земле приобретая форму растет вверх, в сторону или по спирали. Последнему пристально уделил внимание Архимед, составив уравнение. По ряду Фибоначчи устроена шишка, ракушка, ананас, подсолнух, ураган, паутина, молекула ДНК, яйцо, стрекоза, ящерица…Тицириус доказал, что вся наша Вселенная, космос, галактическое пространство, – все спланировано исходя из Золотого принципа. Абсолютно во всем живом и не живом можно прочесть высшую красоту.

Золотое сечение в человеке.

Кости продуманы природой тоже согласно пропорции 5/8. Это и исключает оговорки людей про “кости широкие“. Большинство частей тела в соотношениях применяются к уравнению. Если все частички тела подчиняются Золотой формуле, тогда внешние данные будут весьма привлекательны и идеально сложены.
Отрезок от плеч до верха головы и ее размера = 1:1.618
Отрезок от  пупа до верха головы и от плеч до верха головы = 1:1.618
Отрезок от пупа до коленок и от них до ступней ног = 1:1.618
Отрезок от подбородка до крайней точки верхней губы и от неё до носа = 1:1.618

Все расстояния  лица дают общее представление об идеальных пропорциях, привлекающих взгляд.
Пальцы, ладонь , тоже подчиняются закону. Необходимо ещё отметить, что отрезок расставленных рук с туловищем равен росту человека. Да что там, все органы, кровь, молекулы, соответствуют Золотой формуле. Истинная гармония внутри и снаружи нашего пространства.

Параметры с физической стороны окружающих факторов.

Громкость звука. Высшая точка звука, вызывающая не комфортное ощущение и боль в ушной раковине = 130 децибелам. Это число можно разделить пропорцией 1,618, тогда выходит, что звук человеческого крика будет = 80 децибел.
Тем же методом двигаясь дальше получаем 50 децибел, что характерно для нормальной громкости речи человека. И последний звук, который получим благодаря формуле – приятный звук шепота = 2,618.
По данному принципу можно определить оптимально-комфортное, минимальное и максимальное число температуры, давления, влажности. Простая арифметика гармонии заложена во всем нашем окружении.

Золотое сечение в искусстве.

В архитектуре самые известные здания  и сооружения: египетские пирамиды, пирамиды Майя в Мексике, Нотр-дам де Пари, Парфенон греческий,  Петровский дворец, и другие.

В музыке: Аренский , Бетховен, Гаван , Моцарт, Шопен, Шуберт, и другие.

В живописи: почти все картины  знаменитых художников написаны согласно сечению: разносторонний Леонардо да Винчи и неподражаемый Микеланджело, такие родные в писании Шишкин с Суриковым, идеал чистейшего художества – испанец Рафаэль, и подаривший идеал женской красоты – итальянец Боттичелли, и многие-многие другие.

В поэзии: упорядоченная речь Александра Сергеевича Пушкина, в особенности “Евгений Онегин” и стихотворение “Сапожник”, поэзия замечательных Шота Руставели и Лермонтова, и многих других великих мастеров слова.

В скульптуре: статуя Аполлона Бельведерского, Зевса Олимпийского, прекрасной Афины и грациозной Нефертити, и другие скульптуры и статуи.

В фотографии используется “правило третьей”. Принцип такой: композиция делится на 3 равные части по вертикали и по горизонтали, ключевые моменты располагаются либо на линиях пересечения (горизонт), либо в точках пересечений (объекте). Таким образом пропорции  равны 3/8 и 5/8. В дизайне интерьера согласно Золотого сечения имеется много уловок, которые стоит разобрать детально. Их опишу подробно в следующей статье.

 

Автор : Гумерова Алия

ВЕРНУТЬСЯ К ДРУГИМ СТАТЬЯМ БЛОГА!

Золотое сечение как объяснение пропорций красоты

Над чем работают лучшие умы современной стоматологической науки? Над идеальной улыбкой, воплотившей в себе красоту и здоровье.

Что такое «красота»? Почему лицо и облик одного человека нам нравится, а другого — нет?

На эти вопросы пытались ответить учёные ещё тогда, когда не было ни только стоматологии как направления медицины, но и сама медицина находилась в стадии зарождения.

Оказывается, наше лицо и тело имеет определённые пропорции, кажущиеся на первый взгляд почти мистическими.

Хотя в наш просвещённый век многому можно найти научное и даже математическое объяснение.

Принято считать, что впервые закономерности соотношение размеров тела человека и отдельных его частей обобщил и сформулировал в 1855 г. немецкий исследователь Цейзинг в своём научном труде «Эстетические исследования». За основу своей теории он взял учение о «золотом сечении».

Ещё в VI веке до н.э. древнегреческий философ и математик Пифагор ввёл в научный обиход понятие «золотое деление». «Золотое деление» — это пропорциональное деление отрезка на неравные части. При этом меньший отрезок так относится к большему, как больший отрезок относится ко всему отрезку. a : b = b : c или с : b = b : а.

Так что же особенного в этом соотношении?

Оказывается, что всегда меньший отрезок относится к большему, как 0,382: к 0,618:

То есть, если АВ принять за единицу, АЕ/ЕВ=0,62/0,32 (в практических целях используют приближённые значения).

Один из примеров «золотого деления», с которым наверняка все знакомы, это — пентаграмма и, как представители её, так любимые людьми старшего поколения, «знак качества» и «звезда».

Все диагонали пятиугольника (пятиугольная звезда) делят друг друга на отрезки, связанные между собой «золотой пропорцией».

В настоящее время эта математическая закономерность носит название «золотое сечение», которое ввел в обиход ещё Леонардо да Винчи, который проводил сечения стереометрического тела, образованного правильными пятиугольниками. И каждый раз он получал соотношение сторон в «золотом делении». Он дал этому делению название «золотое сечение», принятое до сих пор.

Но не Пифагор впервые обнаружил закономерность «золотого сечения». Ещё древние египтяне и вавилоняне использовали эти знания в строительстве пирамид и изготовлении предметов обихода. Древние греки при проектировании своих зданий использовали пропорции «золотого сечения». В эпоху возрождения интерес к «золотому сечению» усилился. Художники нашли применение ему в искусстве. Учение о «золотом сечении» связано с именем гениального итальянского математика и монаха Луки Пачоли. В 1509 г. Была издана его книга «Божественная пропорция» с иллюстрациями Леонардо да Винчи (предположительно). Он причислял золотую пропорцию к «божественной сути» через триединство: бог сын, бог отец и святой дух, находящихся между собой в «золотой пропорции».

История «золотого сечения» связана ещё с одним известным итальянским математиком Фибоначчи. До наших времён дошёл ряд чисел: 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55 и т.д., известный, как ряд Фибоначчи.

Особенность последовательности данных чисел заключается в том, что каждый её член, начиная с третьего, равен сумме двух предыдущих (2+3=5, 3+5=8), а отношение смежных чисел ряда приближается к отношению «золотого сечения» (21:34=0,617, а 34:55=0,618). В последствии все исследователи «золотого сечения» в растительном и животном мире, искусстве и анатомии приходили к этому ряду, как арифметическому выражению закона золотого деления. Интересно, что свой закон Фибонначи вывел, подсчитывая количество рождённых кроликов от пары кроликов за год.

Так в чём же ореол таинственности «золотого сечения»?

Всё, что растёт и приобретает какую-либо форму в живом мире нашей планеты — растёт вверх или закручивается по спирали. Спираль (например, морская раковина) — пример соотношения в пропорциях «золотого сечения». Спирали прослеживаются в расположении семян в шишках хвойных деревьев, в семенах подсолнечника и др.

Паук плетёт паутину по спирали, ДНК человека закручено по спирали.

А рост вверх? Растение живёт по тем же законам «золотого сечения». Самый большой участок стебля — до первого листочка. Затем следующие сегменты уменьшаются в пропорции «золотого сечения»: с : в = в : а

Удивительно то, что и человек в соотношении отдельных частей тела и расстояний между ними, подчиняется законам «золотого сечения».

Немецкий учёный Альберт Дюрер доказал, что рост человека делится в золотых пропорциях линией, проходящей через пупок и линией, проходящей через кончики средних пальцев опущенных рук.

Его труды продолжил Цейзинг. Он выяснил, что пропорции мужского тела колеблются в пределах 13 : 8 = 1, 625.

А пропорции женского тела в среднем находятся в соотношении 8 : 5 = 1,6.

Пропорции «золотого сечения» проявляются в отношении длины плеча, предплечья, кисти и пальцев и т.д.

Поразительно, но в лице человека можно проследить множество пропорций, подчиненных «золотому сечению». Причем, чем больше в лице человека соотношений в этой пропорции, тем красивее нам он кажется. Есть лица, при характеристике которых употребляют выражение «правильные черты лица». У этих людей основные пропорции наиболее близки к соотношению 1, 618: или 62 : 38.

Какие же пропорции в лице человека стремятся к «золотому сечению»?

Прежде всего, у людей с красивыми лицами наблюдается:

1. Идеальная пропорция между расстояниями от медиального угла глаза до крыла носа и от крыла носа до подбородка. Это соотношение называется «динамической симметрией» или «динамическим равновесием».
2. Соотношение высоты верхней и нижней губы будет 1,618.
3. Высота надгубной складки (расстояние между верхней губой и нижней границей носа) и высота губ будут составлять соотношение 62 : 38.
4. Ширина одной ноздри суммарно с шириной переносицы относится к ширине другой ноздри в пропорции «золотого сечения».
5. Ширина ротовой щели также относится к ширине между наружными краями глаз, а расстояние между наружными уголками глаз — к ширине лба на уровне линии бровей, как все пропорции «золотого сечения».
6. Расстояние между линии смыкания губ до крыльев носа относится к расстоянию от линии смыкания губ до нижней точки подбородка, как 38 : 62: И к расстоянию от крыльев носа до зрачка — как 38 : 62 = 0.
7. Расстояние между линией верхней части лба до линии зрачков и расстояние между линией зрачков и линией смыкания губ имеет пропорцию «золотого сечения».

Можно продолжить этот список соотношения размеров гармоничного лица. Получается, правильную красоту можно математически просчитать и даже прибегнуть к хирургической корректировке с целью совершенствования внешности.

В настоящее время стоматология, наряду с пластической хирургией, занимается не только лечением заболеваний полости рта, но и эстетической медициной.

Удивительно, но и в стоматологии можно проследить пропорции «золотого сечения».

Красивая улыбка — это не только белоснежные здоровые ровные зубы, но и их правильное соотношение и расположение. И здесь мы опять сталкиваемся с закономерность «золотого сечения».

Вот некоторые примеры соотношений размеров и расстояний между зубами:

1. Ширина верхнего центрального резца относится к ширине нижнего центрального резца, как 62 : 38, т.е. 1, 618:, в соотношении «золотого сечения».
2. В этой же пропорции находится ширина двух верхних резцов к ширине двух нижних.
3. Расстояние между премолярами верхней челюсти относится к ширине четырёх верхних резцов, как 62 : 38.
4. Расстояние между дистальными поверхностями нижних клыков и щечными фиссурами моляров — пропорция 38 : 62.

И этот список можно продолжить.

Как же на практике можно использовать знание о «золотом сечении» и его влиянии на параметры в стоматологии?

Разумеется, искать применение золотых пропорций в эстетической стоматологии.

Расположение, размер и взаимное соотношение зубов в полости рта — всё это подчинено общему закону — «золотому сечению».

Вольно или невольно, осознанно или неосознанно врач использует эти пропорции при восстановлении коронковой части зуба, при протезировании или ортодонтических мероприятиях. Лучше, конечно, чтобы врач применял математическую составляющую в формировании вашей красоты и здоровья.

А мы теперь знаем, что человек — только часть живого мира на нашей планете, подчиняющийся общим законам мироздания. И доказательство тому — учение о «золотом сечении», дошедшее до нас уже даже не из предыдущего тысячелетия.

Время работы

Пн-Пт	10:00 — 22:00
Сб-Вс	10:00 — 20:00

Свистунов Борис Григорьевич Генеральный директор ООО «Стоматология на Смоленке», директор НАО «Демостом», врач стоматолог терапевт

золотого сечения | Примеры, определение и факты

Золотое сечение , также известное как золотое сечение , золотая середина или божественная пропорция , в математике иррациональное число (1 + квадратный корень из √5) / 2 , часто обозначается греческой буквой ϕ или τ, что приблизительно равно 1,618. Это отношение отрезка линии, разрезанного на две части разной длины, при котором отношение всего сегмента к таковому более длинного сегмента равно отношению более длинного сегмента к более короткому.Происхождение этого числа можно проследить до Евклида, который упоминает его как «крайнее и среднее соотношение» в Elements . С точки зрения современной алгебры, если длина более короткого сегмента составляет одну единицу, а длина более длинного сегмента — x единиц, возникает уравнение ( x + 1) / x = x / 1; это может быть преобразовано в квадратное уравнение x ² — x — 1 = 0, для которого положительное решение равно x = (1 + квадратный корень из √5) / 2, золотое сечение.

Древние греки признавали это свойство «разделения» или «разделения на части», фраза, которая в конечном итоге была сокращена до просто «раздел». Прошло более 2000 лет, когда и «сечение», и «сечение» были названы «золотыми» немецким математиком Мартином Омом в 1835 году. Греки также заметили, что золотое сечение обеспечивает наиболее эстетичную пропорцию сторон прямоугольника. , идея, которая была расширена в эпоху Возрождения, например, благодаря работе итальянского эрудита Леонардо да Винчи и публикации De divina пропорционально (1509; Божественная пропорция ), написанной итальянским математиком Лукой Пачоли и проиллюстрированной Леонардо.

Витрувианский человек, рисунок Леонардо да Винчи ( ок. 1509), иллюстрирующий пропорциональный канон, установленный классическим римским архитектором Витрувием; в Академии изящных искусств Венеции.

Foto Marburg / Art Resource, New York

Золотое сечение встречается во многих математических контекстах. Его геометрически можно построить с помощью линейки и циркуля, и это происходит при исследовании архимедовых и платоновых тел. Это предел соотношений последовательных членов последовательности чисел Фибоначчи 1, 1, 2, 3, 5, 8, 13,…, в котором каждый член после второго является суммой двух предыдущих, а также значение самой основной из непрерывных дробей, а именно 1 + 1 / (1 + 1 / (1 + 1 / (1 + ⋯.

В современной математике золотое сечение встречается при описании фракталов, фигур, которые проявляют самоподобие и играют важную роль в изучении хаоса и динамических систем.

Получите подписку Britannica Premium и получите доступ к эксклюзивному контенту. Подпишитесь сейчас

15 удивительных примеров золотого сечения в природе

Знаменитая последовательность Фибоначчи веками очаровывала математиков, художников, дизайнеров и ученых. Также известное как золотое сечение, его повсеместность и поразительная функциональность в природе говорят о его важности как фундаментальной характеристики Вселенной.

Мы уже говорили о рядах Фибоначчи и золотом сечении, но на них стоит сделать небольшой обзор. Последовательность Фибоначчи начинается так: 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55 и так далее до бесконечности. Каждое число представляет собой сумму двух предшествующих ему чисел. Это простой образец, но он кажется своего рода встроенной системой нумерации космоса. Вот 15 поразительных примеров фи в природе.

Леонардо Фибоначчи придумал последовательность при вычислении идеальных пар разложения кроликов в течение одного года.Сегодня его возникающие закономерности и соотношения (phi = 1,61803 …) можно увидеть от микромасштаба до макромасштаба и вплоть до биологических систем и неодушевленных объектов. Хотя золотое сечение не учитывает на каждую структуру или узор во вселенной, оно, безусловно, играет важную роль. Вот несколько примеров.

1. Лепестки цветов

G / O СМИ могут получать комиссию

Количество лепестков в цветке постоянно соответствует последовательности Фибоначчи. Известные примеры включают лилию, у которой три лепестка, лютики, у которых пять (на фото слева), у цикория 21, у ромашек 34 и так далее.Фи появляется в лепестках из-за идеальной упаковки, выбранной с помощью дарвиновских процессов; каждый лепесток размещается на 0,618034 за оборот (из круга на 360 °), что обеспечивает наилучшее воздействие солнечного света и других факторов.

2. Семенные головки

Головка цветка также подвержена фибоначчанским процессам. Обычно семена производятся в центре, а затем перемещаются наружу, заполняя все пространство. Подсолнухи — отличный пример спиралевидного узора.

В некоторых случаях высевные головки настолько плотно упакованы, что их общее количество может достигать 144 и более. И при подсчете этих спиралей общая сумма стремится соответствовать числу Фибоначчи. Интересно, что для оптимизации заполнения требуется очень иррациональное число (а именно такое, которое не будет хорошо представлено дробью). Фи вполне отвечает всем требованиям.

3. Сосновые шишки

Точно так же семенные коробочки на шишке расположены по спирали. Каждый конус состоит из пары спиралей, каждая из которых поднимается вверх в противоположных направлениях.Количество шагов почти всегда будет соответствовать паре последовательных чисел Фибоначчи. Например, конус 3-5 — это конус, который встречается сзади после трех шагов по левой спирали и пяти шагов по правой.

4. Фрукты и овощи

Аналогичным образом спиралевидные узоры можно найти на ананасах и цветной капусте.

5. Ветви деревьев

Последовательность Фибоначчи также можно увидеть в том, как ветви дерева образуются или разделяются. Главный ствол будет расти до тех пор, пока не создаст ветку, которая создаст две точки роста.Затем один из новых стеблей разветвляется на два, а другой находится в состоянии покоя. Этот образец ветвления повторяется для каждого нового стебля. Хороший пример — чиханье. Корневые системы и даже водоросли демонстрируют эту закономерность.

6. Оболочки

Еще один пример — уникальные свойства золотого прямоугольника. Эта форма, прямоугольник, в котором отношение сторон a / b равно золотой середине (фи), может привести к процессу вложенности, который может повторяться до бесконечности и который принимает форму спирали.Это называется логарифмической спиралью, и она изобилует природой.

Раковины улиток и наутилусов следуют по логарифмической спирали, как и улитка внутреннего уха. Его также можно увидеть в рогах некоторых коз и форме паутины некоторых пауков.

7. Спиральные галактики

Неудивительно, что спиральные галактики также следуют знакомому паттерну Фибоначчи. Млечный Путь имеет несколько спиральных рукавов, каждое из которых представляет собой логарифмическую спираль около 12 градусов. Интересно отметить, что спиральные галактики бросают вызов ньютоновской физике.Еще в 1925 году астрономы поняли, что, поскольку угловая скорость вращения галактического диска меняется с расстоянием от центра, радиальные рукава должны становиться искривленными по мере вращения галактик. Впоследствии, после нескольких оборотов, спиральные рукава должны начать закручиваться вокруг галактики. Но они этого не делают — отсюда так называемая проблема намотки. Казалось бы, звезды снаружи движутся со скоростью выше ожидаемой — уникальная черта космоса, которая помогает сохранять его форму.

8. Ураганы

9.Лица

Лица, как человеческие, так и нечеловеческие, изобилуют примерами золотого сечения. Рот и нос расположены на золотых сечениях расстояния между глазами и нижней частью подбородка. Подобные пропорции видны сбоку, и даже глаз и ухо (которое следует по спирали).

Стоит отметить, что тело каждого человека индивидуально, но средние значения для разных популяций имеют тенденцию к фи. Также было сказано, что чем точнее наши пропорции соответствуют фи, тем более привлекательными воспринимаются эти черты.Например, самые «красивые» улыбки — это те, у которых центральные резцы на 1,618 шире, чем боковые резцы, которые на 1,618 шире клыков, и так далее. Вполне возможно, что с эволюционно-психической точки зрения мы настроены любить физические формы, которые придерживаются золотого сечения — потенциального индикатора репродуктивной пригодности и здоровья.

10. Пальцы

Если посмотреть на длину наших пальцев, то каждая часть — от кончика основания до запястья — больше предыдущей примерно на соотношение фи.

11. Тела животных

Даже наши тела имеют пропорции, соответствующие числам Фибоначчи. Например, расстояние от пупка до пола и от макушки до пупка является золотым сечением. Тела животных демонстрируют аналогичные тенденции, включая дельфинов (глаза, плавники и хвост падают на Золотые сечения), морских звезд, морских ежей, муравьев и медоносных пчел.

12. Репродуктивная динамика

Говоря о медоносных пчелах, они следуют Фибоначчи в других интересных направлениях.Самый яркий пример — это деление количества самок в колонии на количество самцов (самок всегда больше, чем самцов). Обычно ответ очень близок к 1,618. Кроме того, генеалогическое древо медоносных пчел также следует знакомому образцу. У самцов один родитель (самка), а у самок — два (самка и самец). Таким образом, когда дело доходит до генеалогического древа, у мужчин есть 2, 3, 5 и 8 бабушек и дедушек, прабабушек и дедушек, gr-gr-grandparents и gr-gr-gr-grandparents соответственно.По той же схеме у женщин 2, 3, 5, 8, 13 и так далее. И, как уже отмечалось, физиология пчел также довольно хорошо следует по Золотой кривой.

13. Драки животных

Когда ястреб приближается к своей добыче, его наиболее резкое изображение находится под углом к ​​направлению полета — углом, который совпадает с углом наклона спирали.

14. Матка

По словам Джаспера Вегутса, гинеколога из университетской больницы Лёвена в Бельгии, врачи могут определить, выглядит ли матка нормальной и здоровой, на основе ее относительных размеров — размеров, которые приблизительно соответствуют золотому сечению.Из Guardian :

За последние несколько месяцев он измерил матки 5000 женщин с помощью ультразвука и составил таблицу среднего отношения длины матки к ее ширине для разных возрастных групп.

Данные показывают, что это соотношение составляет около 2 при рождении, а затем оно неуклонно снижается в течение жизни женщины до 1,46, когда она находится в пожилом возрасте.

Доктор Вергутс был взволнован, обнаружив, что, когда женщины наиболее плодовиты, в возрасте от 16 до 20 лет, отношение длины матки к ширине равно 1.6 — очень хорошее приближение к золотому сечению.

«Это первый раз, когда на это смотрят, поэтому я рад, что все получилось так красиво», — сказал он.

15. Молекулы ДНК

Даже микроскопический мир не застрахован от Фибоначчи. Молекула ДНК имеет размер 34 ангстрем в длину и 21 ангстрем в ширину для каждого полного цикла ее двойной спирали. Эти числа, 34 и 21, являются числами в ряду Фибоначчи, и их отношение 1,61 близко приближается к Phi, 1.6180339.

Спасибо Calvin Dvorsky за помощь в написании статьи!

Источники и изображения: Вверху: Лоскутников / Shutterstock; Лютик: motorolka / shutterstock, ThinkQuest , Shell , Galaxy: FabulousFibonacci , Американский музей естественной истории и здесь , пчелиный мед , ураган : MNN , Faces: Goldennumber and здесь , DNA .

Золотое сечение — что это такое и как его использовать в дизайне

Хороший дизайн обсуждался с тех пор, как мы создаем. Существуют бесконечные форумы, обсуждения в социальных сетях и личные беседы о том, что делает дизайн отличным, и каждый высказывает свою точку зрения.

В этом же прелесть дизайна, правда? Каждый может интерпретировать это по-своему.

Хотя универсального подхода к дизайну никогда не будет, существует конкретный математический подход, который может помочь нам каждый раз на шаг приближаться к созданию потрясающих дизайнерских впечатлений: золотое сечение.

Золотое сечение — это математическое соотношение, которое вы можете найти практически везде, например, в природе, архитектуре, живописи и музыке. Когда он применяется конкретно к дизайну, он создает органичную, сбалансированную и эстетически приятную композицию.

В этой статье мы подробно рассмотрим, что такое золотое сечение, как его рассчитать и как использовать в дизайне, включая удобный список инструментов.

Что такое золотое сечение?

Золотое сечение, также известное как золотое сечение, золотое сечение, божественная пропорция или греческая буква фи, — это особое число, которое приблизительно равно 1.618. Само соотношение происходит от последовательности Фибоначчи, естественной последовательности чисел, которые можно найти везде, от количества листьев на дереве до формы морской ракушки.

Последовательность Фибоначчи — это сумма двух чисел перед ней. Это идет: 0, 1,1, 2, 3, 5, 8, 13, 21 и так далее до бесконечности. На основе этого шаблона греки разработали золотое сечение, чтобы лучше выразить разницу между любыми двумя числами в последовательности.

Как это связано с дизайном? Вы можете найти золотое сечение, если разделите линию на две части, и более длинная часть (a), разделенная на меньшую часть (b), равна сумме (a) + (b), деленной на (a), которые оба равно 1.618. Эта формула может помочь вам при создании фигур, логотипов, макетов и т. Д.

Вы также можете воспользоваться этой идеей и создать золотой прямоугольник. Возьмите квадрат и умножьте одну сторону на 1,618, чтобы получить новую форму: прямоугольник с гармоничными пропорциями.

Если вы положите квадрат на прямоугольник, соотношение между двумя фигурами даст вам золотое сечение.

Если вы продолжите применять формулу золотого сечения к новому прямоугольнику справа, вы получите изображение, состоящее из все более мелких квадратов.

Если вы нарисуете спираль по каждому квадрату, начиная с одного угла и заканчивая в противоположном, вы создадите первую кривую последовательности Фибоначчи (также известную как Золотая спираль).

Как использовать золотое сечение в дизайне

Теперь, когда урок математики окончен, как вы можете применить эти знания в повседневной работе?

Вот четыре способа использования золотого сечения в дизайне:

1. Типографика и определение иерархии

Золотое сечение может помочь вам выяснить, какой размер шрифта вы должны использовать для заголовков и основного текста на веб-сайте, целевой странице, в блоге или даже в печатной кампании.

Допустим, размер вашего основного текста составляет 12 пикселей. Если вы умножите 12 на 1,618, вы получите 19,416, что означает, что размер текста заголовка 19 или 20 пикселей будет соответствовать золотому сечению и сбалансировать размер основного шрифта 12 пикселей.

Если вы хотите выяснить, насколько большим должен быть размер вашего основного текста, вы можете сделать наоборот. Если размер вашего заголовка составляет 25 пикселей, вы можете разделить его на 1,618, чтобы найти основной текст (15 или 16 пикселей).

2. Обрезка и изменение размера изображений

При кадрировании изображения легко выделить белое пространство, которое нужно вырезать.Но как сделать так, чтобы изображение оставалось сбалансированным после изменения его размера? Вы можете использовать Золотую спираль в качестве ориентира для композиции изображения.

Например, если вы наложите золотую спираль на изображение, вы можете убедиться, что точка фокусировки находится в середине спирали.

3. Макет

Использование золотого сечения может помочь вам разработать визуально привлекательный пользовательский интерфейс, который привлекает внимание пользователя к тому, что наиболее важно. Например, страница, которая выделяет широкий блок контента слева и более узкий столбец справа, может соответствовать пропорциям золотого сечения и помочь вам решить, где разместить наиболее важный контент.

4. Разработка логотипа

Если вы разрабатываете новый логотип и чувствуете себя застрявшим, обратитесь к золотому сечению, чтобы набросать пропорции и формы. Многие популярные логотипы следуют золотому сечению, например Twitter, Apple и Pepsi.

Дизайнер Кази Мохаммед Эрфан даже поставил перед собой задачу создать 25 новых логотипов, полностью основанных на золотом сечении. Результат? Простые, сбалансированные и красивые иконки.

Инструменты, которые помогут вам использовать золотое сечение

Вам не нужно выламывать карандаш и бумагу, чтобы вычислить золотое сечение — есть ряд приложений, которые сделают это за вас.

Вот пять инструментов, которые помогут вам использовать золотое сечение в ваших проектах:

• Калькулятор золотого сечения: Вычислите более короткую сторону, длинную сторону и общую длину двух сторон, чтобы вычислить золотое сечение.
• goldenRATIO: Созданное для дизайнеров и разработчиков, это приложение дает вам простой способ создавать веб-сайты, интерфейсы, макеты и многое другое в соответствии с золотым сечением. Он включает в себя встроенный калькулятор с визуальной обратной связью и функциями для хранения положения экрана и настроек, поэтому вам не нужно менять золотое сечение для каждой задачи.
• Калькулятор типографики золотого сечения: Найдите идеальную типографику для своего веб-сайта, указав размер и ширину шрифта. Вы можете оптимизировать на основе размера шрифта, высоты строки, ширины и символов в строке.
• PhiMatrix : Это программное обеспечение для проектирования и анализа Золотого сечения содержит настраиваемые сетки и шаблоны, которые можно накладывать на любое изображение. Его можно использовать для дизайна и композиции, дизайна продукта, разработки логотипа и многого другого.
• Ресурс эскиза Золотого сечения : Загрузите бесплатный файл эскиза Золотой спирали, чтобы помочь с компоновкой изображения и макета.

Начало работы с золотым сечением

Как только вы узнаете, что искать, вы начнете замечать золотое сечение повсюду. (Не верите? Посмотрите на свои руки. Даже ваши пальцы следуют золотому сечению.) Человеческий глаз привык видеть это магическое число, и мы подсознательно положительно на него реагируем.

Как дизайнеры, мы можем использовать это число в своих интересах. Даже небольшие изменения в способе обрезки изображения или разработки макета могут значительно улучшить взаимодействие пользователей с вашим дизайном.

Руководство для дизайнера по золотому сечению [с 14 примерами]

Что общего у раковин улиток, ураганов, Парфенона и Моны Лизы?

Все они следуют золотому сечению.

Дело в том, что независимо от того, являетесь ли вы дизайнером или нет, исследования показали, что ваш мозг, вероятно, запрограммирован на то, чтобы предпочитать природу и произведения искусства, соответствующие золотому сечению. На самом деле искусство, которое следует золотому сечению, часто считается самым красивым. Так что, даже если вы не знаете, что это такое, вы, несомненно, видели это в некоторых из ваших любимых дизайнов и архитектур.

В математике (предмет, в котором я никогда не был так хорош), золотое сечение существует, когда линия делится на две части, и более длинная часть (a), деленная на меньшую часть (b), равна сумме обеих частей. (a) + (b), деленное на (a). Он должен составлять примерно 1,618.

Понял? И я нет. Но для наших целей мы собираемся сконцентрироваться на золотом узоре, как он существует в искусстве — например, в древнеримской архитектуре или картинах Леонардо да Винчи.

Изображение любезно предоставлено Музеем науки .

Если золотое сечение действительно является предпосылкой для создания захватывающего искусства, очевидно, что вы, как человек, занимающийся дизайнерским проектом, должны знать о нем все. Здесь мы разберем примеры золотого сечения в природе, дизайне и даже человеческом лице, чтобы вы могли подумать, как включить золотое сечение в свои собственные маркетинговые проекты.

Что такое золотое сечение в дизайне?

Золотое сечение, также известное как Золотое Сечение, Золотое Сечение или Фи, представляет собой математическое соотношение, которое можно использовать для создания некоторых из самых красивых произведений искусства и архитектуры, таких как Мона Лиза или Парфенон.Наш мозг запрограммирован на то, чтобы предпочитать визуальные эффекты, соответствующие золотому сечению, которое можно найти во многих элементах в природе, и даже в человеческом лице, и поэтому он выглядит чистым и органичным.

Золотое сечение в природе

Золотое сечение проявляется во многих заметных и очевидных объектах природы, включая деревья, сосновые шишки и семена клубники.

Тем не менее, это также можно увидеть в в значительной степени абстрактных местах, например, в точке в черной дыре, где тепло меняется с положительного на отрицательное.Его постоянное присутствие может обозначать золотое сечение как фундаментальную константу природы, что может объяснить, почему наш мозг, кажется, настроен лучше реагировать на визуальные эффекты, соответствующие золотому сечению.

Здесь мы рассмотрим всего несколько примеров золотого сечения в природе:

1. Лепестки цветов

2. Ураганы

3. Спиральные галактики

4. Корпуса Nautilus

5.Семена цветов

6. Шишки сосновые

Значение золотого сечения для человеческого лица

Теперь, когда мы изучили, как природа следует золотому сечению, давайте посмотрим на золотое сечение, как оно существует на человеческом лице.

Предположительно, голова образует золотой прямоугольник с глазами в качестве середины, а рот и нос — в виде золотых отрезков расстояния между глазами и подбородком. Золотое сечение можно найти даже в наших зубах и профиле, когда мы поворачиваем голову в сторону.

Исследования показали, что лица, наиболее близкие к золотому сечению, считаются самыми красивыми.

Доктор Стивен Р. Марквардт, получивший докторскую степень в Калифорнийском университете в Лос-Анджелесе и проводящий исследования привлекательности человека, считает, что золотое сечение — это математическая формула, описывающая красоту лица.

Примеры золотого сечения

1. «Мона Лиза» Леонардо да Винчи
2. Парфенон
3. Раковины улиток
4. Ураганы
5. Семенные головки
6. Лепестки цветов
7. Шишки
8. «Тайная вечеря» Леонардо да Винчи
9. Ветви деревьев
10. Человеческое лицо
11. Спиральная галактика
12. «Сотворение Адама» Микеланджело
13. молекул ДНК
14. «Таинство Тайной вечери» Сальвадора Дали

Следующий курс был разработан совместно с Институтом цифрового маркетинга:

математических мифов: золотое сечение

Большинство из вас слышали о числе, называемом золотым сечением .Он появляется, например, в книге / фильме « Код да Винчи» , а также во многих статьях, книгах и школьных проектах, целью которых является показать, насколько важна математика в реальном мире. Многие авторы (включая автора Кода да Винчи) описывают его как основу всех прекрасных узоров в природе, и иногда его называют божественной пропорцией . Утверждается, что большая часть произведений искусства и архитектуры содержит особенности в пропорциях, заданных золотым сечением.Например, утверждается, что и Парфенон, и пирамиды находятся в этой пропорции. Также утверждалось, что золотое сечение проявляется в человеческом теле, например, как отношение роста взрослого человека к высоте его пупка или длины предплечья к длине кисти.

Тем не менее, за всю свою карьеру применения математики в реальном мире я встречал золотое сечение ровно дважды. Да, дважды! Итак, верны ли какие-либо из этих великих заявлений о золотом сечении?

Какое опять золотое сечение?

Начнем с того, что быстро вспомним, что такое золотое сечение.Это было определено древнегреческим математиком Евклидом следующим образом. Представьте, что у вас есть отрезок линии, который вы хотите разделить на две части. Вы хотите разделить его таким образом, чтобы соотношение между целым сегментом и более длинным из двух кусков было таким же, как соотношение между более длинным из двух кусков и более коротким. Каким должно быть это соотношение?

Мы хотим выбрать A и B так, чтобы ( A + B ) / A = A / B .

Немного математики (см. Здесь) покажет, что соотношение должно быть

Тот факт, что определяется как отношение двух длин, означает, что вы можете искать его всякий раз, когда смотрите на что-то, на котором есть сегменты линий — будь то лицо или здание.

Золотое сечение в человеческом теле

Предполагается, что золотое сечение лежит в основе многих пропорций человеческого тела.К ним относятся форма идеального лица, а также отношение высоты пупка к высоте тела. Действительно, утверждается, что почти каждая пропорция идеального человеческого лица связана с золотым сечением (см. Эту статью, чтобы узнать больше о таких утверждениях).

Вы можете наложить всевозможные прямоугольники на красивое лицо, а затем заявить, что красота проистекает из пропорций прямоугольника.

Однако все это неправда, даже отдаленно.У тела есть много возможных соотношений, многие из которых лежат где-то между 1 и 2. Если вы рассмотрите их достаточно, вы обязательно получите числа, близкие к значению золотого сечения (около 1,618). Это особенно верно, если объекты, которые вы измеряете, не особенно четко определены (как на картинке слева), и можно изменить определение таким образом, чтобы получить пропорции, которые вы хотите найти.

Если вы присмотритесь, вы также обнаружите, что пропорции человеческого тела близки к 1.6, 5/3, 3/2, квадратный корень из 2, 42/26 и т. Д. И т. Д. Действительно, большинство чисел от 1 до 2 будут иметь две части тела, приближающие их в соотношении. Подобные ложные паттерны также наблюдаются в солнечной системе (которая также имеет множество различных соотношений, из которых вы можете выбирать). Также помните, что, поскольку золотое сечение — это иррациональное число (см. Ниже), вы никогда не увидите его точно ни при каких измерениях.

Все это пример того, как человеческий мозг находит ложные корреляции.Действительно, при наличии достаточного количества данных можно найти закономерности, согласующиеся практически с любой гипотезой. Хороший способ убедиться в этом — выйти в погожий солнечный день на улицу и посмотреть на облака. Рано или поздно вы найдете облако, которое соответствует какому-то новому шаблону. В качестве примера посмотрите эту статью BBC News, в которой рассказывается о «королеве-воине», наблюдаемой в облачной структуре.

Это явление на самом деле может быть довольно опасным, когда в данных обнаруживаются ложные корреляции, подтверждающие точку зрения. Например, они могут привести к ложным обвинениям и даже к ложным обвинениям.На этом сайте вы найдете множество примеров ложных корреляций.

Спирали золотые и прочие

Если вы возьмете линию, разделенную на два сегмента, и это будет золотое сечение, а затем сформируете прямоугольник со сторонами и, тогда этот прямоугольник называется золотым прямоугольником .

Золотой прямоугольник состоит из квадрата (белого) и меньшего прямоугольника (серого). Меньший прямоугольник также является золотым.

Золотой прямоугольник, который мы только что сформировали, состоит из квадрата и меньшего прямоугольника, который сам по себе является золотым прямоугольником (подробнее см. Здесь).Этот золотой прямоугольник снова состоит из квадрата и меньшего прямоугольника, который сам по себе является золотым прямоугольником. И так далее.

Используя последовательность все меньших и меньших золотых прямоугольников, мы можем сформировать нечто похожее на спираль. Просто нарисуйте четверть круга в каждом квадрате, который появляется в золотых прямоугольниках.

Спиральная форма, построенная из золотого прямоугольника.

Часто утверждают, что эту спиралевидную форму можно найти во многих местах в природе и искусстве.Например, по форме раковины наутилуса, по форме галактики, по форме урагана или даже волны.

Здесь есть две проблемы. Во-первых, это не спираль. Это последовательность дуг окружности. При переходе от одной дуги к другой кривизна спирали скачет. Вряд ли в каком-либо природном явлении мы увидим такие скачки. Фактически, форма — это только приближение к истинной спирали. Форма спирали, которую он приближает, является примером логарифмической спирали .Такие спирали очень распространены в природе. У них есть полярное уравнение

где — основание натурального логарифма. В природе мы видим такие спирали повсюду, с разной величиной и в зависимости от контекста. Причина, по которой эти спирали настолько распространены, заключается в том, что они обладают свойством самоподобия . Это означает, что если вы повернете спираль на любой фиксированный угол, вы получите спираль, которая является масштабированием оригинала.

Так называемая золотая спираль имеет особое значение

где — золотое сечение (а углы измеряются в радианах).

Нет никаких причин, по которым этот номер был бы каким-то особенным. Оболочка наутилуса представляет собой логарифмическую спираль, потому что свойство самоподобия позволяет оболочке расти без изменения формы. Значения, наблюдаемые для раковины наутилуса, не имеют никакого отношения к приведенному выше значению, при этом значение, наблюдаемое чаще всего в реальных раковинах.

Искусство и архитектура

Здесь надо быть осторожными. Несомненно, некоторые художники, такие как Ле Корбюзье (в его системе Modulor), сознательно использовали золотое сечение в своих произведениях искусства. Это потому, что было заявлено, что пропорции золотого прямоугольника особенно приятны для человеческого глаза, и что с эстетической точки зрения мы предпочитаем золотой прямоугольник всем другим прямоугольникам. Таким образом, имеет смысл использовать их в художественных произведениях. Затем утверждается, что золотое сечение можно увидеть практически в любом другом произведении искусства и архитектуры.

Доказательств того, что золотой прямоугольник особенно хорош, довольно мало. Психологические исследования, показывающие разные прямоугольники группам людей, по-видимому, указывают на то, что существует широкий диапазон предпочтений, причем отношение квадратного корня из двух к одному часто оказывается предпочтительнее других. Проверьте себя на прямоугольниках ниже, чтобы выбрать, какой из них вам больше нравится.

Согласно книге Кейта Девлина Взгляд Девлина: миф, который не исчезнет , идея о том, что золотое сечение вообще имеет какое-либо отношение к эстетике, исходит в первую очередь от двух людей, из которых один был неправильно процитирован, а другой прибегнул к изобретение.Неправильно процитированным автором был Лука Пачоли, который написал книгу под названием De Divina Proportione еще в 1509 году. Книга была названа в честь золотого сечения, но не выступала за теорию эстетики, основанную на золотом сечении, или за то, что она должна применяться к искусству и архитектуре. Такой взгляд был ошибочно приписан Пачоли в 1799 году.

Пачоли был близким другом Леонардо да Винчи, и часто утверждают, что Леонардо сам использовал золотое сечение в своих картинах. Прямых доказательств этому нет.Возможно, самый известный из этих примеров — это модель Vitruvian Man . Однако пропорции на этой картине не соответствуют золотому сечению. Действительно, Леонардо упоминал в своих работах только отношения целых чисел. Предполагаемые примеры золотого сечения, появляющиеся на его картинах, относятся к тому же классу, что и те, которые находят это соотношение в природе.

Девлин приписывает «популяризацию» золотого сечения Адольфу Цайзингу, немецкому психологу 19-го века, который утверждал, что золотое сечение было универсальным законом, описывающим «красоту и завершенность в царствах как природы, так и искусства […], который пронизывает, как высший духовный идеал, все структуры, формы и пропорции, космические или индивидуальные, органические или неорганические, акустические или оптические ». Это был просто пример (как указано выше) наблюдения ложных узоров. эта работа повлияла на многих других и заложила основы большей части современного мифа.

Так называемая золотая спираль, наложенная на Парфенон. Нет никаких доказательств того, что золотое сечение сыграло роль в дизайне этого здания.Основное изображение Парфенона: Ойвинд Солстад, CC BY 2.0.

Другой пример этого мифа — утверждение, что золотое сечение проявляется в пропорциях Парфенона, части Акрополя в Афинах.

Нет никаких свидетельств этого в греческой науке, и идея о том, что Парфенон имеет пропорции, заданные золотым сечением, восходит только к 1850-м годам. Кроме того, фактические размеры Парфенона не дают пропорций, особенно близких к золотому сечению, если вы не будете осторожны с выбором прямоугольников.Фактически, Парфенон имеет свой гармоничный внешний вид благодаря продуманному расположению линий, которые выглядят параллельными, но на самом деле сходятся или изгибаются, поэтому практически невозможно проводить измерения с достаточной точностью, чтобы получить точные соотношения. Поскольку пропорции Парфенона меняются в зависимости от его высоты, просто невозможно найти общую пропорцию, соответствующую золотому сечению.

То же самое относится и к остальной греческой архитектуре: нет никаких свидетельств того, что греки считали золотое сечение эстетически приятным или вообще использовали его в своем искусстве и архитектуре.

Это касается и музыки. Утверждается, что золотое сечение играет важную роль в музыкальной композиции. Об этом мало свидетельств. Однако в композиции важна гамма, а гамма очень тесно связана с корнем двенадцатой степени из 2. Именно это последнее число лежит в основе музыки, а не золотое сечение [ссылка].

В этих упорных мифах о золотом сечении есть реальная опасность. Школьников и многих других обманывают, вводя в заблуждение ложную реальность о том, как работает математика.Рано или поздно они обнаружат, что эта реальность не соответствует действительности, и потеряют веру в вполне реальную способность математики объяснять мир.

Великая реальность

Относясь к золотому сечению довольно пренебрежительно, я хотел бы завершить этот раздел, подчеркнув, насколько удивительным является золотое сечение — ему действительно не нужны все эти ложные утверждения, чтобы сделать его особенным.

Сначала обратимся к природным явлениям, которые действительно связаны с золотым сечением.Золотое сечение тесно связано со знаменитой последовательностью Фибоначчи

.

Подробнее об этой ссылке можно узнать здесь. Последовательность Фибоначчи, безусловно, присутствует в природе, поскольку она связана как с тем, как растет население, так и с тем, как формы могут сочетаться друг с другом. Например, последовательность можно увидеть в спиралях на подсолнечных цветках, которые должны соответствовать друг другу упорядоченным образом, и на листьях некоторых растений, которые необходимо расположить так, чтобы улавливать больше всего солнечного света.В результате можно наблюдать соотношения, близкие к золотому сечению, возникающие в определенных природных явлениях (подробнее здесь).

Эти явления включают распространение трутней среди самок пчел в улье, что связано с тем, как пчелы размножаются на протяжении многих поколений (подробнее см. Здесь). Так что действительно можно увидеть золотое сечение в саду, и для этого есть очень веские математические причины.

Фибоначчи подумал о своей последовательности, рассматривая рост популяции идеализированных кроликов.См. Эту статью, чтобы узнать больше.

Но, возможно, еще более интересными являются многие увлекательные математические свойства золотого сечения. Они исследуются в различных статьях Plus , но я хотел бы указать на одну, которая особенно увлекательна и которая действительно отличает золотое сечение от других чисел: его крайняя иррациональность.

Иррациональные числа — это числа, которые не могут быть представлены дробями и которые имеют бесконечное десятичное расширение, которое не заканчивается повторяющимся блоком.Именно это означает, что иррациональные числа трудно наблюдать в природе. Золотое сечение обладает удивительным свойством быть самым иррациональным числом из всех. Это означает, что это не только невозможно точно представить в виде дроби, но и невозможно легко аппроксимировать дробью. См. Эту статью для математических подробностей.

Сложность аппроксимации золотого сечения дробью делает его очень полезным числом для математиков и ученых, изучающих процесс синхронизации .Это происходит, когда система с собственной частотой форсируется одной из другой частоты и принимает частоту форсирования. Одним из примеров является синхронизация человеческого тела с дневной частотой солнечного света. Второй пример — климат Земли, который синхронизируется с естественными циклами обращения вокруг Солнца.

Однако синхронизация сама по себе может быть проблемой, приводящей к нежелательным резонансам в системе (например, висячий мост сильно вибрирует, если по нему проходит марширующий оркестр).Выбирая две частоты в соотношении, мы можем избежать синхронизации из-за крайней иррациональности золотого сечения. Это очень полезное свойство, по-видимому, используется мозгом и различными видами насекомых, а также учеными-климатологами и даже людьми, производящими самолеты.

Итак, золотое сечение играет главную роль, но не ту, о которой вы часто читаете в связанной с ним мифологии. Какая жалость! Это прекрасный парадокс, но самое интересное в золотом сечении заключается в том, что это не соотношение.

---

---

Об авторе

Крис Бадд.

Эта статья основана на выступлении Бадда в продолжающемся Gresham Цикл лекций колледжа (см. Видео выше). Вы можете увидеть другие статьи, основанные на разговоре, здесь.

Крис Бадд OBE — профессор прикладной математики Университета Бата, вице-президент Института математики и ее приложений, заведующий кафедрой математики Королевского института и почетный член Британской научной ассоциации.Он особенно заинтересован в применении математики в реальном мире и содействии пониманию математики общественностью.

Он является соавтором популярной книги по математике Mathematics Galore! , опубликованный издательством Oxford University Press, совместно с К. Сангвином, и представлен в книге 50 Visions of Mathematics ed. Сэм Парк.

Золотое сечение — определение, формула и решенные примеры

Золотое сечение, которое часто называют золотой серединой, божественной пропорцией или золотым сечением, является особым атрибутом, обозначаемым символом ϕ, и приблизительно равно 1.618. Изучение многих специальных формаций может быть выполнено с использованием специальных последовательностей, таких как последовательность Фибоначчи, и таких атрибутов, как золотое сечение.

Это соотношение встречается в различных искусствах, архитектуре и дизайне. Многие замечательные архитектурные сооружения, такие как Великая пирамида Египта, Парфенон, были частично или полностью спроектированы так, чтобы отразить золотое сечение в их структуре. Великие художники, такие как Леонардо да Винчи, использовали золотое сечение в некоторых своих шедеврах, и в 1500-х годах оно было известно как «Божественная пропорция».Давайте узнаем больше о золотом сечении в этом уроке.

Что такое золотое сечение?

Золотое сечение, которое также называют золотой серединой, божественной пропорцией или золотым сечением, существует между двумя величинами, если их соотношение равно отношению их суммы к большему количеству между ними. Что касается этого определения, если мы разделим линию на две части, части будут в золотом сечении, если:

Отношение длины более длинной части, скажем «a», к длине более короткой части, скажем «b», равно отношению их суммы «(a + b)» к более длинной длине.

Обратитесь к следующей схеме для лучшего понимания вышеупомянутой концепции:

Обозначается греческой буквой ϕ, произносимой как «фи». Примерное значение ϕ равно 1.61803398875 … Он находит применение в геометрии, искусстве, архитектуре и других областях. Таким образом, следующее уравнение устанавливает соотношение для вычисления золотого сечения: ϕ = a / b = (a + b) / a = 1.61803398875 … где a и b — размеры двух величин, а a — большее среди два.

Примеры золотого сечения

Золотое сечение имеет множество применений в области архитектуры. Многие архитектурные чудеса, такие как Великая мечеть Кайруана, были построены с учетом золотого сечения в их структуре. Такие художники, как Леонардо да Винчи, Рафаэль, Сандро Боттичелли и Жорж Сёра использовали это как атрибут в своих произведениях.

Что такое формула золотого сечения?

Формула золотого сечения может использоваться для вычисления значения золотого сечения.Уравнение золотого сечения выводится, чтобы найти общую формулу для расчета золотого сечения.

Уравнение золотого сечения

Из определения золотого сечения,

a / b = (a + b) / a = ϕ

Из этого уравнения получаем два уравнения:

a / b = ϕ → (1)

(a + b) / a = ϕ → (2)

Из уравнения (1),

a / b = ϕ

⇒ a = b

Подставьте это в уравнение (2),

(bϕ + b) / bϕ = ϕ

б (ϕ + 1) / bϕ = ϕ

(ϕ + 1) / ϕ = ϕ

1 + 1 / ϕ = ϕ

1 + 1 / ϕ = ϕ

Как рассчитать золотое сечение?

Значение золотого сечения можно рассчитать разными методами.Начнем с основного.

Метод удара и испытания

Мы угадываем произвольное значение константы, а затем выполняем следующие шаги для вычисления более близкого значения на каждой итерации.

• Вычислите обратное умножение угаданного значения, т. Е. 1 / значение. Это значение будет нашим первым термином.
• Вычислите другой член, прибавив 1 к обратному умножению этого значения.
• Оба члена, полученные на вышеупомянутых шагах, должны быть равны.Если нет, мы будем повторять процесс до тех пор, пока не получим примерно равное значение для обоих терминов.
• Для второй итерации мы будем использовать предполагаемое значение, равное члену 2, полученному на шаге 2, и так далее.

Например,

Так как ϕ = 1 + 1 / ϕ, оно должно быть больше 1. Давайте начнем со значения 1,5 в качестве нашего первого предположения.

• Член 1 = мультипликативная обратная величина 1,5 = 1 / 1,5 = 0,6666 …
• Член 2 = Мультипликативная величина, обратная 1.5 + 1 = 0,6666 .. + 1 = 1,6666 …

Поскольку оба члена не равны, мы повторим этот процесс еще раз, используя предполагаемое значение, равное , член 2 .

В следующей таблице приведены данные расчетов для всех предполагаемых значений до тех пор, пока мы не получим желаемые равные члены:

Итерация	Принятое значение	Клемма 1 (1 / значение)	Клемма 2 (1 / значение + 1)
1.	1,5	11,511,5 = 0,6666 ..	0,6666 .. + 1 = 1,6666 ..
2.	1.6666 ..	11,666..11,666 .. = 0,6	0,6 + 1 = 1,6
3.	1,6	11,611,6 = 0,625	0,625 + 1 = 1,625
4.	1,625	11,62511.625 = 0,61538 ..	0,61538 .. + 1 = 1,61538 ..
5.	1,61538 ..	..	.. и так далее

Чем больше итераций вы выполните, тем ближе приблизительное значение будет к точному. Другие методы обеспечивают более эффективный способ вычисления точного значения.

Уравнение золотого сечения

Другой метод вычисления золотого сечения — решение уравнения золотого сечения.2 — 4ac}} {2a} \)

Подставляя значения a = 1, b = -1 и c = -1, получаем,

ϕ = \ (\ frac {1 \ pm \ sqrt {(1 + 4)}} {2} \)

Решение можно упростить до положительного значения, давая:

ϕ = 1/2 + √5 / 2

Обратите внимание, что мы не рассматриваем отрицательное значение, поскольку \ (\ phi \) — это отношение длин, и оно не может быть отрицательным.

Следовательно, ϕ = 1/2 + √5 / 2

Что такое золотой прямоугольник?

В геометрии золотой прямоугольник определяется как прямоугольник, длина сторон которого находится в золотом сечении.Золотой прямоугольник демонстрирует особую форму самоподобия. Все прямоугольники, которые создаются путем добавления или удаления квадрата, также являются золотыми прямоугольниками.

Построение золотого прямоугольника

Мы можем построить золотой прямоугольник, выполнив следующие шаги:

• Шаг 1: Сначала мы нарисуем квадрат из 1 единицы. На одной из его сторон нарисуйте точку посередине. Теперь мы проведем линию от этой точки до угла другой стороны.

• Шаг 2: Используя эту линию в качестве радиуса и точку посередине в качестве центра, нарисуйте дугу, идущую вдоль стороны квадрата.Длину этой дуги можно вычислить с помощью теоремы Пифагора: √ (1/2) ² + (1) ² = √5 / 2 единиц.
• Шаг 3: Используйте пересечение этой дуги и стороны квадрата, чтобы нарисовать прямоугольник, как показано на рисунке ниже:

Это золотой прямоугольник, потому что его размеры находятся в золотом сечении. т.е. ϕ = (√5 / 2 + 1/2) / 1 = 1.61803

Что такое последовательность Фибоначчи?

Последовательность Фибоначчи — это особый ряд чисел, в котором каждый член (начиная с третьего члена) является суммой двух предыдущих членов.Чтобы найти последовательность Фибоначчи, можно использовать следующие шаги:

• Начнем с того, что в качестве первых двух членов возьмем 0 и 1.
• Таким образом, третий член 1 вычисляется путем сложения 0 и 1.
• Аналогично, следующий член = 1 + 2 = 3 и так далее.

Последовательность Фибоначчи, таким образом, задается как 0, 1, 1, 2, 3, 5, 8, 13, 21, … и так далее. Последовательность Фибоначчи и золотое сечение имеют между собой особую связь. Когда мы начинаем вычислять отношения двух последовательных членов ряда Фибоначчи, значение каждого последующего отношения приближается к точному значению ϕ.

Например,

В следующей таблице приведены значения соотношений, приближенные к значению ϕ. В следующей таблице показаны значения отношений, которые ближе всего подходят к значению ϕ.

Коэффициент

Срок 1	Срок 2	= Срок 2 / Срок 1
2	3	1,5
3	5	1.6666 ..
5	8	1,6
8	13	1,625
13	21	1,61538

Важные темы

Ниже приводится список тем, тесно связанных с золотым сечением. Эти темы также дадут вам представление о том, как такие концепции рассматриваются в Cuemath.

Что такое золотое сечение простыми словами?

Золотое сечение — это математическое соотношение, которое существует между двумя величинами, если их отношение равно отношению их суммы к большему количеству из двух. Другими словами, когда линия делится на две части и более длинная часть «a», деленная на меньшую часть «b», равна сумме (a + b), деленной на «a», это означает, что линия отражающее золотое сечение, равное 1,618.

Что вы имеете в виду под золотым прямоугольником?

В геометрии золотой прямоугольник определяется как прямоугольник, длина сторон которого находится в золотом сечении.Золотой прямоугольник демонстрирует особую форму самоподобия. Все прямоугольники, которые создаются путем добавления или удаления квадрата, также являются золотыми прямоугольниками.

Почему красивое золотое сечение?

Золотое сечение — это соотношение, которое при использовании в различных областях для проектирования объектов делает объекты эстетически привлекательными и приятными на вид. Поэтому золотое сечение считается прекрасным атрибутом. Это можно заметить в различных узорах природы, например, в спиралевидном расположении цветов и листьев.Золотое сечение имеет множество применений в области архитектуры. Многие архитектурные чудеса были построены, чтобы отразить золотое сечение в их структуре, например, Великая пирамида Египта и Великая мечеть Кайруана.

Почему важно золотое сечение?

Золотое сечение — это математическое соотношение, которое обычно встречается в природе и используется в различных областях. Он используется в нашей повседневной жизни, в искусстве и архитектуре. Объекты, созданные с учетом золотого сечения в их структуре и дизайне, более приятны и придают эстетический вид глазам.Это можно заметить в спиралевидном расположении цветов и листьев.

Где в реальной жизни используется золотое сечение?

Золотое сечение широко применяется в области искусства и архитектуры. Многие архитектурные чудеса были построены так, чтобы отразить золотое сечение в их структуре. Такие художники, как Лео да Винчи, Рафаэль, Сандро Боттичелли и Жорж Сёра использовали это как атрибут в своих произведениях. Его можно использовать для изучения структуры многих предметов в нашей повседневной жизни, которые напоминают определенный узор.

Кто открыл золотое сечение?

Древнегреческие математики первыми упомянули золотое сечение в своей работе. Математики V века до нашей эры Гиппак и Евклид внесли большой вклад в свою исследовательскую работу по этой теме.

Что такое формула золотого сечения?

Формула золотого сечения может использоваться для вычисления значения золотого сечения. Формула для расчета золотого сечения имеет вид

.

1 + 1 / ϕ = ϕ

где ϕ обозначает золотое сечение.

Как золотое сечение проявляется в природе

Вселенная может быть хаотичной и непредсказуемой, но это также высокоорганизованный физический мир, связанный законами математики. Один из самых фундаментальных (и поразительно красивых) способов проявления этих законов — это золотое сечение.

Нетрудно найти примеры этого логарифмического явления в природе — будь то простое комнатное растение (например, растение алоэ выше) или обширная спиральная галактика (например, спиральная галактика Мессье 83, показанная ниже), все они происходят из одной и той же математической модели. концепции.

Мессье 83, спиральная галактика, расположенная в 15 миллионах световых лет от Земли. (Фото: НАСА, ЕКА и группа «Наследие Хаббла» (STScI / AURA) / Благодарность: Уильям Блэр, Университет Джона Хопкинса)

Золотое сечение (часто обозначаемое греческой буквой φ) напрямую связано с числовым шаблоном, известным как последовательность Фибоначчи, который представляет собой список, состоящий из чисел, являющихся суммой двух предыдущих чисел в последовательности. Последовательность Фибоначчи, которую часто называют естественной системой нумерации космоса, начинается просто (0 + 1 = 1 , 1 + 1 = 2 , 1 + 2 = 3 , 2 + 3 = 5 , 3 + 5 = 8 …), но вскоре вы обнаружите, что складываете числа в тысячи и миллионы (10946 + 17711 = 28657 , 17711 + 28657 = 46368 , 28657 + 46368 = 75025 …) и это просто продолжается вечно.

Когда число Фибоначчи делится на предшествующее ему число Фибоначчи, оно приближается к золотому сечению, которое является иррациональным числом, которое начинается как 1,6180339887 … и, опять же, продолжается бесконечно.

Когда золотое сечение применяется в качестве фактора роста (как показано ниже), вы получаете тип логарифмической спирали, известный как золотая спираль.

Узнайте больше о последовательности Фибоначчи и естественных спиралях в этой увлекательной серии видеороликов математика Ви Харт, которая говорит быстро, но интересна и напомнит вам о том, как ваш мозг когда-то прыгал от предмета к предмету:

Как объясняет Харт, примеры приблизительных золотых спиралей можно найти в природе, особенно в морских ракушках, океанских волнах, паутинах и даже в хвостах хамелеонов! Продолжайте читать ниже, чтобы увидеть лишь некоторые из способов, которыми эти спирали проявляются в природе.

Хвосты-хамелеоны

Хвост хамелеона славится своей плотной спиралевидной формой. (Фото: Райан М. Болтон / Shutterstock)

Ракушки

Морская ракушка — один из самых известных примеров спирали золотого сечения в природе. (Фото: Tramont_ana / Shutterstock)

Папоротники

Свернувшиеся вверх листья молодого папоротника известны как головастые. (Фото: Zamada / Shutterstock)

Океанские волны

Несмотря на свою бурную природу, океанские волны — еще один пример проявления золотого сечения в природе.(Фото: irabel8 / Shutterstock)

Бутоны цветов

Когда цветок еще не распустился, легко увидеть свидетельство золотого сечения. (Фото: Романцова Ольга / Shutterstock)

Раковины улиток

Раковины улиток — прекрасный пример золотого сечения в природе. (Фото: vvoronov / Shutterstock)

Романеско брокколи

Фрактальные спирали брокколи Романеско (Brassica oleracea). (Фото: Сергей Склезнев / Shutterstock)

Водовороты

Водоворот, показывающий спираль золотого сечения.(Фото: Элейн Дэвис / Shutterstock)

Цветы окопника

Вы можете увидеть спираль стебля этого цветка окопника. (Фото: Михаил Мельников / Shutterstock)

Шишки сосновые

Спирали золотого сечения, если смотреть со дна шишки. (Фото: bzanchi / Shutterstock)

Кочан для подсолнечника

Золотое сечение роста подсолнечника. (Фото: Portogas D Ace / Shutterstock)

Ураган Изабель (2003)

Спираль урагана Изабель в 2003 году. (Фото: Майк Тренчард / НАСА)

Каллы

Спиральное цветение каллы.(Фото: Линн Уотсон / Shutterstock)

Раковины

Колючая раковина со спиралью золотого сечения. (Фото: Fontana / Shutterstock)

Спираль алоэ

Спиральное растение алоэ сидит в садовом горшке. (Фото: PhotoSky / Shutterstock)

Паутина

Эта паутина имеет спиралевидную форму. (Фото: mycteria / Shutterstock)

Лепестки цветов

Среди этих фигурных лепестков цветов много золотых пропорций. (Фото: Ян Грейнджер / Shutterstock) .