Сложные математические формулы: Фото: Наука: Наука и техника: Lenta.ru

Содержание

ТОП-50 Важнейших формул по математике — Математика — Теория, тесты, формулы и задачи

Знание формул по математике является основой для успешной подготовки и сдачи различных экзаменов, в том числе и ЦТ или ЕГЭ по математике. Формулы по математике, которые надежно хранятся в памяти ученика — это основной инструмент, которым он должен оперировать при решении математических задач. На этой странице сайта представлены 50 важнейших формул по математике.

Изучать ТОП-50 Важнейших формул по математике онлайн:

Как успешно подготовиться к ЦТ по физике и математике?

Для того чтобы успешно подготовиться к ЦТ по физике и математике, среди прочего, необходимо выполнить три важнейших условия:

Изучить все темы и выполнить все тесты и задания приведенные в учебных материалах на этом сайте. Для этого нужно всего ничего, а именно: посвящать подготовке к ЦТ по физике и математике, изучению теории и решению задач по три-четыре часа каждый день. Дело в том, что ЦТ это экзамен, где мало просто знать физику или математику, нужно еще уметь быстро и без сбоев решать большое количество задач по разным темам и различной сложности. Последнему научиться можно только решив тысячи задач.
Выучить все формулы и законы в физике, и формулы и методы в математике. На самом деле, выполнить это тоже очень просто, необходимых формул по физике всего около 200 штук, а по математике даже чуть меньше. В каждом из этих предметов есть около десятка стандартных методов решения задач базового уровня сложности, которые тоже вполне можно выучить, и таким образом, совершенно на автомате и без затруднений решить в нужный момент большую часть ЦТ. После этого Вам останется подумать только над самыми сложными задачами.
Посетить все три этапа репетиционного тестирования по физике и математике. Каждый РТ можно посещать по два раза, чтобы прорешать оба варианта. Опять же на ЦТ, кроме умения быстро и качественно решать задачи, и знания формул и методов необходимо также уметь правильно спланировать время, распределить силы, а главное правильно заполнить бланк ответов, не перепутав ни номера ответов и задач, ни собственную фамилию.
Также в ходе РТ важно привыкнуть к стилю постановки вопросов в задачах, который на ЦТ может показаться неподготовленному человеку очень непривычным.

Успешное, старательное и ответственное выполнение этих трех пунктов, а также ответственная проработка итоговых тренировочных тестов, позволит Вам показать на ЦТ отличный результат, максимальный из того, на что Вы способны.

Нашли ошибку?

Если Вы, как Вам кажется, нашли ошибку в учебных материалах, то напишите, пожалуйста, о ней на электронную почту (адрес электронной почты здесь). В письме укажите предмет (физика или математика), название либо номер темы или теста, номер задачи, или место в тексте (страницу) где по Вашему мнению есть ошибка. Также опишите в чем заключается предположительная ошибка. Ваше письмо не останется незамеченным, ошибка либо будет исправлена, либо Вам разъяснят почему это не ошибка.

Все главные формулы по математике — Математика — Теория, тесты, формулы и задачи

Формулы сокращенного умножения

К оглавлению. ..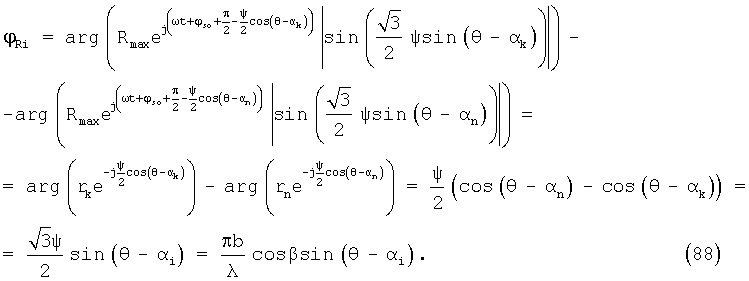

Квадрат суммы:

Квадрат разности:

Разность квадратов:

Разность кубов:

Сумма кубов:

Куб суммы:

Куб разности:

Последние две формулы также часто удобно использовать в виде:

Квадратное уравнение и формула разложения квадратного трехчлена на множители

К оглавлению…

Пусть квадратное уравнение имеет вид:

Тогда дискриминант находят по формуле:

Если D > 0, то квадратное уравнение имеет два корня, которые находят по формуле:

Если

D = 0, то квадратное уравнение имеет один корень (его кратность: 2), который ищется по формуле:

Если D < 0, то квадратное уравнение не имеет корней. В случае когда квадратное уравнение имеет два корня, соответствующий квадратный трехчлен может быть разложен на множители по следующей формуле:

Если квадратное уравнение имеет один корень, то разложение соответствующего квадратного трехчлена на множители задается следующей формулой:

Только в случае если квадратное уравнение имеет два корня (т. е. дискриминант строго больше ноля) выполняется Теорема Виета. Согласно Теореме Виета, сумма корней квадратного уравнения равна:

Произведение корней квадратного уравнения может быть вычислено по формуле:

Парабола

График параболы задается квадратичной функцией:

При этом координаты вершины параболы могут быть вычислены по следующим формулам. Икс вершины:

Игрек вершины параболы:

Свойства степеней и корней

К оглавлению…

Основные свойства степеней:

Последнее свойство выполняется только при n > 0. Ноль можно возводить только в положительную степень.

Основные свойства математических корней:

Для арифметических корней:

Последнее справедливо: если n – нечетное, то для любого a; если же n – четное, то только при a больше либо равном нолю. Для корня нечетной степени выполняется также следующее равенство:

Для корня четной степени имеется следующее свойство:

Формулы с логарифмами

К оглавлению…

Определение логарифма:

Определение логарифма можно записать и другим способом:

Свойства логарифмов:

Логарифм произведения:

Логарифм дроби:

Вынесение степени за знак логарифма:

Другие полезные свойства логарифмов:

Арифметическая прогрессия

К оглавлению…

Формулы n-го члена арифметической прогрессии:

Соотношение между тремя соседними членами арифметической прогрессии:

Формула суммы арифметической прогрессии:

Свойство арифметической прогрессии:

Геометрическая прогрессия

К оглавлению…

Формулы n-го члена геометрической прогрессии:

Соотношение между тремя соседними членами геометрической прогрессии:

Формула суммы геометрической прогрессии:

Формула суммы бесконечно убывающей геометрической прогрессии:

Свойство геометрической прогрессии:

Тригонометрия

К оглавлению. ..

Пусть имеется прямоугольный треугольник:

Тогда, определение синуса:

Определение косинуса:

Определение тангенса:

Определение котангенса:

Основное тригонометрическое тождество:

Простейшие следствия из основного тригонометрического тождества:

Формулы двойного угла

Синус двойного угла:

Косинус двойного угла:

Тангенс двойного угла:

Котангенс двойного угла:

Тригонометрические формулы сложения

Синус суммы:

Синус разности:

Косинус суммы:

Косинус разности:

Тангенс суммы:

Тангенс разности:

Котангенс суммы:

Котангенс разности:

Тригонометрические формулы преобразования суммы в произведение

Сумма синусов:

Разность синусов:

Сумма косинусов:

Разность косинусов:

Сумма тангенсов:

Разность тангенсов:

Сумма котангенсов:

Разность котангенсов:

Тригонометрические формулы преобразования произведения в сумму

Произведение синусов:

Произведение синуса и косинуса:

Произведение косинусов:

Формулы понижения степени

Формула понижения степени для синуса:

Формула понижения степени для косинуса:

Формула понижения степени для тангенса:

Формула понижения степени для котангенса:

Формулы половинного угла

Формула половинного угла для тангенса:

Формула половинного угла для котангенса:

Тригонометрические формулы приведения

Формулы приведения задаются в виде таблицы:

Тригонометрическая окружность

По тригонометрической окружности легко определять табличные значения тригонометрических функций:

Тригонометрические уравнения

К оглавлению. ..

Формулы решений простейших тригонометрических уравнений. Для синуса существует две равнозначные формы записи решения:

Для остальных тригонометрических функций запись однозначна. Для косинуса:

Для тангенса:

Для котангенса:

Решение тригонометрических уравнений в некоторых частных случаях:

Геометрия на плоскости (планиметрия)

К оглавлению…

Пусть имеется произвольный треугольник:

Тогда, сумма углов треугольника:

Площадь треугольника через две стороны и угол между ними:

Площадь треугольника через сторону и высоту опущенную на неё:

Полупериметр треугольника находится по следующей формуле:

Формула Герона

для площади треугольника:

Площадь треугольника через радиус описанной окружности:

Формула медианы:

Свойство биссектрисы:

Формулы биссектрисы:

Основное свойство высот треугольника:

Формула высоты:

Еще одно полезное свойство высот треугольника:

Теорема косинусов:

Теорема синусов:

Радиус окружности, вписанной в правильный треугольник:

Радиус окружности, описанной около правильного треугольника:

Площадь правильного треугольника:

Теорема Пифагора для прямоугольного треугольника (c — гипотенуза, a и b — катеты):

Радиус окружности, вписанной в прямоугольный треугольник:

Радиус окружности, описанной вокруг прямоугольного треугольника:

Площадь прямоугольного треугольника (

h — высота опущенная на гипотенузу):

Свойства высоты, опущенной на гипотенузу прямоугольного треугольника:

Длина средней линии трапеции:

Площадь трапеции:

Площадь параллелограмма через сторону и высоту опущенную на неё:

Площадь параллелограмма через две стороны и угол между ними:

Площадь квадрата через длину его стороны:

Площадь квадрата через длину его диагонали:

Площадь ромба (первая формула — через две диагонали, вторая — через длину стороны и угол между сторонами):

Площадь прямоугольника через две смежные стороны:

Площадь произвольного выпуклого четырёхугольника через две диагонали и угол между ними:

Связь площади произвольной фигуры, её полупериметра и радиуса вписанной окружности (очевидно, что формула выполняется только для фигур в которые можно вписать окружность, т. е. в том числе для любых треугольников):

Свойство касательных:

Свойство хорды:

Теорема о пропорциональных отрезках хорд:

Теорема о касательной и секущей:

Теорема о двух секущих:

Теорема о центральном и вписанном углах (величина центрального угла в два раза больше величины вписанного угла, если они опираются на общую дугу):

Свойство вписанных углов (все вписанные углы опирающиеся на общую дугу равны между собой):

Свойство центральных углов и хорд:

Свойство центральных углов и секущих:

Условие, при выполнении которого возможно вписать окружность в четырёхугольник:

Условие, при выполнении которого возможно описать окружность вокруг четырёхугольника:

Сумма углов n-угольника:

Центральный угол правильного n-угольника:

Площадь правильного n-угольника:

Длина окружности:

Длина дуги окружности:

Площадь круга:

Площадь сектора:

Площадь кольца:

Площадь кругового сегмента:

Геометрия в пространстве (стереометрия)

К оглавлению. ..

Главная диагональ куба:

Объем куба:

Объём прямоугольного параллелепипеда:

Главная диагональ прямоугольного параллелепипеда (эту формулу также можно назвать: «трёхмерная Теорема Пифагора»):

Объём призмы:

Площадь боковой поверхности прямой призмы (P – периметр основания, l – боковое ребро, в данном случае равное высоте h):

Объём кругового цилиндра:

Площадь боковой поверхности прямого кругового цилиндра:

Объём пирамиды:

Площадь боковой поверхности правильной пирамиды (P – периметр основания, l – апофема, т.е. высота боковой грани):

Объем кругового конуса:

Площадь боковой поверхности прямого кругового конуса:

Длина образующей прямого кругового конуса:

Объём шара:

Площадь поверхности шара (или, другими словами, площадь сферы):

Координаты

К оглавлению. ..

Длина отрезка на координатной оси:

Длина отрезка на координатной плоскости:

Длина отрезка в трёхмерной системе координат:

Координаты середины отрезка (для координатной оси используется только первая формула, для координатной плоскости — первые две формулы, для трехмерной системы координат — все три формулы):

Таблица умножения

К оглавлению…

Таблица квадратов двухзначных чисел

К оглавлению…

Расширенная PDF версия документа «Все главные формулы по школьной математике»:

К оглавлению…

Самые красивые физические и математические формулы.: moris_levran — LiveJournal

Это она создает почву, создает каркас для игры видимых красок, ласкающих наши чувства, и без этой поддержки красота мимолетных впечатлений была бы несовершенна как все неотчетливое и преходящее. Напротив красота интеллектуальная дает удовлетворение сама по себе».

П.А.М. Дирак писал: «У теоретической физики есть еще один верный путь развития. Природе присуща та фундаментальная особенность, что самые основные физические законы описываются математической теорией, аппарат которой обладает необыкновенной силой и красотой. Чтобы понять эту теорию, нужно обладать необычайно высокой математической квалификацией. Вы можете спросить: почему природа устроена именно так? На это можно ответить только одно: согласно нашим современным знаниям, природа устроена именно так, а не иначе».

Семь лет назад украинский физик (и художник) Наталия Кондратьева обратилась к ряду ведущих математиков мира с вопросом: «Какие три математические формулы, на ваш взгляд, самые красивые?»
В беседе о красоте математических формул приняли участие сэр Михаэль Атья и Дэвид Элварси из Британии, Яков Синай и Александр Кириллов из США, Фридрих Херцебрух и Юрий Манин из Германии, Давид Рюэль из Франции, Анатолий Вершик и Роберт Минлос из России и другие математики из разных стран. Из украинцев в дискуссии приняли участие академики НАНУ Владимир Королюк и Анатолий Скороход. Часть полученных таким образом материалов и легла в основу изданной Натальей Кондратьевой научной работы «Три самые красивые математические формулы».
— Какую цель вы ставили, обращаясь к математикам с вопросом о красивых формулах?
— Каждое новое столетие приносит обновление научной парадигмы. В самом начале века с ощущением, что мы стоим у порога новой науки, ее новой роли в жизни человеческого общества, я обратилась к математикам с вопросом о красоте идей, стоящих за математическими символами, т.е. о красоте математических формул.
Уже сейчас можно отметить некоторые особенности новой науки. Если в науке ХХ века очень важную роль играла «дружба» математики с физикой, то сейчас математика эффективно сотрудничает с биологией, генетикой, социологией, экономикой… Следовательно, наука будет исследовать соответствия. Математические структуры будут исследовать соответствия между взаимодействиями элементов различных областей и планов. И многое, что раньше мы воспринимали на веру как философские констатации, будет утверждено наукой как конкретное знание.
Этот процесс начался уже в ХХ веке. Так, Колмогоров математически показал, что случайности нет, а есть очень большая сложность. Фрактальная геометрия подтвердила принцип единства в многообразии и т.д.
— Какие же формулы были названы самыми красивыми?
— Сразу скажу, что цели устроить конкурс формулам не было. В своем письме к математикам я писала: «Люди, которые хотят понять, какими законами управляется мир, становятся на путь отыскания гармонии мира. Путь этот уходит в бесконечность (ибо движение вечно), но люди всё равно идут им, т.к. есть особая радость встретить очередную идею или представление. Из ответов на вопрос о красивых формулах, возможно, удастся синтезировать новую грань красоты мира. Кроме того, эта работа может оказаться полезной для будущих ученых как мысль о великой гармонии мира и математики как способе отыскания этой красоты».
Тем не менее среди формул оказались явные фавориты: формула Пифагора и формула Эйлера.
Вслед за ними расположились скорее физические, чем математические формулы, которые в ХХ веке изменили наше преставление о мире, —Максвелла, Шредингера, Эйнштейна.
Также в число самых красивых попали формулы, которые еще находятся на стадии дискуссии, такие, например, как уравнения физического вакуума. Назывались и другие красивые математические формулы.
— Как вы думаете, почему на рубеже второго и третьего тысячелетий формула Пифагора названа одной из самых красивых?
— Во времена Пифагора эта формула воспринималась как выражение принципа космической эволюции: два противоположных начала (два квадрата, соприкасающихся ортогонально) порождают третье, равное их сумме. Можно дать геометрически очень красивые интерпретации.
Возможно, существует какая-то подсознательная, генетическая память о тех временах, когда понятие «математика» означало — «наука», и в синтезе изучались арифметика, живопись, музыка, философия.
Рафаил Хасминский в своем письме написал, что в школе он был поражен красотой формулы Пифагора, что это во многом определило его судьбу как математика.
— А что можно сказать о формуле Эйлера?
— Некоторые математики обращали внимание, что в ней «собрались все», т.е. все самые замечательные математические числа, и единица таит в себе бесконечности! — это имеет глубокий философский смысл.
Недаром эту формулу открыл Эйлер. Великий математик много сделал, чтобы ввести красоту в науку, он даже ввел в математику понятие «градус красоты». Вернее, он ввел это понятие в теорию музыки, которую считал частью математики.
Эйлер полагал, что эстетическое чувство можно развивать и что это чувство необходимо ученому.
Сошлюсь на авторитеты… Гротендик: «Понимание той или иной вещи в математике настолько совершенно, насколько возможно прочувствовать ее красоту».
Пуанкаре: «В математике налицо чувство». Он сравнивал эстетическое чувство в математике с фильтром, который из множества вариантов решения выбирает наиболее гармоничный, который, как правило, и есть верный. Красота и гармония — синонимы, а высшее проявление гармонии есть мировой закон Равновесия. Математика исследует этот закон на разных планах бытия и в разных аспектах. Недаром каждая математическая формула содержит знак равенства.
Думаю, что высшая человеческая гармония есть гармония мысли и чувства. Может быть, поэтому Эйнштейн сказал, что писатель Достоевский дал ему больше, чем математик Гаусс.
Формулу Достоевского «Красота спасет мир» я взяла в качестве эпиграфа к работе о красоте в математике. И он также обсуждался математиками.
— И они согласились с этим утверждением?
— Математики не утверждали и не опровергали этого утверждения. Они его уточнили: «Осознание красоты спасет мир». Здесь сразу вспомнилась работа Юджина Вигнера о роли сознания в квантовых измерениях, написанная им почти пятьдесят лет назад. В этой работе Вигнер показал, что человеческое сознание влияет на окружающую среду, т.е., что мы не только получаем информацию извне, но и посылаем наши мысли и чувства в ответ. Эта работа до сих пор актуальна и имеет как своих сторонников, так и противников. Я очень надеюсь, что в ХХI веке наука докажет: осознание красоты способствует гармонизации нашего мира.

1. Формула Эйлера. Многие видели в этой формуле символ единства всей математики, ибо в ней «-1 представляет арифметику, i — алгебру, π — геометрию и e — анализ».

2. Это простое равенство показывает, величина 0,999 (и так до бесконечности) эквивалентна единице. Многие люди не верят, что это может быть правдой, хотя существует несколько доказательств, основанных на теории пределов. Тем не менее, равенство показывает принцип бесконечности.

3. Это уравнение было сформулировано Эйнштейном в рамках новаторской общей теории относительности в 1915 году. Правая часть этого уравнения описывает энергию, содержащуюся в нашей Вселенной (в том числе» темную энергию»). Левая сторона описывает геометрию пространства-времени. Равенство отражает тот факт, что в общей теории относительности Эйнштейна, масса и энергия определяют геометрию, и одновременно кривизну, которая является проявлением гравитации. Эйнштейн говорил, что левая часть уравнений тяготения в общей теории относительности, содержащая гравитационное поле, красива и как будто вырезана из мрамора, в то время как правая часть уравнений, описывающая материю, всё ещё уродлива, будто сделана из обыкновенной деревяшки.

4. Еще одна доминирующая теория физики — Стандартная модель — описывает электромагнитное, слабое и сильное взаимодействие всех элементарных частиц. Некоторые физики считают, что она отображает все процессы, происходящие во Вселенной, кроме темной материи, темной энергии и не включает в себя гравитацию. В Стандартную модель вписывается и неуловимый до прошлого года бозон Хиггса, хотя не все специалисты уверены в его существовании.

5. Теорема Пифагора — одна из основополагающих теорем евклидовой геометрии, устанавливающая соотношение между сторонами прямоугольного треугольника. Ее мы помним еще со школы и считаем, что автор теоремы — Пифагор. На самом деле этой формулой пользовались еще в Древнем Египте при строительстве пирамид.

6. Теорема Эйлера. Эта теорема заложила фундамент нового раздела математики — топологии. Уравнение устанавливает связь между числом вершин, ребер и граней для многогранников, топологически эквивалентных сфере.

7. Специальная теория относительности описывает движение, законы механики и пространственно-временные отношения при произвольных скоростях движения, меньших скорости света в вакууме, в том числе близких к скорости света. Эйнштейн составил формулу, которая описывает, что время и пространство не являются абсолютными понятиями, а скорее являются относительными в зависимости от скорости наблюдателя. Уравнение показывает, как расширяется или замедляется время в зависимости от того, как и куда движется человек.

8. Уравнение было получено в 1750-х годах Эйлером и Лагранжем при решении задачи об изохроне. Это проблема определения кривой, по которой тяжелая частица попадает в фиксированную точку за фиксированное время, независимо от начальной точки. В общих словах, если ваша система имеет симметрию, есть соответствующий закон сохранения симметрии.

9. Уравнение Каллана — Симанзика. Оно представляет собой дифференциальное уравнение, описывающее эволюцию н-корреляционной функции при изменении масштаба энергий, при которых теория определена и включает в себя бета-функции теории и аномальные размерности. Это уравнение помогло лучше понять квантовую физику.

10. Уравнение минимальной поверхности. Это равенство объясняет формирование мыльных пузырей.

11. Прямая Эйлера. Теорема Эйлера была доказана в 1765 году. Он обнаружил, что середины сторон треугольника и основания его высот лежат на одной окружности.

12. В 1928 году П.А.М. Дирак предложил свой вариант уравнения Шредингера – которое соответствовало теории А. Эйнштейна. Учёный мир был потрясён – Дирак открыл своё уравнение для электрона путём чисто математических манипуляций с высшими математическими объектами, известными как спиноры. И это было сенсацией – до сих пор все великие открытия в физике должны стоять на прочной базе экспериментальных данных. Но Дирак считал, что чистая математика, если она достаточно красива, является надёжным критерием правильности выводов. «Красота уравнений важнее, чем их соответствие экспериментальным данным. … Представляется, что если стремишься получить в уравнениях красоту и обладаешь здоровой интуицией, то ты на верном пути». Именно благодаря его выкладкам был открыт позитрон – антиэлектрон, и предсказал наличие у электрона «спина» — вращения элементарной частицы.

13. Дж. Максвелл получил удивительные уравнения, объединившие все явления электричества, магнетизма и оптики. Замечательный немецкий физик, один из создателей статистической физики, Людвиг Больцман, сказал об уравнениях Максвелла: «Не Бог ли начертал эти письмена?»

14. Уравнение Шредингера.Уравнение, описывающее изменение в пространстве и во времени чистого состояния, задаваемого волновой функцией, в гамильтоновых квантовых системах. Играет в квантовой механике такую же важную роль, как уравнение второго закона Ньютона в классической механике.

Математические формулы по алгебре и геометрии для ЕГЭ

Как выучить все формулы по математике к ЕГЭ

Чтобы сдать ЕГЭ по математике, необходимо знать математические формулы из школьного курса алгебры и геометрии.

Для того, чтобы запомнить формулы школьной математики, желательно держать в течение всего года на видном месте шпаргалку с красиво написанными формулами. Таким образом подключается зрительная память и формулы лучше запоминаются.

Проверяйте себя время от времени: попробуйте написать все важные математические формулы по памяти, а затем проверьте. На самом деле, формул, которые надо выучить наизусть, не так много. И целого учебного года вполне достаточно, чтобы все выучить.

Многие алгебраические, геометрические, тригонометрические формулы можно быстро вывести прямо на экзамене, если Вы их забыли. Но на это придется потратить какое-то время. Поэтому преимущество получают те школьники, которые выучили формулы.
Зная математические формулы наизусть, можно гораздо быстрей решить сложные задачи по алгебре, тригонометрии и геометрии на ЕГЭ.

Мы собрали самые важные формулы из школьного курса математики, которые надо выучить для успешной сдачи ЕГЭ.

Математические формулы школьного курса алгебры

Степени и корни

Формулы сокращенного умножения

Квадратный трехчлен: квадратное уравнение, формулы Виета, разложение на множители

Логарифмические формулы

Формулы тригонометрии

Основные формулы тригонометрии

Тригонометрические уравнения

Значения тригонометрических функций

Формулы приведения

Сумма и разность углов

Формулы двойного и тройного аргумента

Формулы половинного аргумента

Сумма и разность тригонометрических функций

Произведение тригонометрических функций

Формулы дифференциального исчисления

Формулы векторной алгебры из школьного курса математики

Формулы арифметической и геометрической прогрессии

Геометрические формулы школьного курса математики для ЕГЭ

Планиметрия

Стереометрия

Выучить формулы по математике – это еще не все, что надо для успешной сдачи ЕГЭ. Опыт решения задач, знания правил оформления заданий на экзамене не менее важны. Приглашаем всех школьников 11-х классов на курсы подготовки к ЕГЭ ПАРАГРАФ. С нами Вы подготовитесь к ЕГЭ наиболее продуктивно.

Учите формулы по математике и сдавайте ЕГЭ на максимальные баллы!

От красавиц до чудовищ

Некоторое время назад у издателя N + 1 возник спор о математической красоте. Можно ли назвать математику красивой? И если да, то насколько красота математических построений отличается от красоты более привычных нам явлений? Воспринимает ли мозг математика эту красоту так же, как красоту изящной скульптуры или живописного заката? Оказалось, что еще в 2014 году нейробиологи изучили этот вопрос. Выборка у них была небольшая — всего 15 математиков, поэтому всерьез делать выводы о математической красоте на ее основе нельзя (да и сами условия эксперимента потом сильно критиковали). Однако это прекрасный повод посмотреть, какие формулы участники этого исследования назвали красивыми, обычными или некрасивыми. Мы отобрали 10 формул, чтобы наши читатели сами могли решить, какая из них кажется им наиболее совершенной. У вас, кстати, есть возможность проголосовать за любую десяти, но только за одну. Выбирайте мудро!

Тождество Эйлера

Тождество Эйлера испытуемые чаще других называли самым красивым. Причин для этого может быть несколько. Возможно, дело в том, что здесь встретились сразу три важные константы: π, e и i.

Тождество Эйлера

Основное тригонометрическое тождество

Основное тригонометрическое тождество является простой переформулировкой теоремы Пифагора. Его тоже испытуемые довольно часто называли красивым.

Основное тригонометрическое тождество

Формула Эйлера

Формула Эйлера в исследовании проиграла тождеству Эйлера, хотя последнее является частным случаем формулы для x = π. Тем не менее, ее тоже часто называли красивой. Кстати, почти все красивые формулы имеют отношение к условному курсу школьной математики.

Формула Эйлера для экспоненты

Условия Коши-Римана

Условия Коши-Римана — это система дифференциальных уравнений на функции u(x, y) и v(x, y), которая гарантирует, что комплекснозначная функция u(x, y) + iv(x, y) является комплексно-аналитической. Система обладает рядом нетривиальных свойств, которые позволяют объяснить многие удивительные свойства комплексно-аналитических функций.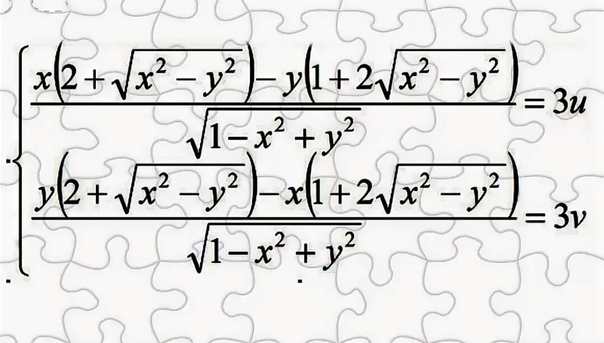 При всей ее значимости для математики, испытуемые оценили эту систему как обычную.

Условия Коши-Римана

Эйлерова характеристика сферы

Еще одна формула, в которой испытуемые не увидели ничего особенного, это эйлерова характеристика сферы. У нее есть несколько интерпретаций. Одна из них такова: если на сфере нарисовать несколько точек, соединить их непересекающимися линиями, а потом посчитать количество вершин (V), количество ребер (E) и количество кусков, на которые разбилась сфера (F), то, независимо от рисунка, окажется выполнено это равенство.

Эйлерова характеристика сферы

Формула Гаусса-Бонне

Формула Гаусса-Бонне, пожалуй, одна из самых сложных в нашем списке.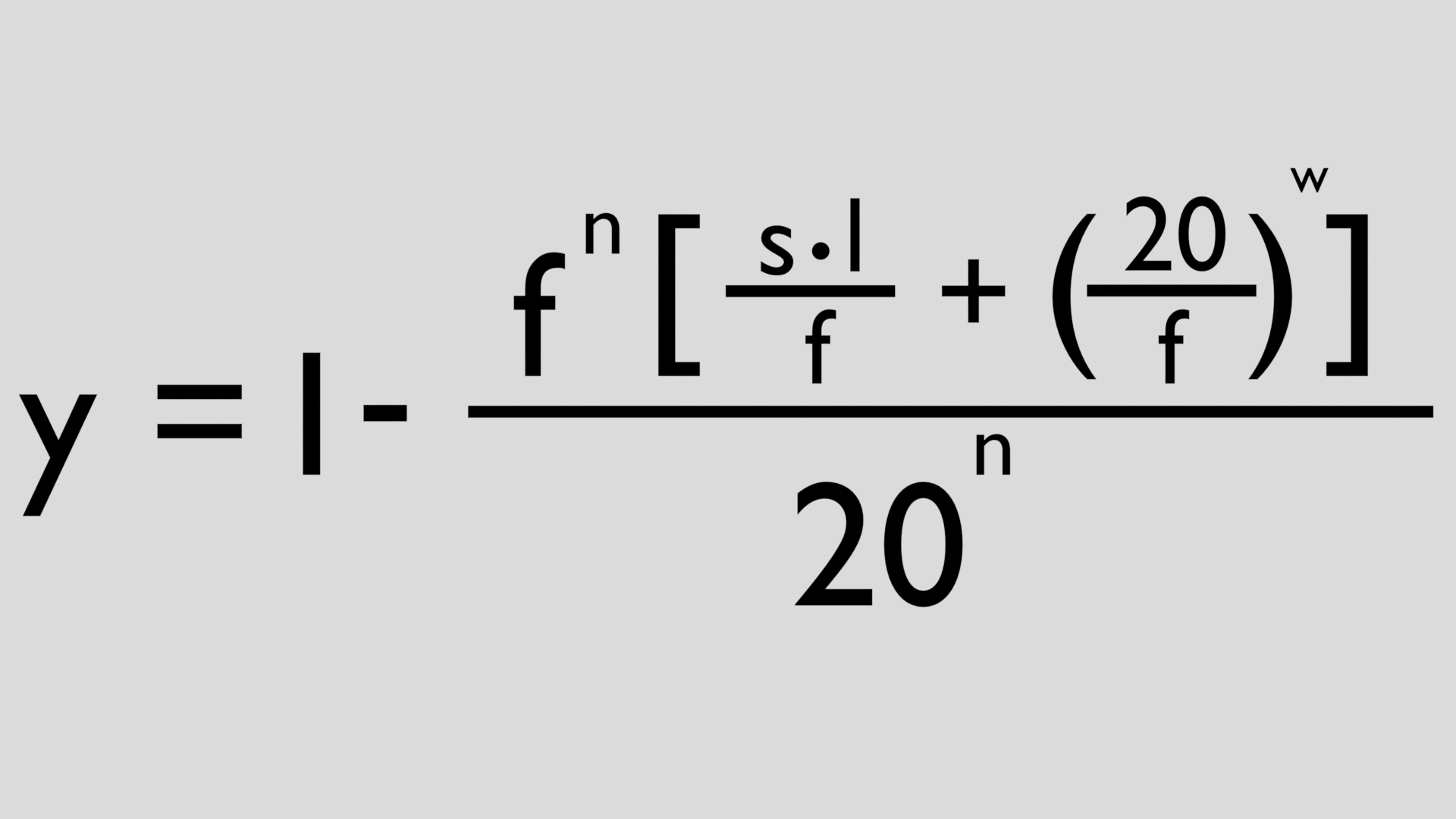 Она работает для двумерных поверхностей и говорит, что сумма интегралов по поверхности от гауссовой кривизны и интеграла по границе от геодезической кривизны не зависят от конкретной реализации поверхности, а определяются ее топологическим типом — эйлеровой характеристикой. Так, для сферы это означает, что интеграл от кривизны по сфере всегда равен 4π. Если мы шевелим сферу, мнем ее, то локально гауссова кривизна меняется. Но при этом интеграл остается неизменным. Несмотря на эти удивительные свойства, формулу тоже зачислили в обычные.

Формула Гаусса-Бонне

Спектральная теорема для ограниченного оператора

А вот это самая сложная формула в нашем списке. В линейной алгебре есть утверждение о том, что самосопряженный оператор на конечномерном пространстве для эрмитова скалярного произведения можно привести к диагональному виду. Представленная выше формула — по сути обобщение этого результата на случай ограниченных операторов на гильбертовом пространстве. Тех самых операторов, которые являются основой квантовой механики. Неудивительно, что и она показалась участникам исследования обычной.

Спектральная теорема для ограниченного оператора

Минимальное число такси

1729 — минимальное число такси. Свое название эти числа получили благодаря истории, которую британский математик Годфри Харди рассказывал про Сриниваса Рамануджана:

«Я помню, пришел раз навестить его, когда Рамануджан лежал в больнице в Питни. Я приехал на такси с номером 1729 и заметил в разговоре, что число скучное, но это, сказал я, надеюсь, не является неблагоприятным знаком. «Нет, — ответил Рамануджан, — число очень интересное, это наименьшее натуральное число, представимое в виде суммы кубов двумя различными способами!»

Соответственно, числами такси называются числа, которые можно представить в виде суммы двух кубов как минимум двумя разными способами. Количество таких чисел бесконечно.

Это формулу испытуемые отнесли к разряду некрасивых.

Минимальное число такси

Короткая точная последовательность

Эта формула — пример важной в алгебре концепции короткой точной последовательности. Здесь целые числа отображаются в целые числа с помощью умножения на два, а после этого все целые числа факторизуются по четным. В этой схеме образ одного отображения — вложения целых в виде четных — совпадает с ядром другого отображения — фактора по четным. И эту формулу испытуемые назвали некрасивой.

Короткая точная последовательность

Формула Рамануджана

И, наконец, формула для числа π, открытая Сринивасом Рамануджаном в 1914 году. Главное свойство этой формулы — быстрая сходимость. Ее испытуемые назвали самой некрасивой из всех.

Формула Рамануджана

Андрей Коняев

Сложные математические формулы.

Все формулы по математике

На этой странице собраны все формулы, необходимые для сдачи контрольных и самостоятельных работ, экзаменов по по алгебре, геометрии, тригонометрии, стереометрии и другим разделам математики.

Здесь вы можете скачать или посмотреть онлайн все основные тригонометрические формулы, формулу площади круга, формулы сокращенного умножения, формула длины окружности, формулы приведения и многие другие.

Можно так же распечатать необходимые сборники математических формул.

Успехов в учебе!

Формулы Арифметики:

Формулы Алгебры:

Геометрические Формулы:

Арифметические формулы:
Законы действий над числами
Переместительный закон сложения: a + b = b + a.
Сочетательный закон сложения: (a + b) + с = a + (b + c).
Переместительный закон умножения: ab = ba.
Сочетательный закон умножения: (ab)с = a(bc).
Распределительный закон умножения относительно сложения: (a + b)с = aс + bс.
Распределительный закон умножения относительно вычитания: (a — b)с = aс — bс.
Некоторые математические обозначения и сокращения:
Признаки делимости
Признаки делимости на «2»
Число, делящееся на «2» без остатка называется чётным , не делящееся – нечётным . Число делится на «2» без остатка, если его последняя цифра чётная (2, 4, 6, 8) или ноль
Признаки делимости на «4»
Число делится на «4» без остатка, если две последние его цифры нули или в сумме образуют число, делящееся без остатка на «4»
Признаки делимости на «8»
Число делится на «8» без остатка, если три последние его цифры нули или в сумме образуют число, делящееся без остатка на «8» (пример: 1 000 — три последние цифры «00», а при делении 1 000 на 8 получается 125; 104 — две последние цифры «12» делятся на 4, а при делении 112 на 4 получается 28; и. т.д.)
Признаки делимости на «3» и на «9»
Без остатка на «3» делятся только те числа, у которых сумма цифр делится без остатка на «3»; на «9» — только те, у которых сумма цифр делится без остатка на «9»
Признаки делимости на «5»
Без остатка на «5» делятся числа, последняя цифра которых «0» или «5»
Признаки делимости на «25»
Без остатка на «25» делятся числа, две последние цифры которых нули или в сумме образуют число, делящееся без остатка на «25» (т.е. числа, оканчивающиеся на «00», «25», «50», «75»
Признаки делимости на «10», «100» и на «1 000»
Без остатка на «10» делятся только те числа, последняя цифра которых ноль, на «100» — только те числа, у которых две последние цифры нули, на «1000» — только те числа, у которых три последние цифры нули
Признаки делимости на «11»
Без остатка на «11» делятся только те числа, у которых сумма цифр, занимающих нечётные места, либо равна сумме цифр, занимающих чётные места, либо отличается от неё на число, делящееся на «11»
Абсолютная величина — формулы ( модуль)
|a| ? 0, причём |a| = 0 только если a = 0; |-a|=|a| |a2|=|a|2=a2 |ab|=|a|*|b| |a/b|=|a|/|b|, причём b ? 0; |a+b|?|a|+|b| |a-b|?|a|-|b|
Формулы Действия с дробями
Формула обращения конечной десятичной дроби в рациональную дробь:
Пропорции
Два равных отношения образуют пропорцию :
Основное свойство пропорции
Нахождение членов пропорции Пропорции , равносильные пропорции : Производная пропорция — следствие данной пропорции в виде
Средние величины
Среднее арифметическое
Двух величин: n величин:
Среднее геометрическое (среднее пропорциональное)
Двух величин: n величин:
Среднее квадратичное
Двух величин: n величин:
Среднее гармоническое
Двух величин: n величин:
Некоторые конечные числовые ряды

Свойства числовых неравенств
1) Если a , то при любом c : a + с .
2) Если a и c > 0 , то aс .
3) Если a и c , то aс > bс .
4) Если a , a и b одного знака, то 1/a > 1/b .
5) Если a и c , то a + с , a — d .
6) Если a , c , a > 0 , b > 0 , c > 0 , d > 0 , то ac .
7) Если a , a > 0 , b > 0 , то
8) Если , то

Формулы Прогрессии:
Производная
Логарифмы:
Координаты и векторы
1. Расстояние между точками A1(x1;y1) и A2(x2;y2) находится по формуле:
2. Координаты (x;y) середины отрезка с концами A1(x1;y1) и A2(x2;y2) находится по формулам:
3. Уравнение прямой с угловым коэффициентом и начальной ординатой имеет вид:
Угловой коэффициент k представляет собой значение тангенса угла, образуемого прямой с положительным направлением оси Ox, а начальная ордината q – значение ординаты точки пересечения прямой с осью Oy.
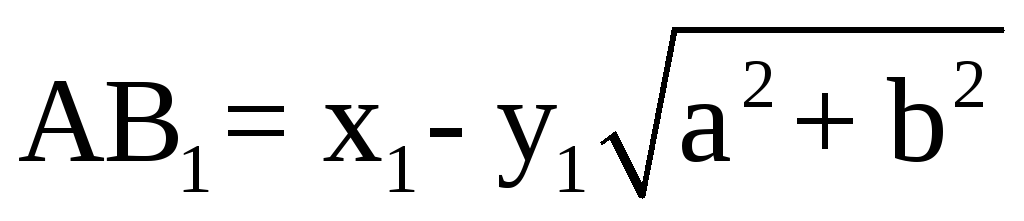
4. Общее уравнение прямой имеет вид: ax + by + c = 0.
5. Уравнения прямых, параллельных соответственно осям Oy и Ox, имеют вид:
Ax + by + c = 0.
6. Условия параллельности и перпендикулярности прямых y1=kx1+q1 и y2=kx2+q2 соответственно имеют вид:
7. Уравнения окружностей с радиусом R и с центром соответственно в точках O(0;0) и C(xo;yo) имеют вид:
8. Уравнение:
представляет собой уравнение параболы с вершиной в точке, абсцисса которой
Прямоугольная декартова система координат в пространстве
1. Расстояние между точками A1(x1;y1;z1) и A2(x2;y2;z2) находится по формуле:
2. Координаты (x;y;z) середины отрезка с концами A1(x1;y1;z1) и A2(x2;y2;z2) находятся по формулам:
3. Модуль вектора заданного своими координатами, находится по формуле:
4. При сложении векторов их соответствующие координаты складываются, а при умножении вектора на число все его координаты умножаются на это число, т.е. справедливы формулы:
5. Единичный вектор сонаправленный с вектором находится по формуле:
6. Скалярным произведением векторов называется число:
где — угол между векторами.
7. Скалярное произведение векторов
8. Косинус угла между векторами и находится по формуле:
9. Необходимое и достаточное условие перпендикулярности векторов и имеет вид:
10. Общее уравнение плоскости, перпендикулярной вектору имеет вид:
Ax + by + cz + d = 0.
11. Уравнение плоскости, перпендикулярной вектору и проходящей через точку (xo;yo;zo), имеет вид:
A(x — xo) + b(y — yo) + c(z — zo) = 0.
12. Уравнение сферы с центром O(0;0;0) записывается в виде.

Видеокурс «Получи пятерку» включает все темы, необходимые для успешной сдачи ЕГЭ по математике на 60-65 баллов. Полностью все задачи 1-13 Профильного ЕГЭ по математике. Подходит также для сдачи Базового ЕГЭ по математике. Если вы хотите сдать ЕГЭ на 90-100 баллов, вам надо решать часть 1 за 30 минут и без ошибок!

Курс подготовки к ЕГЭ для 10-11 класса, а также для преподавателей. Все необходимое, чтобы решить часть 1 ЕГЭ по математике (первые 12 задач) и задачу 13 (тригонометрия). А это более 70 баллов на ЕГЭ, и без них не обойтись ни стобалльнику, ни гуманитарию.

Вся необходимая теория. Быстрые способы решения, ловушки и секреты ЕГЭ. Разобраны все актуальные задания части 1 из Банка заданий ФИПИ. Курс полностью соответствует требованиям ЕГЭ-2018.

Курс содержит 5 больших тем, по 2,5 часа каждая. Каждая тема дается с нуля, просто и понятно.

Сотни заданий ЕГЭ. Текстовые задачи и теория вероятностей. Простые и легко запоминаемые алгоритмы решения задач. Геометрия. Теория, справочный материал, разбор всех типов заданий ЕГЭ. Стереометрия. Хитрые приемы решения, полезные шпаргалки, развитие пространственного воображения. Тригонометрия с нуля — до задачи 13. Понимание вместо зубрежки. Наглядное объяснение сложных понятий. Алгебра. Корни, степени и логарифмы, функция и производная. База для решения сложных задач 2 части ЕГЭ.

Математик Анри Пуанкаре в книге «Наука и метод» писал: «Если бы природа не была прекрасна, она не стоила бы того, чтобы ее знать, жизнь не стоила бы того, чтобы ее переживать. Я здесь говорю, конечно, не о той красоте, которая бросается в глаза… Я имею в виду ту более глубокую красоту, которая открывается в гармонии частей, которая постигается только разумом. Это она создает почву, создает каркас для игры видимых красок, ласкающих наши чувства, и без этой поддержки красота мимолетных впечатлений была бы несовершенна как все неотчетливое и преходящее. Напротив красота интеллектуальная дает удовлетворение сама по себе».

Семь лет назад украинский физик (и художник) Наталия Кондратьева обратилась к ряду ведущих математиков мира с вопросом: «Какие три математические формулы, на ваш взгляд, самые красивые?»
В беседе о красоте математических формул приняли участие сэр Михаэль Атья и Дэвид Элварси из Британии, Яков Синай и Александр Кириллов из США, Фридрих Херцебрух и Юрий Манин из Германии, Давид Рюэль из Франции, Анатолий Вершик и Роберт Минлос из России и другие математики из разных стран. Из украинцев в дискуссии приняли участие академики НАНУ Владимир Королюк и Анатолий Скороход. Часть полученных таким образом материалов и легла в основу изданной Натальей Кондратьевой научной работы «Три самые красивые математические формулы».
— Какую цель вы ставили, обращаясь к математикам с вопросом о красивых формулах?
— Каждое новое столетие приносит обновление научной парадигмы. В самом начале века с ощущением, что мы стоим у порога новой науки, ее новой роли в жизни человеческого общества, я обратилась к математикам с вопросом о красоте идей, стоящих за математическими символами, т.е. о красоте математических формул.
Уже сейчас можно отметить некоторые особенности новой науки. Если в науке ХХ века очень важную роль играла «дружба» математики с физикой, то сейчас математика эффективно сотрудничает с биологией, генетикой, социологией, экономикой… Следовательно, наука будет исследовать соответствия. Математические структуры будут исследовать соответствия между взаимодействиями элементов различных областей и планов. И многое, что раньше мы воспринимали на веру как философские констатации, будет утверждено наукой как конкретное знание.
Этот процесс начался уже в ХХ веке. Так, Колмогоров математически показал, что случайности нет, а есть очень большая сложность. Фрактальная геометрия подтвердила принцип единства в многообразии и т.д.
— Какие же формулы были названы самыми красивыми?
— Сразу скажу, что цели устроить конкурс формулам не было. В своем письме к математикам я писала: «Люди, которые хотят понять, какими законами управляется мир, становятся на путь отыскания гармонии мира. Путь этот уходит в бесконечность (ибо движение вечно), но люди всё равно идут им, т.к. есть особая радость встретить очередную идею или представление. Из ответов на вопрос о красивых формулах, возможно, удастся синтезировать новую грань красоты мира. Кроме того, эта работа может оказаться полезной для будущих ученых как мысль о великой гармонии мира и математики как способе отыскания этой красоты».
Тем не менее среди формул оказались явные фавориты: формула Пифагора и формула Эйлера.
Вслед за ними расположились скорее физические, чем математические формулы, которые в ХХ веке изменили наше преставление о мире, —Максвелла, Шредингера, Эйнштейна.
Также в число самых красивых попали формулы, которые еще находятся на стадии дискуссии, такие, например, как уравнения физического вакуума. Назывались и другие красивые математические формулы.
— Как вы думаете, почему на рубеже второго и третьего тысячелетий формула Пифагора названа одной из самых красивых?
— Во времена Пифагора эта формула воспринималась как выражение принципа космической эволюции: два противоположных начала (два квадрата, соприкасающихся ортогонально) порождают третье, равное их сумме. Можно дать геометрически очень красивые интерпретации.
Возможно, существует какая-то подсознательная, генетическая память о тех временах, когда понятие «математика» означало — «наука», и в синтезе изучались арифметика, живопись, музыка, философия.
Рафаил Хасминский в своем письме написал, что в школе он был поражен красотой формулы Пифагора, что это во многом определило его судьбу как математика.
— А что можно сказать о формуле Эйлера?
— Некоторые математики обращали внимание, что в ней «собрались все», т.е. все самые замечательные математические числа, и единица таит в себе бесконечности! — это имеет глубокий философский смысл.
Недаром эту формулу открыл Эйлер. Великий математик много сделал, чтобы ввести красоту в науку, он даже ввел в математику понятие «градус красоты». Вернее, он ввел это понятие в теорию музыки, которую считал частью математики.
Эйлер полагал, что эстетическое чувство можно развивать и что это чувство необходимо ученому.
Сошлюсь на авторитеты… Гротендик: «Понимание той или иной вещи в математике настолько совершенно, насколько возможно прочувствовать ее красоту».
Пуанкаре: «В математике налицо чувство». Он сравнивал эстетическое чувство в математике с фильтром, который из множества вариантов решения выбирает наиболее гармоничный, который, как правило, и есть верный. Красота и гармония — синонимы, а высшее проявление гармонии есть мировой закон Равновесия. Математика исследует этот закон на разных планах бытия и в разных аспектах. Недаром каждая математическая формула содержит знак равенства.
Думаю, что высшая человеческая гармония есть гармония мысли и чувства. Может быть, поэтому Эйнштейн сказал, что писатель Достоевский дал ему больше, чем математик Гаусс.
Формулу Достоевского «Красота спасет мир» я взяла в качестве эпиграфа к работе о красоте в математике. И он также обсуждался математиками.
— И они согласились с этим утверждением?
— Математики не утверждали и не опровергали этого утверждения. Они его уточнили: «Осознание красоты спасет мир». Здесь сразу вспомнилась работа Юджина Вигнера о роли сознания в квантовых измерениях, написанная им почти пятьдесят лет назад. В этой работе Вигнер показал, что человеческое сознание влияет на окружающую среду, т.е., что мы не только получаем информацию извне, но и посылаем наши мысли и чувства в ответ. Эта работа до сих пор актуальна и имеет как своих сторонников, так и противников. Я очень надеюсь, что в ХХI веке наука докажет: осознание красоты способствует гармонизации нашего мира.

1. Формула Эйлера. Многие видели в этой формуле символ единства всей математики, ибо в ней «-1 представляет арифметику, i — алгебру, π — геометрию и e — анализ».

2. Это простое равенство показывает, величина 0,999 (и так до бесконечности) эквивалентна единице. Многие люди не верят, что это может быть правдой, хотя существует несколько доказательств, основанных на теории пределов. Тем не менее, равенство показывает принцип бесконечности.

3. Это уравнение было сформулировано Эйнштейном в рамках новаторской общей теории относительности в 1915 году. Правая часть этого уравнения описывает энергию, содержащуюся в нашей Вселенной (в том числе» темную энергию»). Левая сторона описывает геометрию пространства-времени. Равенство отражает тот факт, что в общей теории относительности Эйнштейна, масса и энергия определяют геометрию, и одновременно кривизну, которая является проявлением гравитации. Эйнштейн говорил, что левая часть уравнений тяготения в общей теории относительности, содержащая гравитационное поле, красива и как будто вырезана из мрамора, в то время как правая часть уравнений, описывающая материю, всё ещё уродлива, будто сделана из обыкновенной деревяшки.

4. Еще одна доминирующая теория физики — Стандартная модель — описывает электромагнитное, слабое и сильное взаимодействие всех элементарных частиц. Некоторые физики считают, что она отображает все процессы, происходящие во Вселенной, кроме темной материи, темной энергии и не включает в себя гравитацию. В Стандартную модель вписывается и неуловимый до прошлого года бозон Хиггса, хотя не все специалисты уверены в его существовании.

5. Теорема Пифагора — одна из основополагающих теорем евклидовой геометрии, устанавливающая соотношение между сторонами прямоугольного треугольника. Ее мы помним еще со школы и считаем, что автор теоремы — Пифагор. На самом деле этой формулой пользовались еще в Древнем Египте при строительстве пирамид.

6. Теорема Эйлера. Эта теорема заложила фундамент нового раздела математики — топологии. Уравнение устанавливает связь между числом вершин, ребер и граней для многогранников, топологически эквивалентных сфере.

7. Специальная теория относительности описывает движение, законы механики и пространственно-временные отношения при произвольных скоростях движения, меньших скорости света в вакууме, в том числе близких к скорости света. Эйнштейн составил формулу, которая описывает, что время и пространство не являются абсолютными понятиями, а скорее являются относительными в зависимости от скорости наблюдателя. Уравнение показывает, как расширяется или замедляется время в зависимости от того, как и куда движется человек.

8. Уравнение было получено в 1750-х годах Эйлером и Лагранжем при решении задачи об изохроне. Это проблема определения кривой, по которой тяжелая частица попадает в фиксированную точку за фиксированное время, независимо от начальной точки. В общих словах, если ваша система имеет симметрию, есть соответствующий закон сохранения симметрии.

9. Уравнение Каллана — Симанзика. Оно представляет собой дифференциальное уравнение, описывающее эволюцию н-корреляционной функции при изменении масштаба энергий, при которых теория определена и включает в себя бета-функции теории и аномальные размерности. Это уравнение помогло лучше понять квантовую физику.

10. Уравнение минимальной поверхности. Это равенство объясняет формирование мыльных пузырей.

11. Прямая Эйлера. Теорема Эйлера была доказана в 1765 году. Он обнаружил, что середины сторон треугольника и основания его высот лежат на одной окружности.

12. В 1928 году П.А.М. Дирак предложил свой вариант уравнения Шредингера — которое соответствовало теории А. Эйнштейна. Учёный мир был потрясён — Дирак открыл своё уравнение для электрона путём чисто математических манипуляций с высшими математическими объектами, известными как спиноры. И это было сенсацией — до сих пор все великие открытия в физике должны стоять на прочной базе экспериментальных данных. Но Дирак считал, что чистая математика, если она достаточно красива, является надёжным критерием правильности выводов. «Красота уравнений важнее, чем их соответствие экспериментальным данным. … Представляется, что если стремишься получить в уравнениях красоту и обладаешь здоровой интуицией, то ты на верном пути». Именно благодаря его выкладкам был открыт позитрон — антиэлектрон, и предсказал наличие у электрона «спина» — вращения элементарной частицы.

13. Дж. Максвелл получил удивительные уравнения, объединившие все явления электричества, магнетизма и оптики. Замечательный немецкий физик, один из создателей статистической физики, Людвиг Больцман, сказал об уравнениях Максвелла: «Не Бог ли начертал эти письмена?»

14. Уравнение Шредингера.Уравнение, описывающее изменение в пространстве и во времени чистого состояния, задаваемого волновой функцией, в гамильтоновых квантовых системах. Играет в квантовой механике такую же важную роль, как уравнение второго закона Ньютона в классической механике.

На данной странице Вы можете посмотреть или бесплатно скачать самые востребованные математические формулы, таблицы ,а также справочные материалы по высшей математике. Все математические таблицы составлены лично мной и снабжены дополнительными комментариями. Сделано это в целях преодоления трудностей, с которыми часто сталкиваются студенты-заочники в ходе решения задач. Я не претендую на всеобъемлющую полноту материалов, но то, что ОЧЕНЬ ЧАСТО встречается, Вы найдете.

Рассмотрим, например, таблицу тригонометрических формул. Тригонометрических формул достаточно много, они давно известны, и нет никакого смысла переписывать справочники. А вот те формулы, которые очень часто используются для решения задач курса высшей математики, собраны воедино, и могут быть очень полезны при выполнении практических заданий. При этом в комментариях я указываю, в каком разделе высшей математики (пределы, производные, интегралы, и т.д.) практически всегда фигурирует та или иная формула.

Итак, прямо сейчас у Вас есть бесплатный доступ к ценным справочным материалам, возможен, как онлайн просмотр, так и скачивание. Удобнее всего сразу распечатать математические таблицы и справочные материалы, которые Вас заинтересуют. Как показывает практика, информация на экране монитора усваивается хуже, чем на бумаге, да и читать с монитора труднее.

Почти все файлы размещены прямо на сайте, а значит, могут быть получены в максимально короткий срок, ограниченный только скоростью Вашего Интернет-подключения.

! В случае некорректного отображения pdf используйте следующие рекомендации

Рекомендую просмотреть всем. Данные формулы встречаются в ходе решения задач по высшей математике буквально на каждом шагу. Без знания этих формул – никуда. С чего начать изучение высшей математики? С повторения этого. Независимо от уровня Вашей математической подготовки на данный момент, крайне желательно СРАЗУ ВИДЕТЬ возможность выполнения элементарных действий, применения простейших формул в ходе решения пределов, интегралов, дифференциальных уравнений и т.д.

В справочнике есть краткая информация о модуле, формулы сокращенного умножения, алгоритм решения квадратного уравнения, правила упрощения многоэтажных дробей, а также важнейшие свойства степеней и логарифмов.

Приведены самые «ходовые» тригонометрические формулы, которые применяются в ходе решения задач по высшей математике. На самом деле таких формул НЕМНОГО, и, собирать десятки других по различным математическим справочникам – пустая трата времени. Всё (или почти всё), что может потребоваться – здесь.

При выполнении заданий по математике нередко возникает необходимость заглянуть в тригонометрические таблицы. В данном справочном материале представлена таблица значений тригонометрических функций (синуса, косинуса, тангенса и котангенса) при значениях аргумента от нуля до 360 градусов. Держать в памяти данную информацию нет никакого смысла, но некоторые значения тригонометрических функций хорошо бы знать . Также представлены формулы приведения для вышеуказанных тригонометрических функций, иногда (чаще всего при решении пределов) требуются. По просьбам посетителей сайта в pdf-файл добавлена таблица значений обратных тригонометрических функций и две формулы: формула перевода градусов в радианы, формула перевода радианов в градусы.

Методический материал представляет собой обзор графиков основных элементарных функций и их свойств. Будет полезен при изучении практически всех разделов высшей математики, более того, справочное пособие поможет вам намного лучше и качественнее разобраться в некоторых темах. Также вы сможете узнать, какие значения функций следует знать наизусть , чтобы не получить «два автоматом» при ответе на простейший вопрос экзаменатора. Справка выполнена в форме веб страницы и содержит много графиков функций, которые также желательно помнить. По мере развития проекта методичка стала играть роль вводного урока по теме «Функции и графики».

На практике у студентов-заочников практически всегда возникает необходимость использовать первый и второй замечательные пределы, о которых и идет речь в данной справке. Также рассмотрены еще три замечательных предела, которые встречаются значительно реже. Все замечательные пределы снабжены дополнительными важными комментариями. Кроме того, файл дополнен информацией о замечательных эквивалентностях.

В справке приведены правила дифференцирования и таблица производных от основных элементарных функций. Таблица снабжена очень важными примечаниями.

Ваш гид по разделу «Функции и графики». В pdf-ке систематизирована и законспектирована информация об основных этапах исследования функции одной переменной. Руководство сопровождается ссылками, а значит, экономит массу времени. Мануал полезен как чайнику, так и подготовленному читателю.

В общем-то, почти то же самое, что в дифференциальном исчислении. Правила интегрирования и таблица интегралов с моими комментариями.

Справочный материал незаменим при изучении степенных рядов. В таблице представлены разложения в степенной ряд следующих функций: экспоненты, синуса, косинуса, логарифма, арктангенса и арксинуса. Также приведено биномиальное разложение и наиболее распространенные частные случаи биномиального разложения. Разложение функции в ряд является самостоятельным заданием, используется для приближенных вычислений, приближенных вычислений определенного интеграла и в некоторых других задачах.

Основной трудностью при решении неоднородных дифференциальных уравнений второго порядка с постоянными коэффициентами является правильный подбор частного решения по виду правой части. Данная методичка, относится, прежде всего, к уроку Как решить неоднородное уравнение второго порядка? и поможет вам легко разобраться в подборе частного решения. Справка не претендует на основательную научную полноту, она написана простым и понятным языком, однако в 99,99% случаев в ней найдется именно тот случай, который вы ищете.

Справка незаменима в ходе решения прикладных задач комплексного анализа – нахождения частного решения ДУ операционным методом и нахождения частного решения системы ДУ этим же способом. Таблица отличается от аналогов тем, что «заточена» именно под вышеуказанные задания, данная особенность позволяет легко освоить алгоритмы решения. Приведено как прямое, так и обратное преобразование Лапласа для наиболее распространенных функций. В случае если информации окажется недостаточно, рекомендую обратиться к солидному математическому справочнику – полная версия содержит более сотни пунктов.

В справочном материале приведены формулы факториала, количества перестановок, сочетаний, размещений (с повторениями и без повторений), а также содержательные комментарии к каждой формуле, позволяющие понять их суть. + Правила сложения и умножения комбинаций. Кроме того, в pdf-ке есть краткая информация о биноме Ньютона и треугольнике Паскаля с примерами их практического использования.

Файл содержит перечень формул с краткими комментариями по обеим главам тервера – Случайные события и Случайные величины , в том числе приведены формулы и числовые характеристики распространённых дискретных и непрерывных распределений. Справка систематизирует материал и очень удобна для выполнения практических заданий, заглядываем и сразу находим то, что нужно!

Специальные расчётные программы:

В данном разделе вы можете найти вспомогательные программы для решения широких и узколокальных математических задач. Они помогут вам быстро выполнить расчёты и оформить решение.

Универсальный калькулятор реализован в рабочей книге MS Excel, которая содержит три листа. Программа может заменить обычный калькулятор с множеством функций. Любые степени, корни, логарифмы, тригонометрические функции, арки – без проблем! Кроме того, калькулятор в автоматическом режиме выполняет основные действия с матрицами , считает определители (до определителя 5 на 5 включительно), мгновенно находит миноры и алгебраические дополнения матриц. За считанные секунды можно решить систему линейных уравнений с помощью обратной матрицы и по формулам Крамера , посмотреть основные этапы решения. Всё это очень удобно для самопроверки. Просто введите свои числа и получите готовый результат!

Данная полуавтоматическая программа относится к уроку Формула трапеций, формула Симпсона и помогает рассчитать приближенное значение определенного интеграла на 2, 4, 8, 10 и 20 отрезках разбиения. Прилагается видеоурок по работе с калькулятором. Вычислите ваш определенный интеграл в считанные минуты, и даже секунды!

На данный момент пока всё.

Раздел постепенно пополняется дополнительными материалами и полезными программами. Каждое справочное пособие неоднократно редактировалось и улучшалось, в том числе, с учетом ваших пожеланий и замечаний! Если Вы считаете, что упущено что-то важное, нашли какие-либо неточности, а может быть что-то разъяснено недостаточно понятно, обязательно пишите !

С уважением, Емелин Александр

OCR для математических формул — CodeRoad

Я планирую создать программу для генерации отработанных решений задач в учебнике математики, используя OCR для передачи уравнений в Wolfram Alpha, а затем отображая оттуда решения step-by-step. Уравнения не будут слишком сложными

Мне интересно, есть ли подходящая программа OCR (предпочтительно FOSS) или API, которая сможет справиться с этими уравнениями.

ocr
Поделиться Источник Aaron 20 октября 2017 в 05:34
2 ответа
javascript редактор математических формул?
Любой редактор математических формул с открытым исходным кодом javascript можно порекомендовать? Я хочу добавить редактор математических формул на свой веб-сайт, чтобы, когда люди отправляют сообщение с помощью текстового поля, они могли вставить соответствующую математическую формулу. BTW: я…
C++ встраивание математических формул
Я хотел бы знать лучшие практики документирования математических формул в коде C++. В идеале было бы идеально иметь возможность писать уравнения непосредственно в комментарии, но невозможно написать их в удобочитаемой форме. Я посмотрел на LaTex, MathML, и синтаксис сложен при работе со многими…

1

Пожалуйста, обратите внимание на Mathpix ( https://mathpix.com/api.html ). отказ от ответственности: я являюсь основателем Mathpix!
Поделиться nicodjimenez 01 июля 2018 в 07:26
Поделиться rmhrisk 20 октября 2017 в 05:39
Похожие вопросы:

Рендеринг математических формул на чтения компакт-дисков
Есть ли какая-либо поддержка рендеринга/отображения математических формул под iOS? Я предполагаю, что в самом OS нет ничего встроенного, поэтому решение, которое является free-as-in-beer и не…

Рендеринг Математических Формул
Каков был бы наилучший подход к реализации рендеринга математических формул в приложении Cocoa? В комплект поставки MacOS X входит утилита Grapher , которая делает это именно так, как мне нужно (…

OCR lib для математических формул
Мне нужна открытая библиотека OCR, которая способна сканировать сложные печатные математические формулы (например, некоторые формулы, которые были сгенерированы через LaTeX). Я хочу получить…

javascript редактор математических формул?
Любой редактор математических формул с открытым исходным кодом javascript можно порекомендовать? Я хочу добавить редактор математических формул на свой веб-сайт, чтобы, когда люди отправляют…

C++ встраивание математических формул
Я хотел бы знать лучшие практики документирования математических формул в коде C++. В идеале было бы идеально иметь возможность писать уравнения непосредственно в комментарии, но невозможно написать…

Изменение размера шрифта математических формул в RPres
Как я могу изменить размер шрифта математических формул в Rpres? [Примечание редактора: ‘Rpres’-это расширение файла, используемое RStudio для его файлов Presentation. По-видимому, он был принят…

Android studio, создание приложения листа математических формул
Так что я все еще тихий новичок, когда дело доходит до программирования, но мне было любопытно, что было бы лучшей практикой для создания листа формул. Конечно, это будут просто прямые слова, буквы…

добавление плагина математических формул в ckeditor
В настоящее время я делаю приложение для викторины с rails в этом мое требование состоит в том, чтобы иметь богатый текстовый редактор, такой как ckeditor с обработкой файлов и возможностями ввода…

отображение математических формул без webview
Я пишу приложение android, где мне нужно много математических формул. Я искал, как отобразить математические формулы на android, но все возможности, которые я нашел, используют расширение webView,…

сравнение математических формул
Я столкнулся с небольшой проблемой разбора и сравнения математических формул. Предположим, что у нас есть следующие 3 формулы: 2*a+b*c j*i+e+e x+(y*z)+x Мы согласны, что 3 формулы равны. Как мы…
2, завоевавшие большую часть общественной славы, многие менее известные формулы имеют своих чемпионов среди ученых. LiveScience попросил физиков, астрономов и математиков рассказать об их любимых уравнениях; вот что мы обнаружили:
Общая теория относительности
(Изображение предоставлено Shutterstock / RT Wohlstadter)
Уравнение, приведенное выше, было сформулировано Эйнштейном в 1915 году в рамках его новаторской общей теории относительности. сила как искривление ткани пространства и времени.
«Мне до сих пор удивительно, что одно такое математическое уравнение может описать, что такое пространство-время», — сказал астрофизик Института космического телескопа Марио Ливио, который назвал это уравнение своим любимым. «В этом уравнении воплощен весь истинный гений Эйнштейна». [Викторина Эйнштейна: проверьте свои знания о гении]
«Правая часть этого уравнения описывает энергетический состав нашей Вселенной (включая« темную энергию », которая движет текущим космическим ускорением)», — объяснил Ливио.«Левая часть описывает геометрию пространства-времени. Равенство отражает тот факт, что в общей теории относительности Эйнштейна масса и энергия определяют геометрию и, соответственно, кривизну, которая является проявлением того, что мы называем гравитацией». [6 странных фактов о гравитации]
«Это очень элегантное уравнение», — сказал Кайл Кранмер, физик из Нью-Йоркского университета, добавив, что уравнение раскрывает взаимосвязь между пространством-временем, материей и энергией. «Это уравнение говорит вам, как они связаны — как присутствие Солнца искажает пространство-время, так что Земля движется вокруг него по орбите и т. Д.В нем также рассказывается, как эволюционировала Вселенная после Большого взрыва, и предсказывается, что там должны быть черные дыры ».
Стандартная модель
(Изображение предоставлено Shutterstock / RT Wohlstadter)
Еще одна господствующая теория физики, стандартная модель описывает набор фундаментальных частиц, которые, как в настоящее время считается, составляют нашу Вселенную.
Теория может быть заключена в главное уравнение, называемое стандартным модельным лагранжианом (названное в честь французского математика и астронома 18-го века Жозефа Луи Лагранжа), которое было выбрано физик-теоретик Лэнс Диксон из Национальной ускорительной лаборатории SLAC в Калифорнии в качестве своей любимой формулы.
«Он успешно описал все элементарные частицы и силы, которые мы наблюдали в лаборатории на сегодняшний день, за исключением гравитации», — сказал Диксон LiveScience. «Сюда входит, конечно, недавно открытый (подобный) бозон Хиггса, фи в формуле. Это полностью самосогласовано с квантовой механикой и специальной теорией относительности».
Однако стандартная теория моделей еще не объединена с общей теорией относительности, поэтому она не может описывать гравитацию. [Инфографика: объяснение стандартной модели]
Calculus
(Изображение предоставлено Shutterstock / agsandrew)
Хотя первые два уравнения описывают определенные аспекты нашей Вселенной, другое любимое уравнение можно применить ко всем ситуациям.Фундаментальная теорема исчисления составляет основу математического метода, известного как исчисление, и связывает две его основные идеи: понятие интеграла и понятие производной.
«Простыми словами, [он] говорит, что чистое изменение плавной и непрерывной величины, такой как пройденное расстояние, за данный интервал времени (т. Е. Разница в значениях величины в конечные моменты времени интервал) равен интегралу скорости изменения этой величины, т.е.е. интеграл скорости «, — сказала Мелкана Бракалова-Тревитик, заведующая математическим факультетом Фордхэмского университета, которая выбрала это уравнение в качестве своего любимого.» Фундаментальная теорема исчисления (FTC) позволяет нам определить чистое изменение за интервал на основе от скорости изменения в течение всего интервала ».
Зародыши исчисления зародились в древние времена, но большая часть их была собрана в 17 веке Исааком Ньютоном, который использовал расчеты для описания движения планет вокруг Солнца. .
Теорема Пифагора
(Изображение предоставлено Shutterstock / igor. 2
«Самым первым математическим фактом, который меня поразил, была теорема Пифагора, — сказала математик Дайна Таймина из Корнельского университета.«Я тогда был ребенком, и мне казалось таким удивительным, что это работает с геометрией и с числами!» [5 серьезных математических фактов]
1 = 0,999999999….
(Изображение предоставлено: Shutterstock / Турсунбаев Руслан)
Это простое уравнение, которое утверждает, что величина 0,999, за которой следует бесконечная строка девяток, эквивалентна единице, является любимым математиком Стивена Строгаца из Корнельского университета.
«Мне нравится, насколько это просто — все понимают, что в нем говорится, — но насколько это провокационно», — сказал Строгац.«Многие люди не верят, что это может быть правдой. Это также прекрасно сбалансировано. Левая сторона представляет собой начало математики; правая часть представляет тайны бесконечности».
Специальная теория относительности
(Изображение предоставлено Shutterstock / optimarc)
Эйнштейн снова попадает в список со своими формулами специальной теории относительности, которые описывают, что время и пространство не являются абсолютными понятиями, а скорее являются относительными в зависимости от скорости движения. наблюдатель. Приведенное выше уравнение показывает, как время расширяется или замедляется по мере того, как человек движется в любом направлении.
«Дело в том, что это действительно очень просто», — сказал Билл Мюррей, физик элементарных частиц из лаборатории CERN в Женеве. «Там нет ничего, что не мог бы сделать ученик A-level, никаких сложных производных и следовых алгебр. Но то, что он воплощает, — это совершенно новый взгляд на мир, целостное отношение к реальности и наше отношение к ней. неизменный космос сметается и заменяется личным миром, связанным с тем, что вы наблюдаете.Вы переходите от того, чтобы быть вне вселенной, глядя вниз, к одному из компонентов внутри нее.Но концепции и математику может усвоить любой, кто захочет ».
Мюррей сказал, что предпочитает специальные уравнения относительности более сложным формулам более поздней теории Эйнштейна.« Я никогда не смогу следовать математике общей теории относительности », — сказал он. .
Уравнение Эйлера
(Изображение предоставлено: Shutterstock / Jezper)
Эта простая формула инкапсулирует нечто чистое о природе сфер:
«Это говорит о том, что если вы разрежете поверхность сферы на грани, края и вершины и пусть F будет числом граней, E числом ребер и V числом вершин, вы всегда получите V — E + F = 2 «, — сказал Колин Адамс, математик из колледжа Уильямс в Массачусетсе.
«Возьмем, к примеру, тетраэдр, состоящий из четырех треугольников, шести ребер и четырех вершин», — пояснил Адамс. «Если вы сильно дунете в тетраэдр с гибкими гранями, вы можете округлить его до сферы, так что в этом смысле сферу можно разрезать на четыре грани, шесть ребер и четыре вершины. И мы видим, что V — E + F = 2. То же самое верно для пирамиды с пятью гранями — четырьмя треугольными и одним квадратом — восемью ребрами и пятью вершинами »и любой другой комбинацией граней, ребер и вершин.
«Очень крутой факт! Комбинаторика вершин, ребер и граней улавливает кое-что очень фундаментальное о форме сферы», — сказал Адамс.
Уравнения Эйлера-Лагранжа и теорема Нётер
(Изображение предоставлено Shutterstock / Марк Пинтер)
«Это довольно абстрактные, но удивительно мощные», — сказал Кранмер из Нью-Йоркского университета. «Круто то, что этот способ мышления о физике пережил несколько крупных революций в физике, таких как квантовая механика, теория относительности и т. Д.«
Здесь L обозначает лагранжиан, который является мерой энергии в физической системе, такой как пружины, рычаги или фундаментальные частицы.« Решение этого уравнения показывает, как система будет развиваться со временем », — сказал Кранмер.
Побочный результат уравнения Лагранжа называется теоремой Нётер в честь немецкого математика 20 века Эмми Нётер. «Эта теорема действительно фундаментальна для физики и роли симметрии», — сказал Кранмер. обладает симметрией, то существует соответствующий закон сохранения.Например, идея о том, что фундаментальные законы физики сегодня такие же, как и завтра (временная симметрия), подразумевает сохранение энергии. Идея о том, что законы физики здесь такие же, как и в космическом пространстве, подразумевает, что импульс сохраняется. Симметрия, возможно, является движущей концепцией фундаментальной физики, в первую очередь благодаря вкладу [Нётер] ».
Уравнение Каллана-Симанзика
(Изображение предоставлено: Shutterstock / RT Wohlstadter)
« Уравнение Каллана-Симанзика является жизненно важным первым. «Уравнение принципов 1970 года, необходимое для описания того, как наивные ожидания терпят неудачу в квантовом мире», — сказал физик-теоретик Мэтт Страсслер из Университета Рутгерса.
Уравнение имеет множество приложений, в том числе позволяет физикам оценивать массу и размер протона и нейтрона, составляющих ядра атомов.
Основы физики говорят нам, что гравитационная и электрическая сила между двумя объектами пропорциональна обратному квадрату расстояния между ними. На простом уровне то же самое верно и для сильного ядерного взаимодействия, которое связывает протоны и нейтроны вместе, чтобы сформировать ядра атомов, и которое связывает кварки вместе, чтобы сформировать протоны и нейтроны.Однако крошечные квантовые флуктуации могут немного изменить зависимость силы от расстояния, что имеет драматические последствия для сильного ядерного взаимодействия.
«Это предотвращает уменьшение этой силы на больших расстояниях, заставляет ее захватывать кварки и объединять их, чтобы сформировать протоны и нейтроны нашего мира», — сказал Штрасслер. «Уравнение Каллана-Симанзика связывает этот драматический и трудно поддающийся расчету эффект, важный, когда [расстояние] примерно равно размеру протона, с более тонкими, но более простыми для расчета эффектами, которые можно измерить, когда [ расстояние] намного меньше протона.«
Уравнение минимальной поверхности
(Изображение предоставлено Shutterstock / MarcelClemens)
« Уравнение минимальной поверхности каким-то образом кодирует красивые мыльные пленки, которые образуются на границах проводов, когда вы погружаете их в мыльную воду », — сказал математик Фрэнк Морган из Williams. Колледж. «Тот факт, что уравнение является» нелинейным «, включающим степени и произведения производных, является закодированным математическим намеком на удивительное поведение мыльных пленок. Это контрастирует с более знакомыми линейными уравнениями в частных производных, такими как уравнение теплопроводности, волновое уравнение и уравнение Шредингера квантовой физики.2-2bc cos A` Формула Герона `A = sqrt (s (sa) (sb) (sc))`
`s = (a + b + c) / 2` Точные значения` sin (pi / 6) = 1/2` `cos (pi / 6) = sqrt (3) / 2`` tan (pi / 6) = sqrt (3) / 3` `sin (pi / 4) = sqrt (2) / 2` `cos (pi / 4) = sqrt (2) / 2`` tan (pi / 4) = 1` `sin (pi / 3 ) = sqrt (3) / 2` `cos (pi / 3) = 1 / 2`` tan (pi / 3) = sqrt (3) ` Угловые отношения` sin (- альфа) = — sin alpha` `cos (- alpha) = cos alpha`` tan (-alpha) = — tan alpha` `sin (pi — alpha) = sin alpha`` cos (pi — alpha) = — cos alpha` `tan (pi — alpha) = — tan alpha`` sin (pi + alpha) = — sin alpha` `cos (pi + alpha) = -cos alpha` `tan (pi + alpha) = tan alpha`` sin (pi / 2 — alpha) = cos alpha` `cos (pi / 2 — al pha) = sin alpha` `tan (pi / 2 — alpha) = 1 / (tan alpha)` `sin (pi / 2 + alpha) = cos alpha`` cos (pi / 2 + альфа) = — sin alpha` `tan (pi / 2 + alpha) = — 1 / (tan alpha)` `sin ((3pi) / 2 — alpha) = — cos alpha` `cos ((3pi) / 2 — alpha) = — sin alpha`` tan ((3pi) / 2 — alpha) = 1 / (tan alpha) `` sin ((3pi) / 2 + альфа) = — cos alpha` `cos ((3pi) / 2 + alpha) = sin alpha`` tan ((3pi) / 2 + alpha) = — 1 / (tan alpha) ` Тригонометрические уравнения `sin x = sin alpha hArr x = alpha + 2kpi vv x = pi — alpha + 2kpi, k in ZZ` `cos x = cos alpha hArr x = alpha + 2kpi vv x = — alpha + 2kpi, k в ZZ `` tan x = tan alpha hArr x = alpha + kpi, k in ZZ ` Sum Formulas` sin (a + b) = sin a xx cos b + sin b xx cos a` `cos (a + b) = cos a xx cos b — sin a xx sin b` `tan (a + b) = (tan a + tan b) / (1 — tan a xx tan b)` Формулы разности `sin (ab ) = sin a xx cos b — sin b xx cos a` `cos (ab) = cos a xx cos b + sin a xx sin b`` tan (ab) = (tan a — tan b) / (1 + tan a xx tan b) ` Формулы двойных углов` sin (2a) = 2xxsin a xx cos a` `cos (2a) = cos ^ 2 a — sin ^ 2 a` `tan (2a) = (2 xx tan a) / (1 — tan ^ 2 a)`
Формулы Excel: сложные формулы
Урок 3: Сложные формулы
/ ru / excelformulas / простые-формулы / содержание /
Введение
Простая формула — это математическое выражение с одним оператором, например 7 + 9 . 2)
M ultiplication и деление , в зависимости от того, что идет первым A
вычитание , в зависимости от того, что наступит раньше
Мнемоника, которая поможет вам запомнить порядок: PEMDAS или P lease E xcuse M y D ear A Unt32 ally.
Щелкните стрелки в слайд-шоу ниже, чтобы узнать больше о том, как порядок операций используется для вычисления сложных формул.
Хотя эта формула может показаться действительно сложной, мы можем использовать порядок действий шаг за шагом, чтобы найти правильный ответ.
Сначала мы начнем с вычисления всего, что указано в скобках. В этом случае нам нужно вычислить только одно: 6-3 = 3.
Как видите, формула уже выглядит немного проще.2 = 4.
Далее мы решим любое умножение и деление, работая слева направо. Поскольку операция деления предшествует умножению, она вычисляется первой: 3/4 = 0,75.
Теперь посчитаем оставшуюся операцию умножения: 0,75 * 4 = 3.
Затем мы вычислим любое сложение или вычитание, снова работая слева направо. Сначала идет сложение: 10 + 3 = 13.
Наконец, у нас осталась одна операция вычитания: 13-1 = 12.
И теперь у нас есть наш ответ: 12. Это точно такой же результат, который вы получили бы, если бы вводили формулу в электронную таблицу.
Теперь давайте рассмотрим пару примеров, которые показывают, как порядок операций может повлиять на результат.
Использование круглых скобок в формуле может быть очень важным. Из-за порядка действий он может полностью изменить ответ. Давайте попробуем решить ту же задачу, но на этот раз добавим скобки к последней части.
Создание сложных формул
В приведенном ниже примере мы продемонстрируем сложную формулу, используя порядок операций. Здесь мы хотим рассчитать стоимость налога с продаж для счета за питание. Для этого запишем нашу формулу как = (D2 + D3) * 0,075 в ячейку D4 . Эта формула суммирует цены на наши товары, а затем умножает это значение на ставку налога 7,5% (которая записывается как 0,075) для расчета стоимости налога с продаж.
Затем таблица следует порядку операций и сначала добавляет значения в скобках: (44.85 + 39,90) = 84,75 долл. США . Затем он умножает это значение на налоговую ставку: 84,75 доллара * 0,075 . Результат покажет, что налог с продаж составляет $ 6,36 .
Особенно важно вводить сложные формулы с правильным порядком действий. В противном случае таблица не будет точно рассчитывать результаты. В нашем примере, если круглые скобки не включены, умножение вычисляется первым и результат неверный. Скобки — лучший способ определить, какие вычисления будут выполняться в формуле первыми.
Чтобы создать сложную формулу, используя порядок операций:
В нашем примере ниже мы будем использовать ссылку на ячейку вместе с числовыми значениями , чтобы создать сложную формулу, которая вычислит общую стоимость для счета-фактуры общественного питания. Формула рассчитает стоимость каждого пункта меню и сложит эти значения.
Выберите ячейку , которая будет содержать формулу. В нашем примере мы выберем ячейку C4 .
Введите формулу . В нашем примере мы введем = B2 * C2 + B3 * C3 . Эта формула будет следовать порядку операций, сначала выполняя умножение: 2,29 * 20 = 45,80 и 3,49 * 35 = 122,15 . Затем он сложит эти значения, чтобы вычислить итог: 45,80 + 122,15 .
Еще раз проверьте точность формулы, затем нажмите Введите на клавиатуре. Формула вычислит и отобразит результат .В нашем примере результат показывает, что общая стоимость заказа составляет $ 167,95 .
Вы можете добавить круглые скобки к любому уравнению, чтобы облегчить чтение. Хотя это не изменит результат формулы в этом примере, мы могли бы заключить операции умножения в круглые скобки, чтобы уточнить, что они будут вычисляться перед сложением.
Ваша электронная таблица не всегда сообщит вам , если ваша формула содержит ошибку, поэтому вам нужно проверить все свои формулы.Чтобы узнать, как это сделать, ознакомьтесь с уроком «Двойная проверка формул».
Вызов!
Откройте существующую книгу Excel. Если хотите, вы можете использовать файл-пример для этого урока.
Создайте сложную формулу, которая будет выполнять сложение перед умножением. Если вы используете этот пример, создайте формулу в ячейке D6 , которая сначала добавляет значения ячеек D3 , D4 и D5 , а затем умножает их общее количество на 0.075 . Подсказка: вам нужно подумать о порядке операций, чтобы это работало правильно.
/ ru / excelformulas / относительные-абсолютные-ссылки-ячейки / содержание /
Дробное комплексное преобразование для дробно-дифференциальных уравнений | Успехи в разностных уравнениях
Пример 3.1 Рассмотрим следующее уравнение:
{ρt1 / 21.128∂1 / 2u (t, z) ∂t1 / 2 + Dzβu (t, z) = 0, t∈J = [0 , 1] u (0, z) = 0, в окрестности z = 0,
(14)
где u (t, z) — неизвестная функция ρ∈ (0,1) и β∈ (0,1].
Мы предлагаем показать, что уравнение (14) имеет единственное аналитическое решение, с помощью теоремы Банаха о неподвижной точке. Принимая
u (t, z) = μ (z) t + v (t, z) (v (t, z) = O (t2))
в качестве формального решения, где μ (z) = O (zβ), из расчетов следует
t1 / 2∂1 / 2u (t, z) ∂t1 / 2 = 1.128μ (z) t + t1 / 2vα (t, z), α = 1/2,
и
Dzβu (t, z) = Dzβ (μ (z) t + v (t, z)) = tDzβμ (z) + vβ (t, z).
Следовательно, μ (z) удовлетворяет
, что эквивалентно
Dzβμ (z) = g (z, μ (z)),
(15)
, где
Теперь g (z, μ (z)) является сжимающим отображением всякий раз, когда ρ∈ (0,1); поэтому, в силу теоремы Банаха о неподвижной точке, уравнениеУравнение (15) имеет единственное аналитическое решение в единичном круге и, следовательно, задача (14).
Для вычисления индекса фрактальности для уравнения
Dzβμ (z) + ρμ (z) = 0, μ (0) = 1,
(16)
мы предполагаем преобразование Z = zβ и решение может быть выражено в виде ряда в виде
μ (Z) = ∑m = 0∞μmZm,
(17)
где мкм — константы. Подставляя (17) в уравнение. (16) дает
∂∂Z∑m = 0∞θβmμmZm + ρ∑m = 0∞μmZm = 0.
(18)
Так как
θβm = Γ (1 + mβ) mΓ (1 + mβ − β),
, то вычисление устанавливает соотношение
Γ (1 + mβ) Γ (1 + mβ − β) μm + ρμm− 1 = 0
с μ (0) = 1, и, следовательно, получаем
Таким образом, имеем следующее решение:
μ (Z) = ∑m = 0∞ (−ρ) mΓ (1 + mβ) Zm
, что эквивалентно
μ (z) = ∑m = 0∞ (−ρ) mΓ (1 + mβ) zmβ = Eβ (−ρzβ),
, где Eβ — функция Миттаг-Леффлера. Последнее утверждение является точным решением задачи (16), а следовательно, и (14).
Пример 3.2 Рассмотрим следующее уравнение:
{t1 / 2 / 21.128∂1 / 2u (t, z) ∂t1 / 2 + 4z∂u (t, z) ∂z + Dzβu (t, z) = zβt, t∈J = [0,1], u (0, z) = 0, в окрестности z = 0,
(19)
где u (t, z) — неизвестная функция, а β∈ (0,1]. Таким же образом, как в примере 3.1, положим
u (t, z) = μ (z) t + v (t , z) (v (t, z) = O (t2))
как формальное решение, где μ (z) = O (zβ) и
| μ ′ (z) −ν ′ (z) | < λ | μ (z) −ν (z) |, λ <18.
Оценки подразумевают
и
Dzβu (t, z) = Dzβ (μ (z) t + v (t, z)) = tDzβμ (z) + vβ (t, z).
Следовательно, μ (z) удовлетворяет
μ (z) 2 + 4zμ ′ (z) + Dzβμ (z) −zβ = 0,
, что эквивалентно
Dzβμ (z) = G (z, μ (z), zμ ′ (z)),
(20)
, где
G (z, μ (z), zμ ′ (z)) = zβ − 1 / 2μ (z) −4zμ ′ (z).
Теперь, чтобы показать, что G (z, μ (z), zμ ′ (z)) является сжимающим отображением,
Таким образом, ввиду теоремы Банаха о неподвижной точке, уравнениеУравнение (20) имеет единственное аналитическое решение в единичном круге и, следовательно, задача (19).
Чтобы оценить индекс фрактальности для уравнения
Dzβμ (z) + μ (z) 2 + 4zμ ′ (z) −zβ = 0, μ (0) = 1,
(21)
мы предполагаем преобразование Z = zβ и решение можно сформулировать, как в (17). Подставляя (17) в уравнение. (21) имеем
∂∂Z∑m = 0∞θβmμmZm + 12∑m = 0∞μmZm + 4∑m = 1∞mμmZm − Z = 0,
(22)
, где
θβm = Γ (1 + mβ) mΓ (1 + mβ − β).
Следовательно, вычисление накладывает соотношение
(Γ (1 + mβ) Γ (1 + mβ − β) + 4m) μm + 12μm − 1 = 0
с μ (0) = 1, и, следовательно, мы получаем
где Bm через гамма-функцию. Если мы положим B: = maxm {Bm}, то решение приближается к
μ (Z) ≃∑m = 0∞ (B) mΓ (1 + mβ) Zm,
, что эквивалентно
μ (z ) = ∑m = 0∞ (B) mΓ (1 + mβ) zmβ = Eβ (Bzβ).
Последнее утверждение является точным решением задачи (21), а следовательно, и (19).
Далее мы рассмотрим задачу Коши с помощью обобщенного дробно-дифференциального оператора (4).Мы покажем, что решение такой задачи может быть найдено в терминах функции Фокса-Райта [37]:
где Aj> 0 для всех j = 1,…, p, Bj> 0 для всех j = 1, …, Q и 1 + ∑j = 1qBj − ∑j = 1pAj≥0 для подходящих значений | w | <1 и ai, bj - комплексные параметры.
Пример 3.3 Рассмотрим задачу Коши в терминах дифференциального оператора (4)
Dzα, μu (z) = F (z, u (z)),
(23)
, где F (z, u (z)) аналитична в u , а u (z) аналитична в единичном круге.Таким образом, F можно выразить как
Пусть Z = zα (μ + 1). Тогда решение можно сформулировать следующим образом:
где um — константы. Подставляя (24) в уравнение. Из (23) следует
∂∂Z∑m = 0∞Θα, μ, mumZm − ϕ∑m = 0∞umZm = 0.
(25)
Так как
Θα, μ, m = (μ + 1) αΓ (mαμ + 1 + 1) mΓ (nαμ + 1 + 1 − α),
, то расчет дает соотношение
(μ + 1) αΓ (mαμ + 1 + 1) Γ (mαμ + 1 + 1 − α) um − ϕum − 1 = 0;
, следовательно, получаем
um = [ϕ (μ + 1) α] mΓ ((m − 1) αμ + 1 + 1 − α) Γ (mαμ + 1 + 1 − α) Γ ((m − 1 ) αμ + 1 + 1) Γ (mαμ + 1 + 1).
Таким образом, имеем следующее решение:
u (Z) = ∑m = 0∞ [ϕ (μ + 1) α] mΓ ((m − 1) αμ + 1 + 1 − α) Γ (mαμ + 1 + 1 − α) Γ ((m − 1) αμ + 1 + 1) Γ (mαμ + 1 + 1) Zm
, что эквивалентно
u (Z) = ∑m = 0∞ [ϕ (μ +1) α] mΓ (m + 1) Γ ((m − 1) αμ + 1 + 1 − α) Γ (mαμ + 1 + 1 − α) Γ ((m − 1) αμ + 1 + 1) Γ (mαμ + 1 + 1) Змм !.
Поскольку ϕ — произвольная константа, мы предполагаем, что
Таким образом, для подходящего α мы представляем
или
, где | z | <1.
Пример сложных математических формул — математические формулы
Если в формуле более одной операции, порядок операций сообщает вашей электронной таблице, какую операцию нужно вычислить в первую очередь.Как и все тематические разделы в акте, математический раздел представляет собой один законченный раздел, который вы будете изучать сразу.
Математика Физические формулы Отличная компиляция Изучение математики
Сложная формула имеет более одного математического оператора, например 5 2 8.
Пример сложной математической формулы . Формула мощности комплексного числа. Математические уравнения, от формул специальной и общей теории относительности до теоремы Пифагора, мощны и приятны своей красотой для многих ученых.Формула произведения Эйлера.
Excel поставляется с множеством полезных формул, у нас есть категория финансовых логических текстовых ссылок на поиск даты, времени и математических триггеров. Чтобы вспомнить комплексное число, нужно использовать x y 1, где x и y — действительные числа, а i — мнимое число. Формула мощности комплексного числа используется для вычисления значения комплексного числа, которое возводится в степень n.
Теперь рассмотрим несколько простых формул. Полный список наиболее часто используемых основных математических формул.Оказывается, что даже самые сложные формулы могут быть систематически построены в латексе из более простых частей, так что набирать сложные формулы не очень сложно.
i удовлетворяет i 2 1. Чтобы использовать сложные формулы, вам необходимо понимать порядок операций. Более общая формула.
Краткий обзор математического раздела. Символ слева представляет собой бесконечную сумму, а символ справа — бесконечное произведение. Комплексные числа z a b i и z a b i над чертой называются комплексно сопряженными друг другу.
Многие считают его самым красивым уравнением в математике. Комплексное число записывается как abi, где a и b — действительные числа, и i, называемая мнимой единицей, имеет свойство i 2 1. Когда значение равно 1, а равно 0, тождество Эйлера равно 1 1 0.
Подробно примеры формул для ключевых функций, в том числе vlookup index match rank sumproduct medium small large lookup round countifs sumifs choose find. В акте вопросы расположены в порядке возрастания сложности.Каждая отдельная формула достаточно хороша для промежуточных пользователей, когда они сталкиваются с прямыми ситуациями, но по мере того, как вы переходите на следующий уровень, ваши навыки должны повышаться в этом отношении.
Это всегда будет второй раздел теста, и у вас будет 60 минут, чтобы ответить на 60 вопросов. Загрузите наш файл-пример для этого урока. Важно помнить, что латекс имеет свой собственный способ обработки интервалов в математическом режиме.
Таблица законов индекса с примерами, всегда полезными для конкретных целей
Новости Work Flex Переосмысление уравнения трудовой жизни и многое другое
Переход к алгебре Формула Лист Алгебра Формулы Колледж
Купить квадратную формулу Биномиальное разложение Другие разложения
Математические формулы Вопросы по математике И математическая формула Инфографика
Доказательства логарифмических свойств Примеры решений Видео из игр
Статистика для чайников Шпаргалка Статистика Математические методы
6808feb13a70e0d27756a82c092f1d73 Jpg 537 727 пикселей, которые важны для статистических расчетов Ap
для всех электрических уравнений
17 Статистика листа Математика Методы математики
Сложные математические формулы на доске Математика и естественные науки с
Математические формулы Математическая формула Диаграмма Формула Диаграмма Математика
Формулы объема и площади поверхности твердого тела F. Числа для класса Vi
Пример сложного квантового уравнения Huh Quantum
Ssc Adda Алгебраические формулы Часть 1 Изучение математических математических методов
Решите дифференциальное уравнение Бернулли Задача начального значения
Заполните квадрат для вычисления квадратичной формулы Методы
Статистика уравнения регрессии Математика Данные психологического тестирования

Вопрос: Какое уравнение является наиболее сложным?
Физик : Если у вас много места на классной доске и вам нечего больше делать, вы можете записывать числа, буквы (греческие, если вы δυσάρεστος) и математические операторы, и в конечном итоге вы получите самое длинное уравнение, которое когда-либо было записано. .Так что, если вы действительно хотите увидеть самое сложное уравнение, позвоните больному на несколько недель. Лучше задать вопрос: «Какое уравнение является наиболее (но не без нужды) сложным?».
Существует множество бесконечно длинных уравнений, но часто они достаточно простые, чтобы их можно было записать компактно. Например, это уравнение продолжается вечно, но оно довольно прямолинейно: при каждом члене вы переворачиваете знак и увеличиваете знаменатель от одного нечетного числа к другому. Вы можете написать это математическим языком как.Как и сама π, эта сумма продолжается вечно, но это не сложно. Вы можете описать это просто и таким образом, чтобы любой (имея достаточно времени и мелка) мог найти сколько угодно цифр числа π. Это основная идея «Колмогоровской сложности»; длина кратчайшего возможного набора письменных инструкций, которые могут дать заданный результат (неважно, сколько времени уходит на его фактическое вычисление).
Если вы ищете сложное уравнение, лучше всего поискать физику (я имею в виду, для чего еще вам нужен математика ?).Если вы хотите описать поведение мяча, летящего по воздуху, недостаточно сказать «он летит вверх, затем вниз»; для точного расчета траектории падающих объектов требуется минимум математических расчетов, и это намного сложнее.
Возможно, Вселенная довольно сложна. Но, как и π, это обманчиво (мы надеемся). Если вы хотите сделать что-то вроде, скажем, описания гравитационного взаимодействия каждой звезды в галактике, вы должны сделать это, пронумеровав звезды (не торопитесь: звезда 1, звезда 2,…, звезда n), определите положение и масса каждой, и, а затем найти силу, действующую на каждую звезду, создаваемую всеми остальными.На практике это абсурд (в Млечном Пути несколько сотен миллиардов звезд, но мы не можем увидеть большинство из них, потому что на пути есть галактика), но уравнение, которое вы бы использовали, довольно простое. Сила, действующая на звезду k:. Это просто закон всемирного тяготения Ньютона, повторяемый для каждой возможной пары звезд и складывающийся. Итак, хотя сама ситуация сложна, уравнение, описывающее ее, — нет. Очевидно, что если вам нужно уравнение, которое действительно должно быть сложным, вам не нужна сложная ситуация, вам нужна сложная динамика.
Уравнение силы тяжести между множеством объектов — это просто уравнение силы тяжести между каждой сложенной парой. Не намного сложнее.
Весь смысл физики, помимо понимания вещей, состоит в том, чтобы как можно проще описать правила Вселенной. С этой целью физики любят говорить о «лагранжианах». Получив лагранжиан системы, вы можете описать поведение этой системы, применяя «принцип наименьшего действия», который гласит, что поведение системы (орбита, которую принимает планета, путь света через материалы , так далее.) всегда будет таким, что «выбранный» путь будет иметь минимальный общий лагранжиан вдоль этого пути. Это милый рецепт лаконичного и одновременно описывающего множество движущих сил, которыми Колмогоров мог бы гордиться.
Лагранжиан дает каждой точке на этом рисунке значение, а сумма по всему пути является «действием». Принцип наименьшего действия гласит, что путь, по которому система фактически пойдет, имеет наименьшее действие. С помощью этого принципа один лагранжиан может быть использован для вывода многих физических законов одновременно, так что это хороший кандидат для уравнений, которые не являются излишне сложными .
Например, вы можете почти мгновенно резюмировать физику Ньютона. Вместо того, чтобы говорить о кинетической энергии, импульсе и падении, вы можете просто сказать: «Чуваки и дудеты, если позволите, лагранжиан для объекта, летящего по воздуху у поверхности Земли, есть, где m — масса, v — скорость, а z — высота ». Из этой формулы single вы получаете сохранение энергии, сохранение количества движения (при движении вбок), а также ускорение свободного падения. Есть также лагранжианы для всего, от вращения планет до электромагнитных полей.
Как правило, когда вы смотрите на одну и ту же динамику, применяемую снова и снова, соответствующие уравнения не становятся намного сложнее (хотя их решения определенно усложняются). И если вы хотите описать динамику системы, лагранжианы — чрезвычайно компактный способ сделать это. Итак, какое уравнение во Вселенной является самым (но не лишним) сложным? Возможно, это лагранжиан Стандартной модели, который охватывает динамику всех видов частиц и все их взаимодействия. Примечательно, что это не покрывает гравитацию, но круто.Работа продолжается.
Уравнение всего (кроме силы тяжести).
В некотором смысле это уравнение представляет собой сжатые данные. Вся соответствующая динамика есть, но нужно еще многое распаковать, прежде чем это станет отдаленно очевидным. Все уравнения должны иметь некоторый контекст, прежде чем они будут что-либо делать или даже означать что-либо. Вот почему учебники по математике — это в основном слова. «2 + 2 = 4» ничего не значит для инопланетян до тех пор, пока вы не расскажете им, что означает каждый из этих символов и как они используются.В случае лагранжиана Стандартной модели каждый из этих символов много значит, само уравнение использует изящные трюки, и оно даже не описывает динамику само по себе без привязки к Принципу наименьшего действия. Но, учитывая все это, он описывает самую сложную вещь, которую мы можем описать, то есть почти все, без излишней многословности («математика»?).
Ответ Gravy : Это не часть вопроса, но если вы знакомы с физикой, вы, вероятно, видели уравнения для кинетической энергии, импульса и ускорения в однородном гравитационном поле (например, в том, которое вы переживаем прямо сейчас).Но если вы на самом деле не физик, вы, вероятно, никогда не испугались, увидев работу Лагранжа. Эта подливка полна математических расчетов и вводной физики.
«Действие»,, является функцией пути, по которому идет система,. В частности, это интеграл лагранжиана между любыми двумя заданными моментами времени:
, где t ₁ и t ₂ — время начала и остановки, — путь, — производная по времени (скорость) этого пути и является некоторой заданной функцией от и.Если вы хотите выбрать путь, который увеличивает (либо минимизирует, либо максимизирует) S, то вы можете сделать это, решив уравнения Эйлера-Лагранжа:
Это называется уравнениями Эйлера-Лагранжа (множественное число), потому что на самом деле это несколько уравнений. Каждая переменная (x ₁ = x, x ₂ = y, x ₃ = z) говорит вам что-то свое. В обычном исчислении ol ’, если вы хотите найти значение x, которое экстремально увеличивает функцию f (x), вы решаете значение x. Использование уравнений Эйлера-Лагранжа с философской точки зрения аналогично: чтобы найти путь, который увеличивает S, вы решаете путь.
Предыдущий лагранжиан для свободно падающего объекта у поверхности Земли:
Для z:
Итак, уравнение E-L говорит:
или
Другими словами, «все ускоряется вниз с одинаковой скоростью». Проделав то же самое для x или y, вы получите, что гласит: «Вбок не ускоряется». Обе вещи следует знать.
Хочешь быть еще круче, заметьте, что этот лагранжиан не зависит от времени. Это означает, что . Следовательно, применяя цепное правило:
Но у нас есть уравнения E-L! Подключите их:
А следовательно:
В скобках указано постоянное значение (поскольку оно никогда не меняется во времени).В случае, мы обнаруживаем, что эта постоянная величина:
Проницательные студенты физики 1 узнают сумму кинетической энергии плюс гравитационный потенциал. Другими словами: это вывод из закона сохранения энергии для свободно падающих объектов. Более общую трактовку можно провести, используя теорему Нётер, которая гласит, что каждая симметрия производит сохраняющуюся величину. Например, временная симметрия (не изменяется во времени) приводит к сохранению энергии, а пространственная симметрия (не изменяется в каком-либо направлении) приводит к сохранению количества движения в этом направлении.
16 важнейших математических формул ACT Математические формулы, которые вам НЕОБХОДИМО знать
Давайте разберемся, из чего состоит математический раздел ACT. Всего 60 вопросов с множественным выбором из шести областей математики: предалгебра, элементарная алгебра, промежуточная алгебра, координатная геометрия, плоская геометрия и тригонометрия. Таким образом, подсчет очков и математические формулы, которые вам нужно знать, распределяются следующим образом:
Предалгебра / Элементарная алгебра: 24 вопроса, 24 балла
Промежуточная алгебра / координатная геометрия: 18 вопросов, 24 балла
Плоская геометрия / тригонометрия: 18 вопросов, 24 точки
В математическом разделе ACT есть особенность: даже после того, как вы прошли всю подготовку к тесту ACT, ACT не дает вам шпаргалки со всеми математическими формулами, записанными на них.Следовательно, вы должны их запомнить. Но некоторые важные математические формулы ACT требуются чаще, чем другие. Это то, что нужно знать. Хотя может показаться заманчивым просто предположить и уйти, лучше, если вы будете готовы с самого начала.
Давайте посмотрим на самые важные формулы в разделе.
Предалгебра / Элементарная алгебра
Эти формулы включают основы математики и алгебры. Другими словами, от ученика требуется найти неизвестную переменную.
1. Среднее арифметическое (среднее) = сумма значений / количество значений
Специально используется для вычисления среднего значения заданного набора чисел.
Например: (10 + 12 + 14 + 16) / 4 = 13
2. Вероятность = Целевые результаты / Общие результаты
Специально используется для расчета вероятности того, что что-то произойдет из набора возможных результатов.
Например: банка содержит пять синих шариков, пять красных шариков и десять белых шариков.Какова вероятность случайного выбора красного шарика?
5/20 = 0,25 или 25%
3. Квадратичная формула: x = −b ± √b²-4ac / 2a
Специально используется для определения точек пересечения по оси x квадратного (параболического) уравнения.
Например: A = 1, B = 4, C = 4
x = -4 ± √4² — 4 (1) (4) / 2 (1)
х = -4 ± √ 16-4 (4) / 2
х = -4 ± √16 — 16/2
х = -4 ± √ 0/2
х = -4 / 2
х = -2
Промежуточная алгебра / координатная геометрия
Эти формулы помогают вычислять расстояния, длины и свойства точек на плоскости, а также находить переменные в более сложных алгебраических выражениях.
4. Формула расстояния: d = √ (x₁ — x₂) ² + (y₁ — y₂) ²
Специально рассчитывает расстояние между двумя точками на координатной плоскости.
Например: Найдите расстояние между точками (6, 6) и (2, 3)
d = √ (6–2) ² + (6–3) ²
d = √ (4) ² + (3) ²
г = √16 + 3
d = √25
d = 5
5. Формула наклона: Наклон = y₂ — y₁ / x₂ — x₁
В частности, вычисляет наклон (угол) линии, соединяющей две точки на плоскости.
Например: Координаты = (-2, -1) (4, 3)
с = 3 — (-1) / 4 — (-2)
с = 4/6
с = 2/3
6. Пересечение наклона: y = mx + b
Формула, определяющая линию на плоскости с известным наклоном и точкой пересечения по оси Y.
Например: наклон = 2, точка пересечения (0,3)
7. Формула средней точки: (x₁ + x₂) / 2, (y₁ + y₂) / 2
В частности, вычисляет среднюю точку между точками на плоскости.
Например: Найдите середину между (-1, 2) и (3, -6)
(-1 + 3) / 2, (2 + -6) / 2
2/2, -4/2
Середина (1, -2)
Плоская геометрия
Формулы для вычисления атрибутов геометрических фигур на плоскости и решения для переменных на основе углов данной формы (тригонометрические тождества).
8. Площадь треугольника: площадь = (1/2) (основание) (высота)
В частности, вычисляет общую площадь треугольника на основе длин сторон.
Например: база = 5, высота = 8
a = 1/2 (5) (8)
а = 1/2 (40)
а = 20
9. Теорема Пифагора: a² + b² = c²
Используется специально для вычисления длины неизвестной стороны прямоугольного треугольника, если известны две стороны.
Например: a = 3, b = 4
c² = 3² + 4²
c² = 9 + 16
c² = 25
с = √25
с = 5
10.Площадь прямоугольника: площадь = длина x ширина
Конкретно рассчитывает общую площадь прямоугольника.
Например: длина = 5, ширина = 2
11. Площадь параллелограмма: площадь = основание x высота
Специально рассчитывает общую площадь параллелограмма.
Например: основание = 6, высота = 12
12. Площадь круга: π * r²
Специально рассчитывает общую площадь круга.
Например: радиус = 4
a = π x 4²
а = π x 16
а = 50,24
13. Окружность круга: окружность = 2π * r
Вычисляет длину контура круга.
Например: радиус = 7
Тригонометрия
Продолжает работу с предыдущим геометрическим разделом плоскости.
14. Синус (SOH): Синус = противоположный / гипотенуза
Тригонометрическая идентичность, которая представляет относительные размеры сторон треугольника и может также использоваться для вычисления неизвестных сторон или углов треугольника.
Например: напротив = 2,8, гипотенуза = 4,9
15. Косинус (CAH): косинус = смежный / гипотенуза
Тригонометрическая идентичность, которая представляет относительные размеры сторон треугольника и может также использоваться для вычисления неизвестных сторон или углов треугольника.
Например: смежный = 11, гипотенуза = 13
16. Касательная (TOA): Касательная = противоположная / смежная
Тригонометрическая идентичность, которая представляет относительные размеры сторон треугольника и может также использоваться для вычисления неизвестных сторон или углов треугольника.
Например: напротив = 15, рядом = 8
Другие советы
Конечно, есть и другие формулы, которые могут появиться в ACT, но эти самые распространенные. Следовательно, они важнее всего. Запомните эти формулы, изучите, практикуйтесь, и все будет хорошо, когда наступит день экзамена.
Кроме того, убедитесь, что вы хорошо выспались ночью, и приготовьте то, что вам нужно, на ночь вместо утра. Также нет необходимости забивать накануне вечером; вместо этого расслабься! Зубки не работают, и это также лучший способ сделать передышку.
Удачи!
Проверьте, как ваши результаты ACT влияют на ваши шансы зачисления в College Raptor!
.

Сложные математические формулы: Фото: Наука: Наука и техника: Lenta.ru

ТОП-50 Важнейших формул по математике — Математика — Теория, тесты, формулы и задачи

Изучать ТОП-50 Важнейших формул по математике онлайн:

Как успешно подготовиться к ЦТ по физике и математике?

Нашли ошибку?

Все главные формулы по математике — Математика — Теория, тесты, формулы и задачи

Оглавление:

Формулы сокращенного умножения

Квадратное уравнение и формула разложения квадратного трехчлена на множители

Парабола

Свойства степеней и корней

Основные свойства степеней:

Основные свойства математических корней:

Формулы с логарифмами

Определение логарифма:

Свойства логарифмов:

Арифметическая прогрессия

Геометрическая прогрессия

Тригонометрия

Формулы двойного угла

Тригонометрические формулы сложения

Тригонометрические формулы преобразования суммы в произведение

Тригонометрические формулы преобразования произведения в сумму

Формулы понижения степени

Формулы половинного угла

Тригонометрические формулы приведения

Тригонометрическая окружность

Тригонометрические уравнения

Геометрия на плоскости (планиметрия)

Геометрия в пространстве (стереометрия)

Координаты

Таблица умножения

Таблица квадратов двухзначных чисел

Расширенная PDF версия документа «Все главные формулы по школьной математике»:

Самые красивые физические и математические формулы.: moris_levran — LiveJournal

Математические формулы по алгебре и геометрии для ЕГЭ

Как выучить все формулы по математике к ЕГЭ

Математические формулы школьного курса алгебры

Логарифмические формулы

Формулы тригонометрии

Формулы векторной алгебры из школьного курса математики

Формулы арифметической и геометрической прогрессии

Геометрические формулы школьного курса математики для ЕГЭ

От красавиц до чудовищ

Тождество Эйлера

Основное тригонометрическое тождество

Формула Эйлера для экспоненты

Условия Коши-Римана

Эйлерова характеристика сферы

Формула Гаусса-Бонне

Спектральная теорема для ограниченного оператора

Минимальное число такси

Короткая точная последовательность

Формула Рамануджана

Сложные математические формулы.

Формулы Арифметики:

Формулы Алгебры:

Геометрические Формулы:

Арифметические формулы:

Некоторые математические обозначения и сокращения:

Признаки делимости на «2»

Признаки делимости на «4»

Признаки делимости на «8»

Признаки делимости на «3» и на «9»

Признаки делимости на «5»

Признаки делимости на «25»

Признаки делимости на «10», «100» и на «1 000»

Признаки делимости на «11»

Абсолютная величина — формулы ( модуль)

Формулы Действия с дробями

Формула обращения конечной десятичной дроби в рациональную дробь:

Пропорции

Средние величины

Среднее арифметическое

Среднее геометрическое (среднее пропорциональное)

Среднее квадратичное

Среднее гармоническое

Некоторые конечные числовые ряды

Формулы Прогрессии:

OCR для математических формул — CodeRoad