Точка, линия, прямая, луч, отрезок, ломанная
Точка — это абстрактный объект, который не имеет измерительных характеристик: ни высоты, ни длины, ни радиуса. В рамках задачи важно только его местоположение
Точка обозначается цифрой или заглавной (большой) латинской буквой. Несколько точек — разными цифрами или разными буквами, чтобы их можно было различать
точка A, точка B, точка C
ABCточка 1, точка 2, точка 3
123Можно нарисовать на листке бумаги три точки "А" и предложить ребёнку провести линию через две точки "А". Но как понять через какие? AAA
Линия — это множество точек. У неё измеряют только длину. Ширины и толщины она не имеет
Обозначается строчными (маленькими) латинскими буквами
линия a, линия b, линия c
abcЛиния может быть
- замкнутой, если её начало и конец находятся в одной точке,
- разомкнутой, если её начало и конец не соединены
замкнутые линии
разомкнутые линии
Ты вышел из квартиры, купил в магазине хлеб и вернулся обратно в квартиру. Какая линия получилась? Правильно, замкнутая. Ты вернулся в исходную точку. Ты вышел из квартиры, купил в магазине хлеб, зашёл в подъезд и разговорился с соседом. Какая линия получилась? Разомкнутая. Ты не вернулся в исходную точку. Ты вышел из квартиры, купил в магазине хлеб. Какая линия получилась? Разомкнутая. Ты не вернулся в исходную точку.
- самопересекающейся
- без самопересечений
самопересекающиеся линии
линии без самопересечений
- прямой
- ломанной
- кривой
прямые линии
ломанные линии
кривые линии
Прямая линия — это линия которая не искривляется, не имеет ни начала, ни конца, её можно бесконечно продолжать в обе стороны
Даже когда виден небольшой участок прямой, предполагается, что она бесконечно продолжается в обе стороны
Обозначается строчной (маленькой) латинской буквой. Или двумя заглавными (большими) латинскими буквами — точками, лежащими на прямой
прямая линия a
aпрямая линия AB
BAПрямые могут быть
- пересекающимися, если имеют общую точку. Две прямые могут пересекаться только в одной точке.
- перпендикулярными, если пересекаются под прямым углом (90°).
- параллельными, если не пересекаются, не имеют общей точки.
параллельные линии
пересекающиеся линии
перпендикулярные линии
Луч — это часть прямой, которая имеет начало, но не имеет конца, её можно бесконечно продолжать только в одну сторону
У луча света на картинке начальной точкой является солнце
солнышко
Точка разделяет прямую на две части — два луча A A
Луч обозначается строчной (маленькой) латинской буквой. Или двумя заглавными (большими) латинскими буквами, где первая — это точка, с которой начинается луч, а вторая — точка, лежащая на луче
луч a
aлуч AB
BAЛучи совпадают, если
- расположены на одной и той же прямой,
- начинаются в одной точке,
- направлены в одну сторону
лучи AB и AC совпадают
лучи CB и CA совпадают
CBAОтрезок — это часть прямой, которая ограничена двумя точками, то есть она имеет и начало и конец, а значит можно измерить её длину. Длина отрезка — это расстояние между его начальной и конечной точками
Через одну точку можно провести любое число линий, в том числе прямых
Через две точки — неограниченное количество кривых, но только одну прямую
кривые линии, проходящие через две точки
BAпрямая линия AB
BAОт прямой «отрезали» кусочек и остался отрезок. Из примера выше видно, что его длина — наикратчайшее расстояние между двумя точками. ✂ BA✂
Отрезок обозначается двумя заглавными(большими) латинскими буквами, где первая — это точка, с которой начинается отрезок, а вторая — точка, которой заканчивается отрезок
отрезок AB
BAЗадача: где прямая, луч, отрезок, кривая?
Ломанная линия — это линия, состоящая из последовательно соединённых отрезков не под углом 180°
Длинный отрезок «поломали» на несколько коротких
Звенья ломаной (похожи на звенья цепи) — это отрезки, из которых состоит ломанная. Смежные звенья — это звенья, у которых конец одного звена является началом другого. Смежные звенья не должны лежать на одной прямой.
Вершины ломаной (похожи на вершины гор) — это точка, с которой начинается ломанная, точки, в которых соединяются отрезки, образующие ломаную, точка, которой заканчивается ломанная.
Обозначается ломанная перечислением всех её вершин.
ломанная линия ABCDE
вершина ломанной A, вершина ломанной B, вершина ломанной C, вершина ломанной D, вершина ломанной E
звено ломанной AB, звено ломанной BC, звено ломанной CD, звено ломанной DE
звено AB и звено BC являются смежными
звено BC и звено CD являются смежными
звено CD и звено DE являются смежными
ABCDE646212752Длина ломанной — это сумма длин её звеньев: ABCDE = AB + BC + CD + DE = 64 + 62 + 127 + 52 = 305
Задача: какая ломанная длиннее, а у какой больше вершин? У первой линии все звенья одинаковой длины, а именно по 13см. У второй линии все звенья одинаковой длины, а именно по 49см. У третьей линии все звенья одинаковой длины, а именно по 41см.
Многоугольник — это замкнутая ломанная линия
Стороны многоугольника (помогут запомнить выражения: «пойти на все четыре стороны», «бежать в сторону дома», «с какой стороны стола сядешь?») — это звенья ломанной. Смежные стороны многоугольника — это смежные звенья ломанной.Вершины многоугольника — это вершины ломанной. Соседние вершины — это точки концов одной стороны многоугольника.
Обозначается многоугольник перечислением всех его вершин.
замкнутая ломанная линия, не имеющая самопересечения, ABCDEF
многоугольник ABCDEF
вершина многоугольника A, вершина многоугольника B, вершина многоугольника C, вершина многоугольника D, вершина многоугольника E, вершина многоугольника F
вершина A и вершина B являются соседними
вершина B и вершина C являются соседними
вершина C и вершина D являются соседними
вершина D и вершина E являются соседними
вершина E и вершина F являются соседними
вершина F и вершина A являются соседними
сторона многоугольника AB, сторона многоугольника BC, сторона многоугольника CD, сторона многоугольника DE, сторона многоугольника EF
сторона AB и сторона BC являются смежными
сторона BC и сторона CD являются смежными
сторона CD и сторона DE являются смежными
сторона DE и сторона EF являются смежными
сторона EF и сторона FA являются смежными
ABCDEF120605812298141Периметр многоугольника — это длина ломанной: P = AB + BC + CD + DE + EF + FA = 120 + 60 + 58 + 122 + 98 + 141 = 599
Многоугольник с тремя вершинами называется треугольником, с четырьмя — четырёхугольником, с пятью — пятиугольником и т.д.
треугольники
четырёхугольники: квадрат, прямоугольник, дельтоид, ромб, параллелограмм, трапеция
пятиугольники
shpargalkablog.ru
Точка. Кривая. Прямая линия / Виды линий / Справочник по математике для начальной школы
- Главная
- Справочники
- Справочник по математике для начальной школы
- Виды линий
- Точка. Кривая. Прямая линия
Точка
Прямая линия
Прямая линия не имеет ни начала, ни конца.
Прямую линию можно продолжить. Она бесконечна.
Через 2 точки можно провести только одну прямую.
Через 1 точку можно провести много прямых линий.
Расстояние между двумя точками
Поставим две точки на одинаковом расстоянии друг от друга и проведём между ними ломаную линию и прямую линию. Посчитаем расстояние между точками по количеству клеточек.
Вывод: Самое короткое расстояние между двумя точками — это прямая.
Кривая
Через 1 точку можно провести много кривых линий.

Поделись с друзьями в социальных сетях:
Советуем посмотреть:
Отрезок. Луч
Ломаная линия
Длиннее. Короче. Уже. Шире. Одинаковые по длине и ширине
Виды линий
Правило встречается в следующих упражнениях:
1 класс
Страница 40, Моро, Волкова, Степанова, Учебник, 1 часть
Страница 41, Моро, Волкова, Степанова, Учебник, 1 часть
Страница 15, Моро, Волкова, Рабочая тетрадь, 1 часть
Страница 84, Моро, Волкова, Степанова, Учебник, 2 часть
Страница 13, Моро, Волкова, Рабочая тетрадь, 2 часть
2 класс
Страница 28, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, 1 часть
Страница 92, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, 1 часть
Страница 23, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, 2 часть
3 класс
Страница 15, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, 1 часть
© 2019 — budu5.com, Буду отличником!
budu5.com
1 класс. Математика. Точка. Прямая, кривая и ломаная линии. — Прямая линия. Кривая линия. Ломаная линия.
Комментарии преподавателя
На данном уроке Вы изучите простейшие геометрические понятия, о которых вам расскажет мама дракончиков. Вместе с дракончиками Вы изучите такие основные понятия, как прямая линия, луч, отрезок, угол, ломаная и кривая линия. У Вас будет возможность изучить предложенный материал на наглядных примерах.
Тема: Наглядная геометрия
Урок: Начальные геометрические понятия
На этом уроке будут изучены простейшие геометрические понятия. Для лучшего понимания рассмотрим сказку про дракончиков.
Далеко-далеко в горах живет большая-большая семья драконов: папа-дракон, мама-дракониха и много маленьких дракончиков. Когда дракончики были маленькие, они учились ползать, бегать, летать, прыгать, узнавали, что такое снег, дождь, звёзды, учились в горах ориентироваться, учились даже огнём дышать. Когда дракончики немножко подросли, мама решила их научить математики, в том числе геометрии. Дракончики очень удивились, они не поняли о чём идет речь. Мама предложила им сесть на площадке перед большой скалой и смотреть, что она будет рисовать. Она начала рисовать мелом на этом плоском куске скалы различные геометрические вещи, начиная с самых простых. Вначале мама-дракониха нарисовала линию, которая изображена на рисунке. (рис. 1)
Рис. 1
Мама-дракониха сказала, что эта линия называется прямая. Это такое геометрическое понятие.
Прямая линия – это линия, которая совершенно бесконечна.
Прямая линия идет бесконечно в одну сторону и в другую сторону. Есть такое даже выражение «Летит в небе по прямой».
Потом мама нарисовала точку и от неё провела линию. (рис. 2)
Рис. 2
Она объяснила, что точка – это начало, от нее идет линия в бесконечность. Это называется луч.
Луч — это полупрямая, которая имеет точку начала и не имеет конца.
Он так называется потому, что она как луч света. У луча света всегда есть начало. Он всегда начинается либо на солнце, либо на свечки, либо в фонарике, либо на звезде далекой. Дракончики поняли, что такое луч.
Потом мама-дракониха попросила представить дракончиков, что они от прямой отрежут кусочек. Такая фигура называется отрезок. (рис. 3)
Рис. 3
Отрезок — это часть прямой, которая ограничена с двух сторон.
Отрезок может быть длинным или коротким. Дракончики сразу не поняли. Тогда мама нарисовала еще несколько отрезков: длинные и короткие. (рис. 4)
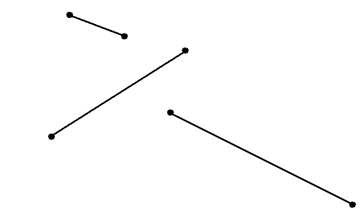
Рис. 4
www.kursoteka.ru
Прямая и ломаная линии | Математика
Прямая линия
Прямая линия есть кратчайшее расстояние между двумя точками.
Это свойство зависит от того, что b) между двумя точками можно провести только одну прямую линию, ибо между двумя точками существует только одно кратчайшее расстояние.
Определение прямой линии, вытекающее из непосредственного усмотрения ее свойства, некоторые называют аксиомой. Это понятие о прямой линии называют иногда основным.
В прямой линии нужно отличить ее положение и ее длину.
Прямую линию можно неопределенно продолжать в обе стороны.
Две точки определяют прямую линии не только в тех точках, которые лежат между ними, но и в тех точках, которые получаются, если неопределенно продолжать прямую линию в обе стороны.
c) Две прямые линии пересекаются в одной точке, ибо точка их пересечения находится на конце прямой линии.
d) Через одну точку можно провести бесчисленное множество прямых линий.
Все линии на чертеже 5 проходят через общую точку A.
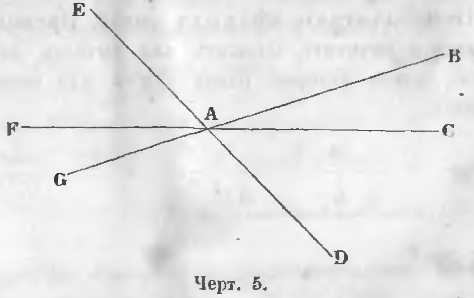
e) Если две прямые имеют две общие точки, то они совпадают всеми остальными точками.
f) Расстояние между двумя точками определяется длиной прямой линии, их соединяющей.
Равные прямые. Две прямые линии, имеющие одинаковую длину, называются равными. Линии AB с CD (черт. 6) будут равными линиями.
Равные прямые совпадают при наложении друг на друга.
Сравнение прямых линий
Чтобы сравнить две данные прямые AB и CD по длине (черт. 7) накладывают линию CD на линию AB так, чтобы точка C совпадала с точкой A.
Здесь могут быть три случая:
Если точка D упадет в точку E, находящуюся между A и B, линия CD меньше AB.
Если точка D упадет в точку B, линия CD равна AB.
Если точка D упадет в точку F, находящуюся на продолжении линии AB, линия CD больше AB.
Сложение и вычитание прямых линий. Прямые линии можно складывать и вычитать. Сложить или вычесть линии значит найти линию, длина которой равна сумме или разности длин данных линий.
Чтобы сложить прямые линии AB, CD, EF (черт. 8), продолжают линию AB и от точки B откладывают линию BG, равную CD, от точки G линию GI равную EF. Линия AI равна сумме всех этих трех линий.
AI = AB + CD + EF.
Чтобы найти разность линий CD и AB, откладывают на линии CD от точки C линию CK, равную AB, тогда линия KD равна разности линий CD и AB.
KD = CD — AB.
Отношение двух прямых линий
Сравнивая две прямые линии по длине, определяют их взаимное отношение. При этом сравнении имеет значение линия, называемая общей мерой двух линий.
Общая мера двух линий есть такая линия, которая содержится целое число раз в обеих линиях.
При определении взаимного отношения двух прямых линий по длине, могут встретиться два случая:
Когда эти линии имеют общую меру.
Когда они ее не имеют.
В первом случае они называются соизмеримыми, во втором — несоизмеримыми. В первом случае отношение двух линий выражается каким-нибудь рациональным, т. е. целым или дробным числом; во втором оно не может быть точно выражено ни целым, ни дробным числом.
Если две прямые линии соизмеримы, то находят их общую меру.
Определение общей меры двух линий
Общая мера двух линий большей AB и меньшей CD (черт. 9) не может быть больше линии CD. Удостоверимся сначала, не будет ли меньшая линия CD этой общей мерой.
Для этого накладывают меньшую линию на большую и определяют, сколько раз она уложится в большей. Если она укладывается ровное число раз, например, m раз, тогда отношение двух линий выражается этим целым числом m.
Действительно, тогда
AB = m * CD и AB/CD = m.
Если же она не укладывается ровное число раз, то последовательно накладывают линию CD до тех пор, пока не получится остатка EB меньшего CD.
Положим, линия CD уложилась в AB два раза и получился еще остаток EB. Общая мера линий AB и CD не может быть более остатка EB.
Действительно, из равенства
AB = 2CD + EB
видно, что общая мера линий AB и CD должна содержаться равное число раз в линии EB. Она может или равняться линии EB или быть меньше ее.
Отсюда заключение:
Общая мера двух линий AB и CD должна быть общей мерой меньшей линии и остатка EB.
Отыскивая общую меру CD и EB, поступаем по предыдущему. Откладываем линию EB на линии CD до тех пор, пока не получится остатка FD, меньшего линии EB. Общая мера CD и EB будет по предыдущему заключению общей мерой EB и FD.
Линию FD снова откладываем по линии EB. Пусть линия FD отложится на линии EB ровно два раза, тогда линия FB и будет этой общей мерой.
Связь между линиями выразится рядом равенств:
AB = 2CD + EB
CD = EB + FD
EB = 2FD
откуда
CD = EB + FD = 2FD + FD = 3FD
AB = 2CD + EB = 2 * 3FD + 3FD = 8FD.
Отношение линий AB и CD выразится равенством:
AB/CD = 8FD/3FD = 8/3.
Мы видим, что при нахождении общей меры нужно поступать точно так же, как при нахождении общего наибольшего делителя между целыми числами. Отсюда
Правило нахождения общей меры двух линий. Чтобы найти общую меру, нужно меньшую линию наложить на большую, первый остаток на меньшую, второй остаток на первый, и поступить так до тех пор, пока последний остаток не уложится ровное число раз в предпоследнем.
Чтобы найти отношение двух линий, нужно при помощи общей меры выразить обе линии и потом найти частное этих выражений.
2-й случай: две прямые линии несоизмеримы. Если две линии несоизмеримы, мы никогда не получим такого остатка, который содержался бы в предпоследнем остатке целое число раз. В этом случае определяют отношение прямых линий с каким угодно приближением. Для этого разделив меньшую линию на n равных частей, накладывают это часть CE на большую линию AB (черт. 10). Положим, что эта часть повторяется в большей линии m раз и еще получается остаток FB меньше CE.
Из равенств
AB = mCE + FB
CD = nCE
имеем
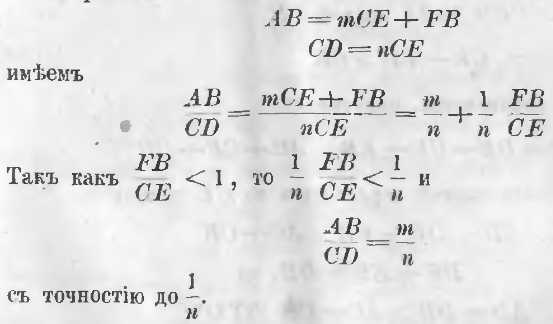
Так как n можно увеличивать произвольно, то и отношение длин двух прямых можно выразить с каким угодно приближением.
(См. о несоизмеримости диагонали квадрата с его стороной).
Измерение линий. Измерить линию значит найти ее отношение к другой линии, принятой за единицу. Это отношение называют длиной данной линии. Длина линии всегда выражается в каких-нибудь единицах.
Ломаные линии
Две линии ACB и ADB (черт. 11), соединяющие концы прямой AB, называются ломаными. При этом линия ACB называется внутренней, а линия ADB внешней ломаной линией.
Теорема 1. Внешняя ломаная больше внутренней.
Даны две ломаные линии: внешняя ADB и внутренняя ACB (черт. 11).
Требуется доказать, что ADB больше ACB или
AD + DB > AC + CB.
Доказательство. Продолжим линию AC до пересечения с линией DB в точке E.
Линия ADE как ломаная больше прямой AE.
AD + DE > AC + CE
Ломаная линия CEB больше прямой CB
CE + EB > CB
Сложив эти неравенства, получим:
AD + DE + CE + EB > AC + CE + CB
Вычтя из обоих частей неравенства по CE, получим:
AD + DE + EB > AC + CB
Так как DE + EB = DB, то
AD + DB > AC + CB.
Что и требовалось доказать.
Теорема 2. Сумма пересекающихся частей ломаных больше суммы непересекающихся.
Даны пересекающиеся ломаные ABC и ADC (черт. 12), AD и BC их пересекающиеся части.
Требуется доказать, что
AD + BC > AB + DC.
Доказательство. Из того, что ломаная AEB больше прямой AB и ломаная CED больше прямой DC вытекают неравенства:
AE + BE > AB
ED + EC > DC
Сложив их, находим:
AE + BE + ED + EC > AB + DC
Так как
AE + ED = AD
BE + EC = BC
то
AD + BC > AB + DC
Что и требовалось доказать.
maths-public.ru
3.2. Прямая линия на плоскости
Прямую линию на плоскости относительно системы прямоугольных декартовых координат можно задать различными способами и в результате получить различные виды уравнения прямой.
 .Общим уравнениемпрямой на плоскости называется уравнение
вида
.Общим уравнениемпрямой на плоскости называется уравнение
вида
. (3.7)
. Уравнение прямой с заданным угловым коэффициентом , (3.8)
г
Рис. 3.1
деугловой коэффициентом прямой, 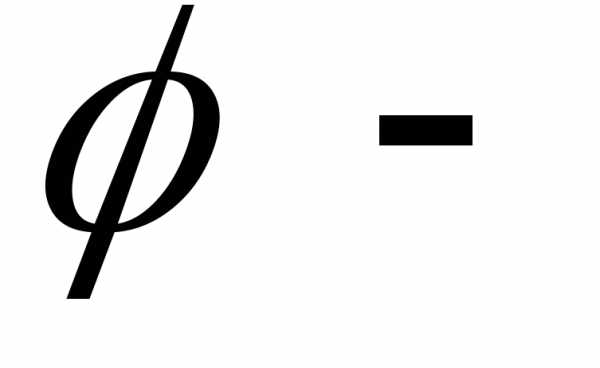 угол наклона прямой к положительному
угол наклона прямой к положительному
направлению оси 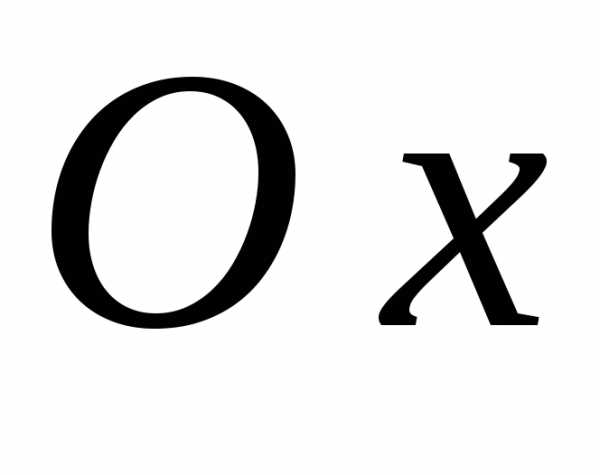 ,
,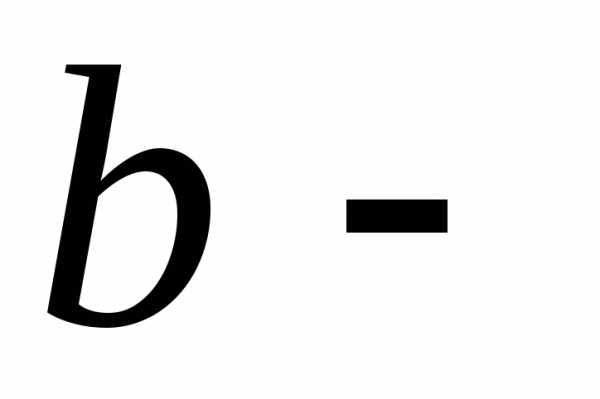 величина отрезка,
величина отрезка,
отсекаемая прямой на оси 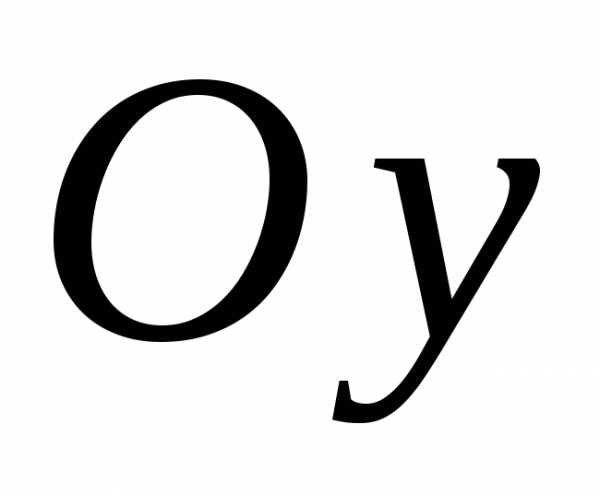 (рис.3.2).
(рис.3.2).
. Уравнение прямой в отрезках на осях
 ,
(3.9)
,
(3.9)
где 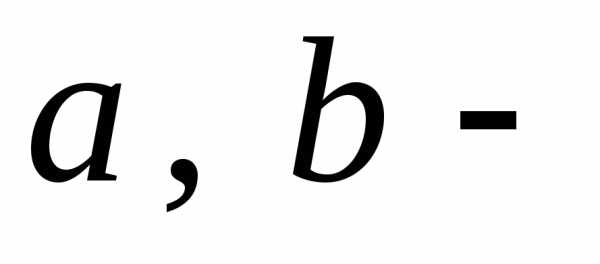 отрезки, отсекаемые прямой на осях
координат (рис. 3.2).
отрезки, отсекаемые прямой на осях
координат (рис. 3.2).
 .
.
Рис. 3.1
Уравнениепрямой, проходящей через две точкии  . (3.10)
. (3.10)
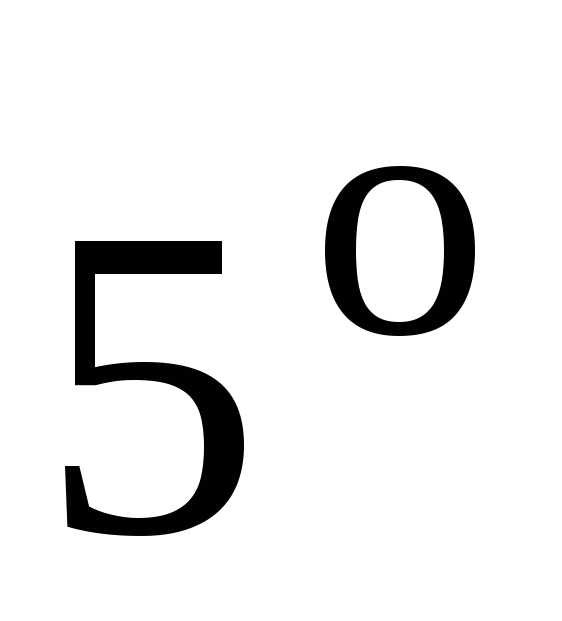 .Нормальное уравнение прямой
.Нормальное уравнение прямой
, (3.11)
где 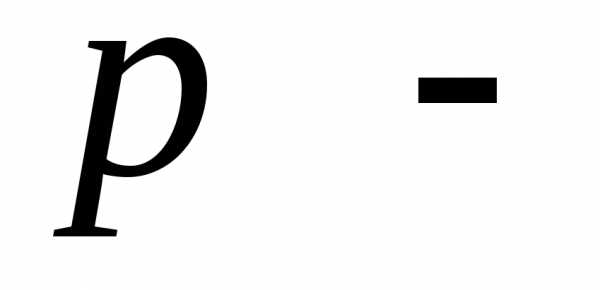 длина перпендикуляра, опущенного
на прямую из начала
длина перпендикуляра, опущенного
на прямую из начала
координат, 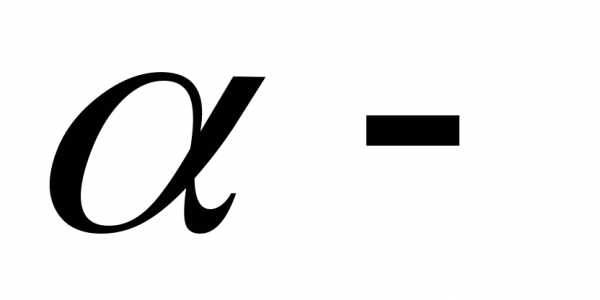 угол, отсчитываемый от положительного
направления оси
угол, отсчитываемый от положительного
направления оси
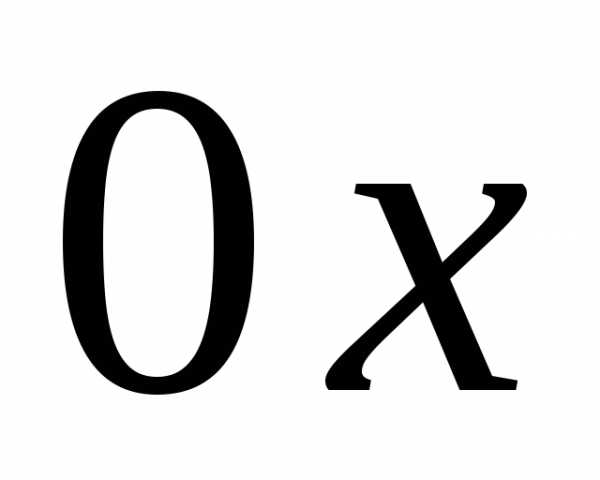 против часовой стрелки до перпендикуляра
против часовой стрелки до перпендикуляра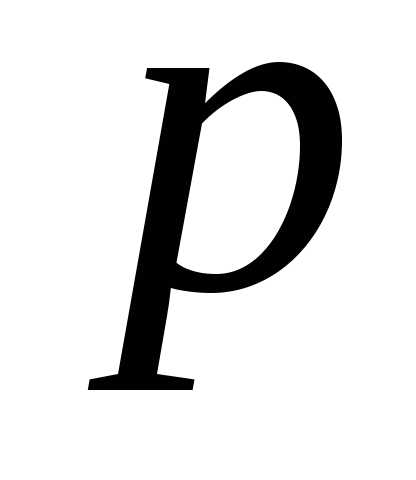 (рис. 3.2).
(рис. 3.2).
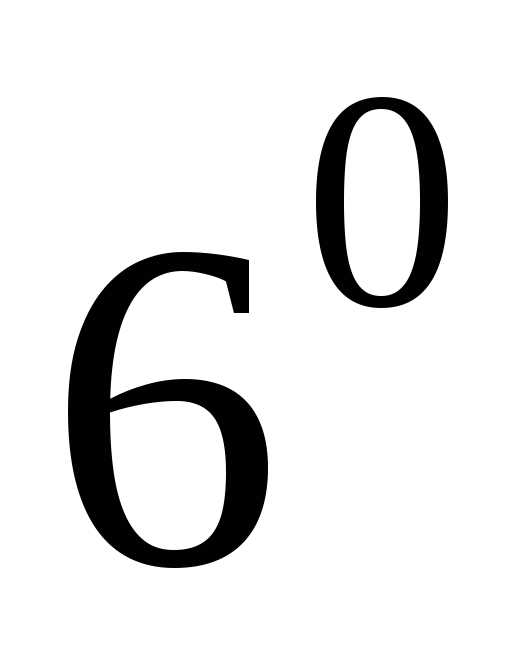 . Задачи на прямую линию
. Задачи на прямую линию
1. Если прямые заданы общими уравнениями и , тоугол между двумя прямыминаходится по формуле
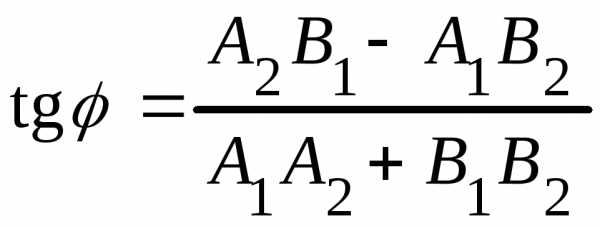 .
(3.12)
.
(3.12)
Если прямые заданы уравнениями
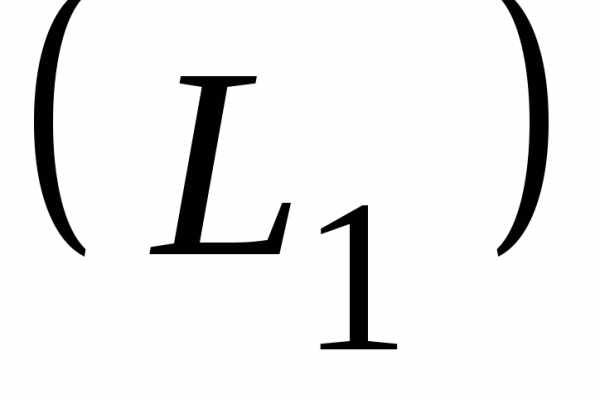 и,
и,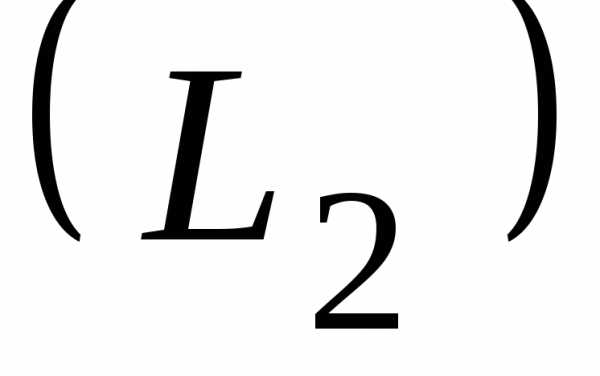
(рис. 3.3) то формула (3.12) принимает вид
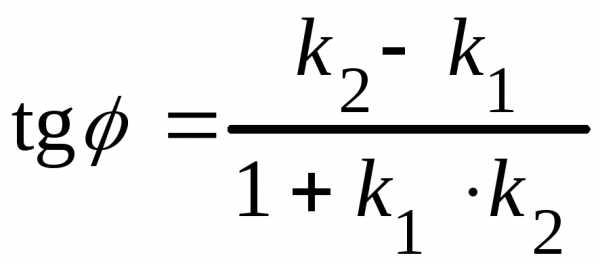 ,
(3.13)
,
(3.13)
где 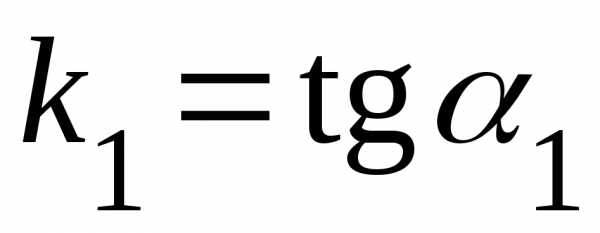 ,
,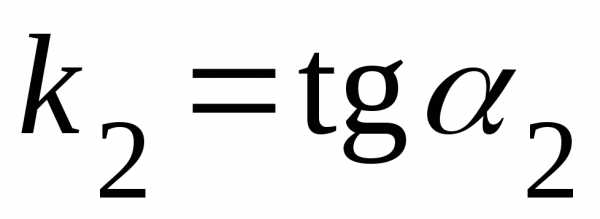 ,
,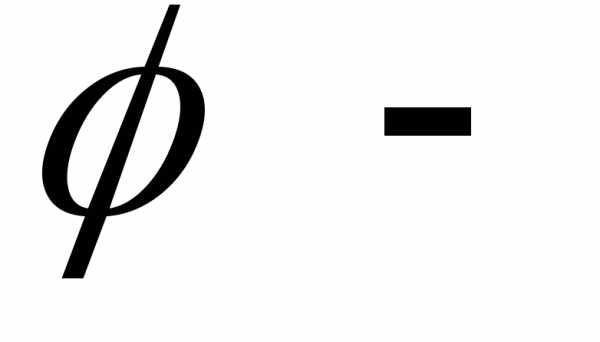 угол, отсчи-
угол, отсчи-
тываемый от прямой 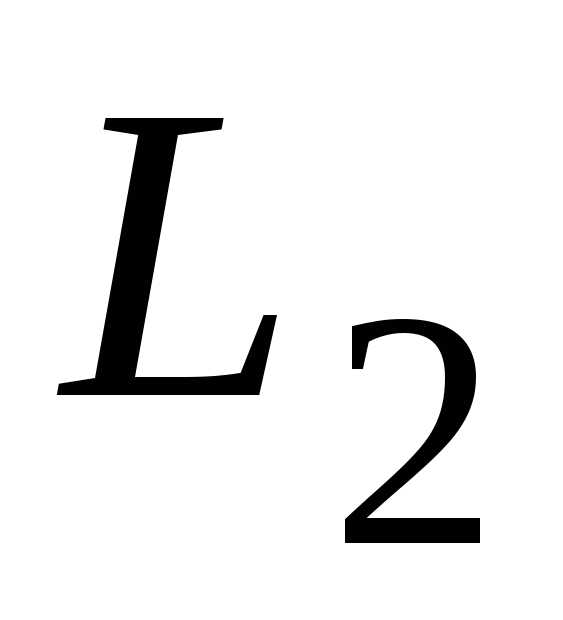 до прямой
до прямой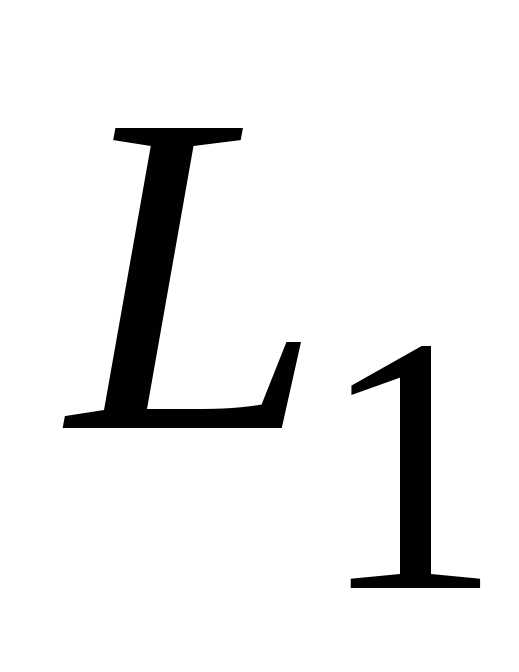 по
по
часовой стрелке.
Условие параллельности прямых
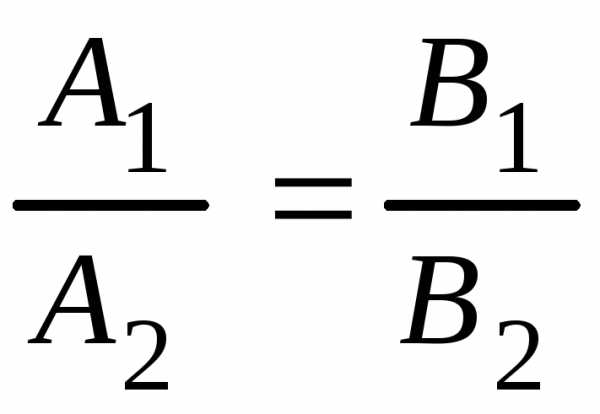 или
или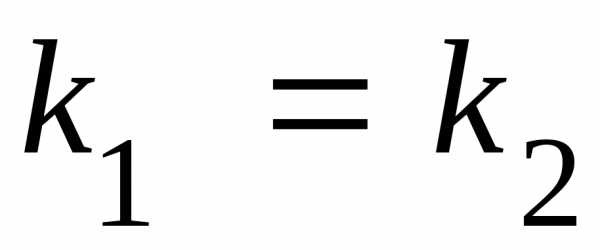 .
(3.14)
.
(3.14)
Условие перпендикулярностипрямых
или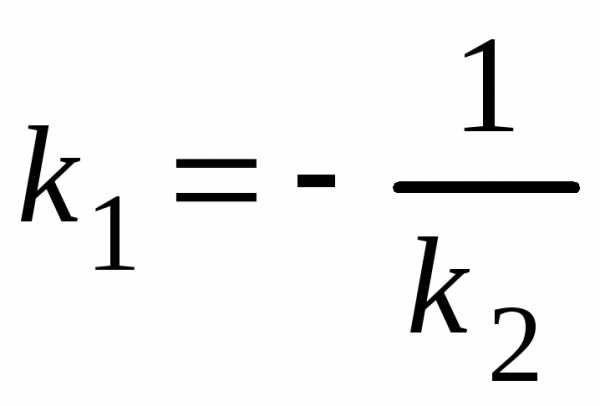 .
(3.15)
.
(3.15)
2. Точка пересечения двух прямых, заданных общими уравнениями
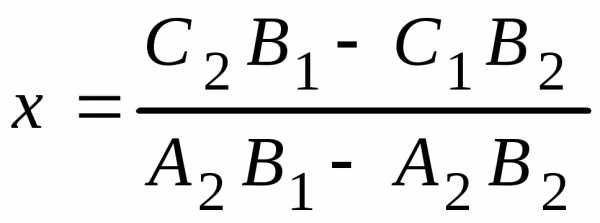 ;
;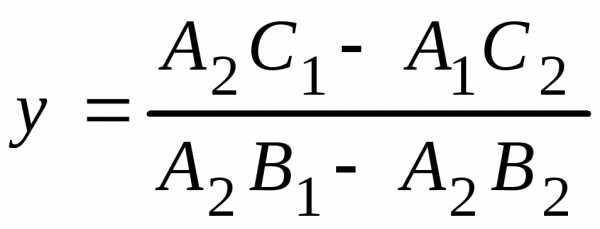 . (3.16)
. (3.16)
3. Уравнение пучка прямых
Пучком прямых, проходящих через заданную точку называют совокупность всех прямых, проходящих через эту точку
. (3.17)
Уравнение пучка прямых, проходящих через точку пересечения двух данных прямых имеет вид
. (3.18)
Здесь параметр  неопределен.
неопределен.
4. Расстояние от данной точки до прямой
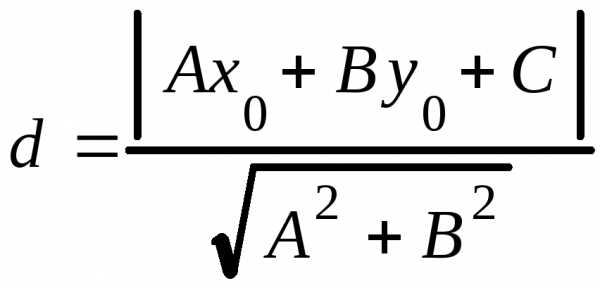 . (3.19)
. (3.19)
3.2.1. Решение типовых примеров задания 5 РГР
1. Даны
координаты вершин треугольника 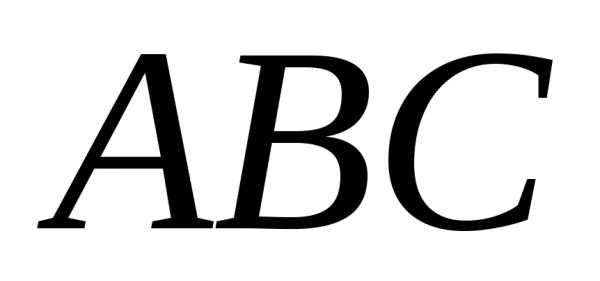 :,
,.Найти: 1) длину стороны
:,
,.Найти: 1) длину стороны 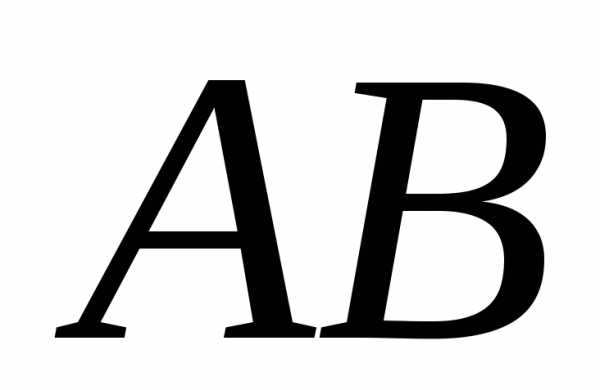 ;
2) уравнение стороны
;
2) уравнение стороны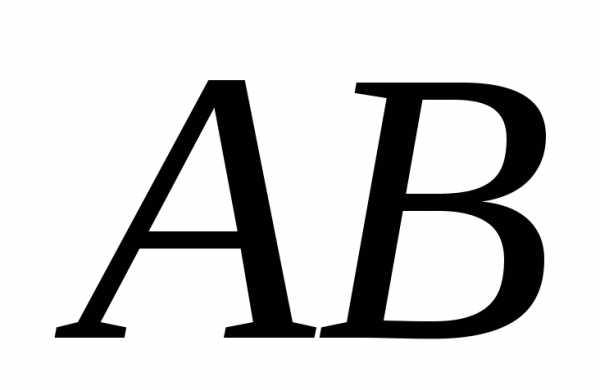 и ее угловой коэффициент; уравнение
стороны
и ее угловой коэффициент; уравнение
стороны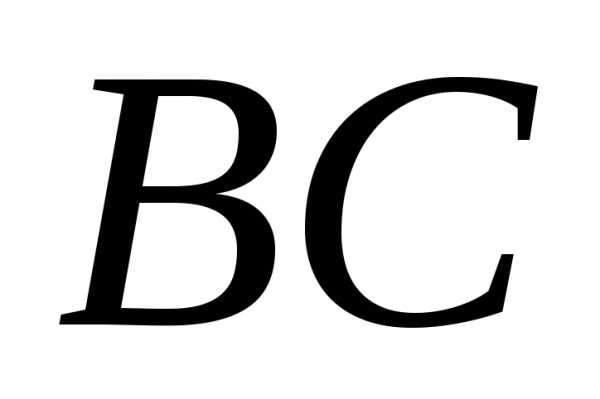 ;
3) угол
;
3) угол в градусах;4)
уравнение высоты
в градусах;4)
уравнение высоты 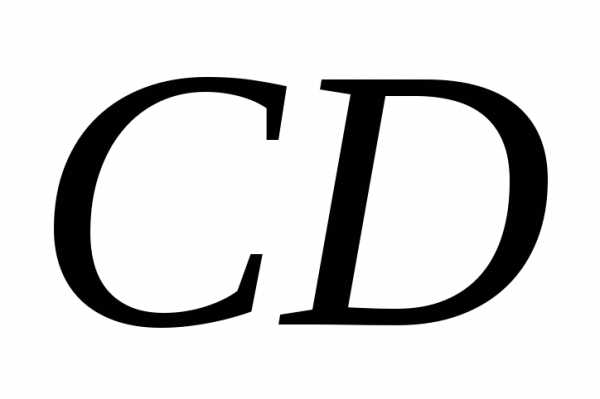 и ее длину; 5) уравнение медианы
и ее длину; 5) уравнение медианы и координаты точки
и координаты точки ,
пересечения этой медианы с высотой
,
пересечения этой медианы с высотой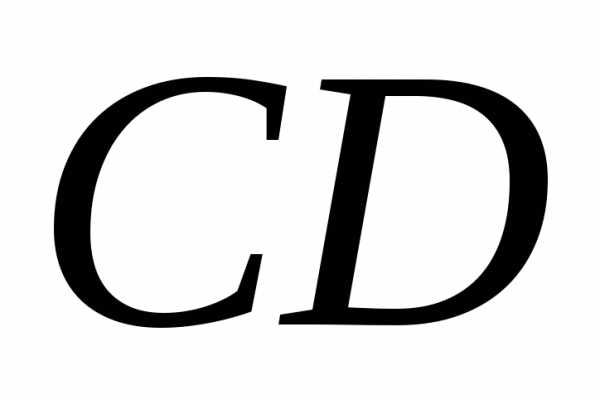 ;
6) уравнение прямой
;
6) уравнение прямой ,
проходящей через точку
,
проходящей через точку ,
параллельно стороне
,
параллельно стороне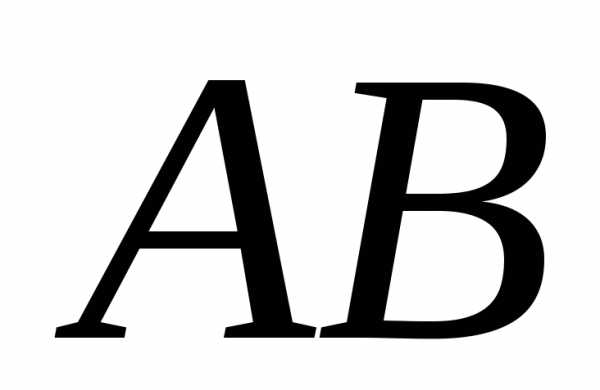 .
.
Решение.1. Расстояние между точками
между точками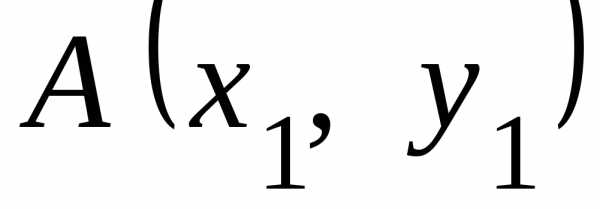 иравно
иравно
.
В нашем случае
,и длина стороны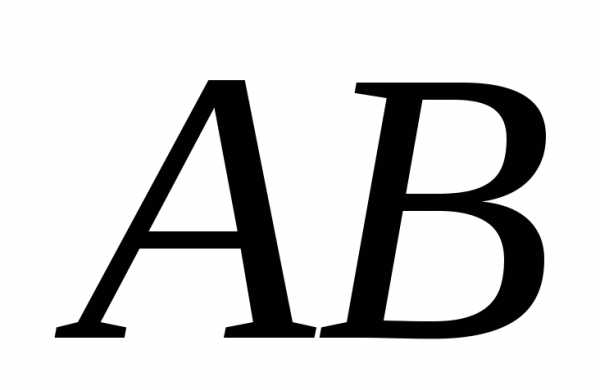
15 ед. длины.
2. Запишем уравнение прямой, проходящей черези
;.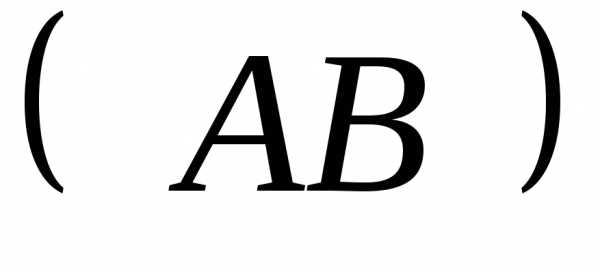 .
.
Решив последнее уравнение относительно у, находим:
; ,
откуда
,
откуда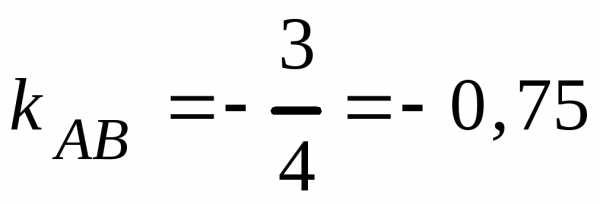 .
.
Подставив в (3.10) координаты точек  и
и ,
получим уравнение
,
получим уравнение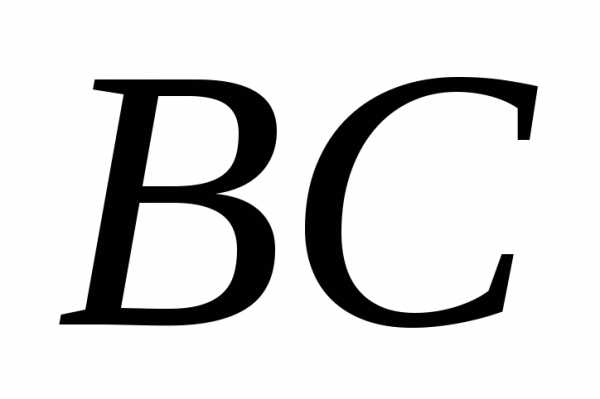 :
:
;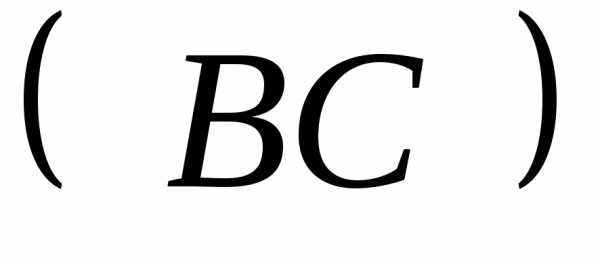 .
.
Искомый 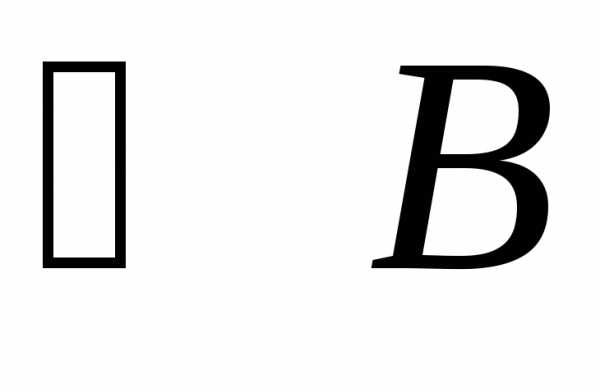 образован прямыми
образован прямыми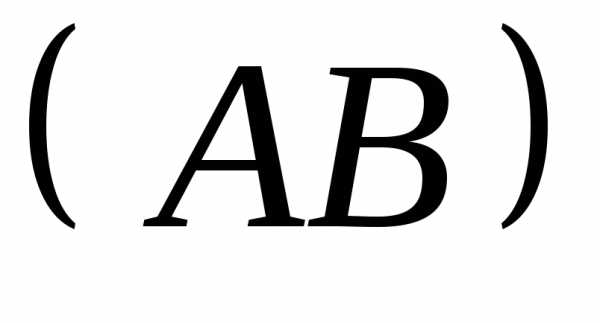 и
и 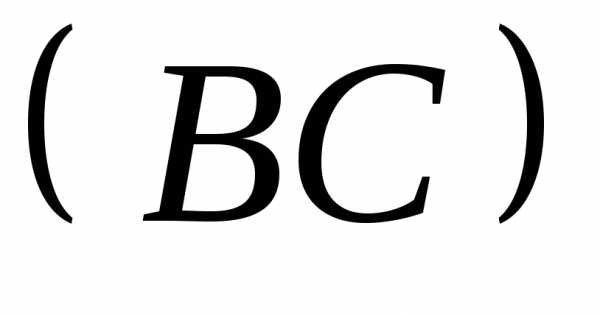 ,
коэффициенты которых
,
коэффициенты которых 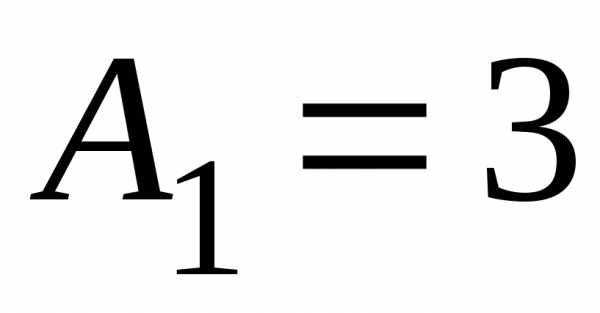 ,
,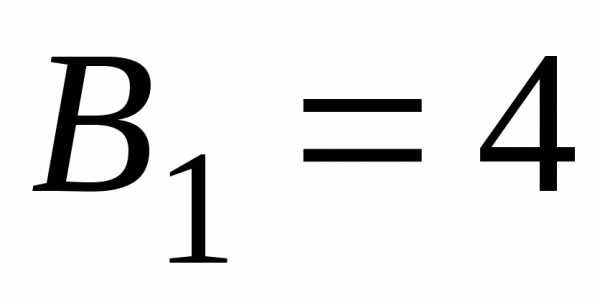 ,,
,,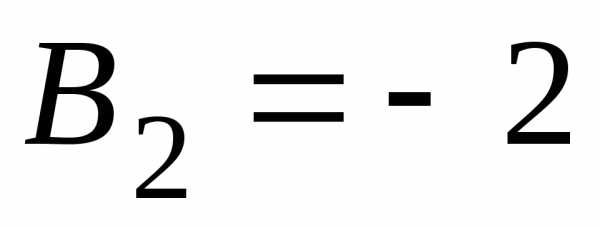 .
Подставив значения угловых коэффициентов
в (3.12), получим
.
Подставив значения угловых коэффициентов
в (3.12), получим
; рад или.
4.
Высота  перпендикулярна стороне
перпендикулярна стороне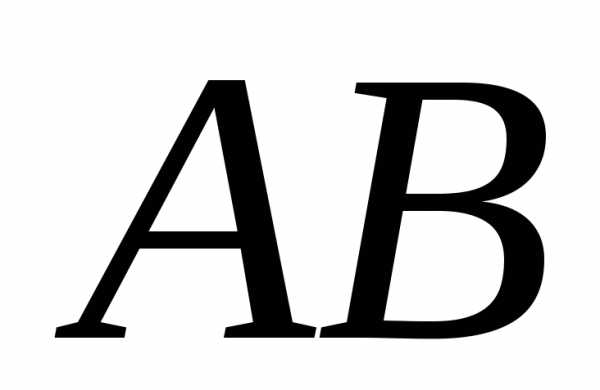 . Чтобы найти ее угловой коэффициент,
воспользуемся условием перпендикулярности
прямых
. Чтобы найти ее угловой коэффициент,
воспользуемся условием перпендикулярности
прямых
.
Подставив в уравнение пучка прямых
координаты точки  и найден-ный угловой коэффициент, получим
уравнение высоты
и найден-ный угловой коэффициент, получим
уравнение высоты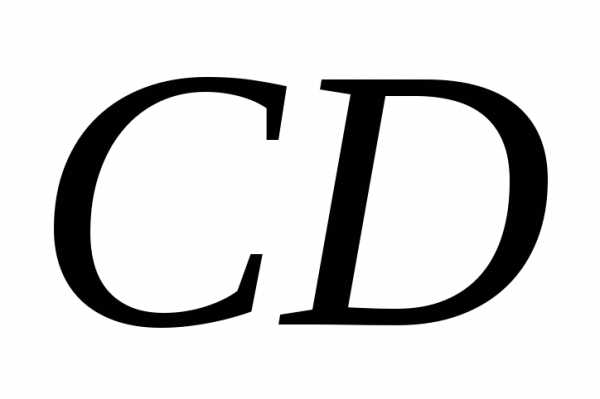
 .
.
Длину высоты 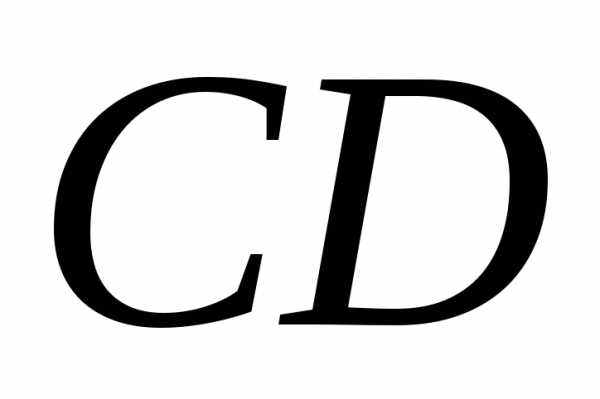 найдем как расстояние от точки
найдем как расстояние от точки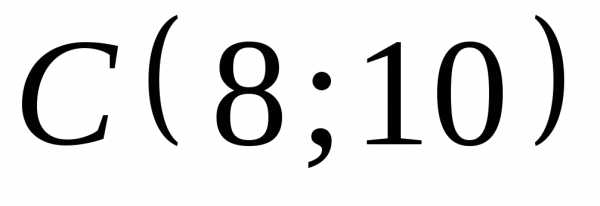 до прямой
до прямой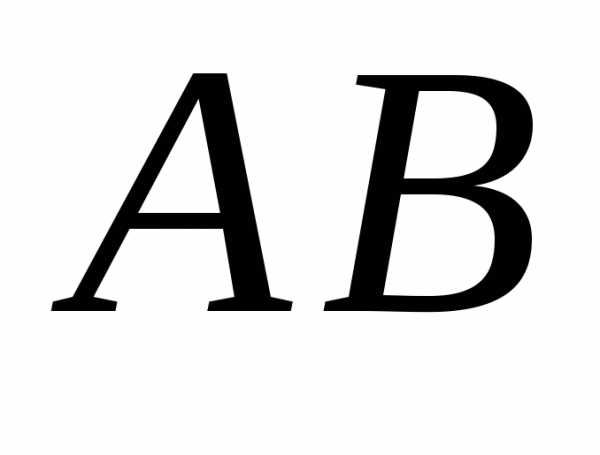 по формуле (3.19), где
по формуле (3.19), где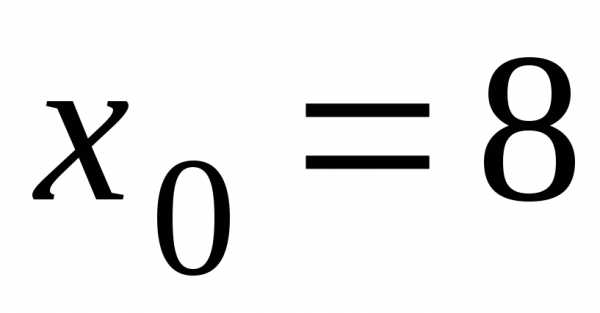 ,
,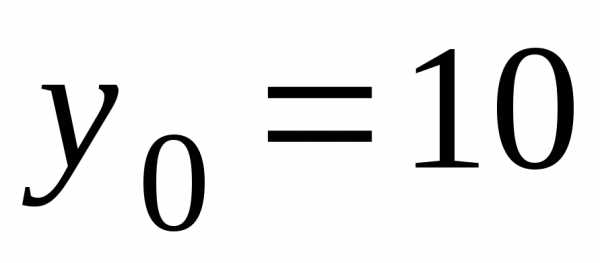 ,
, ,
,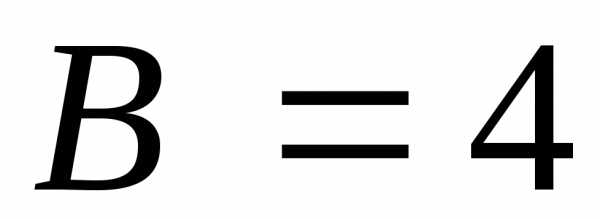 ,
,
(ед. длины).
5. Найдем координаты точки  ,
принадлежащей медиане
,
принадлежащей медиане :
:
.
Подставив в (3.10) координаты точек  и
и ,
находим уравнение медианы:
,
находим уравнение медианы:
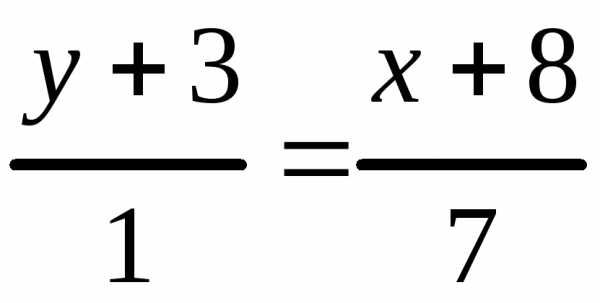 ;
; .
.
Координаты точки  пересечения высоты
пересечения высоты и медианы
и медианы найдем, учитывая, что в данном случае
найдем, учитывая, что в данном случае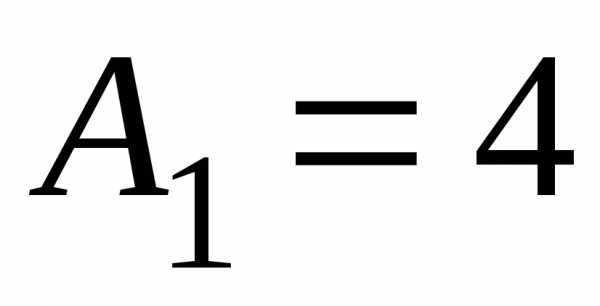 ,
,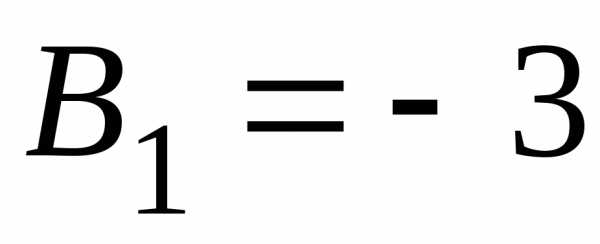 ,
, ;
;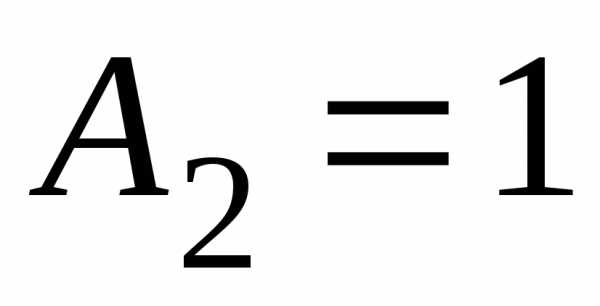 ,
,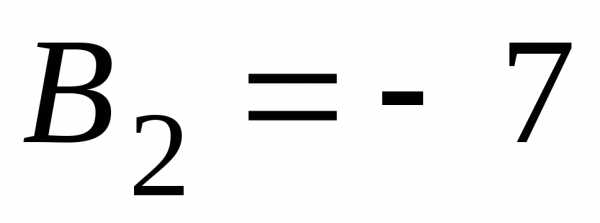 ,
,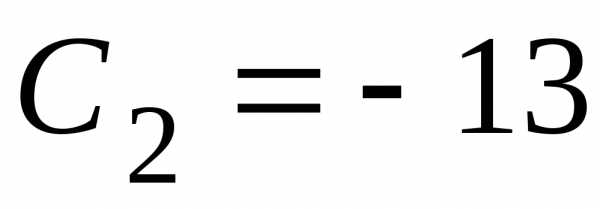
;;.
6. Так как искомая прямая параллельна
стороне
, то ее угловой коэффициент равен
угловому коэффициенту прямой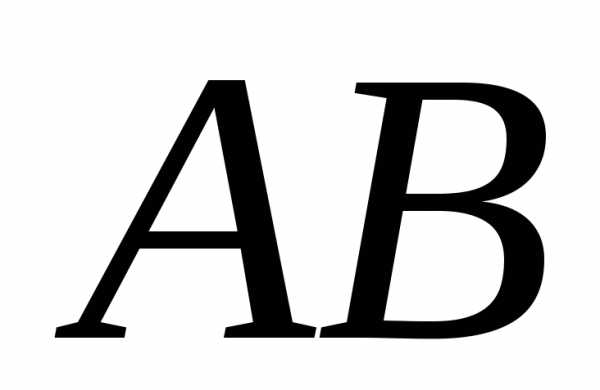 :
:
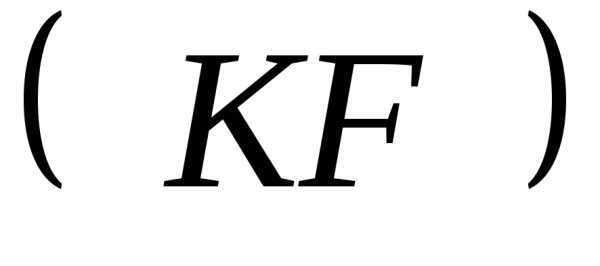 .
.
Треугольник 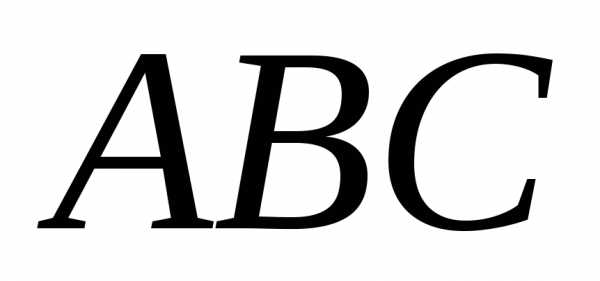 ,высота
,высота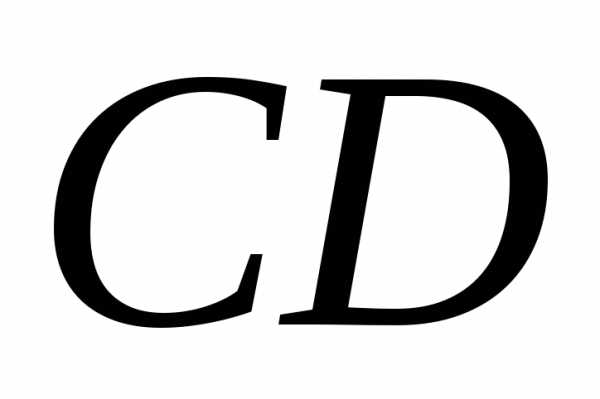 ,
медиана
,
медиана ,прямая
,прямая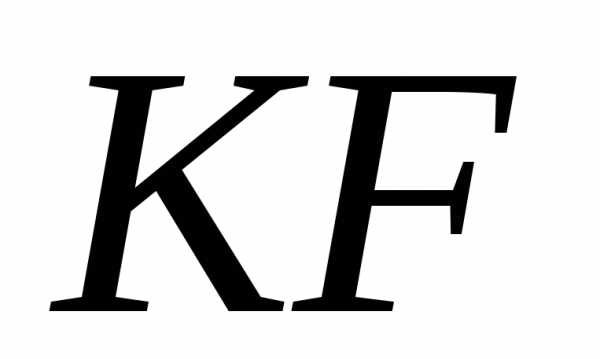 и точкаМпостроены в системе
координатхОуна рис.3.4.
и точкаМпостроены в системе
координатхОуна рис.3.4.
Рис. 3.4
studfiles.net
Прямая линия — это… Что такое Прямая линия?
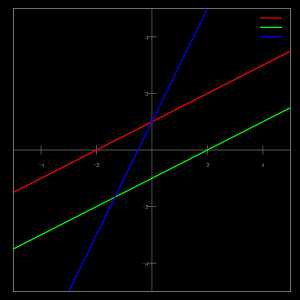
Прямая — одно из основных понятий геометрии.
При систематическом изложении геометрии прямая линия обычно принимается за одно из исходных понятий, которое лишь косвенным образом определяется аксиомами геометрии.
Если основой построения геометрии служит понятие расстояния между двумя точками пространства, то прямую линию можно определить как линию, путь вдоль которой равен расстоянию между двумя точками.
Аналитически прямая задаётся уравнением (в трёхмерном пространстве — системой уравнений) первой степени.
- Через любые две несовпадающие точки можно провести единственную прямую.
- Две несовпадающие прямые на плоскости или пересекаются в единственной точке, или являются параллельными.
- В трёхмерном пространстве существуют три варианта взаимного расположения двух прямых:
- Прямая линия — алгебраическая линия первого порядка: в декартовой системе координат прямая линия задается на плоскости уравнением первой степени (линейное уравнение).
Уравнения прямой на плоскости
 Способы задания прямой:
Способы задания прямой:или
Общее уравнение прямой линии на плоскости в декартовых координатах:
где A и B одновременно не равны нулю. При C = 0 прямая проходит через начало координат.
Уравнение прямой с угловым коэффициентом. Прямая линия, пересекающая ось Oy в точке и образующая угол φ с положительным направлением оси Ox:
Коэффициент k называется угловым коэффициентом прямой. В этом виде невозможно представить прямую, параллельную оси Oy.
Уравнение прямой в отрезках. Прямая линия, пересекающая ось Ox в точке и ось Oy в точке :
В этом виде невозможно представить прямую, проходящую через начало координат.
Нормальное уравнение прямой:
где p — длина перепендикуляра, опущенного на прямую из начала координат, а θ — угол (измеренный в положительном направлении) между положительным направлением оси Ox и направлением этого перпендикуляра. Если p = 0, то прямая проходит через начало координат, а угол задаёт угол наклона прямой.
Если прямая задана общим уравнением Ax + By + C = 0, то отрезки a и b, отсекаемые ею на осях, угловой коэффициент k, расстояние прямой от начала координат p, cosθ и sinθ выражаются через коэффициенты A, B и C следующим образом:
Во избежание неопределённости знак перед радикалом выбирается так, чтобы соблюдалось условие p > 0. В этом случае cosθ и sinθ являются направляющими косинусами положительной нормали прямой — перпендикуляра, опущенного из начала координат на прямую. Если C = 0, то прямая проходит через начало координат и выбор положительного напрвления произволен.
Уравнение прямой, проходящей через две заданные несовподающие точки и
или
или в общем виде
Параметрические уравнения прямой могут быть записаны в виде:
где t — производный параметр, при этом
Уравнение прямой в полярных координатах ρ и φ:
или
Тангенциальное уравнение прямой на плоскости:
- ξx + ηy = 1
Числа ξ и η называются её тангенциальными, линейными или плюккеровыми координатами.
Уравнения прямой в пространстве
Каноническое уравнение прямой в пространстве:
- Пусть M(x0,y0,z0) — точка, лежащая на прямой, и — вектор, ей коллинеарный. Тогда уравнение прямой имеет вид:
Взаимное расположение точек и прямых
Три точки и лежат на одной прямой тогда и только тогда, если выполняется условие
Отклонение точки от прямой Ax + By + C = 0 может быть найдено по формуле
где знак перед радикалом противоположен знаку C. Отклонение по модулю равно расстоянию между точкой и прямой; оно положительно, если точка и начало координат лежат по разные стороны от прямой, и отрицательно, если по одну сторону.
Взаимное расположение нескольких прямых
Две прямые, заданные уравнениями
или
пересекаются в точке
Угол γ12 между пересекающимися прямыми определяется формулой
При этом под γ12 понимается угол, на который надо повернуть первую прямую (заданную параметрамиA1, B1, C1, k1 и b1) вокруг точки пересечения против часовой стрелки до первого совмещения со второй прямой.
Эти прямые параллельны, если A1B2 − A2B1 = 0 или k1 = k2, и перпендикулярны, если A1A2 + B1B2 = 0 или
Любую прямую, паралельную A1x + B1y + C1 = 0, можно выразить уравнением A1x + B1y + C = 0. При этом расстояние между ними будет равно
Если знак перед радикалом противоположен C1, то δ будет положительным, когда вторая прямая и начало координат лежат по разные стороны от первой прямой.
Для того, чтобы три прямые
пересекались в одной точке или были параллельны друг другу, необходимо и достаточно, чтобы выполнялось условие
См. также
Ссылки
Wikimedia Foundation. 2010.
dic.academic.ru
Прямая — это… Что такое Прямая?
Прямая — одно из основных понятий геометрии, то есть точного универсального определения не имеет.
При систематическом изложении геометрии прямая линия обычно принимается за одно из исходных понятий, которое лишь косвенным образом определяется аксиомами геометрии.
Если основой построения геометрии служит понятие расстояния между двумя точками пространства, то прямую линию можно определить как линию, путь вдоль которой равен расстоянию между двумя точками.
Аналитически прямая задаётся уравнением (в трёхмерном пространстве — системой уравнений) первой степени.
- Через любые две несовпадающие точки можно провести единственную прямую.
- Две несовпадающие прямые на плоскости или пересекаются в единственной точке, или являются параллельными.
- В трёхмерном пространстве существуют три варианта взаимного расположения двух прямых:
- Прямая линия — алгебраическая линия первого порядка: в декартовой системе координат прямая линия задается на плоскости уравнением первой степени (линейное уравнение).
Уравнения прямой на плоскости
 Способы задания прямой:
Способы задания прямой:или .
Общее уравнение прямой
Общее уравнение прямой линии на плоскости в декартовых координатах:
где , и — произвольные постоянные, причем постоянные и не равны нулю одновременно. Вектор с координатами точки называется нормальным вектором, он перпендикулярен прямой.
При прямая проходит через начало координат. Также уравнение можно переписать в виде
Уравнение прямой с угловым коэффициентом
Уравнение прямой линии, пересекающей ось в точке и образующей угол с положительным направлением оси :
Коэффициент называется угловым коэффициентом прямой. В этом виде невозможно представить прямую, параллельную оси
Получение уравнения прямой в отрезкахУравнение прямой в отрезках
Уравнение прямой линии, пересекающей ось в точке и ось в точке :
В этом виде невозможно представить прямую, проходящую через начало координат.
Нормальное уравнение прямой
где — длина перпендикуляра, опущенного на прямую из начала координат, а — угол (измеренный в положительном направлении) между положительным направлением оси и направлением этого перпендикуляра. Если , то прямая проходит через начало координат, а угол задаёт угол наклона прямой.
Вывод нормального уравнения прямой
Если прямая задана общим уравнением то отрезки и отсекаемые ею на осях, угловой коэффициент расстояние прямой от начала координат и выражаются через коэффициенты , и следующим образом:
Во избежание неопределённости знак перед радикалом выбирается так, чтобы соблюдалось условие В этом случае и являются направляющими косинусами положительной нормали прямой — перпендикуляра, опущенного из начала координат на прямую. Если то прямая проходит через начало координат и выбор положительного направления произволен.
Уравнение прямой, проходящей через две заданные несовпадающие точки
Если заданы две несовпадающие точки с координатами и , то прямая, проходящая через них, задаётся уравнением
или
или в общем виде
Векторное параметрическое уравнение прямой
Векторное параметрическое уравнение прямой задается вектором конец которого лежит на прямой, и направляющим вектором прямой Параметр пробегает все действительные значения.
Параметрические уравнения прямой
Параметрические уравнения прямой могут быть записаны в виде:
где — производный параметр, — координаты и направляющего вектора прямой. При этом
Смысл параметра аналогичен параметру в векторно-параметрическом уравнении.
Каноническое уравнение прямой
Каноническое уравнение получается из параметрическиx уравнений делением одного уравнения на другое:
где — координаты и направляющего вектора прямой, и координаты точки, принадлежащей прямой.
Уравнение прямой в полярных координатах
Уравнение прямой в полярных координатах и :
или
Тангенциальное уравнение прямой
Тангенциальное уравнение прямой на плоскости:
Числа и называются её тангенциальными, линейными или плюккеровыми координатами.
Уравнения прямой в пространстве
Векторное параметрическое уравнение прямой в пространстве:
где — радиус-вектор некоторой фиксированной точки лежащей на прямой, — ненулевой вектор, коллинеарный этой прямой (называемый её направляющим вектором), — радиус-вектор произвольной точки прямой.
Параметрические уравнения прямой в пространстве:
где — координаты некоторой фиксированной точки лежащей на прямой; — координаты вектора, коллинеарного этой прямой.
Каноническое уравнение прямой в пространстве:
где — координаты некоторой фиксированной точки лежащей на прямой; — координаты вектора, коллинеарного этой прямой.
Общее векторное уравнение прямой[уточнить] в пространстве:
- Поскольку прямая является пересечением двух различных непараллельных плоскостей, заданных соответственно общими уравнениями:
- и
то уравнение прямой можно задать системой этих уравнений:
Векторное уравнение прямой в пространстве[1]:196-199:
- Уравнение прямой в пространстве можно записать в виде векторного произведения радиуса-вектора произвольной точки этой прямой на фиксированный направляющий вектор прямой :
где фиксированный вектор , ортогональный вектору , можно найти, подставляя в это уравнение радиус-вектор какой-нибудь одной известной точки прямой.
Взаимное расположение точек и прямых на плоскости
Три точки , и лежат на одной прямой тогда и только тогда, когда выполняется условие
Отклонение точки от прямой может быть найдено по формуле
где знак перед радикалом противоположен знаку Отклонение по модулю равно расстоянию между точкой и прямой; оно положительно, если точка и начало координат лежат по разные стороны от прямой, и отрицательно, если по одну сторону.
В пространстве расстояние от точки до прямой, заданной параметрическим уравнением
можно найти как минимальное расстояние от заданной точки до произвольной точки прямой. Коэффициент этой точки может быть найден по формуле
Взаимное расположение нескольких прямых на плоскости
Две прямые, заданные уравнениями
или
пересекаются в точке
Угол между пересекающимися прямыми определяется формулой
При этом под понимается угол, на который надо повернуть первую прямую (заданную параметрами , , , и ) вокруг точки пересечения против часовой стрелки до первого совмещения со второй прямой.
Эти прямые параллельны, если или , и перпендикулярны, если или .
Любую прямую, параллельную прямой с уравнением можно выразить уравнением При этом расстояние между этими прямыми будет равно
Если знак перед радикалом противоположен то будет положительным, когда вторая прямая и начало координат лежат по разные стороны от первой прямой.
Для того, чтобы три прямые
пересекались в одной точке или были параллельны друг другу, необходимо и достаточно, чтобы выполнялось условие
Если и , то прямые и перпендикулярны.
См. также
Примечания
Ссылки
dic.academic.ru
