Пример журнала: Образец оформления журнала «Интернаука»

Пример статьи для журнала Скопус (международного журнала)

 Скачать пример научной статьи для журнала из списка Скопус (международного журнала)

---

полный текст доступен по ссылке выше

ИССЛЕДОВАНИЕ ОСНОВНЫХ ХАРАКТЕРИСТИК БОРТОВОЙ ДРОССЕЛЬНОЙ СИСТЕМЫ ОХЛАЖДЕНИЯ ИК-ПРИЕМНИКА НА ОСНОВЕ  БАЛЛОНА С КРИОГЕННОЙ ЗАПРАВКОЙ

А.И. Довгялло, С.О. Некрасова, Д.В. Сармин, Д.А. Угланов

Самарский государственный аэрокосмический университет имени академика С.П. Королева (национальный исследовательский университет), г. Самара, Московское шоссе 34

 

Abstract: В этой статье описывается новый резервуар с криогенной заправкой (жидкий азот). На основании этого резервуара, предлагается создать систему охлаждения заслонки, которая может иметь улучшенные характеристики по сравнению с системой охлаждения на основе высокого давления. Данная статья посвящена первым результатам испытаний резервуаров с криогенной заправкой (жидкий азот), которые были сделаны на уровне давления до 4 МПа. Также показано, что поведение параметров в баке во времени соответствует расчетной модели.

Keywords: Баллон с криогенной заправкой, дроссельная система охлаждения, криогенная техника, холодопроизводительность

1. Введение

В настоящее время обеспечение охлаждения  ИК – приемников, элементов оптических систем и других устройств, устанавливаемых на летательных аппаратах, является важнейшим требованием, предъявляемым ко многим аэрокосмическим проектам [1]. Система охлаждения может иметь различные параметры по массе, потребляемой мощности, габаритам, надежности, холодопроизводительности и температуры термостатирования.
Бортовые системы охлаждения можно разделить на три основных типа:  

термомеханические системы охлаждения с замкнутым циклом;

системы охлаждения одноразового действия с разомкнутым циклом, использующие, например, газ высокого давления;

вихревые системы охлаждения [8].

Эти системы используют хладагенты, находящиеся либо в субкритическом, либо в суперкритическом состоянии, отвержденные хладагенты, а также жидкие, сохраняемые при комнатных температурах.
Простейшей и наименее дорогой системой охлаждения одноразового действия является система охлаждения, основанная на эффекте Джоуля – Томпсона и использующая газ под высоким давлением от 7 до 60 МПа.
Использование гелия, водорода, аргона или азота дает возможность обеспечить температурный уровень охлаждения от 74К до 4,2К при суммарной мощности тепловыделения объекта от 0,1 до 10 Вт.
К  рабочим телам баллонных дроссельных систем предъявляются повышенные требования по их чистоте, что осуществляется за счет их регазификации из криогенно-жидкого состояния, после чего они заправляются в баллон компримированием или перепуском из аккумуляторов высокого давления.

Время функционирования дроссельных систем охлаждения зависит от массы заправки и потребной холодопроизводительности.
Использование в космической технике криогенных жидкостей для  систем охлаждения  на борту летательных аппаратов также имеет место. Но по некоторым требованиям эксплуатации их применение вызывает определенные трудности.
Таким образом, из приведенного выше следует, что объективно полезным и своевременным  будет разработка и создание универсального оборудования, способного удовлетворять существующим технологиям применения компримированных газов и криогенных жидкостей.
Так, например, на газонаполнительных компрессорных станциях при существующей  инфраструктуре и технологиях заправки было бы уместно совместить применяемый в настоящее время способ наполнения баллонов компримированием  с заправкой из криогенно – жидкого состояния.

2. Баллон с криогенной заправкой

3.Дроссельная система охлаждения на основе баллона с криогенной заправкой  

4.Имитационные испытания баллона с криогенной заправкой для дроссельной системы охлаждения

5.Технико-экономическая оценка применения баллона с криогенной заправкой

6.Выводы

7. Заключение

Конфликт интересов

Благодарности

ССЫЛКИ

[1] Красночуб, Е.К. Микрокриогенные системы охлаждения космических летательных аппаратов инфракрасного наблюдения на основе микрокриогенных систем [Текст] / Е.К. Красночуб // Полет. – Самара, 2004. – №11. – С. 41-48.
[2] Патент  2163699, Российская  Федерация,   МПК 7F17C9/02/ Топливный баллон [Текст]  / А.И. Довгялло, С.В. Лукачев и др.  заявитель и  патентообладатель  СГАУ.  –  №9911457706 заявл. 02.07.1997, опубл. 27.02.2001. Бюл. №6

[3] Довгялло А.И., Угланов Д.А. Теплообмен и термоциклическая прочность  в топливном баллоне с криогенной заправкой// Вестник СГАУ. – 2007. — №2.
[4] А.И. Довгялло, А.П. Логашкин, Д.В. Сармин, Д.А. Угланов. Анализ работы баллоного микроохладителя при использовании азота с околокритическими параметрами. Вестник Самарского государственного аэрокосмического университета им. С.П. Королева, 2009, №3 (Ч.2), с. 143-146.
[5] А.И. Довгялло, Д.В. Сармин, Д.А.Угланов. Предварительные исследования тепловых процессов в баллоне с криогенной заправкой   бортовой дроссельной системы// Вестник Самарского государственного аэрокосмического университета им. С.П. Королева, – 2011 —  №3 (Ч.4), с. 78-85
[6] Д.В. Сармин., С.О. Некрасова Д.А. Угланов, А.И. Довгялло /Имитационные испытания баллона с криогенной заправкой для дроссельной системы охлаждения и ее сравнительные характеристики [Текст]  // Прикладная физика, 2013. – № 4. – С. 54-59.
[7] А.И. Довгялло, А.П. Логашкин, Д.В. Сармин,  Д.А. Угланов , Е.С. Шатохин Сравнение  массовых характеристик баллона с криогенной заправкой и баллона высокого давления для дроссельной системы охлаждения Вестник Самарского государственного аэрокосмического университета им. С.П. Королева., 2013, №3,  112-118
[8] Biryuk, V.V.Vortex effect of gas energy separation in aircraft engineering and technology;(1993) Izvestiya Vysshikh Uchebnykh Zavedenij. Aviatsionnaya Tekhnika, (2), pp. 20-23.  

---

Образцы и бланки журналов регистраций 2023 года

Журнал регистрации нужен для отражения факта формирования/поступления в компанию какого-либо документа. Он подразделяется на множество видов. Некоторые виды книг нужно вести на протяжении всего года, другие заводятся на короткий срок. Журналы позволяют упорядочить документооборот, систематизировать его по хронологическому принципу.

Функции журнала регистрации

Журнал регистрации наделен следующими функциями:

• Фиксация даты регистрации, от которой будет отсчитываться срок выполнения документа.
• Упорядочивание справочных данных о документации.
• Быстрый и простой поиск нужной бумаги.
• Упорядочивание всей документации.

Регистрация представляет собой присвоение документу определенного регистрационного номера. Последний включает в себя 12 символов. Эти 12 символов могут быть дополнены указанием наименования документа, ФИО подписавшего, корреспондента, исполнителя. Регистрировать требуется все документы, которые были созданы в компании или поступили извне.

Регистрация – это внесение записи о документе в журнале, присвоение номера и проставление его на бумаге. Наличие номера обозначает, что бумага входит в документооборот компании. Регистрационный номер может составляться несколькими фирмами. В этом случае каждая компания ставит свой регистрационный номер. Можно указывать обозначения через черту.

ВНИМАНИЕ! Где проставлять номер? Все зависит от конкретного документа, его формы.

Какие журналы должны быть в компании?

В любой организации должен быть обязательный перечень журналов:

• По учету входящей корреспонденции.
• По учету исходящей корреспонденции.
• По учету приказов, касающихся главной деятельности компании.
• По учету соглашений.

Рассмотренный перечень книг используется в работе практически любой организации. При этом не имеет значение размер компании, размер ее штата, форма собственности.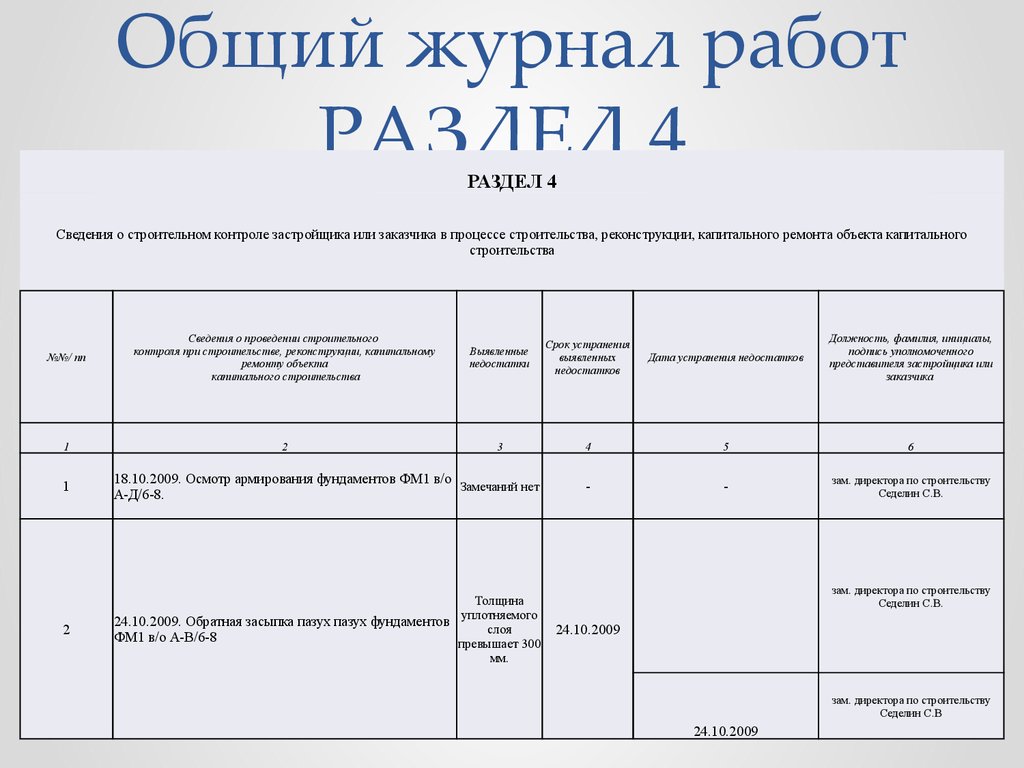 При этом нужно учитывать, что чем больше фирма, тем большее количество видов журналов она использует. Формы этих книг не утверждены, а потому организация может определять их самостоятельно. При этом следует пользоваться образцом.

Требуется ли регистрировать каждый документ?

Компания имеет полное право регистрировать каждый документ. Однако делать это в обязательном порядке не требуется. Более того, регистрация каждой бумаги даже не желательна. Связано это с тем, что регистрация занимает много времени. Она заставляет сотрудников компании бросать свои дела ради рутинной работы.

Как определить, какой документ нуждается в регистрации? Регистрировать следует те бумаги, которые потенциально нужно будет отслеживать.

Электронная или бумажная форма?

Журналы регистрации могут вестись и в бумажной, и в электронной форме. Большая часть фирм уже использует электронную форму. Она более проста, более удобна в использовании. Для ведения таких книг нужны специальные программы.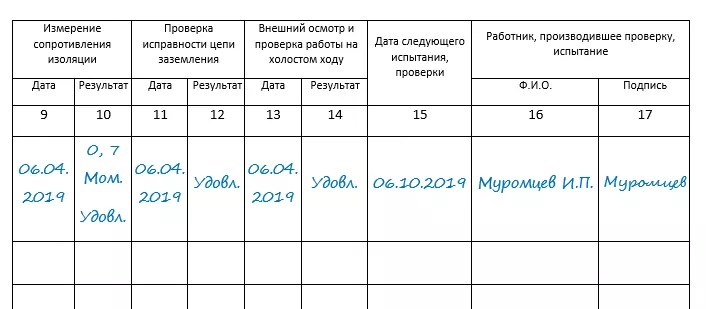 Они могут быть как простейшими, так и сложными.

Однако остались еще предприятия, которые ведут бумажный документооборот. Он актуален для тех книг, в которых нужно ставить росписи сотрудников. К примеру, к таким книгам относится Журнал регистрации печатей и штампов. Для ведения бумажных книг могут использоваться тетради, специальные журналы.

Как хранить журналы?

Все журналы нужно внести в номенклатуру. Электронные книги требуется включить в систему электронного документооборота. Срок хранения документов установлен Перечнем типовых бумаг, утвержденным приказом Минкультуры №558 от 25 августа 2010 года. Для обычных книг этот срок составляет 5 лет. Если это журнал регистрации приказов о приеме/увольнении, срок увеличивается до 75 лет.

Программы

Ведение электронных книг осуществляется посредством специальных программ:

• Microsoft Excel. В этой программе реализован самый минимум функций, который потребуется секретарю.
• Microsoft Access. Программа с расширенным функционалом. Поможет сформировать единую базу данных. Позволяет связывать регистрационные журналы между собой, фильтровать бумаги по определенным параметрам.
• Гугл.Драйв и Яндекс.Диск. Системы работают по принципу, аналогичному Excel. Отличие заключается в том, что с этими программами можно работать удаленно.

Это наиболее экономичные решения, которые подходят небольшим компаниям. Но большие предприятия пользуются более серьезными системами.

Логарифм | Правила, примеры и формулы

Ключевые люди:

Джон Напье Генри Бриггс Йоост Бюрги

Похожие темы:

натуральный логарифм мантисса десятичный логарифм власть

Просмотреть весь связанный контент →

логарифм , показатель степени или степень, в которую нужно возвести основание, чтобы получить заданное число. Выражаясь математически, x — это логарифм n по основанию b , если b ^x  =  n , и в этом случае записывается 0 5 0 9 0 9 0 0 1 9 9 0 0 2 0 б   n . Например, 2 ³  = 8; следовательно, 3 — это логарифм 8 по основанию 2, или 3 = log ₂  8. Таким же образом, поскольку 10 ²  = 100, то 2 = log ₁₀  100. Логарифмы последнего вида (что логарифмы с основанием 10) называются обычными или бриггсовскими логарифмами и записываются просто log н .

Логарифмы, изобретенные в 17 веке для ускорения вычислений, значительно сократили время, необходимое для умножения многозначных чисел. Они были основными в численной работе более 300 лет, пока совершенствование механических вычислительных машин в конце 19 века и компьютеров в 20 веке не сделало их устаревшими для крупномасштабных вычислений. Однако натуральный логарифм (с основанием

e ≅ 2,71828 и записанный как ln n ) продолжает оставаться одной из самых полезных функций в математике с приложениями к математическим моделям в физических и биологических науках.

Свойства логарифмов

Логарифмы были быстро приняты учеными из-за различных полезных свойств, которые упрощали длительные и утомительные вычисления.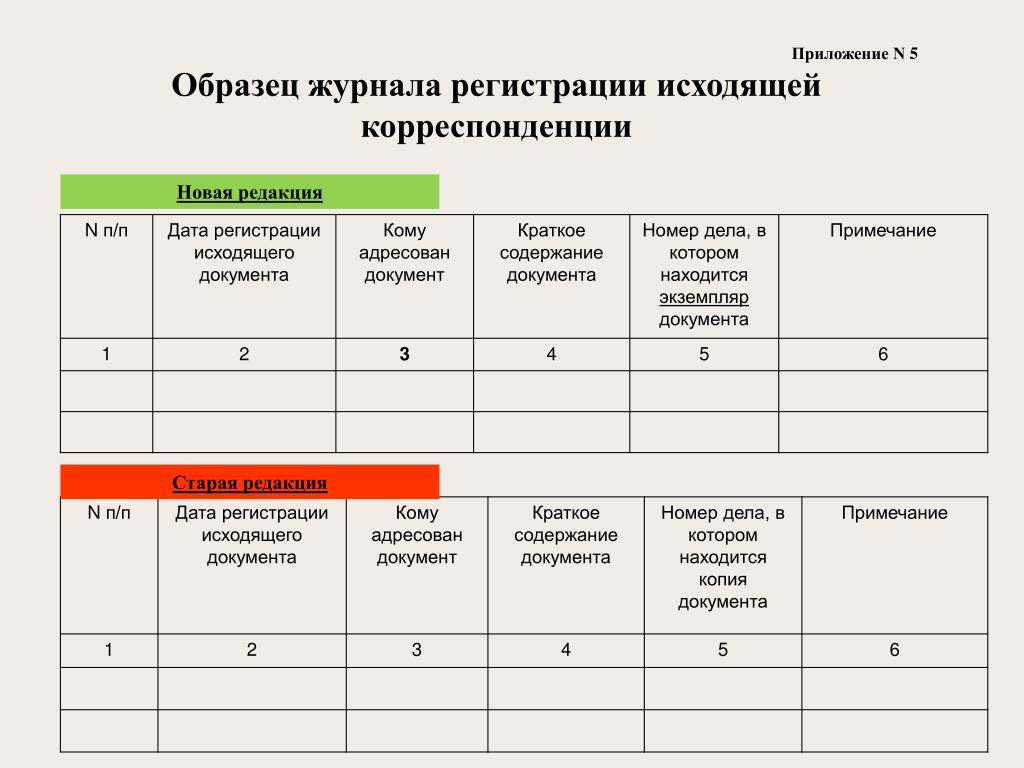 В частности, ученые могли найти произведение двух чисел m и n , просматривая логарифм каждого числа в специальной таблице, складывая логарифмы вместе, а затем снова сверяясь с таблицей, чтобы найти число с этим вычисленным логарифмом (известным как его антилогарифм). Выраженная в виде десятичных логарифмов, эта связь определяется как log м n  = log м  + log n . Например, 100 × 1000 можно вычислить, найдя логарифмы 100 (2) и 1000 (3), сложив логарифмы (5), а затем найдя антилогарифм (100 000) в таблице. Точно так же задачи деления преобразуются в задачи вычитания с логарифмами: log m / n = log m − log n . Это еще не все; вычисление степеней и корней можно упростить с помощью логарифмов. Логарифмы также можно преобразовывать между любыми положительными основаниями (за исключением того, что 1 нельзя использовать в качестве основания, поскольку все его степени равны 1), как показано в Щелкните здесь, чтобы увидеть полноразмерную таблицу логарифмических законов.

В таблицы логарифмов обычно включались только логарифмы чисел от 0 до 10. Чтобы получить логарифм некоторого числа за пределами этого диапазона, число сначала было записано в научной записи как произведение его значащих цифр и его экспоненциальной степени — например, 358 будет записано как 3,58 × 10 ² , а 0,0046 будет можно записать как 4,6 × 10 ⁻³ . Затем в таблице можно было найти логарифм значащих цифр — десятичную дробь от 0 до 1, известную как мантисса. Например, чтобы найти логарифм числа 358, нужно найти log 3,58 ≅ 0,55388. Следовательно, log 358 = log 3,58 + log 100 = 0,55388 + 2 = 2,55388. В примере числа с отрицательным показателем степени, например 0,0046, можно найти log 4,6 ≅ 0,66276. Следовательно, log 0,0046 = log 4,6 + log 0,001 = 0,66276 — 3 = -2,33724.

История логарифмов

Предвестником изобретения логарифмов стало сравнение арифметических и геометрических последовательностей. В геометрической последовательности каждый член образует постоянное отношение со своим последующим; например, …1/1000, 1/100, 1/10, 1, 10, 100, 1000… имеет обыкновенное отношение 10. В арифметической последовательности каждый последующий член отличается на константу, известную как общая разность; например, …−3, −2, −1, 0, 1, 2, 3… имеет общую разность 1. Обратите внимание, что геометрическую последовательность можно записать в терминах ее знаменателя; для приведенного выше примера геометрической последовательности: …10 ⁻³ , 10 ⁻² , 10 ⁻¹ , 10 ⁰ , 10 ¹ , 10 ² , 10 ^{3 …} . Умножение двух чисел в геометрической последовательности, скажем, 1/10 и 100, равносильно сложению соответствующих показателей степени обыкновенного отношения, -1 и 2, чтобы получить 10 ¹  = 10. Таким образом, умножение превращается в сложение. Однако первоначальное сравнение двух серий не было основано на каком-либо явном использовании экспоненциальной записи; это была более поздняя разработка. В 1620 г. швейцарский математик Йост Бюрги опубликовал в Праге первую таблицу, основанную на концепции соотношения геометрических и арифметических последовательностей.

Шотландский математик Джон Нейпир опубликовал свое открытие логарифмов в 1614 году. Его цель состояла в том, чтобы помочь в умножении величин, которые тогда назывались синусами. Весь синус был величиной стороны прямоугольного треугольника с большой гипотенузой. (Первоначальная гипотенуза Непера была равна 10 ⁷ .) Его определение было дано в терминах относительных скоростей.

Оформите подписку Britannica Premium и получите доступ к эксклюзивному контенту. Подписаться сейчас

Таким образом, логарифм любого синуса представляет собой число, очень точно выражающее линию, которая одинаково увеличивалась в течение определенного времени, в то время как линия всего синуса пропорционально убывала в этом синусе, причем оба движения имеют одинаковое время и одинаково смещаются в начале.

В сотрудничестве с английским математиком Генри Бриггсом Нейпир привел свой логарифм в его современную форму. Для логарифма Напера сравнение будет между точками, движущимися по градуированной прямой линии, 9Точка 0019 L (для логарифма) движется равномерно от минус бесконечности до плюс бесконечности, точка X (для синуса) движется от нуля до бесконечности со скоростью, пропорциональной ее расстоянию от нуля. Кроме того, L равно нулю, когда X равно единице, и их скорости в этой точке равны. Суть открытия Непера состоит в том, что оно представляет собой обобщение отношения между арифметическим и геометрическим рядами; т. е. умножение и возведение в степень значений 9Точка 0019 X соответствует сложению и умножению значений точки L соответственно. На практике удобно ограничить движение L и X требованием, чтобы L  = 1 при X  = 10 в дополнение к условию, что X  = 1 при L  = 0. Это изменение привело к бриггсовскому или десятичному логарифму.

Нейпир умер в 1617 году, и Бриггс продолжил работу в одиночку, опубликовав в 1624 году таблицу логарифмов, рассчитанных до 14 знаков после запятой для чисел от 1 до 20 000 и от 9.от 0 000 до 100 000. В 1628 году голландский издатель Адриан Влак опубликовал 10-местную таблицу для значений от 1 до 100 000, добавив недостающие 70 000 значений. И Бриггс, и Влак занимались созданием логарифмических тригонометрических таблиц. Такие ранние таблицы были либо с точностью до одной сотой градуса, либо с точностью до одной угловой минуты. В 18 веке таблицы были опубликованы для 10-секундных интервалов, которые были удобны для таблиц с семью десятичными знаками. В общем случае требуются более тонкие интервалы для вычисления логарифмических функций меньших чисел, например, при вычислении функций log sin x и логарифмический тангенс x .

Наличие логарифмов сильно повлияло на форму плоской и сферической тригонометрии. Процедуры тригонометрии были переработаны для получения формул, в которых операции, зависящие от логарифмов, выполняются одновременно. Тогда обращение к таблицам состояло всего из двух шагов: получения логарифмов и, после выполнения вычислений с логарифмами, получения антилогарифмов.

Фрэнсис Дж. Мюррей

Логарифм (Журналы) — Примеры | Натуральное бревно и обыкновенное бревно

Логарифмы — это еще один способ записи показателей степени. Мы знаем, что 2 ⁵ = 32.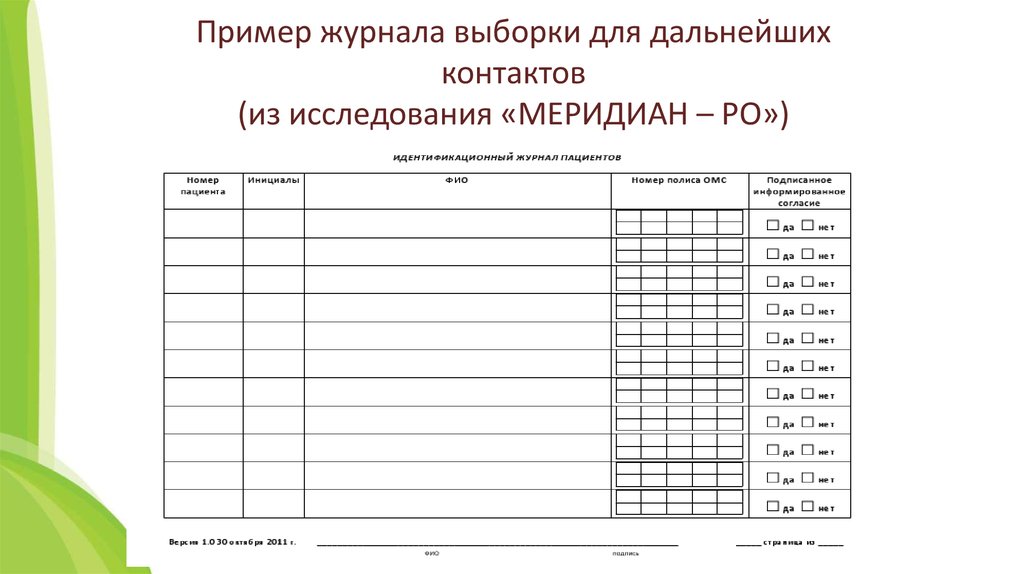 Но если нас попросят найти, какое число заменяет вопросительный знак в 2 ^? = 32, то методом проб и ошибок мы можем просто найти, что ответ равен 5. Но что, если нас попросят найти вопросительный знак в 2 ^? = 30? Существует ли такое число, что при возведении к нему 2 будет 30? Нет, тогда как решить? Решение — логарифмы (или журналы).

Давайте узнаем больше о логарифмах и их свойствах на примерах.

1.	Что такое логарифм?
2.	Определение журналов
3.	Натуральное бревно и обыкновенное бревно
4.	Правила журналов
5.	Как сжимать/расширять логарифмы?
6.	Часто задаваемые вопросы о логарифмах

Что такое логарифм?

Логарифм — это не что иное, как другой способ выражения показателей степени, и его можно использовать для решения задач, которые нельзя решить, используя только понятие показателей степени. Разобраться в логах не так уж и сложно. Чтобы понимать логарифмы, достаточно знать, что логарифмическое уравнение — это просто еще один способ записи показательного уравнения.

Логарифм и показатель степени являются обратными формами друг друга. Это можно понять из раздела ниже. Первоначально математик по имени Джон Нейпир ввел логарифмы для упрощения расчетов, и эта концепция быстро была принята другими учеными, инженерами и т. д.

Вот математическое определение бревен.

Определение журналов

Логарифм определяется с помощью показателя степени.

• б ^х = а ⇔ log _б а = х

Здесь «log» означает логарифм. Правая часть стрелки читается как «Логарифм а по основанию b равен х».

Очень простой способ запомнить это: «база остается базой в обеих формах» и «база не остается с показателем степени в логарифмической форме». Обратите внимание, что «b» является основанием как в левой, так и в правой частях подразумеваемого символа, а в логарифмической форме видно, что основание b и показатель степени x не остаются на одной стороне уравнения.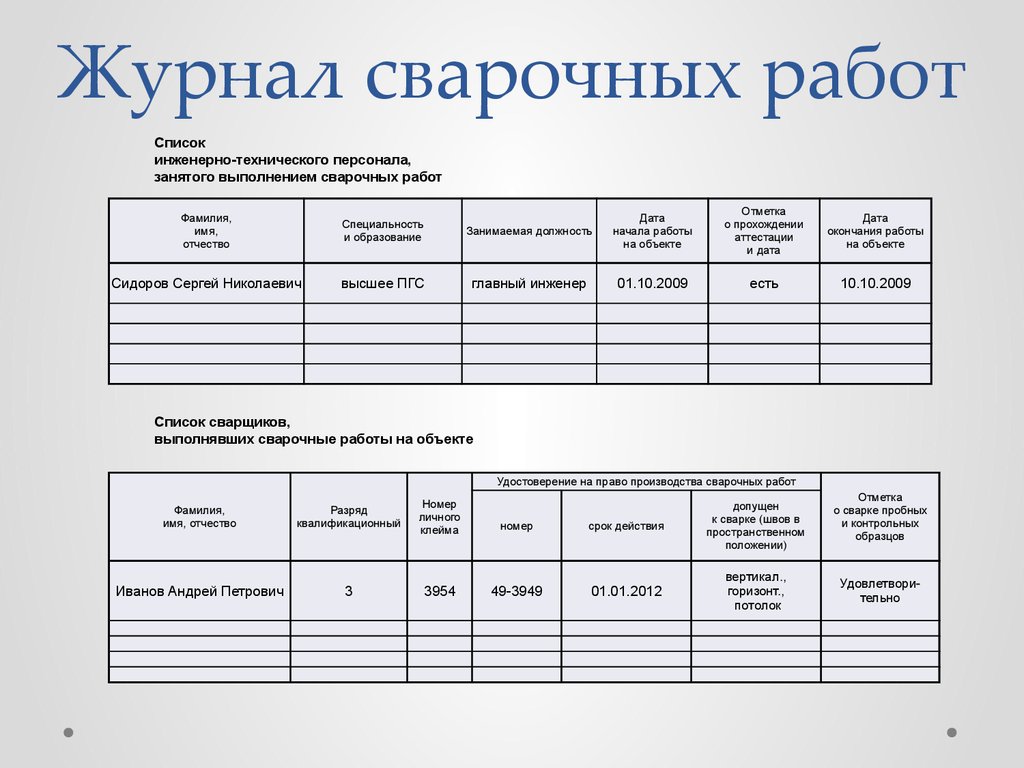

Здесь

• a и b — два положительных действительных числа.
• х — действительное число.
• а, который внутри лога называется «аргумент».
• б, который внизу журнала называется «база».

В приведенном выше уравнении нужно понимать две вещи (из символа ⇔):

• b ^x = a ⇒ log _b a = x. Это называется «экспоненциальной формой в логарифмическую форму»
• log _б а = х ⇒ б ^х = а . Это называется «переведение в экспоненциальную форму»

Вот таблица для понимания преобразований из одной формы в другую.

Экспоненциальная форма	Логарифмическая форма
2 5 = 32	журнал 2 32 = 5
6 2 = 36	журнал 6 36 = 2
3 -2 = 1/9	журнал 3 (1/9) = -2
e 2 = 7,389	журнал e 7,389 = 2
10 3 = 1000	журнал 10 1000 = 3

Натуральное бревно и обыкновенное бревно

Обратите внимание на две последние строки приведенной выше таблицы.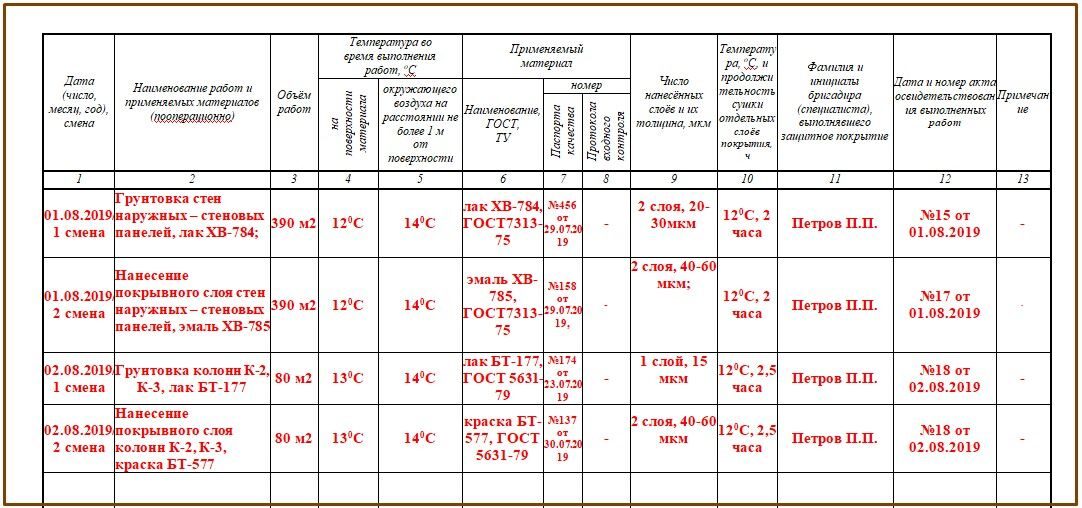 У них лог _e и журнал ₁₀ . Эти два журнала имеют особое значение и определенные имена в логарифмах.

• бревно _e называется натуральным бревном
• журнал ₁₀ называется общим журналом

Давайте узнаем больше о каждом из них.

Натуральный логарифм

Натуральный логарифм есть не что иное, как логарифм с основанием e. То есть натуральный логарифм означает log _e . Но обычно он не представляется как log _{e 9.0038 . Вместо этого он представлен как пер. т. е.}

• log _e = ln

Примеры:

• e ^x = 2 ⇒ log _e 2 = x (или) ln 2 = x.
• e ^x = 7 ⇒ log _e 7 = x (или) ln 7 = x.

Десятичный логарифм

Десятичный логарифм есть не что иное, как логарифм с основанием 10. То есть десятичный логарифм означает log ₁₀ .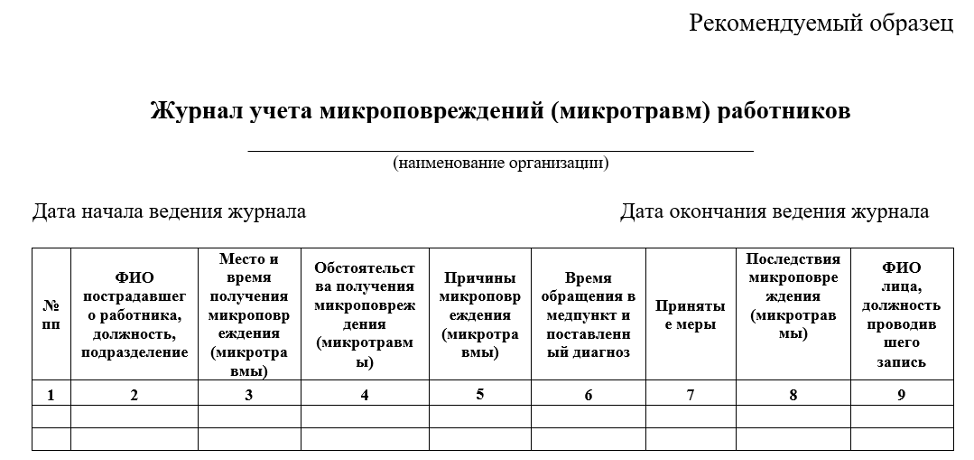 Но обычно вместо записи log 9 достаточно написать «log».0035 10 . т. е.

• логарифм ₁₀ = логарифм

т.е. если нет базы для лога значит его лог ₁₀ . Другими словами, это десятичный логарифм.

Примеры:

• 10 ² = 100 ⇒ log ₁₀ 100 = 2 (или) log 100 = 2
• 10 ^-2 = 0,01 ⇒ log ₁₀ 0,01 = -2 (или) log 0,01 = -2

Обратите внимание, что в этих примерах мы не написали 10 в качестве основы, потому что это очевидно.

Правила журналов

Правила журналов используются для упрощения логарифма, расширения логарифма или сжатия группы логарифмов в один логарифм. Вот правила (или) свойства журналов. Если вы хотите увидеть, как выводятся все эти правила, нажмите здесь.

Давайте рассмотрим каждое из этих правил одно за другим.

Log 1

Значение log 1 независимо от основания равно 0. Поскольку из свойств показателей мы знаем, что ⁰ = 1 для любого «а». Преобразовав это в логарифмическую форму, запишите _a 1 = 0 для любого «а». Очевидно, что при a = 10 log ₁₀ 1 = 0 (или) просто log 1 = 0.

Если мы расширим это до натурального логарифма, то получим, поскольку e ⁰ = 1 ⇒ ln 1 = 0

Log

_a a

Поскольку a ¹ = a, для любого «a», преобразуя это уравнение в логарифмическую форму, log _a a = 1. Таким образом, логарифм любого числа к одному и тому же основание всегда равно 1. Например:

• журнал ₂ 2 = 1
• журнал ₃ 3 = 1
• журнал 10 = 1
• лн е = 1

Логарифм произведения

Логарифм произведения двух чисел равен сумме логарифмов отдельных чисел, т. е.

Обратите внимание, что основания всех журналов здесь должны быть одинаковыми. Это напоминает / получено из правила произведения показателей степени: x ^м ⋅ х ⁿ = х ^м+n .

Примеры:

• log 6 = log (3 x 2) = log 3 + log 2
• логарифм (5x) = логарифм 5 + логарифм x

Правило частного логарифма

Логарифм частного двух чисел представляет собой разность между логарифмами отдельных чисел, т. е. _и п

Обратите внимание, что основания всех журналов здесь также должны быть одинаковыми. Это напоминает / получено из частного правила показателей степени: x ^м / х ^н = х ^м-н .

Примеры:

• лог. 4 = лог. (8/2) = лог. 8 — лог. 2
• лог (х/2) = лог х — лог 2

Степенное правило логарифма

Показатель степени аргумента логарифма можно поставить перед логарифмом, т. е.

• log _a m ⁿ = n log 92318 m a

Здесь основания должны быть одинаковыми с обеих сторон. Это напоминает / происходит из правила степени степени показателей: (x ^м ) ^н = х ^мн .

Правило изменения основания

С помощью этого свойства можно изменить основание логарифма. Он говорит:

• log _b a = (log꜀ a) / (log꜀ b)

Другой способ записи этого правила: log _b a · log꜀ b = log꜀ a.

Используя это свойство, мы можем изменить основание на любое другое число. Следовательно, мы также можем изменить основание на 10. Тогда получаем: log _b а = (логарифм а) / (логарифм б). Таким образом:

• log ₂ 3 = (log 3) / (log 2)
• журнал ₃ 2 = (лог 2) / (лог 3)

Правило равенства логарифмов

Это правило используется при решении уравнений с логарифмами. т. е.

• log _b a = log _b c ⇒ a = c

Это своего рода журнал отмены с обеих сторон.

Число поднято до свойства журнала

Когда в логарифм возводится число, основание которого совпадает с числом, результатом является просто аргумент логарифма.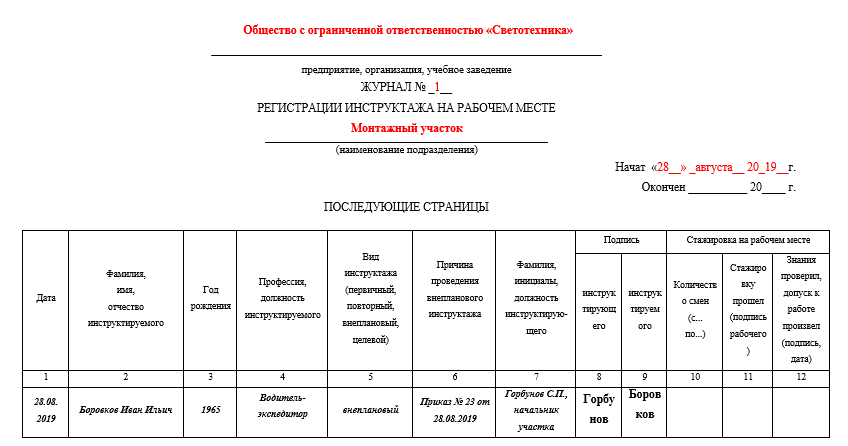 т. е.

• a ^{log _a x} = x

Вот несколько примеров этого свойства.

• 2 ^{журнал ₂ 5} = 5
• 10 ^{журнал 6} = 6
• е ^{пер. 3} = 3

Свойство отрицательного журнала

Негативные журналы имеют форму -log _б а. Мы можем вычислить это, используя правило степени логарифмов.

−log _b a = log _b a ^-1 = log _b (1/a)

Таким образом, 038 (1/ а)

т. е., чтобы преобразовать отрицательный журнал в положительный, мы можем просто взять обратное значение аргумента. Кроме того, чтобы преобразовать отрицательный логарифм в положительный логарифм, мы можем взять обратное основание, то есть

• −log _b a = log _1/b a

Как сжимать/расширять логарифмы?

Мы можем либо сжать группу журналов в один журнал, либо развернуть один журнал в группу журналов, используя приведенные выше правила журналов. Но важные правила, которые мы используем в этом процессе, следующие:

• log _a mn = log _a m + log _a n (правило произведения логарифмов)
• журнал _a m/n = log _a m — log _a n (частное правило логарифмов)
• log _a m ⁿ = n log _a m (Степенное правило логарифмов)

Расширение логарифмов

Расширим логарифм (3x ² y ³ ).

журнал (3x ² и ³ )
= log (3) + log (x ² ) + log (y ³ ) (по правилу произведения)
= log 3 + 2 log x + 3 log y (по степенному правилу)

Сокращение логарифмов

Давайте просто возьмем приведенную выше сумму логарифмов и сократим ее. Мы должны вернуть лог (3x ² y ³ ).

лог. 3 + 2 лог. x + 3 лог. у
= log (3) + log (x ² ) + log (y ³ ) (по степенному правилу)
= log (3x ² y ³ ) (По правилу произведения)

Важные примечания по логарифмам:

• Логарифм 0 НЕ определяется, так как одно число, возведенное в другое число, никогда не дает 0 в результате.
• Экспоненциальное уравнение преобразуется в логарифмическое уравнение и наоборот, используя b ^x = a ⇔ log _b a = x.
• Обыкновенный логарифм — это логарифм по основанию 10, т. е. логарифм ₁₀ = логарифм.
• Натуральный логарифм — это логарифм по основанию e, т. е. log _e = ln.
• Логарифмы используются для самых сложных вычислений умножения и деления.

☛ Похожие темы:

• Общий калькулятор журнала
• Калькулятор естественного бревна

Часто задаваемые вопросы о логарифмах

Что такое журналы в математике?

Журналы — это другой способ записи показателя степени. Формула преобразования экспоненциальной формы в логарифмическую: b ^x = a ⇔ log _b a = x. Логарифмы очень полезны при решении уравнений с показателями степени.

Каковы значения логарифмов log 0, log 1, log 2, log 3, log 4, log 5, log 10, log 100 и log inf?

Вот значения данных журналов:

• log 0 не определен ни для какой базы, потому что число, увеличенное до любого числа, не дает 0.
• журнал 1 = 0 как 10 ⁰ = 1
• log 2 ≈ 0,3010 (с помощью калькулятора)
• log 3 ≈ 0,4771 (с помощью калькулятора)
• log 4 ≈ 0,6021 (с помощью калькулятора)
• log 5 ≈ 0,6990 (с помощью калькулятора)
• log 10 = 1 как 10 ¹ = 10
• log 100 = 2 как 10 ² = 100
• журнал ∞ = ∞

Что такое ln в математике?

Ln в математике используется для представления натуральных логарифмов. т. е. ln = «логарифм с основанием e». Например, e ² = x ⇔ ln x = 2.

Какие 3 типа логарифмов существуют?

Существуют три основных типа логарифмов:

• Десятичный логарифм, который записывается как логарифм без основания. Например: журнал 2
• Натуральный логарифм, который записывается как «ln» (означает log _и ). Например: пер. 2
• Логарифм по любому другому основанию (без конкретного названия). Например: журнал ₃ 2.

Каковы значения логарифмов ln e, ln 1 и ln от 0?

Здесь значения заданных натуральных бревен.

• In e = 1 как e ¹ = e
• In 1 = 0 как e ⁰ = 1
• In 0 НЕ определено

Что такое важные логарифмические свойства?

Важными логарифмическими свойствами являются:

• Правило произведения: log _a mn = log _a m + log _a n
• Частное правило: log _a m/n = log _a m — log _a n
• Степенное правило: log _a m ⁿ = n log _a m

Как рассчитать журналы?

Мы можем вычислять журналы, используя свойства логарифмов. т. е., используя правила журналов, мы можем либо сжать набор логарифмов в один, либо разложить один логарифм на множество. Мы также используем логарифмическую таблицу и антилогарифмическую таблицу в расчетах.

Какая производная от ln x и log x?

Вот производные:

• Производная от ln x равна d/dx (ln x) = 1/x.