Логический сдвиг — это… Что такое Логический сдвиг?
Би́товый сдвиг — изменение позиций битов в слове на одну и ту же величину.
В основной своей массе компьютеры не могут напрямую адресовать биты, которые содержатся группами по 8, 16, 32 битов в словах. Для обеспечения работы с битами существует множество команд, к которым относятся и сдвиги: Все сдвиги похожи друг на друга поведением средних битов: они просто сдвигаются влево или вправо на определённую величину. И различаются поведением крайних битов: одного, который уходит из слова, и второго, который должен появиться в слове.
Логический сдвиг
Логический сдвиг влево | Логический сдвиг вправо |
Сдвиг, при котором уходящий бит уходит, не влияя на оставшееся биты, а на место появившегося бита записывается бит 0.
Пример работы операции сдвига:
- Пусть у нас есть число 10101010b (в двоичной системе).

- Если сделать сдвиг влево на 1 бит, то получим число 01010100b
- Если сделать сдвиг вправо на 1 бит, то получим число 01010101b
В большинстве процессоров уходящий бит сохраняется в флаге переноса. Эта функция широко используется при работе с многобайтовыми числами.
Арифметический сдвиг
Арифметический сдвиг влево | Арифметический сдвиг вправо |
При этом сдвиге слово рассматривается не просто как группа битов, а как целое число в дополнительном коде. При сдвиге влево ведёт себя как логический сдвиг, при сдвиге вправо: уходящий бит уходит, не влияя на оставшееся биты, а на место появившегося бита устанавливается бит, соответствующий знаку.
Пример работы операции сдвига:
- Пусть у нас есть число 11111010b=−6 (в двоичной системе).
- Если сделать сдвиг влево на 1 бит, то получим число 11110100b=−12
- Если сделать сдвиг вправо на 1 бит, то получим число 11111101b=−3
Легко заметить, что при арифметическом сдвиге сдвиг влево соответствует умножению на 2, а сдвиг вправо делению на 2 (в общем случае — на основание системы счисления).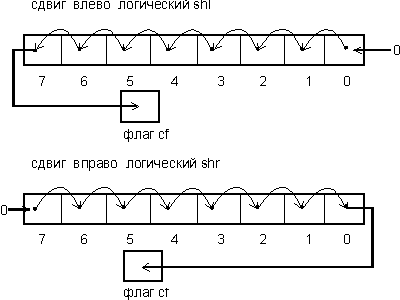 Исключение:
Исключение: −1 >>a 1 = −1 (в общем случае это относится к числам от −1 до −p+1, где p — основание системы счисления).
Схемотехническая реализация операций сдвига очень проста. Именно поэтому эти операции рекомендуют использовать для операций умножения и деления целых чисел на числа равные степени 2 (2, 4, 8, 16, 32, 64 и т. д.).
Циклический сдвиг
Циклический сдвиг влево | Циклический сдвиг вправо |
При этом сдвиге уходящий бит появляется на месте появившегося.
Пример работы операции сдвига:
- Пусть у нас есть число 11111010b (в двоичной системе).
- Если сделать сдвиг влево на 1 бит, то получим число 11110101b
- Если сделать сдвиг вправо на 1 бит, то получим число 01111101b
Циклический сдвиг через бит переноса
Циклический сдвиг влево через бит переноса | Циклический сдвиг вправо через бит переноса |
В архитектуру многих процессоров входит флаг переноса в следующий разряд (например, cf на n+1)-битным числом, состоящим из регистра и флага переноса.
Например, если у нас в регистре число 11111010b, флаг переноса равен 0:
- После сдвига влево на 1 бит: в регистре 11110100b, флаг переноса равен 1
- После сдвига вправо на 1 бит: в регистре 01111101b, флаг переноса равен 0
Операция циклического сдвига через бит переноса используется при работе с многобайтовыми числами. В частности, чтобы сдвинуть вправо на 1 бит длинное число, нужно очистить[1]cf (в случае деления числа со знаком нужно записать в cf старший бит старшего слова) и циклически сдвинуть на единицу через cf каждое слово, начиная с верхнего. Например, пусть у нас есть число 011000111100b, занимающее три 4-битных слова:
Было: HI=0110, MED=0011, LO=1100, cf=0 После сдвига HI: HI=0011, MED=0011, LO=1100, cf=0 После сдвига MED: HI=0011, MED=0001, LO=1100, cf=1 После сдвига LO: HI=0011, MED=0001, LO=1110, cf=0
Сдвиги через регистр флагов более чем на 1 бит практически не используются.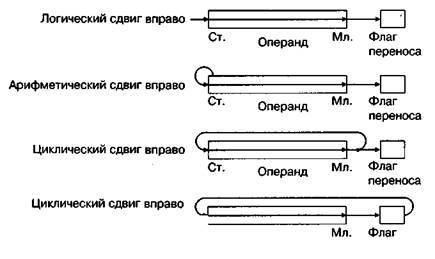
Примечания
- ↑ Можно вместо очистки флага для первого обрабатываемого слова использовать арифметический\логический сдвиг, если он присваивает флагу
Источник
Wikimedia Foundation. 2010.
Логический сдвиг — это… Что такое Логический сдвиг?
Би́товый сдвиг — изменение позиций битов в слове на одну и ту же величину.
В основной своей массе компьютеры не могут напрямую адресовать биты, которые содержатся группами по 8, 16, 32 битов в словах. Для обеспечения работы с битами существует множество команд, к которым относятся и сдвиги: Все сдвиги похожи друг на друга поведением средних битов: они просто сдвигаются влево или вправо на определённую величину. И различаются поведением крайних битов: одного, который уходит из слова, и второго, который должен появиться в слове.
Логический сдвиг
Логический сдвиг влево | Логический сдвиг вправо |

Пример работы операции сдвига:
- Пусть у нас есть число 10101010b (в двоичной системе).
- Если сделать сдвиг влево на 1 бит, то получим число 01010100b
- Если сделать сдвиг вправо на 1 бит, то получим число 01010101b
В большинстве процессоров уходящий бит сохраняется в флаге переноса. Эта функция широко используется при работе с многобайтовыми числами.
Арифметический сдвиг
Арифметический сдвиг влево | Арифметический сдвиг вправо |
При этом сдвиге слово рассматривается не просто как группа битов, а как целое число в дополнительном коде. При сдвиге влево ведёт себя как логический сдвиг, при сдвиге вправо: уходящий бит уходит, не влияя на оставшееся биты, а на место появившегося бита устанавливается бит, соответствующий знаку.
Пример работы операции сдвига:
- Пусть у нас есть число 11111010b=−6 (в двоичной системе).
- Если сделать сдвиг влево на 1 бит, то получим число 11110100b=−12
- Если сделать сдвиг вправо на 1 бит, то получим число 11111101b=−3
Легко заметить, что при арифметическом сдвиге сдвиг влево соответствует умножению на 2, а сдвиг вправо делению на 2 (в общем случае — на основание системы счисления). Исключение: −1 >>a 1 = −1 (в общем случае это относится к числам от −1 до −p+1, где p — основание системы счисления).
Схемотехническая реализация операций сдвига очень проста. Именно поэтому эти операции рекомендуют использовать для операций умножения и деления целых чисел на числа равные степени 2 (2, 4, 8, 16, 32, 64 и т. д.).
Циклический сдвиг
Циклический сдвиг влево | Циклический сдвиг вправо |
При этом сдвиге уходящий бит появляется на месте появившегося.
Пример работы операции сдвига:
- Пусть у нас есть число 11111010b (в двоичной системе).

- Если сделать сдвиг влево на 1 бит, то получим число 11110101b
- Если сделать сдвиг вправо на 1 бит, то получим число 01111101b
Циклический сдвиг через бит переноса
Циклический сдвиг влево через бит переноса | Циклический сдвиг вправо через бит переноса |
В архитектуру многих процессоров входит флаг переноса в следующий разряд (например, cf
Например, если у нас в регистре число 11111010b, флаг переноса равен 0:
- После сдвига влево на 1 бит: в регистре 11110100b, флаг переноса равен 1
- После сдвига вправо на 1 бит: в регистре 01111101b, флаг переноса равен 0
Операция циклического сдвига через бит переноса используется при работе с многобайтовыми числами. В частности, чтобы сдвинуть вправо на 1 бит длинное число, нужно очистить[1]cf (в случае деления числа со знаком нужно записать в cf старший бит старшего слова) и циклически сдвинуть на единицу через cf каждое слово, начиная с верхнего. Например, пусть у нас есть число 011000111100b, занимающее три 4-битных слова:
Например, пусть у нас есть число 011000111100b, занимающее три 4-битных слова:
Было: HI=0110, MED=0011, LO=1100, cf=0 После сдвига HI: HI=0011, MED=0011, LO=1100, cf=0 После сдвига MED: HI=0011, MED=0001, LO=1100, cf=1 После сдвига LO: HI=0011, MED=0001, LO=1110, cf=0
Сдвиги через регистр флагов более чем на 1 бит практически не используются.
Примечания
- ↑ Можно вместо очистки флага для первого обрабатываемого слова использовать арифметический\логический сдвиг, если он присваивает флагу
cfзначение вышедшего бита.
Источник
Wikimedia Foundation. 2010.
Логический сдвиг — это… Что такое Логический сдвиг?
Би́товый сдвиг — изменение позиций битов в слове на одну и ту же величину.
В основной своей массе компьютеры не могут напрямую адресовать биты, которые содержатся группами по 8, 16, 32 битов в словах. Для обеспечения работы с битами существует множество команд, к которым относятся и сдвиги: Все сдвиги похожи друг на друга поведением средних битов: они просто сдвигаются влево или вправо на определённую величину.
Логический сдвиг
Логический сдвиг влево | Логический сдвиг вправо |
Сдвиг, при котором уходящий бит уходит, не влияя на оставшееся биты, а на место появившегося бита записывается бит 0.
Пример работы операции сдвига:
- Пусть у нас есть число 10101010b (в двоичной системе).
- Если сделать сдвиг влево на 1 бит, то получим число 01010100b
- Если сделать сдвиг вправо на 1 бит, то получим число 01010101b
В большинстве процессоров уходящий бит сохраняется в флаге переноса. Эта функция широко используется при работе с многобайтовыми числами.
Арифметический сдвиг
Арифметический сдвиг влево | Арифметический сдвиг вправо |
При этом сдвиге слово рассматривается не просто как группа битов, а как целое число в дополнительном коде. При сдвиге влево ведёт себя как логический сдвиг, при сдвиге вправо: уходящий бит уходит, не влияя на оставшееся биты, а на место появившегося бита устанавливается бит, соответствующий знаку.
При сдвиге влево ведёт себя как логический сдвиг, при сдвиге вправо: уходящий бит уходит, не влияя на оставшееся биты, а на место появившегося бита устанавливается бит, соответствующий знаку.
Пример работы операции сдвига:
- Пусть у нас есть число 11111010b=−6 (в двоичной системе).
- Если сделать сдвиг влево на 1 бит, то получим число 11110100b=−12
- Если сделать сдвиг вправо на 1 бит, то получим число 11111101b=−3
Легко заметить, что при арифметическом сдвиге сдвиг влево соответствует умножению на 2, а сдвиг вправо делению на 2 (в общем случае — на основание системы счисления). Исключение: −1 >>a 1 = −1 (в общем случае это относится к числам от −1 до −p+1, где p — основание системы счисления).
Схемотехническая реализация операций сдвига очень проста. Именно поэтому эти операции рекомендуют использовать для операций умножения и деления целых чисел на числа равные степени 2 (2, 4, 8, 16, 32, 64 и т. д.).
Циклический сдвиг
Циклический сдвиг влево | Циклический сдвиг вправо |
При этом сдвиге уходящий бит появляется на месте появившегося.
Пример работы операции сдвига:
- Пусть у нас есть число 11111010b (в двоичной системе).
- Если сделать сдвиг влево на 1 бит, то получим число 11110101b
- Если сделать сдвиг вправо на 1 бит, то получим число 01111101b
Циклический сдвиг через бит переноса
Циклический сдвиг влево через бит переноса | Циклический сдвиг вправо через бит переноса |
В архитектуру многих процессоров входит флаг переноса в следующий разряд (например, cf на n+1)-битным числом, состоящим из регистра и флага переноса.
Например, если у нас в регистре число 11111010b, флаг переноса равен 0:
- После сдвига влево на 1 бит: в регистре 11110100b, флаг переноса равен 1
- После сдвига вправо на 1 бит: в регистре 01111101b, флаг переноса равен 0
Операция циклического сдвига через бит переноса используется при работе с многобайтовыми числами. В частности, чтобы сдвинуть вправо на 1 бит длинное число, нужно очистить[1]
В частности, чтобы сдвинуть вправо на 1 бит длинное число, нужно очистить[1]cf (в случае деления числа со знаком нужно записать в cf старший бит старшего слова) и циклически сдвинуть на единицу через cf каждое слово, начиная с верхнего. Например, пусть у нас есть число 011000111100b, занимающее три 4-битных слова:
Было: HI=0110, MED=0011, LO=1100, cf=0 После сдвига HI: HI=0011, MED=0011, LO=1100, cf=0 После сдвига MED: HI=0011, MED=0001, LO=1100, cf=1 После сдвига LO: HI=0011, MED=0001, LO=1110, cf=0
Сдвиги через регистр флагов более чем на 1 бит практически не используются.
Примечания
- ↑ Можно вместо очистки флага для первого обрабатываемого слова использовать арифметический\логический сдвиг, если он присваивает флагу
cfзначение вышедшего бита.
Источник
Wikimedia Foundation. 2010.
Побитовые операторы в C++: И, ИЛИ, НЕ и исключающее ИЛИ | Уроки С++
Обновл. 11 Сен 2020 |
11 Сен 2020 |
Побитовые операторы манипулируют отдельными битами в пределах переменной.
Примечание: Для некоторых этот материал может показаться сложным. Если вы застряли или что-то не понятно — пропустите этот урок (и следующий), в будущем сможете вернуться и разобраться детально. Он не столь важен для прогресса в изучении языка C++, как другие уроки, и изложен здесь в большей мере для общего развития.
Зачем нужны побитовые операторы?
В далеком прошлом компьютерной памяти было очень мало и ею сильно дорожили. Это было стимулом максимально разумно использовать каждый доступный бит. Например, в логическом типе данных bool есть всего лишь два возможных значения (true и false), которые могут быть представлены одним битом, но по факту занимают целый байт памяти! А это, в свою очередь, из-за того, что переменные используют уникальные адреса памяти, а они выделяются только в байтах. Переменная bool занимает 1 бит, а другие 7 бит — тратятся впустую.
Используя побитовые операторы, можно создавать функции, которые позволят уместить 8 значений типа bool в переменную размером 1 байт, что значительно сэкономит потребление памяти. В прошлом такой трюк был очень популярен. Но сегодня, по крайней мере, в прикладном программировании, это не так.
Теперь памяти стало существенно больше и программисты обнаружили, что лучше писать код так, чтобы было проще и понятнее его поддерживать, нежели усложнять его ради незначительной экономии памяти. Поэтому спрос на использование побитовых операторов несколько уменьшился, за исключением случаев, когда необходима уж максимальная оптимизация (например, научные программы, которые используют огромное количество данных; игры, где манипуляции с битами могут быть использованы для дополнительной скорости; встроенные программы, где память по-прежнему ограничена).
В языке С++ есть 6 побитовых операторов:
| Оператор | Символ | Пример | Операция |
| Побитовый сдвиг влево | << | x << y | Все биты в x смещаются влево на y бит |
| Побитовый сдвиг вправо | >> | x >> y | Все биты в x смещаются вправо на y бит |
| Побитовое НЕ | ~ | ~x | Все биты в x меняются на противоположные |
| Побитовое И | & | x & y | Каждый бит в x И каждый соответствующий ему бит в y |
| Побитовое ИЛИ | | | x | y | Каждый бит в x ИЛИ каждый соответствующий ему бит в y |
| Побитовое исключающее ИЛИ (XOR) | ^ | x ^ y | Каждый бит в x XOR с каждым соответствующим ему битом в y |
В побитовых операциях следует использовать только целочисленные типы данных unsigned, так как C++ не всегда гарантирует корректную работу побитовых операторов с целочисленными типами signed.
Правило: При работе с побитовыми операторами используйте целочисленные типы данных unsigned.
Побитовый сдвиг влево (<<) и побитовый сдвиг вправо (>>)
В языке C++ количество используемых бит основывается на размере типа данных (в 1 байте находятся 8 бит). Оператор побитового сдвига влево (<<) сдвигает биты влево. Левый операнд является выражением, в котором они сдвигаются, а правый — количество мест, на которые нужно сдвинуть. Поэтому в выражении 3 << 1 мы имеем в виду «сдвинуть биты влево в литерале 3 на одно место».
Примечание: В следующих примерах мы будем работать с 4-битными двоичными значениями.
Рассмотрим число 3, которое в двоичной системе равно 0011:
3 = 0011
3 << 1 = 0110 = 6
3 << 2 = 1100 = 12
3 << 3 = 1000 = 8
В последнем третьем случае один бит перемещается за пределы самого литерала! Биты, сдвинутые за пределы двоичного числа, теряются навсегда.
Оператор побитового сдвига вправо (>>) сдвигает биты вправо. Например:
12 = 1100
12 >> 1 = 0110 = 6
12 >> 2 = 0011 = 3
12 >> 3 = 0001 = 1
В третьем случае мы снова переместили бит за пределы литерала. Он также потерялся навсегда.
Хотя в примерах, приведенных выше, мы смещаем биты только в литералах, мы также можем смещать биты и в переменных:
unsigned int x = 4; x = x << 1; // x должен стать равным 8
unsigned int x = 4; x = x << 1; // x должен стать равным 8 |
Следует помнить, что результаты операций с побитовыми сдвигами в разных компиляторах могут отличаться.
Что!? Разве операторы << и >> используются не для вывода и ввода данных?
И для этого тоже.
Сейчас польза от использования побитовых операторов не так велика, как это было раньше. Сейчас в большинстве случаев оператор побитового сдвига влево используется для вывода данных. Например, рассмотрим следующую программу:
Сейчас в большинстве случаев оператор побитового сдвига влево используется для вывода данных. Например, рассмотрим следующую программу:
#include <iostream> int main() { unsigned int x = 4; x = x << 1; // оператор << используется для побитового сдвига влево std::cout << x; // оператор << используется для вывода данных в консоль return 0; }
#include <iostream> int main() { unsigned int x = 4; x = x << 1; // оператор << используется для побитового сдвига влево std::cout << x; // оператор << используется для вывода данных в консоль return 0; } |
Результат выполнения программы:
8
А как компилятор понимает, когда нужно применить оператор побитового сдвига влево, а когда выводить данные? Всё очень просто.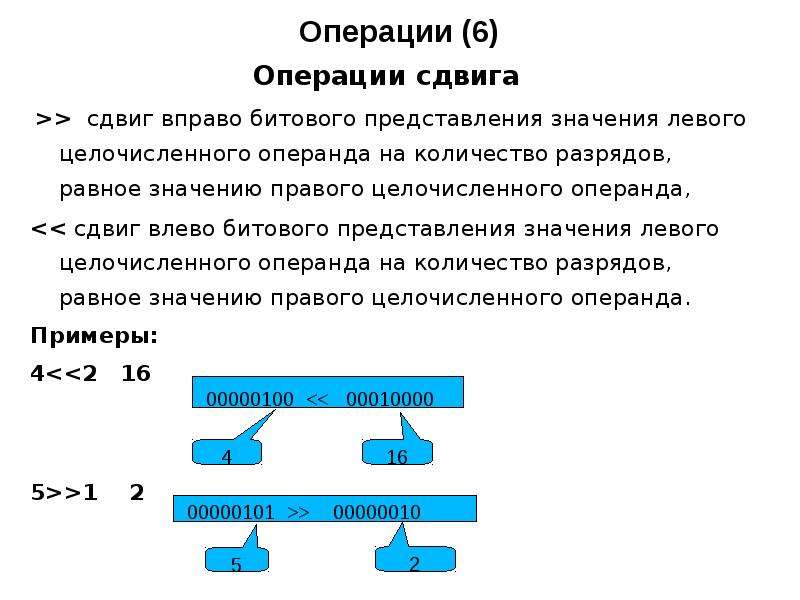 std::cout переопределяет значение оператора
std::cout переопределяет значение оператора << по умолчанию на новое (вывод данных в консоль). Когда компилятор видит, что левым операндом оператора << является std::cout, то он понимает, что должен произойти вывод данных. Если левым операндом является переменная целочисленного типа данных, то компилятор понимает, что должен произойти побитовый сдвиг влево (операция по умолчанию).
Побитовый оператор НЕ
Побитовый оператор НЕ (~), пожалуй, самый простой для объяснения и понимания. Он просто меняет каждый бит на противоположный, например, с 0 на 1 или с 1 на 0. Обратите внимание, результаты побитового НЕ зависят от размера типа данных!
Предположим, что размер типа данных составляет 4 бита:
4 = 0100
~ 4 = 1011 (двоичное) = 11 (десятичное)
Предположим, что размер типа данных составляет 8 бит:
4 = 0000 0100
~ 4 = 1111 1011 (двоичное) = 251 (десятичное)
Побитовые операторы И, ИЛИ и исключающее ИЛИ (XOR)
Побитовые операторы И (&) и ИЛИ (|) работают аналогично логическим операторам И и ИЛИ. Однако, побитовые операторы применяются к каждому биту отдельно! Например, рассмотрим выражение
Однако, побитовые операторы применяются к каждому биту отдельно! Например, рассмотрим выражение 5 | 6. В двоичной системе это 0101 | 0110. В любой побитовой операции операнды лучше всего размещать следующим образом:
0 1 0 1 // 5
0 1 1 0 // 6
А затем применять операцию к каждому столбцу с битами по отдельности. Как вы помните, логическое ИЛИ возвращает true (1), если один из двух или оба операнды истинны (1). Аналогичным образом работает и побитовое ИЛИ. Выражение 5 | 6 обрабатывается следующим образом:
0 1 0 1 // 5
0 1 1 0 // 6
-------
0 1 1 1 // 7
Результат:
0111 (двоичное) = 7 (десятичное)
Также можно обрабатывать и комплексные выражения ИЛИ, например, 1 | 4 | 6. Если хоть один бит в столбце равен 1, то результат целого столбца — 1. Например:
0 0 0 1 // 1
0 1 0 0 // 4
0 1 1 0 // 6
--------
0 1 1 1 // 7
Результатом 1 | 4 | 6 является десятичное 7. 7. Если единиц в столбце чётное количество, то результатом будет 0, если же нечётное количество, то результат — 1. Например:
7. Если единиц в столбце чётное количество, то результатом будет 0, если же нечётное количество, то результат — 1. Например:
0 0 0 1 // 1
0 0 1 1 // 3
0 1 1 1 // 7
--------
0 1 0 1 // 5
Побитовые операторы присваивания
Как и в случае с арифметическими операторами присваивания, язык C++ предоставляет побитовые операторы присваивания для облегчения внесения изменений в переменные.
| Оператор | Символ | Пример | Операция |
| Присваивание с побитовым сдвигом влево | <<= | x <<= y | Сдвигаем биты в x влево на y бит |
| Присваивание с побитовым сдвигом вправо | >>= | x >>= y | Сдвигаем биты в x вправо на y бит |
| Присваивание с побитовой операцией ИЛИ | |= | x |= y | Присваивание результата выражения x | y переменной x |
| Присваивание с побитовой операцией И | &= | x &= y | Присваивание результата выражения x & y переменной x |
| Присваивание с побитовой операцией исключающего ИЛИ | ^= | x ^= y | Присваивание результата выражения x ^ y переменной x |
Например, вместо х = х << 1; мы можем написать х <<= 1;.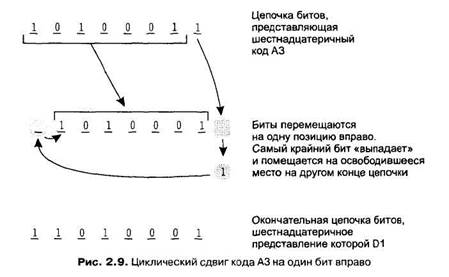 12:
12:
0 1 0 1
1 1 0 0
--------
1 0 0 1 // 9 (десятичное)
Оценить статью:
Загрузка…Поделиться в социальных сетях:
Битовые операторы | Кодкамп
Введение
Примеры
Побитовое И
& Оператор выполнит двоичный И, где бит копируется , если она существует в обоих операндов. Это означает:
# 0 & 0 = 0
# 0 & 1 = 0
# 1 & 0 = 0
# 1 & 1 = 1
# 60 = 0b111100
# 30 = 0b011110
60 & 30
# Out: 28
# 28 = 0b11100
bin(60 & 30)
# Out: 0b11100 Побитовое ИЛИ
| Оператор выполнит двоичное «или», где бит копируется, если он существует в любом из операндов. Это означает:
# 0 | 0 = 0
# 0 | 1 = 1
# 1 | 0 = 1
# 1 | 1 = 1
# 60 = 0b111100
# 30 = 0b011110
60 | 30
# Out: 62
# 62 = 0b111110
bin(60 | 30)
# Out: 0b111110 Побитовое XOR (исключающее ИЛИ)
^ Оператор будет выполнять двоичный XOR , в котором двоичный 1 копируется тогда и только тогда , когда это значение ровно один операнд.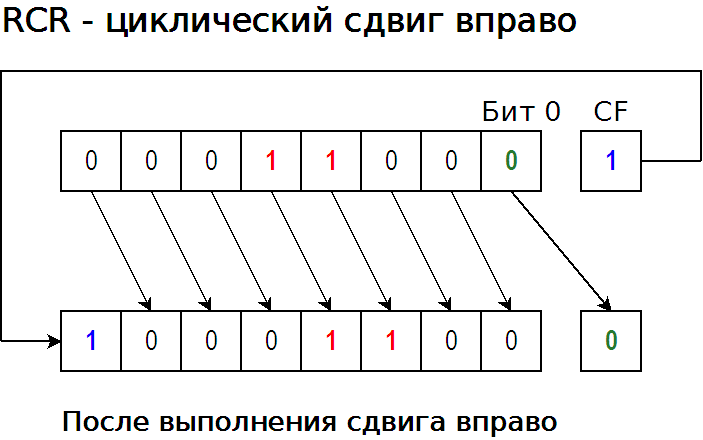 30)
# Out: 0b100010
30)
# Out: 0b100010
Побитовый сдвиг влево
<< оператор выполняет побитовое «сдвиг влево» , где значение левого операнда перемещается влево на число битов данных в правом операнде.
# 2 = 0b10
2 << 2
# Out: 8
# 8 = 0b1000
bin(2 << 2)
# Out: 0b1000
Выполнение левого разрядное смещение 1 эквивалентно умножению на 2 :
7 << 1
# Out: 14
Выполнение левого разрядного смещения n эквивалентно умножения на 2**n :
3 << 4
# Out: 48 Побитовый сдвиг вправо
>> оператор выполняет побитовое «сдвиг вправо» , где значение левого операнда перемещается вправо на число битов данных в правом операнде.
# 8 = 0b1000
8 >> 2
# Out: 2
# 2 = 0b10
bin(8 >> 2)
# Out: 0b10
Выполнение правильного битового смещения 1 эквивалентно целочисленного деления на 2 :
36 >> 1
# Out: 18
15 >> 1
# Out: 7
Выполнение правильного битового смещения n эквивалентно целочисленное деление на 2**n :
48 >> 4
# Out: 3
59 >> 3
# Out: 7 Побитовое НЕ
~ Оператор переворачивает все биты числа. Поскольку компьютеры используют прямой код — прежде всего, в дополнении до двух обозначений для кодирования отрицательных двоичных чисел , где отрицательные числа записываются с ведущим один (1) вместо ведущего нуля (0).
Поскольку компьютеры используют прямой код — прежде всего, в дополнении до двух обозначений для кодирования отрицательных двоичных чисел , где отрицательные числа записываются с ведущим один (1) вместо ведущего нуля (0).
Это означает , что если вы используете 8 бит для представления номера вашего дополнительного кода комплемента, вы бы относиться к модели от 0000 0000 до 0111 1111 для представления чисел от 0 до 127 и резервного 1xxx xxxx для представления отрицательных чисел.
Восьмиразрядные числа с двумя дополнительными числами
Биты Значение без знака Значение двух дополнений 0000 0000 0 0 0000 0001 1 1 0000 0010 2 2 0111 1110 126 126 0111 1111 127 127 1000 0000 128 -128 1000 0001 129 -127 1000 0010 130 -126 1111 1110 254 -2 1111 1111 255 -1
По существу, это означает , что в то время как 1010 0110 имеет беззнаковое значение 166 (прибыл в путем добавления (128 * 1) + (64 * 0) + (32 * 1) + (16 * 0) + (8 * 0) + (4 * 1) + (2 * 1) + (1 * 0) ), оно имеет значение дополнительного код дополнение -90 (прибыли в добавлении (128 * 1) - (64 * 0) - (32 * 1) - (16 * 0) - (8 * 0) - (4 * 1) - (2 * 1) - (1 * 0) , и дополняя значение).
Таким образом, отрицательные числа в диапазоне до -128 ( 1000 0000 ). Ноль (0) представляется в виде 0000 0000 , и минус один (-1) , как 1111 1111 .
В целом, однако, это означает , ~n = -n - 1 .
# 0 = 0b0000 0000
~0
# Out: -1
# -1 = 0b1111 1111
# 1 = 0b0000 0001
~1
# Out: -2
# -2 = 1111 1110
# 2 = 0b0000 0010
~2
# Out: -3
# -3 = 0b1111 1101
# 123 = 0b0111 1011
~123
# Out: -124
# -124 = 0b1000 0100
Обратите внимание, что общий эффект этой операции при нанесении на положительные числа можно суммировать:
~n -> -|n+1|
И затем, применительно к отрицательным числам, соответствующий эффект:
~-n -> |n-1|
Следующие примеры иллюстрируют это последнее правило …
# -0 = 0b0000 0000
~-0
# Out: -1
# -1 = 0b1111 1111
# 0 is the obvious exception to this rule, as -0 == 0 always
# -1 = 0b1000 0001
~-1
# Out: 0
# 0 = 0b0000 0000
# -2 = 0b1111 1110
~-2
# Out: 1
# 1 = 0b0000 0001
# -123 = 0b1111 1011
~-123
# Out: 122
# 122 = 0b0111 1010
Операции на месте
Все операторы Побитового (кроме ~ ) имеет свои собственные места версии
a = 0b001
a &= 0b010
# a = 0b000
a = 0b001
a |= 0b010
# a = 0b011
a = 0b001
a <<= 2
# a = 0b100
a = 0b100
a >>= 2
# a = 0b001
a = 0b101
a ^= 0b011
# a = 0b110Синтаксис
Параметры
Примечания
Циклический сдвиг через бит переноса
Логический сдвиг
Сдвиг, при котором уходящий бит исчезает, не влияя на оставшиеся биты, а на месте появившегося бита записывается бит 0.
Пример работы операции сдвига:
· Пусть у нас есть число 10101010b (в двоичной системе).
· Если сделать сдвиг влево на 1 бит, то получим число 01010100b.
· Если сделать сдвиг исходного числа вправо на 1 бит, то получим число 01010101b.
В большинстве процессоров уходящий бит сохраняется во флаге переноса. Эта функция широко используется при работе со многобайтовыми числами.
Логический сдвиг влево Логический сдвиг вправо
Арифметический сдвиг
При этом сдвиге слово рассматривается не просто как группа битов, а как целое число в дополнительном коде. При сдвиге влево ведёт себя как логический сдвиг, при сдвиге вправо уходящий бит исчезает, не влияя на оставшиеся биты, а на месте появившегося бита устанавливается бит, соответствующий знаку.
Арифметический сдвиг влево Арифметический сдвиг вправо
Пример №1
Пример работы операции сдвига 8 битного числа в прямом коде:
· Пусть у нас есть 8 битное число: 0000 0010b = 2. (записанное в двоичной системе, в прямом коде).
(записанное в двоичной системе, в прямом коде).
· Cдвиг влево на 1 бит, дает число: 00000100b = 4.
· Сдвиг вправо на 1 бит, дает число: 00000001b = 1.
Пример №2
Пример работы операции сдвига 8 битного числа записанного в дополнительном до 2х коде:
· Пусть у нас есть число 11111010b = −6 (в двоичной системе, в дополнительном коде).
· Если сделать сдвиг влево на 1 бит, то получим число 11110100b = −12.
· Если сделать сдвиг исходного числа вправо на 1 бит, то получим число 11111101b = −3.
Циклический сдвиг
При этом сдвиге уходящий бит появляется на месте появившегося свободного на другом конце числа.
Циклический сдвиг влево Циклический сдвиг вправо
Пример
- Пусть у нас есть число 11111010b (в двоичной системе).
- Если сделать сдвиг влево на 1 бит, то получим число 11110101b.
- Если сделать сдвиг вправо на 1 бит, то получим число 01111101b.

Циклический сдвиг через бит переноса
При нём первый бит по направлению сдвига получает значение из бита переноса, а значение последнего бита сдвигается в бит переноса.
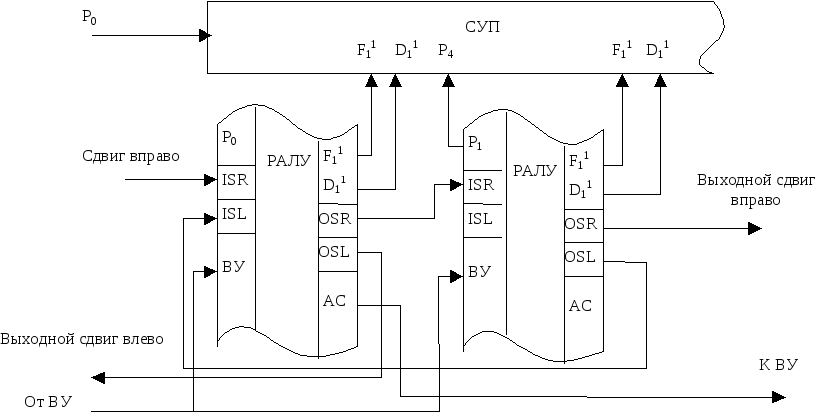
В архитектуру многих процессоров входит флаг переноса в следующий разряд (например, cf на x86). Данная операция выполняет циклический сдвиг над (n+1)-битным числом, состоящим из регистра и флага переноса.
Флаг переноса CF (англ. Carry flag) в микропроцессорах — битовый флаг, который устанавливается, если в результате арифметической операции в (n + 1)-м значащем бите появилась единица (соответственно, в результате двоичного сдвига из разрядной сетки ушла единица).
Например, если у нас в регистре число 11111010b, флаг переноса циклического сдвига вправо равен 0.
После сдвига влево на 1 бит в регистре 11110101b, флаг переноса равен 1.
После сдвига вправо на 1 бит в регистре 01111101b, флаг переноса равен 1.
Операция циклического сдвига через бит переноса используется при работе с многобайтовыми числами. В частности, чтобы сдвинуть вправо на 1 бит длинное число, нужно очистить[1] cf (в случае деления числа со знаком нужно записать в cf старший бит старшего слова) и циклически сдвинуть на единицу через cf каждое слово, начиная с верхнего. Например, пусть у нас есть число 011000111100b, занимающее три 4-битных слова:
Было: HI=0110, MED=0011, LO=1100, cf=0
После сдвига HI: HI=0011, MED=0011, LO=1100, cf=0
После сдвига MED: HI=0011, MED=0001, LO=1100, cf=1
После сдвига LO: HI=0011, MED=0001, LO=1110, cf=0
Сдвиги через регистр флагов более чем на 1 бит практически не используются.
MSLibrary. Реализация множественного выбора условий с помощью битовых масок, для iOS и не только…
Мы продолжаем публикацию материалов, от разработчиков библиотеки MSLibrary for iOS. Тема этой статьи не случайна, проблема выбора нескольких условий из заданного множества, не редко встречается в нашей работе. Простейший пример — выбор партнера для игры (свидания, путешествия и тд). Выбор надо осуществлять из нескольких групп, сформированных по уровню подготовленности (здесь могут быть и возрастные группы и все что угодно). Условие — дать пользователю возможность выбрать партнера из одной или нескольких групп одновременно. Другим примером могут служить константы NSRegularExpressionOptions проверки типа данных для класса NSRegularExpression. При подстановке этих констант в методы класса, мы можем записать:
Простейший пример — выбор партнера для игры (свидания, путешествия и тд). Выбор надо осуществлять из нескольких групп, сформированных по уровню подготовленности (здесь могут быть и возрастные группы и все что угодно). Условие — дать пользователю возможность выбрать партнера из одной или нескольких групп одновременно. Другим примером могут служить константы NSRegularExpressionOptions проверки типа данных для класса NSRegularExpression. При подстановке этих констант в методы класса, мы можем записать:NSRegularExpressionCaseInsensitive | NSRegularExpressionDotMatchesLineSeparators
Объединив константы знаком логического «ИЛИ» мы будем уверены, что проверим анализируемую строку на соответствие обоим из заданных условий.
Один из способов реализации подобной задачи — использование списка констант в виде перечисления enum, в котором элементы перечисления представляют собой двоичные числа с одним установленным битом. Сделать это не очень сложно, но сначала немного теории. Вспомним такие битовые операции, как «СДВИГ», «И», «ИЛИ».
Вспомним такие битовые операции, как «СДВИГ», «И», «ИЛИ».
Побитовые логические операции с двоичными числами
ЛОГИЧЕСКИЙ БИТОВЫЙ «СДВИГ (SHIFT)»
При логическом сдвиге значение последнего бита по направлению сдвига теряется (копируясь в бит переноса), а первый приобретает нулевое значение.
На картинке изображен логический сдвиг влево на один разряд.
Для полноты картины можно сказать, что при сдвиге влево на один разряд исходное число 01010101 превращается в 10101010. В привычной нам шестнадцатеричный системе (Hex) число 0x55 превращается в 0xAA или в десятичной системе 85 превращается в 170, то есть умножается на 2, что вполне логично.
ПОБИТОВОЕ «ИЛИ (OR)»
Это — бинарная операция, действие которой эквивалентно применению логического ИЛИ к каждой паре битов, которые стоят на одинаковых позициях в двоичных представлениях операндов. Другими словами, если оба соответствующих бита операндов равны 0, двоичный разряд результата равен 0; если же хотя бы один бит из пары равен 1, двоичный разряд результата равен 1.
Визуально это выглядит так:
Применение операции побитового «ИЛИ» к исходным числам 01100110 и 10101010 дает результат 11101110. В шестнадцатеричный системе (Hex) исходные числа 0x66 и 0xAA, результат 0xEE или в десятичной системе исходные числа 102 и 170, результат 238.
ПОБИТОВОЕ «И (AND)»
Это — бинарная операция, действие которой эквивалентно применению логического «И» к каждой паре битов, которые стоят на одинаковых позициях в двоичных представлениях операндов. Другими словами, если оба соответствующих бита операндов равны 1, результирующий двоичный разряд равен 1; если же хотя бы один бит из пары равен 0, результирующий двоичный разряд равен 0.
Применение операции побитового «И» к исходным числам 01100110 и 10101010 дает результат 00100010. В шестнадцатеричный системе (Hex) исходные числа 0x66 и 0xAA, результат 0x22 или в десятичной системе исходные числа 102 и 170, результат 34.
Двоичные числа с одним установленным битом
Теперь посмотрим что же получается в случае применения этих операций к двоичным числам с одним установленным битом.
ПОРАЗРЯДНЫЙ (ПОБИТОВЫЙ) СДВИГ
Примененный к числу 00000001 поразрядный сдвиг даст следующий результат:
Операции битовых сдвигов обозначаются, в зависимости от направления сдвига, знаками «<<» и «>>»:
двоичноеЧисло << n // битовый сдвиг влево на "n" позиций (разрядов) двоичноеЧисло >> n // битовый сдвиг вправо на "n" позиций (разрядов)
Число 00000001 это десятичная 1. Поэтому числа с одним установленным битом и битовым сдвигом влево принято обозначать следующим образом:
1 << n //где "n" количество позиций (разрядов) на которое осуществляется сдвиг 1 << 0 // 00000001 сдвиг на 0 разрядов 1 << 1 // 00000001 сдвиг на 1 разрядов 1 << 3 // 00000001 сдвиг на 3 разряда 1 << 5 // 00000001 сдвиг на 5 разрядов
ПОБИТОВОЕ ЛОГИЧЕСКОЕ «ИЛИ (OR)»
Возьмем несколько чисел с одним установленным битом и применим к ним операцию побитового логического «ИЛИ (OR)». Записывается это так:
1<<0 | 1<<3 | 1<<5
а выглядит так:
Замечательное свойство такой операции — в результате получается уникальное значение в данном диапазоне чисел.
Результат, полученный от применения операции побитового логического «ИЛИ» к разным числам с одним установленным битом из заданного множества чисел, всегда уникален
ПОБИТОВОЕ ЛОГИЧЕСКОЕ «И (AND)»
Второе свойство чисел с одним установленным битом — применив операцию побитового логического «И (AND)» к любому из чисел, входящих в операцию «ИЛИ (OR)» и полученному результату, мы получим исходное число:
1 << 0 & (1 << 0 | 1 << 3 | 1 << 5) = 1 << 0 1 << 3 & (1 << 0 | 1 << 3 | 1 << 5) = 1 << 3 1 << 5 & (1 << 0 | 1 << 3 | 1 << 5) = 1 << 5
В то время, как другие числа с одним установленным битом этому условию не удовлетворяют:
1 << 1 & (1 << 0 | 1 << 3 | 1 << 5) ≠ 1 << 1 1 << 2 & (1 << 0 | 1 << 3 | 1 << 5) ≠ 1 << 2 1 << 4 & (1 << 0 | 1 << 3 | 1 << 5) ≠ 1 << 4
Для наглядности:
Это свойство числа, полученного в результате применения операции побитового логического «ИЛИ (OR)», позволяет использовать его в качестве «БИТОВОЙ МАСКИ».
БИТОВАЯ МАСКА
Это — определённые данные, которые используются для маскирования — выбора отдельных битов или полей из нескольких битов из двоичной строки или числа.
Другим словами, результат, полученный от применения операции побитового логического «ИЛИ» к разным числам с одним установленным битом из заданного множества чисел, может быть использован в качестве битовой маски.
Применив операцию побитового логического «ИЛИ (OR)» к нескольким числам с одним установленным битом, можно использовать полученный результат в качестве битовой маски для фильтрации исходных чисел из множества других.
Перейдем к практике.
Перечисления enum с двоичными числами с одним установленным битом
Для определения набора констант, с заданным количеством конкретных значений, удобно использовать перечисляемый тип или перечисление enum. Запишем перечисление для умозрительного примера, приведенного в начале статьи. Допустим нам надо определить пять групп пользователей. Записывается это так:
Допустим нам надо определить пять групп пользователей. Записывается это так:
enum Groups {
group_0 = 0,
group_1 = 1
group_2 = 2,
group_3 = 3,
group_4 = 4,
};Мы можем использовать «Groups » для выбора подходящей группы пользователей, но не можем объединять эти группы, то есть мы не можем выбрать пользователей из групп «group_2» и «group_3» и организовать фильтрацию всех пользователей по этим параметрам. Мы можем вычислить контрольное число произведя операцию (2 + 3) = 5, но оно не будет уникальным, группы «group_1» и «group_4» дадут тот же результат: (1 + 4) = 5. Модифицируем выражение, указав в качестве значений числа с одним установленным битом и используя побитовый сдвиг влево.
enum Groups {
group_0 = 1 << 0,
group_1 = 1 << 1,
group_2 = 1 << 2,
group_3 = 1 << 3,
group_4 = 1 << 4
};В этом случае мы можем легко создать «БИТОВУЮ МАСКУ», применив операции побитового «ИЛИ (OR)» к выбранным параметрам.
 Допустим, мы выбрали те же «group_2» и «group_3»:
Допустим, мы выбрали те же «group_2» и «group_3»:(1 << 2 | 1 << 3) = 0x55 1 << 2 & (1 << 2 | 1 << 3) = 1 << 2 1 << 3 & (1 << 2 | 1 << 3) = 1 << 3 1 << 1 & (1 << 2 | 1 << 3) ≠ 1 << 1 1 << 4 & (1 << 2 | 1 << 3) ≠ 1 << 4
или, подставив константы:
(group_2 | group_3) = 0x55 group_2 & (group_2 | group_3) = group_2 group_3 & (group_2 | group_3) = group_3 group_1 & (group_2 | group_3) ≠ group_1 group_4 & (group_2 | group_3) ≠ group_4
Аналогично устроены многие битовые константы, в частности упоминавшиеся в начале статьи NSRegularExpressionOptions:
typedef NS_OPTIONS(NSUInteger, NSRegularExpressionOptions) {
NSRegularExpressionCaseInsensitive = 1 << 0, // Match letters in the pattern independent of case
NSRegularExpressionAllowCommentsAndWhitespace = 1 << 1, // Ignore whitespace and #-prefixed comments in the pattern
NSRegularExpressionIgnoreMetacharacters = 1 << 2, // Treat the entire pattern as a literal string
NSRegularExpressionDotMatchesLineSeparators = 1 << 3, // Allow . and $ to match the start and end of lines
NSRegularExpressionUseUnixLineSeparators = 1 << 5, // Treat only \n as a line separator (otherwise, all standard line separators are used)
NSRegularExpressionUseUnicodeWordBoundaries = 1 << 6 // Use Unicode TR#29 to specify word boundaries (otherwise, traditional regular expression word boundaries are used)
};
and $ to match the start and end of lines
NSRegularExpressionUseUnixLineSeparators = 1 << 5, // Treat only \n as a line separator (otherwise, all standard line separators are used)
NSRegularExpressionUseUnicodeWordBoundaries = 1 << 6 // Use Unicode TR#29 to specify word boundaries (otherwise, traditional regular expression word boundaries are used)
}; или NSTextCheckingResult:
typedef NS_OPTIONS(uint64_t, NSTextCheckingType) { // a single type
NSTextCheckingTypeOrthography = 1ULL << 0, // language identification
NSTextCheckingTypeSpelling = 1ULL << 1, // spell checking
NSTextCheckingTypeGrammar = 1ULL << 2, // grammar checking
NSTextCheckingTypeDate = 1ULL << 3, // date/time detection
NSTextCheckingTypeAddress = 1ULL << 4, // address detection
NSTextCheckingTypeLink = 1ULL << 5, // link detection
NSTextCheckingTypeQuote = 1ULL << 6, // smart quotes
NSTextCheckingTypeDash = 1ULL << 7, // smart dashes
NSTextCheckingTypeReplacement = 1ULL << 8, // fixed replacements, such as copyright symbol for (c)
NSTextCheckingTypeCorrection = 1ULL << 9, // autocorrection
NSTextCheckingTypeRegularExpression = 1ULL << 10, // regular expression matches
NSTextCheckingTypePhoneNumber = 1ULL << 11, // phone number detection
NSTextCheckingTypeTransitInformation = 1ULL << 12 // transit (e. g. flight) info detection
};
g. flight) info detection
}; Вернемся к нашему примеру с группами пользователей. Мы создали битовую маску, теперь надо написать код для ее использования. Если два подхода для решения этой задачи, первый — использующий операторы «if(){}» и второй — в котором применяется связка операторов «for(){}» и «switch(){}», рассмотрим оба.
Использование оператора «if(){}»
Этот подход довольно несложен. Нижеприведенный код в особых комментариях не нуждается:
NSInteger group_masck = (group_2 | group_3) = 0x55;
if ((group_masck & group_0) == group_0) {
// действие, совершаемое в случае соответствия константы и маски
}
if ((group_masck & group_1) == group_1) {
// действие, совершаемое в случае соответствия константы и маски
}
if ((group_masck & group_2) == group_2) {
// действие, совершаемое в случае соответствия константы и маски
}
if ((group_masck & group_3) == group_3) {
// действие, совершаемое в случае соответствия константы и маски
}
if ((group_masck & group_4) == group_4) {
// действие, совершаемое в случае соответствия константы и маски
}
Подставив в этот код значения констант мы увидим, как он работает:
NSInteger group_masck = (1 << 2 | 1 << 3) = 0x55
if (((1 << 2 | 1 << 3) & 1 << 0) == 1 << 0) {
// действие, совершаемое в случае соответствия константы и маски
}
if (((1 << 2 | 1 << 3) & 1 << 1) == 1 << 1) {
// действие, совершаемое в случае соответствия константы и маски
}
if (((1 << 2 | 1 << 3) & 1 << 2) == 1 << 2) {
// действие, совершаемое в случае соответствия константы и маски
}
if (((1 << 2 | 1 << 3) & 1 << 3) == 1 << 3) {
// действие, совершаемое в случае соответствия константы и маски
}
if (((1 << 2 | 1 << 3) & 1 << 4) == 1 << 4) {
// действие, совершаемое в случае соответствия константы и маски
}
Таким образом, некие действия выполняются во всех случаях соответствия константы и маски, в нашем примере для пользователей из групп «group_2» и «group_3».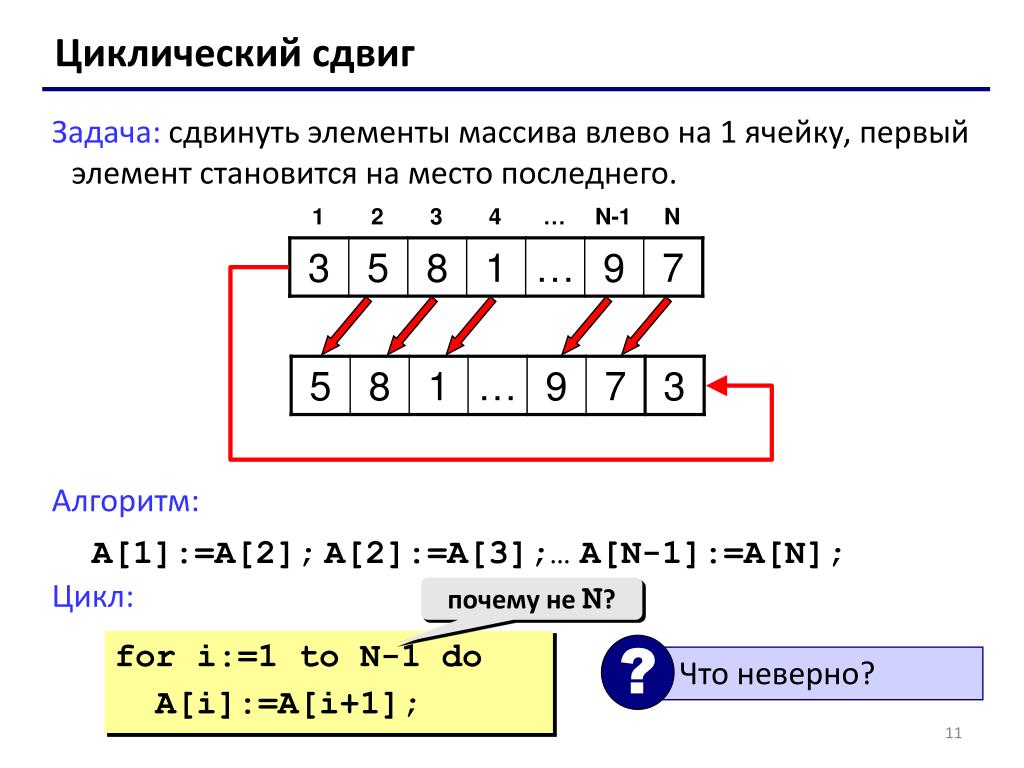
Использование операторов «for(){}» и «switch(){}»
Второй подход заключается в использовании связки операторов «for(){}» и «switch(){}». Преимущество этого варианта в том, что если для разных констант «Groups» необходимо совершать идентичные действия, например применять одни и те же функции, отличающиеся только некими переменными, то данный подход позволяет создать более компактный и изящный код:
NSInteger group_masck = (group_2 | group_3) = 0x55;
id variable;
for (int i = 0; i <= 4; i++) {
switch (i) {
case 0: {
variable = value_0;
}
break;
case 1: {
variable = value_1;
}
break;
case 2: {
variable = value_2;
}
break;
case 3: {
variable = value_3;
}
break;
case 4: {
variable = value_4;
}
break;
default: {
//действие, совершаемое в случае ошибки
}
break;
}
if ((group_masck & 1ULL << i) == 1ULL << i) {
// выполняется некое действие с подстановкой переменной "variable"
}
}
По такому же принципу организованы многие методы и функции нашей библиотеки MSLibrary for iOS.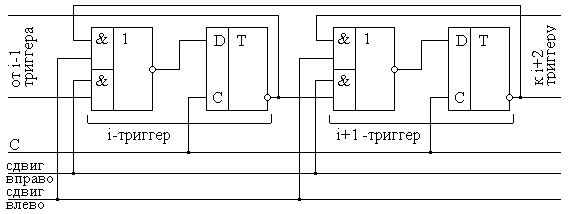 Для примера, функция: msfDDstringCheckingStyle() принимает значения «YES» или «NO» в зависимости от того, выполняются ли в анализируемой строке заданные условия.
Для примера, функция: msfDDstringCheckingStyle() принимает значения «YES» или «NO» в зависимости от того, выполняются ли в анализируемой строке заданные условия.
BOOL msfDDstringCheckingStyle(NSString *string, tMSstringCheckingStyle stringCheckingStyle, BOOL allConditionsIsRequired, NSInteger minLengthOfString)где
string — анализируемая строка
stringCheckingStyle — константы, накладывающие некие ограничения
allConditionsIsRequired — флаг, в случае если он имеет значение «YES», выполнение условий определяемых всеми константами «stringCheckingStyle» обязательно, если он имеет значение «NO», может быть выполнено любое одно или несколько, заданных условий
minLengthOfString — минимальная длина строки
Константы «stringCheckingStyle» заданы так:
typedef enum tMSstringCheckingStyle: NSInteger {
kMSstringCheckingStyle_digits = 1ULL << 0, // must-have only a digits
kMSstringCheckingStyle_englishLetters = 1ULL << 1, // must-have only a English letters
kMSstringCheckingStyle_russianLetters = 1ULL << 2, // must-have only a Russian letters
kMSstringCheckingStyle_startWithLetter = 1ULL << 3, // the string necessarily start with a letter
kMSstringCheckingStyle_upperAndLowerCaseLetters = 1ULL << 4, // must-have a uppercase and a lowercase letters
kMSstringCheckingStyle_specialSymbols = 1ULL << 5, // must-have one or more special symbols "-" "." "+" "_"
} tMSstringCheckingStyle;
Таким образом, например, записав функцию с виде:
msfDDstringCheckingStyle(NSString *string, tMSstringCheckingStyle kMSstringCheckingStyle_digits | kMSstringCheckingStyle_englishLetters, BOOL YES, NSInteger 8)мы получим положительный результат только в случае, если строка «string» будет иметь не менее 8 знаков и в ней будут обязательно содержаться буквы английского алфавита и цифры, что полезно, к примеру, при проверке новых паролей.
Как видите вопрос решается всего в одну строку кода.
Надеемся, что материал был для вас полезен, команда MSLibrary for iOS
Другие статьи:
Захват и верификация телефонных номеров с помощью регулярных выражений, для iOS и не только… Часть 1
Захват и верификация телефонных номеров с помощью регулярных выражений, для iOS и не только… Часть 2
ПРОСТО: удаляем из строки ненужные символы, для iOS и не только…
Создание и компиляция кроссплатформенных (универсальных) библиотек в Xcode
сдвиг вправо логический
SRL используется для смены 32 бита в регистре, указанном операндом 1 справа. Количество сдвинутых битов равно обозначается операндом 2. Второй адрес операнда , а не , используемый для адресные данные; вместо этого вычисляется базовый адрес / адрес смещения и крайние правые 6 бит обрабатываются как двоичное целое число, которое представляет количество биты, которые нужно сдвинуть. Мы назовем это оцените коэффициент сдвига.Это ведет к два различных способа кодирования коэффициента сдвига:
1) Непосредственно — Коэффициент сдвига кодируется как смещение. Рассмотреть возможность пример ниже.
SRL R9,8
В указанную выше смену второй операнд, 8, рассматривается как адрес основания / смещения, где 8 — это смещение и базовый регистр опускаются. Действующий адрес — 8. (См. Explicit Обращаясь к .) При представлении в виде адреса крайние правые 6 бит по-прежнему представляют собой число 8, поэтому биты в регистр 9 сдвинут вправо на 8 бит.
2) Косвенно — Смена коэффициент помещается в регистр, и регистр упоминается как базовый Зарегистрируйтесь в базовом / замещающем адресе.
L R5, FACTOR PUT SHIFT FACTOR IN REG
SRL R9,0 (R5) ТЕПЕРЬ ПЕРЕМЕСТИТЬ КОСВЕННО
…
КОЭФФИЦИЕНТ DC F8 КОЭФФИЦИЕНТ СМЕЩЕНИЯ 8 БИТ
В этом случае эффективный адрес вычисляется путем сложения содержимого базового регистра 5 (который равен 8), со смещением 0.В эффективный адрес снова 8, и крайние правые 6 бит этого адреса указывают что коэффициент сдвига равен 8.
Каждый метод имеет свое применение. Прямой метод полезен в ситуациях, когда количество бит, которое вы хочу сдвинуть фиксируется. Кодирование напрямую позволяет посмотреть инструкцию, чтобы определить коэффициент сдвига. С другой стороны, косвенный метод позволяет определить коэффициент сдвига во время выполнения программы. Если коэффициент сдвига не может быть определен пока программа не будет запущена, необходимо использовать косвенный метод.
При логическом сдвиге биты, сдвинутые вправо, теряются, а 0s заменяют биты слева.
Рассмотрим следующую инструкцию.
SRL R8,6
Эта инструкция представляет сдвиг вправо регистра 8 с использованием коэффициента сдвига 6. Коэффициент сдвига был закодирован напрямую. В итоге 6 бит, 110000, сдвинуты из регистра справа. Освободившиеся битовые позиции слева заменяются нулями.Это показано на диаграмме ниже.
Эта инструкция имеет RS , но 4 младших бита второго байта не используются.
Некоторые несвязанные SRL
R5 = B111111111111111111111111111111
R6 = B11110000111100001111000011110000
SRL R5,1 R5 = B01111111111111111111111111111111
SRL R5,2 R5 = B001111111111111111111111111111
SRL R5,3 R5 = B00011111111111111111111111111111
SRL R5,31 R5 = B00000000000000000000000000000001
SRL R5,32 R5 = B00000000000000000000000000000000
SRL R6,4 R6 = B00001111000011110000111100001111
л R9, = F3
SRL R5,0 (R9) R5 = B00011111111111111111111111111111
л R3, = F5
SRL R5,0 (R3) R5 = B00000111111111111111111111111111
Логические и арифметические сдвиги — Уроки C
Это руководство по C объясняет логические и арифметические сдвиги в языке C с примерами.Одиночный бит — это основная единица памяти, в которой хранится либо 1, либо 0. Поэтому, когда биты перемещаются влево или вправо в значении определенного типа, а именно. integer, char и т. д. меняются их значения. Перемещение битов в значении на языке C выполняется с помощью операторов сдвига влево или вправо. Поскольку эти операторы работают с отдельными битами, они называются побитовыми операторами. Эти операторы работают с отдельными битами значений переменных целочисленного типа данных в их знаковой или беззнаковой форме. Символы внутренне являются целыми числами, и поэтому эти операторы работают с ними.
Оператор сдвига влево обозначается символом «>». Эти операторы являются двоичными, требуют двух операндов с каждой стороны, и оба должны быть целыми числами. Синтаксис сдвига влево и вправо следующий:
имя переменной оператор сдвига вправо / влево без битов для сдвига;
val >> 5; / * сдвигаем значение в val вправо на 5 бит * /
число << 5; / * сдвигаем значение в num влево на 5 бит * / Сдвиг называется логическим, когда выполняется с целыми числами без знака в любом направлении, вправо или влево.В логическом сдвиге при сдвиге на любую сторону пустые слоты дополняются нулями. Например:
/ * * rlshift.c - программа использует операторы сдвига влево и вправо с беззнаковыми * целые числа * / #includeint main (пусто) { unsigned int b = 16, результат; printf ("значение exp. result = b >> 3 равно% d \ n", result = b >> 3); printf ("значение b после сдвига вправо на 3 бита,% d \ n", b); printf ("значение exp. result = b << 3 равно% d \ n", result = b << 3); printf ("значение b после сдвига влево на 3 бита,% d \ n", b); / * обратите внимание, что значение b остается неизменным после сдвига влево или вправо * / / * только результат изменения * / возврат 0; }
Сдвиг значения вправо на n битов приводит к делению значения на степень 2, возведенной в n, а смещение значения влево на n битов дает эффект умножения значения на степень 2, возведенную в n. Например:
/ * * rlshift_effect.c - программа отображает результат сдвига влево или вправо * значения беззнаковых целых чисел * / #includeint main (пусто) { беззнаковое int b = 16; printf ("значение exp. b >> = 3 равно% d \ n", b >> = 3); printf ("значение b после сдвига вправо на 3 бита,% d \ n", b); printf ("значение exp. b << = 3 равно% d \ n", b << = 3); printf ("значение b после сдвига влево на 3 бита,% d \ n", b); / * * обратите внимание, что значение b после сдвига вправо на 3 бита равно * деление на 2 возводится в 3 * и сдвиг влево на 3 бита приводит к тому, что * умножено на 2 и увеличено до 3 * / возврат 0; }
Теперь мы рассмотрим , что происходит, когда значение в переменной сдвигается в любую сторону, кроме отрицательного числа, или что происходит, когда количество сдвигов превышает количество бит в операнде. Например:
мальчиков >> -6;
мальчики << -6;
мальчики >> 35 лет; В стандарте указано, что поведение таких сдвигов зависит от реализации. Мы должны избегать использования таких типов сдвигов, потому что их эффекты непредсказуемы и непереносимы.
Арифметические сдвиги
До сих пор мы рассматривали сдвиг беззнаковых целых чисел вправо или влево на заданные биты и заполняли таким образом образовавшиеся пустые места нулями. Когда арифметический сдвиг вправо выполняется для отрицательного числа, то бит знака копируется в пустые слоты, созданные при сдвиге. Например:
/ * rshift_negtive_val.c - программа выполняет сдвиг вправо для -ve целых чисел * / #includeint main (пусто) { int hall = -16; printf ("значение exp. hall >> = 3 равно% d \ n", hall >> = 3); printf ("значение холла, -ve значение, после сдвига вправо на 3 бита," "is% d \ n", холл); / * * отрицательные числа сохраняются в компьютере в форме дополнения до 2 * сдвига вправо числа -ve равно -ve, потому что знаковый бит 1 копируется * в пустые слоты * / возврат 0; }
Арифметический и логический сдвиги влево идентичны.Различаются только правые сдвиги, и то только для отрицательных значений. Следовательно, программы , которые сдвигают вправо для значений со знаком, по своей сути непереносимы.
Использование операторов смены:
Например:
/ * count_one_bit.c: Программа считает 1 бит в заданном целом числе без знака * / #includevoid count1bits (int); int main (пусто) { int num; printf ("введите какое-нибудь беззнаковое целое число \ n"); scanf ("% d", & num); count1bits (число); / * призыв к веселью.* / возврат 0; } void count1bits (int num1) { int ones = 0; while (num1! = 0) { если (число1% 2! = 0) единицы ++; число1 >> = 1; } printf ("Количество Единиц в Значении% d \ n", единиц); }
Sanfoundry Global Education & Learning Series - Учебники по 1000 C.
Если вы хотите просмотреть все учебные пособия по C, перейдите к учебным пособиям по C. Примите участие в конкурсе сертификации Sanfoundry, чтобы получить бесплатную Почетную грамоту. Присоединяйтесь к нашим социальным сетям ниже и будьте в курсе последних конкурсов, видео, стажировок и вакансий!Rotators - обзор | Темы ScienceDirect
Схема системы представлена на рисунке 1.Сточные воды, поступающие с бумажной фабрики и поступающие на очистные сооружения, состоят из растворимых волокон, нерастворимых волокон, небольших кусочков пластика и песка. Блок 1 представляет собой фильтр-вращатель, в котором удаляются мелкие кусочки пластика и песок. Блок 2 представляет собой резервуар с мешалкой для гомогенизации сточных вод. В блоке 3 растворимое волокно осаждается путем добавления куагулянта (катионного биополимера) для нейтрализации электрических зарядов волокна, затем добавляется флокулянт (полиалюминийхлорид) для связывания коагулянта-волокна с другими связями.Осажденное волокно отправляется обратно на бумажный завод для повторного использования, в то время как часть осветленной воды блоком 3 направляется непосредственно на бумажный завод, а другая часть отправляется в аэробный биореактор (блок 4), где происходят реакции описать уравнением. (1) - (6) имеют место. Кислород добавляется компрессором прямого вытеснения (установка 8). Фосфат аммония добавляется, потому что концентрации азота и фосфора в биореакторе очень низкие. Блок 5, вторичный отстойник, питается выходным потоком блока 4, а остальная часть направляется в блок 7, варочный котел, для уменьшения концентрации биомассы.Затем его отправляют на окончательную утилизацию (сушильные кровати). Осветленная вода из блока 5 направляется в резервуар хлорирования (блок 6), где патогенные микроорганизмы погибают при добавлении гипохлорита натрия. Динамическая модель для биореактора этого процесса дается формулой. (1) - (7).
(1) dVbdt = Fi + Fr + Fn + Fai − Fob − Fao
(2) dSbdt = FiVb * Si + FrVb * Ss − FobVb * Sb − rs
(3) dNTbdt = FiVb * NTi + FnV * NTn + FrVb * NTs − FobVb * NTb − rNT
(4) dPO42 − bdt = FiVb * PO42 − i + FnVb * PO42 − n + FrVb * PO42 − s − FobVb * PO42 − b − rpo42−
( 5) dXbdt = FrVb * Xs − FobVb * Xb + rX
(6) dO2bdt = kLa * (O2 * −O2b) −VCO− (FobVb * O2b)
(7) dSSTbdt = FiVb * SSTi + FsrV −FobVb * SSTb
где, V b - объем биореактора, м 3 ; t - время, сутки; F i - входной объемный расход, м 3 · d −1 ; F r - оборотный расход, м 3 · d −1 ; F ob - расход на выходе, м 3 · d -1 ; S b - концентрация субстрата, кг · м −3 ; S льдина - выход осветленной воды с концентрацией субстрата первичного отстойника, кг · м −3 ; S r - концентрация субстрата в рециркулируемом потоке, кг · м −3 ; r s - скорость реакции субстрата, кг · сут -1 ; NT b - концентрация общего азота, кг · м −3 ; NT p floe - выход осветленной воды из первичного отстойника с концентрацией общего азота, кг · м −3 ; F n - объемный расход внешней дозировки фосфата амония, м 3 · сутки −1 ; NT n - концентрация общего азота при внешней дозе, кг · м −3 ; NT r - концентрация общего рециркулируемого азота, кг · м −3 ; r NT - скорость реакции общего азота, кг · сут -1 ; PO 4b - концентрация фосфора, кг · м −3 ; PO 4i - выход осветленной воды первичного отстойника с концентрацией фосфора, кг · м −3 ; PO 4n - внешняя дозированная концентрация фосфора, кг · м −3 ; PO 4r - концентрация рециркулируемого фосфора, кг · м −3 ; r PO4 - скорость реакции фосфора, кг · сут -1 ; X b - концентрация биомассы, кг · м −3 ; X r - концентрация рециркулируемой биомассы, кг · м −3 ; r x - скорость роста биомассы, кг · сут -1 ; O 2 концентрация кислорода, кг · м −3 ; O 2 * - равновесная концентрация кислорода, кг · м −3 ; k La - коэффициент массообмена, d -1 ; r O2 - скорость реакции кислорода, кг · сут −1 ; SST b - общая концентрация взвешенных веществ, кг · м −3 ; SST i - выход осветленной воды из первичного отстойника с общей концентрацией взвешенных веществ, кг · м −3 ; и SST r - общая рециклированная концентрация взвешенных твердых частиц, кг · м -3 .Кинетические выражения, взятые и модифицированные путем добавления зависимости от температуры и pH, были взяты из Mannina et al. (2012), и даются определяющим уравнением. (8) - (12). В таблице 1 приведены соответствующие значения и значения кинетических параметров.
Таблица 1. Числовые значения параметров
| Число | Символ | Значение | Значение | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1. | μ H | Скорость роста 1 | .8 d -1 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 2. | μ AUT | Максимальная скорость роста нитрификаторов + | 1,09 d -1 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 3 9038 | Константа скорости гидролиза * | 2,76 d −1 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 4. | K X | Константа насыщения гидролиза * | 0,036 кг X кг S| 5. | K OH | Коэффициент насыщения кислородом для гетеротрофной биомассы * | 0,29 кгO2 / м −3 | 6. | η N03H | . 0,72 | 7. | K F | Коэффициент насыщения для S f (COD) + | 7,55 кгCOD / м −3 | K p04 | Коэффициент насыщения для PO4 * | 1,13e −5 кгPO4 / м −3 | 9. | K коэффициент насыщения | общий | Nh5 9038 азот * | 1,41 кгNh5 / м −3 | 10. | q PP | Константа скорости накопления PO4 + | 1,34 d −1 | μ PAO | Максимальная скорость роста биомассы, накапливающей PO4 | 0,912 d −1 | 12. | η N03PAass0 | N03PAass0 | Пониженный коэффициент накопления PO4 0,5 | 13. | b H | Константа скорости распада гетеротрофной биомассы + | 0,264 d −1 | 14. | b AUT | Константа скорости распада автотрофной биомассы + | 0,05 d -1 | 15. | b pAO константа накапливается биомассы | 0,1 d −1 | 16. | i NBM | Общее содержание азота в биомассе * | 1.0e −3 кгNT / кгX | 17368 | Y PHA | Эффективность хранения PO4 + | 0,15 кг DQO / кг PO4 | 18. | i PBM | содержание фосфора | в биомассе | биомасса | 4 / кг X | 19. | Y A | Эффективность автотрофных микроорганизмов + | 0,23 | 20. | Y микроорганизмы.* 0,45 | 21. | k La | Объемный коэффициент массопереноса * | 6,0 d −1 | |
(8) rs / XKHH + rs / X / XHX * (O2bKOH + O2b + ηNO3HKOHKOH + SO2)] - [1YH * μHSbKF + SbO2bKOH + O2bPO4bKPO4 + PO4 + PO4bNTbKNh5 + NTbX * (1 + ηNO3HKNh5 + NTbX * (1 + ηNO3HBNHKOH) (9000) rNO3 9000) (9000) + iNO3 9000) (9000) μAUTO2bKOH + O2bPO4bKPO4bNTbKNh5 + NTbXAUT - [iNBM * μHSbKF + SbO2bKOH + PO4bNTbKNh5 + NTbXH * (1 + ηNO3HKOHKOH + O2B)]
(10) rPO4 = -qPPO2bKOH + O2bPO4bKPO4 + PO4bXPAO - [iPBM * μPAOO2bKOH + O2bPO4bKPO4 + PO4bNTbKNh5 + NTbXPAO * (1 + ηNO3PAO)] - iPBM * bAUTXAUT
(11) rx = [μHSbKF + SbO2bKOH + O2bPO4bKPO4b + PO4bNTbKNh5b + NTbX * 0.33 * (1 + ηNO3HKOHKOH + O2b)] - 0,33bHX + [O2bKOH + O2bPO4bKPO4 + PO4bX * 0,33 * (μPAO * NTbKNh5 + NTb * (1 + ηNO3PAO) + qPP)] - 0,33bKNObUT2Ob + μPObObObUT2BOb + μPObObObOb2 * 0,33−0,33bAUTX
(12) rO2 = [(1−1YH) ((PO4bKPO4 + PO4bNTbKNh5 + NTb) * (μHSbKF + SbO2bKOH + O2bXH + μPAOO2bKOHO + O2bXPAO2HPO + O2bXPAO)) * - - [(4.75 − YAYA) * μAUTO2bKOH + O2bPO4bKPO4 + SpoPO4b4NTbKNh5 + NTbXAUT]
Фундаментальный C - сдвигает и вращает
| Указатель статей |
|---|
| Фундаментальный C - сдвигает и вращает |
| Вращается |
Страница 2 из 2
Нормализующие маски
Обычно сдвиги могут быть полезны при нормализации значений после извлечения битов с использованием маски. Например, рассмотрим проблему разделения значений RGB, приведенную ранее:
int RGBcolor = 0x010203; int B = цвет RGB & 0x0000FF; int G = цвет RGB & 0x00FF00; int R = цвет RGB & 0xFF0000; G >> = 8; R = (без знака) R >> 16; int data = -1; данные << = 1;
Теперь R равно 1, G равно 2 и B равно 3, как требуется.Обратите внимание, что мы можем сдвинуть G, не беспокоясь о знаковом бите, потому что он должен быть 0. Когда мы сдвигаем R, мы должны использовать логический сдвиг, чтобы он не интерпретировался как отрицательное значение.
Конечно, вы можете объединить операции в одно выражение:
int RGBcolor = 0x010203; int B = цвет RGB & 0x0000FF; int G = (цвет RGB & 0x00FF00) >> 8; int R = ((без знака) RGBcolor & 0xFF0000) >> 16;
Поскольку оператор сдвига имеет более высокий приоритет, чем логическое &, скобки необходимы.
Повернуть
Существует еще одна форма сдвига - левый или правый поворот - и хотя у большинства процессоров есть инструкция, которая будет выполнять этот тип сдвига за одну операцию, по причинам истории C не имеет оператора поворота.
При повороте вправо все биты сдвигаются вправо и используется младший значащий бит, который был сдвинут в качестве нового наиболее значимого. То есть бит младшего разряда сдвигается в бит старшего разряда. Вы можете видеть, что это вращение долот.
Аналогичным образом поворот влево сдвигает все биты влево и перемещает бит высокого порядка, чтобы он стал новым битом низкого порядка. Снова вы можете видеть, что это вращает биты в другом направлении. Вращения не соответствуют простому умножению или делению, и они не так полезны, как сдвиги влево и вправо для разделения битов. Они используются для криптографии и обработки сигналов.
C может не иметь оператора поворота. но легко реализовать поворот, используя поворот влево и вправо и логические операторы.
Например, поворот вправо:
беззнаковые данные int = 0xF; данные = данные >> 1 | данные << 31;
Идея достаточно проста для понимания. Сначала мы выполняем логический сдвиг вправо, при котором самый старший бит обнуляется. Затем мы выполняем логический сдвиг влево 31 раз, чтобы переместить младший значащий бит в самый старший значащий бит. Они объединяются по ИЛИ, чтобы получить результат 0x80000007.
Вы можете увидеть общий принцип.Если вы хотите повернуть вправо n бит 32-битного int, используйте:
data = data >> n | data << 32-n;
Аналогично, если вы хотите повернуть влево n бит 32-битного значения, используйте:
data = data << n | данные >> 32-н;
Обратите внимание, что n не может быть отрицательным или равным 32, что приведет к неопределенному поведению. Также обратите внимание, что данные должны быть без знака, чтобы использовать логические сдвиги.
Говорят, что большинство компиляторов обнаруживают вышеуказанные идиомы и преобразуют инструкции в инструкцию поворота машинного кода, если это возможно.GCC выполняет эту оптимизацию, но только если вы убедитесь, что вращение положительное. То есть:
беззнаковые данные int = 0x0F; данные = данные >> (без знака) 1 | данные << (без знака) 31;
компилируется в:
ror% eax
, где ror - инструкция поворота вправо. Если вы оставите беззнаковые квалификаторы, строка компилируется в эквивалентные сдвиги вправо и влево, соединенные ИЛИ.
Было бы лучше, если бы в C был оператор поворота.
Проверка долота
Окончательная версия в книге
Порядок байтов
Окончательная версия в книге
Некоторые примеры.
Опции
Среднее без переполнения
Вычисление контрольной суммы
Окончательная версия в книге
Сводка
Есть четыре побитовых логических оператора &, |, ^ и ~.Их не следует путать с логическими операторами &&, || а также !.
Поразрядные логические операторы по-разному работают со знаковыми и беззнаковыми типами.
Маска - это способ управления битами, на которые влияет побитовая операция.
Есть два оператора сдвига: << арифметический или логический сдвиг влево и >> арифметический сдвиг вправо.
Арифметический сдвиг влево соответствует умножению целочисленного типа на 2, а арифметический сдвиг вправо делит на 2.
Арифметический сдвиг вправо - это не совсем то же самое, что целочисленное деление на 2 для отрицательных значений, поскольку он округляется до отрицательной бесконечности.
В C нет оператора поворота, но вы можете его создать.
Маски также могут использоваться для проверки состояния бита или группы битов.
Не существует стандарта для порядка, в котором хранятся части многобайтового значения. Little endian сначала сохраняет младшие биты, а big endian сначала хранит старшие биты.
Фундаментальный C: приближение к машине
Теперь доступен в мягкой обложке и электронной книге на Amazon.
- О C
Extract Dependent v Independent
& Undefined Behavior - Начало работы с C с использованием NetBeans
- Управляющие структуры и данные
- Переменные
Извлечь переменные - Арифметика и представление
Извлечение арифметики и представления - Операторы и выражение
Извлечение побочных эффектов, точек последовательности и отложенного вычисления
Первый черновик главы: Низкие данные - Объем функций и срок службы
- Массивы
Извлечь простые массивы
Извлечь перечисления - Строки
Извлечь простые строки - Указатели
Извлечь начальные указатели
Извлечь указатели, преобразование типов и типов - Структуры
Извлечь основные структуры
Извлечь Typedef - Обработка битов
Извлечение базовых битов *** НОВИНКА
Извлечение сдвигает и поворачивает - Файлы
Извлечь файлы Компиляция C - препроцессор, компилятор, компоновщик
Компиляция извлечения и препроцессор
См. Также сопутствующий том: Применение C
Статьи по теме
Удаленная разработка на C / C ++ с помощью NetBeans
Raspberry Pi и Интернет вещей в C
Начало работы с C / C ++ на Micro: бит
Чтобы быть в курсе новых статей на I Programmer, подпишитесь на нашу еженедельную рассылку новостей, подпишитесь на RSS-канал и подпишитесь на нас в Twitter, Facebook или Linkedin.
Комментарии
Добавление комментариев или просмотр существующих комментариев с помощью Disqus
или отправьте свой комментарий по адресу: [email protected]
Двоичный сдвиг | Schoolcoders вики
Двоичный сдвиг - это простой, но полезный метод манипуляции битами, часто используемый вместе с побитовые логические операции.
Обычная операция сдвига битов иногда называется логическим сдвигом , потому что она обрабатывает байт как набор независимых логических битов. Альтернативой является арифметический сдвиг, при котором байт рассматривается как число.
Все примеры здесь используют байты. Вы также можете применить ту же технику к 16-битным словам, 32-битным словам или любому другому размеру слова.
Логический сдвиг влево
Операция сдвига влево сдвигает каждый бит на одну позицию влево:
- То, что было в позиции бита 0, перемещается в позицию бита 1.
- То, что было в битовой позиции 1, перемещается в битовую позицию 2.
- и т.д…
- То, что было в позиции бита 7 (самый левый бит), выпадает из конца и теряется навсегда.
- 0 перемещается в позицию 0 бита.
В этом примере вы заметите, что байт изначально имел денарное значение 29. После сдвига он имеет денарное значение 58, т.е. ровно вдвое больше первоначальной стоимости. Так будет всегда.
Это не должно вызывать удивления, потому что то же самое происходит и с основанием 10.Если мы возьмем число 237 и сдвинем каждую цифру на 1 позицию влево, добавив ноль в правую часть, мы получим 2370. Это, конечно, в 10 раз больше начального значения - именно так вы умножаете на 10. В двоичной системе сдвиг влево умножается на 2, а не на 10, потому что мы работаем с основанием 2.
Что произойдет, если мы сдвинемся влево на 3 бита? Взгляните:
Каждый бит сдвигается на 3 позиции влево. 3 бита справа от байта сдвигаются с конца и теряются.Три 0 бита помещается в битовые позиции 0, 1, 2.
Переход на 3 места точно такой же, как переход на 1 место, 3 раза!
Если посмотреть на денарное значение, то начальный байт имеет значение 14. После сдвига на 3 новое значение будет 112 (14x8). Как и следовало ожидать, смещение слева на 3 эквивалентно умножению на 2x2x2 (три сдвига на 1 бит).
Сдвиг влево на n битов эквивалентен умножению на 2 в степени n.
Логический сдвиг вправо
Операция сдвига вправо сдвигает каждый бит на одну позицию влево:
- То, что было в позиции бита 0 (самый правый бит), выпадает из конца и теряется навсегда.
- То, что было в битовой позиции 1, перемещается в битовую позицию 0.
- То, что было в позиции бита 2, перемещается в позицию бита 1.
- и т.д…
- 0 перемещается в битовую позицию 7.
В этом примере байт изначально имел денарное значение 52. После сдвига он имеет денарное значение 26, что составляет половину исходного значения. ровно вдвое больше первоначальной стоимости. Так будет всегда.
И снова то же самое происходит с основанием 10. Если мы возьмем число 350 и сдвинем каждую цифру на 1 позицию вправо, мы получим 35. Это, конечно же, десятая часть стартовой стоимости. В двоичном формате сдвиг вправо делится на 2, а не на 10, потому что мы работаем с основанием 2.
Что произойдет, если исходное число не будет точным? Вот пример. Сдвинем двоичное значение 00010110 вправо на 2:
.Поскольку это сдвиг на 2 бита, мы ожидаем, что значение будет разделено на 2 в степени 2 - (2x2), то есть 4.
Однако в этом случае начальное значение 22 не делится на 4. Правильным результатом будет 5,5, но на самом деле мы получим 5.
При использовании сдвига вправо для деления числа на степень 2 результатом будет , округленное вниз до целого числа.
Арифметический сдвиг вправо
Это более сложная тема, которая может вам не понадобиться для GCSE.
Если вы имеете дело с байтами или словами, которые представляют целое число со знаком , логический сдвиг вправо не будет работать для отрицательных чисел. Например:
Проблема здесь в том, что бит 7, знак , бит устанавливается в 0. Это дает неверный результат - вместо небольшого отрицательного значения вы получаете большое положительное значение.
При арифметическом сдвиге знаковый бит остается таким же, как сдвиг данных. Если бит знака был 0, он будет заполнен 0, но если он был 1, он будет быть заполненным 1:
Отрицательные числа округляются с вниз до , как и положительные значения. Для ясности:
- Если 3 сдвинуто вправо один раз, это дает 1 (потому что 1,5, округленное в меньшую сторону, равно 1).
- Если -3 сдвинуть вправо один раз, он дает -2 (потому что -1.5 округляется в меньшую сторону - это -2).
В действительности арифметический сдвиг влево не нужен, потому что логический сдвиг влево делает то же самое.
80386 Справочное руководство программиста - раздел 3.4
; Вставить выровненную по правому краю битовую строку из регистра в ; битовая строка памяти. ; ; Предположения: ; 1) База строкового массива выровнена по двойному слову, и ; 2) длина битовой строки является непосредственным значением ; но битовое смещение хранится в регистре.; ; Регистр ESI содержит выровненную по правому краю битовую строку ; быть вставленным. ; Регистр EDI содержит битовое смещение начала ; подстрока. ; Регистры EAX и ECX также используются этим ; операция "вставка". ; MOV ECX, EDI; сохранить исходное смещение для дальнейшего использования SHR EDI, 3; смещение деления со знаком на 8 (адрес байта) И CL, 7H; изолировать три младших бита смещения в CL MOV EAX, [EDI] strg_base; переместить строковое двойное слово в EAX ROR EAX, CL; выровнять по правому краю старое битовое поле SHRD EAX, ESI, длина; принести новые биты ROL EAX, длина; выравнивание по правому краю новое битовое поле ROL EAX, CL; довести до окончательного положения MOV [EDI] strg_base, EAX; заменить двойное слово в памяти
; Вставить выровненную по правому краю битовую строку из регистра в ; битовая строка памяти. ; ; Предположения: ; 1) База строкового массива выровнена по двойному слову, и ; 2) длина битовой строки является непосредственным значением ; но битовое смещение хранится в регистре. ; ; Регистр ESI содержит выровненную по правому краю битовую строку ; быть вставленным. ; Регистр EDI содержит битовое смещение начала ; подстрока. ; Регистры EAX, EBX, ECX и EDI также используются ; эта операция "вставки".; MOV ECX, EDI; временное хранилище для смещения SHR EDI, 5; смещение деления со знаком на 32 (адрес двойного слова) SHL EDI, 2; умножить на 4 (в формате байтового адреса) И CL, 1FH; изолировать младшие пять бит смещения в CL MOV EAX, [EDI] strg_base; переместить двойное слово с низкой строкой в EAX MOV EDX, [EDI] strg_base + 4; другое строковое слово в EDX MOV EBX, EAX; временное хранилище для части строки + поворот SHRD EAX, EDX, CL; двойной сдвиг по смещению внутри dword + EDX: EAX SHRD EAX, EBX, CL; двойной сдвиг по смещению в пределах двойного слова + вправо SHRD EAX, ESI, длина; принести новые биты ROL EAX, длина; выравнивание по правому краю новое битовое поле MOV EBX, EAX; временное хранилище для части строки + поворот SHLD EAX, EDX, CL; двойной сдвиг назад по смещению внутри слова + EDX: EAX SHLD EDX, EBX, CL; двойной сдвиг назад по смещению внутри слова + влево MOV [EDI] strg_base, EAX; заменить двойное слово в памяти MOV [EDI] strg_base + 4, EDX; заменить двойное слово в памяти
; Вставить выровненную по правому краю битовую строку из регистра в ; битовая строка памяти. ; ; Предположения: ; 1) База строкового массива выровнена по двойному слову, и ; 2) длина битовой строки 32 ; но битовое смещение хранится в регистре. ; ; Регистр ESI содержит 32-битную строку, которую нужно вставить. ; Регистр EDI содержит битовое смещение начала ; подстрока. ; Регистры EAX, EBX, ECX и EDI также используются ; эта операция "вставки". ; MOV EDX, EDI; сохранить исходное смещение для дальнейшего использования SHR EDI, 5; смещение деления со знаком на 32 (адрес двойного слова) SHL EDI, 2; умножить на 4 (в формате байтового адреса) И CL, 1FH; изолировать младшие пять бит смещения в CL MOV EAX, [EDI] strg_base; переместить двойное слово с низкой строкой в EAX MOV EDX, [EDI] strg_base + 4; другое строковое слово в EDX MOV EBX, EAX; временное хранилище для части строки + поворот SHRD EAX, EDX; двойной сдвиг по смещению внутри dword + EDX: EAX SHRD EDX, EBX; двойной сдвиг по смещению в пределах двойного слова + вправо MOV EAX, ESI; переместить 32-битное поле на место MOV EBX, EAX; временное хранилище для части строки + поворот SHLD EAX, EDX; двойной сдвиг назад по смещению внутри слова + EDX: EAX SHLD EDX, EBX; двойной сдвиг назад по смещению внутри слова + влево MOV [EDI] strg_base, EAX; заменить двойное слово в памяти MOV [EDI] strg_base, + 4, EDX; заменить двойное слово в памяти
; Извлечь выровненную по правому краю битовую строку из бита памяти ; строка в регистр ; ; Предположения: ; 1) База строкового массива выровнена по двойному слову, и ; 2) длина битовой строки является непосредственным значением ; но битовое смещение хранится в регистре. ; ; Регистр EAX содержит выровненные по правому краю и дополненные нулями ; битовая строка, которая была извлечена. ; Регистр EDI содержит битовое смещение начала ; подстрока. ; Регистры EDI и ECX также используются этой «выдержкой»." ; MOV ECX, EDI; временное хранилище для смещения SHR EDI, 3; смещение деления со знаком на 8 (адрес байта) И CL, 7H; изолировать три младших бита смещения MOV EAX, [EDI] strg_base; переместить строковое двойное слово в EAX SHR EAX, CL; сдвиг по смещению в пределах двойного слова AND EAX, маска; извлеченное битовое поле в EAX
; Извлечь выровненную по правому краю битовую строку из бита памяти ; строка в регистр.; ; Предположения: ; 1) База строкового массива выровнена по двойному слову, и ; 2) длина битовой строки является непосредственной ; значение, но битовое смещение хранится в регистре. ; ; Регистр EAX содержит выровненные по правому краю и дополненные нулями ; битовая строка, которая была извлечена. ; Регистр EDI содержит битовое смещение начала ; подстрока. ; Регистры EAX, EBX и ECX также используются этим «извлечением». MOV ECX, EDI; временное хранилище для смещения SHR EDI, 5; смещение деления со знаком на 32 (адрес двойного слова) SHL EDI, 2; умножить на 4 (в формате байтового адреса) И CL, 1FH; изолировать младшие пять бит смещения в CL MOV EAX, [EDI] strg_base; переместить двойное слово с низкой строкой в EAX MOV EDX, [EDI] strg_base + 4; другое строковое слово в EDX SHRD EAX, EDX, CL; двойной сдвиг вправо по смещению внутри двойного слова AND EAX, маска; извлеченное битовое поле в EAX
SETcc (установить байт при условии cc) установить байт в единицу, если условие cc истинно; в противном случае устанавливает байт в ноль.См. Приложение D для определения возможные условия.
Логический сдвиг вправо - BeebWiki
Логический сдвиг вправо, >>> , это побитовый оператор для сдвига двоичного файла значение справа, без расширения знака.
| Наличие | BASIC V | |
| Синтаксис | БАЗОВЫЙ V | >>> |
| Токен (шестнадцатеричный) | БАЗОВЫЙ V | 3E 3E 3E (оператор) |
| Описание | БАЗОВЫЙ V | Возвращает первый операнд, при этом биты его двоичного представления смещены в сторону младшего значащего конца на количество разрядов, указанных во втором операнде, и нули сдвинуты в самый старший значащий конец. |
| Связанные ключевые слова | << , >> , AND , DIV , EOR , НЕ , OR | |
Описание
>>> принимает два целых значения и возвращает первое значение со сдвигом вправо на количество двоичных разрядов, указанных во втором
операнд. Например, в заявлении
ПЕЧАТЬ ~ & 87654321 >>> 4
двоичные цифры & 87654321, 10000111011001010100001100100001, перемещаются четыре места справа в реестре.В этом случае четыре наименее значащие биты (0001) отбрасываются, а шестнадцатая позиция (бит 4) становится местом единиц (бит 0) возвращаемого значения. Поскольку это логический сдвиг , нули сдвигаются вверху, так что биты с 28 по 31 результата - все нули. BASIC выполняет сдвиг в одной инструкции, но если рассматривать сдвиг как пошаговый расчет, он может быть представлен как:
Операнд 10000111011001010100001100100001
\
1-я смена 01000011101100101010000110010000 â † ’
\
2-я смена 00100001110110010101000011001000 â † ’
\
3-я смена 00010000111011001010100001100100 â † ’
\
4-я смена 00001000011101100101010000110010 â † ’
Вывод из инструкции:
> ПЕЧАТЬ ~ & 87654321 >>> 4 8765432
Банкноты
>>> принимает два дополнения к отрицательному расстоянию сдвига.
На процессорах ARM возвращается расстояние сдвига от 32 до 255 включительно.
нуль; любое большее или отрицательное расстояние N% имеет тот же эффект
как N% И 255 . BASIC на других архитектурах может давать разные
результат, когда второй операнд больше 31 или меньше 0.
Как оператор Группы 5 >>> не связан с другой Группой 5
операторы, поэтому круглые скобки должны использоваться, когда операнд имеет такой оператор
по обе стороны. Например:
ЕСЛИ (двойное слово% >>> 24) = 1 ТО...
Подробнее см. = .
Двойной знак «больше» делает арифметический оператор сдвига вправо , >> , что больше всего дублирует
значащий бит для выполнения расширения знака.
(((num% + (num% <0)) DIV2) AND & 7FFFFFFF) действует так же, как (num% >>> 1) и может использоваться на всех BASIC BBC.
- beardo 02:54, 3 сентября 2011 г. (UTC)
.
