Логический сдвиг влево: Логический сдвиг | это… Что такое Логический сдвиг?

Логический сдвиг | это… Что такое Логический сдвиг?

Би́товый сдвиг — изменение позиций битов в слове на одну и ту же величину.

В основной своей массе компьютеры не могут напрямую адресовать биты, которые содержатся группами по 8, 16, 32 битов в словах. Для обеспечения работы с битами существует множество команд, к которым относятся и сдвиги: Все сдвиги похожи друг на друга поведением средних битов: они просто сдвигаются влево или вправо на определённую величину. И различаются поведением крайних битов: одного, который уходит из слова, и второго, который должен появиться в слове.

Содержание 1 Логический сдвиг 2 Арифметический сдвиг 3 Циклический сдвиг 4 Циклический сдвиг через бит переноса 5 Примечания 6 Источник

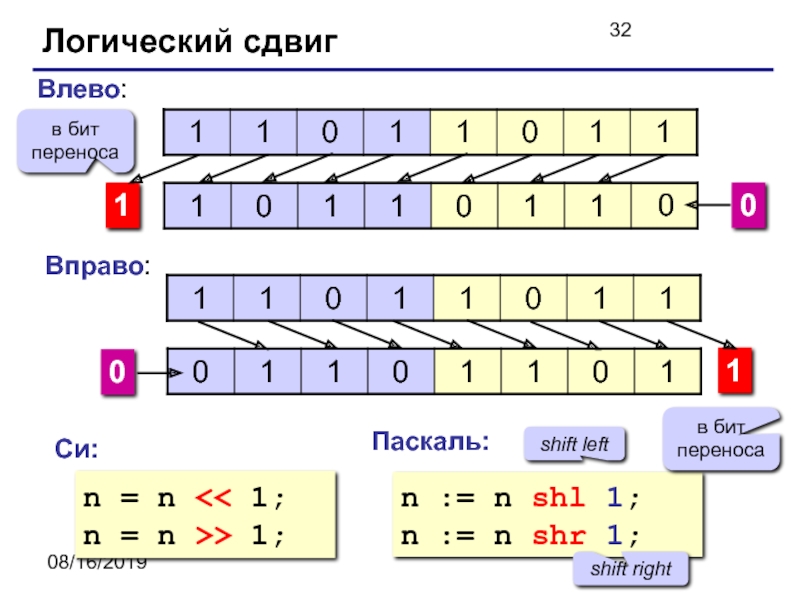
Логический сдвиг

Логический сдвиг влево

Логический сдвиг вправо

Сдвиг, при котором уходящий бит уходит, не влияя на оставшееся биты, а на место появившегося бита записывается бит 0.

Пример работы операции сдвига:

Пусть у нас есть число 10101010b (в двоичной системе).

Если сделать сдвиг влево на 1 бит, то получим число 01010100b

Если сделать сдвиг вправо на 1 бит, то получим число 01010101b

В большинстве процессоров уходящий бит сохраняется в флаге переноса. Эта функция широко используется при работе с многобайтовыми числами.

Арифметический сдвиг

Арифметический сдвиг влево

Арифметический сдвиг вправо

При этом сдвиге слово рассматривается не просто как группа битов, а как целое число в дополнительном коде. При сдвиге влево ведёт себя как логический сдвиг, при сдвиге вправо: уходящий бит уходит, не влияя на оставшееся биты, а на место появившегося бита устанавливается бит, соответствующий знаку.

Пример работы операции сдвига:

Пусть у нас есть число 11111010b=−6 (в двоичной системе).

Если сделать сдвиг влево на 1 бит, то получим число 11110100b=−12

Если сделать сдвиг вправо на 1 бит, то получим число 11111101b=−3

Легко заметить, что при арифметическом сдвиге сдвиг влево соответствует умножению на 2, а сдвиг вправо делению на 2 (в общем случае — на основание системы счисления). Исключение: −1 >>a 1 = −1 (в общем случае это относится к числам от −1 до −p+1, где p — основание системы счисления).

Схемотехническая реализация операций сдвига очень проста. Именно поэтому эти операции рекомендуют использовать для операций умножения и деления целых чисел на числа равные степени 2 (2, 4, 8, 16, 32, 64 и т. д.).

Циклический сдвиг

Циклический сдвиг влево

Циклический сдвиг вправо

При этом сдвиге уходящий бит появляется на месте появившегося.

Пример работы операции сдвига:

Пусть у нас есть число 11111010b (в двоичной системе).

Если сделать сдвиг влево на 1 бит, то получим число 11110101b

Если сделать сдвиг вправо на 1 бит, то получим число 01111101b

Циклический сдвиг через бит переноса

Циклический сдвиг влево через бит переноса

Циклический сдвиг вправо через бит переноса

В архитектуру многих процессоров входит флаг переноса в следующий разряд (например, cf на n+1)-битным числом, состоящим из регистра и флага переноса.

Например, если у нас в регистре число 11111010b, флаг переноса равен 0:

После сдвига влево на 1 бит: в регистре 11110100b, флаг переноса равен 1

После сдвига вправо на 1 бит: в регистре 01111101b, флаг переноса равен 0

Операция циклического сдвига через бит переноса используется при работе с многобайтовыми числами. В частности, чтобы сдвинуть вправо на 1 бит длинное число, нужно очистить^[1]cf (в случае деления числа со знаком нужно записать в cf старший бит старшего слова) и циклически сдвинуть на единицу через cf каждое слово, начиная с верхнего. Например, пусть у нас есть число 011000111100b, занимающее три 4-битных слова:

Было:              HI=0110, MED=0011, LO=1100, cf=0
После сдвига HI:   HI=0011, MED=0011, LO=1100, cf=0
После сдвига MED:  HI=0011, MED=0001, LO=1100, cf=1
После сдвига LO:   HI=0011, MED=0001, LO=1110, cf=0

Сдвиги через регистр флагов более чем на 1 бит практически не используются.

Примечания

1. ↑ Можно вместо очистки флага для первого обрабатываемого слова использовать арифметический\логический сдвиг, если он присваивает флагу cf значение вышедшего бита.

Источник

• Лекция: «Битовые операции»
• «Assembler&Win32. Курс молодого бойца.» Урок 11. «Биты, сдвиг логический, арифметический и циклический.»

Логический сдвиг | это… Что такое Логический сдвиг?

Би́товый сдвиг — изменение позиций битов в слове на одну и ту же величину.

В основной своей массе компьютеры не могут напрямую адресовать биты, которые содержатся группами по 8, 16, 32 битов в словах. Для обеспечения работы с битами существует множество команд, к которым относятся и сдвиги: Все сдвиги похожи друг на друга поведением средних битов: они просто сдвигаются влево или вправо на определённую величину. И различаются поведением крайних битов: одного, который уходит из слова, и второго, который должен появиться в слове.

Содержание 1 Логический сдвиг 2 Арифметический сдвиг 3 Циклический сдвиг 4 Циклический сдвиг через бит переноса 5 Примечания 6 Источник

Логический сдвиг

Логический сдвиг влево

Логический сдвиг вправо

Сдвиг, при котором уходящий бит уходит, не влияя на оставшееся биты, а на место появившегося бита записывается бит 0.

Пример работы операции сдвига:

Пусть у нас есть число 10101010b (в двоичной системе).

Если сделать сдвиг влево на 1 бит, то получим число 01010100b

Если сделать сдвиг вправо на 1 бит, то получим число 01010101b

В большинстве процессоров уходящий бит сохраняется в флаге переноса. Эта функция широко используется при работе с многобайтовыми числами.

Арифметический сдвиг

Арифметический сдвиг влево

Арифметический сдвиг вправо

При этом сдвиге слово рассматривается не просто как группа битов, а как целое число в дополнительном коде. При сдвиге влево ведёт себя как логический сдвиг, при сдвиге вправо: уходящий бит уходит, не влияя на оставшееся биты, а на место появившегося бита устанавливается бит, соответствующий знаку.

Пример работы операции сдвига:

Пусть у нас есть число 11111010b=−6 (в двоичной системе).

Если сделать сдвиг влево на 1 бит, то получим число 11110100b=−12

Если сделать сдвиг вправо на 1 бит, то получим число 11111101b=−3

Легко заметить, что при арифметическом сдвиге сдвиг влево соответствует умножению на 2, а сдвиг вправо делению на 2 (в общем случае — на основание системы счисления). Исключение: −1 >>a 1 = −1 (в общем случае это относится к числам от −1 до −p+1, где p — основание системы счисления).

Схемотехническая реализация операций сдвига очень проста. Именно поэтому эти операции рекомендуют использовать для операций умножения и деления целых чисел на числа равные степени 2 (2, 4, 8, 16, 32, 64 и т. д.).

Циклический сдвиг

Циклический сдвиг влево

Циклический сдвиг вправо

При этом сдвиге уходящий бит появляется на месте появившегося.

Пример работы операции сдвига:

Пусть у нас есть число 11111010b (в двоичной системе).

Если сделать сдвиг влево на 1 бит, то получим число 11110101b

Если сделать сдвиг вправо на 1 бит, то получим число 01111101b

Циклический сдвиг через бит переноса

Циклический сдвиг влево через бит переноса

Циклический сдвиг вправо через бит переноса

В архитектуру многих процессоров входит флаг переноса в следующий разряд (например, cf на n+1)-битным числом, состоящим из регистра и флага переноса.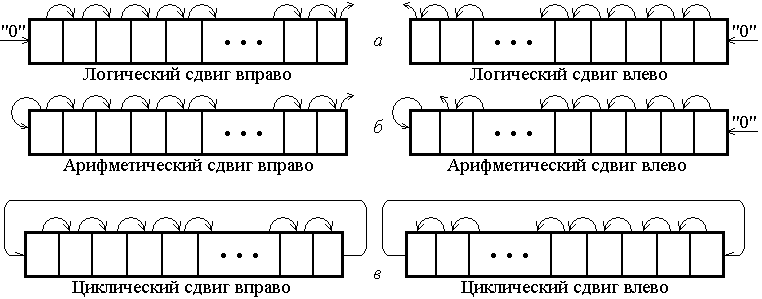

Например, если у нас в регистре число 11111010b, флаг переноса равен 0:

После сдвига влево на 1 бит: в регистре 11110100b, флаг переноса равен 1

После сдвига вправо на 1 бит: в регистре 01111101b, флаг переноса равен 0

Операция циклического сдвига через бит переноса используется при работе с многобайтовыми числами. В частности, чтобы сдвинуть вправо на 1 бит длинное число, нужно очистить

[1]cf (в случае деления числа со знаком нужно записать в cf старший бит старшего слова) и циклически сдвинуть на единицу через cf каждое слово, начиная с верхнего. Например, пусть у нас есть число 011000111100b, занимающее три 4-битных слова:

Было:              HI=0110, MED=0011, LO=1100, cf=0
После сдвига HI:   HI=0011, MED=0011, LO=1100, cf=0
После сдвига MED:  HI=0011, MED=0001, LO=1100, cf=1
После сдвига LO:   HI=0011, MED=0001, LO=1110, cf=0

Сдвиги через регистр флагов более чем на 1 бит практически не используются.

Примечания

1. ↑ Можно вместо очистки флага для первого обрабатываемого слова использовать арифметический\логический сдвиг, если он присваивает флагу cf значение вышедшего бита.

Источник

• Лекция: «Битовые операции»
• «Assembler&Win32. Курс молодого бойца.» Урок 11. «Биты, сдвиг логический, арифметический и циклический.»

Сдвиг битов (сдвиг влево, сдвиг вправо)

Сдвиг бит перемещает каждую цифру в двоичное представление числа слева или справа. Различают три основных вида смен:

Левые сдвиги

При сдвиге влево старший бит теряется, и 0 бит вставляется на другом конце.

Оператор сдвига влево обычно записывается как «<<».

0010 << 1 → 0100 0010 << 2 → 1000

Одиночный сдвиг влево умножает двоичное число на 2:

0010 << 1 → 0100 0010 это 2 0100 это 4

Логические сдвиги вправо

При сдвиге вправо с логическим сдвигом вправо , младший бит теряется и 0 вставляется с другого конца.

1011 >>> 1 → 0101 1011 >>> 3 → 0001

Для положительных чисел один логический сдвиг вправо делит число на 2, отбрасывая все остатки.

0101 >>> 1 → 0010 0101 это 5 0010 это 2

Арифметические сдвиги вправо

При сдвиге вправо с арифметическим значением вправо сдвиг , младший бит теряется и старший бит скопирован .

Языки обрабатывают арифметические и логические сдвиги вправо в различные пути. Java предоставляет два оператора сдвига вправо: >> делает арифметический сдвиг вправо и >>> делает логических сдвигов вправо.

1011 >> 1 → 1101 1011 >> 3 → 1111 0011 >> 1 → 0001 0011 >> 2 → 0000

Первые два числа имели 1 как наиболее значащий бит, поэтому было вставлено больше единиц во время смены. Последние два числа имели 0 как старший бит, поэтому сдвиг вставляется больше 0.

Если число закодировано с помощью два дополнения, тогда арифметический сдвиг вправо сохраняет знак числа, в то время как логический сдвиг вправо делает число положительным.

// Арифметический сдвиг 1011 >> 1 → 1101 1011 это -5 1101 это -3 // Логический сдвиг 1111 >>> 1 → 0111 1111 это -1 0111 это 7

Поделиться Твитнуть Доля

Смотрите также:

• Двоичные числа
• Побитовое И
• Побитовое ИЛИ
• Побитовое НЕ
• Побитовое XOR (исключающее ИЛИ)

Что дальше?

Если вы готовы начать применять эти концепции к некоторым проблемам, ознакомьтесь с нашими пробными вопросами для собеседования по программированию.

Они имитируют настоящее интервью, предлагая подсказки, когда вы застряли или вам не хватает оптимизации.

Попробуйте задать несколько вопросов прямо сейчас

{«id»:30034749,»username»:»2023-06-09_02:27:37_pep@6w»,»email»:null,»date_joined»:»2023-06-09T02:27:37.458567+00: 00″,»first_name»:»»,»last_name»:»»,»full_name»:»»,»short_name»:»друг»,»is_anonymous»:true,»is_on_last_question»:false,»percent_done»:0, «num_questions_done»:0,»num_questions_remaining»:46,»is_full_access»:false,»is_student»:false,»first_payment_date»:null,»last_payment_date»:null,»num_free_questions_left»:3,»terms_has_agreed_to_latest»:false,»preferred_content_language «:»»,»preferred_editor_language»:»»,»is_staff»:false,»auth_providers_human_readable_list»:»»,»num_auth_providers»:0,»auth_email»:»»}

Сдвиг влево (

Оператор сдвиг влево ( << ) возвращает число или BigInt, двоичное представление которого является первым операндом, сдвинутым на указанное число битов влево.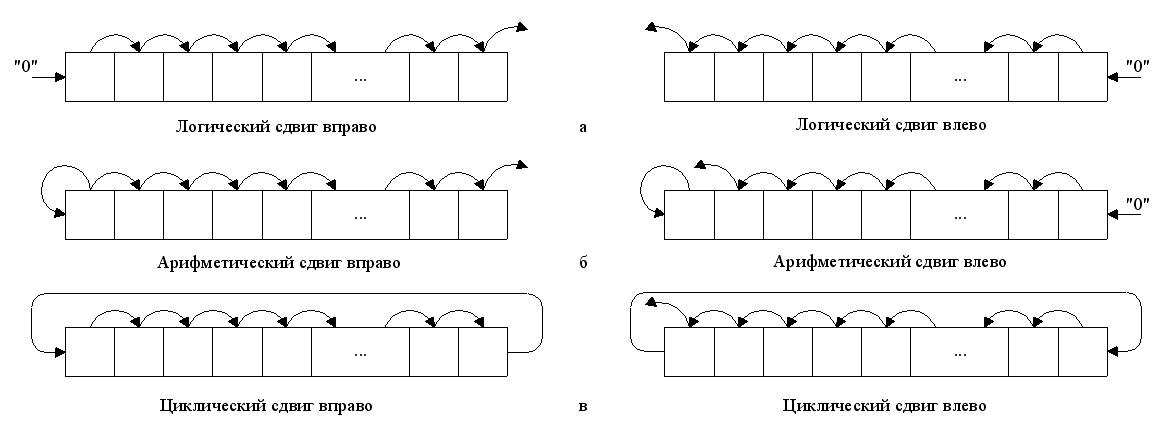 Лишние биты, сдвинутые влево, отбрасываются, а нулевые биты сдвигаются справа

 x << y
 

Оператор << перегружен для двух типов операндов: числа и BigInt. Для чисел оператор возвращает 32-битное целое число. Для BigInts оператор возвращает BigInt. Сначала он приводит оба операнда к числовым значениям и проверяет их типы. Он выполняет сдвиг влево BigInt, если оба операнда становятся BigInts; в противном случае он преобразует оба операнда в 32-битные целые числа и выполняет сдвиг числа влево. А TypeError выдается, если один операнд становится BigInt, а другой становится числом.

Оператор работает с битовым представлением левого операнда в дополнении до двух. Например, 9 << 2 дает 36:

 9 (по основанию 10): 000000000000000000000000000001001 (по основанию 2)
                  --------------------------------
9 << 2 (по основанию 10): 0000000000000000000000000000100100 (по основанию 2) = 36 (по основанию 10)
 

Побитовое 32-битное целое число x влево на y бит дает x * 2 ** y .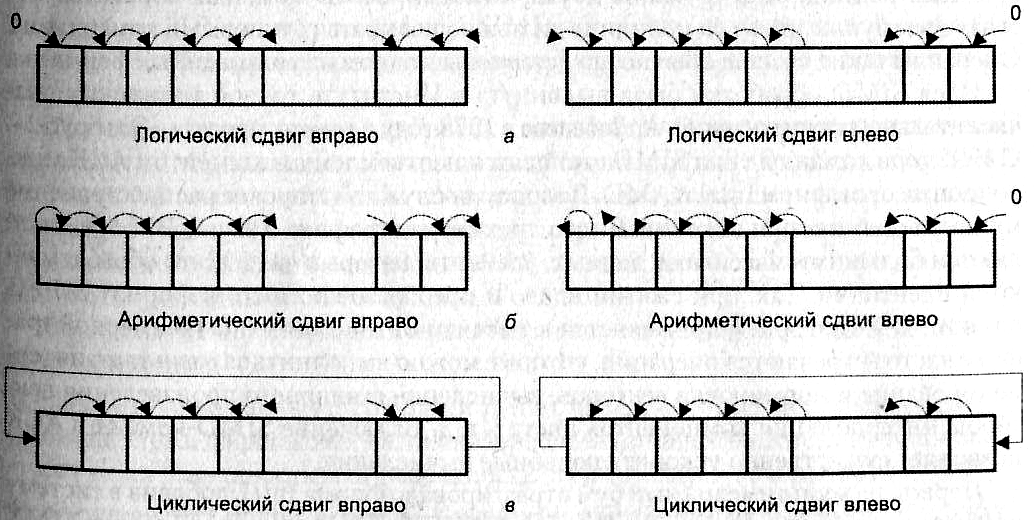 Так, например, 9 << 3 эквивалентно 9 * (2 ** 3) = 9 * (8) = 72 .

Если левый операнд представляет собой число длиной более 32 бит, в нем будут отброшены самые значащие биты. Например, следующее целое число длиной более 32 бит будет преобразовано в 32-битное целое:

 До: 1110011011111010000000000000001100000000000001
После: 10100000000000000110000000000001
 

Правый операнд будет преобразован в 32-битное целое число без знака, а затем взят по модулю 32, поэтому фактическое смещение сдвига всегда будет положительным целым числом от 0 до 31 включительно. Например, 100 << 32 совпадает с 100 << 0 (и дает 100 ), потому что 32 по модулю 32 равно 0.

Для BigInts усечение отсутствует. Концептуально следует понимать, что положительные BigInts имеют бесконечное число ведущих 0 бит, а отрицательные BigInts имеют бесконечное количество ведущих 1 бит.

Сдвиг влево любого числа x на 0 возвращает x , преобразованное в 32-битное целое число.