Логические операции си: Логические операторы в C | Microsoft Learn

Начинаем изучать STM32: битовые операции / Хабр

Небольшое отступление…

В прошлом уроке мы рассмотрели с чего начать, если вы решили изучать микроконтроллеры STM32: как настроить IDE, как создать простой проект, как откомпилировать программу и как запустить программу на выполнение. После полюбовались на перемигивание светодиодов на Discovery-плате )

Начиная новую статью, я задумывал сразу же перейти к подробному разбору листинга программы, который заставлял попеременно перемигиваться наши светодиоды, но уже перейдя к написанию, я вдруг осознал для себя, что есть большое количество вопросов без ответа на которые — перейти к рассмотрению программы было бы преждевременно. И для себя я определил целый перечень таких вопросов:

1. Что же такое битовые операции? Как ими пользоваться?
2. Что такое регистры и как они связаны с битовыми операциями?
3. Из чего состоят микроконтроллеры STM32F0xx-серии, как осуществляется тактирование и чем обеспечена жизнь внутри МК?
4. Как происходит стартовая инициализация МК, зачем нужен startup-файл, что делает функция SystemInit? Объяснение на пальцах.
5. Из чего состоит библиотека CMSIS? Как в ней ориентироваться? Что полезного можно из нее извлечь и как ей пользоваться?

Именно с рассмотрения этих вопросов я хотел бы продолжить повествование о программировании STM32.

Список статей:

1. Начинаем изучать STM32 или Управляем светом по-умному
2. Начинаем изучать STM32: битовые операции
3. Начинаем изучать STM32: Что такое регистры? Как с ними работать?

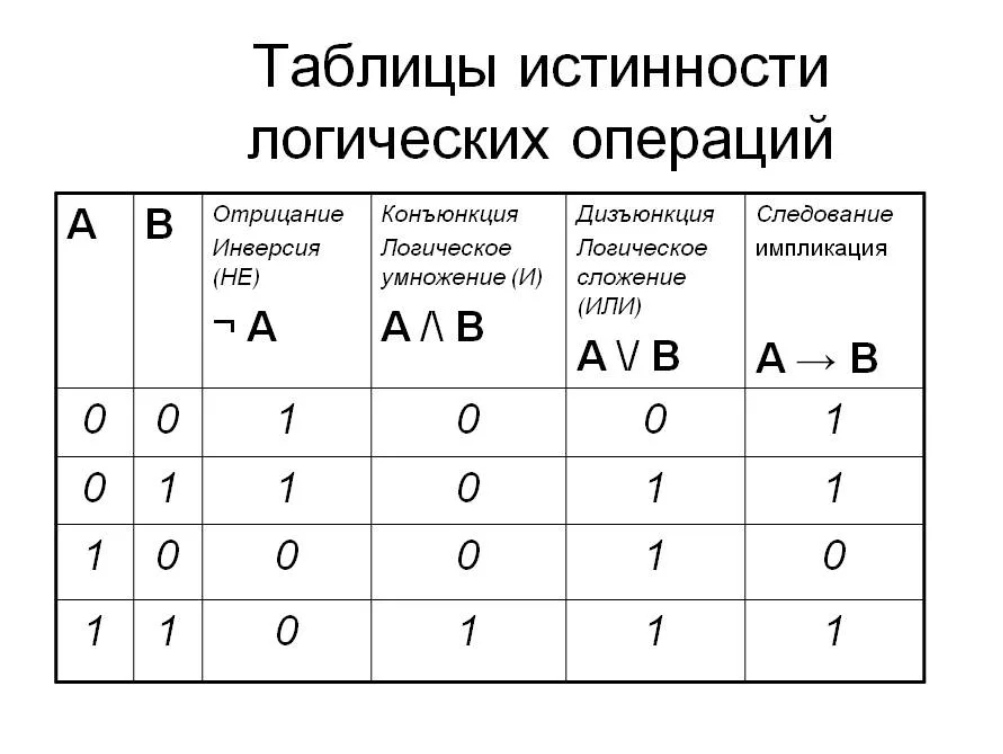
Основные логические операции

Только начиная изучать микроконтроллеры, слова «регистр» и «битовые операции» для меня казались чем-то таинственно загадочным и я долго не хотел переходить к рассмотрению данной темы. Но когда я более-менее разобрался с тем, что это такое я понял что зря откладывал изучение такой важной темы в дальний ящик. Битовые операции наверное самые распространенные операции в микроконтроллере и знание того, как и зачем их можно применять в нашей работе — откроет перед нами огромный потенциал возможностей для управления всем и вся в нашем МК!

Все мы на уроках информатики в школе знакомились с тем, что такое цифровая техника, почему она так называется, какие существуют основные логические операции. Все современные цифровые технологии основаны на двоичной математике и логических схемах.

Микроконтроллер всегда оперирует только двумя состояниями: «ноль» — нет напряжения, «единица» — есть напряжение. Давайте немного освежим в голове знания о основных логических операциях т.к. они составляют основу всей цифровой техники.

• Конъюнкция — обозначается как «Логическое И» или «Логическое умножение» . В сущности, результат от выполнения данной логической операции двух для выражений А и В подобен их умножению. То есть, выражение примет значение «1» в случае только если и А, и В имеют значение «1». Во всех других случаях будет значение «0». Может обозначаться как И, &&, AND, &
• Дизъюнкция — обозначается как «Логическое ИЛИ» или «Логическое сложение». Результат от выполнения данной логической операции двух для выражений А и В подобен их сложению. То есть, выражение примет значение «1» в случае если хотя бы одно из выражений А и В имеют значение «1». .

Битовые операции

Битовые операции — практически то же самое, что и логические операции только лишь с той разницей, что применяются они к битам и к числам двоичной системы.

К слову говоря, для простоты изучения битовых операций я использовал программу 32-bit ASM Calculator от ManHunter. С помощью данной программы можно проверять результаты выполнения битовых операций, переводить числа из одной системы счисления в другую. Программа имеет интуитивно понятный интерфейс и после знакомства программа стала одним из основных инструментов в моей работе с микроконтроллерами. Небольшое пояснение к интерфейсу программы данно на изображении ниже:

Битовая операция «НЕ» — «~»

Если бит равен «1», то после выполнения операции «НЕ» он будет равен «0», и наоборот. Операция сразу же выполняется над всеми битами двоичного числа. Например, инвертируем число FF:

Битовая операция «И» — «&»

Если оба бита в разряде равны «1», то после выполнения операции «И» результат в разряде будет равен «1», но если хотя бы один из битов равен «0» тогда и результат будет равен «0».

Операция так же выполняется поразрядно. Например, «умножим» два числа 0xFF0 и 0xF0F:

В результате мы увидим, что в тех разрядах где были единицы в обоих числах, в результате получились единицы, во всех остальных случаях — нули.

Рассмотрим варианты практического применения:

• В ситуации, если нам необходимо сбросить конкретный бит или группу битов в ноль мы можем использовать маску. Думаю, будет нагляднее показать это на примере. Допустим, мы берем число и 0xF8F и нам надо чтобы 7-й бит стал вместо единицы нулем. Нет проблем, накидываем маску и снимаем галочку с нужного бита. Умножаем числа и получаем результат:
  
  
• Если нам необходимо проверить конкретный бит в числе на 0 или 1 — мы так же используя маску проводим умножение. В маске мы устанавливаем бит, который хотели бы проверить. Если требуемый бит равен «0» — то результатом вычисления будет «0», если «1» то, соответственно, «1». Если мы хотим узнать, равен ли 7-й бит единицы — делаем соответствующую маску и умножаем наше число на маску.
  Все просто:
  
  Если нам нужно проверить четность числа(имеется ввиду способность числа делиться на два) — то мы таким же образом проверяем 1-й бит, если он равен «1» — то число нечетное, если там «0» то число четное. Попробуйте сами, в целях обучения и формирования навыков, сделать данную проверку.
  

Битовая операция «ИЛИ» — «|»

Если один или оба из пары битов равен «1» то результат будет «1», иначе если оба бита равны «0» то результат будет равен «0». То есть, грубо говоря, производится сложение всех единиц в разрядах. Например если мы складываем два числа 0xF8F и 0x7F, то получим следующий результат:

Рассмотрим вариант практического применения:

• Если нам необходимо
  установит конкретный бит в числе на 1 — мы так же используя маску проводим сложение. Например, чтобы выставить 15-й бит в числе 0xFF0 нужно провести операцию логического сложения и мы получим требуемый результат:

Попробуйте самостоятельно поиграться с различными числами и понаблюдать за результатами. «

Если биты в разряде отличаются и не равны тогда результат будет «1», иначе «0». Например, если мы делаем XOR числа 0xF8F и 0x7F, то мы увидим что в разрядах в которых находятся отличные биты то там в результате получается «1» и в местах где биты одинаковые, будь то «0» или «1» — получился «0», в итоге мы получим следующий результат:

Рассмотрим варианты практического применения:

• Если нам понадобилось инвертировать какие-либо биты в числе, можно используя маску с легкостью сделать это используя операцию XOR. Давайте сделаем инверсию 6 и 7 разряда в числе 0xF8 используя маску 0xC0. Результат вы можете посмотреть на изображении:
• Бывают ситуации когда необходимо сравнить два регистра и определить равны они или нет. В этом случае нам необходимо значения регистров подвергнуть операции XOR. Если результат получился «0» — тогда регистры равны, иначе — не равны:
  
  

Битовые операции сдвига
Существует ряд интересных и порой чрезвычайно полезных битовых операций именуемых как операции сдвига. Двигать разряды можно как вправо, так и влево. В ходе данной операции происходит сдвиг всех разрядов двоичного числа на указанное количество позиций, при этом, в случае если сдвиг идёт влево — старший бит (самый левый) теряется, а в младший (самый правый) записывается «0». При логическом сдвиге вправо происходит обратная ситуация — младший бит (самый правый) теряется, а в старший записывается «0». Дополнительно хотелось бы отметить, что в случае 32-разрядных слов сдвигаются все 32 разряда целиком. Рассмотрим операции сдвига подробнее.

Cдвиг влево — «<<«

То, как происходит сдвиг вы можете увидеть на изображении ниже. Думаю, что всё достаточно очевидно:

При двоичном сдвиге можно заметить одну интересную особенность. Сдвиг на один разряд умножает наше число на 2. Если сдвинуть на n разрядов наше число x то получится x * (2 * n). Попробуйте самостоятельно отследить эту закономерность через нашу утилку для подсчета. =)

Cдвиг вправо — «>>»

То, что получается в результате сдвига вправо достаточно наглядно отражено на изображении:

При двоичном сдвиге вправо можно заметить что происходит ситуация обратная сдвигу влево — число делится на 2 с при сдвиге в 1 разряд и после на 2 * n, где n — количество разрядов на которые произведен сдвиг. Так же попробуйте самостоятельно поиграться с числами и которые заведомо делятся на 2 нацело. И вопрос на засыпку — какой результат будет если вы поделите таким образом нечетное число?

Важное замечание. Если вы будете делать сдвиг для переменной с отрицательным знаком (signed) — освободившиеся позиции будут заполняться единичками.

В качестве заключения…

Многим начинающим данная тема может показаться дико скучной и может сложиться ощущение что ну вообще не понятно где и как можно применить эти знания. Спешу вас обнадежить, в ситуациях когда нужно поднять ту или иную ногу МК или записать параметр в какой-нить периферийный блок или модуль — там кругом и всюду будут требоваться знания битовых операций. Так как статья получилась достаточно объемной, рассмотрение регистров мы перенесем на следующий урок. Ну и в последующем можно использовать эту статью как шпаргалку.

В качестве домашнего задания попробуйте самостоятельно разобрать код нашей программы в блоке while(1) {… } и понять как же битовыми операциями мы включаем и выключаем наши светодиоды. Ну а на следующем уроке я расскажу как оно происходит на самом деле!

Список статей:

1. Начинаем изучать STM32 или Управляем светом по-умному
2. Начинаем изучать STM32: битовые операции
3. Начинаем изучать STM32: Что такое регистры? Как с ними работать?

Что такое логическая операция?

Обновлено: 16.11.2019, автор: Computer Hope

Логическая операция — это специальный символ или слово, соединяющее две или более фразы информации. Он используется для проверки того, является ли определенное отношение между фразами истинным или ложным.

В вычислениях логические операции необходимы, потому что они моделируют способ передачи информации через электрические цепи, например, внутри ЦП. Эти типы операций называются булевыми операциями.

Элементы схемы, которые ведут себя в соответствии с булевой логикой, называются логическими вентилями.

Основные логические операции

Следующие семь логических операций принимают входные данные, которые являются либо истинными (1), либо ложными (0) и производят одно выходное значение, которое также является истинным или ложным.

Большинство этих операций могут принимать более двух входных данных, за исключением операции НЕ, которая принимает только один входной сигнал. Ниже приведены примеры использования только одного или двух входов, что обычно происходит внутри компьютера.

Операции перечислены ниже. Нажмите на ссылку операции, чтобы узнать больше.

• И
• ИЛИ
• НЕ
• НЕ-И
• НИ
• Исключающее ИЛИ
• Исключающее ИЛИ

И

Логическая операция И возвращает значение «истина», только если любой из ее входов истинен. Если какой-либо из входов ложен, выход также ложен.

В компьютерном программировании операция И обычно записывается как && (два амперсанда).

В булевой алгебре операция И двух входов A и B может быть записана как AB .

Ниже приведена таблица истинности для операции И и принципиальная схема логического элемента И.

И
А	Б	АВ
0	0	0
1	0	0
0	1	0
1	1	1

ИЛИ

Логическая операция ИЛИ возвращает истину, если любой из ее входов истинен. Если все входы ложны, выход также ложен.

В компьютерном программировании операция ИЛИ обычно записывается как || (две вертикальные полосы).

В булевой алгебре значение ИЛИ двух входов A и B может быть записано как A+B .

Примечание

Не путайте операцию ИЛИ с арифметическим сложением, даже если в обеих операциях используется символ « + «. Это разные операции.

Ниже приведена таблица истинности для операции ИЛИ и принципиальная схема логического элемента ИЛИ.

ИЛИ
А	Б	А+В
0	0	0
1	0	1
0	1	1
1	1	1

НЕ

Логическая операция НЕ возвращает истину, если ее вход ложный, и ложь, если ее вход истинен.

В компьютерном программировании операция НЕ обычно записывается как ! (восклицательный знак).

В булевой алгебре НЕ значение ввода A может быть записано как A̅ (A с зачеркиванием).

Ниже приведена таблица истинности для операции НЕ и принципиальная схема логического элемента НЕ.

НЕ
А	А̅
0	1
1	0

НЕ-И

Логическая операция И-НЕ (что означает «НЕ И») возвращает значение «истина», если ее входы ложны, и ложь, если любой из ее входов истинен.

Кончик

Флэш-память NAND — это тип флэш-памяти, основанный на логических элементах NAND.

В булевой алгебре значение НЕ-И двух входов A и B может быть записано как (AB с зачеркиванием).

NAND отличается тем, что является одним из двух «универсальных» логических элементов, потому что любая другая логическая операция может быть создана с использованием только вентилей NAND. (Другой универсальный логический элемент — НЕ-ИЛИ.)

Ниже приведена таблица истинности для операции И-НЕ и принципиальная схема логического элемента И-НЕ.

НЕ-И
А	Б	___ АБ
0	0	1
1	0	1
0	1	1
1	1	0

НОР

Логическая операция НЕ-ИЛИ (что означает «НЕ ИЛИ») возвращает значение «истина», если ее входные данные ложны, и ложь, если любой из ее входов истинен.

Кончик

NOR Flash — тип флэш-памяти, основанный на логических элементах NOR.

В булевой алгебре значение NOR двух входов A и B может быть записано как (A+B с зачеркиванием).

NOR отличается тем, что является одним из двух «универсальных» логических вентилей, потому что любая другая логическая операция может быть создана с использованием только вентилей NOR. (Другой универсальный логический вентиль — И-НЕ.)

Ниже приведена таблица истинности для операции ИЛИ-ИЛИ и принципиальная схема логического элемента ИЛИ-НЕ.

НО
А	Б	_____ А+В
0	0	1
1	0	0
0	1	0
1	1	0

Исключающее ИЛИ

Логическая операция XOR (расшифровывается как «исключающее ИЛИ») возвращает истину, если какие-либо из ее входных данных различаются, и ложь, если все они одинаковы. Другими словами, если ее входные данные представляют собой комбинацию истинного и ложного, выход XOR истина. Если все его входные данные истинны или все ложны, выход XOR ложен.0003

В булевой алгебре значение XOR двух входов A и B может быть записано как A⊕B (символ XOR ⊕ напоминает знак плюс внутри круга).

Ниже приведена таблица истинности для операции XOR и ее принципиальная схема.

Исключающее ИЛИ
А	Б	А⊕В
0	0	0
1	0	1
0	1	1
1	1	0

Исключающее ИЛИ

Логическая операция ИСКЛЮЧАЮЩЕЕ ИЛИ (что означает «исключительное НЕ ИЛИ») возвращает истину, если любой из ее входов совпадает, и ложь, если какой-либо из них отличается. Другими словами, если ее входы представляют собой комбинацию истинного и ложного, выход ИСКЛЮЧАЮЩЕЕ ИЛИ-НЕ является ложным. Если все его входы истинны или все ложны, выход ИСКЛЮЧАЮЩЕЕ ИЛИ является истинным.0003

В булевой алгебре значение исключающего ИЛИ двух входов A и B можно записать как (символ исключающего ИЛИ ⊕ напоминает знак плюс внутри круга с чертой над всем).

Ниже приведена таблица истинности для операции XNOR и ее принципиальная схема.

Исключающее ИЛИ
А	Б	_____ А⊕В
0	0	1
1	0	0
0	1	0
1	1	1

• Как создать компьютерную программу.

Аккумулятор, побитовый оператор, логическое значение, идемпотентность, оператор, термины программирования

1.1 Логические операции

Математика обычно включает в себя объединение истинных (или гипотетически истинных) утверждения различными способами для получения (или доказательства) новых истинных утверждений. Начнем с разъяснения некоторых из этих фундаментальных идей.

Под предложением мы подразумеваем утверждение, имеющее определенное истинностное значение , истина (T) или ложь (F) — например,

«В 1492 году Колумб плыл по синему океану». (T)

«Наполеон выиграл битву при Ватерлоо». (Ф)

В более общем смысле под формулой мы подразумеваем утверждение, возможно, с некоторыми переменными, которое либо истинно, либо false всякий раз, когда мы присваиваем определенные значения каждой из переменных. Мы будем использовать заглавные буквы для обозначения формул. Если правда а формула зависит от значений, скажем, $x$, $y$ и $z$, мы будем использовать обозначение типа $P(x,y,z)$ для обозначения формулы. 92+y = 12$», то $P(2,8)$ и $P(3,3)$ верно, а $P(1,4)$ и $P(0,6)$ ложны. Если $Q(x,y,z)$ равно «$x+y

Является ли предложение истинным или ложным, обычно зависит от того, что мы говорят о том, что одно и то же предложение может быть истинным или ложным в зависимости от по контексту; например, формула $x|y$ означает, что `$x$ делит $у$’. То есть $x|y$, если существует некоторый $z$ такой, что $y=x\cdot z$. Сейчас, правда ли, что $3|2$? Это зависит: если мы говорим о целых числах, ответ — нет; если мы говорим о рациональных числах, то ответ да, потому что $2=3\cdot(2/3)$. (Конечно, если $x\not=0$ и $y$ любые рациональных чисел, затем $x|y$, так что это не очень полезное понятие. При обычном использовании внешний вид формулы «$x|y$» подразумевает , что $x$ и $y$ являются целыми числами.)

Вселенная дискурса для конкретной области математики представляет собой набор, который содержит все, что представляет интерес для этой темы. Когда мы изучение математических формул типа «$x$ делит $y$» на переменные предполагается, что они принимают значения в любом дискурсивном универсуме подходит для конкретного предмета. Вселенная дискурса обычно ясно из обсуждения, но иногда нам нужно будет идентифицируйте его явно для ясности. Вселенная дискурса обычно обозначается $U$.

Сложные предложения и формулы составляются из более простых, используя небольшое количество логических операций . Просто горстка этих операций позволит нам сказать все, что мы должны сказать в математика.

Если $P$ — это формула, то «не $P$» — это другая формула. формула, которую мы символически запишем как $\lnot P$. Конечно, $\lне P$ ложно, если $P$ истинно, и наоборот, например,

«6 не является простым числом» или «Неверно, что 6 премьер» или «$\lnot(\hbox{6 простое число})$» (T)

«Рональд Рейган не был президентом». (Ф)

Предположим, что $P$ и $Q$ — формулы. Затем «$P$ и $Q$» — это формула, записанная символически как $P\land Q$, называемое соединением из $P$ и $Q$. Чтобы $P\land Q$ были истинными как $P$, так и $Q$ должно быть истинным, иначе оно ложно, например,

«5 долларов = 6 долларов и 7 долларов = 8 долларов». (F)

«Сиэтл находится в Вашингтоне, а Бойсе — в Айдахо». (T)

«Толстой был русским, а Диккенс был Французский.» (Ф)

Если $P$ и $Q$ являются формулами, то формула «$P$ или $Q$» записывается символически как $P\lor Q$, называемая дизъюнкция $P$ и $Q$. Это важно отметить, что это включительно или, то есть, «либо или оба». Итак, если $P$, $Q$ или оба $P$ и $Q$ верны, то же самое и с $P\lor Q$. Единственный случай, когда $P\lor Q$ может быть ложным, состоит в том, что оба $P$ и $Q$ ложны, например,

«Вашингтон в Канаде или Лондон в Англии». (T)

«$5

«Ленин был испанцем или Ганди был итальянцем». (Ф)

Если $P$ и $Q$ — формулы, то «если $P$, то $Q$» или «$P$ означает, что $Q$» написано $P\подразумевает Q$, используя условное обозначение , $\подразумевает$. Не очевидно (по крайней мере, для большинства людей), под чем обстоятельства $P\имеет Q$ должно быть правдой. Отчасти это потому, что «if… then» используется в обычном английском языке более чем одним способом, однако нам нужно исправить правило, которое позволит нам точно знать, когда $P\ подразумевает Q$ верно. Конечно, если $P$ истинно, а $Q$ ложно, $P$ не может подразумевают $Q$, поэтому $P\implis Q$ в этом случае ложно. Чтобы помочь нам с в других случаях рассмотрим следующее утверждение:

«Если $x$ меньше 2, то $x$ меньше 4».

Это утверждение должно быть верным независимо от значения $x$. (при условии, что вселенная дискурса является чем-то знакомым, например целые числа). Если $x$ равно 1, оно оценивается как $\rm T\имплицитно T$, если $x$ равно 3, оно становится $\rm F\implis T$, а если $x$ равно 5, становится $\rm F\ подразумевает F$. Таким образом, оказывается, что $P\implis Q$ истинно, если только $P$ истинно, а $Q$ ложно. Это правило, которое мы принимаем.

Наконец, biconditional , написанный $\Leftrightarrow$, соответствует фраза «если и только если» или «если» для краткости. Таким образом, $P \Leftrightarrow Q$ истинно, когда и $P$, и $Q$ имеют одинаковое истинностное значение, иначе оно ложно.

Пример 1.1.2 Предположим, что $P(x,y)$ равно «$x+y=2$» и $Q(x,y)$ равно «$xy>1$». Тогда, когда $x=1$ и $y=1$, $\lnot P(x,y)$, $P(x,y)\land Q(x,y)$, $P(x,y)\lor Q(x,y)$, $P(x,y)\имеет Q(x,y)$ и $P(x,y)\Leftrightarrow Q(x,y)$ имеют значения истинности F, F, T, F, F соответственно, а когда $x=2$ и $y=3$ имеют истинностные значения Т, Ф, Т, Т, Ф соответственно. $\квадрат$

Используя операции $\lnot$, $\land$, $\lor$, $\implies$, $\Leftrightarrow$, мы можем построить составных выражений, таких как $$ (P\land (\lnot Q))\ подразумевает ((\lnot R)\lor ((\lnot P)\land Q)). $$ Как показывает этот пример, иногда необходимо включать много круглых скобок, чтобы группировать термины в формуле ясно. Как и в алгебре, где умножение имеет приоритет перед сложением, мы можем убрать некоторые скобки согласование определенного порядка, в котором логически операции выполняются. Мы будет применять операции в этом порядке, начиная с от первого к последнему: $\lnot$, $\land$, $\lor$, $\implies$ и $\Leftrightarrow$. Так $$A\подразумевает B\или C\земля \lне D $$ сокращение от $$A\подразумевает (B\или (C\land (\lnot D))). $$ Как и в алгебре, часто разумно включать несколько дополнительных скобок, чтобы убедиться, что предполагаемый смысл понятен. Большая часть информации, которую мы обсудили, может быть резюмирована в таблицы истинности . Например, таблица истинности для $\lnot P$:

$P$	$\lnot P$
Т	Ж
Ф	Т

В этой таблице две строки, потому что есть только две возможности для истинное значение $P$. Другие логические операции используют две переменные, поэтому им требуется 4 строки в их таблицах истинности.

$P$	$Q$	$P\land Q$	$P\lor Q$	$P\Rightarrow Q$	$P\Leftrightarrow Q$
Т	Т	Т	Т	Т	Т
Ф	Т	Ф	Т	Т	Ф
Т	Ж	Ж	Т	Ж	Ж
Ж	Ж	Ж	Ж 9п$ строки в таблице, потому что есть много разных способов назначить T и F для $n$ простых формул в составном выражении. Таблица истинности для $(P\land Q)\lor \lnot R$ такова: $P$ $Q$ $R$ $P \land Q$ $\lnot R$ $(P \land Q)\lor\lnot R$ Т Т Т Т Ф Т Ф Т Т Ф Ф Ф Т Ф Т Ф Ф Ф Ф Ф Т Ф Ф Ф Т Т Ф Т Т Т Ф Т Ф Ф Т Т Т Ф Ф Ф Т Т Ф Ф Ф Ф Т Т Обратите внимание, как включение промежуточных шагов облегчает работу с таблицей. посчитай и прочитай. Тавтология — это логическое выражение, которое всегда оценивается как T, то есть последний столбец его таблицы истинности состоит только из Т. Иногда говорят, что тавтология равна 9.0005 действительный ; хотя «действительный» используется в других контекстах как ну, это не должно вызывать путаницы. Например, $(P\land Q)\lor P\Leftrightarrow P$ является тавтологией, поскольку ее таблица истинности такова: $P$ $Q$ $P\land Q$ $(P\land Q)\lor P$ $(P\land Q)\lor P\Leftrightarrow P$ Т Т Т Т Т Ф Т Ф Ф Т Т Ж Ж Т Т Ф Ф Ф Ф Т Мы перечисляем несколько важных тавтологий в следующей теореме. Теорема 1.1.3. Справедливы следующие утверждения. а) $P\стрелка влево \lnot\lnot P$ б) $P\lor Q\Leftrightarrow Q\lor P$ c) $P\land Q\Стрелка влево Q\land P$ d) $(P\land Q)\land R\Стрелка влево P\land(Q\land R)$ e) $(P\lor Q)\lor R\Стрелка влево P\lor(Q\lor R)$ f) $P\land (Q\lor R)\Leftrightarrow (P\land Q)\lor (P\land R)$ g) $P\lor (Q\land R)\Стрелка влево (P\lor Q)\land (P\lor R)$ h) $(P\подразумевает Q)\Стрелка влево (\lnot P\lor Q)$ i) $P\имеет (P\или Q)$ j) $P\land Q\подразумевает Q$ k) $(P\стрелка влево Q)\стрелка влево ((P\подразумевает Q)\land (Q\подразумевает P))$ l) $(P\подразумевается Q)\стрелка влево (\lnot Q\подразумевается \lnot P)$ Доказательство. Доказательства оставлены в качестве упражнений. $\qed$ Заметим, что (b) и (c) — коммутативные законы, (d) и (e) — ассоциативные законы и (е) и (ж) говорят, что $\land$ и $\lor$ распределяются друг над другом. Это говорит о том, что существует форма алгебры для логических выражений, аналогичная алгебре для числовых выражений. Этот предмет называется Булева алгебра и имеет множество применений. особенно в информатике. Если две формулы всегда принимают одно и то же истинностное значение независимо от того, элементы из вселенной дискурса, которые мы заменяем различными переменные, то мы говорим, что они эквивалентны . Стоимость эквивалента формулы в том, что они говорят одно и то же. Это всегда правильный шаг в доказательстве заменить некоторую формулу эквивалентной. Кроме того, многие тавтологии содержат важные идеи для построения доказательств. Для например, (k) говорит, что если вы хотите показать, что $P\Leftrightarrow Q$, это можно (и часто целесообразно) разбить доказательство на два части, одна из которых доказывает импликацию $P\implis Q$, а вторая доказывая обратное , $Q\подразумевает P$. При чтении теоремы 1.1.3 у вас может возникнуть заметил, что $\land$ и $\lor$ обладают многими схожими свойствами. Они называются «двойственными» понятиями — для любого свойства один, есть почти идентичное свойство, которому удовлетворяет другой, экземпляры двух операций поменялись местами. Это часто означает, что когда мы доказываем результат, включающий одно понятие, мы получаем соответствующий результат для своего двойственного без дополнительной работы. Джордж Буль. Буль (1815–1864) имел только обычное школьное образование, хотя и выучил Греческий и латынь самостоятельно. Он начал свою карьеру в качестве элементарного школьным учителем, но решил, что ему нужно больше узнать о математики, поэтому он начал изучать математику, а также языки, необходимые ему для чтения современной литературы на математика. В 1847 году он опубликовал короткую книгу «Математический анализ». Анализ логики , который, можно справедливо сказать, лег в основу исследования. математической логики. Ключевой вклад работы заключался в переопределить «математику» так, чтобы она означала не просто «изучение чисел и величина», но изучение символов и манипулирование ими в соответствии с к определенным правилам. Важность этого уровня абстракции для будущее математики трудно переоценить. Вероятно, на Благодаря этой работе он перешел на должность в Куинс-колледж в Корке. В «Исследовании законов мысли» , опубликованном в 1854 г., Буль установил настоящую формальную логику, развивая то, что сегодня называется Булева алгебра или иногда алгебра множеств . Он использовал символы для сложение и умножение как операторы, но в совершенно абстрактном смысл. Сегодня эти символы все еще иногда используются в булевых выражениях. алгебре, хотя символы `$\land$’ и `$\lor$’, и `$\cap$’ и `$\cup$’ также используются. Буль применил алгебраическую манипуляцию к процесс рассуждения. Вот простой пример типа манипуляцию, которую он проделал: уравнение $xy=x$ (которое сегодня можно было бы записать $x\land y = x$ или $x\cap y = x$) означает, что «все вещи, удовлетворяющие $x$ удовлетворяет $y$’, или, говоря нашим языком, $x\имеет y$. Если также $yz=y$ (что есть $y\implis z$), то подстановка $y=yz$ в $xy=x$ дает $x(yz)=x$ или $(xy)z=x$. Заменив $xy$ на $x$, получим $xz=x$, или $x\подразумевает z$. Этот простой пример логического рассуждения используется более и далее по математике. 92+bD+c=0$, обработка $D$ как номер , предоставляет информацию о решениях для дифференциальное уравнение. Информация здесь взята из A History of Mathematics, by Карл Б. Бойер, Нью-Йорк: John Wiley and Sons, 1968. Подробнее информацию см. в Lectures on Ten British Mathematics , by Александр Макфарлейн, Нью-Йорк: John Wiley & Sons, 1916. Пример 1.1.1 Постройте таблицы истинности для следующих логических выражений: а) $(P\land Q)\или \lnot P$ б) $P\имеет (Q\land P)$ c) $(P\land Q)\Стрелка влево (P\lor \lnot R)$ d) $\lnot P\имеет в виду \lnot(Q\lor R)$ Пример 1.1.2 Проверьте тавтологии в теореме 1.1.3. Пример 1.1.3 Предположим, что $P(x,y)$ — это формула «$x+y=4$», а $Q(x,y)$ — это формула «$x $P(x,y)\land Q(x,y)$,    $\lnot P(x,y)\lor Q(x,y)$, $P(x,y)\подразумевает \lnot Q(x,y)$,    $\lnot(P(x,y)\Leftrightarrow Q(x,y))$, , используя значения: а) $x=1, y=3$ c) $x=1, y=2$ б) $x=3, y=1$ 9007 0 г) $x=2, y=1$ Пример 1. Оставить комментарий Добавить комментарий Отменить ответ Ваш адрес email не будет опубликован. Обязательные поля помечены * Комментарий * Имя * Email * Сайт