Кодирование слов: Задача №5. Кодирование в различных системах счисления, расшифровка сообщений, выбор кода.

Задача №5. Кодирование в различных системах счисления, расшифровка сообщений, выбор кода.

Автор материалов — Лада Борисовна Есакова.

Кодирование – это перевод информации, представленной символами первичного алфавита, в последовательность кодов.

Декодирование (операция, обратная кодированию) – перевод кодов в набор символов первичного алфавита.

Кодирование может быть равномерное и неравномерное. При равномерном кодировании каждый символ исходного алфавита заменяется кодом одинаковой длины. При неравномерном кодировании разные символы исходного алфавита могут заменяться кодами разной длины.

Код называется однозначно декодируемым, если любое сообщение, составленное из кодовых слов, можно декодировать единственным способом.

Равномерное кодирование всегда однозначно декодируемо.

Для неравномерных кодов существует следующее достаточное (но не необходимое) условие однозначного декодирования:

Сообщение однозначно декодируемо с начала, если выполняется

условие Фано: никакое кодовое слово не является началом другого кодового слова.

Сообщение однозначно декодируемо с конца, если выполняется обратное условие Фано: никакое кодовое слово не является окончанием другого кодового слова.

 

Кодирование в различных системах счисления

Пример 1.

Для кодирования букв О, В, Д, П, А решили использовать двоичное представление

чисел 0, 1, 2, 3 и 4 соответственно (с сохранением одного незначащего нуля в случае одноразрядного представления). Если закодировать последовательность букв ВОДОПАД таким способом и результат записать восьмеричным кодом, то получится

1) 22162

2) 1020342

3) 2131453

4) 34017

Решение:

Представим коды указанных букв в дво­ич­ном коде, добавив незначащий нуль для одноразрядных чисел:

О	В	Д	П	А
0	1	2	3	4
00	01	10	11	100

Закодируем по­сле­до­ва­тель­ность букв: ВО­ДО­ПАД — 010010001110010.

Разобьём это пред­став­ле­ние на трой­ки спра­ва на­ле­во и пе­ре­ведём каждую тройку в восьмеричное число.

010 010 001 110 010 — 22162.

Пра­виль­ный ответ ука­зан под но­ме­ром 1.

Ответ:

1

Пример 2.

Для пе­ре­да­чи по ка­на­лу связи со­об­ще­ния, со­сто­я­ще­го толь­ко из сим­во­лов А, Б, В и Г, ис­поль­зу­ет­ся по­сим­воль­ное ко­ди­ро­ва­ние: А-10, Б-11, В-110, Г-0. Через канал связи пе­ре­даётся со­об­ще­ние: ВАГ­БА­А­ГВ. За­ко­ди­руй­те со­об­ще­ние дан­ным кодом. По­лу­чен­ное дво­ич­ное число пе­ре­ве­ди­те в шест­на­дца­те­рич­ный вид.

            1) D3A6

2) 62032206

3) 6A3D

4) CADBAADC

 

Решение:

За­ко­ди­ру­ем по­сле­до­ва­тель­ность букв: ВАГ­БА­А­ГВ — 1101001110100110. Разобьем это пред­став­ле­ние на четвёрки спра­ва на­ле­во и пе­ре­ведём каждую четверку в шестнадцатеричное число:

 

1101 0011 1010 0110₂ = D3A6₁₆

 

Пра­виль­ный ответ ука­зан под но­ме­ром 1.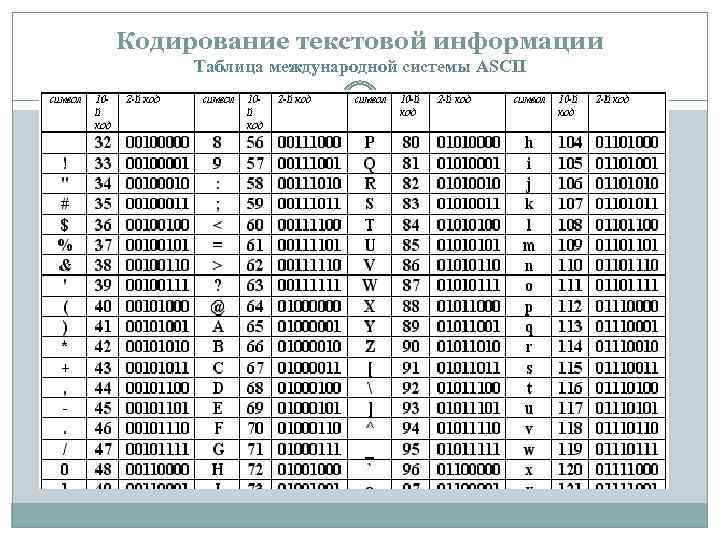

Ответ: 1

Расшифровка сообщений

Пример 3.

Для 5 букв ла­тин­ско­го ал­фа­ви­та за­да­ны их дво­ич­ные коды (для не­ко­то­рых букв – из двух бит, для не­ко­то­рых – из трех). Эти коды пред­став­ле­ны в таб­ли­це:

 

a	b	c	d	e
100	110	011	01	10

Опре­де­ли­те, какой набор букв за­ко­ди­ро­ван дво­ич­ной стро­кой 1000110110110, если из­вест­но, что все буквы в по­сле­до­ва­тель­но­сти – раз­ные:

1) cbade

2) acdeb

3) acbed

4) bacde

 

Решение:

Мы видим, что усло­вия Фано и об­рат­ное усло­вие Фано не вы­пол­ня­ют­ся, зна­чит код можно рас­ко­ди­ро­вать не­од­но­знач­но.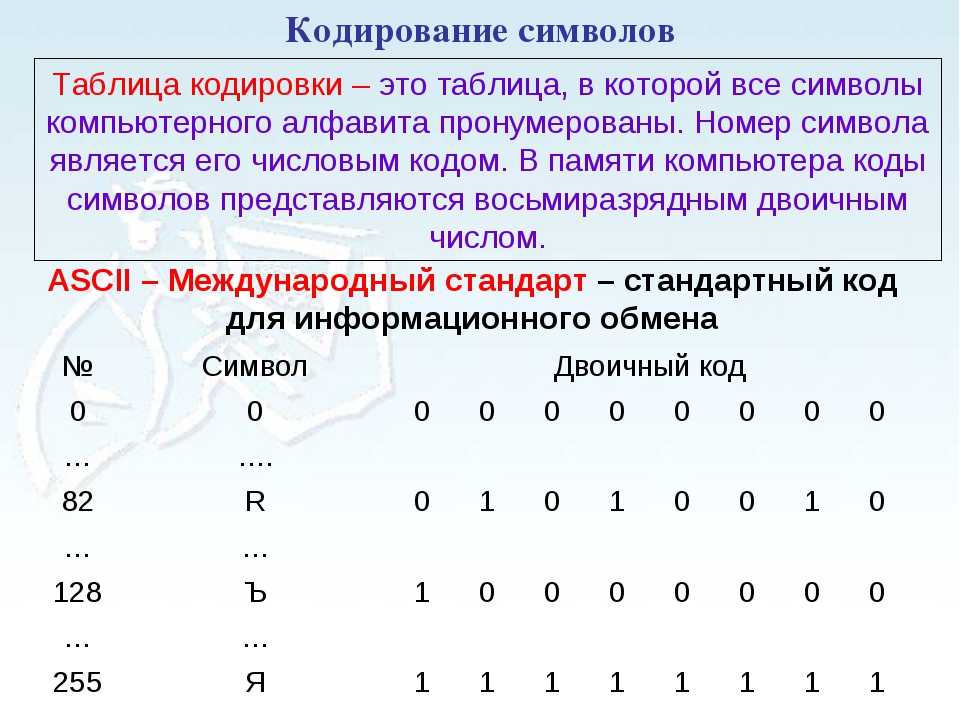

Значит, будем перебирать варианты, пока не получим подходящее слово :

1) 100 011 01 10 110

Пер­вая буква опре­де­ля­ет­ся од­но­знач­но, её код 100: a.

Пусть вто­рая буква — с, тогда сле­ду­ю­щая буква — d, потом — e и b.

Такой ва­ри­ант удо­вле­тво­ряет усло­вию, зна­чит, окон­ча­тель­но по­лу­чи­ли ответ: acdeb.

 

Ответ: 2

Пример 4.

Для пе­ре­да­чи дан­ных по ка­на­лу связи ис­поль­зу­ет­ся 5-би­то­вый код. Со­об­ще­ние со­дер­жит толь­ко буквы А, Б и В, ко­то­рые ко­ди­ру­ют­ся сле­ду­ю­щи­ми ко­до­вы­ми сло­ва­ми: А — 11010, Б — 10111, В — 01101.

При пе­ре­да­че воз­мож­ны по­ме­хи. Од­на­ко не­ко­то­рые ошиб­ки можно по­пы­тать­ся ис­пра­вить. Любые два из этих трёх ко­до­вых слов от­ли­ча­ют­ся друг от друга не менее чем в трёх по­зи­ци­ях. По­это­му если при пе­ре­да­че слова про­изо­шла ошиб­ка не более чем в одной по­зи­ции, то можно сде­лать обос­но­ван­ное пред­по­ло­же­ние о том, какая буква пе­ре­да­ва­лась.

(Го­во­рят, что «код ис­прав­ля­ет одну ошиб­ку».) На­при­мер, если по­лу­че­но ко­до­вое слово 10110, счи­та­ет­ся, что пе­ре­да­ва­лась буква Б. (От­ли­чие от ко­до­во­го слова для Б толь­ко в одной по­зи­ции, для осталь­ных ко­до­вых слов от­ли­чий боль­ше.) Если при­ня­тое ко­до­вое слово от­ли­ча­ет­ся от ко­до­вых слов для букв А, Б, В более чем в одной по­зи­ции, то счи­та­ет­ся, что про­изо­шла ошиб­ка (она обо­зна­ча­ет­ся ‘х’).

 

По­лу­че­но со­об­ще­ние 11000 11101 10001 11111. Де­ко­ди­руй­те это со­об­ще­ние — вы­бе­ри­те пра­виль­ный ва­ри­ант.

 

1) АххБ

2) АВхБ

3) хххх

4) АВББ

 

Решение:

Де­ко­ди­ру­ем каж­дое слово со­об­ще­ния. Пер­вое слово: 11000 от­ли­ча­ет­ся от буквы А толь­ко одной по­зи­ци­ей. Вто­рое слово: 11101 от­ли­ча­ет­ся от буквы В толь­ко одной по­зи­ци­ей. Тре­тье слово: 10001 от­ли­ча­ет­ся от любой буквы более чем одной по­зи­ци­ей. Четвёртое слово: 11111 от­ли­ча­ет­ся от буквы Б толь­ко одной по­зи­ци­ей.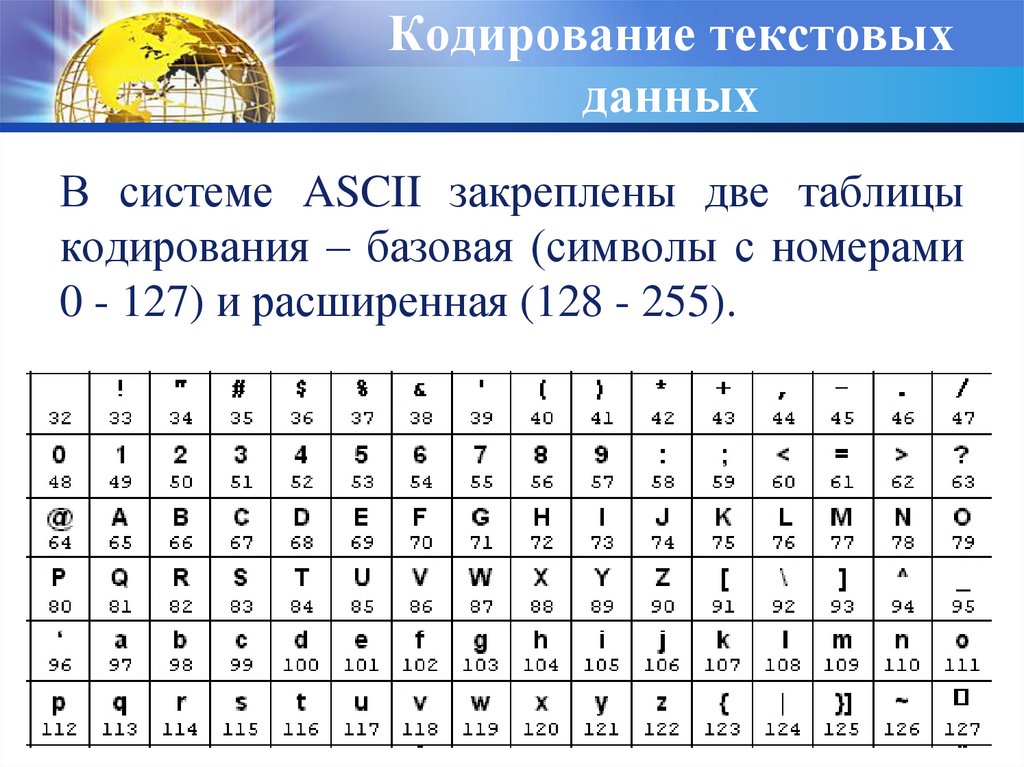

Таким об­ра­зом, ответ: АВхБ.

Ответ: 2

Однозначное кодирование

Пример 5.

Для пе­ре­да­чи по ка­на­лу связи со­об­ще­ния, со­сто­я­ще­го толь­ко из букв А, Б, В, Г, ре­ши­ли ис­поль­зо­вать не­рав­но­мер­ный по длине код: A=1, Б=01, В=001. Как нужно за­ко­ди­ро­вать букву Г, чтобы длина кода была ми­ни­маль­ной и до­пус­ка­лось од­но­знач­ное раз­би­е­ние ко­ди­ро­ван­но­го со­об­ще­ния на буквы?

1) 0001

2) 000

3) 11

4) 101

 

Решение:

Для анализа соблюдения условия однозначного декодирования (условия Фано) изобразим коды в виде дерева. Тогда однозначность выполняется, если каждая буква является листом дерева:

 

Видим, что ближайший от корня дерева свободный лист (т.е. код с минимальной длиной) имеет код 000.

Ответ: 2

Пример 6.

Для ко­ди­ро­ва­ния не­ко­то­рой по­сле­до­ва­тель­но­сти, со­сто­я­щей из букв У, Ч, Е, Н, И и К, ис­поль­зу­ет­ся не­рав­но­мер­ный дво­ич­ный пре­фикс­ный код. Вот этот код: У — 000, Ч — 001, Е — 010, Н — 100, И — 011, К — 11. Можно ли со­кра­тить для одной из букв длину ко­до­во­го слова так, чтобы код по-преж­не­му остал­ся пре­фикс­ным? Коды осталь­ных букв ме­нять­ся не долж­ны.

Вы­бе­ри­те пра­виль­ный ва­ри­ант от­ве­та.

При­ме­ча­ние. Пре­фикс­ный код — это код, в ко­то­ром ни одно ко­до­вое слово не яв­ля­ет­ся на­ча­лом дру­го­го; такие коды поз­во­ля­ют од­но­знач­но де­ко­ди­ро­вать по­лу­чен­ную дво­ич­ную по­сле­до­ва­тель­ность.

1) ко­до­вое слово для буквы Е можно со­кра­тить до 01

2) ко­до­вое слово для буквы К можно со­кра­тить до 1

3) ко­до­вое слово для буквы Н можно со­кра­тить до 10

4) это не­воз­мож­но

 

Решение:

Для анализа соблюдения условия однозначного декодирования (условия Фано) изобразим коды в виде дерева. Тогда однозначность выполняется, если каждая буква является листом дерева:

 

Легко заметить, что если букву Н перенести в вершину 10, она останется листом. Т.е. ко­до­вое слово для буквы Н можно со­кра­тить до 10.

Пра­виль­ный ответ ука­зан под но­ме­ром 3.

Ответ: 3

Благодарим за то, что пользуйтесь нашими статьями. Информация на странице «Задача №5. Кодирование в различных системах счисления, расшифровка сообщений, выбор кода.» подготовлена нашими редакторами специально, чтобы помочь вам в освоении предмета и подготовке к экзаменам. Чтобы успешно сдать необходимые и поступить в ВУЗ или колледж нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий. Также вы можете воспользоваться другими материалами из разделов нашего сайта.

Публикация обновлена: 07.04.2023

Кодирование для чайников, ч.1 / Хабр

Не являясь специалистом в обозначенной области я, тем не менее, прочитал много специализированной литературы для знакомства с предметом и прорываясь через тернии к звёздам набил, на начальных этапах, немало шишек. При всём изобилии информации мне не удалось найти простые статьи о кодировании как таковом, вне рамок специальной литературы (так сказать без формул и с картинками).

Статья, в первой части, является ликбезом по кодированию как таковому с примерами манипуляций с битовыми кодами, а во второй я бы хотел затронуть простейшие способы кодирования изображений.

0. Начало

Поскольку я обращаюсь к новичкам в этом вопросе, то не посчитаю зазорным обратиться к Википедии. А там, для обозначения кодирования информации, у нас есть такое определение — процесс преобразования сигнала из формы, удобной для непосредственного использования информации, в форму, удобную для передачи, хранения или автоматической переработки.

Чего мне не хватало в 70-80-е, так это в школе, пусть не на информатике, а, например, на уроках математики — базовой информации по кодированию. Дело в том, что кодированием информации каждый из нас занимается ежесекундно, постоянно и в целом — не концентрируясь на самом кодировании. То есть в быту мы это делаем постоянно. Так как это происходит?

Мимика, жесты, речь, сигналы разного уровня — табличка с надписью, знак на дороге, светофоры, и для современного мира — штрих- и бар-коды, URL, хэш-тэги.

Давайте рассмотрим некоторые более подробно.

1.1 Речь, мимика, жесты

Удивительно, но всё это — коды. С помощью них мы передаём информацию о своих действиях, ощущениях, эмоциях. Самое важное, чтобы коды были понятны всем. Например, родившись в густых лесах у Амазонки и не видя современного городского человека, можно столкнуться с проблемой непонимания кода — улыбка, как демонстрация зубов, будет воспринята как угроза, а не как выражение радости.

Следуя определению, что же происходит когда мы говорим? Мысль — как форма, удобная для непосредственного использования, преобразуется в речь — форму удобную для передачи. И, смотрите, так как у звука есть ограничение как на скорость, так и на дальность передачи, то, например, жест, в какой-то ситуации, может быть выбран для передачи той же информации, но на большее расстояние.

Но мы всё еще будем ограничены дальностью остроты нашего зрения, и тогда — человек начинает придумывать другие способы передачи и преобразования информации, например огонь или дым.

1.2 Чередующиеся сигналы

Индеец пингует

В примитивном виде кодирование чередующимися сигналами используется человечеством очень давно. В предыдущем разделе мы сказали про дым и огонь. Если между наблюдателем и источником огня ставить и убирать препятствие, то наблюдателю будет казаться, что он видит чередующиеся сигналы «включено/выключено». Меняя частоту таких включений мы можем выработать последовательность кодов, которая будет однозначно трактоваться принимающей стороной.

Наряду с сигнальными флажками на морских и речных судах, при появлении радио начали использовать код Морзе. И при всей кажущейся бинарности (представление кода двумя значениями), так как используются сигналы точка и тире, на самом деле это тернаный код, так как для разделения отдельных кодов-символов требуется пауза в передаче кода. То есть код Морзе кроме «точка-тире», что нам даёт букву «A» может звучать и так — «точка-пауза-тире» и тогда это уже две буквы «ET».

1.3 Контекст

Когда мы пользуемся компьютером, мы понимаем, что информация бывает разной — звук, видео, текст. Но в чем основные различия? И до того, как начать информацию кодировать, чтобы, например, передавать её по каналам связи, нужно понять, что из себя представляет информация в каждом конкретном случае, то есть обратить внимание на содержание. Звук — череда дискретных значений о звуковом сигнале, видео — череда кадров изображений, текст — череда символов текста. Если мы не будем учитывать контекст, а, например, будем использовать азбуку Морзе для передачи всех трёх видов информации, то если для текста такой способ может оказаться приемлемым, то для звука и видео время, затраченное на передачу например 1 секунды информации, может оказаться слишком долгим — час или даже пара недель.

2. Кодирование текста

От общего описания кодирования перейдём к практической части. Из условностей мы за константу примем то, что будем кодировать данные для персонального компьютера, где за единицу информации приняты — бит и байт. Бит, как атом информации, а байт — как условный блок размером в 8 бит.

Текст в компьютере является частью 256 символов, для каждого отводится один байт и в качестве кода могут быть использованы значения от 0 до 255. Так как данные в ПК представлены в двоичной системе счисления, то один байт (в значении ноль) равен записи 00000000, а 255 как 11111111. Чтение такого представления числа происходит справа налево, то есть один будет записано как 00000001.

Итак, символов английского алфавита 26 для верхнего и 26 для нижнего регистра, 10 цифр. Так же есть знаки препинания и другие символы, но для экспериментов мы будем использовать только прописные буквы (верхний регистр) и пробел.

Тестовая фраза «ЕХАЛ ГРЕКА ЧЕРЕЗ РЕКУ ВИДИТ ГРЕКА В РЕЧКЕ РАК СУНУЛ ГРЕКА РУКУ В РЕКУ РАК ЗА РУКУ ГРЕКУ ЦАП».

2.1 Блочное кодирование

Информация в ПК уже представлена в виде блоков по 8 бит, но мы, зная контекст, попробуем представить её в виде блоков меньшего размера. Для этого нам нужно собрать информацию о представленных символах и, на будущее, сразу подсчитаем частоту использования каждого символа:

Символ	Количество
ПРОБЕЛ	18
Р	12
К	11
Е	11
У	9
А	8
Г	4
В	3
Ч	2
Л	2
И	2
З	2
Д	1
Х	1
С	1
Т	1
Ц	1
Н	1
П	1

Всего нами использовано 19 символов (включая пробел).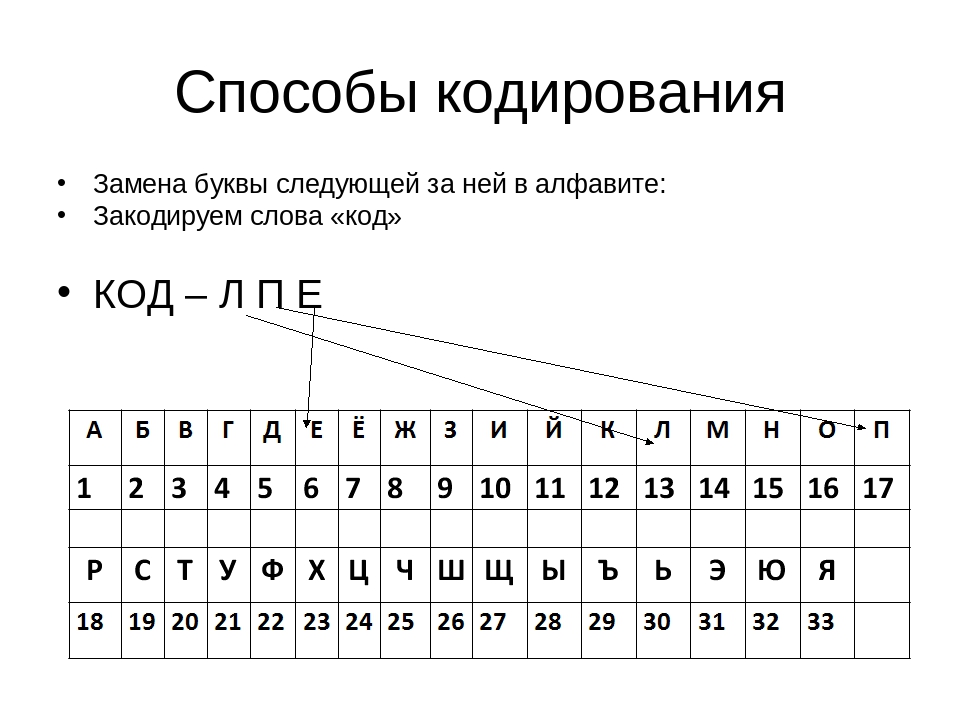 Для хранения в памяти ПК будет затрачено 18+12+11+11+9+8+4+3+2+2+2+2+1+1+1+1+1+1+1=91 байт (91*8=728 бит).

Эти значения мы берём как константы и пробуем изменить подход к хранению блоков. Для этого мы замечаем, что из 256 кодов для символов мы используем только 19. Чтобы узнать — сколько нужно бит для хранения 19 значений мы должны посчитать LOG₂(19)=4.25, так как дробное значение бита мы использовать не можем, то мы должны округлить до 5, что нам даёт максимально 32 разных значения (если бы мы захотели использовать 4 бита, то это дало бы лишь 16 значений и мы не смогли бы закодировать всю строку).

Нетрудно посчитать, что у нас получится 91*5=455 бит, то есть зная контекст и изменив способ хранения мы смогли уменьшить использование памяти ПК на 37.5%.

К сожалению такое представление информации не позволит его однозначно декодировать без хранения информации о символах и новых кодах, а добавление нового словаря увеличит размер данных. Поэтому подобные способы кодирования проявляют себя на бОльших объемах данных.

Кроме того, для хранения 19 значений мы использовали количество бит как для 32 значений, это снижает эффективность кодирования.

2.2 Коды переменной длины

Воспользуемся той же строкой и таблицей и попробуем данные закодировать иначе. Уберём блоки фиксированного размера и представим данные исходя из их частоты использования — чем чаще данные используются, чем меньше бит мы будем использовать. У нас получится вторая таблица:

Символ	Количество	Переменный код, бит
ПРОБЕЛ	18	0
Р	12	1
К	11	00
Е	11	01
У	9	10
А	8	11
Г	4	000
В	3	001
Ч	2	010
Л	2	011
И	2	100
З	2	101
Д	1	110
Х	1	111
С	1	0000
Т	1	0001
Ц	1	0010
Н	1	0011
П	1	0100

Для подсчёта длины закодированного сообщения мы должны сложить все произведения количества символов на длины кодов в битах и тогда получим 179 бит.

Но такой способ, хоть и позволил прилично сэкономить память, но не будет работать, потому что невозможно его раскодировать. Мы не сможем в такой ситуации определить, что означает код «111», это может быть «РРР», «РА», «АР» или «Х».

2.3 Префиксные блочные коды

Для решения проблемы предыдущего примера нам нужно использовать префиксные коды — это такой код, который при чтении можно однозначно раскодировать в нужный символ, так как он есть только у него. Помните ранее мы говорили про азбуку Морзе и там префиксом была пауза. Вот и сейчас нам нужно ввести в обращение какой-то код, который будет определять начало и/или конец конкретного значения кода.

Составим третью таблицу всё для той же строки:

Символ	Количество	Префиксный код с переменными блоками, бит
ПРОБЕЛ	18	0000
Р	12	0001
К	11	0010
Е	11	0011
У	9	0100
А	8	0101
Г	4	0110
В	3	0111
Ч	2	10001
Л	2	10010
И	2	10011
З	2	10100
Д	1	10101
Х	1	10110
С	1	10111
Т	1	11000
Ц	1	11001
Н	1	11010
П	1	11011

Особенность новых кодов в том, что первый бит мы используем для указания размера следующего за ним блока, где 0 — блок в три бита, 1 — блок в четыре бита. Нетрудно посчитать, что такой подход закодирует нашу строку в 379 бит. Ранее при блочном кодировании у нас получился результат в 455 бит.

Можно развить этот подход и префикс увеличить до 2 бит, что позволит нам создать 4 группы блоков:

Символ	Количество	Префиксный код с переменными блоками, бит
ПРОБЕЛ	18	000
Р	12	001
К	11	0100
Е	11	0101
У	9	0110
А	8	0111
Г	4	10000
В	3	10001
Ч	2	10010
Л	2	10011
И	2	10100
З	2	10101
Д	1	10110
Х	1	10111
С	1	11000
Т	1	11001
Ц	1	11010
Н	1	11011
П	1	11100

Где 00 — блок в 1 бит, 01 — в 2 бита, 10 и 11 — в 3 бита. Подсчитываем размер строки — 356 бит.

В итоге, за три модификации одного способа, мы регулярно уменьшаем размер строки, от 455 до 379, а затем до 356 бит.

2.4 Код Хаффмана

Один из популярнейших способов построения префиксных кодов. При соблюдении определенных условий позволяет получить оптимальный код для любых данных, хотя и допускает вольные модификации методов создания кодов.

Такой код гарантирует, что для каждого символа есть только одна уникальная последовательность значений битов. При этом частым символам будут назначены короткие коды.

Символ	Количество	Код
ПРОБЕЛ	18	00
Р	12	101
К	11	100
Е	11	011
У	9	010
А	8	1111
Г	4	11011
В	3	11001
Ч	2	111011
Л	2	111010
И	2	111001
З	2	111000
Д	1	1101011
Х	1	1101010
С	1	1101001
Т	1	1101000
Ц	1	1100011
Н	1	1100010
П	1	110000

Считаем результат — 328 бит.

Заметьте, хоть мы и стали использовать коды в 6 и 7 бит, но их слишком мало, чтобы повлиять на исход.

2.5.1 Строки и подстроки

До сих пор мы кодировали данные, рассматривая их как совокупность отдельных символов. Сейчас мы попробуем кодировать целыми словами.

Напомню нашу строку: «ЕХАЛ ГРЕКА ЧЕРЕЗ РЕКУ ВИДИТ ГРЕКА В РЕЧКЕ РАК СУНУЛ ГРЕКА РУКУ В РЕКУ РАК ЗА РУКУ ГРЕКУ ЦАП».

Составим таблицу повторов слов:

Слово	Количество
ПРОБЕЛ	18
ГРЕКА	3
В	2
РАК	2
РЕКУ	2
РУКУ	2
ВИДИТ	1
ГРЕКУ	1
ЕХАЛ	1
ЗА	1
РЕЧКЕ	1
СУНУЛ	1
ЦАП	1
ЧЕРЕЗ	1

Для кодирования нам нужно придумать концепцию, например — мы создаём словарь и каждому слову присваиваем индекс, пробелы игнорируем и не кодируем, но считаем, что каждое слово разделяется именно символом пробела.

Сначала формируем словарь:

Слово	Количество	Индекс
ГРЕКА	3	0
В	2	1
РАК	2	2
РЕКУ	2	3
РУКУ	2	4
ВИДИТ	1	5
ГРЕКУ	1	6
ЕХАЛ	1	7
ЗА	1	8
РЕЧКЕ	1	9
СУНУЛ	1	10
ЦАП	1	11
ЧЕРЕЗ	1	12

Таким образом наша строка кодируется в последовательность:

7, 0, 12, 3, 5, 0, 1, 9, 2, 10, 0, 4, 1, 3, 2, 8, 4, 6, 11

Это подготовительный этап, а вот то, как именно нам кодировать словарь и данные уже после подготовительного кодирования — процесс творческий. Мы пока останемся в рамках уже известных нам способов и начнём с блочного кодирования.

Индексы записываем в виде блоков по 4 бита (так можно представить индексы от 0 до 15), таких цепочек у нас будет две, одна для закодированного сообщения, а вторая для соответствия индексу и слову. Сами слова будем кодировать кодами Хаффмана, только нам еще придется задать разделитель записей в словаре, можно, например, указывать длину слова блоком, самое длинное слово у нас в 5 символов, для этого хватит 3 бита, но так же мы можем использовать код пробела, который состоит из двух бит — так и поступим. В итоге мы получаем схему хранения словаря:

Индекс / биты	Слово / биты	Конец слова / биты
0 / 4	ГРЕКА / 18	ПРОБЕЛ / 2
1 / 4	В / 5	ПРОБЕЛ / 2
2 / 4	РАК / 10	ПРОБЕЛ / 2
3 / 4	РЕКУ / 12	ПРОБЕЛ / 2
4 / 4	РУКУ / 12	ПРОБЕЛ / 2
5 / 4	ВИДИТ / 31	ПРОБЕЛ / 2
6 / 4	ГРЕКУ / 17	ПРОБЕЛ / 2
7 / 4	ЕХАЛ / 20	ПРОБЕЛ / 2
8 / 4	ЗА / 10	ПРОБЕЛ / 2
9 / 4	РЕЧКЕ / 18	ПРОБЕЛ / 2
10 / 4	СУНУЛ / 26	ПРОБЕЛ / 2
11 / 4	ЦАП / 17	ПРОБЕЛ / 2
12 / 4	ЧЕРЕЗ / 21	ПРОБЕЛ / 2

7

0

12

3

5

0

1

9

2

10

0

4

1

3

2

8

4

6

11

и само сообщение по 4 бита на код.

Считаем всё вместе и получаем 371 бит. При этом само сообщение у нас было закодировано в 19*4=76 бит. Но нам всё еще требуется сохранять соответствие кода Хаффмана и символа, как и во всех предыдущих случаях.

Послесловие

Надеюсь статья позволит составить общее впечатление о кодировании и покажет, что это не только военный-шифровальщик или сложный алгоритм для математических гениев.

Периодически сталкиваюсь с тем, как студенты пытаются решить задачи кодирования и просто не могут абстрагироваться, подойти творчески к этому процессу. А ведь кодирование, это как причёска или модные штаны, которые таким образом показывают наш социальный код.

UPD:

Так как редактор Хабра уничтожил написанную вторую часть, а администрация не отреагировала на моё обращение, то продолжение (написанное еще в январе) скорее всего никогда не увидит свет (две недели непрерывной работы). Писать снова, считать таблицы, писать софт для проверки и скриншотов стимулов у меня нет, как нет желания писать что-то на ресурсе, на котором несогласные с «линией партии» получают отрицательную карму.

Введение в обработку естественного языка — как кодировать значение слова | Лили Чен

Понимание математики и реализации Word2Vec

Изображение автора

Мужчина для короля, а женщина для чего?

Как обучить алгоритм машинного обучения правильно предсказывать правильный ответ «королева»?

В этой статье я расскажу о модели обработки естественного языка — Word2Vec — которую можно использовать для таких прогнозов.

В модели Word2Vec каждое слово словаря представлено вектором. Длина этого вектора — это гиперпараметр, который мы, люди, устанавливаем. Давайте использовать 100 в этой статье.

Поскольку каждое слово представляет собой вектор из 100 чисел, вы можете представить каждое слово как точку в 100-мерном пространстве.

Конечная цель Word2Vec состоит в том, чтобы похожие слова имели схожие векторы и, таким образом, группировались ближе друг к другу в этом 100-мерном пространстве.

Итак, как обучить алгоритм, чтобы у похожих слов были похожие векторы? И как это помогает решить проблему аналогии «мужчина относится к королю, как женщина к чему?»

Для обучения Word2Vec необходим большой объем текста. Например, Коричневый корпус. NLTK составил список корпусов, доступных для доступа.

По своей сути Word2Vec предназначен для прогнозирования вероятности появления одного слова рядом с другим словом (в предложении).

Изображение автора

В приведенном выше примере: «…лелеять бледно-голубую точку, единственный дом, который мы когда-либо знали» , «синий» — это центральное слово , а «бледный» — за пределами или . контекст слово. Мы хотим, чтобы алгоритм предсказывал вероятность того, что «бледный» является контекстным словом «синий». Примечание: в этой статье я буду использовать вне слов и контекст слов взаимозаменяемо.

Мы рассчитываем вероятность для каждого контекстного слова, которое находится в пределах определенного размера окна. Если размер окна равен 1, мы хотим предсказать вероятность слова, непосредственно предшествующего центральному слову и следующего за ним. Если размер окна равен 2, мы хотим предсказать вероятность двух слов, непосредственно предшествующих и следующих за центральным словом.

Таким образом, для алгоритма мы перебираем каждое слово в корпусе. В каждой позиции t мы вычисляем вероятность контекстных слов в пределах окна w при заданном центральном слове в позиции t .

Изображение автора

Хорошая модель даст высокую вероятность для этих контекстных слов, а плохая модель — низкую вероятность.

Разница между фактическим и прогнозируемым учитывается в потерях, которые используются в градиентном спуске для обновления параметров (тета) модели. И вот оно, центральная тема многих алгоритмов обучения с учителем.

Градиентный спуск

Что такое тета в Word2Vec? И какова функция потерь?

Параметры и функция потерь Word2Vec

Напомним, что каждое слово представлено вектором из 100 чисел. Также помните, что каждое слово может служить центральным словом или словом контекста. Таким образом, каждое уникальное слово в корпусе представлено двумя векторами : один вектор для него как центральное слово, а другой для него как контекстное слово.

Параметры тета

Параметры тета Word2Vec являются центральным и внешним векторами всех уникальных слов в корпусе. Размеры тета в 2 раза больше длины словарных строк и 100 столбцов.

На изображении я использовал строчные буквы v для представления вектора центрального слова слова и строчные буквы u для представления контекстного вектора слова слова. Таким образом, v_zebra является вектором для зебры, когда зебра является центральным словом. u_zebra — это вектор для зебры, когда зебра является контекстным словом какого-то другого центрального слова. Позже я буду использовать заглавную U для обозначения матрицы, содержащей все внешние векторы u .

Функция потерь, которую мы будем использовать, представляет собой потерю отрицательного логарифмического правдоподобия (NLL). NLL используется во многих алгоритмах машинного обучения, таких как логистическая регрессия. Уравнение для NLL: центральное слово по индексу t .

Таким образом, потеря одного контекстного слова при наличии центрального слова составляет:

Как вычислить вероятность? Мы используем уравнение Softmax. Ниже показано, как вычислить вероятность контекстного слова (o) при наличии центрального слова (c).

Номинатор является показателем скалярного произведения вектора контекста для контекстного слова o с центральным вектором для центрального слова c . Знаменатель представляет собой сумму показателя степени скалярного произведения вектора контекста каждого словарного слова с центральным вектором слова. Вау, это был полный рот!

Как вы, наверное, уже догадались, эту наивную вероятность softmax вычислять дорого, так как нам нужно суммировать по всему словарю. Есть еще один более эффективный способ проиграть; Я опишу это позже.

В градиентном спуске вы берете производную функции потерь по параметрам, чтобы узнать, как обновлять параметры на каждой итерации.

Для заданного центрального слова нам необходимо вычислить градиент как для вектора центрального слова, так и для всех векторов контекстных слов.

производная функции потерь для вычисления градиентов

Я не буду здесь делать выводы, но чтобы вычислить градиент для вектора центра, вы берете скалярное произведение U и (y_hat минус y). U — это, как я уже говорил, матрица всех внешних векторов всего словаря. Чтобы вычислить градиенты внешних векторов, вы берете скалярное произведение центрального вектора и (y_hat минус y) транспонированные. y_hat в данном случае — это Softmax скалярного произведения U и центрального вектора.

В целом алгоритм работает следующим образом:

Для каждой итерации:

1. Рассчитайте потери и градиенты мини-партии (например, размером 50).
2. Обновите параметры модели следующим образом:

тета = тета — скорость_обучения * градиенты

Чтобы вычислить градиенты мини-пакета размером 50, вы выполняете 50 итераций, и во время каждой итерации вы:

1. Получить случайное центральное слово и его контекстные слова.
2. Для каждого контекстного слова рассчитайте градиенты (взяв производную функции потерь).
3. Агрегировать все градиенты контекстных слов.

Агрегированные градиенты мини-пакета затем используются для обновления тета.

Вот суть Github с некоторыми соответствующего кода. Примечание. Я исключил некоторые части, такие как синтаксический анализ корпуса и код уравнения Softmax.

Алгоритм, который я только что описал, называется алгоритмом Skip-Gram. В Skip-Gram вы предсказываете вероятность контекстного слова с учетом центрального слова. Существует также другой алгоритм, называемый CBOW, в котором вместо этого вы предсказываете вероятность центрального слова с учетом его контекста.

Как я уже говорил, вычисление функции потерь, которую мы использовали, требует больших затрат. Существует еще один метод обучения Word2Vec, который называется «отрицательная выборка». При отрицательной выборке вместо кросс-энтропийной потери (т. е. отрицательной логарифмической вероятности функции Softmax) вы тренируете бинарную логистическую регрессию для истинной пары по сравнению с несколькими шумовыми парами. Истинная пара — это центральное слово и одно из его контекстных слов. Шумовая пара — это одно и то же центральное слово и случайное слово. При отрицательной выборке функция потерь работает намного эффективнее, поскольку вы не суммируете весь словарь.

Loss fxn для отрицательной выборки

Мужчина для короля, как женщина для чего?

Когда вы просите алгоритм Word2Vec решить эту аналогию, вы, по сути, просите его найти слово, наиболее ПОДХОДЯЩЕЕ на «король» и «женщина», но НАИБОЛЕЕ ОТЛИЧНОЕ на «мужчина». Сходство здесь относится к косинусному сходству двух векторов .

https://en.wikipedia.org/wiki/Cosine_similarity

Таким образом, после обучения вектор слов для «королевы» больше всего похож на векторы для «король» и «женщина», но не похож на «мужчина».

Кроме того, поскольку похожие слова сгруппированы вместе в многомерном пространстве, вы можете думать о векторе для «королевы» примерно как векторе для «короля» минус вектор для «мужчины» плюс вектор для «женщины».

Изображение автора

И вот, как мы можем обучить компьютеры решать аналогии!

Поиск похожих слов и решение аналогий — это всего лишь два основных применения Word2Vec. Вложения Word2Vec также можно использовать для более сложных задач, таких как анализ тональности. Для анализа настроений функции будут средними по всем векторам слов в предложении. Ярлык, конечно же, будет настроением (положительным, отрицательным, нейтральным). Затем вы можете выполнить многоклассовую классификацию с помощью таких классификаторов, как случайный лес, регрессия Softmax или даже нейронная сеть!

Следите за новыми статьями о НЛП!

Откройте документ Word и укажите кодировку с помощью PowerShell

спросил 6 лет, 3 месяца назад

Изменено 6 лет, 3 месяца назад

Просмотрено 3к раз

Я пытаюсь заставить PowerShell открыть текстовый файл и выбрать определенный вариант кодировки.

По умолчанию при открытии этого текстового файла в Word вручную он пытается открыть его с японской кодировкой, поэтому некоторые символы отображаются неправильно.

Я пробовал много разных вещей, но ничего не работает, так что я полностью застрял.

Этот текстовый файл, среди прочего, необходимо ежедневно преобразовывать в PDF.

Мой текущий сценарий выглядит следующим образом:

 $wdFormatPDF = 17
$word = New-Object -ComObject Word.Application
$word.Visible = $true
$folderpath = "C:\Users\smirabile\Downloads\report-testing-destination\*"
$fileTypes = "принято.spl"
Get-ChildItem -Path $folderpath -Include $fileTypes | ForEach-Object {
    $path = ($_.FullName).Substring(0, ($_.FullName).LastIndexOf("."))
    $doc = $word.Documents.Open($_.FullName)
    $Word.Selection.PageSetup.Orientation = 1
    $Word.Selection.PageSetup.LeftMargin = 20
    $Word.Selection.PageSetup.RightMargin = 20
    $doc.Выбрать()
    $Word.Selection.Font.Size = 9$doc.SaveAs([ref]$path, [ref]$wdFormatPDF)
    $doc. Закрыть()
}
$слово.Выйти()
Stop-Process -Name WINWORD -Force
 

• powershell
• кодировка
• кодировка символов
• ms-word

Если сомневаетесь, прочтите документацию:

Синтаксис

 выражение.Open(FileName, ConfirmConversions, ReadOnly, AddToRecentFiles,
    PasswordDocument, PasswordTemplate, Revert, WritePasswordDocument,
    WritePasswordTemplate, Format, Encoding, Visible, OpenConflictDocument,
    OpenAndRepair, DocumentDirection, NoEncodingDialog)
 

[…]
Кодировка | Дополнительно | Вариант | Кодировка документа (кодовая страница или набор символов), используемая Microsoft Word при просмотре сохраненного документа. Может быть любой допустимой константой MsoEncoding . […] Значение по умолчанию — системная кодовая страница.

Используйте [Type]::Missing для параметров, которые вы хотите использовать со значением по умолчанию.