Каких параметров функций не существует в си: Функции (C++) | Microsoft Learn

Функции в программировании. Урок 11 курса «Python. Введение в программирование»

Функция в программировании представляет собой обособленный участок кода, который можно вызывать, обратившись к нему по имени, которым он был назван. При вызове происходит выполнение команд тела функции.

Функции можно сравнить с небольшими программками, которые сами по себе, то есть автономно, не исполняются, а встраиваются в обычную программу. Нередко их так и называют – подпрограммы. Других ключевых отличий функций от программ нет. Функции также при необходимости могут получать и возвращать данные. Только обычно они их получают не с ввода (клавиатуры, файла и др.), а из вызывающей программы. Сюда же они возвращают результат своей работы.

Существует множество встроенных в язык программирования функций. С некоторыми такими в Python мы уже сталкивались. Это print(), input(), int(), float(), str(), type(). Код их тела нам не виден, он где-то «спрятан внутри языка». Нам же предоставляется только интерфейс – имя функции.

С другой стороны, программист всегда может определять свои функции. Их называют пользовательскими. В данном случае под «пользователем» понимают программиста, а не того, кто пользует программу. Разберемся, зачем нам эти функции, и как их создавать.

Предположим, надо три раза подряд запрашивать на ввод пару чисел и складывать их. С этой целью можно использовать цикл:

i = 0
while i < 3:
    a = int(input())
    b = int(input())
    print(a+b)
    i += 1

Однако, что если перед каждым запросом чисел, надо выводить надпись, зачем они нужны, и каждый раз эта надпись разная. Мы не можем прервать цикл, а затем вернуться к тому же циклу обратно. Придется отказаться от него, и тогда получится длинный код, содержащий в разных местах одинаковые участки:

print("Сколько бананов и ананасов для обезьян?")
a = int(input())
b = int(input())
print("Всего", a+b, "шт.
  ")
 
print("Сколько жуков и червей для ежей?")
a = int(input())
b = int(input())
print("Всего", a+b, "шт.")
 
print("Сколько рыб и моллюсков для выдр?")
a = int(input())
b = int(input())
print("Всего", a+b, "шт.")

Пример исполнения программы:

Сколько бананов и ананасов для обезьян?
15
5
Всего 20 шт.
Сколько жуков и червей для ежей?
50
12
Всего 62 шт.
Сколько рыб и моллюсков для выдр?
16
8
Всего 24 шт.

Внедрение функций позволяет решить проблему дублирования кода в разных местах программы. Благодаря им можно исполнять один и тот же участок кода не сразу, а только тогда, когда он понадобится.

Определение функции. Оператор def

В языке программирования Python функции определяются с помощью оператора def. Рассмотрим код:

def count_food():
    a = int(input())
    b = int(input())
    print("Всего", a+b, "шт.")

Это пример определения функции. Как и другие сложные инструкции вроде условного оператора и циклов функция состоит из заголовка и тела.

Заголовок оканчивается двоеточием и переходом на новую строку. Тело имеет отступ.

Ключевое слово def сообщает интерпретатору, что перед ним определение функции. За def следует имя функции. Оно может быть любым, также как и всякий идентификатор, например, переменная. В программировании весьма желательно давать всему осмысленные имена. Так в данном случае функция названа «посчитать_еду» в переводе на русский.

После имени функции ставятся скобки. В приведенном примере они пустые. Это значит, что функция не принимает никакие данные из вызывающей ее программы. Однако она могла бы их принимать, и тогда в скобках были бы указаны так называемые параметры.

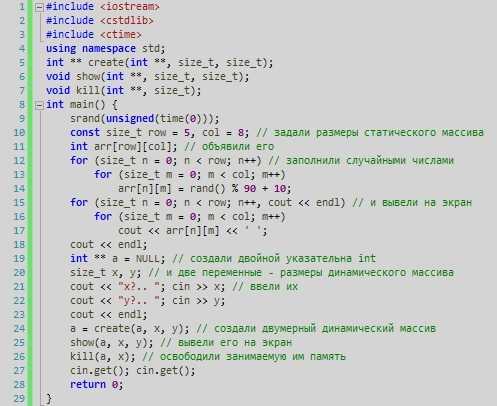
После двоеточия следует тело, содержащее инструкции, которые выполняются при вызове функции. Следует различать определение функции и ее вызов. В программном коде они не рядом и не вместе. Можно определить функцию, но ни разу ее не вызвать. Нельзя вызвать функцию, которая не была определена.

Определив функцию, но ни разу не вызвав ее, вы никогда не выполните ее тела.

Вызов функции

Рассмотрим полную версию программы с функцией:

def count_food():
    a = int(input())
    b = int(input())
    print("Всего", a+b, "шт.")
 
print("Сколько бананов и ананасов для обезьян?")
count_food()
 
print("Сколько жуков и червей для ежей?")
count_food()
 
print("Сколько рыб и моллюсков для выдр?")
count_food()

После вывода на экран каждого информационного сообщения осуществляется вызов функции, который выглядит просто как упоминание ее имени со скобками. Поскольку в функцию мы ничего не передаем скобки опять же пустые. В приведенном коде функция вызывается три раза.

Когда функция вызывается, поток выполнения программы переходит к ее определению и начинает исполнять ее тело. После того, как тело функции исполнено, поток выполнения возвращается в основной код в то место, где функция вызывалась. Далее исполняется следующее за вызовом выражение.

В языке Python определение функции должно предшествовать ее вызовам. Это связано с тем, что интерпретатор читает код строка за строкой и о том, что находится ниже по течению, ему еще неизвестно. Поэтому если вызов функции предшествует ее определению, то возникает ошибка (выбрасывается исключение NameError):

print("Сколько бананов и ананасов для обезьян?")
count_food()
 
print("Сколько жуков и червей для ежей?")
count_food()
 
print("Сколько рыб и моллюсков для выдр?")
count_food()
 
def count_food():
    a = int(input())
    b = int(input())
    print("Всего", a+b, "шт.")

Результат:

Сколько бананов и ананасов для обезьян?
Traceback (most recent call last):
  File "test.py", line 2, in <module>
    count_food()
NameError: name 'count_food' is not defined

Для многих компилируемых языков это не обязательное условие. Там можно определять и вызывать функцию в произвольных местах программы. Однако для удобочитаемости кода программисты даже в этом случае предпочитают соблюдать определенные правила.

Функции придают программе структуру

Польза функций не только в возможности многократного вызова одного и того же кода из разных мест программы. Не менее важно, что благодаря им программа обретает истинную структуру. Функции как бы разделяют ее на обособленные части, каждая из которых выполняет свою конкретную задачу.

Пусть надо написать программу, вычисляющую площади разных фигур. Пользователь указывает, площадь какой фигуры он хочет вычислить. После этого вводит исходные данные. Например, длину и ширину в случае прямоугольника. Чтобы разделить поток выполнения на несколько ветвей, следует использовать оператор if-elif-else:

figure = input("1-прямоугольник, 
2-треугольник, 3-круг: ")
 
if figure == '1':
  a = float(input("Ширина: "))
  b = float(input("Высота: "))
  print("Площадь: %.2f" % (a*b))
elif figure == '2':
  a = float(input("Основание: "))
  h = float(input("Высота: "))
  print("Площадь: %.2f" % (0.5 * a * h))
elif figure == '3':
  r = float(input("Радиус: "))
  print("Площадь: %. 2f" % (3.14 * r**2))
else:
  print("Ошибка ввода")

Здесь нет никаких функций, и все прекрасно. Но напишем вариант с функциями:

def rectangle():
    a = float(input("Ширина: "))
    b = float(input("Высота: "))
    print("Площадь: %.2f" % (a*b))
 
def triangle():
    a = float(input("Основание: "))
    h = float(input("Высота: "))
    print("Площадь: %.2f" % (0.5 * a * h))
 
def circle():
    r = float(input("Радиус: "))
    print("Площадь: %.2f" % (3.14 * r**2))
 
figure = input("1-прямоугольник, 
2-треугольник, 3-круг: ")
if figure == '1':
  rectangle()
elif figure == '2':
  triangle()
elif figure == '3':
  circle()
else:
  print("Ошибка ввода")

Он кажется сложнее, а каждая из трех функций вызывается всего один раз. Однако из общей логики программы как бы убраны и обособлены инструкции для нахождения площадей. Программа теперь состоит из отдельных «кирпичиков Лего». В основной ветке мы можем комбинировать их как угодно. Она играет роль управляющего механизма.

Если нам когда-нибудь захочется вычислять площадь треугольника по формуле Герона, а не через высоту, то не придется искать код во всей программе (представьте, что она состоит из тысяч строк кода как реальные программы). Мы пойдем к месту определения функций и изменим тело одной из них.

Если понадобиться использовать эти функции в какой-нибудь другой программе, то мы сможем импортировать их туда, сославшись на данный файл с кодом (как это делается в Python, будет рассмотрено позже).

Практическая работа

В программировании можно из одной функции вызывать другую. Для иллюстрации этой возможности напишите программу по следующему описанию.

Основная ветка программы, не считая заголовков функций, состоит из одной строки кода. Это вызов функции test(). В ней запрашивается на ввод целое число. Если оно положительное, то вызывается функция positive(), тело которой содержит команду вывода на экран слова «Положительное».

Если число отрицательное, то вызывается функция negative(), ее тело содержит выражение вывода на экран слова «Отрицательное».

Понятно, что вызов test() должен следовать после определения функций. Однако имеет ли значение порядок определения самих функций? То есть должны ли определения positive() и negative() предшествовать test() или могут следовать после него? Проверьте вашу гипотезу, поменяв объявления функций местами. Попробуйте объяснить результат.

Примеры решения и дополнительные уроки в pdf-версии и android-приложении курса

Производная функции. Геометрический смысл производной.

Производная функции — одна из сложных тем в школьной программе. Не каждый выпускник ответит на вопрос, что такое производная.

В этой статье просто и понятно рассказано о том, что такое производная и для чего она нужна

. Мы не будем сейчас стремиться к математической строгости изложения. Самое главное — понять смысл.

Запомним определение:

Производная — это скорость изменения функции.

На рисунке — графики трех функций. Как вы думаете, какая из них быстрее растет?

Ответ очевиден — третья. У нее самая большая скорость изменения, то есть самая большая производная.

Вот другой пример.

Костя, Гриша и Матвей одновременно устроились на работу. Посмотрим, как менялся их доход в течение года:

На графике сразу все видно, не правда ли? Доход Кости за полгода вырос больше чем в два раза. И у Гриши доход тоже вырос, но совсем чуть-чуть. А доход Матвея уменьшился до нуля. Стартовые условия одинаковые, а скорость изменения функции, то есть производная, — разная. Что касается Матвея — у его дохода производная вообще отрицательна.

Определение.

Производная – это скорость изменения функции.

Интуитивно мы без труда оцениваем скорость изменения функции.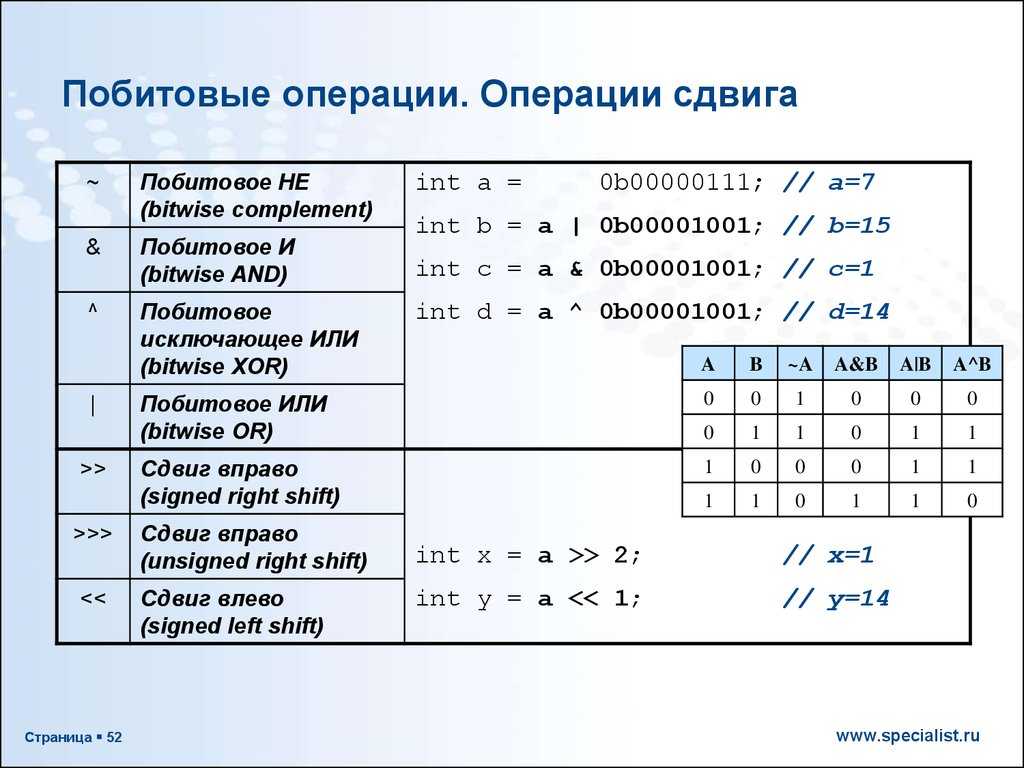 Но как же это делаем?

На самом деле мы смотрим, насколько круто идет вверх (или вниз) график функции. Другими словами — насколько быстро меняется у с изменением х. Очевидно, что одна и та же функция в разных точках может иметь разное значение производной — то есть может меняться быстрее или медленнее.

Производная функции обозначается .

Покажем, как найти с помощью графика.

Нарисован график некоторой функции . Возьмем на нем точку А с абсциссой . Проведём в этой точке касательную к графику функции. Мы хотим оценить, насколько круто вверх идет график функции. Удобная величина для этого — тангенс угла наклона касательной.

Производная функции в точке  равна тангенсу угла наклона касательной, проведённой к графику функции в этой точке.

Обратите внимание — в качестве угла наклона касательной мы берем угол между касательной и положительным направлением оси ОХ.

Иногда учащиеся спрашивают, что такое касательная к графику функции.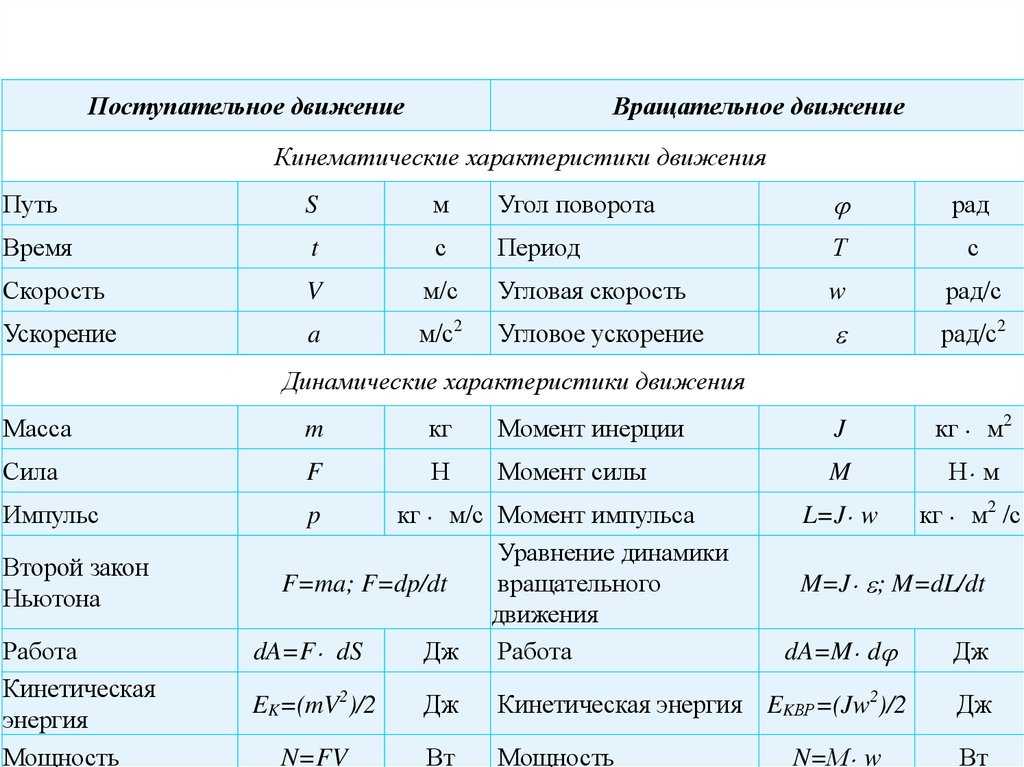 Это прямая, имеющая на данном участке единственную общую точку с графиком, причем так, как показано на нашем рисунке. Похоже на касательную к окружности.

Найдем . Мы помним, что тангенс острого угла в прямоугольном треугольнике равен отношению противолежащего катета к прилежащему. Из треугольника

Мы нашли производную с помощью графика, даже не зная формулу функции. Такие задачи часто встречаются в ЕГЭ по математике.

Есть и другое важное соотношение. Вспомним, что прямая задается уравнением

.

Величина k в этом уравнении называется угловым коэффициентом прямой. Она равна тангенсу угла наклона прямой к оси X.

.

Мы получаем, что

Запомним эту формулу. Она выражает геометрический смысл производной.

Производная функции в точке  равна угловому коэффициенту касательной, проведенной к графику функции в этой точке.

Другими словами, производная равна тангенсу угла наклона касательной.

Мы уже сказали, что у одной и той же функции в разных точках может быть разная производная.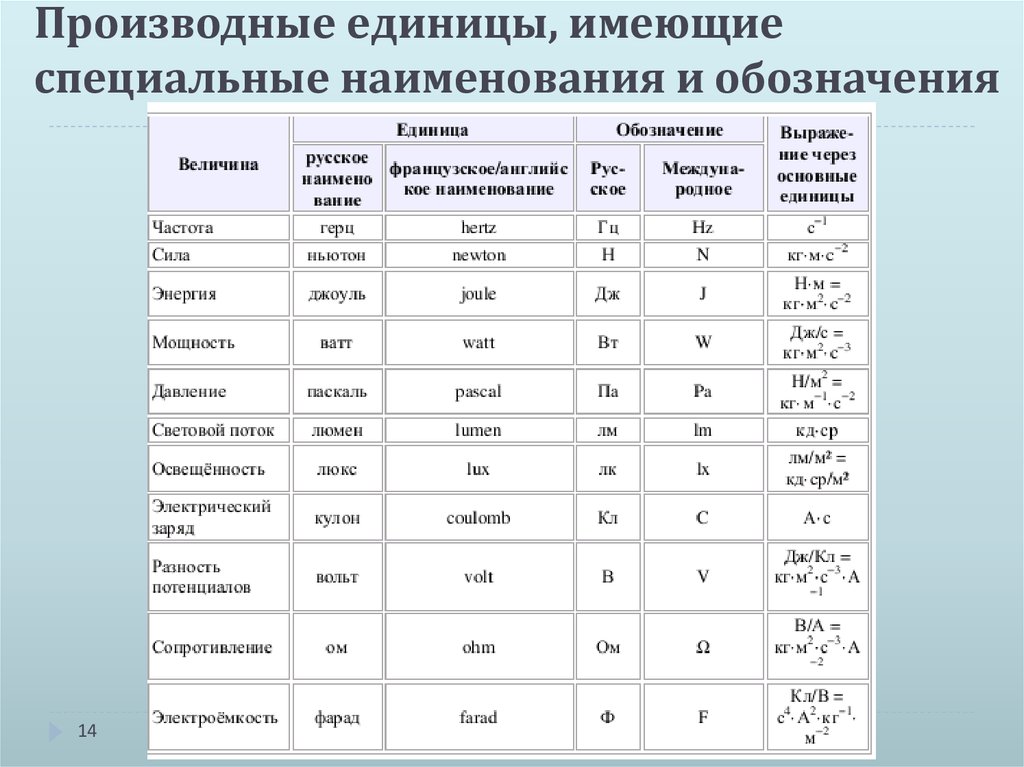 Посмотрим, как же связана производная с поведением функции.

Нарисуем график некоторой функции . Пусть на одних участках эта функция возрастает, на других — убывает, причем с разной скоростью. И пусть у этой функции будут точки максимума и минимума.

В точке A функция возрастает. Касательная к графику, проведенная в точке A, образует острый угол  с положительным направлением оси X. Значит, в точке A производная положительна.

В точке B наша функция убывает. Касательная в этой точке образует тупой угол  с положительным направлением оси X. Поскольку тангенс тупого угла отрицателен, в точке B производная отрицательна.

Вот что получается:

Если функция возрастает, ее производная положительна.

Если убывает, ее производная отрицательна.

А что же будет в точках максимума и минимума? Мы видим, что в точках C (точка максимума) и D (точка минимума) касательная горизонтальна. Следовательно, тангенс угла наклона касательной в этих точках равен нулю, и производная тоже равна нулю.

Точка С — точка максимума. В этой точке возрастание функции сменяется убыванием. Следовательно, знак производной меняется в точке С с «плюса» на «минус».

В точке D — точке минимума — производная тоже равна нулю, но ее знак меняется с «минуса» на «плюс».

Вывод: с помощью производной можно узнать о поведении функции всё, что нас интересует.

Если производная положительна, то функция возрастает.

Если производная отрицательная, то функция убывает.

В точке максимума производная равна нулю и меняет знак с «плюса» на «минус».

В точке минимума производная тоже равна нулю и меняет знак с «минуса» на «плюс».

Запишем эти выводы в виде таблицы:

	возрастает	точка максимума	убывает	точка минимума	возрастает
	+	0	—	0	+

Сделаем два небольших уточнения. Одно из них понадобится вам при решении задач ЕГЭ. Другое — на первом курсе, при более серьезном изучении функций и производных.

1. Возможен случай, когда производная функции в какой-либо точке равна нулю, но ни максимума, ни минимума у функции в этой точке нет. Это так называемая точка перегиба:

В точке E касательная к графику горизонтальна, и производная равна нулю. Однако до точки E функция возрастала — и после точки E продолжает возрастать. Знак производной не меняется — она как была положительной, так и осталась.

2. Бывает и так, что в точке максимума или минимума производная не существует. На графике это соответствует резкому излому, когда касательную в данной точке провести невозможно.

А как найти производную, если функция задана не графиком, а формулой? В этом случае применяется таблица производных. В ней вы найдете производные всех элементарных функций и правила взятия производных, то есть дифференцирования.

Геометрический смысл производной, задачи

Покажем, что такое геометрический смысл производной, на примере нескольких задач из Банка заданий ФИПИ.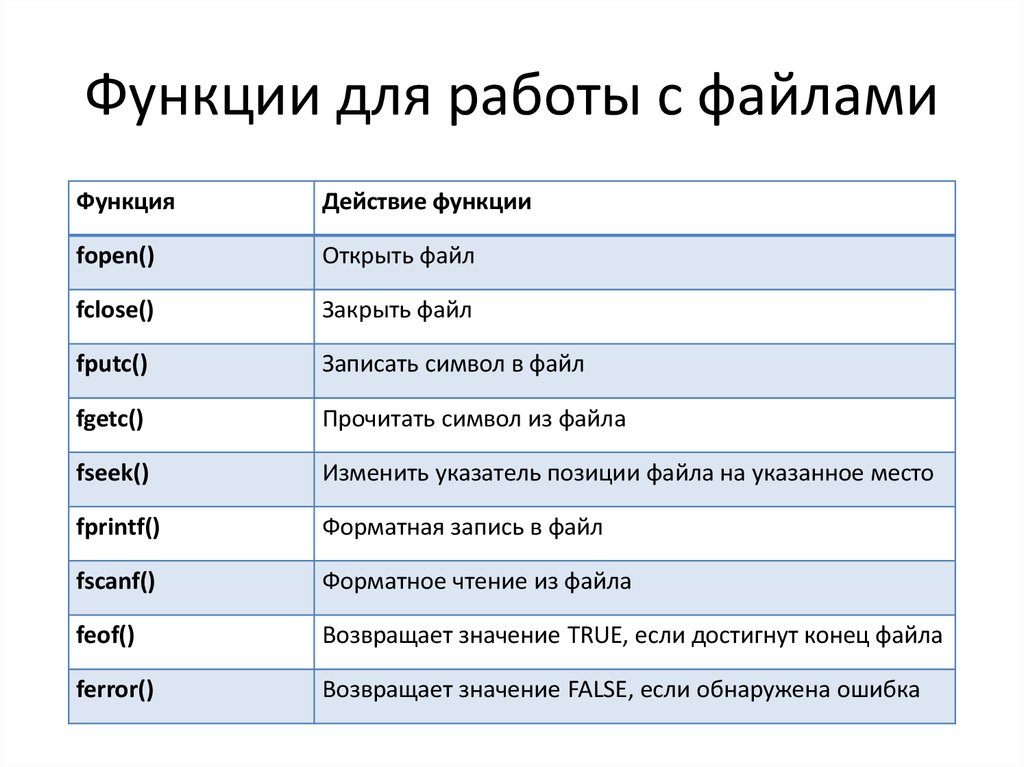

Задача 1. На рисунке изображен график функции ). Найдите количество решений уравнения )=0 на отрезке [-2,5; 9,5].

Решение:

Производная функции равна нулю в точках максимума и минимума функции Таких точек на графике 5.

Ответ: 5.

Задача 2. На рисунке изображен график функции y= ) — производной функции ). Сколько точек максимума имеет функция ) на отрезке ? В ответе запишите это число.

Решение:

Обратите внимание, что на этом рисунке изображен не график функции, а график ее производной.

В вариантах ЕГЭ по математике таких задач много. Пользуясь графиком производной, надо ответить на вопрос о поведении функции.

В точке максимума функции производная равна нулю и меняет знак с «плюса» на «минус». Такая точка на отрезке на графике одна.

Ответ: 1.

Задача 3. На рисунке изображены график функции и касательная к нему в точке с абсциссой Найдите значение производной функции в точке

Решение:

Вспомним определение.

Производная функции в точке равна тангенсу угла наклона касательной, проведенной к графику функции в этой точке (то есть угловому коэффициенту касательной).

Это геометрический смысл производной.

В точке функция y = f(x) убывает. Касательная, проведенная к ее графику в этой точке, образует тупой угол с положительным направлением оси Х. Найдем тангенс острого угла смежного с углом

Ответ: -0,5.

Задача 4. На рисунке изображен график производной функции определенной на отрезке В какой точке отрезка принимает наименьшее значение?

Решение:

На рисунке изображен график производной. Если функция возрастает — ее производная положительна. Если функция убывает — ее производная отрицательна. В точке минимума производная равна нулю и меняет знак с «минуса» на «плюс».

На рисунке есть такая точка, и это x = 1,5.

Слева от этой точки, на отрезке [1; 1,5] производная отрицательна, и функция убывает. Справа от этой точки, на интервале [1,5; 5), производная положительна, и функция возрастает.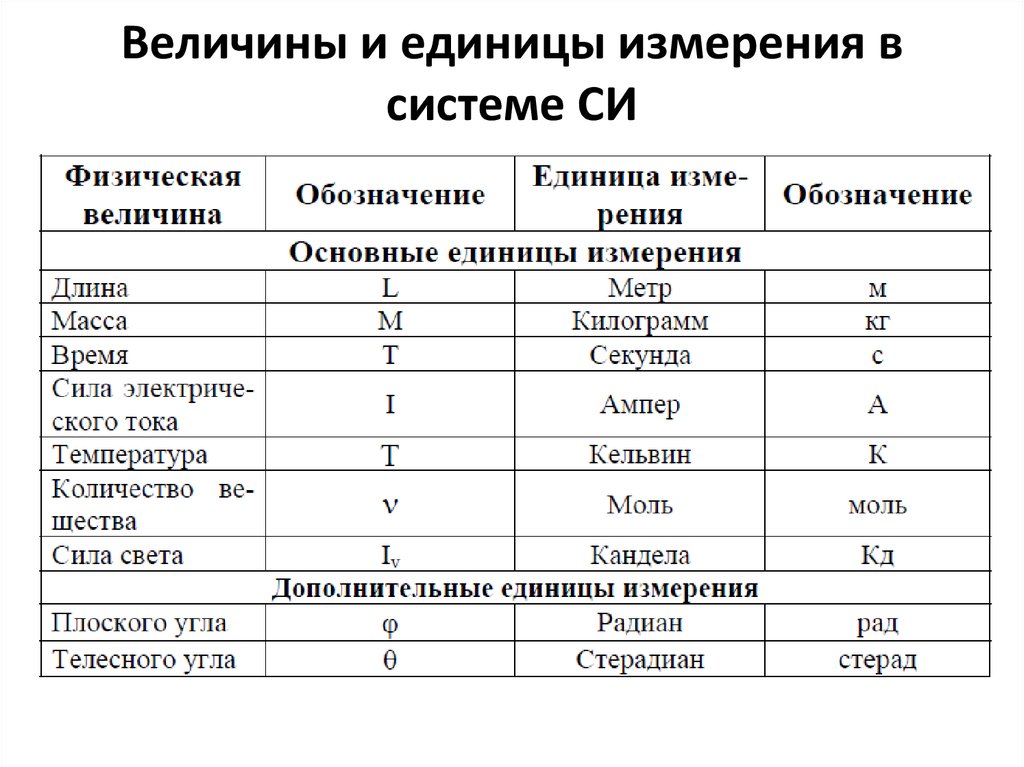

Значит, — точка минимума функции

Поэтому и свое наименьшее значение функция принимает в точке 1,5.

Ответ: 1,5.

Задача 5. На рисунке изображен график — производной функции В какой точке отрезка функция принимает наименьшее значение?

Решение:

На рисунке изображен график производной. Если функция возрастает — ее производная положительна. Если функция убывает — ее производная отрицательна. В точке минимума производная равна нулю и меняет знак с «минуса» на «плюс».

На рисунке есть такая точка, и это x = 3.

Слева от этой точки производная отрицательна, и функция убывает. Справа от точки x = 3 производная положительна, и функция возрастает.

Значит, — точка минимума функции

Кстати, вид графика функции определить нетрудно. Это квадратичная парабола с ветвями вверх.

Ответ: 3.

Задача 6. На рисунке изображен график производной непрерывной функции В какой точке отрезка функция принимает наибольшее значение?

Решение:

На отрезке расположена точка в которой производная равна нулю и меняет знак с «+» на «-».

Это значит, что — точка максимума функции на отрезке и наибольшее значение функция принимает именно в этой точке.

Ответ: — 2,5.

Задача 7. На рисунке изображен график производной функции определенной на интервале (-3;7). В какой точке отрезка [-2; 4] функция принимает наименьшее значение?

Решение:

Точка минимума функции f(x) — это x = 0. В этой точке производная равна 0 и меняет знак с «минуса» на «плюс».

Слева от точки 0 производная отрицательна, функция убывает. Справа от этой точки производная положительна, функция возрастает.

Наименьшее значение на отрезке достигается при x = 0.

Ответ: 0.

Задача 8. На рисунке изображены график функции и касательная к нему в точке с абсциссой Найдите значение производной функции в точке

Решение:

Производная функции в точке равна тангенсу угла наклона касательной, проведенной к графику функции в этой точке.

— касательная к

В точке производная отрицательная, т. к. функция — убывает в этой точке.

— угол, который образует касательная с положительным направлением оси Х.

Угол — тупой, а смежный с ним угол — острый.

Ответ: -0,375.

Задача 9. На рисунке изображен график непрерывной функции f(x) и касательные CD и MN, проведенные к ее графику в точках А и В. Найдите отношение значений производной функции f(x) в точках А и В.

Решение:

Найдём значения производных в точках А и В с помощью графика.

где — угол наклона касательной к графику функции в точке с абсциссой

Для точки А:

Для точки В:

Отношение производных:

Ответ: 0,15.

Условия касания

Пусть прямая касается графика функции в точке Тогда для точки выполняются условия касания:

Первое уравнение показывает, что значения функций и в точке равны друг другу. Это верно, поскольку эта точка лежит и на одном, и на другом графике.

Второе условие показывает, что производная функции в точке равна угловому коэффициенту касательной, то есть k.

Задача 10. Прямая касается графика функции причем абсцисса точки касания положительна. Найдите b.

Решение:

Запишем условие касания:

Начнем со второго уравнения:

Т.к. то

Найдем подставив в первое уравнение:

отсюда

Ответ: -7.

Условия касания встречаются нам не только в заданиях 1 части ЕГЭ по математике, но и в задачах с параметрами. Более того, это один из приемов решения уравнений и неравенств с параметрами.

Физический смысл производной

Мы узнали, что такое геометрический смысл производной. Научились находить производную с помощью графика функции и решать задачи ЕГЭ. Производная помогает нам исследовать функции, находить их точки максимума и минимума, строить графики функций.

И оказывается, что с производной вы познакомились намного раньше — в школьном курсе физики. Вы уже пользовались этим математическим понятием, но не называли его словом «производная».

Вспомним тему «Кинематика» в физике. Это раздел физики, описывающий механическое движение. Величины, которыми описывается движение какого-либо тела, — это скорость v, время t, координата х, если тело движется вдоль прямой. Или координаты x и y, если оно движется по плоскости.

Вспомним формулу для равномерного прямолинейного движения: где x — координата.

Пусть 3 материальных точки — например, три автомобиля — одновременно выезжают с постоянными скоростями из точки А и едут по прямолинейному шоссе. На графике показано, как меняется их координата x с течением времени. У какого из автомобилей скорость больше?

Очевидно, у третьего. Считая, что x = vt, для первого автомобиля найдем = 20 км/ч. Возможно, это машина, которая поливает или чистит дорогу, и поэтому так медленно едет. Для второго автомобиля = 40 км/ч, для третьего = 75 км/ч.

Но если пройденный путь, то есть изменение координаты тела, мы разделим на время, то найдем тангенс угла наклона для каждой из этих прямых. Так и есть.

Скорость тела — это производная от его координаты по времени.

А теперь пусть тело, например, автомобиль, движется вдоль оси x, причем его скорость не является постоянной. Зависимость его координаты от времени x(t) показана на графике.

Возьмем на графике точку, соответствующую моменту времени и проведем в этой точке касательную к графику функции.

Тангенс угла наклона этой касательной численно равен мгновенной скорости тела в момент

Мы получили, что мгновенная скорость — это производная от координаты по времени.

Это физический смысл производной.

Но не только скорость в физике является производной от другой физической величины, координаты.

Ускорение — это производная от скорости по времени. Сила тока — производная от заряда по времени.

Изучая курс физики в школе и в вузе, вы увидите множество уравнений, связывающих одни физические величины с производными других физических величин. Такие уравнения называются дифференциальными. А само действие взятия производной называется дифференцированием.

Вот задача из вариантов ЕГЭ по математике, где используется физический смысл производной.

Задача 11. Материальная точка M начинает движение из точки A и движется по прямой на протяжении 12 секунд. График показывает, как менялось расстояние от точки A до точки M со временем. На оси абсцисс откладывается время t в секундах, на оси ординат — расстояние s.

Определите, сколько раз за время движения скорость точки M обращалась в ноль (начало и конец движения не учитывайте).

Решение:

Производная — это скорость изменения функции. Мгновенная скорость движущегося тела (материальной точки) является производной от его координаты по времени. Это физический смысл производной.

Найдем на графике s(t) точки, в которых производная функции s(t) равна нулю. Таких точек 6. Это точки максимума и минимума функции s(t).

Ответ: 6.

Изучая высшую математику в вузе, вы узнаете еще одно определение производной.

Производной функции f(x) в точке называется предел отношения приращения функции к приращению аргумента при приращении аргумента, стремящемся к нулю.

Это определение есть в вашем школьном учебнике алгебры. Но намного важнее не механически его запомнить, а понять его смысл. Первые шаги к этому мы сделали, определив производную как скорость изменения функции. Мы также узнали, что такое геометрический смысл производной и физический смысл производной.

Проверка путей к файлам и папкам в параметрах PowerShell — 4sysops

Принятие путей к файлам и папкам в качестве параметра — довольно распространенное явление в сценариях PowerShell. Без проверки этих параметров ваш сценарий может работать не так, как предполагалось.

• Автор
• Последние сообщения

Мика Райрдон

Я фанатик PowerShell, в настоящее время работаю над управлением клиентами Windows в компании Haworth, расположенной в Голландии, штат Мичиган. Я копаюсь и документирую свои выводы на tiberriver256.github.io, и вы можете найти меня в Твиттере @tiberriver256. 9

Проблема с принятием параметра заключается в том, что вы не можете быть уверены, что вызов функции передает фактический путь к файлу. Мы принимаем все, что является строкой, и мы начнем работать с этой строкой, полагая, что пользователь скрипта не допустил ошибок при вводе пути. Это может привести к неожиданным результатам.

Например, если ваш сценарий запрашивает путь к папке, а пользователь вводит что-то неожиданное, ваш сценарий не сможет выполнить намеченную задачу. В приведенном ниже примере сценарий не может создать папку, если пользователь вводит недопустимые символы в именах папок. 9

Начнем с того, что зададим несколько вопросов об ожидаемом нами пути:

• Должен ли путь всегда указывать на файл или всегда быть папкой — или мы берем и то, и другое?
• Должен ли файл или папка существовать или нет?
• Если это всегда будет файл, а не папка, какие расширения файлов нам нужны?
• Если мы создаем файлы/папки, как нам проверить, нет ли в пути недопустимых символов?

Теперь, когда у нас есть ответы на основные вопросы относительно типа пути, который мы ожидаем для аргумента, мы можем приступить к написанию атрибутов проверки для нашего параметра. Атрибуты проверки — это атрибуты, которые вы можете добавить к параметрам при написании функции PowerShell (прекрасное введение см. в этой записи блога 4sysops, написанной Адамом Бертрамом). 9

Для этой задачи нам не нужны никакие сценарии проверки. Класс .NET System.IO.FileInfo позаботится об этой задаче за нас.

 функция Invoke-Task {
параметр(
[System.IO.FileInfo]$Путь
)
} 

Если вы передадите недопустимый путь в качестве аргумента, PowerShell выдаст следующее сообщение об ошибке:

 PS C:\> Invoke-Task -Path C:\Users
Invoke-Task: невозможно обработать преобразование аргумента для параметра «Путь». Не удается преобразовать значение «CC:\Users» в тип «System.IO.FileInfo». Ошибка: «Данный
формат пути не поддерживается."
В строке:1 символ:19 
 Мы можем сделать это относительно просто, используя  Test-Path  . Вы также можете легко отменить это, чтобы убедиться, что файл или папка не существует.  
 
 функция Invoke-Task {
параметр(
[Проверить скрипт({
если(-Не ($_ | Путь к тесту)){
выкинуть "Файл или папка не существует"
}
вернуть $true
})]
[System.IO.FileInfo]$Путь
)
} 
 При передаче несуществующей папки или файла в качестве аргумента вы получите следующее сообщение об ошибке:
 PS C:\> Invoke-Task -Path C:\FolderThatDoesNotExist
Invoke-Task: невозможно проверить аргумент параметра «Путь». Файл или папка не существует
В строке:1 символ:19
+ Invoke-Task -Path C:\FolderThatDoesNotExist
+                  ~~~~~~~~~~~~~~~~~~~~~~~~~~
+ CategoryInfo          : InvalidData: (:) [Invoke-Task], ParameterBindingValidationException
+ FullyQualifiedErrorId: ParameterArgumentValidationError,Invoke-Task
 
 Подтвердить, что путь существует и является ли он файлом или папкой
 Мы можем использовать параметр  PathType  командлета  Test-Path , чтобы проверить, является ли путь листовым (файл) или контейнерным (папка) типом.
 Если вы немного изучили параметры проверки, вы, возможно, уже знаете, что мы можем использовать атрибут ValidatePattern  для легкого выполнения этой задачи. Однако  ValidateScript  позволяет отображать более описательное сообщение об ошибке.
 функция Invoke-Task {
параметр(
[Проверить скрипт({
if(-Not ($_ | Путь к тесту)){
выкинуть "Файл или папка не существует"
}
if(-Not ($_ | Test-Path -PathType Leaf)){
throw «Аргумент Path должен быть файлом. Пути к папкам не допускаются».
}
если($_ -не соответствует "(\.msi|\.exe)"){
throw «Файл, указанный в аргументе пути, должен быть типа msi или exe»
}
вернуть $true
})]
[System.IO.FileInfo]$Путь
)
}
 
 Если имя файла не имеет необходимого расширения, вы увидите следующее сообщение об ошибке:
 Подпишитесь на информационный бюллетень 4sysops! 
 PS C:\> Invoke-Task -Path C:\Users\desktop.ini
Invoke-Task: невозможно проверить аргумент параметра «Путь».  Файл, указанный в аргументе пути, должен быть типа msi или exe.
В строке:1 символ:19
+ Invoke-Task -Путь C:\Users\desktop.ini
+                  ~~~~~~~~~~~~~~~~~~~~~
+ CategoryInfo          : InvalidData: (:) [Invoke-Task], ParameterBindingValidationException
+ FullyQualifiedErrorId: ParameterArgumentValidationError,Invoke-Task
 9 
 Проверка путей к файлам и папкам очень важна, поскольку в противном случае сценарий PowerShell может привести к неожиданным и нежелательным результатам. Вы можете использовать встроенные функции PowerShell для проверки ввода пользователя или написать сценарий проверки. 
  
 Проверка PowerShell для проверки существования файла (примеры) 
  
 Используете ли вы PowerShell для создания, чтения, обновления и удаления файлов? Если это так, вы, вероятно, сталкивались с ошибками, когда целевые файлы не существуют или уже существуют. К счастью для вас, в PowerShell есть способы проверить, существует ли файл, прежде чем что-либо с ним делать. 
 

Не читатель? Посмотрите соответствующий видеоурок!
 
 
   Не видите видео? Убедитесь, что ваш блокировщик рекламы отключен.    
 
 Например, вместо того, чтобы позволить вашему коду сразу создать файл, лучше проверить, что файл уже существует. Как показано на снимке экрана ниже, вы можете написать более качественный код и добиться четкого вывода. 
 Создание уже существующего файла 
 В этой статье вы узнаете о различных способах использования PowerShell для проверки существования файла. Вы также узнаете, как использовать каждый из этих способов для создания более качественного кода и результатов с помощью логики обработки ошибок. 
 
 Содержание 
  
 Предварительные условия 
 
 
  Если вы ИТ-специалист, которому приходится сталкиваться со слишком большим количеством запросов на сброс пароля в Active Directory, ознакомьтесь со Specops uReset, безопасным решением SSPR.  
 
 
 Эта статья представляет собой практическое руководство, в котором вы учитесь на различных примерах. А для выполнения примеров вам понадобится следующее: 
 
 
 Редактор кода.  Рекомендуемыми являются  Visual Studio Code  и  Atom, , которые работают на разных платформах. Вы также можете использовать Windows PowerShell ISE, если работаете на компьютере с Windows. 
 
  Windows PowerShell 5.1  (настольный) или  PowerShell 7.1 (базовый)  . Команды и сценарии в этой статье применимы к обоим выпускам PowerShell. Независимо от того, используете ли вы Windows, Linux или macOS, все будет в порядке, если у вас установлен PowerShell. 
 
 
   Связано: Как загрузить и установить PowerShell 7 в Windows, Linux и macOS   
 
 Использование PowerShell для проверки существования файла . Использование этих трех методов различается по использованию, но концепция и конечная цель одинаковы. Вот эти три способа: 
 
 
  Test-Path  Командлет. 
 
  Get-Item  и  Get-ChildItem  Командлет. 
 
  System.IO.File  Класс. 
 
 
 Будут приведены примеры и демонстрации каждого из этих трех методов, включая способы их использования с обработкой ошибок.  
 
 Использование Test-Path 
  
 Первый способ — это командлет  Test-Path , специально разработанный для определения существования пути или файла. При использовании этого командлета для проверки существования файла результат равен 9.0065 истина  или  ложь  . Результат показывает, существует файл или нет. 
 
 Ниже приведен основной синтаксис, позволяющий командлету  Test-Path  работать с проверкой файла. 
 
 Test-Path -Path <ПУТЬ к ФАЙЛУ> -PathType Leaf 
 Например, если вам нужно проверить существование такого файла с именем  C:\temp\important_file.txt , используйте приведенный ниже код. Обратите внимание, что часть  -PathType Leaf  указывает командлету проверять файл, а не каталог явно.
 Test-Path -Path C:\temp\important_file.txt -PathType Leaf 
 Когда вы запускаете приведенную выше команду в PowerShell, результат возвращает  True , если файл существует. В противном случае результатом будет  False , как вы можете видеть на скриншоте ниже.
 Использование Test-Path в PowerShell для проверки существования файла.0002 Этот пример является типичным вариантом использования для создания файлов в указанном месте. Чтобы избежать ошибки  «Файл  уже существует», скрипт проверяет, существует ли уже файл перед его созданием. Если файл существует, сценарий показывает сообщение и больше не пытается создать файл.
 Скопируйте приведенный ниже код и сохраните его в файле с именем  Create-NewFile.ps1  . Обязательно измените значение переменной  $path , если вы хотите изменить расположение вывода файла. После сохранения скрипта запустите его в PowerShell для проверки.
 # Создать-НовыйФайл.ps1
# Полный путь к файлу
$file = 'c:\temp\important_file.txt'
#Если файл не существует, создайте его.
if (-not(Test-Path -Path $file -PathType Leaf)) {
     пытаться {
         $null = New-Item -ItemType File -Path $file -Force -ErrorAction Stop
         Write-Host "Файл [$file] создан. "
     }
     ловить {
         бросить $_.Exception.Message
     }
 }
# Если файл уже существует, показать сообщение и ничего не делать.
 еще {
     Write-Host «Невозможно создать [$file], так как файл с таким именем уже существует».
 } 
 На приведенном ниже снимке экрана показаны два разных выхода. Первый — при запуске скрипта, когда файл не существует. Второй — после создания файла, а он уже существует.
 Запуск скрипта PowerShell для создания файла
   Связано: Назад к основам: Как запустить скрипт PowerShell предмет в указанном месте  . Для сравнения,  Командлет Get-ChildItem  предназначен для  получения элементов и дочерних элементов в одном или нескольких указанных местоположениях  . Функциональность этих двух командлетов не заключается в том, чтобы явно проверять, существуют ли файлы.
 Что произойдет, если вы используете  Get-Item  или  Get-ChildItem  для получения несуществующего элемента? Вы получите сообщение об ошибке для каждого отсутствующего файла. Возьмите приведенные ниже команды в качестве примера.
 $file = 'c:\temp\important_file.txt'
Get-Item -Path $file
Get-ChildItem -Path $file 
 Предположим, что файл  c:\temp\important_file.txt  не существует. Каждая из приведенных выше команд возвращает ошибку. Как видно из приведенного ниже примера, сообщение об ошибке для обеих команд одинаковое.
 Использование Get-Item и Get-ChildItem в PowerShell для проверки существования файла
 Пример: архивирование существующего файла и создание нового файла 
 В этом примере сценарий использует  Get-Item  и  Test-Path  командлеты. Логика этого скрипта заключается в следующем:
 Проверить, существует ли архивная папка, используя  Test-Path  .
 Если папка архива не существует, скрипт создает новую папку архива в таком формате —  гггг-МММ-дд_чч-мм-сс-тт  .
 Затем скрипт перемещает старый файл в папку архива.
 Проверить, существует ли файл, используя  Get-Item  .
 Если файл существует, сценарий сначала перемещает его в папку архива. Затем сценарий создает новый файл в исходном месте.
 Если файл не существует, сценарий создает новый файл.
 Скопируйте приведенный ниже код и сохраните его как  Create-NewFileAfterArchive.ps1  . После сохранения скрипта запустите его в PowerShell и проверьте результаты.
 # Create-NewFileAfterArchive.ps1
# Полный путь к файлу
$file = 'c:\temp\important_file.txt'
#Полный путь к папке архивации
$archiveFolder = "c:\temp\archive_$(get-date -Format 'yyyy-MMM-dd_hh-mm-ss-tt')\"
# Если файл существует, переместите его в папку архива, а затем создайте новый файл.
если (Get-Item -Path $file -ErrorAction Ignore) {
    пытаться {
        ## Если папка Архив не существует, создайте ее сейчас.
        if (-not(Test-Path -Path $archiveFolder -PathType Container)) {
            $null = New-Item -ItemType Directory -Path $archiveFolder -ErrorAction STOP
        }
        ## Переместите существующий файл в архив. 
        Move-Item -Path $file -Destination $archiveFolder -Force -ErrorAction STOP
        Write-Host "Старый файл [$file] был заархивирован в [$archiveFolder]"
     } ловить {
        бросить $_.Exception.Message
     }
 }
 Создайте новый файл
 пытаться {
     $null = New-Item -ItemType File -Path $file -Force -ErrorAction Stop
     Write-Host "Новый файл [$file] создан."
 } ловить {
    Write-Host $_.Exception.Message
 } 
  Совет. Параметр  -ErrorAction Ignore  подавляет ошибку (не отображается в консоли), а также не записывает ошибку в автоматическую переменную  $error   .
 На снимке экрана ниже первый запуск скрипта создал файл  c:\temp\important_file.txt.  Последующие выполнения сценария каждый раз создают новую папку архива, перемещают существующий файл в папку архива, а затем создают новый файл в  c:\temp\important_file.txt. 
 Запуск скрипта в PowerShell для проверки существования файла с помощью Get-Item
 Использование метода [System.
 IO.File]::Exists() .NET
 Последний метод, который следует изучить в этой статье, — это  System.IO. .File  Класс .NET, в частности метод  Exists() . Одной из сильных сторон PowerShell является возможность импорта и использования классов и методов .NET.
 Например, чтобы использовать метод  Exists()  в PowerShell для проверки существования файла, используйте приведенный ниже код.
 [System.IO.File]::Exists("PATH") 
 Приведенный выше метод дает логический результат –  true  или  false  . Если результат возвращает  true  , это означает, что целевой файл существует. В противном случае возвращается результат  false , когда целевой файл не существует.
 В приведенном ниже примере кода команда проверяет наличие файла  c:\temp\important_file.txt  .
 $file = 'c:\temp\important_file.txt'
[System.IO.File]::Exists($file)
 
 Как видно из приведенного ниже результата, результат возвращает true, подтверждая, что файл существует.
 Использование класса System.IO.File в PowerShell
 С помощью этого метода .NET вы также можете использовать троичные операции, как в примере ниже. Вместо того, чтобы показывать истинные или ложные результаты по умолчанию, вы можете настроить сообщение о результатах с более короткой реализацией. Однако тернарный оператор в этом примере применим только к PowerShell 7+.
 $file = 'c:\temp\important_file.txt'
[System.IO.File]::Exists($file) ? «Файл существует». : "Файл не существует." 
 Пример: обновление содержимого файла, если файл существует 
 Этот пример сценария обновляет текстовый файл, добавляя новое значение GUID. Однако обновление содержимого происходит только в том случае, если файл существует. В противном случае скрипт показывает сообщение и больше ничего не делает.
 Скопируйте приведенный ниже сценарий и сохраните его как  Update-FileContents.ps1  . При необходимости измените значение пути к файлу переменной  $file . Затем запустите скрипт в PowerShell для проверки.
 # Update-FileContents.ps1
#Полный путь к файлу
$file = 'c:\temp\important_file.txt'
# Если файл существует, добавьте новое значение GUID в файл.
если ([System.IO.File]::Exists($file)) {
    пытаться {
        $newValue = ((Новый-Guid).Guid)
        Add-Content -Path $file -Value $newValue -ErrorAction STOP
        Write-Host "Файл [$file] был обновлен с помощью [$newValue]"
     } ловить {
        бросить $_.Exception.Message
     }
 }
# Если файл не существует, показать сообщение и ничего не делать.
 еще {
     Write-Host «Не удалось обновить файл [$file], так как он не существует».
 } 
 На скриншоте ниже видно, что скрипт обновлял файл при каждом запуске. Обновление произошло потому, что метод  [System.IO.File]::Exists()  подтвердил существование файла  c:\temp\important_file.txt .
 В конце концов, использование команды  gc c:\temp\important_file.txt  для чтения содержимого файла подтвердило, что сценарий обновил файл значениями GUID.
 Использование метода .NET [System.IO.File]::Exists() в PowerShell
   Связано: Использование ускорителей типов данных PowerShell для ускорения написания кода  
 Заключение 
  Если вы ИТ-специалист, которому приходится сталкиваться со слишком большим количеством запросов на сброс пароля в Active Directory, попробуйте Specops uReset, безопасное решение SSPR. 
 Из этой статьи вы узнали, что существует несколько способов использования PowerShell для проверки существования файла. Хорошей практикой является проверка наличия файла перед выполнением каких-либо изменений, связанных с файлом.
 Вы узнали об использовании командлетов  Get-Item  ,  Get-ChildItem  и  Test-Path  . А также метод  [System.IO.File]::Exists() .NET . Примеры показали вам, как использовать методы и как сочетать их с логикой обработки ошибок.
 Прекратите терпеть эти сообщения об ошибках.