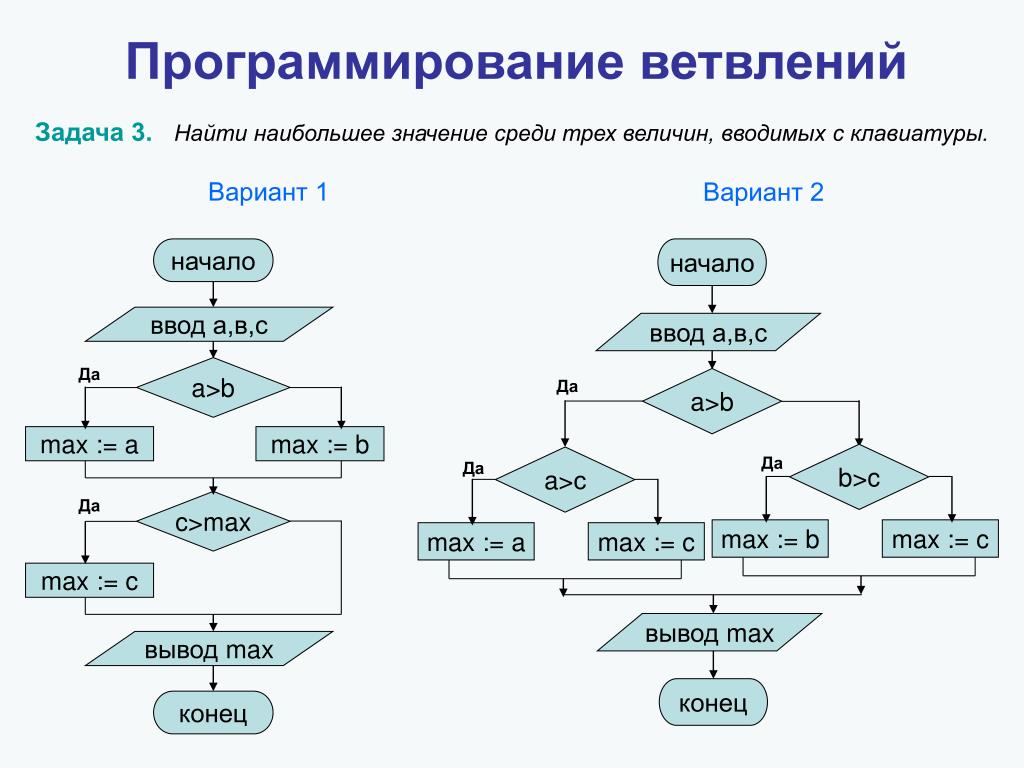
Основы логики — что это, определение и ответ
Математическая логика (она же булева алгебра) является неотъемлемым блоком знаний как в школьном курсе информатики, так и в ЕГЭ. В чистом виде логика в экзамене представлена в двух заданиях: №2 и №15, которые идут по увеличению сложности. Кроме этого, логика в том или ином виде встречается и в других разделах экзамена – от кодирования информации до программирования.
Цель логики как науки – определить, истинно или ложно некоторое высказывание, а также прослеживать связь между высказываниями относительно друг друга. Высказывания обозначаются логическими переменными, которые могут принимать лишь два значения:
Истина = 1, Ложь = 0
Логические выражения (которые состоят из более чем одного высказывания) на естественном языке образуются с помощью связок «И», «ИЛИ», «НЕ». В математической логике аналогом этих связок являются базовые логические операции – конъюнкция, дизъюнкция и инверсия. Чтобы определить значение составного логического выражения, надо знать значения входящих в него логических переменных (высказываний). Чтобы рассмотреть все возможные случаи, в булевой алгебре есть специальный аппарат – таблица истинности. Таблица истинности строится следующим образом: в столбцах записываются логические переменные и само выражение, а в строках – всевозможные комбинации переменных и соответствующий для них результат выражения. Для выражения, содержащего n переменных, количество комбинаций для них будет равно 2n. Подробнее про таблицы истинности написано ниже.
Чтобы рассмотреть все возможные случаи, в булевой алгебре есть специальный аппарат – таблица истинности. Таблица истинности строится следующим образом: в столбцах записываются логические переменные и само выражение, а в строках – всевозможные комбинации переменных и соответствующий для них результат выражения. Для выражения, содержащего n переменных, количество комбинаций для них будет равно 2n. Подробнее про таблицы истинности написано ниже.
Логическое умножение. Конъюнкция
Конъюнкция (логическое умножение, логическое «И») обозначает объединение двух или нескольких высказываний в одно таким образом, что результат будет истинным тогда и только тогда, когда истинны все входящие в него высказывания. Пусть есть два высказывания:
Эти высказывания истинны. Значит, их объединение с помощью конъюнкции («В ЕГЭ по информатике есть программирование И логика») – истинно.
Операцию конъюнкции в булевой алгебре принято обозначать знаком « /\ » или, реже, « & » (амперсанд). Операция логического умножения, аргументами которой являются логические переменные А и В, записываются следующей формулой: A /\ B. Таблица истинности для конъюнкции:
Операция логического умножения, аргументами которой являются логические переменные А и В, записываются следующей формулой: A /\ B. Таблица истинности для конъюнкции:
| A | B | A /\ B |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
Логическое сложение. Дизъюнкция
Дизъюнкция (логическое сложение, логическое «ИЛИ») обозначает объединение двух или нескольких высказываний в одно таким образом, что результат будет истинным тогда, когда истинно хотя бы одно входящее в него высказывание.
Операцию дизъюнкции в булевой алгебре принято обозначать знаком « \/ ». Операция логического сложения, аргументами которой являются логические переменные А и В, записывается следующей формулой: A \/ B.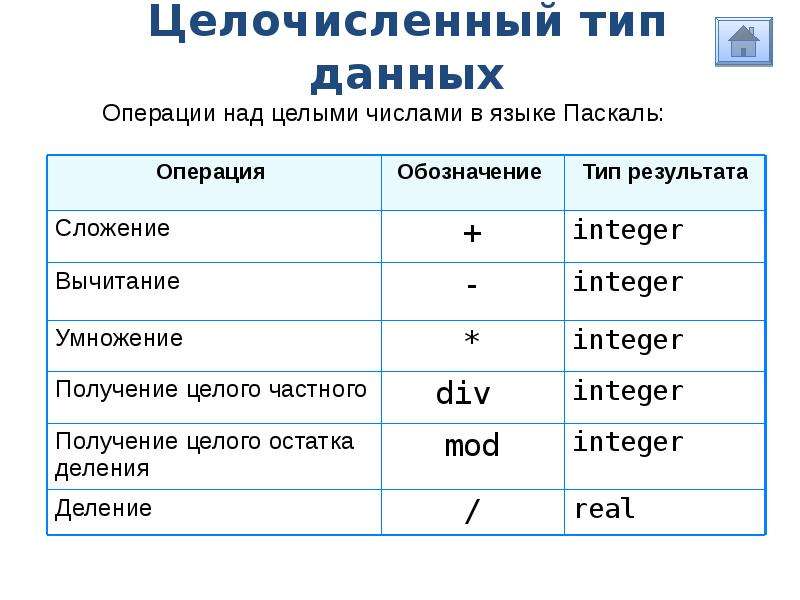 Таблица истинности для дизъюнкции:
Таблица истинности для дизъюнкции:
| A | B | A \/ B |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 1 |
Логическое отрицание. Инверсия
Инверсия (логическое отрицание, логическое «НЕ») получает из истинного высказывания ложное и, наоборот, из ложного – истинное. Например, высказывание «Москва – столица России» истинно, а данное высказывание, образованное с помощью логического отрицания («Москва – не столица России») – ложно. Ложное высказывание можно сделать истинным с помощью инверсии:
Операцию инверсии в булевой алгебре принято обозначать знаком « ¬ ». Операция логического отрицания, аргументом которой является логическая переменная А, записывается следующей формулой: ¬A. Результатом операции логического отрицания является Истина, когда аргумент Ложь, и значение Ложь, когда аргумент Истина. Таблица истинности для инверсии:
Результатом операции логического отрицания является Истина, когда аргумент Ложь, и значение Ложь, когда аргумент Истина. Таблица истинности для инверсии:
| A | ¬A |
|---|---|
| 0 | 1 |
| 1 | 0 |
Построение таблиц истинности логических выражений
Для каждого логического выражения можно построить таблицу истинности, которая определяет его истинность или ложность при всех возможных комбинациях исходных значений логических переменных. Алгоритм построения таблиц истинности:
Определить количество строк, которое равно количеству возможных комбинаций значений логических переменных, входящих в логическое выражение (если переменных n штук, то количество строк будет равно 2n). Еще одну строку стоит добавить для указания самих переменных, итого строк в таблице будет 2n + 1.

Определить количество столбцов, которое равно количеству логических переменных плюс количество логических операций. Это нужно для того, чтобы вычислять значение логического выражения поэтапно, последовательно выполняя все логические операции над исходными переменными.
Построить таблицу с указанным количеством столбцов и строк и внести всевозможные наборы логических переменных. Наборы входных переменных рекомендуется заполнять следующим образом:
разделить столбец значений первой переменной пополам и заполнить верхнюю часть колонки нулями, а нижнюю – единицами;
разделить столбец значений второй переменной на четыре части и заполнить четверти чередующимися группами нулей и единиц;
продолжать деление столбцов значений последующих переменных на 8, 16, 32 и т.д. частей.
Заполнить таблицу истинности по столбцам, выполняя базовые логические операции в необходимой последовательности и в соответствии с таблицей истинности.

Порядок выполнения логических операций, содержащих конъюнкцию, дизъюнкцию и инверсию
При определении значения сложных логических выражений стоит соблюдать строгий порядок выполнения входящих в выражение операций:
Инверсия
Конъюнкция
Дизъюнкция
Более сложные логические операции, о которых поговорим чуть позже.
Аналогично тому, как это делается в арифметике, приоритет выполнения логических операций можно менять с помощью скобок.
Например, у выражения A \/ B /\ (С \/¬D) будет следующий порядок действий:
2. (С \/¬D)
3. B /\ (С \/¬D)
4. A \/ B /\ (С \/¬D)
Алгебра логики в программировании — Умскул Учебник
На этой странице вы узнаете- Что не так с импликацией и эквиваленцией?
- Какое применение алгебра логики может найти в программировании?
В статье «Алгебра логики» мы выучили основы этого непростого раздела математики. Разобравшись в той теме, пора пойти дальше и заговорить на понятном компьютеру языке — языке программирования.
Разобравшись в той теме, пора пойти дальше и заговорить на понятном компьютеру языке — языке программирования.
| Мы говорили, что алгебра логики оперирует истиной и ложью, которым также могут соответствовать числа 1 и 0. В Python эта логика сохраняется. В нем есть логический тип данных bool, который может принимать значение True или False — истина и ложь соответственно. Последние также эквивалентны числам 1 и 0. |
Как логические операторы записываются в программе Python и в чем их отличие?
Логические операторы в Python мы уже упоминали в статье «Основы программирования. Часть 2». Давайте их вспомним:
| Что не так с импликацией и эквиваленцией? Проблема в том, что для импликации и эквиваленции нет специальных логических операторов, но для них можно использовать математические: Но несмотря на схожесть работы, это все еще математические операторы, из-за чего нарушается привычный приоритет. Так что в программе он будет следующим: |
Самый практичный совет по записи логических уравнений в программе — не стесняйтесь использовать скобки, если используете математические операторы.
Например:
- простое логическое уравнение только из конъюнкции, дизъюнкции и инверсии в лишних скобках не нуждается (кроме тех, конечно, что уже есть в уравнении):
- при появлении импликации и эквиваленции подключаем скобки, чтобы сохранить приоритет и этих, и других логических операторов:
| Какое применение алгебра логики может найти в программировании? Между программированием и алгеброй логики установлен довольно приятный союз: — С одной стороны, в больших и запутанных программах может быть много логических зависимостей, распутать которые поможет знание алгебры логики. |
Например, очень популярная задача алгебры логики — построение таблицы истинности. Давайте попробуем предположить, что нам может понадобиться, чтобы программа смогла это сделать?
Давайте попробуем предположить, что нам может понадобиться, чтобы программа смогла это сделать?
- Нужен перебор логических переменных по совсем небольшому диапазону — от 0 до 1.
- Правильно записанное логическое уравнение, чтобы проверить его при каждом наборе истины и лжи.
Вопрос встает только о конкретной реализации. Python — очень гибкий язык. Для разных формулировок задачи он может предложить разные инструменты, при использовании которых написание кода станет еще приятнее.
Начнем с обобщенной задачи — построение таблицы истинности. На этом примере можно показать, что математические операторы путают приоритет логических. Так что давайте составим таблицу истинности для уравнения A ≡ B ∧ C ⇒ A.
Перебор устроим с помощью вложенных циклов for. Они будут перебирать отдельные переменные, которые потом будут поставляться в логическое уравнение.
print("A B C")
for A in range(0, 2):
for B in range(0, 2):
for C in range(0, 2):
result = A == ((B and C) <= A)
print(A, B, C, result)
Вывод:
A B C
0 0 0 False
0 0 1 False
0 1 0 False
0 1 1 True
1 0 0 True
1 0 1 True
1 1 0 True
1 1 1 True
Мы заранее подписали каждый столбец, так что не запутаться в выводе будет проще.
Да, промежуточных результатов при такой реализации у нас нет. А зачем они нам? Нам важен итоговый результат — мы его получили.
У меня есть ощущение, что этот код не очень красивый. Он однозначно рабочий, но все-таки слишком много вложенных циклов. Как это можно решить?
В статье «Комбинаторика в информатике» мы обсуждали такую вещь, как модуль itertools, который содержит функции для работы с различными комбинациями. Как раз наш случай — мы используем различные комбинации 1 и 0

Сейчас нам пригодится функция product, которая создаст различные комбинации из указанных элементов. Изначально запишем их в отдельный массив для удобства:
from itertools import product
print("A B C")
d = [0, 1]
for i in product(d, repeat = 3):
A, B, C = i
result = A == ((B and C) <= A)
print(A, B, C, result)
Вывод:
A B C
0 0 0 False
0 0 1 False
0 1 0 False
0 1 1 True
1 0 0 True
1 0 1 True
1 1 0 True
1 1 1 True
Как видите, результат мы получили тот же, но смогли избавиться от некрасивого массива вложенных циклов. С еще большим количеством переменных в уравнении было бы нагляднее.
Пожалуй, стоит подробнее рассказать про строку:
A, B, C = i.
Мы точно знаем, что i — это массив с 3 элементами, так как мы изначально задали создание наборов длиной 3. Если указать перед ним ровно столько же переменных, им можно присвоить соответствующие элементы массива в одну строку.
Выше мы обсуждали, почему в этом уравнении обязательно должны быть скобки. Давайте докажем это. Построим таблицу истинности для того же уравнения, но не будем ставить скобки.
Давайте докажем это. Построим таблицу истинности для того же уравнения, но не будем ставить скобки.
from itertools import product
print("A B C")
d = [0, 1]
for i in product(d, repeat = 3):
A, B, C = i
result = A == B and C <= A
print(A, B, C, result)
Вывод:
A B C
0 0 0 True
0 0 1 False
0 1 0 False
0 1 1 False
1 0 0 False
1 0 1 False
1 1 0 True
1 1 1 True
Не вышло: итоговые значения таблиц истинности разные. Значит, приоритет действительно нарушается.
Другая наша возможная цель — проверить, будет ли выражение истинным всегда?
Как и в прошлый раз, у нас есть не один вариант реализации. Будем анализировать выражение А ∧ (В ∨ С) ≡ В.
Первый вариант:
- перебор всех наборов — вложенными циклами или с помощью product;
- сохранение всех результатов уравнения от каждого набора;
- проверка, чтобы ни одно значение не было ложным — для сохранения всех результатов можно использовать список.

from itertools import product
d = [0, 1]
all_results = []
for i in product(d, repeat = 3):
A, B, C = i
result = (A and (B or C)) == B
all_results.append(result)
if False not in all_results:
print("Функция полностью истинна")
else:
print("Функция истинна не всегда")
Вывод: Функция истинна не всегдаPython не был бы Python, если бы не дал нам возможность записать все практически в одну строку.
Второй вариант — функция all. Она возвращает True, если все значения внутри нее равны True — как раз наш случай. Чтобы записать программу максимально коротко, прямо внутри нее можно прописать и уравнение, и перебор его элементов:
from itertools import product
d = [0, 1]
result = all((A and (B or C)) == B for A, B, C in product(d, repeat = 3))
if result:
print("Функция полностью истинна")
else:
print("Функция истинна не всегда")
Здесь в переменную result записывается логическое значение True, если для всех наборов А, В, С из комбинаций d длиной 3 результат логического уравнения равен True. Если же среди всех результатов есть хоть один False — функция all даст нам False.
Если же среди всех результатов есть хоть один False — функция all даст нам False.
Для похожей задачи — чтобы не все значения уравнения были ложными — можно использовать функцию
from itertools import product
d = [0, 1]
result = any((A and (B or C)) == B for A, B, C in product(d, repeat = 3))
if result:
print("Функция не всегда ложна")
else:
print("Функция всегда ложна")
Вывод: Функция не всегда ложна
Python — гибкий язык. Если вам важнее видеть алгоритм работы кода более явно — используйте вложенные циклы, массивы для хранения значений и будьте более, чем на 100% уверены в каждом шаге. Если же вы хотите использовать дополнительные инструменты для сокращения объема кода и, как следствие, более быстрого его написания — вам в помощь комбинации product из itertools и инструменты массовой проверки all и any.
- Для импликации и эквиваленции в Python используются математические операторы сравнения, что немного нарушает их общий приоритет. Сохранить его можно с помощью скобок.
- Значения истины и лжи в Python являются логическим типом данных, который может принимать значение True или False и соответствует 1 и 0.
- Функция all проверяет, все ли переданные ей значения истинны. Функция any проверяет, есть ли среди всех переданных значений хоть одно истинное.
Задание 1.
Для выражения А ∨ В ∧ ¬(В ∧ А) выберите верную запись на языке Python (с сохранением порядка действий):
- A and B or not B or A
- A and B or not (B or A)
- A or B and not B and A
- A or B and not (B and A)
Задание 2.
Для выражения ¬А ⇒ В ≡ А ∧ В выберите верную запись на языке Python (с сохранением порядка действий):
- not (А <= В == А and В)
- not А <= В == (А and В)
- ((not A) <= B) == (A and B)
- (not А) <= (В == (А and В))
Задание 3.
Чему будет равен последний столбец таблицы истинности для уравнения:
A ∧ B ⇒ C ∧ D ∨ D ∧ A?
- 11101101
- 11101111
- 00000011
- 11000111
Задание 4.
Выберите уравнение, которое во всех случаях принимает значение истины:
- ¬(A ∧ B) ∧ ¬(C ∧ ¬A)
- ¬(A ∧ B) ∨ ¬(C ∧ ¬A)
- A ∧ B ∧ ¬(C ∧ ¬A)
- ¬(A ∧ B) ∨ ¬(C ∧ A)
Ответ: 1. — 4; 2. — 3; 3. — 1; 4. — 2.
Что такое оператор И в компьютерах?
Оператор И связывает фразы с помощью «и» в предложение. Например, «Джон и Джулия пошли в кино». Оператор возвращает истину, когда оба входных значения истинны. Так же, как тип значения 0x1, также известный как Boolean. Оставайтесь с нами, чтобы узнать больше об операторе И в информатике!
Что такое оператор И? Оператор И — это логический оператор, который сравнивает два значения и возвращает значение «истина», если оба значения истинны. И символ оператора « и ».
И символ оператора « и ».
Оператор AND обычно используется с логическими значениями, но его также можно использовать с другими типами данных, такими как числа и строки.
При использовании с логическими значениями оператор И возвращает значение true, если оба операнда имеют значение true, и значение false, если хотя бы один из операндов имеет значение false.
Таблица истинности для оператора AND показана ниже:
A B A AND B
—————————–
T T T
T F F
F T F
F F F
Как работает оператор И?«Операция И в компьютерах — это логический оператор, который возвращает ИСТИНА, если оба операнда ИСТИНА, и ЛОЖЬ в противном случае. Операнды могут быть логическими выражениями, переменными или константами».
В программировании оператор И — это логический оператор, который возвращает ИСТИНА, если оба операнда ИСТИНА, и ЛОЖЬ в противном случае. Операнды могут быть логическими выражениями, переменными или константами.
Например, выражение (A && B) вернет значение TRUE, только если оба значения A и B равны TRUE. Если либо A, либо B равно FALSE, то выражение вернет FALSE.
Каковы преимущества использования оператора И?Оператор И — это логический оператор, который позволяет вам комбинировать два или более условий для создания более точного поиска. Например, если вы ищете документы, в которых упоминаются как «кошки», так и «собаки», вы должны использовать оператор И между двумя терминами.
Преимущества использования оператора И заключаются в том, что он может помочь вам сузить результаты поиска и быстрее найти наиболее релевантную информацию. Это также может быть полезно при логическом поиске, когда вы пытаетесь найти документы, соответствующие определенным критериям.
Как я могу использовать оператор И на своем компьютере? Оператор AND — это логический оператор, который можно использовать в компьютерном программировании. Оператор AND принимает два логических значения и возвращает одно логическое значение, являющееся конъюнкцией двух входных значений. Другими словами, если оба входных значения истинны, то и выходное значение будет истинным. Если одно из входных значений ложно, то и выходное значение будет ложным.
Другими словами, если оба входных значения истинны, то и выходное значение будет истинным. Если одно из входных значений ложно, то и выходное значение будет ложным.
Оператор И может использоваться в компьютерном программировании по-разному. Например, его можно использовать для проверки того, верны ли оба условия, прежде чем предпринимать какие-либо действия. Его также можно использовать для объединения двух или более логических значений в одно составное логическое значение.
В большинстве языков программирования оператор И представлен символом && (два амперсанда).
ЗаключениеОператор И является одним из самых основных и важных операторов в компьютерном программировании. Он позволяет комбинировать два логических значения для получения одного выходного значения. Другими словами, он позволяет вам проверить, верны ли оба условия. Если вы только начинаете программировать, понимание оператора AND — отличный первый шаг.
Приложение Noon — это бесплатное образовательное онлайн-приложение для учащихся, которое делает процесс обучения увлекательным и интерактивным. С более чем 10 000 лекций, доступных в автономном режиме, вы можете легко учиться из любой точки мира. Кроме того, благодаря возможности найти учителей по всему миру вы можете настроить процесс обучения в соответствии со своими потребностями. И так, чего же ты ждешь? Загрузите приложение Noon прямо сейчас и начните учиться!
С более чем 10 000 лекций, доступных в автономном режиме, вы можете легко учиться из любой точки мира. Кроме того, благодаря возможности найти учителей по всему миру вы можете настроить процесс обучения в соответствии со своими потребностями. И так, чего же ты ждешь? Загрузите приложение Noon прямо сейчас и начните учиться!
java — Какая польза от & в языках программирования?
спросил
Изменено 11 лет, 10 месяцев назад
Просмотрено 3к раз
Я видел использование и во многих языках программирования, и, поскольку я очень люблю groovy, я попробовал следующий код, чтобы найти применение и :
a = 1; println a & 2
Я получаю вывод как 0 . Когда я меняю значения на , я получаю разные ответы.
Итак, кто-нибудь может сказать, в чем польза и в языках программирования, таких как Groovy, на простом английском, возможно, с простым примером на любом языке?
Заранее спасибо.
- Java
- отличный
и обычно представляют собой либо побитовое И (для целочисленных аргументов), либо логическое И без короткого замыкания (для логических аргументов).
bitwise-and возвращает серию битов (обычно представляемых как тип int ), которые имеют только биты в общем наборе
18 == 10010 6 == 00110 18 и 6 == 2 == 00010
Похоже, это то, что происходит в вашем коде Groovy. 1 и 2 == 0 , так как 1 и 2 не имеют общих битов.
Логика без короткого замыкания и аналогична && , но
if (f() && g()) // g вызывается, только если f возвращает false if (f() & g()) // g вызывается, даже если f возвращает false
В языках, допускающих перегрузку операторов, библиотеки иногда перегружали и для выполнения пересечения множеств или поэлементного битового пересечения.
При поиске «Groovy Operator» в Google первый результат дает: http://groovy.codehaus.org/Operators
В целом все операторы, поддерживаемые в Java, идентичны в Groovy.
Далее в http://download.oracle.com/javase/tutorial/java/nutsandbolts/operators.html:
побитовое И &
При поиске «Побитовое И» в Google первый результат: http://en.wikipedia.org/wiki/Bitwise_operation#AND
И
Побитовое И принимает два двоичных представления одинаковой длины и выполняет логическую операцию И над каждой парой соответствующих битов. Для каждой пары результат равен 1, если первый бит равен 1 И второй бит равен 1; в противном случае результат равен 0. Например:
0101 (десятичное число 5) И 0011 (десятичное число 3) = 0001 (десятичная 1)
это займет менее 5 минут.
Зарегистрируйтесь или войдите в систему
Зарегистрируйтесь с помощью Google Зарегистрироваться через Facebook Зарегистрируйтесь, используя электронную почту и парольОпубликовать как гость
Электронная почтаТребуется, но не отображается
Опубликовать как гость
Электронная почтаТребуется, но не отображается
Нажимая «Опубликовать свой ответ», вы соглашаетесь с нашими условиями обслуживания и подтверждаете, что прочитали и поняли нашу политику конфиденциальности и кодекс поведения.