Функции язык си: 13) Функции в Си — CoderLessons.com

Обработка ошибок в языке Си

24.11.2021 | Категория Программирование

В языке Си нет никакой нативной обработки ошибок, а значит приходится пользоваться всякими костылями, чтобы эту обработку ошибок сделать. Например, в задании на квадратные уравнения вы пользовались чем-то, похожим на это:

Оказывается, этот подход очень распространен в библиотечном коде проекта GNU. Например, если мы посмотрим на документацию функции `fopen(…)`

то есть, функция `fopen()` вернет:

• Указатель типа `FILE*`, если программа отработала верно 
• `NULL`, если во время выполнения возникла ошибка (например, файл который мы пытаемся открыть, не существует). Часть про `errno` пока что игнорируем.
  

А это значит, что обработка ошибок функции fopen должна происходить примерно вот так:

Файл `blabla.txt` я специально не создал, а значит, моя программа ожидаемо закончится с сообщением `something went wrong with fopen()!`.

Но бывают (почти всегда) ситуации, в которых об ошибке хочется знать чуть больше, чем просто то что она произошла. Тут и вступает в дело переменная `errno`, которая глобальная и определена во всех больших хедерах (в том числе в `stdlib.h` и `stdio.h`, но не в `string.h` — подумайте, почему). Где-то в недрах `errno.h` есть специальный массив строк под названием `sys_errlist`, к которому у вас, как у программиста, строго говоря, нет доступа. Строки в этом массиве — сообщения об ошибках, а `errno`, которая выставилась в результате ошибки — индекс в этом массиве, который указывает на описание ошибки, которая возникла. Существуют специальные функции, которые помогают вам выводить ошибки, например `perror()`. Перепишем наш код с обработкой ошибок через `perror()`

Теперь при ошибке, при открытии файла, вызовется функция `perror()`, она проверит чему равна переменная `errno`(которая, повторюсь, глобальная и хитро определена в заголовке как `stdio.h`, так и `errno.

h`), и она найдет нужное сообщение об ошибке, то есть `main: No such file or directory`. В данном случае, я посчитал, что ошибка критическая, поскольку любое продолжение программы приведет к Segmentation fault, поэтому после вывода сообщения об ошибке, программа завершается с кодом errno (что, в принципе, необязательно). Узнать что делает аргумент функции `perror()` остается заданием для читателя. Узнать это можно в man-страницах 😉

Более лаконично этот код записывается так:

а ЕЩЕ более лаконично

(Это решение плохо тем, что иногда в случае ошибки функции возвращают `NULL`, а иногда `-1` в случае ошибок, такие штуки ВСЕГДА надо проверять в man-страницах.)

Важные замечания:

• НЕ стоит проверять значение `errno` в случае успешного выполнения функции, потому что оно, строго говоря, не определено в этом случае (хотя, в большинстве случаев оно будет значения `Success`)
• Если у вас несколько функций подряд, которые используют errno, то проверять наличие ошибки нужно после КАЖДОЙ из них.

Есть ли альтернативы? Ну, пока не придумали. Даже язык Go, по идеологии внук языка Cи, страдает от постоянных

А этот язык сейчас один из самых популярных! (Хотя в Go2 придумали безумно интересный механизм обработки ошибок, кардинально отличающийся от того, что написано здесь и других прочих объектно-ориентированных exception-handling).

Существует механизм `SJLJ`, пользоваться которым без надобности не рекомендуется.

Берегите себя и пишите безопасный код 😉

Построение и решение графиков Функций

Понятие функции

Функция — это зависимость y от x, где x является независимой переменной или аргументом функции, а y — зависимой переменной или значением функции. Функция — это соответствие между двумя множествами, причем каждому элементу первого множества соответствует один и только один элемент второго множества.

Задать функцию значит определить правило, в соответствии с которым по значениям независимой переменной можно найти соответствующие значения функции. Вот, какими способами ее можно задать:

• Табличный способ — помогает быстро определить конкретные значения без дополнительных измерений или вычислений.

• Графический способ — наглядно.

• Аналитический способ — через формулы. Компактно, и можно посчитать функцию при произвольном значении аргумента из области определения.

• Словесный способ.

Область определения функции — это множество всех допустимых значений аргумента (переменной x). Геометрически — это проекция графика функции на ось Ох.

Например, для функции вида область определения выглядит так

Область значений функции — множество всех значений, которые функция принимает на области определения. Геометрически — это проекция графика функции на ось Оy.

Например, естественная область значений функции y = x² — это все числа больше либо равные нулю. Можно записать вот так: Е (у): [0; +∞).

Реши домашку по математике на 5.

Подробные решения помогут разобраться в самой сложной теме.

Понятие графика функции

Графиком функции y = f(x) называется множество точек (x; y), координаты которых связаны соотношением y = f(x). Само равенство y = f(x) называется уравнением данного графика.

График функции — это множество точек (x; y), где x — это аргумент, а y — значение функции, которое соответствует данному аргументу.

Проще говоря, график функции показывает множество всех точек, координаты которых можно найти, просто подставив в функцию любые числа вместо x.

Для примера возьмём самую простую функцию, в которой аргумент равен значению функции, то есть y = x.

В этом случае нам не придётся вычислять для каждого аргумента значение функции, так как они равны, поэтому у всех точек нашего графика абсцисса будет равна ординате.

Отметим любые три точки на координатной плоскости, например: L (-2; -2), M (0; 0) и N (1; 1).

Если мы последовательно от наименьшего значения аргумента к большему соединим отмеченные точки, то у нас получится прямая линия. Значит графиком функции y = x является прямая. На графике это выглядит так:

Надпись на чертеже y = x — это уравнение графика. Ставить надпись с уравнением на чертеже удобно, чтобы не запутаться при решении задач.

Важно отметить, что прямая линия бесконечна в обе стороны. Хоть мы и называем часть прямой графиком функции, на самом деле на чертеже изображена только малая часть графика.

Запоминаем!

Не обязательно делать чертеж на целый тетрадный лист, можно выбрать удобный для вас масштаб, который отразит суть задания.

Исследование функции

Важные точки графика функции y = f(x):

Стационарные точки — точки, в которых производная функции f(x) равна нулю.

Критические точки — точки, в которых производная функции f(x) равна нулю либо не существует. Стационарные точки являются подмножеством множества критических точек.

Экстремум в математике — максимальное или минимальное значение функции на заданном множестве. Точка, в которой достигается экстремум, называется

точкой экстремума. Соответственно, если достигается минимум — точка экстремума называется точкой минимума, а если максимум — точкой максимума.

Нули функции — это значения аргумента, при которых значение функции равно нулю.

Асимптота — прямая, которая обладает таким свойством, что расстояние от точки графика функции до этой прямой стремится к нулю при неограниченном удалении точки графика от начала координат. По способам их отыскания выделяют три вида асимптот: вертикальные, горизонтальные, наклонные.

Функция непрерывна в точке k, если предел функции в данной точке равен значению функции в этой точке:

Если функция f(x) не является непрерывной в точке x = a, то говорят, что f(x) имеет разрыв в этой точке

.

Если нам нужно построить график незнакомой функции, когда заранее невозможно представить вид графика, полезно применять схему исследования свойств функции. Она поможет составить представление о графике и приступить к построению по точкам.

Схема построения графика функции:

 

1. Найти область определения функции.

2. Найти область допустимых значений функции.

3. Проверить не является ли функция четной или нечетной.

4. Проверить не является ли функция периодической.

5. Найти точку пересечения с осью OY (если она есть).

6. Вычислить производную и найти критические точки, определить промежутки возрастания и убывания.

7. Промежутки знакопостоянства.

8. Асимптоты.

9. На основании проведенного исследования построить график функции.

Построение графика функции

Чтобы понять, как строить графики функций, потренируемся на примерах или воспользуйтесь онлайн тренажером.

Задача 1. Построим график функции

Как решаем:

Упростим формулу функции:

при х ≠ -1.

График функции — прямая y = x — 1 с выколотой точкой M (-1; -2).

Задача 2. Построим график функции

Как решаем:

Выделим в формуле функции целую часть:

График функции — гипербола, сдвинутая на 3 вправо по x и на 2 вверх по y и растянутая в 10 раз по сравнению с графиком функции

Задача 3. Построить графики функций:

а) y = 3x — 1

б) y = -x + 2

в) y = 2x

г) y = -1

Как решаем:

Воспользуемся методом построения линейных функций «по точкам».

а) y = 3x — 1

x	y
0	-1
1	2

Как видим, k = 3 > 0 и угол наклона к оси Ox острый, b = -1 — смещение по оси Oy.

б) y = -x + 2

x	y
0	2
1	1

k = -1 > 0 и b = 2 можно сделать аналогичные выводы, как и в первом пункте.

в) y = 2x

x	y
0	0
0	2

k = 2 > 0 — угол наклона к оси Ox острый, b = 0 — график проходит через начало координат.

г) y = -1

k = 0 — константная функция, прямая проходит через точку b = -1 и параллельно оси Ox.

Задача 4. По виду графика определить знаки коэффициентов общего вида функции y = ax² + bx + c.

 

Как решаем:

Вспомним, как параметры a, b и c определяют положение параболы.

1. Ветви вниз, следовательно, a < 0.

   Точка пересечения с осью Oy — c = 0.

   Координата вершины

2. Ветви вверх, следовательно, a > 0.

   Точка пересечения с осью Oy — c > 0.

   Координата вершины , т.к. неизвестное число при делении на положительное дает отрицательный результат, то это число отрицательное, следовательно, b > 0.

3. Ветви вниз, следовательно, a < 0.

   Точка пересечения с осью Oy — c > 0.

   Координата вершины , т. к. неизвестное число при делении на отрицательное дает в результате положительное, то это число отрицательное, следовательно, b < 0.

Задача 5. Построить графики функций:

а) y = x² + 1

б)

в) y = (x — 1)² + 2

г)

д)

Как решаем:

Построить графики можно при помощи элементарных преобразований.

Если построен график функции y = f(x), то при a > 0 следующие графики получаются с помощью сдвига графика f(x).

• y = f(x) + a — график функции y = f(x) сдвигается на a единиц вверх;

• y = f(x) − a — график функции y = f(x) сдвигается на a единиц вниз;

• y = f(x + a) — график функции y = f(x) сдвигается на a единиц влево;

• y = f(x − a) — график функции у = f(x) сдвигается на a единиц вправо.

Преобразование график по типу y = mf(x): y = f(x) → y = mf(x), где m — положительное число.

• Если m > 1, то такое преобразование графика называют растяжением вдоль оси y с коэффициентом m.

• Если m < 1, то такое преобразование графика называют сжатием к оси x с коэффициентом 1/m.

а)

Преобразование в одно действие типа f(x) + a.

y = x²

Сдвигаем график вверх на 1:

y = x² + 1

б)

Преобразование в одно действие типа f(x — a).

Сдвигаем график вправо на 1:

в) y = (x — 1)² + 2

В этом примере два преобразования, выполним их в порядке действий: сначала действия в скобках f(x — a), затем сложение f(x) + a.

y = x²

Сдвигаем график вправо на 1:

y = (x — 1)²

Сдвигаем график вверх на 2:

y = (x — 1)² + 2

г)

Преобразование в одно действие типа

y = cos(x)

Растягиваем график в 2 раза от оси ординат вдоль оси абсцисс:

д)

Мы видим три преобразования вида f(ax), f (x + a), -f(x).

Чтобы выполнить преобразования, посмотрим на порядок действий: сначала умножаем, затем складываем, а уже потом меняем знак. Чтобы применить умножение ко всему аргументу модуля в целом, вынесем двойку за скобки в модуле.

Сжимаем график в два раза вдоль оси абсцисс:

Сдвигаем график влево на 1/2 вдоль оси абсцисс:

Отражаем график симметрично относительно оси абсцисс:

Общие сведения о функциях — Видеоруководство по C

Из курса: C Essential Training

Понимание функций

“

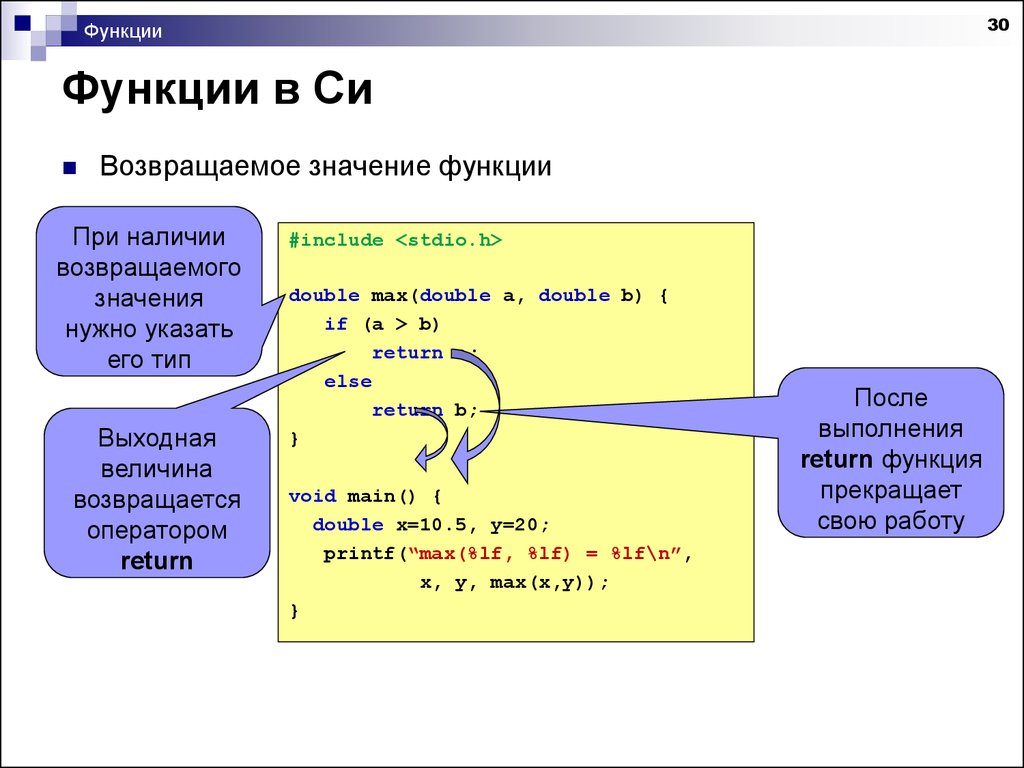
— [Инструктор] Можно написать код, в котором используются только ключевые слова языка C, но для реального программирования вы используете функцию. Функция — это машина программирования, которая что-то делает, например мини-программа. Функция может принимать входные данные, функция может генерировать выходные данные. Он может делать и то, и другое, или не может ни то, ни другое. Библиотека C поставляется с множеством встроенных функций. Они прототипированы в различных заголовочных файлах, но код функции хранится в библиотеках, смешанных с компоновщиком. Вы используете эти библиотечные функции, но вы также можете создавать свои собственные функции для выполнения определенных задач. Все программы на C имеют и используют по крайней мере одну функцию, главную функцию, с которой начинается выполнение кода. Как и все функции C, функция main имеет тип данных, такой же, как переменная. Тип данных сообщает, какое значение генерирует функция, если таковое имеется. Для основной функции она выводит целочисленное значение, установленное в строке семь оператором return. Тип данных функции и ее выходные данные должны совпадать. В этом упражнении показаны пять функций, каждая из которых относится к разным базовым типам. Функция valchar — это символьная функция, возвращающая символьное значение. Valint — целочисленная функция, возвращающая целое число. Valfloat возвращает значение с плавающей запятой. И valdouble возвращает значение двойной точности. Функция типа данных void, valvoid, ничего не возвращает, она недействительна. Независимо от типа функции C могут возвращать только одно значение. Ключевое слово return отправляет значение, которое может быть литералом, значением, хранящимся в переменной или возвращаемым из другой функции, обратно в вызывающий оператор. Основная функция возвращает свое значение операционной системе. Функции, принимающие входные данные, имеют значения, указанные в скобках. Они называются аргументами. Функция повтора в этом упражнении принимает один аргумент — целочисленное значение. Переменная R представляет это значение внутри функции. В строке 15 вызывается функция повтора. Его аргумент указан в скобках. Это может быть буквальное значение, переменная или выражение, но значение должно соответствовать типу данных аргумента функции.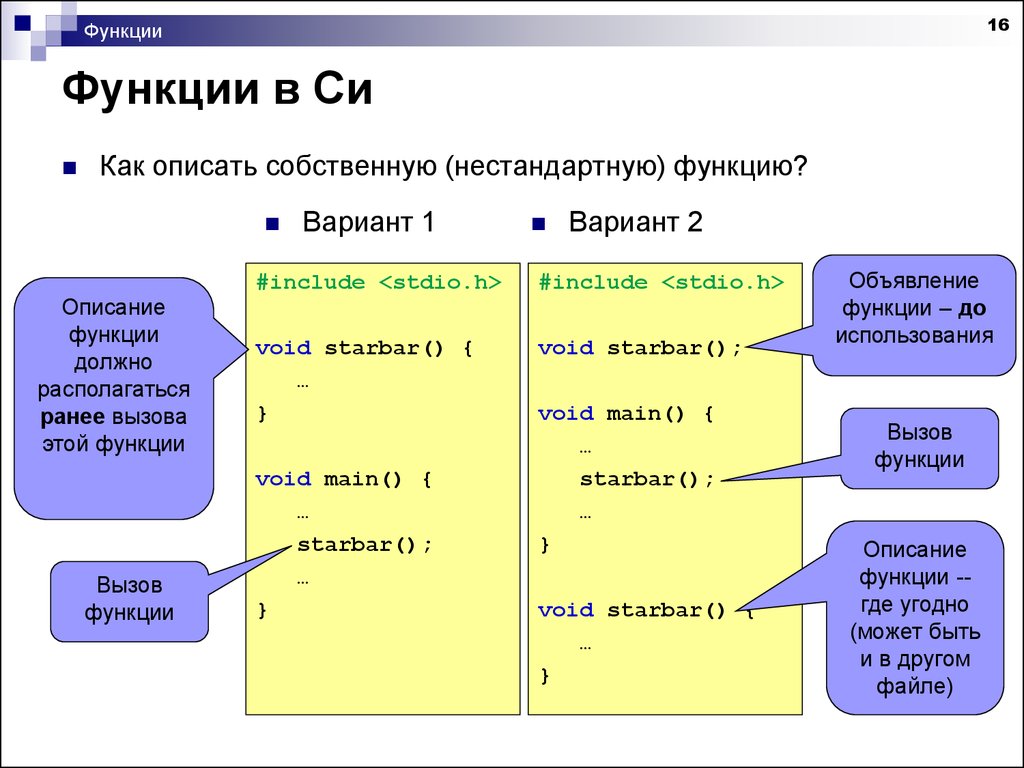 Целое число здесь. Функция может принимать любое количество аргументов или ни одного. Здесь функция total принимает пять аргументов, каждый из которых имеет тип данных и имя переменной. Функция вызывается в строке 17 в основной функции. Он вызывается внутри этой функции printf, которая разбита на несколько строк. Функция заголовка — это символьная функция. Он возвращает указатель, строку. Его аргумент недействителен, что означает, что у него нет аргумента. Он ничего не ожидает, поэтому вызов этой функции в строке 16 ничего не показывает в скобках. Значение, возвращаемое такой функцией, можно использовать немедленно, как здесь, в этом операторе printf, или оно может быть сохранено в другой переменной или даже отброшено. Внутрь или наружу или вообще никак. Вот как функции в C возвращают значения и обрабатывают аргументы.

Содержание

Функция, рекурсивное программирование, упражнения и решения на C

Категории Программирование на C Чтение: 3 мин. 15 января 2023 г. 9 марта 2016 г. В серии изучения программирования на C мы уже использовали многие функции по незнанию. Такие функции, как – printf() , scanf() , sqrt() , pow() или, что наиболее важно, функция main() . Каждая программа на C имеет по крайней мере одну функцию, то есть функцию main() .

Функция обеспечивает модульность нашей программы. Разделение программы на разные модули облегчает сопровождение, отладку и понимание кода.

Функции в программировании на C подразделяются на две категории: библиотечные функции и пользовательские функции. В этом упражнении мы сосредоточимся на определяемых пользователем функциях и научимся писать собственные функции.

Не стесняйтесь оставлять свои вопросы и предложения ниже в разделе комментариев. Я постараюсь помочь как можно скорее.

Необходимые знания

Основы программирования на C, функции, возврат значения из функции, рекурсия

Список упражнений по программированию функций и рекурсий

1. Напишите программу на C, чтобы найти куб любого числа с помощью функции.
2. Напишите программу на C для определения диаметра, длины окружности и площади круга с помощью функций.
3. Напишите программу на C, чтобы найти максимум и минимум между двумя числами с помощью функций.
4. Напишите программу на C, чтобы проверить, является ли число четным или нечетным, используя функции.
5. Напишите программу на C, чтобы проверить, является ли число простым, Армстронгом или совершенным числом, используя функции.
6. Напишите программу на C, чтобы найти все простые числа между заданным интервалом, используя функции.
7. Напишите программу на C для вывода всех сильных чисел между заданным интервалом с помощью функций.
8. Напишите программу на C для вывода всех чисел Армстронга между заданным интервалом с помощью функций.
9. Напишите программу на C для вывода всех совершенных чисел между заданным интервалом с помощью функций.
10. Напишите программу на C для нахождения степени любого числа с помощью рекурсии.
11. Напишите программу на C для вывода всех натуральных чисел от 1 до n с использованием рекурсии.
12. Напишите программу на C для вывода всех четных и нечетных чисел в заданном диапазоне с использованием рекурсии.
13. Напишите программу на C, чтобы найти сумму всех натуральных чисел от 1 до n с помощью рекурсии.
14. Напишите программу на C, чтобы найти сумму всех четных или нечетных чисел в заданном диапазоне, используя рекурсию.
15. Напишите программу на C, чтобы найти обратную сторону любого числа с помощью рекурсии.
16. Напишите программу на C, чтобы проверить, является ли число палиндромом или не использует рекурсию.
17. Напишите программу на C для нахождения суммы цифр заданного числа с помощью рекурсии.
18. Напишите программу на C для нахождения факториала любого числа с помощью рекурсии.