Деление в питоне: Остаток от деления в Python 3 и целая часть при делении

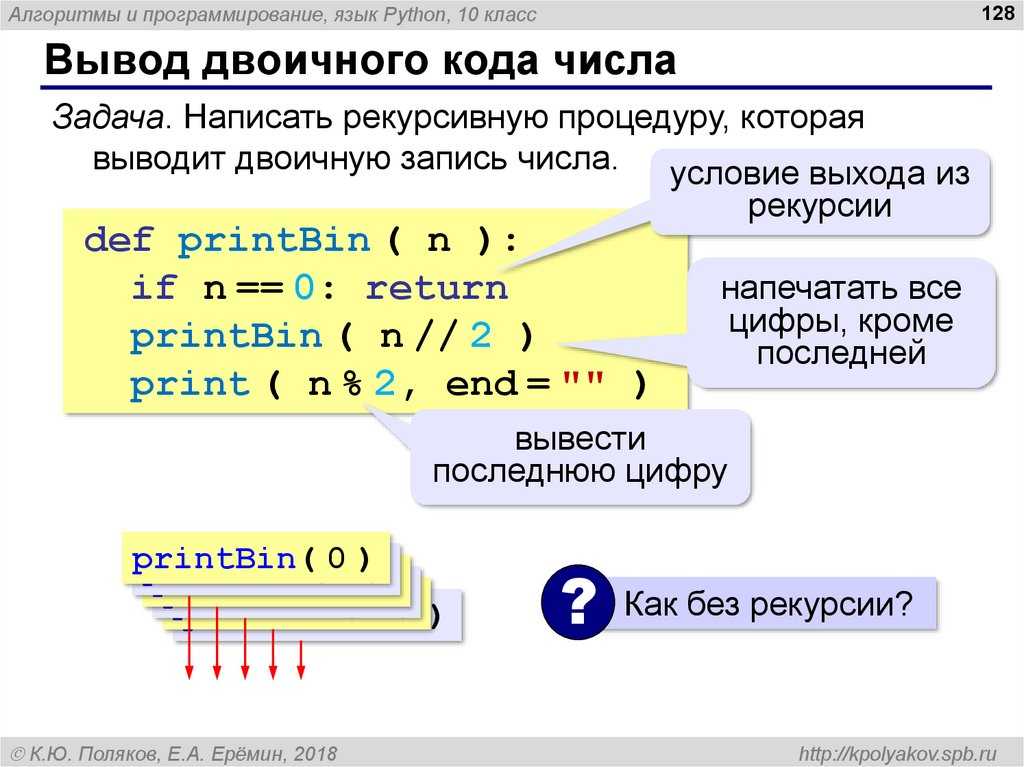
Остаток от деления в Python 3 и целая часть при делении

Python — популярный высокоуровневый язык программирования. Он обладает большим набором инструментов, имеет динамическую типизацию и используется для решения любых видов задач.

Деление в Python разделяется на три вида: обычное, целочисленное и взятие остатка. Программисту не нужно заботиться о типах операндов, Python сам определяет их и приводит результат к нужному виду. Как это делается, разберемся в этой статье.

Оператор деления

Деление в Python обозначается косой чертой «/». Примечательно, что результат в консоле всегда приводится к типу «float», даже если оба операнда были целочисленного типа, об этом свидетельствует появление «.0» у полученного значения.

Это появилось в 3-ей версии Python, ранее результатом деления целых чисел было только целое число, чтобы получить дробный результат, программисты явно указывали одному из операндов тип «float», в противном случае дробная часть просто отбрасывалась.

Важно понимать, что деление в Python, как и другие операции, работает медленнее, чем в более низкоуровневых языках программирования. Это связано с высоким уровнем автоматизации и абстракции, из-за динамической типизации интерпретатор вынужден приводить числа к дробному типу «float», который требует большего количества памяти.

Деление в представлении человека отличается от его представления в компьютере. Компьютер устроен так, что все арифметические операции могут выполняться только через сложение. Это значит, что быстрее всего выполняется сложение, затем вычитание, где необходимо менять знак операндов, умножение, где число складывается много раз. Деление выполняется дольше всех, потому что помимо многократно повторяющейся операции сложения необходимо также менять знак операндов, что требует больше памяти и действий.

Примеры:

print(int(1) / int(2))
print(5 / 5)
print(1 / 3)

0.5
1.0
0.3333333333333333

Из примера видно, что не смотря на то, что во всех случаях операция была между целыми числами, результатом деления в Python 3 является вещественное число.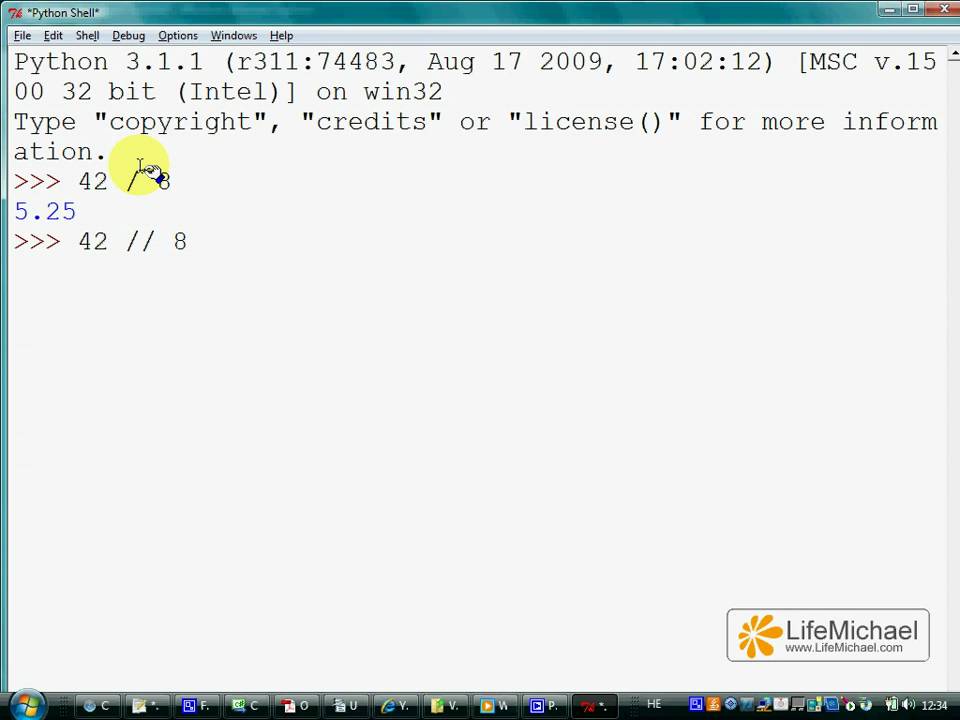 В первом случае мы даже специально использовали приведение к типу int.

Дополнительно хотелось бы отметить, что если точности типа данных float не достаточно, можно воспользоваться библиотекой decimal. В частности мы её использовали при написании программы «калькулятор» в отдельной статье.

Чтобы выполнить деление на цело в Python, можно воспользоваться целочисленным делением. В этом случае результатом будет целое число, без остатка. Целочисленное деление в Python обозначается двумя косыми чертами «//».

В отличие от других языков программирования Python позволяет результату целочисленного деления быть как целым (int), так и дробным (float) числом. В обоих случаях дробная часть отбрасывается и получается число с окончанием «.0».

Примеры нахождения целой части от деления:

print(5 // 2)
print(0 // 2)
print(1234 // 5.0)

2
0
246.0

В первых двух случаях деление осуществлялось между целыми числами. Поэтому в результате было получено целое число. В третьем примере одно из чисел вещественное. В этом случае в результате получаем так же вещественное число (типа float), после запятой у которого 0.

Для получения остатка от деления в Python 3 используется операция, обозначающаяся символом процента «%». Остаток — это оставшаяся после целочисленного деления часть числа. Операция взятия остатка используется для решения различных видов задач.

Примеры:

print(10 % 3)
print(5 % 10)
print(5 % 0.25)

1
5
0.0

Определение остатка от деления очень часто используется в программах для нахождения, допустим, чётных чисел. Или, например, если обработка данных выполняется в цикле, и нужно выводить в консоль сообщение о ходе обработки не каждый раз, а на каждой 10-ой итерации.

Вот пример вывода чётных чисел из списка в консоль:

example_list = [3, 7, 2, 8, 1, 12]
for value in example_list:
    if value % 2 == 0:
        print(value)

2
8
12

Проблемы чисел с плавающей точкой

Компьютер устроен так, что на аппаратном уровне понимает только две цифры: один и ноль.

Из-за этого при делении и других операциях с дробями часто возникают проблемы. Например, 1/10 в двоичном представлении является неправильной бесконечной дробью. Её нельзя написать полностью, поэтому приходится округлять, а выбор значения при округлении ограничен нулем и единицей.

Что говорить о делении, если ошибки возникают и при операции сложения. Если сложить число «0.1» с самим собой четырнадцать раз, то получиться 1.400…01. Откуда взялась эта единица? Она появилась при переводе числа из двоичного вида в десятичный.

a = 0.1
for i in range(13):
    a += 0.1
print(a)

1.4000000000000001

Более технически сложное деление приводит к подобным неточностям гораздо чаще. Обычно Python округляет результат так, что пользователь не замечает этой проблемы, но если получается достаточно длинное число, то проблема проявляется.

Деление комплексных чисел

Комплексные числа — это числа вида «a + b·i». Они занимают наивысшую ступень в иерархии чисел, арифметические операции над ними существенно отличаются от операций над обычными числами.

Деление комплексного числа на обычное меняет лишь длину радиус вектора, но не его направление.

Пример:

print((5 + 8j) / 2)

(2.5+4j)

Сокращенные операции деления

Чтобы упростить жизнь программистов, разработчики Python включили в язык «сокращенные операции». Их используют если надо выполнить операцию над переменной и полученный результат записать в эту же переменную.  То, что записывается в длинной форме, можно записать в более короткой по следующим правилам:

	Полная форма	Краткая форма
Деление	a = a / b	a /= b
Целая часть	a = a // b	a //=b
Остаток	a = a % b	a %= b

Приведём пример:

a = 245
a %= 17
print(a)

7

Деление на ноль

Если попробовать в Python выполнить деление на 0, то мы получим исключение ZeroDivisionError.

Исключение следует обрабатывать, это можно сделать так:

try:
    print(24 / 0)
except Exception as e:
    print(e)

division by zero

Но в этом случае мы обрабатываем все исключения. Зачастую так делать не совсем корректно. Мы знаем, что в нашем коде возможно деление на 0 и, чтобы отловить именно эту ошибку, следует заменить except Exception as e: на except ZeroDivisionError as e:.
Но можно и проверять перед выполнением операции, что делитель не равен 0. Например так:

a = 14
b = None
if a == 0:
    print('делитель равен нулю!')
else:
    b = 345/a
    print('Операция выполнена, результат = ' + str(b))

Операция выполнена, результат = 24.642857142857142

Как найти в Python остаток от деления?

Python — простой и современный язык для написания кода. В нем есть мощные библиотеки, которые могут оценивать любое выражение. Python — главный конкурент Matlab и Octave.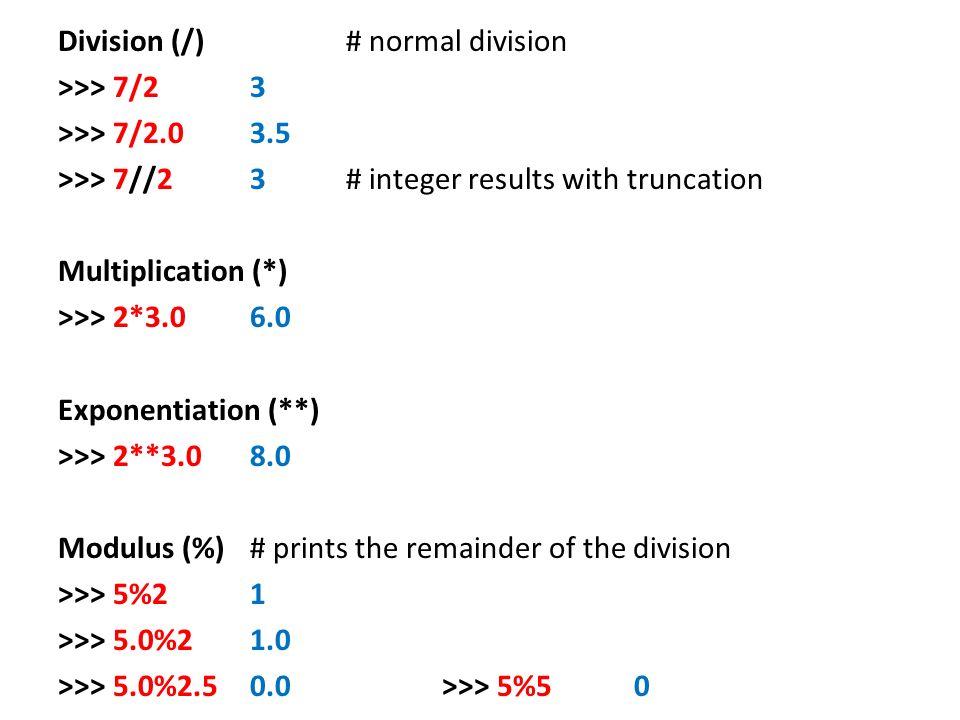 Запуская Python в интерактивном режиме, пользователь может легко найти оставшуюся часть раздела. Но это еще не все! Python может быть мощным калькулятором.

Понятие оператора

Чтобы легко найти остальную часть деления в Python, вам нужно понять некоторые определения. Оператор: знак или строка, позволяющая выполнять математические, побитовые, логические и другие вычисления. Выражения или числа, введенные пользователем для поиска остатка, комбинации или сравнения в Python 3, называются операндами.

Подразделяются на следующие типы операторов:

• операторы присваивания;
• арифметика;
• логические;
• сравнения;
• членство;
• личность.
• мало по малу;

Проще говоря, в примере «15-5» оператором является знак «-», операнды — 15 и 5. Это арифметическая операция с целыми числами. Если мы примем во внимание выражение «Истина и Истина», то здесь будет оператор «И», а операнды — «Истина» и «Истина». Этот пример можно отнести к логическому типу.

Целые и вещественные числа. Математические операции и вывод результата

Если мы рассматриваем математические операции над целыми и дробными числами, то это операторы +, -, *, /, **, //,%. С первыми тремя все понятно. Они обозначают соответственно сложение, вычитание, умножение. Оператор ** указывает на необходимость возведения в степень.

Одиночное (/) и двойное (//) деление различаются. Если первое дает действительное число в решении, второе необходимо, чтобы найти целую часть деления. Например, 9 // 4 = 2. Этот оператор соответствует функции div в Turbo Pascal. Но закономерность есть. Знак «/» напечатает целое число в результате, если и делитель, и делимое являются целыми числами. Чтобы найти остаток от деления в Python, вам нужно использовать оператор «%». По аналогии с тем же «Турбо Паскалем» «%» сравним с функцией мода. Например, 9% 2 = 1, то есть в Python остаток от деления в данном случае равен 1. Рассмотрим еще несколько примеров.

Для деления без остатка Python предлагает использовать функцию divmod (x, y). В этом случае x — делимое, y — делитель. Для divmod (9,3) программа выдает следующий результат (3,0). Это означает, что все деление равно 3, а остаток равен 0.

Математические операции могут выполняться без присвоения значения переменной. Затем результат выводится автоматически. Если ваш код содержит присвоение переменной, вы можете отобразить результат на экране с помощью оператора печати.

Модуль math

Для удобства пользователей разработчики предлагают мощный математический модуль, который может работать с любым типом чисел и выполнять дополнительные функции.

Для подключения библиотеки необходимо в начале кода программы написать следующую строку: import math. Эта команда позволит вам загрузить в программный код все функции, доступные в математическом модуле. Итак, чтобы подключить конкретный блок из библиотеки, нужно постоянно его регистрировать. Например, x = math.ceil (5.6).

Если программа будет часто использовать один и тот же блок, вы можете только импортировать его. Например, вам нужно округлить до ближайшего целого числа. Тогда код записывается следующим образом: из math import ceil или из math import *. В обоих случаях это не повлияет на дополнительный код округления.

Стандартные функции арифметики в Python

Чтобы вычислить остаток от целочисленного деления в Python, не всегда необходимо загружать математическую библиотеку. Некоторые функции интегрированы.

Интегрированные функции	Их цель	Примеры
целое число (х)	Преобразует действительное число в целое, т. Е. Дробная часть «усекается».	интервал (5.3) >>> 5 интервал (5.6) >>> 5 интервал (5,987) >>> 5
круглый (х)	Выражение округляется до ближайшего целого числа.	круглый (5,4) >>> 5,0 круглый (5,7) >>> 6,0 круглый (5. 5) >>> 6.0 круглый (5,987) >>> 6,0
круглый (х, п)	Используется для округления дробной части до n десятичных знаков	круглый (5.8776.2) >>> 5,88 круглый (5.9876.3) >>> 5,988
брюшной (х)	Найдите форму выражения	брюшной пресс (-7) >>> 7 брюшной пресс (7,8) >>> 7,8 абс (-66,55) >>> 66,55

Функции, для которых библиотека должна быть связана (сначала необходимо ввести из математического импорта *), показаны в следующей таблице.

Функции	Их цель
потолок (x)	Функция нужна для округления числа до большего целого числа («вверх»)
самолет (x)	Функция нужна для округления числа до наименьшего целого числа («вниз»)
квадрат (x)	Вычислить корень числа
регистр (х)	Требовалось найти логарифм. Если указать базу, расчет будет соответствующим.
а также	Возвращает основание натурального логарифма
грех (х)	Вычислить тригонометрические функции, где x в радианах
cos (x)
загар (х)
asin (х)
acos (x)
атан (х)
atan2 (х, у)	Найдите полярный угол точки, заданной x и y
градусы (x)	Требуется для преобразования угла из радиан в градусы
радианы (х)	Функция, необходимая для преобразования угла из градусов в радианы
пи	Печатает значение константы π

В качестве примера ниже приведен код, в котором используются математические операторы.

Результат отображается следующим образом.

В математическом модуле есть много других функций. Здесь перечислены наиболее распространенные.

Операторы деления

в Python — GeeksforGeeks

Операторы деления позволяют разделить два числа и вернуть частное, т. е. первое число или число слева делится на второе число или число справа и возвращает частное.

Существует два типа операторов деления:

(i)

Деление с плавающей запятой:  

Частное, возвращаемое этим оператором, всегда представляет собой число с плавающей запятой, независимо от того, являются ли два числа целыми. Например:

 >>>5/5
1,0
>>>10/2
5,0
>>>-10/2
-5,0
>>>20.0/2
10.0 

(ii)

Целочисленное деление (этажное деление): 

Частное, возвращаемое этим оператором, зависит от передаваемого аргумента. Если какое-либо из чисел является числом с плавающей запятой, он возвращает вывод в формате с плавающей запятой. Это также известно как деление на пол, потому что, если какое-либо число отрицательное, выход будет половинчатым. Например:

 >>>5//5
1
>>>3//2
1
>>>10//3
3 

Рассмотрим приведенные ниже инструкции в Python.

Python3

print ( 5 / / 2 ) print ( - 5 / / 2 )

Выход

 2
-3 

Выход:

 2
-3 

Первый вывод в порядке, но второй может удивить, если мы приближаемся к миру Java/C++. В Python оператор «//» работает как деление пола для аргументов с целыми числами и числами с плавающей запятой. Однако оператор деления ‘/’ всегда возвращает значение с плавающей запятой.

Примечание: Оператор «//» используется для возврата ближайшего целого числа, которое меньше или равно указанному выражению или значению. Таким образом, из приведенного выше кода 5//2 возвращает 2. Вы знаете, что 5/2 равно 2,5, а ближайшее целое число, меньшее или равное, равно 2[5//2]. (это обратно к обычной математике, в обычной математике значение равно 3).

Example

Python3

print ( 5.0 / 2 ) print ( - 5.0 / 2 )

Выход

 2,5
-2.5 

Реальный оператор разделения этажей — «//». Он возвращает минимальное значение как для целых аргументов, так и для аргументов с плавающей запятой.

Python3

print ( 5 / / 2 ) print ( - 5 / / 2 ) print ( 5.0 / / 2 ) print ( - 5.0 / / 2 )

Выход

 2
-3
2. 0
-3.0 

См. например.

Возможен ли оператор деления для логических значений?:

В Python оператор деления (/) не определен для логических значений. Если вы попытаетесь разделить два логических значения, вы получите TypeError.

Однако, если вы хотите перегрузить оператор деления для пользовательского класса с логическими значениями, вы можете определить специальный метод __truediv__. Вот пример:

Python

class MyClass:      def __init__( self , value):          self .value = Значение DEF __truediv __ ( Self , другие): Вернуть . 0034 MyClass( self .value and other.value)   a = MyClass( True ) b = MyClass ( False ) C = A / B

в этом примере. логический. Затем мы перегружаем оператор /, определяя метод __truediv__ для выполнения логической операции и над атрибутом значения двух экземпляров MyClass.

Когда мы вызываем a / b, вызывается метод __truediv__ с a в качестве первого аргумента и b в качестве второго аргумента. Метод возвращает новый экземпляр MyClass с атрибутом значения, который является логическим и имеет значения a.value и b. value.

Обратите внимание, что перегрузка оператора деления для логических значений не имеет смысла или пользы, поскольку деление не определено для логических значений в математике или в Python. Приведенный выше пример — просто демонстрация того, как перегрузить оператор в пользовательском классе.

Преимущества оператора деления:

Оператор деления (/) — это основной арифметический оператор в языках программирования, который выполняет операцию деления над числовыми значениями. Вот некоторые преимущества использования оператора деления:

1. Основные арифметические операции: Оператор деления — это одна из основных арифметических операций, которая используется в математике, технике и других областях. Он позволяет делить одно число на другое для выполнения вычислений, таких как вычисление среднего значения набора чисел или масштабирование значения.
2. Выразительный синтаксис : Оператор деления обеспечивает краткий и выразительный синтаксис для выполнения операций деления в коде. Вместо написания сложного выражения с несколькими арифметическими операциями вы можете использовать оператор деления для выполнения деления в одной строке кода.
3. Контроль точности: Оператор деления позволяет контролировать точность вычислений, используя различные типы данных или стратегии округления. Например, вы можете использовать деление с плавающей запятой (/) для вычисления десятичного частного или целочисленное деление (//) для вычисления усеченного частного.
4. Алгоритмическая эффективность: Оператор деления может использоваться для реализации эффективных алгоритмов численных вычислений, таких как умножение матриц, линейная алгебра и численное интегрирование. Используя оператор деления в этих алгоритмах, вы можете уменьшить количество арифметических операций и повысить производительность своего кода.
5. Математическое моделирование: Оператор деления используется в математическом моделировании и имитационном моделировании для представления взаимосвязей между переменными, такими как скорость изменения, скорость роста или вероятности. Используя оператор деления в этих моделях, вы можете моделировать и анализировать сложные системы и явления.

В целом оператор деления является мощным и универсальным оператором, предоставляющим широкий спектр преимуществ в программировании и математике.

Python Двойная косая черта (//) Оператор: Floor Division — LearnDataSci

Автор: Alfie Grace
Data Scientist

операторы

floor целочисленное деление ) с использованием оператора // . Этот оператор разделит первый аргумент на второй и округлит результат до ближайшего целого числа, что сделает его эквивалентным 9.0033 функция math.floor() .

См. краткий пример ниже:

 15 // 4 

То же, что:

 import math
math.floor(15 / 4) 

Результат обычного деления (с использованием оператора /) равен $\frac{15}{4} = 3,75$, но использование // уменьшило 3,75$ до 3$ $.

Результат обычного деления всегда число с плавающей запятой, тогда как если один из операндов является числом с плавающей запятой в делении пола , то результатом будет число с плавающей запятой.

Ниже показан пример этого:

 print("Обычное деление")
print(2 / 2, "\это число с плавающей запятой")
print("\nРазделение этажа")
print(15 // 4, "\это целое число")
print(15.0 // 4, "\tis a float.") 

Out:

 Обычное деление
1.0 — это число с плавающей запятой.
Разделение этажа
3 является инт.
3.0 - плавающий. 

Когда операнд отрицательный, деление на пол возвращает наибольшее целое число меньшее или равное результат обычного деления. Давайте используем те же операнды, что и раньше, чтобы показать, как это работает:

 печать(15/4)
печать (15 // 4)
print(-15 // 4) 

Выход:

 3,75
3
-4 

Глядя на результат обычного деления, когда оба числа положительны, $\frac{15}{4}=3,75$, деление по полу возвращает $3$, так как это наибольшее целое число, меньшее или равное $3,75$. Когда один из операндов отрицательный, результат нормального деления отрицательный ($-3,75$), поэтому наибольшее целое число, меньшее или равное, равно $-4$.

Мы рассмотрим, где разделение этажей может быть полезным, а также рассмотрим другие подходы, которые можно использовать для достижения аналогичных результатов.

При использовании Python вы часто будете сталкиваться с ошибками, когда функции несовместимы с числами с плавающей запятой. Например, допустим, вы хотите использовать функцию диапазона с частным из двух чисел:

 для значения в диапазоне (25/5):
    print(value) 

Out:

 ------------------------------------------------------- --------------------------------------------------
TypeError Traceback (последний последний вызов)
 в ()
----> 1 для значения в диапазоне (25/5):
      2 печать (значение)
TypeError: объект 'float' не может быть интерпретирован как целое число 

Чтобы наша программа работала правильно, нам нужно сначала преобразовать частное в целочисленный тип , чего мы можем добиться с помощью оператора // :

 для значения в диапазоне (25 // 5):
    печать(значение) 

Выход:

 0
1
2
3
4 

Другая область, в которой вы можете захотеть использовать оператор этажа, — это индексация списков:

 x = list(range(100))
x[len(x) / 10] 

Выход:

 -------------------------------------------------- ----------------------------------------
TypeError Traceback (последний последний вызов)
 в <модуле>
      1 х = список (диапазон (100))
      2
----> 3 х [длина (х) / 10]
TypeError: индексы списка должны быть целыми числами или срезами, а не числами с плавающей запятой 

Один из способов решить эту проблему — использовать оператор деления пола:

 x[len(x) // 10] 

Исходящий:

 10 

лучший вариант. В следующем разделе мы рассмотрим различные функции, которые могут дать аналогичный результат.

Иногда вы обнаружите, что работаете с наборами данных, которые содержат как целые числа, так и числа с плавающей запятой, например, если вы использовали беспорядочные данные.

При таких обстоятельствах // оператор выдаст противоречивые результаты, выводя как числа с плавающей запятой, так и целые числа. Таким образом, если ваша программа зависит от целых чисел, то использование оператора // потребует дополнительных шагов для обеспечения согласованного вывода.

Есть несколько других способов манипулирования частными двух чисел для правильной работы с вашей программой. Например, вы не всегда можете округлять значение в меньшую сторону, поэтому использование различных подходов может дать вам больший контроль над результатами.

math.floor() дает тот же результат, что и оператор деления пола, округляя аргумент до ближайшего целого числа.

Одним существенным отличием использования math.floor() является то, что он всегда выводит целое число, независимо от типа входных данных. При работе как с целыми числами, так и с числами с плавающей запятой math.floor() более полезен, поскольку обеспечивает более согласованный вывод.

Ниже показано, как мы можем вычислить результат обычного деления:

 импорт математики
math.floor(15 / 4) 

Как и при использовании оператора Floor, math.floor по-прежнему будет округлять в меньшую сторону, когда ввод отрицательный.

В качестве альтернативы math.floor() мы также можем использовать math.ceil() , который всегда будет округлять до ближайшего целого числа, а не вниз.

Например:

 math.ceil(15 / 4) 

Подобно math. floor , math.ceil всегда выводит результат в виде целого числа, независимо от типов данных аргументов. math.ceil будет округлять отрицательные числа в большую сторону, поэтому math.ceil(-15 / 4) даст в результате -3 .

Для быстрого исправления можно преобразовать float в int . Передача числа с плавающей запятой в int() приводит к целому числу, в котором все обрезается после десятичного числа входного числа с плавающей запятой.

В следующем примере $\frac{15}{4}=3,75$, но приведение к целому числу отрезает $.75$:

 int(15 / 4) 

int() работает аналогично math.floor() , за исключением того, что int() эффективно округляет отрицательные числа вверх, а не вниз:

 print(math. floor(-15 / 4))
печать (целое (-15 / 4)) 

Выход:

 -4
-3 

В качестве альтернативы математическим функциям мы также можем использовать round() для округления значений и последующего вывода результата в виде целого числа.

Отличие от round() заключается в том, что будет использоваться обычное округление, т. е. любое десятичное число .5 и больше округляется в большую сторону.

Ниже показано использование round() :

 round(3.5) 

Мы также можем указать, до скольких десятичных знаков следует округлить ввод.

Пример ниже показывает, как можно округлить результат деления 15 на 4 ( 3,75 ) до 1 десятичной цифры: Добавление 1 после запятой сообщает, что мы хотели бы, чтобы результат имел 1 десятичную точку, но мы могли бы использовать любое число.