отрицательное число
Отрицательное число — это число, указывающее на противоположное. Если положительное число — это расстояние вверх, то отрицательное — это расстояние вниз. Если положительное число — это расстояние справа, то отрицательное — это расстояние слева. Если положительное число — это депозит на банковский счет, то отрицательное число — это снятие средств с этого банковского счета. Если положительное число — это количество минут в будущем, то отрицательное число — это количество минут в прошлом. Если положительное число означает сложение, то отрицательное — вычитание.
Счетные числа (1, 2, 3 и т.д.) — это все положительные числа. Положительные числа, отрицательные числа и вместе взятое нулевое число называются «знаковыми числами» или целыми числами.
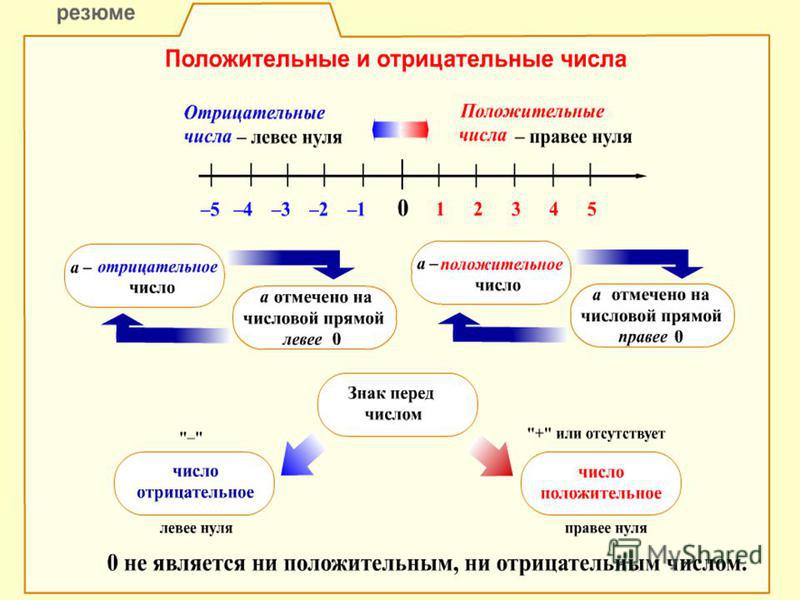
Число ноль не является ни положительным, ни отрицательным. Ноль — это его собственная противоположность, то есть +0 = -0. То есть нулевой шаг вправо — это то же самое, что нулевой шаг влево.
Отрицательное число всегда меньше нуля.
Отрицательное число записывается путем проставления знака минуса «-» перед положительным числом. Например, 3 — положительное число, а -3 — отрицательное. Оно читается как «отрицательная тройка» или «минус тройка»; это означает противоположность знаку 3.
Отрицательные числа в числовой строке оставляют ноль. Число и его противоположность всегда находятся на одном и том же расстоянии от нуля. Отрицательное число -3 находится слева от нуля, а 3 справа от нуля:
Иногда для выделения мы пишем пару противоположных чисел как -3 и +3.
Число и его противоположность всегда складываются к нулю. Таким образом, сумма -3 и +3 равна 0. Можно записать это либо как -3 + 3 = 0, либо как 3 + (- 3) = 0. Кроме того, число и его противоположность говорят, что «аннулируют друг друга».
арифметика с отрицательными числами
- Добавление отрицательного числа к чему-то — это то же самое, что и вычитание положительного числа из него. Например, прибавление отрицательного числа «-1» к числу «9» равнозначно вычитанию одного из девяти.
В символах:
В символах:9 + (−1) = 9 − 1 = 8
- Вычитание отрицательного числа из чего-то — то же самое, что и добавление к нему положительного числа. Например, вычитание отрицательного числа «-8» из числа «6» равнозначно сложению числа «6» и числа «8». В символах:
6 − (−8) = 6 + 8 = 14
- Отрицательное число, умноженное на другое отрицательное число, дает положительное число. Например, умножить отрицательное число «-3» на отрицательное число «-2» то же самое, что умножить число «3» на число «2». В символах:
(−3) × (−2) = 3 × 2 = 6
- Отрицательное число, умноженное на положительное, дает отрицательное число. Например, умножение отрицательного числа «-4» на положительное число «5» аналогично умножению числа «4» на число «5», но ответ отрицательный. В символах:
(−4) × 5 = −(4 × 5) = −20
Использование отрицательных чисел
Когда человек беден, люди иногда говорят, что у него отрицательная сумма денег.
Автор
Alegsaonline.com — отрицательное число — Leandro Alegsa — 2020-11-18 21:36:32 — url: https://ru.alegsaonline.com/art/69018Библиографические ссылки
— www.mathleague.com — Math league website discussion of negative numbers- www.purplemath.com — Purple Math website about negative numbersИСТОРИЯ ВОЗНИКНОВЕНИЯ ОТРИЦАТЕЛЬНЫХ И ПОЛОЖИТЕЛЬНЫХ ЧИСЕЛ
- Авторы
- Руководители
- Файлы работы
- Наградные документы
Семенов Д.У. 1
1
Джамбаева Ф.Н. 1
1
Автор работы награжден дипломом победителя III степени
Диплом школьникаСвидетельство руководителя
Текст работы размещён без изображений и формул.
Полная версия работы доступна во вкладке «Файлы работы» в формате PDF
Мир чисел очень загадочен и интересен.
В прошлом году на уроках математики мы начали изучать тему «Положительные и отрицательные числа». У меня возник вопрос, когда возникли отрицательные числа, в какой стране, какие ученые занимались этим вопросом. В Википедии я прочитал, что отрицательное число — элемент множества отрицательных чисел, которое (вместе с нулём) появилось в математике при расширении множества натуральных чисел. Цель расширения: обеспечить выполнение операции вычитания для любых чисел. В результате расширения получается множество (кольцо) целых чисел, состоящее из положительных (натуральных) чисел, отрицательных чисел и нуля.
В итоге я решил исследовать историю возникновения отрицательных чисел.
Целью данной работы является исследование истории возникновения отрицательных и положительных чисел.
Объект исследования — отрицательные числа и положительные числа
История положительных и отрицательных чисел
Люди долго не могли привыкнуть к отрицательным числам. Отрицательные числа казались им непонятными, ими не пользовались, просто не видели в них особого смысла. Эти числа появились значительно позже натуральных чисел и обыкновенных дробей.
Первые сведения об отрицательных числах встречаются у китайских математиков во II в. до н. э. и то, были известны лишь правила сложения и вычитания положительных и отрицательных чисел; правила умножения и деления не применялись.
Положительные количества в китайской математике называли «чен», отрицательные – «фу»; их изображали разными цветами: «чен» — красным, «фу» — черным. Это можно заметить в книге «Арифметика в девяти главах» (Автор Чжан Цань).
Такой способ изображения использовался в Китае до середины XII столетия, пока Ли Е не предложил более удобное обозначение отрицательных чисел – цифры, которые изображали отрицательные числа, перечеркивали черточкой наискось справа налево.
Лишь в VII в. индийские математики начали широко использовать отрицательные числа, но относились к ним с некоторым недоверием. Бхасхара прямо писал: «Люди не одобряют отвлеченных отрицательных чисел…». Вот как индийский математик Брахмагупта излагал правила сложения и вычитания: «имущество и имущество есть имущество, сумма двух долгов есть долг; сумма имущества и нуля есть имущество; сумма двух нулей есть нуль… Долг, который отнимают от нуля, становится имуществом, а имущество – долгом. Если нужно отнять имущество от долга, а долг от имущества, то берут их сумму». «Сумма двух имуществ есть имущество».
(+х) + (+у) = +(х + у) (-х) + (-у) = — (х + у)
(-х) + (+у) = — (х — у) (-х) + (+у) = +(у — х)
0 – (-х) = +х 0 – (+х) = -х
Индийцы называли положительные числа «дхана» или «сва» (имущество), а отрицательные – «рина» или «кшайя» (долг).
Индийские ученые, стараясь найти и в жизни образцы такого вычитания, пришли к толкованию его с точки зрения торговых расчетов. Если купец имеет 5000 р. и закупает товара на 3000 р., у него остается 5000 — 3000 = 2000, р. Если же он имеет 3000 р., а закупает на 5000 р., то он остается в долгу на 2000 р. В соответствии с этим считали, что здесь совершается вычитание 3000 — 5000, результатом же является число 2000 с точкой наверху, означающее «две тысячи долга». Толкование это носило искусственный характер, купец никогда не находил сумму долга вычитанием 3000 — 5000, а всегда выполнял вычитание 5000 — 3000.
Чуть позже в Древней Индии и Китае догадались вместо слов «долг в 10 юаней» писать просто «10 юаней», но рисовать эти иероглифы черной тушью. А знаков «+» и «–» в древности не было ни для чисел, ни для действий.
Греки тоже поначалу знаков не использовали. Древнегреческий ученый Диофант вообще не признавал отрицательные числа, и если при решении уравнения получался отрицательные корень, то он отбрасывал его как «недоступный».
Правила действий с положительными и отрицательными числами были предложены уже в III веке в Египте. Введение отрицательных величин впервые произошло у Диофанта. Он даже использовал специальный символ для них. В то же время Диофант употребляет такие обороты речи, как «Прибавим к обеим сторонам отрицательное», и даже формулирует правило знаков: «Отрицательное, умноженное на отрицательное, дает положительное, тогда как отрицательное, умноженное на положительное, дает отрицательное».
В Европе отрицательными числами начали пользоваться с XII–XIII вв., но до XVI в. большинство ученых считали их «ложными», «мнимыми» или «абсурдными», в отличие от положительных чисел – “истинных”. Положительные числа так же толковались как «имущество», а отрицательные – как «долг», «недостача».
Признанию отрицательных чисел способствовали работы французского математика, физика и философа Рене Декарта. Он предложил геометрическое истолкование положительных и отрицательных чисел – ввел координатную прямую.
(1637 г.).
Положительные числа изображаются на числовой оси точками, лежащими вправо от начала 0, отрицательные – влево. Геометрическое истолкование положительных и отрицательных чисел способствовало к их признанию.
В 1544 году немецкий математик Михаил Штифель впервые рассматривает отрицательные числа как числа, меньшие нуля (т. е. « меньшие, чем ничто »). С этого момента отрицательные числа рассматриваются уже не как долг, а совсем по-новому. Сам Штифель писал: «Нуль находится между истинными и абсурдными числами…»
Почти одновременно со Штифелем защищал идею отрицательных чисел Бомбелли Раффаэле (около 1530—1572), итальянский математик и инженер, переоткрывший сочинение Диофанта.
Так же и Жирар считал отрицательные числа вполне допустимыми и полезными, в частности, для обозначения недостачи чего-либо.
Всякий физик постоянно имеет дело с числами: он всегда что-то измеряет, вычисляет, рассчитывает. Везде в его бумагах — числа, числа и числа. Если приглядеться к записям физика, то обнаружится, что при записи чисел он часто использует знаки «+» и «-«. (Например: термометр, шкала глубин и высот)
Только в начале XIX в. теория отрицательных чисел закончила свое развитие, и «абсурдные числа» получили всеобщее признание.
Определение понятия числа
В современном мире человек постоянно пользуется числами, даже не задумываясь об их происхождении. Без знания прошлого нельзя понять настоящее. Число является одним из основных понятий математики. Понятие числа развивалось в тесной связи с изучением величин; эта связь сохраняется и теперь. Во всех разделах современной математики приходится рассматривать разные величины и пользоваться числами.
Число — абстракция, используемая для количественной характеристики объектов. Возникнув ещё в первобытном обществе из потребностей счёта, понятие числа изменялось и обогащалось и превратилось в важнейшее математическое понятие.
Существует большое количество определений понятию «число».
Первое научное определение числа дал Евклид в своих «Началах», которое он, очевидно, унаследовал от своего соотечественника Эвдокса Книдского (около 408 – около 355 гг. до н. э.): «Единица есть то, в соответствии с чем каждая из существующих вещей называется одной. Число есть множество, сложенное из единиц». Так определял понятие числа и русский математик Магницкий в своей «Арифметике» (1703 г.). Еще раньше Евклида Аристотель дал такое определение: «Число есть множество, которое измеряется с помощью единиц». В своей «Общей арифметике» (1707 г) великий английский физик, механик, астроном и математик Исаак Ньютон пишет: «Под числом мы подразумеваем не столько множество единиц, сколько абстрактное отношение какой-нибудь величины к другой величине такого же рода, взятой за единицу.
Число бывает трех видов: целое, дробное и иррациональное. Целое число есть то, что измеряется единицей; дробное – кратной частью единицы, иррациональное – число, не соизмеримое с единицей».
Мариупольский математик С.Ф.Клюйков также внес свой вклад в определение понятия числа: «Числа – это математические модели реального мира, придуманные человеком для его познания». Он же внес в традиционную классификацию чисел так называемые «функциональные числа», имея в виду то, что во всем мире обычно именуют функциями.
Натуральные числа возникли при счете предметов. Об этом я узнала в 5 классе. Затем я узнала, что потребность человека измерять величины не всегда выражается целым числом. После расширения множества натуральных чисел до дробных стало возможным делить любое целое число на другое целое число (за исключением деления на нуль). Появились дробные числа. Вычитать же целое число из другого целого числа, когда вычитаемое больше уменьшаемого, долгое время казалось невозможным.
Интересным для меня оказался тот факт, что долгое время многие математики не признавали отрицательных чисел, считая, что им не соответствуют какие-либо реальные явления.
Происхождение слов «плюс» и «минус»
Термины произошли от слов plus – «больше», minus – «меньше». Сначала действия обозначали первыми буквами p; m. Многие математики предпочитали или Возникновение современных знаков «+», «–» не совсем ясно. Знак «+», возможно, происходит от сокращенной записи et, т.е. «и». Впрочем, может быть он возник из торговой практики: проданные меры вина отмечались на бочке «–», а при восстановлении запаса их перечеркивали, получался знак «+».
Италии ростовщики, давая деньги в долг, ставили перед именем должника сумму долга и черточку, вроде нашего минуса, а когда должник возвращал деньги, зачеркивали ее, получалось что-то вроде нашего плюса.
Современные знаки «+» и появились в Германии в последнее десятилетие XVв. в книге Видмана, которая была руководством по счету для купцов (1489г.). Чех Ян Видман уже писал «+» и «–» для сложения и вычитания.
Чуть позднее немецкий ученый Михель Штифель написал «Полную Арифметику», которая была напечатана в 1544 году. В ней встречаются такие записи для чисел: 0-2; 0+2; 0-5; 0+7. Числа первого вида он назвал «меньше, чем ничего» или «ниже, чем ничего». Числа второго вида назвал «больше, чем ничего» или «выше, чем ничего». Вам, конечно, понятны эти названия, потому что «ничего» – это 0.
Отрицательные числа в Египте
Однако, не смотря на такие сомнения, правила действий с положительными и отрицательными числами были предложены уже в III веке в Египте. Введение отрицательных величин впервые произошло у Диофанта.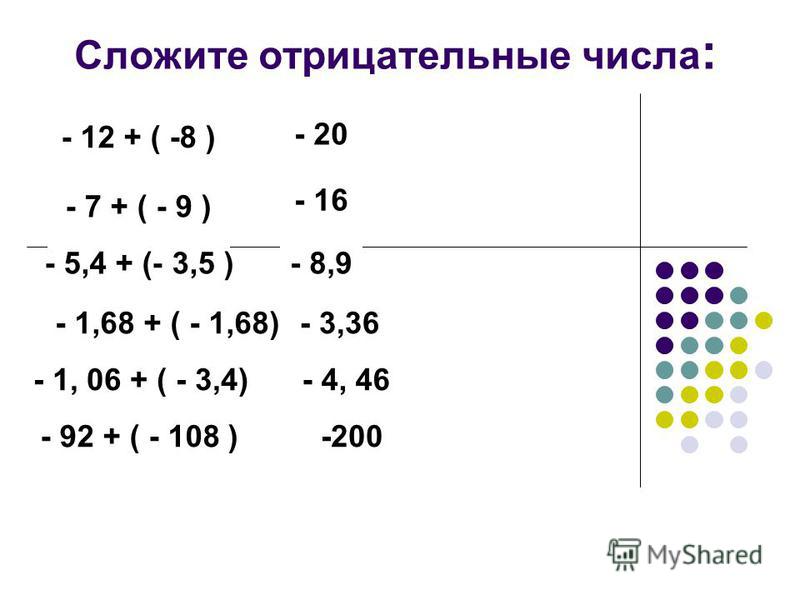
Он даже использовал специальный символ для них (сейчас мы в этом качестве используем знак «минус»). Правда, ученые спорят, обозначал ли символ Диофанта именно отрицательное число или просто операцию вычитания, потому что у Диофанта отрицательные числа не встречаются изолированно, а только в виде разностей положительных; и в качестве ответов в задачах он рассматривает только рациональные положительные числа. Но в то же время Диофант употребляет такие обороты речи, как «Прибавим к обеим сторонам отрицательное», и даже формулирует правило знаков: «Отрицательное, умноженное на отрицательное, дает положительное, тогда как отрицательное, умноженное на положительное, дает отрицательное» (то, что сейчас обычно формулируют: «Минус на минус дает плюс, минус на плюс дает минус»).
(–) (–) = (+), (–) (+) = (–).
Отрицательные числа в Древней Азии
Положительные количества в китайской математике называли «чен», отрицательные – «фу»; их изображали разными цветами: «чен» — красным, «фу» — черным.
Такой способ изображения использовался в Китае до середины XII столетия, пока Ли Е не предложил более удобное обозначение отрицательных чисел – цифры, которые изображали отрицательные числа, перечеркивали черточкой наискось справа налево. Индийские ученые, стараясь найти и в жизни образцы такого вычитания, пришли к толкованию его с точки зрения торговых расчетов.
Если купец имеет 5000 р. и закупает товара на 3000 р., у него остается 5000 — 3000 = 2000, р. Если же он имеет 3000 р., а закупает на 5000 р., то он остается в долгу на 2000 р. В соответствии с этим считали, что здесь совершается вычитание 3000 — 5000, результатом же является число 2000 с точкой наверху, означающее «две тысячи долга».
Толкование это носило искусственный характер, купец никогда не находил сумму долга вычитанием 3000 — 5000, а всегда выполнял вычитание 5000 — 3000. Кроме того, на этой основе можно было с натяжкой объяснить лишь правила сложения и вычитания «чисел с точками», но никак нельзя было объяснить правила умножения или деления.
В V-VI столетиях отрицательные числа появляются и очень широко распространяются в индийской математике. В Индии отрицательные числа систематически использовали в основном так, как это мы делаем сейчас. Индийские математики используют отрицательные числа с VII в. н. э.: Брахмагупта сформулировал правила арифметических действий с ними. В его произведении мы читаем: « имущество и имущество есть имущество, сумма двух долгов есть долг; сумма имущества и нуля есть имущество; сумма двух нулей есть нуль… Долг, который отнимают от нуля, становится имуществом, а имущество – долгом. Если нужно отнять имущество от долга, а долг от имущества, то берут их сумму».
Индийцы называли положительные числа «дхана» или «сва» (имущество), а отрицательные – «рина» или «кшайя» (долг). Впрочем, и в Индии с пониманием и принятием отрицательных чисел были проблемы.
Отрицательные числа в Европе
Не одобряли их долго и европейские математики, потому что истолкование «имущество-долг» вызывало недоумения и сомнения.
В самом деле, как можно «складывать» или «вычитать» имущества и долги, какой реальный смысл может иметь «умножение» или «деление» имущества на долг? (Г.И. Глейзер, История математики в школе IV-VI классы. Москва, Просвещение, 1981)
Вот почему с большим трудом завоевали себе место в математике отрицательные числа. В Европе к идее отрицательного количества достаточно близко подошел в начале XIII столетия Леонардо Фибоначчи Пизанский, однако в явном виде отрицательные числа применил впервые в конце XV столетия французский математик Шюке. Автор рукописного трактата по арифметике и алгебре «Наука о числах в трёх частях». Символика Шюке приближается к современной (Математический энциклопедический словарь. М., Сов. энциклопедия, 1988)
Современное истолкование отрицательных чисел
В 1544 году немецкий математик Михаил Штифель впервые рассматривает отрицательные числа как числа, меньшие нуля (т.
е. « меньшие, чем ничто »). С этого момента отрицательные числа рассматриваются уже не как долг, а совсем по-новому. Сам Штифель писал: «Нуль находится между истинными и абсурдными числами…» (Г.И. Глейзер, История математики в школе IV-VI классы. Москва, Просвещение, 1981)
После этого Штифель полностью посвящает свою работу математике, в которой он был гениальным самоучкой. Один из первых в Европе после Николы Шюке начал оперировать отрицательными числами.
Знаменитый французский математик Рене Декарт в «Геометрии» (1637 год) описывает геометрическое истолкование положительных и отрицательных чисел; положительные числа изображаются на числовой оси точками, лежащими вправо от начала 0, отрицательные – влево. Геометрическое истолкование положительных и отрицательных чисел привело к более ясному пониманию природы отрицательных чисел, способствовало их признанию.
Почти одновременно со Штифелем защищал идею отрицательных чисел Р.
Бомбелли Раффаэле (около 1530—1572), итальянский математик и инженер, переоткрывший сочинение Диофанта.
Бомбелли и Жирар, напротив, считали отрицательные числа вполне допустимыми и полезными, в частности, для обозначения недостачи чего-либо. Современное обозначение положительных и отрицательных чисел со знаками « + » и « — » применил немецкий математик Видман. Выражение «ниже, чем ничего» показывает, что Штифель и некоторые другие мысленно воображали положительные и отрицательные числа точками на вертикальной шкале (вроде шкалы термометра). Развитое затем математиком А. Жираром представление об отрицательных числах как о точках на некоторой прямой, располагающихся по другую сторону от нуля, чем положительные, оказалось решающим в обеспечении этим числам прав гражданства, особенно в результате развития метода координат у П. Ферма и Р. Декарта.
Вывод
В своем работе я исследовал историю возникновения отрицательных чисел.
В ходе исследования я сделал вывод:
Современная наука встречается с величинами такой сложной природы, что для их изучения приходится изобретать все новые виды чисел.
При введении новых чисел большое значение имеют два обстоятельства:
а) правила действий над ними должны быть полностью определены и не вели к противоречиям;
б) новые системы чисел должны способствовать или решению новых задач, или усовершенствовать уже известные решения.
К настоящем у времени существует семь общепринятых уровней обобщения чисел: натуральные, рациональные, действительные, комплексные, векторные, матричные и трансфинитные числа. Отдельными учеными предлагается считать функции функциональными числами и расширить степень обобщения чисел до двенадцати уровней.
Все эти множества чисел я постараюсь изучить.
Приложение
СТИХОТВОРЕНИЕ
«Сложение отрицательных чисел и чисел с разными знаками»
Если уж захочется вам сложить
Числа отрицательные, нечего тужить:
Надо сумму модулей быстренько узнать,
К ней потом знак «минус» взять да приписать.
Если числа с разными знаками дадут,
Чтоб найти их сумму, все мы тут как тут.
Больший модуль быстро очень выбираем.
Из него мы меньший вычитаем.
Самое же главное – знак не позабыть!
— Вы какой поставите? – мы хотим спросить
— Вам секрет откроем, проще дела нет,
Знак, где модуль больше, запиши в ответ.
Правила сложения положительных и отрицательных чисел
Минус с минусом сложить,
Можно минус получить.
Если сложишь минус, плюс,
То получится конфуз?!
Знак числа ты выбирай
Что сильнее, не зевай!
Модули их отними,
Да все числа помири!
— Правила умножения можно истолковать и таким образом:
«Друг моего друга — мой друг»: + ∙ + = + .
«Враг моего врага — мой друг»: ─ ∙ ─ = +.
«Друг моего врага — мой враг»: + ∙ ─ = ─.
«Враг моего друга – мой враг»: ─ ∙ + = ─.
Знак умножения есть точка, в ней три знака:
Прикрой из них два, третий даст ответ.
Например.
Как определить знак произведения 2∙(-3)?
Закроем руками знаки «плюс» и «минус». Остаётся знак «минус»
Список литературы
-
«История древнего мира», 5 класс. Колпаков, Селунская.
-
«История математики в древности», Э. Кольман.
-
«Справочник школьника». ИД «ВЕСЬ», Санкт-Петербург. 2003 г.
-
Большая математическая энциклопедия.
Якушева Г.М. и др.
-
Большая математическая энциклопедия. Якушева Г.М. и др.
-
Вигасин А.А,.Годер Г.И., «История древнего мира» учебник 5 класса, 2001г.
-
Википедия. Свободная энциклопедия.
-
Возникновение и развитие математической науки: Кн. Для учителя. – М.: Просвещение, 1987.
-
Возникновение и развитие математической науки: Кн. Для учителя. – М.: Просвещение, 1987.
-
Гельфман Э.Г. «Положительные и отрицательные числа», учебное пособие по математике для 6-го класса, 2001.
-
Глав. ред. М. Д. Аксёнова. – М.: Аванта+,1998.
-
Глав. ред. М. Д. Аксёнова. – М.: Аванта+,1998.
-
Глейзер Г. И. «История математики в школе», Москва, «Просвещение», 1981 г.
-
Детская энциклопедия «Я познаю мир», Москва, «Просвещение», 1995г.
-
История математики в школе , IV-VI классы. Г.И. Глейзер, Москва, Просвещение, 1981.
-
История математики в школе , IV-VI классы. Г.И. Глейзер, Москва, Просвещение, 1981.
-
М.: Филол. О-во «СЛОВО»: ОЛМА-ПРЕСС, 2005.
-
Малыгин К.А.
-
Математический энциклопедический словарь.
М., Сов. энциклопедия, 1988.
-
Нурк Э.Р., Тельгмаа А.Э. «Математика 6 класс», Москва, «Просвещение»,1989г
-
Учебник 5 класс. Виленкин, Жохов, Чесноков, Шварцбурд.
-
Фридман Л. М.. «Изучаем математику», учебное издание, 1994 г.
-
Э.Г. Гельфман и др., Положительные и отрицательные числа в театре Буратино. Учебное пособие по математике для 6 класса. 3-е издание, испр., — Томск: Издательство Томского университета, 1998г.
-
Энциклопедия для детей. Т.11. Математика
Якушева Г.М. и др.
М., Сов. энциклопедия, 1988.
17
Просмотров работы: 25974
Что такое отрицательные числа? | TheSchoolRun
Мы объясняем, что такое отрицательные числа и как можно научить детей этому понятию с помощью числовой прямой, а также рассмотрим типы вопросов, которые детям могут задавать с отрицательными числами.
или Зарегистрируйтесь, чтобы добавить к своим сохраненным ресурсам
Что такое отрицательные числа?
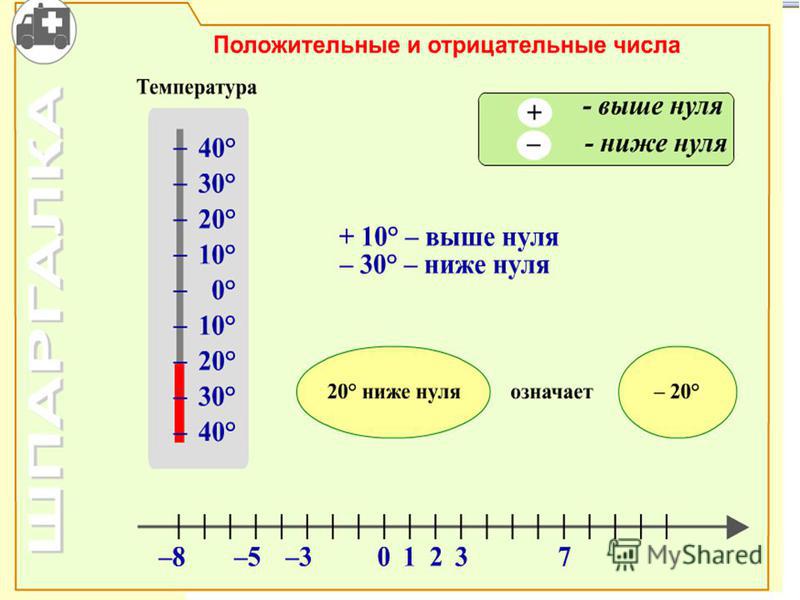
Отрицательное число — это число меньше нуля.
Можно продемонстрировать детям с помощью горизонтального числовая строка или вертикальная числовая строка ( числовая лестница ):
Повысьте уровень обучения вашего ребенка уже сегодня!
- Начните обучение своего ребенка с индивидуальной программы обучения
- Получайте еженедельные материалы по английскому языку и математике, которые отправляются прямо на ваш почтовый ящик
- Поддерживайте процесс обучения вашего ребенка сегодня 9003 БЕСПЛАТНАЯ пробная версия 9003
Что такое числовая линия?
Цепочки чисел
Упорядочивание положительных и отрицательных чисел
Сложение и вычитание отрицательных чисел
Что такое целое число?
Различия между положительными и отрицательными числами
Математика для 6 класса: чему учит ваш ребенок
Вычитание отрицательных чисел
Советы учителей по математике KS2
- Проверить отрицательные целые числа и обвести их кругом для символа «-».
- Положительные целые числа, скорее всего, не будут иметь знак.
- Посмотрите на обведенные цифры. Вы можете захотеть нарисовать такую диаграмму:
- Затем вы можете поставить числа в каждом столбце.
отрицательные числа в начальной школе
Отрицательные числа вводятся в 4-м классе , где детей просят расположить по порядку различные отрицательные и положительные числа в числовой строке.
Детей также можно попросить решить задачи, связанные с отрицательными и положительными температурами.
Дети обычно используют числовые ряды, подобные приведенным выше, чтобы помочь им с этими задачами. Пример одной из таких проблем:
Температура в понедельник утром -5˚C. Температура в пятницу утром 1˚C. Насколько теплее утро пятницы, чем утро понедельника?
(ответ: 6˚C)
В 6-м классе дети должны будут считать в уме отрицательные числа , поэтому их попросят найти разницу между отрицательным числом и положительным числом, или два отрицательных числа. Они обычно начинают с использования числовой прямой для выполнения этих вычислений, но позже переходят к их обработке в уме.
Примеры вопросов могут включать:
Сколько будет 6 минус 12? (-6)
Сколько будет -7 плюс 18? (11)
Температура составляет 5˚C, а затем падает на 9˚.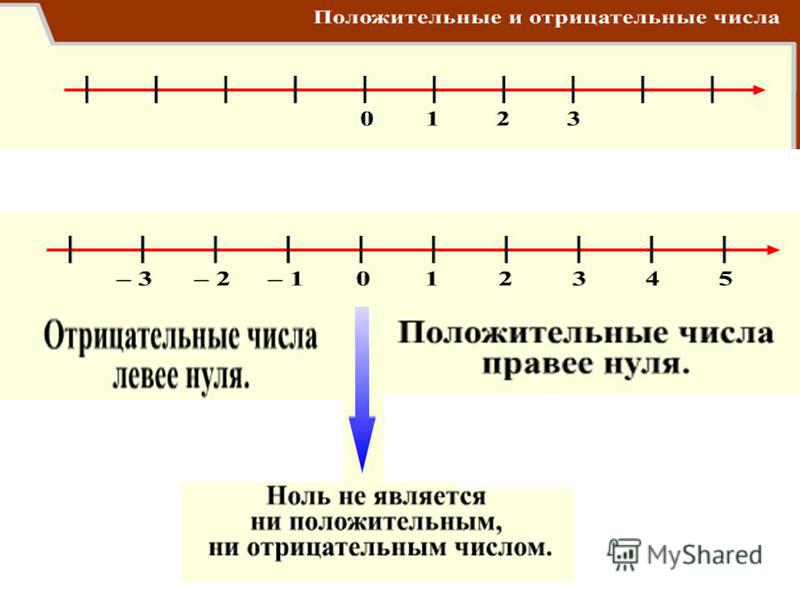
Какая сейчас температура? (-4˚C)
К 6-му классу детей просят считать положительные и отрицательные температуры на линейном графике , таком как:
Если вашему ребенку нравится практиковать математические понятия в играх, мы рекомендуем бесплатный онлайн игра Minus Miners, в которой игрокам предлагается сбежать из подземной шахты, а в процессе они узнают все об отрицательных числах.
Больше похоже на это
С ай
каждое целое число вслух или про себя. «Посмотрите, у меня есть четыре номера, я нужно сказать каждый из них про себя. первое число минус три и шесть десятых, следующий две и восемь десятых, третий отрицательный одна и две десятых, а последний — одна и пять десятых. P мазь к каждому целому числу и найдите минус знаки.
I идентифицировать
является ли каждое целое число положительным или отрицательным.
E оценка значение каждого целого числа с использованием правил значения. «Посмотрим. Я нарисую числовую линию, чтобы помочь мне оценить. Я поставлю ноль в посередине, и, как и в моей таблице t, поставьте + справа и — справа слева от нуля.» «Правило №1 гласит, что положительные целые числа всегда больше. |
У меня есть два положительных целых числа, 2,8 и 1,5, поэтому я
поместите их в числовую строку первыми. Я знаю, что эти двое будут больше
чем два отрицательных числа, -3,6 и -1,2». Правило № 2 гласит, что при положительном
числа, целое число дальше от нуля имеет большую ценность. Для двух положительных целых чисел
если я проведу линию от нуля до каждого из них, 2,8 будет дальше всего от
нуль. Используя это правило, 2,8 является наибольшим из двух положительных чисел.
Для отрицательных чисел это противоположно положительным числам. Правило
# 3 говорит, что с отрицательными числами целое число ближайший до нуля имеет большее значение. Для двух отрицательных целых чисел, если
Я провожу линию от нуля к каждому из них, -1,2 ближе всего к нулю. С использованием
по этому правилу -1,2 больше из двух отрицательных чисел.