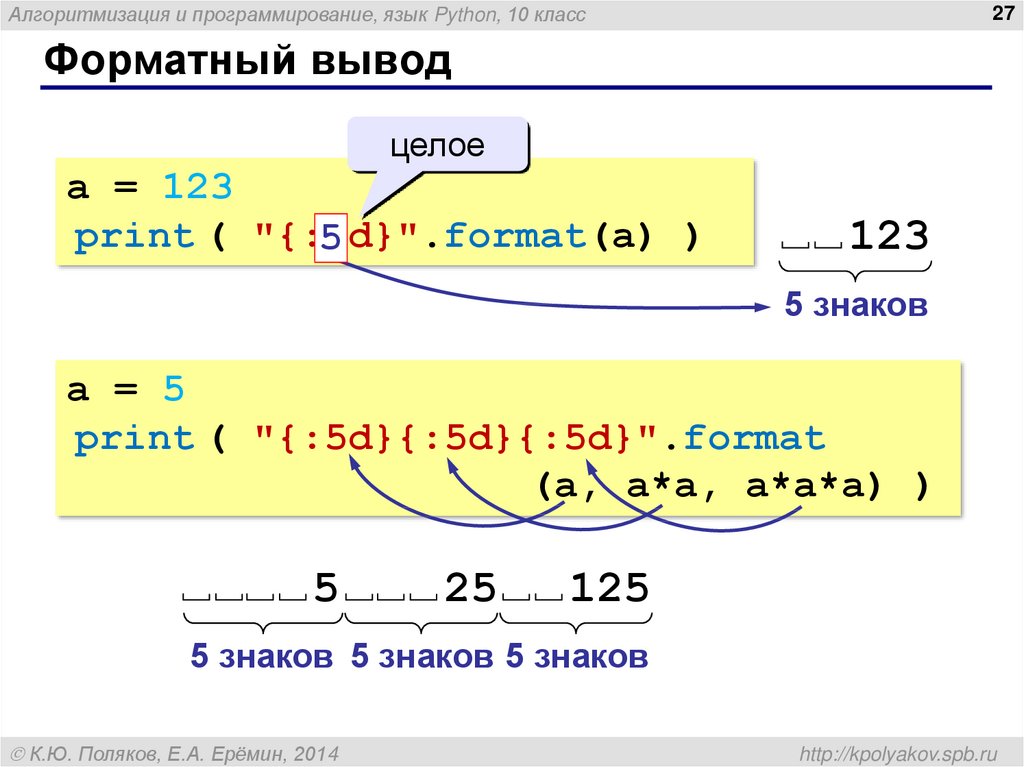
Как найти в Python остаток от деления?
Python — простой и современный язык для написания кода. В нем есть мощные библиотеки, которые могут оценивать любое выражение. Python — главный конкурент Matlab и Octave. Запуская Python в интерактивном режиме, пользователь может легко найти оставшуюся часть раздела. Но это еще не все! Python может быть мощным калькулятором.
Понятие оператора
Чтобы легко найти остальную часть деления в Python, вам нужно понять некоторые определения. Оператор: знак или строка, позволяющая выполнять математические, побитовые, логические и другие вычисления. Выражения или числа, введенные пользователем для поиска остатка, комбинации или сравнения в Python 3, называются операндами.
Подразделяются на следующие типы операторов:
- операторы присваивания;
- арифметика;
- логические;
- сравнения;
- членство;
- личность.
- мало по малу;
Проще говоря, в примере «15-5» оператором является знак «-», операнды — 15 и 5. Это арифметическая операция с целыми числами. Если мы примем во внимание выражение «Истина и Истина», то здесь будет оператор «И», а операнды — «Истина» и «Истина». Этот пример можно отнести к логическому типу.
Это арифметическая операция с целыми числами. Если мы примем во внимание выражение «Истина и Истина», то здесь будет оператор «И», а операнды — «Истина» и «Истина». Этот пример можно отнести к логическому типу.
Целые и вещественные числа. Математические операции и вывод результата
Если мы рассматриваем математические операции над целыми и дробными числами, то это операторы +, -, *, /, **, //,%. С первыми тремя все понятно. Они обозначают соответственно сложение, вычитание, умножение. Оператор ** указывает на необходимость возведения в степень.
Одиночное (/) и двойное (//) деление различаются. Если первое дает действительное число в решении, второе необходимо, чтобы найти целую часть деления. Например, 9 // 4 = 2. Этот оператор соответствует функции div в Turbo Pascal. Но закономерность есть. Знак «/» напечатает целое число в результате, если и делитель, и делимое являются целыми числами. Чтобы найти остаток от деления в Python, вам нужно использовать оператор «%». По аналогии с тем же «Турбо Паскалем» «%» сравним с функцией мода. Например, 9% 2 = 1, то есть в Python остаток от деления в данном случае равен 1. Рассмотрим еще несколько примеров.
Например, 9% 2 = 1, то есть в Python остаток от деления в данном случае равен 1. Рассмотрим еще несколько примеров.
Для деления без остатка Python предлагает использовать функцию divmod (x, y). В этом случае x — делимое, y — делитель. Для divmod (9,3) программа выдает следующий результат (3,0). Это означает, что все деление равно 3, а остаток равен 0.
Математические операции могут выполняться без присвоения значения переменной. Затем результат выводится автоматически. Если ваш код содержит присвоение переменной, вы можете отобразить результат на экране с помощью оператора печати.
Модуль math
Для удобства пользователей разработчики предлагают мощный математический модуль, который может работать с любым типом чисел и выполнять дополнительные функции.
Для подключения библиотеки необходимо в начале кода программы написать следующую строку: import math. Эта команда позволит вам загрузить в программный код все функции, доступные в математическом модуле. Итак, чтобы подключить конкретный блок из библиотеки, нужно постоянно его регистрировать. Например, x = math.ceil (5.6).
Итак, чтобы подключить конкретный блок из библиотеки, нужно постоянно его регистрировать. Например, x = math.ceil (5.6).
Если программа будет часто использовать один и тот же блок, вы можете только импортировать его. Например, вам нужно округлить до ближайшего целого числа. Тогда код записывается следующим образом: из math import ceil или из math import *. В обоих случаях это не повлияет на дополнительный код округления.
Стандартные функции арифметики в Python
Чтобы вычислить остаток от целочисленного деления в Python, не всегда необходимо загружать математическую библиотеку. Некоторые функции интегрированы.
Интегрированные функции | Их цель | Примеры |
целое число (х) | Преобразует действительное число в целое, т. Е. Дробная часть «усекается». | интервал (5.3) >>> 5 интервал (5.6) >>> 5 интервал (5,987) >>> 5 |
круглый (х) | Выражение округляется до ближайшего целого числа. | круглый (5,4) >>> 5,0 круглый (5,7) >>> 6,0 круглый (5.5) >>> 6.0 круглый (5,987) >>> 6,0 |
круглый (х, п) | Используется для округления дробной части до n десятичных знаков | круглый (5.8776.2) >>> 5,88 круглый (5.9876.3) >>> 5,988 |
брюшной (х) | Найдите форму выражения | брюшной пресс (-7) >>> 7 брюшной пресс (7,8) >>> 7,8 абс (-66,55) >>> 66,55 |
Функции, для которых библиотека должна быть связана (сначала необходимо ввести из математического импорта *), показаны в следующей таблице.
Функции | Их цель |
потолок (x) | Функция нужна для округления числа до большего целого числа («вверх») |
самолет (x) | Функция нужна для округления числа до наименьшего целого числа («вниз») |
квадрат (x) | Вычислить корень числа |
регистр (х) | Требовалось найти логарифм. |
а также | Возвращает основание натурального логарифма |
грех (х) | Вычислить тригонометрические функции, где x в радианах |
cos (x) | |
загар (х) | |
asin (х) | |
acos (x) | |
атан (х) | |
atan2 (х, у) | Найдите полярный угол точки, заданной x и y |
градусы (x) | Требуется для преобразования угла из радиан в градусы |
радианы (х) | Функция, необходимая для преобразования угла из градусов в радианы |
пи | Печатает значение константы π |
В качестве примера ниже приведен код, в котором используются математические операторы.
Результат отображается следующим образом.
В математическом модуле есть много других функций. Здесь перечислены наиболее распространенные.
python — Целочисленное деление отрицательных целых чисел
Вопрос возник при решении задачи о палиндроме. Вот решение
def palindrom(param):
# convert to str
word = str(param)
# in cycle char by char comparing from start and from end to middle of the word
return True if word[:len(word)//2] == word[:-len(word)//2-1:-1] else False
if palindrom(input("give me a word: ")):
print("Палиндром")
else:
print("Та ну не")
которое работает для слов четной длины, и не работает для слов с нечтным количеством символов.
Оказалось, что 7//2==3, а -7//2==-4
то есть задачу то я решил:
return word[:len(word)//2] == word[:-(len(word)//2)-1:-1]
но почему так реализовано целочисленное деление?
Хотелось бы -7//2 ==-3.
Какой тут глубинный смысл? А то ведь
7//2 + (- 7//2) == -1 7//2 - 7//2 == 0
P. S.: признателен gil9red за подсказки и краткое решение задачи о палиндроме в примечаниях ниже.
S.: признателен gil9red за подсказки и краткое решение задачи о палиндроме в примечаниях ниже.
P.P.S.: что интересно, операции побитового двоичного сдвига тоже соблюдают данное правило:
7>>1 == 3 -7>>1 == -4
- python
4
Дело в том, как определяется целочисленное деление.
Определение
Разделить целое число a на целое число b!=0 с остатком — это значит
найти такие два целых q и r, которые удовлетворяют следующим условиям:
1) a = b * q + r;
2) 0 <= r < |b|.
Тогда из определения будет:
-7 // 2 = -4
Объяснение:
- При делении отрицательного числа на положительное, получится отрицательное число
- Можно предположить, что правильный ответ
-3, но в этом случае умножив-3 * 2мы получим-6. Чтобы получить исходное
Чтобы получить исходное -7нужно к результату прибавить число-1, но остаток не может быть отрицательным по определению(r>=0). По этому в данном случае остаток равен1и частное равно-4.
3
Вот что у меня получилось. Как оказалось законы математики и формула в Python по вычислению остатка разные. Общая формула a%b=r (a=b*q+r), где q неполное частное, r остаток. Для математики, в которой по правилам остаток не может быть отрицательным:
-19%5=1 (-19=5*(-4)+1) 19%-5=4 (-21=5*(-5)+4) -19%-5=1 (-19=(-5)*4+1) -5%19=14 (-5=19*(-1)+14) 5%-19=5 (5=(-19)*0+5) -5%-19=14 (-5=(-19)*1+14)
Для Python, где остаток может быть отрицательным:
-19%5=1 (-19=5*(-4)+1) сходится 19%-5=-1 (19=(-5)*(-4)-1) не сходится -19%-5=-4 (-19=(-5)*3-4) не сходится -5%19=14 (-5=19*(-1)+14) сходится 5%-19=-14 (5=(-19)*(-1)-14) не сходится -5%-19=-5 (-5=(-19)*0-5) не сходится
Итого: неполное частное «q» округляется в меньшую целую сторону, так же как и с делением нацело. Т.е. если у вас одно число помещается в другом -3,XX раза, берется -4, если 3,XX раза, берется 3, если 0,xx раз, берется 0. Моя логика так нарисовала)
Т.е. если у вас одно число помещается в другом -3,XX раза, берется -4, если 3,XX раза, берется 3, если 0,xx раз, берется 0. Моя логика так нарисовала)
2
Зарегистрируйтесь или войдите
Регистрация через Google
Регистрация через Facebook
Регистрация через почту
Отправить без регистрации
Почта
Необходима, но никому не показывается
Отправить без регистрации
Почта
Необходима, но никому не показывается
Нажимая на кнопку «Отправить ответ», вы соглашаетесь с нашими пользовательским соглашением, политикой конфиденциальности и политикой о куки
Python Двойная косая черта (//) Оператор: Floor Division — LearnDataSci
Автор: Alfie Grace
Data Scientist
operator
) с помощью оператора // . Этот оператор разделит первый аргумент на второй и округлит результат до ближайшего целого числа, что сделает его эквивалентным
Этот оператор разделит первый аргумент на второй и округлит результат до ближайшего целого числа, что сделает его эквивалентным math.floor() 9Функция 0017.
См. краткий пример ниже:
15 // 4
То же, что:
import math math.floor(15 / 4)
Результат обычного деления (с использованием оператора /) равен $\frac{15}{4} = 3,75$, но использование // уменьшило 3,75$ до 3$ $.
Результат обычного деления всегда число с плавающей запятой, тогда как если один из операндов является числом с плавающей запятой в делении пола , то результатом будет число с плавающей запятой.
Ниже показан пример этого:
print("Обычное деление")
print(2 / 2, "\это число с плавающей запятой")
print("\nРазделение этажа")
print(15 // 4, "\это целое число")
print(15. 0 // 4, "\tis a float.")
0 // 4, "\tis a float.") Out:
Обычное деление 1.0 — это число с плавающей запятой. Разделение этажа 3 является инт. 3.0 - плавающий.
Когда операнд отрицательный, деление на пол возвращает наибольшее целое число меньшее или равное результат обычного деления. Давайте используем те же операнды, что и раньше, чтобы показать, как это работает:
печать(15/4) печать (15 // 4) print(-15 // 4)
Выход:
3,75 3 -4
Глядя на результат обычного деления, когда оба числа положительны, $\frac{15}{4}=3,75$, деление по полу возвращает $3$, так как это наибольшее целое число, меньшее или равное $3,75$. Когда один из операндов отрицательный, результат нормального деления отрицательный ($-3,75$), поэтому наибольшее целое число, меньшее или равное, равно $-4$.
Мы рассмотрим, где разделение этажей может быть полезным, а также рассмотрим другие подходы, которые можно использовать для достижения аналогичных результатов.
При использовании Python вы часто будете сталкиваться с ошибками, когда функции несовместимы с числами с плавающей запятой. Например, допустим, вы хотите использовать функцию диапазона с частным из двух чисел:
для значения в диапазоне (25/5):
print(value) Out:
------------------------------------------------------- -------------------------------------------------- TypeError Traceback (последний последний вызов)в () ----> 1 для значения в диапазоне (25/5): 2 печать (значение) TypeError: объект 'float' не может быть интерпретирован как целое число
Чтобы наша программа работала правильно, нам нужно сначала преобразовать частное в целочисленный тип , чего мы можем добиться с помощью оператора // :
для значения в диапазоне (25 // 5):
печать(значение) Выход:
0 1 2 3 4
Еще одна область, в которой вы можете захотеть использовать оператор Floor, — это индексирование списков:
x = list(range(100)) x[len(x) / 10]
Выход:
-------------------------------------------------- ---------------------------------------- TypeError Traceback (последний последний вызов)в <модуле> 1 х = список (диапазон (100)) 2 ----> 3 х [длина (х) / 10] TypeError: индексы списка должны быть целыми числами или срезами, а не числами с плавающей запятой
Один из способов решить эту проблему — использовать оператор деления пола:
x[len(x) // 10]
Исходящий:
10
лучший вариант. В следующем разделе мы рассмотрим различные функции, которые могут дать аналогичный результат.
В следующем разделе мы рассмотрим различные функции, которые могут дать аналогичный результат.
Иногда вы обнаружите, что работаете с наборами данных, которые содержат как целые числа, так и числа с плавающей запятой, например, если вы использовали беспорядочные данные.
При таких обстоятельствах // оператор выдаст противоречивые результаты, выводя как числа с плавающей запятой, так и целые числа. Таким образом, если ваша программа зависит от целых чисел, то использование оператора // потребует дополнительных шагов для обеспечения согласованного вывода.
Есть несколько других способов манипулирования частными двух чисел для правильной работы с вашей программой. Например, вы не всегда можете округлять значение в меньшую сторону, поэтому использование различных подходов может дать вам больший контроль над результатами.
math.floor() дает тот же результат, что и оператор деления пола, округляя аргумент в меньшую сторону до ближайшего целого числа.
Одним существенным отличием использования math.floor() является то, что он всегда выводит целое число, независимо от типа входных данных. При работе как с целыми числами, так и с числами с плавающей запятой math.floor() более полезен, поскольку обеспечивает более согласованный вывод.
Ниже показано, как мы можем вычислить результат обычного деления:
импорт математики math.floor(15 / 4)
Как и при использовании оператора Floor, math.floor по-прежнему будет округлять в меньшую сторону, когда ввод отрицательный.
В качестве альтернативы math.floor() мы также можем использовать math.ceil() , который всегда будет округлять до ближайшего целого числа, а не вниз.
Например:
math.ceil(15 / 4)
Подобно math. ,  floor
floor math.ceil всегда выдает выходные данные в виде целого числа, независимо от типов данных аргументов. math.ceil будет округлять отрицательные числа в большую сторону, поэтому math.ceil(-15 / 4) даст в результате -3 .
Для быстрого исправления можно преобразовать float в int . Передача числа с плавающей запятой в int() приводит к целому числу, в котором все обрезается после десятичного числа входного числа с плавающей запятой.
В следующем примере $\frac{15}{4}=3,75$, но приведение к целому числу отрезает $.75$:
int(15 / 4)
int() работает аналогично math.floor() , за исключением того, что int() эффективно округляет отрицательные числа вверх, а не вниз:
print(math.floor(-15 / 4)) печать (целое (-15 / 4))
Выход:
-4 -3
В качестве альтернативы математическим функциям мы также можем использовать round() для округления значений и последующего вывода результата в виде целого числа.
Отличие от round() заключается в том, что будет использоваться обычное округление, т. е. любое десятичное число .5 и больше округляется в большую сторону.
Ниже показано использование round() :
round(3.5)
Мы также можем указать, до скольких десятичных знаков ввод должен быть округлен.
В приведенном ниже примере показано, как можно округлить результат деления 15 на 4 ( 3,75 ) до 1 десятичной цифры: Добавление 1 после запятой означает, что мы хотели бы, чтобы результат имел 1 десятичную точку, но мы могли бы использовать любое число. Например, мы можем округлить число пи до девяти знаков после запятой: 9.0008
Например, мы можем округлить число пи до девяти знаков после запятой: 9.0008
round(math.pi, 9)
Out:
3.141592654
Оператор деления пола ( // ) в основном используется, когда вам требуется целое число или нужно вернуть наименьшее целое число, меньшее или равное вход.
Если оба операнда являются целыми числами, то на выходе будет целое число. Если любой из операндов является числом с плавающей запятой, то вывод будет числом с плавающей запятой.
Строки, использующие оператор // , легко читаются и идиоматичны, но в случаях, когда вы работаете с непоследовательными и беспорядочными наборами данных, может быть лучше использовать math.floor() , math.ceil() , int() или round() .
Что означает // в Python?
Что делает оператор Python // ?
Чем он отличается от оператора /?
Оператор
/ Оператор / является оператором деления в Python.
Когда / используется между двумя числами, вы всегда получите точный (настолько точный, насколько Python может управлять) результат обратно:
>>> 5 / 2 2,5
В отличие от некоторых языков программирования, / в Python не действуют иначе при использовании между целыми числами; в Python 3 то есть.
В Python 2 деление на два целых числа приведет к уменьшению до ближайшего целого числа:
>>> 5 / 2 # Python 2 2
Но в Python 3 деление двух целых чисел всегда возвращает число с плавающей запятой с точным результатом:
>>> 4 / 2 2.0
Оператор
// между целыми числами Оператор // — это оператор деления пола в Python.
Когда // используется между двумя целыми числами, вы всегда получите целое число:
>>> 5 // 2 2
Оператор // обеспечивает деление при округлении результата до ближайшего целого числа. Это часто называют целочисленным делением или делением пола .
Это часто называют целочисленным делением или делением пола .
При использовании // с числом с плавающей запятой, вы получите обратно число с плавающей запятой:
>>> 5.0 // 2 2.0
Но, как и в случае с целыми числами, это число с плавающей запятой будет , а будет округленным в меньшую сторону до ближайшего целого числа .
Когда следует использовать
// в Python?Если вы когда-нибудь видели такой код:
>>> n = 5 >>> целое(n / 2) 2
Тогда вы, вероятно, видели возможность использовать // оператор.
Если вы делите, а затем сразу же конвертируете результат в целое число, вы, вероятно, могли бы использовать вместо этого оператор // .
В этой функции split_in_half мы используем функцию int , чтобы убедиться, что значение mid_point является целым числом:
def split_in_half(sequence):
"""Вернуть две половины заданной последовательности (список, строка и т. д.)"""
mid_point = int (len (последовательность) / 2)
возвращаемая последовательность[:mid_point], последовательность[mid_point:]
д.)"""
mid_point = int (len (последовательность) / 2)
возвращаемая последовательность[:mid_point], последовательность[mid_point:]
Оба числа, которые мы делим, являются целыми, поэтому мы могли бы использовать // , чтобы получить целочисленный результат:
def split_in_half(sequence):
"""Вернуть две половины заданной последовательности (список, строка и т.д.)"""
mid_point = len(последовательность) // 2
возвращаемая последовательность[:mid_point], последовательность[mid_point:]
Это немного эффективнее, чем деление для получения точного числа с плавающей запятой, а затем деление этого числа с плавающей запятой, чтобы вернуться к целому числу.
Обратите внимание, что
// всегда округляется в меньшую сторону Прежде чем вы замените все случаи использования int(a / b) в вашем коде на a // b , вы должны отметить, что эти два действия действуют по-разному, когда результат деление является отрицательным числом:
Допустим, мы делим и получаем -2,5 :
>>> a = -5 >>> б = 2 >>> а/2 -2,5
При использовании / и int мы получим -2 , но при делении на // вместо этого получим -3 :
>>> int(a / 2) -2 >>> а // 2 -3
Оператор // всегда округляет в меньшую сторону. Он действует не столько как встроенная функция
Он действует не столько как встроенная функция int , сколько как math.floor :
>>> from math import floor >>> этаж(а/2) -3 >>> а // 2 -3
Также помните, что a // b возвращает число с плавающей запятой, когда либо a , либо b — числа с плавающей запятой.
>>> а = 52,0 >>> б = 4 >>> а // б 13,0
Таким образом, вы, скорее всего, захотите использовать // только для деления между положительными целыми числами .
Использование
divmod вместо Что делать, если вам нужно целочисленное деление (с // ) и остаток от этого деления (с % ):
>>> duration = 500
>>> минуты = продолжительность // 60
>>> секунды = продолжительность % 60
>>> print(f"{минуты}:{секунды}")
8:20
Вместо того, чтобы использовать // и % по отдельности, вы можете использовать функцию divmod , чтобы получить оба результата одновременно:
>>> duration = 500
>>> минуты, секунды = divmod(длительность, 60)
>>> print(f"{минуты}:{секунды}")
8:20
Теоретически это можно оптимизировать для одновременного выполнения обеих операций, но на практике CPython не выполняет эту оптимизацию, поэтому в первую очередь касается читабельности .
Иногда divmod может значительно улучшить читаемость кода.
Например, здесь мы используем // и % , чтобы получить часы, минуты и секунды:
>>> duration = 9907
>>> часы = продолжительность // (60 * 60)
>>> минуты = (длительность // 60) % 60
>>> секунды = продолжительность % 60
>>> print(f"{часы}:{минуты:02d}:{секунды:02d}")
2:46:07
Но мы могли бы использовать divmod дважды вместо этого:
>>> продолжительность = 9907
>>> минуты, секунды = divmod(длительность, 60)
>>> часы, минуты = divmod(минуты, 60)
>>> print(f"{часы}:{минуты:02d}:{секунды:02d}")
2:46:07
Я считаю, что подход divmod намного понятнее, чем альтернативное использование // и % .
Если вам нужно как частное (если использовать математический термин), так и остаток от деления, рассмотрите возможность использования divmod .
Примечание : если вам это интересно 9Синтаксис 0016 :02d выше, см.