Арифметический сдвиг: Что такое арифметический сдвиг влево 01001001?

Арифметические операции с фиксированной точкой: Операции сдвига

Операции сдвигов появились вместе с компьютерами. Они легко реализовываются на цифровых схемах и существуют практически на всех типах процессоров. В математике они заменяются операциями умножения и деления. Операции сдвигов удобно рассматривать на битовом представлении числа. При сдвиге все биты числа сдвигаются либо влево, либо вправо. Сдвиг на один бит влево равнозначен умножению на 2, сдвиг на один бит вправо равнозначен делению на 2. Есть отличия при операциях с беззнаковыми целыми числами и с целыми числами со знаком.

Логический (или беззнаковый) сдвиг влево

Логический сдвиг влево применяется при операциях над беззнаковыми целыми числами. При сдвиге влево все биты сдвигаются влево на один бит, старший бит отбрасывается, а в младший бит записывается 0. Если до операции в старшем бите была единица, то число после операции становится меньше исходного. В случае отбрасывания старшей единицы устанавливается флаг Carry.

Логический (беззнаковый) сдвиг вправо

Логический сдвиг вправо применяется при операциях над беззнаковыми целыми числами. При сдвиге вправо все биты сдвигаются вправо, отбрасывается младший бит, а в старший записывается 0. Если в младшем бите до операции была 1, то устанавливается флаг Carry.

Арифметический (для чисел со знаком) сдвиг вправо

Арифметический сдвиг вправо применяется при операциях со знаковыми целыми числами. При сдвиге вправо все биты сдвигаются вправо, отбрасывается младший бит, а старший бит дублируется, тем самым сохраняя знак. Арифметический сдвиг вправо равнозначен выполнению операции деления на 2.

Арифметический (для чисел со знаком) сдвиг влево

Арифметический сдвиг влево применяется при операциях со знаковыми целыми числами. При сдвиге влево все биты сдвигаются влево на один бит, старший бит отбрасывается, а в младший бит записывается 0. Если при сдвиге влево изменяется знаковый бит (с 1 на 0 или с 0 на 1), то происходит ситуация насыщение — устанавливается флаг Overflow и значение результата заменяется на максимальное целое число в случае, если до начала операции число было положительное или на минимальное целое, если до начала операции число было отрицательным.

Арифметический сдвиг влево равнозначен выполнению операции умножения на 2.

Примеры

Рассмотрим использование арифметических и логических сдвигов. Для рассмотрения примеров выберем формат представления fractional данных.

Введем произвольное значение вещественного числа в формате float-point. После введения, число автоматически конвертируется в формат fractional и его бинарное представления. Если исходное вещественное число выходит за пределы допустимого представления в формате fractional, то оно будет автоматически приведено к допустимым пределам. Например, попробуйте ввести 1 при выбранном формате Q1.15.

Логический сдвиг — это… Что такое Логический сдвиг?

Би́товый сдвиг — изменение позиций битов в слове на одну и ту же величину.

В основной своей массе компьютеры не могут напрямую адресовать биты, которые содержатся группами по 8, 16, 32 битов в словах. Для обеспечения работы с битами существует множество команд, к которым относятся и сдвиги: Все сдвиги похожи друг на друга поведением средних битов: они просто сдвигаются влево или вправо на определённую величину.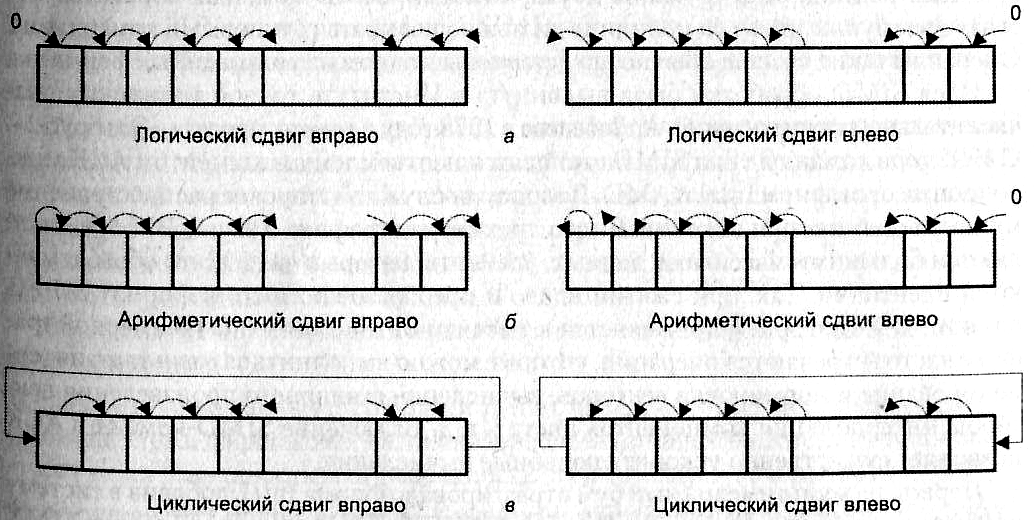 И различаются поведением крайних битов: одного, который уходит из слова, и второго, который должен появиться в слове.

Логический сдвиг

Логический сдвиг влево

Логический сдвиг вправо

Сдвиг, при котором уходящий бит уходит, не влияя на оставшееся биты, а на место появившегося бита записывается бит 0.

Пример работы операции сдвига:

Пусть у нас есть число 10101010b (в двоичной системе).

Если сделать сдвиг влево на 1 бит, то получим число 01010100b

Если сделать сдвиг вправо на 1 бит, то получим число 01010101b

В большинстве процессоров уходящий бит сохраняется в флаге переноса. Эта функция широко используется при работе с многобайтовыми числами.

Арифметический сдвиг

Арифметический сдвиг влево

Арифметический сдвиг вправо

При этом сдвиге слово рассматривается не просто как группа битов, а как целое число в дополнительном коде. При сдвиге влево ведёт себя как логический сдвиг, при сдвиге вправо: уходящий бит уходит, не влияя на оставшееся биты, а на место появившегося бита устанавливается бит, соответствующий знаку.

Пример работы операции сдвига:

Пусть у нас есть число 11111010b=−6 (в двоичной системе).

Если сделать сдвиг влево на 1 бит, то получим число 11110100b=−12

Если сделать сдвиг вправо на 1 бит, то получим число 11111101b=−3

Легко заметить, что при арифметическом сдвиге сдвиг влево соответствует умножению на 2, а сдвиг вправо делению на 2 (в общем случае — на основание системы счисления). Исключение: −1 >>a 1 = −1 (в общем случае это относится к числам от −1 до −p+1, где p — основание системы счисления).

Схемотехническая реализация операций сдвига очень проста. Именно поэтому эти операции рекомендуют использовать для операций умножения и деления целых чисел на числа равные степени 2 (2, 4, 8, 16, 32, 64 и т. д.).

Циклический сдвиг

Циклический сдвиг влево

Циклический сдвиг вправо

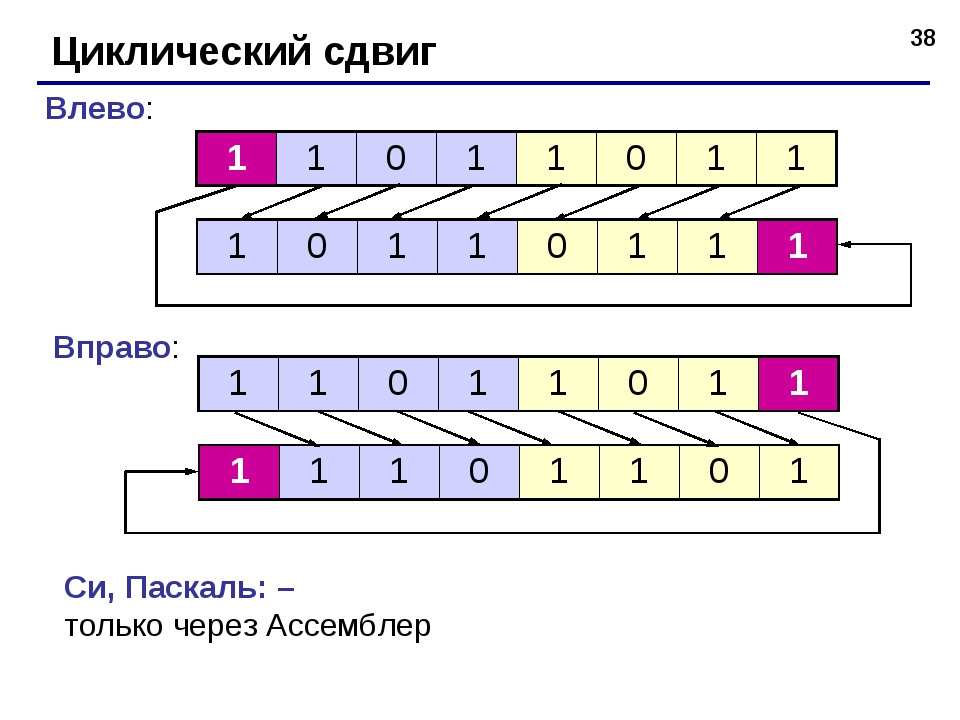
При этом сдвиге уходящий бит появляется на месте появившегося.

Пример работы операции сдвига:

Пусть у нас есть число 11111010b (в двоичной системе).

Если сделать сдвиг влево на 1 бит, то получим число 11110101b

Если сделать сдвиг вправо на 1 бит, то получим число 01111101b

Циклический сдвиг через бит переноса

Циклический сдвиг влево через бит переноса

Циклический сдвиг вправо через бит переноса

В архитектуру многих процессоров входит флаг переноса в следующий разряд (например, cf на n+1)-битным числом, состоящим из регистра и флага переноса.

Например, если у нас в регистре число 11111010b, флаг переноса равен 0:

После сдвига влево на 1 бит: в регистре 11110100b, флаг переноса равен 1

После сдвига вправо на 1 бит: в регистре 01111101b, флаг переноса равен 0

Операция циклического сдвига через бит переноса используется при работе с многобайтовыми числами. В частности, чтобы сдвинуть вправо на 1 бит длинное число, нужно очистить^[1]cf (в случае деления числа со знаком нужно записать в cf старший бит старшего слова) и циклически сдвинуть на единицу через cf каждое слово, начиная с верхнего. Например, пусть у нас есть число 011000111100b, занимающее три 4-битных слова:

Было:              HI=0110, MED=0011, LO=1100, cf=0
После сдвига HI:   HI=0011, MED=0011, LO=1100, cf=0
После сдвига MED:  HI=0011, MED=0001, LO=1100, cf=1
После сдвига LO:   HI=0011, MED=0001, LO=1110, cf=0

Сдвиги через регистр флагов более чем на 1 бит практически не используются.

Примечания

1. ↑ Можно вместо очистки флага для первого обрабатываемого слова использовать арифметический\логический сдвиг, если он присваивает флагу
   cf значение вышедшего бита.

Источник

Wikimedia Foundation. 2010.

Битовый сдвиг — это.

.. Что такое Битовый сдвиг?

Би́товый сдвиг — изменение позиций битов в слове на одну и ту же величину.

Большинство компьютеров не могут напрямую адресовать биты, которые содержатся группами по 8, 16, 32 или 64 битов в словах. Для обеспечения работы с битами существует множество машинных инструкций, включающие различные типы сдвигов. Все сдвиги похожи друг на друга поведением средних битов, которые просто сдвигаются влево или вправо на определённую величину. Однако, поведение крайних битов, которые уходят из слова и которые появляются в слове, зависит от типа сдвига.

В электронике битовые сдвиги осуществляются в регистрах сдвига.

Логический сдвиг

Логический сдвиг влево

Логический сдвиг вправо

Сдвиг, при котором уходящий бит уходит, не влияя на оставшееся биты, а на место появившегося бита записывается бит 0.

Пример работы операции сдвига:

Пусть у нас есть число 10101010b (в двоичной системе).

Если сделать сдвиг влево на 1 бит, то получим число 01010100b

Если сделать сдвиг исходного числа вправо на 1 бит, то получим число 01010101b

В большинстве процессоров уходящий бит сохраняется во флаге переноса. Эта функция широко используется при работе со многобайтовыми числами.

Арифметический сдвиг

Арифметический сдвиг влево

Арифметический сдвиг вправо

При этом сдвиге слово рассматривается не просто как группа битов, а как целое число в дополнительном коде. При сдвиге влево ведёт себя как логический сдвиг, при сдвиге вправо: уходящий бит уходит, не влияя на оставшиеся биты, а на место появившегося бита устанавливается бит, соответствующий знаку.

Пример работы операции сдвига:

Пусть у нас есть число 11111010b = −6 (в двоичной системе).

Если сделать сдвиг влево на 1 бит, то получим число 11110100b = −12

Если сделать сдвиг исходного числа вправо на 1 бит, то получим число 11111101b = −3

Легко заметить, что при арифметическом сдвиге сдвиг влево соответствует умножению на 2, а сдвиг вправо — делению на 2 (в общем случае — на основание системы счисления) с округлением к −∞.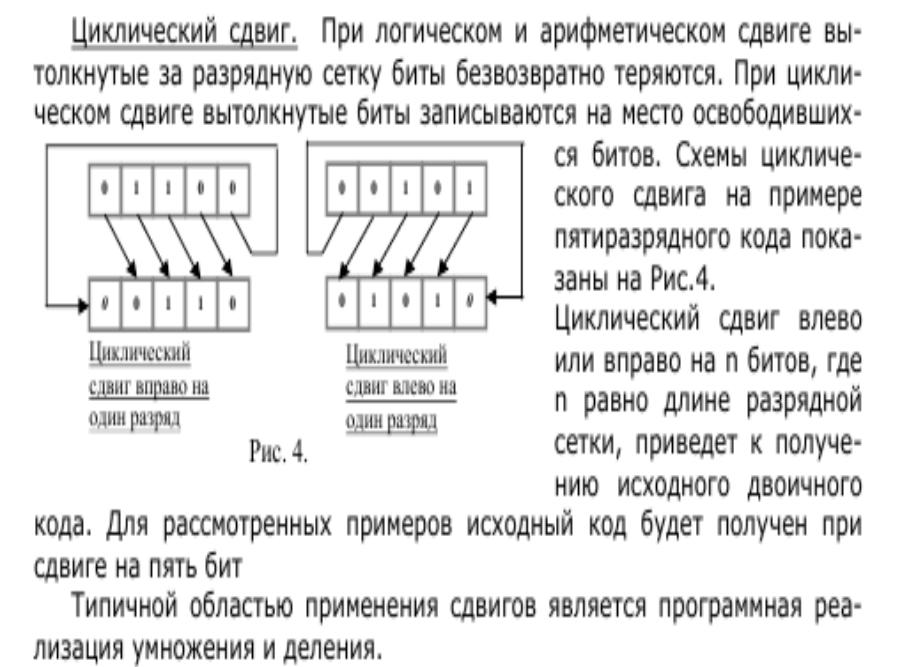 Например:

 1011 = −5          1111 = −1
>>a 1              >>a 1
 ----               ----
 1101 = −3          1111 = −1

Схемотехническая реализация операций сдвига очень проста. Именно поэтому эти операции рекомендуют использовать для операций умножения и деления целых чисел на числа, равные степени 2 (2, 4, 8, 16, 32, 64 и т. д.) — если, конечно, такое округление отрицательных чисел не мешает.

Циклический сдвиг

Циклический сдвиг влево

Циклический сдвиг вправо

При этом сдвиге уходящий бит появляется на месте появившегося.

Пример работы операции сдвига:

Пусть у нас есть число 11111010b (в двоичной системе).

Если сделать сдвиг влево на 1 бит, то получим число 11110101b

Если сделать сдвиг вправо на 1 бит, то получим число 01111101b

Циклический сдвиг через бит переноса

Циклический сдвиг влево через бит переноса

Циклический сдвиг вправо через бит переноса

В архитектуру многих процессоров входит флаг переноса в следующий разряд (например, cf на x86). Данная операция выполняет циклический сдвиг над (n+1)-битным числом, состоящим из регистра и флага переноса.

Например, если у нас в регистре число 11111010b, флаг переноса равен 0:

После сдвига влево на 1 бит: в регистре 11110101b, флаг переноса равен 1

После сдвига вправо на 1 бит: в регистре 01111101b, флаг переноса равен 0

Операция циклического сдвига через бит переноса используется при работе с многобайтовыми числами. В частности, чтобы сдвинуть вправо на 1 бит длинное число, нужно очистить^[1]cf (в случае деления числа со знаком нужно записать в cf старший бит старшего слова) и циклически сдвинуть на единицу через cf каждое слово, начиная с верхнего. Например, пусть у нас есть число 011000111100b, занимающее три 4-битных слова:

Было:              HI=0110, MED=0011, LO=1100, cf=0
После сдвига HI:   HI=0011, MED=0011, LO=1100, cf=0
После сдвига MED:  HI=0011, MED=0001, LO=1100, cf=1
После сдвига LO:   HI=0011, MED=0001, LO=1110, cf=0

Сдвиги через регистр флагов более чем на 1 бит практически не используются.

См. также

Примечания

1. ↑ Можно вместо очистки флага для первого обрабатываемого слова использовать арифметический\логический сдвиг, если он присваивает флагу cf значение вышедшего бита.

Ссылки

Assembler: 30. Команды сдвига и циклического сдвига

Логический сдвиг операнда влево/вправо

SHL операнд, количество_сдвигов 
SHR операнд, количество_сдвигов 

SHL и SHR сдвигают биты операнда (регистр/память) влево или вправо соответственно на один разряд и изменяют флаг переноса cf. При логическом сдвиге все биты равноправны, а освободившиеся биты заполняются нулями. Указанное действие повторяется количество раз, равное значению второго операнда.

Пример: 
; al = 01011011 (двоичное) 
shr al, 3 

Это означает: сдвиг всех битов регистра al на 3 разряда вправо. Так что al станет 00001011. Биты слева заполняются нулями, а биты справа выдвигаются. Последний выдвинутый бит, становится значением флага переноса cf.

Команда shl такая же, как и shr, но сдвигает влево. 
; bl = 11100101 (двоичное) 
shl bl, 2 

После выполнения команды регистр bl будет равен 10010100 (двоичное). Два последних бита заполнились нулями, флаг переноса установлен, потому, что последний выдвинутый слева бит был равен 1

Арифметический сдвиг влево/вправо

SAL операнд, количество_сдвигов 
SAR операнд, количество_сдвигов 

Команда SAR — сдвигает биты операнда (регистр/память) вправо на один разряд, значение последнего вытолкнутого бита попадает в флаг переноса, а освободившиеся биты заполняются знаковым битом.

Пример: 
; al = 10100110 
sar al, 3 
; al = 11110100 
sar al, 2 
; al = 11111101 

; bl = 00100110 
sar bl, 3 
; bl = 00000010

Команда SAL — сдвигает биты операнда (регистр/память) влево на один разряд, значение последнего вытолкнутого бита попадает в флаг переноса, а освободившиеся биты заполняются нулями, при этом знаковый бит не двигается.

Пример: 
; al = 10100110 
sal al, 3 
; al = 10110000
sal al, 4 
; al = 10000000

Команды циклического сдвига

rol операнд, количество_сдвигов 
ror операнд, количество_сдвигов 
rcl операнд, количество_сдвигов 
rcr операнд, количество_сдвигов 

Циклический сдвиг напоминает смещение, выдвигаемые биты, снова вдвигаются с другой стороны:

Пример: команды ror (циклический сдвиг вправо)

Из рисунка выше, биты вращаются, то есть каждый бит, который выталкивается снова вставляется с другой стороны. Флаг переноса cf содержит значение последнего выдвинутого бита.

ROL и ROR сдвигают все биты операнда влево(для ROL) или вправо(для ROR) на один разряд, при этом старший(для ROL) или младший(для ROR) бит операнда вдвигается в операнд справа(для ROL) или слева(для ROR) и становится значением младшего(для ROL) или старшего(для ROR) бита операнда; одновременно выдвигаемый бит становится значением флага переноса cf. Указанные действия повторяются количество раз, равное значению второго операнда.

RCL и RCR сдвигают все биты операнда влево (для RCL) или вправо (для RCR) на один разряд, при этом старший(для RCL) или младший(для RCR) бит становится значением флага переноса cf; одновременно старое значение флага переноса cf вдвигается в операнд справа(для RCL) или слева(для RCR) и становится значением младшего(для RCL) или старшего(для RCR) бита операнда. Указанные действия повторяются количество раз, равное значению второго операнда.

Операция — арифметический сдвиг — Большая Энциклопедия Нефти и Газа, статья, страница 1

Операция — арифметический сдвиг

Cтраница 1

Операция арифметического сдвига заключается в перемещении влево или вправо двоичных разрядов с одних позиций на другие с сохранением порядка их следования относительно друг друга за исключением знакового разряда. Операции сдвига выполняются командами: SLA ( SHIFT LEFT SINGLE ALGEBRAIC) — СДВИГ ВЛЕВО АРИФМЕТИЧЕСКИЙ, SRA ( SHIFT RIGHT SINGLE ALGEBRAIC) — СДВИГ ВПРАВО АРИФМЕТИЧЕСКИЙ, SLDA ( SHIFT LEFT DOUBLE ALGEBRAIC) — СДВИГ ВЛЕВО ДВОЙНОЙ АРИФМЕТИЧЕСКИЙ, SLDA ( SHIFT RIGHT DOUBLE ALGEBRAIC) — СДВИГ ВПРАВО ДВОЙНОЙ АРИФМЕТИЧЕСКИЙ. Эти команды применяются для изменения или уравнивания масштабов, так как они обеспечивают умножение или деление операндов на 2, где k есть число двоичных сдвигов.  [1]

Операция арифметического сдвига, заключается в перемещении влево или вправо двоичных разрядов с одних позиций на другие с сохранением порядка их следования относительно друг друга за исключением знакового разряда. Операции сдвига выполняются командами: SLA ( SHIFT LEFT SINGLE ALGEBRAIC) — СДВИГ ВЛЕВО АРИФМЕТИЧЕСКИЙ, SRA ( SHIFT RIGHT SINGLE ALGEBRAIC) — СДВИГ ВПРАВО АРИФМЕТИЧЕСКИЙ, SLDA ( SHIFT LEFT DOUBLE ALGEBRAIC) — СДВИГ ВЛЕВО ДВОЙНОЙ АРИФМЕТИЧЕСКИЙ, SRDA ( SHIFT RIGHT DOUBLE ALGEBRAIC) — СДВИГ ВПРАВО ДВОЙНОЙ АРИФМЕТИЧЕСКИЙ. Эти команды применяются для изменения или уравнивания масштабов, так как они обеспечивают умножение или деление операндов на 2ft, где k есть число двоичных сдвигов.  [2]

Операции арифметического сдвига влево SLA ( Left Algebraic) и арифметического сдвига вправо SRA ( Right Algebraic) производят сдвиг влево или вправо значащей части дополнительного кода числа. При сдвиге вправо пропадает значение из разряда тридцать один, а в разряд один поступает код знакового разряда. Разряд знака при этом не изменяется. Сдвигаемый код находится в регистре RI, а величина сдвига указывается шестью младшими двоичными разрядами адреса второго операнда. Операции SLDA и SRDA производят двойной ( Double) арифметический сдвиг соответственно влево и вправо. Сдвигаемый код состоит из 64 битов и занимает два общих регистра. Старшая часть находится в регистре с четным номером Ri, а младшая — в регистре со следующим нечетным номером.  [3]

Операция арифметического сдвига эквивалентна умножению числа с фиксированной запятой, находящегося на сумматоре, на 2 или 2 — п, в зависимости от направления сдвига.  [4]

Запуск операции арифметического сдвига ( логического сдвига) происходит при записи числа сдвигов по адресу 777316 ( 777314) При этом знак числа сдвигов определяет направление сдвигов. Tlpt выполнении этих операций 32-разрядное содержимое регистров АК и МЧ сдвигается на соответствующее число разрядов.  [5]

Использование операций арифметического сдвига при программировании достаточно очевидно.  [6]

Различие между операциями логического и арифметического сдвига заключается в обработке знакового разряда — первого разряда слова. При логическом сдвиге первый разряд сдвигается вместе с другими разрядами, поскольку ему не приписывается особый смысл. При арифметическом сдвиге знаковый разряд должен рассматриваться отдельно. В случае арифметического сдвига вправо освобождаемые разряды с левой стороны накапливающего сумматора заполняются с учетом значения знакового разряда, сохраняя таким образом алгебраический знак содержимого сумматора.  [7]

Микросхема PS состоит из дешифраторов вида сдвига ОСТ и выбора величины сдвига и знака DCF, входного MUXI и выходного MUXO мультиплексоров, блока выбора знака и блока знакового разряда. Вход S / используется для определения знака операций арифметического сдвига и распространения знакового разряда.  [9]

В связи с этим для более эффективной реализации указанных действий в машине предусмотрены две операции арифметического сдвига, используемые в командах формата RS. При выполнении этих команд преобразуемое число х выбирается из регистра ль а в качестве значения k принимается исполнительный адрес 5з, заданный в команде, — этот адрес является непосредственным операндом. Результат выполнения операции помещается в регистр г; регистр г2 в этих операциях не используется, и поэтому в записи команды на автокоде он не указывается. При выполнении этих операций новое значение ш не вырабатывается.  [10]

Однако в некоторых арифметических операциях байтами можно манипулировать прямо, применяя байтовые инструкции. В двойные ( длинные) слова помещается произведение ( при умножении) или делимое — при выполнении операции деления.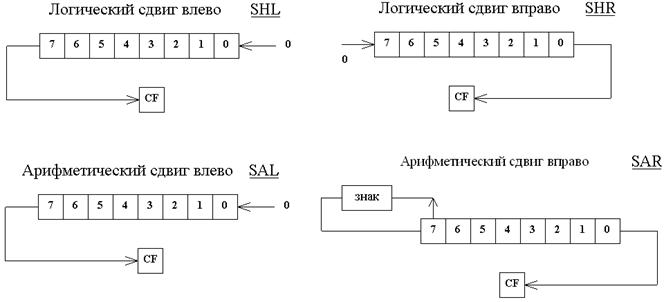 Над двойными словами допустимы операции прямого арифметического сдвига, сложения или вычитания слова посредством команд сложения / вычитания слов. Набор команд, обеспечивающий условный переход по знаку, позволяет в программе передавать управление в зависимости от результатов арифметических операций. Заметим, что самый старший бит в числе с дополнением до двух всегда указывает знак числа.  [11]

Бит 11, флаг переполнения OF ( overflow flag), в первую очередь служит индикатором ошибки при выполнении операций над числами со знаком. Флаг OF равен 1, если результат сложения двух чисел с одинаковым знаком или результат вычитания двух чисел с противоположными знаками выйдет за пределы допустимого диапазона значений операндов. Кроме того, OF 1, если старший, ( знаковый) бит операнда изменился в результате операции арифметического сдвига.  [13]

Страницы:      1

Алгоритмические языки — 4й семестр

Двоичная арифметика

Современные процессоры семейства IA-32

При программировании аппаратных средств важно уметь быстро переводить числа из двоичной в восьмеричную или шестнадцатеричную системы и обратно. Чтобы перевести двоичное число в восьмеричное, надо разбить его на группы по три бита, начиная с наименее значащих, затем каждую группу по отдельности перевести в восьмеричную цифру. Получившиеся восьмеричные цифры образуют запись исходного числа в восьмеричной системе. Примеры: Чтобы перевести двоичное число в шестнадцатеричное, надо разбить его на группы по четыре бита, начиная с наименее значащих, затем каждую группу по отдельности перевести в шестнадцатеричную цифру. Получившиеся шестнадцатеричные цифры образуют запись исходного числа в шестнадцатеричной системе. Примеры:

hex dec oct bin 0 1 2 3 4 5 6 7 8 9 A B C D E F 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 0 1 2 3 4 5 6 7 10 11 12 13 14 15 16 17 0000 0001 0010 0011 0100 0101 0110 0111 1000 1001 1010 1011 1100 1101 1110 1111

Обратный перевод выполняется аналогично.сдвиг влево SHL<<сдвиг вправо SHR>>

При побитовом отрицании в двоичном представлении числа каждый бит меняет значение на противоположное.

Примеры:

0010 1110 1101 0001 NOT $2E = $D1

1000 1101 0011 1001 0111 0010 1100 0110 NOT $8D39 = $72C6

При побитовом «И» биты результата вычисляются по битам исходных чисел независимо друг от друга. Единица получается только в том случае, если в соответствующих разрядах исходных чисел обе единицы. В остальных случаях — ноль.

Примеры:

0010 1110 0011 0111 0010 0110 $2E AND $37 = $26

1000 1101 0011 1001 1010 0110 0100 1100 1000 0100 0000 1000 $8D39 AND $A64C = $8408

Побитовое «И» используется, чтобы определить значение определенного бита числа. В этом случае в качестве второго операнда (маски) выбирают число, в котором выставлен в 1 только интересующий разряд. В результате будет получен 0, если в исходном числе интересующий разряд был равен 0. Если интересующий разряд был равен 1, то результат выражения равен второму операнду.

xxxX xxxx 0001 0000 000X 0000 a AND $10 = ?

xxxx XXXX xxxx xxxx 0000 1111 0000 0000 0000 XXXX 0000 0000 b AND $0F00 = ?

Побитовое «И» используется, чтобы сбросить в 0 определенные биты числа, не меняя остальные. В этом случае в качестве второго операнда (маски) выбирают число, в котором все биты, кроме битов, соответствующих сбрасываемым, установлены в 1.

xxxx xXxx 1111 1011 xxxx x0xx a := a AND $FD

xxxx xxxx XXxx xxxx 1111 1111 0011 1111 xxxx xxxx 00xx xxxx b := b AND $FF3F

При побитовом «ИЛИ» биты результата вычисляются по битам исходных чисел независимо друг от друга. Ноль получается только в том случае, если в соответствующих разрядах исходных чисел оба нуля, в других случаях — единица.

Примеры:

0010 1110 0011 0111 0011 1111 $2E OR $37 = $3F

1000 1101 0011 1001 1010 0110 0100 1100 1010 1111 0111 1101 $8D39 OR $A64C = $AF7D

Побитовое «ИЛИ» используется, чтобы установить в 1 определенный бит числа, не меняя остальные. В этом случае в качестве второго операнда (маски) выбирают число, в котором выставлен в 1 только интересующий бит, а остальные сброшены.

Xxxx xxxx 1000 0000 1xxx xxxx a := a OR $80

XXXx xxxx xxxx xxxx 1110 0000 0000 0000 111x xxxx xxxx xxxx b := b OR $E000

Побитовое исключающее «ИЛИ» отличается от обычного «ИЛИ» тем, что два единичных бита дают в результате этой операции 0.

Примеры:

0010 1110 0011 0111 0001 1001 $2E XOR $37 = $19

1000 1101 0011 1001 1010 0110 0100 1100 0010 1011 0111 0101 $8D39 XOR $A64C = $2D75

Побитовое исключающее «ИЛИ» используется, чтобы изменить определенный бит числа (инвертировать), не меняя остальные. В этом случае в качестве второго операнда (маски) выбирают число, в котором выставлен в 1 только интересующий бит, а остальные сброшены.

xxxx xxXx 0000 0010 xxxx xxYx a := a XOR $02

xxxx xxxx xxxx XXXX 0000 0000 0000 1111 xxxx xxxx xxxx YYYY b := b XOR $000F

При побитовом сдвиге влево на 1 разряд в двоичной записи первого аргумента справа добавляется 0, а выходящий за разрядную сетку старший бит отбрасывается. Второй аргумент операции сдвига задает, сколько раз необходимо проделать такую процедуру. Сдвиг влево на n бит эквивалентен умножению числа на 2ⁿ и имеет то преимущество, что вычисляется процессором гораздо быстрее, чем целочисленное умножение.

Примеры:

0010 1110 SHL 1 0101 1100 $2E SHL 1 = $5C

1000 1101 0011 1001 SHL 3 0110 1001 1100 1000 $8D39 SHL 3 = $69C8

Сдвиг влево используют, чтобы «собрать» многобайтное число из отдельных байтов. Например:
$78 + $56 SHL 8 + $34 SHL 16 + $12 SHL 24 = $12345678

Различают два типа побитовых сдвигов вправо: арифметический и логический. При арифметическом сдвиге вправо на 1 разряд в двоичной записи первого аргумента слева дублируется старший разряд (бит знака), а младший бит числа отбрасывается. При логическом сдвиге вправо на 1 разряд в двоичной записи первого аргумента слева добавляется 0, а младший бит числа отбрасывается. Второй аргумент операции сдвига задает, сколько раз необходимо проделать такую процедуру. Арифметический сдвиг вправо на n бит эквивалентен делению числа на 2ⁿ с учетом знака, а логический — беззнаковому делению. В Паскале используется логический сдвиг, а в Си — арифметический.

Примеры:

0010 1110 SHR 1 0001 0111 $2E SHR 1 = $17

1000 1101 0011 1001 (логический) SHR 2 0010 0011 0100 1110 $8D39 SHR 2 = $234E

1000 1101 0011 1001 (арифметический) >> 2 1110 0011 0100 1110 -29383 >> 2 = -7346

Совместно с побитовым «И» сдвиг вправо используют, чтобы «разобрать» многобайтное число на отдельные байты. Например:
$12345678 AND $000000FF = $78
$12345678 AND $0000FF00 SHR 8 = $56
$12345678 AND $00FF0000 SHR 16 = $34
$12345678 AND $FF000000 SHR 24 = $12

Арифметические и логические (битовые) операции. Маски

Содержание урока

§26. Особенности представления чисел в компьютере

§27. Хранение в памяти целых чисел

§28. Операции с целыми числами

Сложение и вычитание

Умножение и деление

Сравнение

Поразрядные логические операции

Сдвиги

Вопросы и задания

Задачи

§29. Хранение в памяти вещественных чисел

§28. Операции с целыми числами

Сдвиги

Об операции сдвига вспоминают гораздо реже, чем она того заслуживает. Перечитайте ещё раз алгоритм умножения, описанный выше, и вы убедитесь, что он весь построен на сдвигах. Сдвиги незаменимы тогда, когда требуется проделать ту или иную обработку каждого бита, входящего в число. Наконец, сдвиги двоичного числа позволяют быстро умножить или разделить число на степени двойки: 2, 4, 8 и т. д. Поэтому программисты очень ценят и широко применяют всевозможные разновидности сдвигов.

Идея операции сдвига довольно проста: все биты кода одновременно сдвигаются в соседние разряды ¹ влево или вправо (рис. 4.16).

---

¹ Аппаратно сдвиг реализуется необычайно просто и изящно: регистр, содержащий число, сбрасывается в ноль, при этом из тех разрядов, где исчезла единица, электрический импульс проходит в соседние и устанавливает их в единицу. При этом важно, что все разряды обрабатываются одновременно.

---

Рис. 4.16

Отдельно надо поговорить о двух крайних битах, у которых «нет соседей». Для определённости обсудим сдвиг влево. Для самого младшего бита (на рис. 4.16 он крайний справа) данные взять неоткуда, поэтому в него просто заносится ноль. Самый старший (крайний слева) бит должен потеряться, так как его некуда сохранить. Чтобы данные не пропали, содержимое этого разряда копируется в специальную ячейку процессора — бит переноса ² С (от англ, carry — перенос), с которым может работать процессор.

---

² При программировании на языках высокого уровня бит переноса недоступен.

---

Рассмотренный тип сдвига обычно называется логическим сдвигом. Его можно использовать для быстрого умножения и деления. Рассмотрим, например, 8-разрядный двоичный код 0000 1100, который представляет число 12₁₀. Выполнив логический сдвиг влево, получим 0001 1000, т. е. число 24₁₀, которое вдвое больше! Это не случайность: вспомните, что происходит, если к десятичному числу справа приписать дополнительный ноль, например 34 -> 340.

При сдвиге вправо любое чётное число уменьшается ровно в 2 раза. В случае нечётного значения происходит деление нацело, при котором остаток отбрасывается. Например, из 0001 0001 = 17₁₀ при сдвиге вправо получается 0000 1000 = 8₁₀.

Логический сдвиг влево на 1 разряд увеличивает целое положительное число вдвое, а сдвиг вправо делит на 2 нацело.

Пример. Для умножения числа, находящегося в ячейке Z, на 10 можно использовать такой алгоритм:

1. Сдвиг влево Z (в ячейке Z получаем 2Z₀, где Z₀ — исходное число).

2. X = Z (сохраним 2Z₀).

3. Сдвиг на 2 бита влево X (вычислили 8Z₀).

4. X = X + Z (X = 8Z₀ + 2Z₀ = 10Z₀).

Для некоторых компьютеров такая последовательность выполняется быстрее, чем стандартная операция умножения.

Посмотрим, что получится для отрицательных чисел. Сдвинем влево код 1111 1000 (8-разрядное представление числа —8):

получится 1111 0000. Легко проверить, что это дополнительный код числа -16, т. е. значение удвоилось! Но со сдвигом вправо ничего не получается: из 1111 1000 получаем 0111 1100 — это код положительного числа! Дело в том, что при сдвиге вправо отрицательных чисел, в отличие от положительных, старший разряд надо заполнять не нулём, а единицей! Чтобы исправить положение, вводится ещё одна разновидность сдвига — арифметический сдвиг. Его единственное отличие от логического состоит в том, что старший (знаковый) бит не меняется, т. е. знак числа остаётся прежним (рис. 4.17).

Рис. 4.17

Если применить арифметический сдвиг к коду 1111 1000, получается 1111 1100 — дополнительный код числа -4, т. е. произошло деление на 2. В качестве упражнения проверьте, как ведёт себя отрицательное нечётное число при арифметическом сдвиге вправо.

Арифметический сдвиг влево не требуется, поскольку он ничем не отличается от обычного логического сдвига.

То, что в результате логических сдвигов содержимое крайних разрядов теряется, не всегда удобно. Поэтому в компьютере предусмотрен циклический сдвиг, при котором бит из одного крайнего разряда переносится в другой («по циклу», рис. 4.18).

Рис. 4.18

Циклический сдвиг позволяет «просмотреть» все биты и вернуться к исходному значению. Если сделать последовательно 8 циклических сдвигов 8-битного числа, каждый его бит на каком-то шаге окажется на месте младшего разряда, где его можно выделить с помощью логической операции «И» с маской 1. Так можно «просматривать» не только младший, но и любой другой разряд (например, для выделения старшего разряда нужно использовать маску 80₁₆).

Следующая страница Вопросы и задания

Cкачать материалы урока

Logical Vs. Арифметический сдвиг — Open4Tech

Логический сдвиг и Арифметический сдвиг — это операции манипулирования битами (побитовые операции).

Логический сдвиг

• A Логический сдвиг влево одной позиции перемещает каждый бит влево на один. Свободный младший значащий бит (LSB) заполняется нулем, а самый старший бит (MSB) отбрасывается.
• A Логический сдвиг вправо одной позиции перемещает каждый бит вправо на один.Младший значащий бит отбрасывается, а свободный старший бит заполняется нулем.

Рис. 1 Логический сдвиг на один бит

Арифметический сдвиг

• A Арифметический сдвиг влево одной позиции перемещает каждый бит влево на один. Свободный младший значащий бит (LSB) заполняется нулем, а самый старший бит (MSB) отбрасывается. Он идентичен левому логическому сдвигу.
• A Арифметический сдвиг вправо одной позиции перемещает каждый бит вправо на один.Младший значащий бит отбрасывается, а свободный старший бит заполняется значением предыдущего (теперь сдвинутого на одну позицию вправо) старшего бита.

Рис. 1 Арифметический сдвиг влево и вправо на один бит

Операции арифметического сдвига можно использовать для деления или умножения целочисленной переменной.

Умножение на сдвиг влево:

Результат операции сдвига влево — умножение на 2 ⁿ , где n — количество сдвинутых битовых позиций.

Пример:

Возьмем десятичное число 2, представленное как 4-битное двоичное число 0010 . Сдвинув влево на одну позицию, мы получим 0100 , что равно 4 в десятичном представлении. Если мы сдвинем его еще раз, мы получим двоичное значение 1000 , которое в десятичном представлении равно 8.

Для представления без знака, когда первая «1» сдвинута с левого края, операция переполнилась. Результат умножения больше максимально возможного.

Сдвиг влево для значений со знаком также работает, но происходит переполнение, когда наиболее значимый бит изменяет значения (с 0 на 1 или с 1 на 0).

Разделение сдвигом вправо:

Результатом операции сдвига вправо является деление на 2 ⁿ , где n — количество сдвинутых битовых позиций.

Пример:

Если у нас есть двоичное число 01110101 (117 десятичных) и мы выполняем арифметический сдвиг вправо на 1 бит, мы получаем двоичное число 00111010 (58 десятичное).Итак, мы разделили исходное число на 2.

Если у нас есть двоичное число 1010 (-6 десятичное) и мы выполняем арифметический сдвиг вправо на 1 бит, мы получаем двоичное число 1101 (-3 десятичное) . Итак, мы разделили исходное отрицательное число на 2.

Примечание. В приведенных выше примерах используется представление с дополнением до двух.

Была ли эта статья полезной?

Если у вас есть предложения или вопросы, оставьте комментарий ниже.

Сдвиг и вращение бит — онлайн-инструменты

Битовый сдвиг включает перемещение битов на один или несколько шагов влево или вправо. Когда биты сдвигаются на один шаг, бит, который находится дальше всего в направлении сдвига, отпадет, и новый бит будет добавлен на противоположном конце. Значение нового бита зависит от того, какой тип операции сдвига используется.

Логический сдвиг

Логический сдвиг влево Логический сдвиг вправо

При логических сдвигах новые сдвинутые биты всегда получают нулевое значение. ⁿ , где n — количество шагов, если результат соответствует количеству используемых битов. Если умножение или деление можно заменить операцией сдвига, компьютер часто вычисляет немного быстрее.

Арифметический сдвиг

Левый арифметический сдвиг Правый арифметический сдвиг

Арифметические сдвиги подходят для целых чисел со знаком (т. Е. Целых чисел, которые могут быть как положительными, так и отрицательными), которые используют представление дополнения до двух для отрицательных чисел.

Арифметический сдвиг влево идентичен логическому сдвигу влево и может использоваться таким же образом для умножения как положительных, так и отрицательных значений на два.

При арифметическом сдвиге вправо новые биты получают то же значение, что и знаковый бит (крайний левый бит). Это гарантирует, что знак (+/−) остается неизменным до и после. Один шаг с арифметическим сдвигом вправо равен почти , как целочисленное деление на два. Разница в том, что результат всегда округляется в меньшую сторону (в сторону минус бесконечности), а не в сторону нуля.

Круговой сдвиг

Левый круговой сдвиг Круговой сдвиг вправо

Круговые сдвиги, также называемые поворотами на , используют бит, который был сдвинут на одном конце, и вставляет его обратно как новое значение бита на другом конце. Круговые сдвиги часто используются для криптографических приложений и подходят, когда желательно не терять никаких битовых значений.

Переносное вращение

Перенос влево Перенос вправо

Значение последнего сдвинутого бита обычно сохраняется во флаге переноса.Особый тип кругового сдвига, называемый , вращение через перенос , использует старое значение этого флага для сдвигаемого бита.

Сквозной перенос с поворотом можно использовать для смещения значений, больших, чем обычно может обрабатывать компьютер. Например, если компьютер может выполнять сдвиги только 32 бита за раз, но мы хотим выполнить арифметический сдвиг вправо для 64-битного значения, мы можем выполнить вычисления в два этапа. Сначала мы выполняем арифметический сдвиг вправо на половине, содержащей наиболее значимые биты.Сдвинутый бит будет сохранен во флаге переноса. Чтобы завершить расчет, мы затем выполняем операцию поворота на через перенос во второй половине.

битовый сдвиг (левый сдвиг, правый сдвиг)

битовый сдвиг (левый сдвиг, правый сдвиг) | Торт для интервью

Сдвиг бит перемещает каждую цифру в двоичное представление числа слева или справа. Есть три основных типа смен:

Левый сдвиг

При сдвиге влево старший бит теряется, и На другом конце вставлен 0 бит.

Оператор сдвига влево обычно записывается как «<<».

0010 << 1 → 0100 0010 << 2 → 1000

Один сдвиг влево умножает двоичное число на 2:

0010 << 1 → 0100 0010 это 2 0100 это 4

Логические сдвиги вправо

При сдвиге вправо с логическим сдвигом вправо , наименее значимый бит теряется, и 0 вставлен на другом конце.

1011 >>> 1 → 0101 1011 >>> 3 → 0001

Для положительных чисел один логический сдвиг вправо делит число на 2, выбрасывая остатки.

0101 >>> 1 → 0010 0101 это 5 0010 это 2

Арифметические сдвиги вправо

При переключении вправо с арифметической вправо shift , наименее значимый бит теряется и старший бит копируется .

Языки обрабатывают арифметику и логический сдвиг вправо. различные пути. Java предоставляет два оператора сдвига вправо: >> делает арифметический сдвиг вправо и >>> выполняет логический сдвиг вправо на .

1011 >> 1 → 1101 1011 >> 3 → 1111 0011 >> 1 → 0001 0011 >> 2 → 0000

Первые два числа имели 1 как наибольшую значащий бит, поэтому было вставлено больше единиц во время смены. Последние два числа имели 0 как самый старший бит, поэтому сдвиг вставлен больше 0-х.

Если число закодировано с использованием два дополнения, то арифметический сдвиг вправо сохраняет знак числа, в то время как логический сдвиг вправо делает число положительным.

// Арифметический сдвиг 1011 >> 1 → 1101 1011 это -5 1101 это -3 // Логический сдвиг 1111 >>> 1 → 0111 1111 это -1 0111 это 7

Скоро интервью?

Пройдите бесплатный 7-дневный ускоренный курс по электронной почте. Вы научитесь мыслить алгоритмически , чтобы разбить сложное собеседование по кодированию вопросов.

Никакого предварительного обучения информатике не требуется — мы быстро научим вас, пропуская все чрезмерно академический материал.

Без спама. Отказ от подписки в один клик в любое время.

Ты в! Зайдите в свой почтовый ящик прямо сейчас, чтобы прочитать день первый!

{«id»: 20601036, «username»: «2021-04-30_01: 50: 33__w06 *)», «email»: null, «date_joined»: «2021-04-30T01: 50: 33.438918 + 00: 00» , «first_name»: «», «last_name»: «», «full_name»: «», «short_name»: «friend», «is_anonymous»: true, «is_on_last_question»: false, «percent_done»: 0, «num_questions_done «: 0,« num_questions_remaining »: 46,« is_full_access »: false,« is_student »: false,« first_payment_date »: null,« last_payment_date »: null,« num_free_questions_left »: 3,« terms_has_agreed_to_lage »: false «», «предпочтительный_ редактор_языка»: «», «is_staff»: false, «auth_providers_human_readable_list»: «», «num_auth_providers»: 0, «auth_email»: «»}

×

Войти / зарегистрироваться

Всего за пару кликов.

Мы никогда не будем публиковать сообщения у вас на стене или писать сообщения вашим друзьям.

Где мне ввести свой пароль?

На самом деле, не поддерживает вход по паролю. Никогда не было. Только методы OAuth, указанные выше. Почему?

1. Легко и быстро. Нет потока «сброса пароля». Нет пароля, который нужно забыть.
2. Это позволяет нам избежать хранения паролей, к которым могут получить доступ хакеры, и использовать их, чтобы попытаться войти в электронную почту или банковские счета наших пользователей.
3. Одному человеку становится сложнее поделиться платной учетной записью Interview Cake с несколькими людьми.

«Я так привык думать, что у меня просто нет умения решать вопросы на собеседовании, но вы помогли мне это понять.«Я в долгу перед тобой, чувак! — Ноам

. . .

Сборка

— Примеры арифметического сдвига вправо в моем учебнике сдвиг в единицах, когда MSB был равен нулю

Говоря о C, это было бы ошибкой в ​​книге по стандарту:

• Сдвиг для беззнаковых типов работает так, как вы ожидаете (количество бит для сдвига должно быть меньше ширины сдвигаемого числа и быть неотрицательным).
• Сдвиг на типах со знаком отличается. Если число, которое нужно сдвинуть, отрицательное, то левый сдвиг не определен, однако правый сдвиг определяется реализацией.

Итак, сдвиг для чисел без знака четко определен, но не для чисел со знаком (точнее, нет общего определения).

Для полноты картины в стандарте указано:

Результатом E1 >> E2 являются битовые позиции E2 со смещением вправо E1. Если E1 имеет беззнаковый тип или если E1 имеет знаковый тип и неотрицательное значение, значение результата является неотъемлемой частью частного E1 / 2E2.Если E1 имеет тип со знаком и отрицательное значение, результирующее значение определяется реализацией ().

Итак, принимая во внимание пример OP (положительные числа), нет причин заполнять их одним.

Говоря об арифметическом сдвиге (давайте возьмем x86 в качестве примера):

При арифметическом сдвиге (также называемом сдвигом со знаком), как и при логическом сдвиге, биты, которые соскальзывают с конца, исчезают (за исключением последнего, который входит во флаг переноса). Но при арифметическом сдвиге пробелы заполняются таким образом, чтобы сохранить знак сдвигаемого числа.По этой причине арифметические сдвиги лучше подходят для чисел со знаком в формате дополнения до двух.

Команда SAR заполнится единицей, когда число отрицательное (для сохранения знака), например:

sar 10110011b, 2 # результат 11101100b

( shr 10110011b, 2 # результат 00101100b )

Но опять же, пример OP говорит о положительных числах, поэтому нет причин заполнять их одним.

Подводя итог, можно заполнить единицей при сдвиге вправо, но не в тех случаях.

Арифметический сдвиг — Организация и структура данных — Eduqas — GCSE Computer Science Revision — Eduqas

Двоичные числа умножаются и делятся с использованием арифметических сдвигов, также известных как двоичные сдвиги.

Умножение и деление двоичных чисел с использованием арифметических сдвигов, также известных как двоичные сдвиги

Умножение

Для умножения числа арифметический сдвиг перемещает все цифры двоичного числа влево и заполняет пробелы после сдвига на 0 :

• для умножения на два, все цифры сдвигаются на одну позицию влево
• для умножения на четыре, все цифры сдвигаются на две позиции влево
• для умножения на восемь, все цифры сдвигаются на три позиции влево
• и так на

Пример — вычислить 00001100 (денаринг 12) × 2

Разместите значение	128	64	32	16	8	4	2
Значение					1	1	0	0

Результат: shiftin g на одну позицию слева дает 00011000 (денар 24)

Место значение	128	64	32	16	8	4	2	1 43	60 Значение				1	1	0	0	0

Пример: 00010110 (десятичный 22) × 4

903 903 903 903 903 903 903

Поместите значение	32	16	8	4	2	1
Значение				1	0	1	1	Результат сдвиг на две позиции влево дает 1011000 (денар 88) 90 493 1622 0 смещение за пределы доступных значений заголовка может привести к ошибке переполнения. Деление Чтобы разделить число, арифметический сдвиг перемещает все цифры в двоичном числе вправо: для деления на два, все цифры сдвигаются на одну позицию вправо для деления на четыре, все цифры сдвигаются на две позиции вправо для деления на восемь, все цифры сдвигаются на три позиции вправо и так далее Пример: 100100 (денар 36) ÷ 2 Разрядное значение 128 64 32 8 4 2 1 Значение 1 0 1 1 0 0 9058 Разрядное значение 128 64 32 16 8 4 2 1 Значение 1 0 Результат: сдвиг на одну позицию вправо дает 10010 (денар 18) Пример: денарный 15) ÷ 2 Разрядное значение 128 64 32 9034 3 16 8 4 2 1 Значение 1 0 0 1 0 903 Разрядное значение 128 64 32 16 8 4 2 1 1 1 1 1 Результат: сдвиг на два места вправо дает 111 (денарное 7).Примечание — 15 ÷ 2 = 7,5. Однако в этой двоичной форме десятичные дроби не используются, поэтому десятичные дроби отбрасываются. 1 9037 1 Разрядное значение 128 64 32 16 8 4 2 1 1 Пример: 110110 (денар 54) ÷ 4 Место значение 128 64 32 16 8 4 1 Значение 1 1 0 1 1 0 Результат: сдвиг на два места вправо дает 1101 9080 6 1 Разрядное значение 128 64 32 16 8 4 2 Значение 1 1 0 1 Цифровые схемы и обработка информации Операции арифметического сдвига ARM имеет две операции арифметического сдвига, а именно ASL (арифметический сдвиг влево) и ASR (арифметический сдвиг вправо). ASL — это арифметический сдвиг влево на 0 до 31 места. Освободившиеся биты в самом младшем конце слова заполняются нулями. Он идентичен LSL. В терминах кода это записано в той же синтаксической форме: MOV r0, r1, ASL № 3 ; сдвинуть значение в r1 на 3 позиции влево и заполнить свободные места нулями MOV r0, r1, ASL r2 ; сдвинуть значение в r1 на количество мест, заданных в r2, и заполнить свободные места нулями Арифметический сдвиг влево ASR — это арифметический сдвиг вправо на 0 на 32 места.Освободившиеся биты в самом старшем конце слова заполняются нулями, если исходное значение (исходный операнд) было положительным. Освободившиеся биты заполняются единицами, если исходное значение было отрицательным. Это известно как «расширение знака», потому что самый старший бит исходного значения является битом знака для дополнительных чисел до 2, то есть 0 для положительных чисел и 1 для отрицательных чисел. Следовательно, арифметический сдвиг сохраняет знак чисел. MOV r0, r1, ASR № 3 ; сдвинуть значение в r1 на 3 позиции вправо и заполнить пустые биты копиями исходного старшего бита MOV r0, r1, ASR r2 ; сдвинуть значение в r1 вправо на количество разрядов, заданных в r2, заполнить пустые биты копиями исходного старшего бита Арифметический сдвиг вправо положительное значение Арифметический сдвиг вправо отрицательное значение Чтобы показать разницу между логическим и арифметическим сдвигом вправо, рассмотрим LSR и ASR, где сдвигается значение 112, а сдвиг — 3 разряда.3). Повторное выполнение ASL # 3 преобразует битовый шаблон в 0000 1110 (или 1410). Что будет, если число -112? Сначала создайте битовую комбинацию дополнения до 2 для -112, перевернув битовую комбинацию 112 и прибавив 1: 0111 0000 становится 1000 1111 + 1 становится 1001 0000 Теперь выполните операцию LSR # 3 на 1001 0000. Это сдвигает биты на 3 позиции вправо и заполняет освободившиеся биты нулями: 1001 0000 становится 0001 0010, то есть +1810 Теперь вместо этого выполните операцию ASR # 3 на 1001 0000.3. Руководство пользователя Assembler: Операции сдвига Операции сдвига регистра перемещают биты в регистре влево или вправо на заданное количество бит, называемое длиной сдвига. Возможен сдвиг регистра: Непосредственно по инструкции ASR , LSR , LSL , ROR и RRX , и результат записывается в регистр назначения. При вычислении Operand2 инструкциями, указывающими второй операнд как регистр со сдвигом.Результат используется инструкцией. Допустимая продолжительность смен зависит от типа смены и инструкции, см. описание отдельной инструкции или гибкую описание второго операнда. Если длина сдвига равна 0, сдвига не происходит. Операции сдвига регистров обновляют флаг переноса, кроме случаев, когда указанная длина смены — 0. Арифметический сдвиг вправо (ASR) Арифметический сдвиг вправо на n бит перемещает левые 32-n бит регистра вправо на n мест, в правые 32-n бит результата.Копирует исходный бит [31] регистр в левые n бит результата. Вы можете использовать операцию ASR # n , чтобы разделить значение на регистр Rm на 2 n , с результатом округляется к отрицательной бесконечности. Когда инструкция ASRS или когда ASR # n используется в Operand2 с инструкции MOVS , MVNS , ANDS , ORRS , ORNS , EORS , BICS , TEQ или TST , флаг переноса обновлено до последнего сдвинутого бита, бит [ n -1], регистра Rm . Примечание Если n равно 32 или больше, то все биты в результате устанавливаются в значение бита [31] Rm . Если n равно 32 или больше и флаг переноса обновлен, он обновляется до значение бита [31] Rm . Рисунок 10-1 ASR № 3 Логический сдвиг вправо (LSR) Логический сдвиг вправо на n бит перемещает левые 32-n битов регистра вправо на n помещает в правые 32-n бита результата.Он устанавливает левые n бит результат к 0. Вы можете использовать операцию LSR # n , чтобы разделить значение на регистр Rm на 2 n , если значение рассматривается как целое число без знака. Когда инструкция LSRS или когда LSR # n используется в Operand2 с инструкции MOVS , MVNS , ANDS , ORRS , ORNS , EORS , BICS , TEQ или TST , флаг переноса обновлено до последнего сдвинутого бита, бит [ n -1], регистра Rm . Примечание Если n равно 32 или больше, то все биты в результате сбрасываются на 0. Если n равно 33 или больше и флаг переноса обновлен, он обновляется до 0. Рисунок 10-2 LSR № 3 Логический сдвиг влево (LSL) Логический сдвиг влево на n бит перемещает правые 32-n битов регистра влево на n помещает, в левые 32-n бита результата.Он устанавливает правую n бит результата до 0. Вы можете использовать операцию LSL # n для умножения значения в регистре Rm на 2 n , если значение равно рассматривается как целое число без знака или целое число со знаком с дополнением до двух. Может произойти переполнение без предупреждения. Когда инструкция LSLS или LSL # n , с ненулевым n , используется в Operand2 с инструкциями MOVS , MVNS , ANDS , ORRS , ORNS , EORS , BICS , TEQ или TST , флаг переноса обновляется до последнего сдвинутого бита, бит [ 32 — n ] регистра Rm .Эти инструкции не влияют на флаг переноса при использовании с LSL. # 0. Примечание Если n равно 32 или больше, то все биты в результате сбрасываются на 0. Если n равно 33 или больше и флаг переноса обновлен, он обновляется до 0. Рисунок 10-3 LSL # 3 Повернуть вправо (ROR) Повернуть вправо на n бит перемещает левые 32-n бит регистра вправо на n помещает в правые 32-n бита результата.Он также перемещает правые n бит регистр в левые n бит результата. Когда инструкция RORS или когда ROR # n используется в Operand2 с инструкции MOVS , MVNS , ANDS , ORRS , ORNS , EORS , BICS , TEQ или TST , флаг переноса обновлено до последнего чередования бит, бит [ n -1], регистра Rm . Примечание Если n равно 32, то значение результата такое же, как и значение в Rm , и если флаг переноса обновлен, он обновляется до бита [31] из Rm . ROR с длиной смены, n , более 32 — это То же, что и ROR с длиной смены n -32. Рисунок 10-4 ROR № 3 Повернуть вправо с выдвижением (RRX) Повернуть вправо с расширением перемещает биты регистра вправо на один бит. Копирует флаг переноса в бит [31] результата. Когда инструкция RRXS или когда RRX используется в Operand2 с инструкциями MOVS , MVNS , ANDS , ORRS , ORNS , EORS , BICS , TEQ или TST , флаг переноса обновляется до бита [0] регистра Rm . Оставить комментарий Добавить комментарий Отменить ответ Ваш адрес email не будет опубликован. Обязательные поля помечены * Комментарий * Имя * Email * Сайт