Aeyrwbz c: Функции (C++) | Microsoft Learn

Что такое Функция в Алгебре?

Понятие функции

Определение функции можно сформулировать по-разному. Рассмотрим несколько вариантов, чтобы усвоить наверняка.

1. Функция — это взаимосвязь между величинами, то есть зависимость одной переменной величины от другой.

Знакомое обозначение y = f (x) как раз и выражает идею такой зависимости одной величины от другой. Величина у зависит от величины х по определенному закону, или правилу, которое обозначается f.

Вывод: меняя х (независимую переменную, или аргумент) — меняем значение у.

2. Функция — это определенное действие над переменной.

Значит, можно взять величину х, как-то над ней поколдовать — и получить соответствующую величину

у.

В технической литературе можно встретить такие определения функции для устройств, в которых на вход подается х — на выходе получается у. Схематично это выглядит так:

В этом значении слово «функция» используют и в далеких от математики областях. Например, так говорят о функциях ноутбука, костей в организме или даже о функциях менеджера в компании. В каждом перечисленном случае речь идет именно о неких действиях.

3. Функция — это соответствие между двумя множествами, причем каждому элементу первого множества соответствует один элемент второго множества. Это самое популярное определение в учебниках по математике.

Например, функция у = 2х каждому действительному числу x ставит в соответствие число y, которое в два раза больше, чем

х.

Область определения — множество х, то есть область допустимых значений выражения, которое записано в формуле.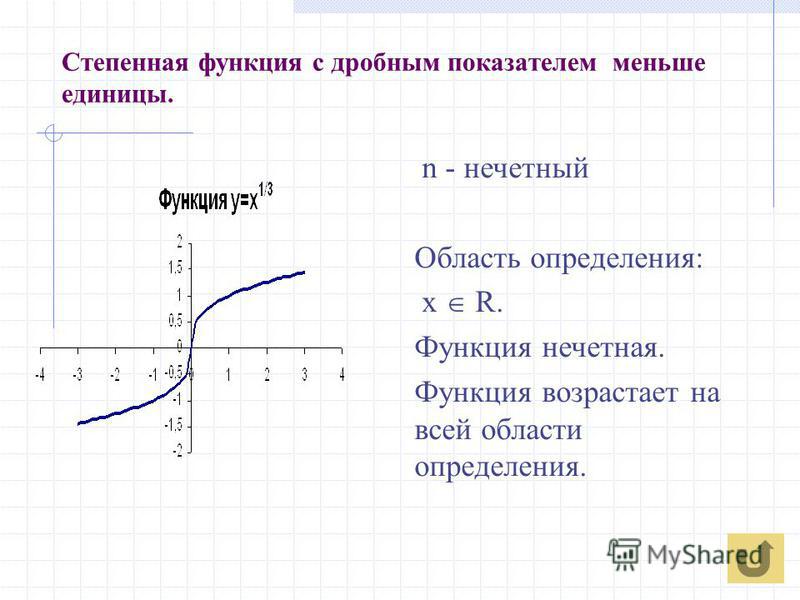

Например, для функции вида

область определения выглядит так:

• х ≠ 0 (потому что на ноль делить нельзя)

И записать это можно так: D (y): х ≠ 0.

Область значений — множество у, то есть это значения, которые может принимать функция.

Например, естественная область значений функции y = x2 — это все числа больше либо равные нулю. Можно записать вот так: Е (у): у ≥ 0.

Для примера рассмотрим соответствие между двумя множествами — человек-владелец странички в инстаграм и сама страничка, у которой есть владелец. Такое соответствие можно назвать взаимно-однозначным — у человека есть страничка, и это можно проверить. И наоборот — по аккаунту в инстаграм можно проверить, кто им владеет.

В математике тоже есть такие взаимно-однозначные функции. Например, линейная функция у = 3х +2. Каждому значению х соответствует одно и только одно значение у. И наоборот — зная у, можно сразу найти х.

х	-3	-2	-1	0	1	2
у = 3х +2	-7	-4	-1	2	5	8

Рассмотрим другие типы соответствий между множествами.

Например, фрукты и цвет каждого:

У каждого фрукта есть свой цвет. Но такое соответствие нельзя назвать взаимно-однозначным. Например, яблоко может быть и красным, и желтым и даже зеленым.

Пример такого соответствия в математике — функция у = х2. Один и тот же элемент второго множества у = 4 соответствует двум разным элементам первого множества: х = 2 и х = -2.

Так на примере с фруктами можно показать соответствие, которое нельзя назвать функцией:

Видно, что в первом множестве есть элементы, которым соответствует два или три элемента из второго множества. Описать такое соответствие математически было бы сложнее.

Демоурок по математике

Узнайте, какие темы у вас «хромают», а после — разбирайте их без зубрежки формул и скучных лекций.

Способы задания функции

Функция — это зависимость «y» от «x», где «x» является переменной или аргументом функции, а «y» — зависимой переменной

или значением функции.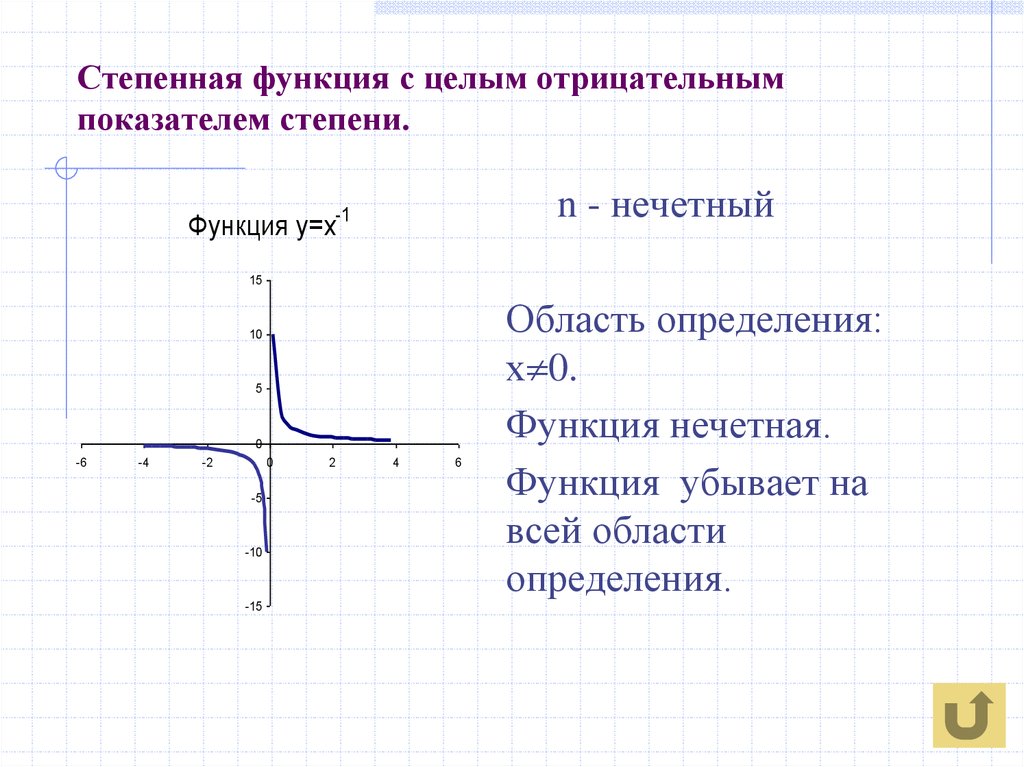

Задать функцию значит определить правило, в соответствии с которым по значениям независимой переменной можно найти соответствующие ее значения. Вот, какими способами ее можно задать:

• Табличный способ — помогает быстро определить конкретные значения без дополнительных измерений или вычислений.
• Графический способ — самый наглядный. На графике сразу видно возрастание и убывание функции, наибольшие и наименьшие значения, точки максимума и минимума.
• Аналитический способ — через формулы. Компактно, и можно посчитать функцию при произвольном значении аргумента из области определения.
• Словесный способ.

Нужно быстро привести знания в порядок перед экзаменом? Записывайтесь на курсы ЕГЭ по математике в Skysmart!

Задать функцию формулой

Через аналитический способ задания функции можно сразу по конкретному значению аргумента «x» найти значение функции «y».

Пример. Дана функция: y(x) = 32x + 5.

Найти: значения функции «y» при x = 0.

Как рассуждаем:

Подставим в формулу вместо «x» число «0». Запишем расчет.

y(0) = 32 * 0 + 5 = 5

Ответ: y = 5.

Задать функцию таблицей

Любую функцию можно записать с помощью таблицы. Для этого достаточно найти несколько значений «y» для произвольно выбранных значений «x».

Пример. Дана функция: y(x) = −x + 4.

Найти: значения «y» при x = -1, x = 0 и x = 1.

Как рассуждаем:

1. Подставим в функцию y(x) = −x + 4 вместо «x» первое число -1.

2. Продолжим подставлять в функцию y(x) = −x + 4 данные значения x (0 и 1).
y(0) = −0 + 4 = 4
y(1) = −1 + 4 = 3

Не путаем знаки!

Когда в функцию нужно подставить отрицательное число — включаем внимательность на максимум. Возьмите нужное число в скобки, чтобы точно не потерять знак минус.

3. Запишем полученные результаты в таблицу:

x	y
−1	5
0	4
1	3

Так мы получили табличный способ задания функции y(x) = −x + 4.

Задать функцию графиком

График функции — это объединение всех точек, когда вместо «x» можно подставить произвольные значения и найти координаты этих точек.

График функции показывает множество всех точек, координаты которых можно найти, просто подставив в функцию любые числовые значения вместо «x».

Пример. Дана функция: y(x) = −2x + 1.

Найти: значения «y» для произвольных «x», а именно −1, 0, 1.

Как рассуждаем:

1. Подставим данные значения х в функцию и запишем результаты:

x	Рассчет
−1	y(−1) = −2 * (−1) + 1 = 2 + 1 = 3
0	y(0) = −2 * 0 + 1 = 0 + 1 = 1
1	y(1) = −2 * 1 + 1 = −2 + 1 = −1

2. Каждая пара значений «x» и «y» — это координаты точек по оси Ox (абсцисса точки) и Oy (ордината точки).

Дадим названия каждой точке и запишем их координаты:

Имя точки	x	y
A	−1	3
B	0	1
C	1	−1

3. Отметим точки А (-1; 3), B (0; 1) и С (1; -1) на прямоугольной системе координат.

4. Соединим отмеченные точки прямой.

Проведенная прямая будет графиком функции y(x) = −2x + 1.

Степенная функция с нечетным показателем степени , ее свойства и график 9 класс онлайн-подготовка на Ростелеком Лицей |

 

 

Тема: Числовые функции

 

Урок: Степенная функция с нечетным показателем степени её свойства и график

 

1. Введение

 

 

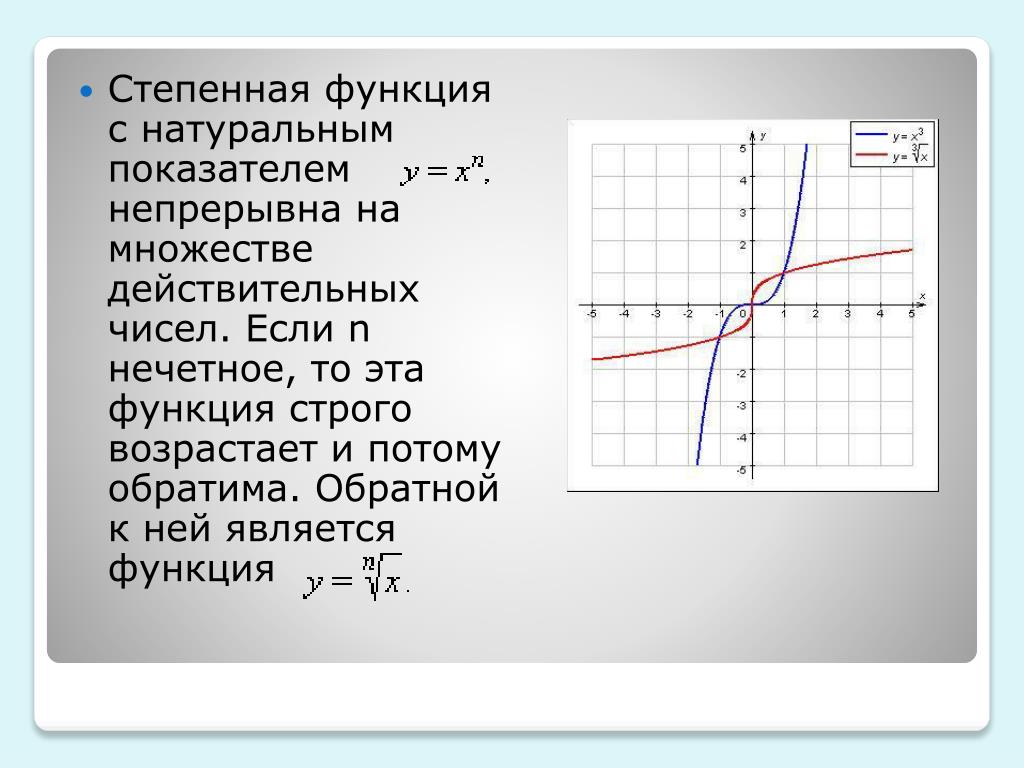
Мы рассмотрим свойства и график степенной функции с нечетным показателем степени т.е. функции вида

 

 

2. Функция и её свойства

 

 

Рассмотрим функцию  (рис. 1).

 

График проходит через три фиксированные характерные точки:

Прочтем график и сформулируем свойства функции.

2. Функция нечетная, График симметричен относительно начала координат.

3. Функция возрастает.

4. Не ограничена ни сверху, ни снизу.

5 .Не имеет ни наибольшего, ни наименьшего значения.

6. Функция непрерывна. Это значит, что кривую можно изобразить, не отрывая карандаша от бумаги.

7.

8. Выпукла вверх при выпукла вниз при .

 

3. Функция и её свойства

 

 

Рассмотрим свойства иных степенных функций с нечетным показателем степени.

 

Функция

1.

2. Функция нечетная,

3. График проходит через три фиксированные точки:

4. Функция возрастает.

5. Не ограничена ни сверху, ни снизу.

6. Нет ни наибольшего, ни наименьшего значения.

7. Функция непрерывна.

8.

9. Выпукла вверх при выпукла вниз при

 

4. Примеры

 

 

Рассмотрим взаимное расположение кривых на примере функций (рис. 2).

 

Например,

Рассмотренное свойство является ключом к решению ряда задач.

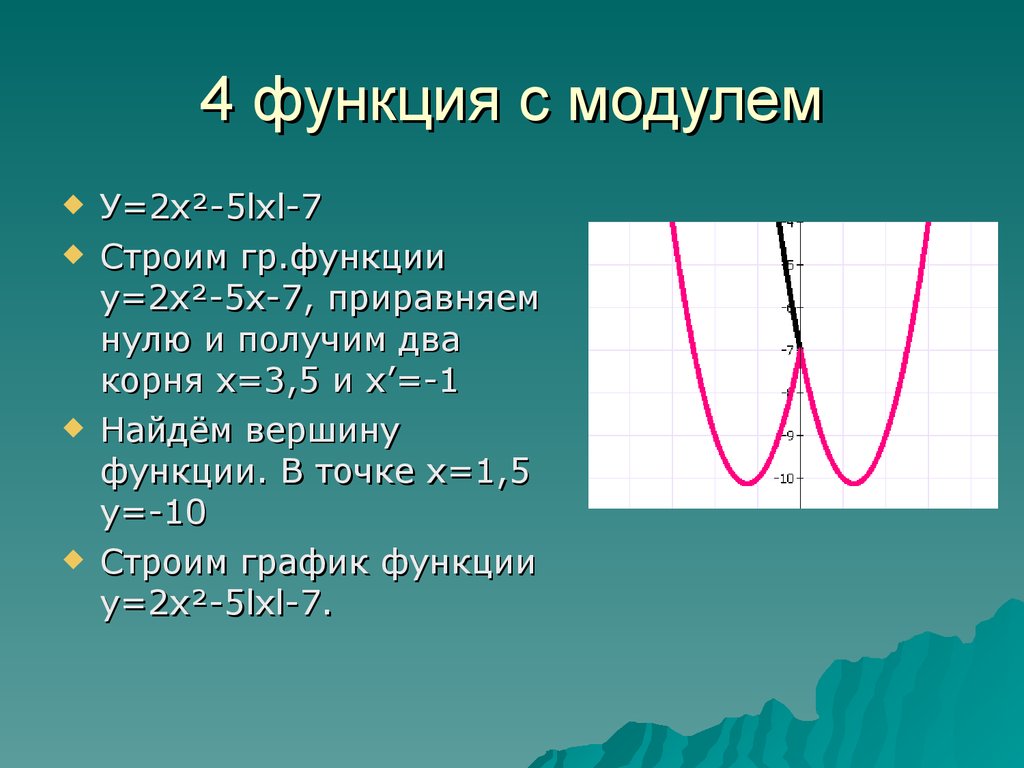
1. Найдитеи постройте график функции.

Решение:

График получим из известного нам графика  путем сдвига на две единицы вправо (рис. 3).

 

Отметим точки пересечения с осями.

Ответ:

2.  График данной функции получаем из графика функции  сдвигом на одну единицу вверх (рис. 4).

 

Ответ:

 

5. Свойство функции с нечетным показателем

 

 

Мы изучаем степенные функции с нечетным показателем степени. Все они монотонно возрастают на всей области определения. Отметим важное свойство:

 

Если функция возрастает, а функция  убывает, и если уравнение имеет корень, то этот корень – единственный (рис. 5).

 

6. Решение задач

 

 

Рассмотрим примеры:

 

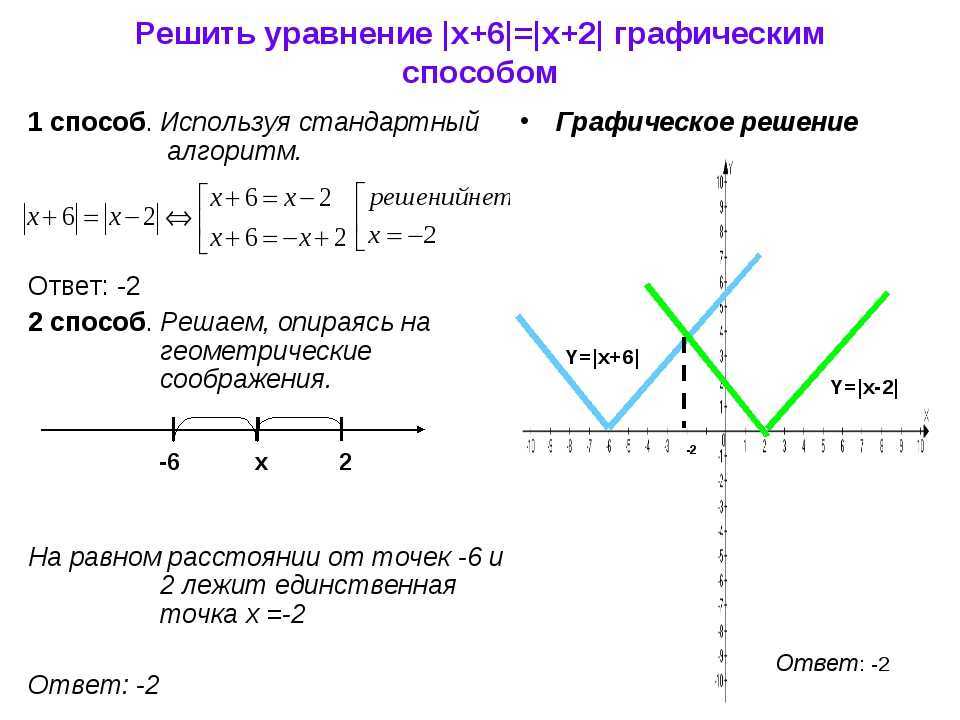
1. Решить уравнение

решить неравенство

Решение:

Корень

Функция  монотонно возрастает, функция  монотонно убывает, корень есть, значит, он единственный.

Решением неравенства является луч

Ответ:

2. Построить график кривой

Решить уравнение

Решить неравенство

Решение:

Построим график функции  Для этого график функции  сдвинем на 3 вправо вдоль оси x и на 1 вниз вдоль оси y(рис. 7).

 

Функция монотонно возрастает, поэтому прямая пересекает кривую только в одной точке. Это точка

Решением неравенства является луч  На этом промежутке кривая расположена выше оси x.

Ответ:

3. Найти область значений функции  где

Решение:

Если x то yвозрастает и

Ответ:

4. Определить число решений системы

Решение:

Построим график каждой функции. График функции симметричное отображение графика  относительно оси x.Если  монотонно возрастает, то  монотонно убывает.

График функции  получаем сдвигом графика  на 6 вниз вдоль оси у(рис. 9).

Функция  монотонно возрастает, и если кривые пересекаются, то только в одной точке.

Ответ: Система имеет только одно решение.

 

7. Заключение

 

 

Мы рассмотрели график и свойства степенной функции с нечетным показателем степени. На следующем уроке мы рассмотрим задачи на степенную функцию с натуральным показателем.

 

 

Список рекомендованной литературы

1. Мордкович А.Г. и др. Алгебра 9 кл.: Учеб.для общеобразоват. учреждений.- 4-е изд. – М.: Мнемозина, 2002.-192 с.: ил.

2. Мордкович А.Г. и др. Алгебра 9 кл.: Задачник для учащихся общеобразовательных учреждений / А. Г. Мордкович, Т. Н. Мишустина и др. — 4-е изд. — М.: Мнемозина, 2002.-143 с.: ил.

3. Макарычев Ю. Н. Алгебра. 9 класс : учеб.для учащихся общеобразоват. учреждений / Ю. Н. Макарычев, Н. Г. Миндюк, К. И. Нешков, И. Е. Феоктистов. — 7-е изд., испр. и доп. — М.: Мнемозина, 2008.

4 .Алимов Ш.А., Колягин Ю.М., Сидоров Ю.В. Алгебра. 9 класс. 16-е изд. — М., 2011. — 287 с.

5. Мордкович А. Г. Алгебра. 9 класс. В 2 ч.