Золотое сечение примеры: что это такое, пропорции, принцип, применение в архитектуре и строительстве

Примеры золотого сечения в архитектуре, его применение

Примеры золотого сечения в архитектуре найти можно везде, когда умеешь его видеть. Выяснить это даже школьнику по силам. В 2013 году ученица 10 класса Сивакова Елена провела собственное исследование зданий 19-20 веков. Проследим, как она это сделала, и научимся видеть и определять его в архитектурных сооружениях за 5 минут. После прочтения статьи не останется вопросов о том, что это такое, и можно ли его необычные свойства использовать в своей жизни.

Содержание

7+ примеров золотого сечения в архитектуре России

Санкт-Петербург

Здания исторического центра Санкт-Петербурга построены в разных архитектурных стилях, таких как барокко, классицизм, ампир, эклектика, необарокко, неоготика. Подчиняются ли они золотому правилу?

Исаакиевский собор

Придворный архитектор Александра I Огюст Монферран строил этот собор с 1819 по 1858 гг. Стиль позднего классицизма, в котором уже проявлены черты неоренессанса и эклектики. Елена задалась вопросом: «В чём же причина гармонии довольно громоздкого здания?»

Свой поиск она начала, как рекомендуется в методике профессора Московского архитектурного института Ю.Н.Герасимова, с фасада собора. На чертеже просматриваются три ряда Золотого сечения.

Первый ряд определён шириной здания, которая принята за 400 ед. и представляет такие цифры 400, 247, 153, 94, 58…

Если 400 разделим на число ≈1,618, то получим приблизительно 247; повторяем действие со следующим числом: 247: 1.618≈153.

И так находим все числа. Теперь смотрим на рисунок. Основная часть с колоннами вписывается в прямоугольник со сторонами 400 и 247. Поскольку стороны находятся в соотношении Ф≈1.618, то они образуют Золотой прямоугольник.

Следующий ряд представлен высотой здания: 370, 228, 140, 87, 53, 33, 20, 12. Эти размеры заложены в более мелкие детали. По вертикали Исаакиевский собор делится Золотым сечением у основания купола, что делает соотношение основной части и купола гармоничным.

Третий ряд размеров начинается со 113, и являет ширину основания главного купола: 113, 69, 42, 26, 16. Числа этого ряда встречаются в размерах окон, в высотах колонн и других деталей собора.

Золотые прямоугольный и равнобедренный треугольники имеют место в здании Исаакиевского собора, как видно из рисунка.

Кунсткамера

На Университетской набережной Васильевского острова стоит здание Кунсткамеры, заложенное в 1718 году под руководством немецкого архитектора Георга Маттарнови: Петровское барокко, два 3-этажных корпуса и сложная многоярусная купольная башня.

Исследование начинается с главных величин: высоты и длины здания, от которых строится золотой ряд. Длина — 450 ед., далее 277, 170, 105, 65, 40, 24. Такие размеры можно видеть в высоте и широте разных уровней башни, длине корпусов. Сама башенная часть вписана в золотой равнобедренный треугольник от основания до вершины. Золотое сечение просматривается в большей степени именно в этом главном элементе, что правильно с точки зрения архитектуры.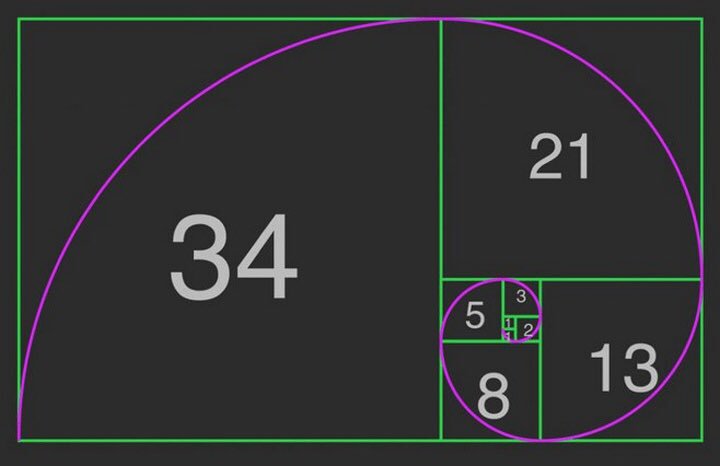 Вывод: основа Кунсткамеры подчиняется золотому правилу и сохраняет композиционную гармоничность.

Новый золотой ряд начинает высота здания: 211, 130, 80, 49, 30. Глядя на размеры чертежа, становиться понятно, что выбор трёхэтажного вида корпусов обусловлен соразмерностью с башней.

Торговый дом «Эсдерс и Схейфальс» на пересечении Мойки и Гороховой

Построено в 1907 году по проекту Владимира Александровича Липского и Константина Николаевича де Рошефора (Рошфора). В 1905 г. бельгиец С. Эсдерс и нидерландец Н. Схейфальс подали прошение о разрешении построить пятиэтажное здание с куполом и шпилем на угловой башне для их торгового дома вместо старого.

С длины здания в 671 ед. начинается ряд Золотого сечения, наблюдаемого в размерах: 671, 414, 256, 158, 98, 60, 37, 23. Обращаем внимание на основной элемент — шпиль. Убеждаемся, что композиционное решение завершено гармоничным сочетанием высотных величин.

Дом Советов на Московской площади

Построен в 1941г по проекту Ноя Абрамовича Троцкого. Здание советского периода рассматривают как творческую интерпретацию классики. Центральный портик с четырнадцатью колоннами завершает скульптурный ансамбль на тему строительства социализма и гербом Российской Советской Федеративной Социалистической Республики.

По бокам симметрично расположены пятиэтажные корпуса. Длина Дома достигает 1472 ед., из которого методом деления на число Ф получается ряд размеров элементов здания: 1472, 909, 562, 34, 214, 132, 81, 50 (Приложение 21): высоты сооружения, высоты входа и др.

Вершина Золотого равнобедренного треугольника совпадает с вершиной здания, а его стороны проходят через вехние точки главного входа. Прямоугольный золотой треугольник образован вершинами в верхушке здания и в конце внутренней части бокового крыла. Пропорциональность очевидна, хотя и не имеет большой композиционной значимости.

Москва

Московский Государственный Университет на Воробьёвых горах

Над его проектом работал коллектив под управлением Б. М.Иофана, которого позже сместили с должности главного архитектора. Образец послевоенной советской архитектуры выстроен с 1949 по 1953 годы.

Б.М.Иофан предложил композицию из пяти составляющих с центральной башней. В годы строительства это было самое высокое здание в Европе.

Длина здания равна 1472 ед. и начинает ряд: 909, 562, 347, 214, 132, 81, 50. Золотому сечению подчиняются, в основном высотные размеры. Из ширины башни проистекает другой ряд: 538, 332, 205, 126, который видим в широтных размерах.

Золотой прямоугольный треугольник гипотенузой проходит через угол здания и захватывает пристройки.

Таким образом, во всех исследуемых зданиях ученица обнаружила Золотое сечение, сохраняющее гармонию.

5 примеров дополнительно

Чтобы упростить задачу поиска ЗС, можно брать рациональные дроби 3/2; 5/3; 8/5; 13/8; 21/13; 34/21; 55/34; 89/55; и так дальше. Закономерность ясна: 3+2 =5; 5+3=8; 8+5=13… Или ещё проще. Сделайте себе циркуль для определения пропорции по инструкции в видео. Времени уйдет минут 10. Как пользоваться этим циркулем для определения пропорциональности элементов тоже расскажут и покажут.

Применяя этот способ, находим золотую пропорцию русского зодчего Матвея Казакова в кремлёвском здании сената, да и во всех остальных работах: Пречистенском дворце в Москве, Благородном собрании, Голицынской больнице (им. Пирогова)…

Созданный другим великим архитектором Василием Ивановичем Баженовым дом Пашкова в Москве (Российская государственная библиотека) причисляют к образцам совершенных архитектурных памятников, в котором легко определить ЗС.

Ужасный символ Парижа и золотое сечение

Когда в Париже собирали металлическую Эйфелеву башню, многие французы возмущались. Критики писали о ней, как об «уродстве города», «сраме Парижа», «тощей пирамиде из металлических лестниц». В их числе были Эмиль Золя, Дюма-младший, Ги де Мопассан. Сейчас этот самый посещаемый памятник является гордостью парижан. Может быть виной тому «божественная» пропорция?

Она же наблюдается и самом знаменитом французском соборе Нотр-Дам-Де-Пари.

Вся правда о древних строителях

Интуитивно или сознательно великие архитекторы строили здания с учётом этих пропорций? Античные математики знали о золотом сечении со времён Пифагора. Находятся всё новые подтверждения его применения в архитектурных пропорциях. Однако не найти ни одной древней записи с прямой рекомендацией использовать “божественную пропорцию”. Нет таковой и у Витрувия (I век до н. э.), написавшего «Десять книг об архитектуре», в которых он рассматривал пропорциональности в том числе. Странный факт, не правда ли?

Может все выше приведённые исследования являются подгонкой под известный результат? Не так сложно выбрать из множества архитектурных элементов те, которые подтверждают гипотезу, т. к. абсолютной точности никто не требует. Логично задуматься над вопросом: «Что если греки НЕ применяли золотое сечение?»

Собственно говоря, и для Луки Пачоли, написавшего в 1509 году труд «Божественная пропорция», не столь важно было его прикладное значение. Важно было обосновать её мистическую природу. А применять его осознанно стали только с момента издания книги.

Тайна архитектуры Древней Греции

Красивые и гармоничные объекты всегда отвечают правилу ЗС, а при анализе величин определяется эта пропорциональность. Искусствоведы внимательно изучили греческий Парфенон, возведённый в честь победы над персами — храм богини Афины. Отношение длины храма к ширине даёт золотое число с маленькой погрешностью. Если отнять от длины сооружения 14 см и прибавить к ширине, то получится полное совпадение с математической величиной. Фасад здания немного сужается кверху, отклоняется от прямоугольной формы. Учитывая визуальное восприятие, сделано это строителями сознательно. Поэтому считать его прямоугольником золотого сечения не совсем корректно. Но пропорции соблюдаются, так что логично предположить, что архитекторы Иктин и Калликрат умышленно заложили правило в проект?

Мифы и диковинные факты о пирамиде

Пирамида Хеопса также выстроена с учётом этого условия. Не вдаваясь в математическое доказательство наличия золотой формулы, скажем только, что в нём присутствуют прямоугольный золотой треугольник, сторонами которого являются высота и половина стороны основания строения. Ничего удивительного?

Но тогда возникает вопрос об уровне древнеегипетской математики. Выходит, что теорема Пифагора была им известна за два тысячелетия до рождения самого учёного. Внимание привлекает факт, что наследники Хеопса строили свои пирамиды уже с другими пропорциями. Почему?

Установлено, что сооружения пирамидальной формы с ЗС оказывают на находящихся в них феноменальное воздействие: растения лучше растут, металлы становятся прочнее, вода долго остаётся свежей. Учёные много лет работают с этими загадками, но тайна остаётся.

Замечено, что пирамида приводит структуру пространства в слаженное состояние. Всё, что попадает в зону действия, тоже организуется подобным образом: психоэмоциональное состояние людей улучшается, вредные для человека излучения уменьшаются, исчезают геопатогенные зоны. Интернет утверждает, что если размер фигуры увеличивается в два раза, то влияние пирамиды усиливается в сто раз.

Как же всё-таки построить «Золотой» дом для себя?

Правильное распределение энергий внутри дома, гармоничные конструкции в сочетании с экологией и безопасностью строительных материалов побуждают современных архитекторов и дизайнеров использовать принципы и понятия Золотого сечения. Это увеличивает смету и создаёт впечатление глубокой проработки проекта. Стоимость возрастает на 60-80%.

Для талантливых художников и архитекторов правило сохраняется интуитивно во время творческого процесса. Однако некоторые из них сознательно реализуют это положение.

В природе подобная соразмерность встречается везде. Тот, кто чувствует гармонию пространства, создаст пропорциональное здание без специальных для этого усилий.

Например, наши предки строили хоромы соразмерные человеку. Мерили высоту и длину в саженях, локтях, аршинах, пядях. Никто не возражает, что в человеческом теле соблюдена золотая пропорция? Длина руки от кончиков пальцев до подмышки относится к расстоянию от той же точки до локтя как эта величина к размеру ладони.

Известный французский архитектор Ле Корбюзье для расчёта параметров будущего дома и интерьера использовал в качестве отправной единицы рост хозяина. Все его работы по-настоящему индивидуальны и гармоничны.

5 способов соблюдать правило в интерьере

1. В доме, построенном без учёта соотношения, можно сделать перепланировку комнат, чтобы пропорции соответствовали.
2. Иногда достаточно переставить мебель или сделать дополнительную перегородку.
3. Аналогичным образом меняется высота и длина окон и дверей.
4. В цветовом оформлении получение упрощённого соотношения достигается за счёт 60% основного цвета, 30% — оттеняющего, и остальных 10% — усиливающих восприятие тонов.
5. Высота и длина мебели должна соизмеряться высотой потолков и шириной простенков.

Приложение этой нормы в интерьере, как архитектурно оформленном пространстве, объединяют с понятиями самоорганизации, рекурсии, асимметрии, красоты.

О золотом сечении простыми словами

Что же это такое? Отрезки золотой пропорции выражаются бесконечной иррациональной дробью, десятичное значение которой равно приближённо числу Ф≈1,618 или Ф≈1,62. Другими словами: если берём целое и делим его на две части так, что одна из них составляет 62%, а другая — 38%, получаем Золотую пропорцию.

Золотой прямоугольник: когда длину большей стороны делим на длину меньшей и получаем число Ф. При делении меньшей на большую получается обратное значение φ ≈ 0,618.

Золотой равнобедренный треугольник: если отношение размера одной боковой стороны и размера основания составляет золотое число Ф; угол между равными сторонами равен 36°.

Золотой прямоугольный треугольник Кеплера объединяет в себе теорему Пифагора и ЗС: соотношение квадратов его сторон составляет 1,618.

Оцените полезность статьи, поделитесь с друзьями и добавьте в закладки, чтобы было легко найти.

Смотрите познавательное видео по теме

Золотое сечение: пропорции и примеры

С давних времен идеальными чертами лица назывались те, которые соответствуют так называемому правилу «золотого сечения». Считается, что лица, максимально приближенные к таким пропорциям, воспринимаются окружающими как более привлекательные. Об этом стандарте красоты 1 февраля рассказал «Известиям» пластический и реконструктивный хирург клиники эстетической медицины «Время Красоты» Рашид Велиханов.

«Для начала следует разобраться, что же понимается под «золотым сечением». Если говорить на языке геометрии, то это пропорциональное деление отрезка (в нашем случае лица) на неравные части, при котором меньший отрезок так относится к большему, как больший ко всему.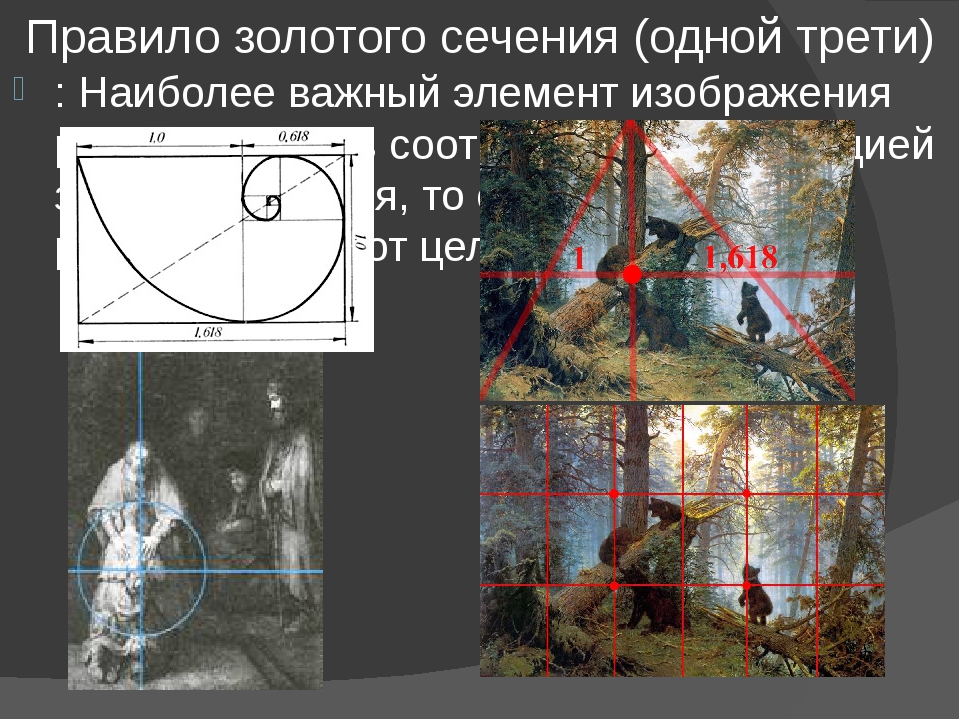 Если в результате таких вычислений получается примерно 1,618 (1,62, если округлить), то это и есть «золотое сечение». Чтобы было понятнее, давайте рассмотрим эти вычисления на примере лица», — предложил врач.

Так, для определения того, насколько лицо подходит под этот стандарт красоты, необходимо провести следующие вычисления: разделить высоту лица на ширину лица, ширину рта на ширину носа, расстояние между зрачками на расстояние между бровями. Чем ближе полученное число будет к 1,62 в каждом конкретном случае, тем больше черты лица подходят под «золотое сечение».

Как уточнил хирург, при расчетах также учитываются второстепенные соотношения.

«Измеряется расстояние между внутренними углами глаз, которое должно быть равно длине глаза и ширине носа. Высота подбородка должна быть равна длине глаза. Кроме того, лицо условно делится на три горизонтальных участка: лоб от линии роста волос до бровей, затем от бровей до кончика носа, а от него до подбородка. В идеале эти три части должны быть равны друг другу. Помимо этого, проводятся две вертикальные прямые линии вниз от зрачков, которые должны пересекаться с уголками рта. Таким образом, идеальным считается овальное лицо с правильными чертами», — объяснил Велиханов.

Специалист перечислил некоторых звезд, чьи лица максимально соответствуют «золотому сечению»: Эмбер Херд, Скарлет Йохансон, Эмили Ротаковски, Белла Хадид, Ким Кардашьян, Девид Бекхем, Бред Питт, Хью Джекман, Роберт Паттисон.

«Сегодня принципы «золотого сечения» активно используется в практике пластических хирургов, косметологов и визажистов. У пластических хирургов, например, есть специальная программа, накладывающая маску с идеальными пропорциями на лицо пациента. Благодаря этому можно смоделировать результаты планируемой операции и подогнать их под «золотое сечение». Кроме того, на просторах интернета можно без проблем найти калькуляторы симметричности лица, с помощью которых каждый человек может сопоставить свои данные и получить результат», — отметил хирург.

По его словам, помимо симметричного лица на привлекательность большое значение также оказывают состояние и тон кожи, прическа и другие факторы.

Кроме того, каждый человек индивидуален, и если его черты лица не подходят под «золотое сечение», то это вовсе не значит, что он не красив, добавил Велиханов.

23 декабря хирург Амжад Аль-Юсеф назвал самые популярные пластические операции на лице. Так, в тройке лидеров прочно закрепилась операция по коррекции носа — ринопластика.

13 реальных примеров золотого сечения, которые вы будете рады узнать

Золотое сечение выведено из последовательности Фибоначчи и проявляется повсеместно в различных природных элементах. Это часть естественных измерений большинства биологических и небиологических сущностей на этой планете.

«Геометрия имеет два великих сокровища: одно — теорема Пифагора; другой — деление линии на крайнее и среднее отношение. Первую мы можем сравнить с мерой золота; второе мы можем назвать драгоценным камнем».
―Иоганн Кеплер

Золотое сечение обозначается множеством различных терминов, таких как золотое сечение, золотое сечение, срединное сечение, божественная пропорция, золотое сечение, а также крайнее и среднее соотношение. Все эти названия указывают на то, что это соотношение размеров данного объекта, но это описание кажется расплывчатым. Более точным способом его описания было бы назвать его соотношением отрезков прямой, когда прямая делится на две части (а и b), так что отношение «а» к «b» такое же, как отношение от (а+б) до «а». Это соотношение называется золотым сечением и обозначается греческой буквой фи (Φ). Его математическое значение равно 1,6180339.8… Для общих целей значение принимается равным 1,618. Это значение можно получить, используя основные квадратные уравнения, геометрию или анализируя последовательность Фибоначчи. Эта последовательность представляет собой ряд чисел, где каждое число является суммой двух предшествующих ему чисел. Начальная последовательность следующая — 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144 и так далее. Интересным аспектом этого ряда является то, что после первых четырех-пяти чисел, если каждое число разделить на его непосредственное предыдущее число, оно дает значение, близкое к 1,618. Это значение приближается к золотому сечению по мере продвижения серии.

Представление золотого сечения

Ряд Фибоначчи часто визуально представляется так, как указано выше. Каждое число представлено в виде квадрата, сторона которого равна значению числа. Затем эти квадраты размещаются рядом по мере развития ряда, чтобы получить так называемый прямоугольник Фибоначчи. Если через углы каждого квадрата провести спираль, получится спираль Фибоначчи. Точно так же, как соотношение чисел ряда дает золотую пропорцию, так и в случае с этой спиралью. Отношение каждого витка спирали или отношение ее увеличивающихся радиусов дает золотое сечение. Это обычная форма проявления божественного соотношения в природных элементах

Выяснение взаимосвязи между золотым сечением и последовательностью Фибоначчи имеет жизненно важное значение для обнаружения и идентификации проявления этого конкретного отношения в природе.

Реальные примеры золотого сечения

Цветочные лепестки

Почти у всех цветковых растений количество лепестков на цветке равно числу Фибоначчи. Крайне редко количество лепестков может быть не таким. Примеры этого явления: бархатцы, цинерария и маргаритки имеют 13 лепестков; у астры и цикория по 21 лепестку; цветы подорожника и пиретума имеют 34 лепестка и т. д. Золотое сечение видно в этих цветах с точки зрения расположения лепестков. Все лепестки изогнуты примерно на 1,618034°, чтобы оптимизировать воздействие солнечного света.

Кроме того, цветы с несколькими слоями лепестков демонстрируют последовательность Фибоначчи для каждого слоя, а вид сверху на цветок представляет собой спираль Фибоначчи. Соотношение лепестков между каждым слоем является золотым сечением. То же самое относится и к расположению листьев большинства растений.

Соцветия семени

Спиралевидные узоры соцветий, как у подсолнухов, являются прекрасным примером процесса Фибоначчи и божественного соотношения. В семенной головке, как правило, новые семена образуются в центре и мигрируют наружу радиальным образом по мере взросления. Поскольку каждая мутовка семенных головок следует последовательности, логически следует, что отношение любых двух соседних мутовок является золотым сечением. Семенные головки также имеют две различные радиальные ориентации. Если сравнить общее количество семенных головок, ориентированных в двух направлениях, получится божественная пропорция.

Сосновые шишки

Подобно спиралевидным узорам семенных головок, стручки сосновых шишек также расположены по спирали Фибоначчи. Каждая шишка состоит из пар чередующихся оборотов, каждый из которых ориентирован в направлении, противоположном другому обороту. Соотношение оборотов каждого стручка и отношение числа стручков в последовательных мутовках есть золотое сечение, т. е. 1,618.

Фрукты и овощи

Та же картина наблюдается и в случае фракталоподобных фруктов и овощей. Наиболее распространенными примерами являются ананас, красная капуста, артишоки и цветная капуста по-румынски (изображение). В этих фруктах и ​​овощах легко визуализировать спиральные узоры на их поверхности.

Схема ветвления деревьев

Когда основной ствол дерева разветвляется, он дает начало боковой ветви, которая в дальнейшем делится и дает еще две ветви. Одна из этих ветвей разделится и сформирует две новые точки роста, а другая ветвь останется бездействующей. Это происходит в каждом случае ветвления по длине дерева в течение его жизни. Это порождает ответвления, количество которых соответствует прогрессии Фибоначчи. Это означает, что в каждом узле ветвления отношение новых ветвей к старым составляет 1,618.

Раковины

Внешняя известковая раковина улиток, морских раковин и других подобных образцов также имеет спираль Фибоначчи. Очевидными примерами являются раковины улиток и наутилусов, где хорошо видна спираль. Каждая камера наутилуса по сравнению с его непосредственным преемником раскрывает золотое сечение. То же самое верно и в случае с улитками. У моллюсков двустворчатого типа, у которых на раковине имеются бороздки, отношение борозд к гребням равно золотой середине. То же явление наблюдается и в случае рогов баранов и коз, формы некоторых паутин и внутренней улитки уха.

Спиральные галактики

Спираль Фибоначчи также наблюдается в случае спиральной галактики. Наша собственная галактика — Млечный Путь — является одним из таких небесных образований. Некоторые другие сущности в галактике также демонстрируют золотое сечение. Он находится в соотношении диаметров Сатурна и его колец. Это также отношение расстояний Венеры и Земли от Солнца. Интересно, что соотношение оборотов этих двух планет также дает золотое сечение.

Ураганы

Как и в случае с раковинами и спиральными галактиками, движение воздуха и ветра в ураганах также следует спирали Фибоначчи, раскрывая золотое сечение. Спиральный характер урагана во многом обусловлен одновременным движением воздуха и атмосферных элементов между областью низкого давления (эпицентром урагана) и окружающей областью высокого давления.

Лица

Различные черты человеческого лица демонстрируют божественные пропорции. Это видно, если сравнить взаимное расположение черт лица. Некоторые распространенные примеры таких соотношений:

► Центр зрачка ● Нижняя часть зубов ● Нижняя часть подбородка
► Внешний и внутренний край глаза ● Центр носа
► Внешние края губ ● Верхний край губ
► Ширина центра зуб ● Ширина второго зуба
► Ширина глаза ● Ширина радужной оболочки

Наряду с этим, человеческое лицо также имеет золотое сечение с точки зрения соотношения сторон по вертикали и горизонтали. Кроме того, форма уха напоминает форму спирали Фибоначчи. Многочисленные исследования пришли к выводу, что лица с чертами лица, которые демонстрируют точное золотое сечение, считаются очень привлекательными и считаются чрезвычайно красивыми.

Динамика воспроизводства

В популяциях медоносных пчел соотношение самок и самцов составляет 1,618. Кроме того, в соответствии с репродукцией пчел оплодотворенные яйца становятся самками пчел, а неоплодотворенные — самцами. Поэтому. У самок есть два родителя, а у самца только один родитель. Следовательно, если бы кто-то изучил генеалогическое древо отдельных пчел, число родителей увеличилось бы от самых новых до самых старых в последовательности Фибоначчи.

ДНК

Молекула ДНК имеет длину 34 Å и ширину 21 Å. Соотношение примерно равно золотому сечению. То же верно и для соотношения двух борозд спиральной молекулы ДНК, т. е. большой (21 Å) и малой (13 Å) бороздки.

Тела животных

Тело животных может быть разным. Несмотря на этот широкий диапазон, они все еще демонстрируют божественную пропорцию в различных частях своего тела. Вот некоторые примеры:

► Дельфины: Размеры (длина:ширина) глаз, плавников, а также хвостовой части.
► Пингвины: соотношение положения отметин на теле у глаз, клюва и крыльев по сравнению с его общей высотой.
► Тигр: Почти все черты лица и их положения показывают золотое сечение, включая соотношение длины и ширины лица.
► Насекомые: Соотношение сегментов тела (голова, грудь и брюшко) друг к другу соответствует золотому сечению.

Человеческие тела

Золотые пропорции, наблюдаемые в человеческом теле, следующие:

► С головы до пят ● С головы до пупка
► Соотношение длины каждого пальца пальца
► Плечо к кончику пальца ● Плечо к локтю
► От бедра до пятки ● От бедра до колена
► Длина груди ● Длина от талии

В дополнение к этим примерам божественные пропорции также видны в различных архитектурных чудесах, таких как греческий Парфенон, картинах, таких как Тайная вечеря, в музыкальных симфониях и инструментах, и даже в библейских текстах (размеры Ноева ковчега). Это соотношение почиталось как божественное и называлось «отпечаток пальца Бога» из-за его проявления в многочисленных живых и неживых существах. Некоторые утверждают, что это свидетельство присутствия Бога и его разумного замысла вселенной, тогда как другие в то же время указывают, что это просто статистические манипуляции. Как бы то ни было, интересно отметить наличие этого отношения в столь разнообразных формах в природе.

Реальные примеры золотого сечения в повседневной жизни

Амина Решма Последнее обновление: 18 июля 2022 г., 10:10 CST

3 минут чтения

Золотое сечение имеет место, когда отношение суммы двух величин равно отношению количества в целом, что символизируется числом 1,618 или греческой буквой «фи». Он использовался для создания того, что считается наиболее эстетичным дизайном, демонстрирующим идеальную симметрию в архитектуре и искусстве, а также применялся для измерения человеческой красоты. Вы, вероятно, не знаете о математике, которая делает золотое сечение таким привлекательным, потому что оно создает вещи и музыку, которые естественным образом привлекательны без каких-либо причин для оправдания этого.

¹

Большинство из вас наверняка слышали о золотом сечении. Его можно найти, например, в «Код да Винчи» и во многих статьях, книгах и школьных проектах, иллюстрирующих, насколько математика важна для общества. Его иногда называют божественной пропорцией, и многие авторы считают его основой всех красивых узоров в природе. Говорят, что многие произведения искусства и архитектуры содержат элементы, соответствующие пропорциям золотого сечения. Говорят, что при строительстве Парфенона и пирамид использовалось золотое сечение. Также предполагалось, что в человеческом теле есть примеры золотого сечения, и говорят, что природа тоже наполнена этой божественной пропорцией.

2

Тем не менее, всякий раз, когда вы думаете о применении математики к реальному миру, вы, возможно, скупо сталкиваетесь с золотым сечением, что, вероятно, побуждает вас усомниться в правдивости великих заявлений, сделанных о золотом сечении.

Но это правда, что из-за его распространенности в природе и в человеческой анатомии золотое сечение часто называют Божественным сечением. Тот факт, что золотое сечение можно найти во многих живых существах, привело к благоговению перед этим необычным соотношением, которое до сих пор является источником вдохновения для современных художников и творцов. Итак, давайте посмотрим на некоторые реальные примеры золотого сечения, которые можно найти повсюду в классической архитектуре, произведениях искусства, природе и даже музыке.

1. Золотое сечение в архитектуре

В природе и искусстве золотое сечение обеспечивает почти безупречную красоту. Ища примеры золотого сечения в повседневной жизни, вы можете быть удивлены тем, сколько раз оно использовалось для строительства многочисленных монументальных зданий и сооружений. Когда золотое сечение используется в архитектуре, структура называется сакральной архитектурой. Вот некоторые примеры: ^{3, 1}

• Парфенон
• Великая пирамида в Гизе
• Шартрский собор
• Портик Девы
• Тадж-Махал
• Здание Организации Объединенных Наций

9011 7 Нотр-Дам
• Большая мечеть Кайруана

2. Золотое сечение in Art

Существует множество примеров мастеров-художников, которые использовали золотое сечение в своем искусстве.

Эти произведения искусства были созданы с использованием пропорций золотого прямоугольника и золотого треугольника. Искусство, основанное на золотом сечении, более привлекательно для человеческого глаза. Некоторые примеры искусства, изображающие золотое сечение: ¹

• Мона Лиза и Витрувианский человек Леонардо Ди Винчи
• Распятие Рафаэля
• Автопортрет Рембрандта
• Рождение Венеры Боттичелли
• Давид, Святое семейство Микеланджело
• Таинство последнего «Ужин» и «Постоянство памяти» Сальвадора Дали

3. Золотое сечение в музыке

Когда для построения музыкального произведения используется золотое сечение, оно превращает произведение в живую иллюстрацию математики, как создается музыка числовых значений. Золотое сечение процветало в музыке 20-го века, и некоторые из самых известных композиторов — Дебюсси, Штокхаузен, Барток, Стравинский, Манцони и Лигети — сознательно решили использовать эти таинственные пропорции.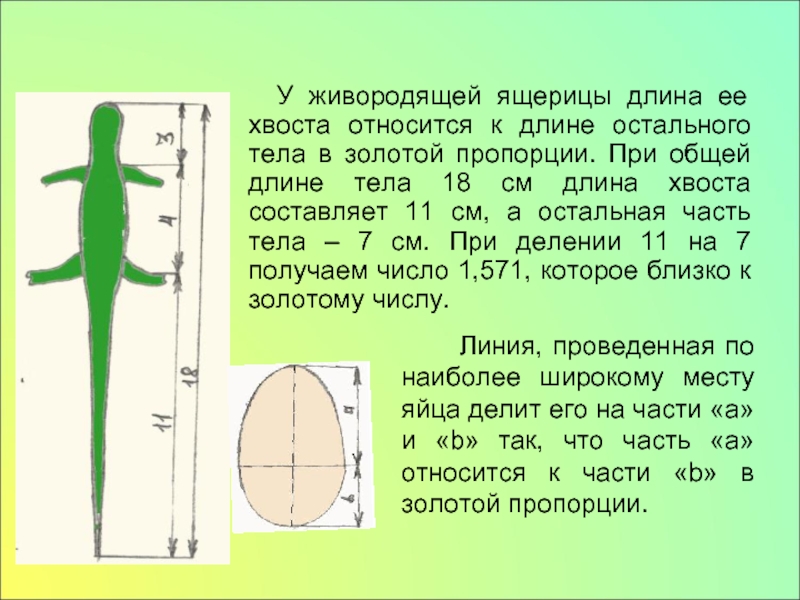

Несколько хорошо известных случаев включают в себя: ^{4 1}

• «Диалог моря и ветра» Клода Дебюсси
• Музыка Бартока для струнных, перкуссии и челесты, первая часть
• Соната Моцарта сущ. 1 до мажор
• Пятая симфония Бетховена, первая часть
• Эрик Сати и Sonneries de la Rose+Croix

тему и читать следующие блоги, чтобы узнать больше.

Парфенон в Греции и тайна идеальных пропорций

Закономерности в природе: красота чисел Фибоначчи и золотое сечение

Вы можете прочитать больше и другие интересные статьи о математике в блоге FutureSchool BYJU.

Каталожные номера:

1. Примеры золотого сечения в архитектуре и природе | LoveToKnow . (н.д.). Получено 13 июля 2022 г. с https://feng-shui.lovetoknow.com/Examples_of_Golden_Ratio
9.0117 Мифы математики: Золотое сечение | plus.maths.org . (н.д.). Получено 13 июля 2022 г. с https://plus.maths.org/content/myths-maths-golden-ratio
2. Суть золотого сечения в повседневной жизни.